- 快召唤伙伴们来围观吧
- 微博 QQ QQ空间 贴吧
- 文档嵌入链接
- 复制
- 微信扫一扫分享
- 已成功复制到剪贴板
incremental-fisher
展开查看详情
1 . Incremental, Approximate Database Queries and Uncertainty for Exploratory Visualization Danyel Fisher Microsoft Research ABSTRACT 1.1 Interaction Assists Exploratory Visualization Exploratory data visualization calls for iterative analyses, but very Several projects have attempted to distinguish between large databases are often far too slow to allow interactive exploratory visualization and presentation (e.g. [22]). In exploration. Incremental, approximate database queries exchange presentations, the audience and presenters expect precision: the precision for speed: by sampling from the full database, the visualization should be based on the best data possible. system can resolve queries rapidly. As the sample gets broader, In contrast, exploratory visualization can be understood as the precision increases at the cost of time. As the precision of the iterating through a series of visualizations rapidly enough to make sample value can be estimated, we can represent the range of a decision based on data. In many cases, knowing a correct possible values. This range may be visually represented using answer within some percentage may be sufficient for decision- uncertainty visualization techniques. This paper outlines the making. Consider a sales manager examining recent sales tables: current literature in both incremental approximate queries and in learning that her branch sold approximately five times as many uncertainty visualization. The two fields mesh well: incremental widgets as sprockets will allow her to dive further into the widgets techniques can collect data in interactive time, and uncertainty category without worrying much about sprockets. techniques can show bounded error. We might draw an analogy to a computer-graphics artist looking at a rapidly-generated wireframe, rather than a full render Keywords: Uncertainty visualization, incremental visualization, of an animated scene. The wireframe can be generated rapidly, approximate visualization, very large data, exploratory data and may give the artist enough information to move props or analysis. actors around. Approximate results can help make decisions about datasets Index Terms: H.2.4 [Database Management]: Systems—Query rapidly. In the data cleaning phase, an analyst can discover that Processing; H.5.2 [Information Interfaces] User Interfaces— some messy items swamp the dataset. In exploration, a quick Graphical User Interfaces. overview can help an analyst realize they have issued the wrong 1 INTRODUCTION query—and, once they have the right one, quick overviews can help decide which region of the data is worthwhile focusing on. In We live in an era of ever-faster computing systems, but larger some cases, approximate results might allow a time-critical storage and information lead to slower database queries. This is decision to be made faster without having to wait for a long unfortunate, as the field of visual analytics has often focused on processing job. the value of exploratory visualization: a process of iterating Today, analysts will sometimes separate a tractable subset of through queries to learn more about a dataset. Users expect to ask their database, and work off of that subset, creating data cleaning a question of the data, get a response, and then generate a new round of questions. Getting one result from a dataset serves as a scripts and preliminary graphs. They then run those same scripts cue for the next query. on the full database. The analyst must judge how large a sample Very large databases make interactivity much more difficult, as of data to collect, and must decide whether the sample is a full query across the entire dataset can be very slow. Several representative. In few cases does the analyst expect to make data analysis systems, such as Tableau, Vertica, and Microsoft’s decisions based on a sample. Incremental processing allows a PowerPivot, have incorporated high-speed in-memory column- user to work off of increasingly-large samples, and thus oriented storage in order to scale to interactive queries across increasingly-certain results. millions of rows. Beyond this range, however, there is a more In general, we wish to visualize data rapidly enough to fundamental issue: a database simply cannot produce a full encourage the user to be able to string tasks together interactively. response to a query in interactive time. Card et al suggest a timing model which describes how long a In this paper, we take as a primary goal the idea of presenting user might stay on task [2] (and later work on timing by Seow, useful results to the user at interactive speeds. We accept that [25]). Responses less than 0.1 seconds are perceived as nearly there will always be some queries that are too slow to fully instantaneous; anything less than one second is understood as an complete as rapidly as a user might wish; we look for ways to prompt response. On the other hand, if a system takes more than reduce the impact of these limitations. Enabling these scenarios ten seconds to reply to a query, the user will perceive the will require both new designs for visualization and system design. questioning and answering as separate tasks. 1.2 Big Data: Hard for Databases and Visualizations That sort of timing is an ambitious goal. Any compute job that danyelf@microsoft.com touches large data—in the terabyte range and up—requires a 1 Microsoft Way, Redmond, Washington. 98052 USA substantial amount of time. Disks are limited in reading speed; networks are limited in throughput. In distributed networks, such as Hadoop, Amazon EC2, or Microsoft’s Azure, there can be individual machines may run slowly; consolidating data from
2 .multiple machines may also saturate bandwidth. While increased Two fields of research converge to make this possible. On the bandwidth, parallelism, or clever storage schemes may one hand, the database community has carried on a tradition of temporarily achieve interactive rates against large datasets, ever- research looking at incremental and online data querying larger datasets keep pace with innovations. techniques, examining systems and situations where it works well. In the visualization community, large data has also been a These techniques have not yet become mainstream. On the other challenge. Information visualization research was forced to face hand, the data visualization community has wrestled with issues of scale over a decade ago, when datasets grew larger than concepts of collecting and visualizing data that is subject to the number of pixels on screen: a threshold crossed around a ‘uncertainty’; however, the field seems to have had limited million items, or a few megabytes of data. Pioneering work by success in finding useful examples of uncertain data. This paper Shneiderman [26] and others argued that it is critical to unifies these literatures, suggesting interactions between them. summarize data, either by ordering it hierarchically, or allowing Aspects of this have been mentioned before. The CONTROL users to filter and zoom deeper into the dataset. project [9][11] is a major inspiration for the area of online, These techniques are limited by data constraints: a treemap may interactive data analysis. The CONTROL project is motivated in be a good overview technique, but requires that each node have an part by allowing users to interactively generate visualizations. accurate count of the sizes of its children. Depending on the size However, the authors have not presented appropriate and storage of a dataset, that can be a very expensive visualizations that would go with their interactive database. computation. In this paper, we identify classes of visualization Olston and Mackinlay [20] mention incremental sampling as a techniques that work well when our ability to collect data rapidly potential motivator for their visualization of uncertainty, and refer is limited. back to the CONTROL project, but provide little detail on how those techniques might be carried out in practice. In this paper, we 1.3 Approximate Visualizations of Incremental Data attempt to overview both literatures, in an attempt to describe the We can use incremental data sampling to generate approximate costs and benefits of incremental visualizations. answers for many types of queries. While it is possible to generate We propose a workflow as in Table 2: the user begins a a visualization based on a sample of a dataset, we wish to allow computation process that iteratively updates a visualization with users to interactively choose to trade time for accuracy. For ever better estimates and confidence bounds. appropriately-formed queries, many queries should be able to This paper intends to motivate incremental analysis from both produce an approximate answer rapidly; as the data request the data side and the visualization side, and argues that the two progresses, the user can get a more detailed, and more accurate, should be brought together. First, the paper contributes as a response. The user can choose to interrupt at any moment, when review of techniques for handling large data, including pre- they have enough information to act on the data, create a new aggregation and online querying; it discusses statistical bounds query, or decide to wait for more detailed data. that help describe the range of the data, and discusses the implications for arranging data in disks and networks. Second, it reviews the visualization literature on uncertainty and on aggregation, and links the notion of uncertainty to the probabilistic results produced in the previous section. Last, it introduces a prototype system, “TeraSim,” that generates iterative, convergent data for visualization. While TeraSim is still in construction, its design illustrates how a pipeline from data through visualization can be brought together. Table 2. Workflow for incremental visualization system. SQL syntax is for illustration only. Incremental Visualization System 1. Large Data is stored on disk or distributed system 2. User selects a dataset within their visualization system; system issues aggregate query SELECT APPROXIMATE CATEGORY, SUM(*) Figure 1. Hypothetical comparison on quality of answers for a FROM Table T system computing incremental results. While the traditional, WHERE Condition=C GROUP BY CATEGORY fixed system generates a complete answer sooner, the incremental system has fairly tight bounds much earlier. 3. Database begins to produce histograms of (CATEGORY, SUM, CONFIDENCE BOUNDS). Figure 1 illustrates a (hypothetical) accuracy-vs-time trade-off 4. Visualization updates to reflect categories and curve. The Y axis represents the degree of accuracy of the query values from the database. response, expressed as a fraction of the true value. In the 5. If the user chooses to interrupt, then the incremental case, the system produces useful results almost visualization stops; otherwise, repeat step 3 with more detail. immediately (solid line); at a later time, the full query (dotted line) 6. User issues new query, or waits for computation to returns. At that moment, the full query is more accurate (but only complete. slightly) than the incremental partial results had been. These techniques apply to data and queries where a sample can 2 DEALING WITH LARGE DATA be visualized usefully, such as aggregate visualizations. In contrast, visualizations that emphasize individual datapoints will The notion of “large” data changes with computer technologies. be much less successful. Papers in the VLDB (“Very Large Databases”) conference of 1975 referred to tables of millions of entries [27]; current work
3 .looks at analyses of web-scale datasets—a handful of orders of user can choose from a very broad selection of choices, then the magnitude larger. During the intervening 35 years, the use of amount of data to be prefetched will be similarly large. multiple parallel data stores and networked databases has stayed constant. Separating data onto multiple disks and network means 2.2 Parallel Computation for Big Data that any query against the data will be costly. One way to handle very large datasets is to parallelize storage and computation. Rather than storing all the data on a single 2.1 Pre-Aggregation is Fast, but Inflexible machine—limited by the one machine’s memory, disk bandwidth, This problem has been recognized for a very long time. OLAP [3] and computation speed—large datasets can be spread across a is a technology that partially pre-aggregates data into ‘cubes’, distributed database. In the last few years, the MapReduce [5] stored in a ‘data warehouse’. The cubes are chosen to expose concept has become a popular way to store large data in parallel. major facets of the data, while reducing the number of individual Distributed machines each store a portion of the dataset, and a elements. For example, a retailer might store individual sales query is run against each distributed machine separately. Each transactions in a transactional database; the warehouse might then machine runs the query locally (“map”), and then an aggregation store all transactions aggregated by product, sales date, and retail site brings together all of these results into a single result set outlet. This warehouse would be very quick to reply to queries (“reduce”). One major advantage of this scheme is that data size is like “how many widgets were sold on Wednesday?” However, it no longer a problem: each machine handles a constant amount of would be unable to address queries that require dimensions not data. stored in the cube, such as “how many customers from ZIP code Several query languages have been written specifically against 98052 purchased a widget?” While an offline data warehouse is a MapReduce-type clusters. Sawzall [21] is a specialized language fast way to handle data, we are particularly concerned that the for MapReduce, which allows users to precisely express each step user be able to formulate queries based on dimensions that were as simple syntax. DryadLINQ [34] extends C#’s LINQ not previously expected. (“Language INtegrated Query”) syntax to allow users to write As an example from the Information Visualization field, the queries that have a parallel component; the system then Hotmap [8] project visualized where users downloaded tiles from propagates the query across multiple machines in parallel. Microsoft’s Bing Maps. While the datasource started with raw DryadLINQ also computes a full directed graph of maps and HTTP logs, they were pre-processed offline into a fixed data reduces, allowing multiple-step mappings and reductions. structure to allow for quick retrieval. Hotmap needed to know the Dremel [18] is also designed as a rapid query language against number of hits at each latitude and longitude, as a result, location large databases; while other systems are agnostic to underlying was used as a primary key. While this new format allowed for data structures, Dremel requires that the data table be formatted as interactive navigation speeds, the pre-computation phase was very a particular column-oriented database; while the pre-processing long (eliminating the possibility of looking at daily changes) and for this column-orientation can be slow, the results allow for fast allowed only a certain set of queries. For example, the system queries. could address queries about the date of the web hit, but not the IP These parallel systems make linear queries fast, limited only by address of the requestor (a field that was not indexed). This pre- the read speed of their system. However, contemporary aggregation limited the analyses that could be done with the implementations do not have mechanisms for reporting system without extensive manual labor and slow computation. incremental results: they touch every row before returning complete results. Of course, any of these systems might be modified to allow progressive queries: recently, MapReduce Online [6] has offered online incremental queries against Hadoop architectures; it allows increasingly-accurate results as further time runs. In general, this paper addresses precisely this issue: what would the cost, and the value, be of adding progressive callbacks to MapReduce-type systems and large data queries? In the next section, we look first at approximate queries against large datasets. 3 APPROXIMATE QUERIES FOR LARGE DATASETS As we have noted above, serial scans of large datasets look at individual records very rapidly. Rather than waiting until the scan has touched the entire database, it might be possible to return partial results. If that partial result is based on a fair random sample of the dataset, it will have statistical bounds and properties that can be used to approximate the remainder of the dataset. Unfortunately, this is frequently not the case: data often comes Figure 2. The Hotmap project. Brighter spots have had more ordered on disk. In the next sections, we will discuss the people look at them. operations that are possible on such a sample, the challenges of Some issues with speed can be alleviated by carefully planning getting data into randomized order, and the sorts of statistical out a sequence of queries. Chan et al [4] show a system which statements that we can make about these aggregations. keeps ahead of viewers by adaptively prefetching data near where 3.1 Operations on Samples they currently are. This means that users will always have the illusion of available data. This solution, like other forms of pre- Working from a sample of data implies that we can only carry out aggregation, works best when the user’s options are limited: if the some operations: we can use the limited sample to extrapolate
4 .what the rest of the database looks like. We can then predict specify a fraction of the result set to return. This random selection bounds on the remainder of the dataset, and visualize these can then be joined with other tables; the query could be repeated bounds. to get a broader random sample. The TABLESAMPLE function takes a random selection of pages in the database. 3.1.1 Using Aggregate Queries It might be possible to get rapid, partial answers by pre- Aggregate queries are of particular interest precisely because they computing a large random sample of the database, especially in can reasonably be predicted from a limited subset of a database. cases where a full OLAP cube would still be too big (or too slow) Computing the sum, count, and average are very common to be practicable. Recent work [14] explores creating and aggregate queries, and can be computed both easily and precisely maintaining these random samples. online. For sum, count, and average queries against a random sample, the size of the confidence interval inversely proportional 3.3 Joining Sampled Data to the square root of the size of the sample, and proportional to the The join operation is critical to sophisticated data analysis. To variance of the dataset. Thus, as the sample grows, the confidence understand the importance of the ‘join’ operation, recall the interval decreases, allowing the user to see values converging. marketing scenario from before. To examine customers who These queries can be applied well to a variety of different types returned for a second visit, or those who bought a t-shirt in the of visualizations. A histogram, for example, can be understood as same visit as a pair of pants, they will need to construct a join a count query, separated by categories. Many popular statement: two different tables will need to be linked together. visualizations are one- or two-dimensional histograms: faceted Join operations are also needed to fill in metadata about columns, browsers, such as FacetMap [29], are simply histograms of navigate graph data structures, and link together different sources categories across different dimensions. Hotmap, discussed above, of data. is a two-dimensional histogram across a fairly large number of While joining is a fundamental relational database operation, possible buckets. While both of these projects showed precise joining can be difficult on both Map-Reduce and in sampled results, they would have worked well as approximations. datasets. On parallel Map-Reduce systems, join operations often Some queries are harder. Percentile and median queries can be require substantial network bandwidth and computation to first estimated incrementally, but with diminished precision and ill- hash, then join entries together. defined bounds. Operations like finding the largest or smallest Joins cut substantially down on the size of samples, too: a values, or top-N lists, requires looking at every point, and so random 10% sample of two datasets to be joined together has just cannot be reasonably approximated with samples. a 1% chance of finding a row that matches between both datasets. We can also approximate some queries with others. While A system will need to keep intermediate join results in memory, finding a particular outlier is difficult, finding values that fall looking for matches—and data collection will be especially slow outside a percentile range is entirely plausible. if one of the joined attributes is highly filtered. Much of the research from the CONTROL project tried to 3.1.2 Appropriate Data Characteristics establish ways to handle joining rapidly. One CONTROL Beyond the type of query, the type of data matters, too. It is technique was the Hash Ripple Join [9]. In a typical join, a desirable to have a finite number of categories: many of the database looks at all of the index values of one dimension into techniques discussed here cannot apply to histograms that are memory (perhaps in portions), and then matches them against the wider than memory. In the example looking at corporate sales, a other dimension. The hash ripple join, in contrast, alternately histogram of product by number of people who bought it would reads sets of rows from each dimension, incrementally building a be easy to generate. On the other hand, a histogram of street larger pool of rows that might match each other. The Ripple Join address by number of purchases made from it may well suffers when it runs out of memory, however; the Scalable Hash overwhelm the histogram. Ripple Join [17] addresses issues with both memory usage by As the confidence level is a function of the variance of the data, falling back to disk storage, and adds a capability to join across a the distribution of the data columns also matter: the bounds of a distributed system. highly skewed distribution will converge much more slowly than The Sort-Merge-Shrink Join [13] is an alternate strategy that, a more balanced distribution. similarly, works when the set of keys is larger than memory; in addition, the Sort-Merge-Shrink Join offers robust statistical 3.2 Randomly Selecting from Databases estimates of both progress and running totals. However, it requires The question of efficient random sampling from database files is the data on disk to be arranged in random order. well-known ([19] has a survey of techniques from 1990). It is a These methods might potentially be parallelized or run on a slow process to individually read random rows of a database; the distributed system. This line of research suggests that incremental database system is optimized for reading continuous chunks of queries against joined data may be possible, and can be made both memory. The quality of the random values can be traded for fast and memory efficient. speed, however: taking random pages from a disk table introduces some bias, but is much faster than taking random rows. A second 3.4 Convergent Bounds on Values trade-off is whether to sample with or without replacement. An estimate is of limited utility if it does not allow us to also Sampling with replacement can be statistically desirable; understand how good an estimate it is. We can use confidence however, sampling without replacement ensures that the process bounds to control the visualization. Both the Ripple Join [9] and will eventually cover all rows and eventually converge at the true Sort-Merge-Shrink [13] papers provide discussions of their answer. (For small numbers of rows—a few percent of the statistical estimators. These estimators are complex, as they need database—sampling with and without replacement are nearly to account for the statistical properties of the JOIN operation from identical.) two different, dependent samples. Random sampling is implemented in major commercial The notion of a ‘central limit theorem’ states that the databases: the TABLESAMPLE keyword is now available in DB2 distribution of the mean of a sample of data is normally [10], SQL Server, and Oracle. Each of these allows a user to distributed, with a variance proportional to the variance of the
5 .dataset. This means that the mean of the full dataset can be visualizations we discuss here, although the navigation techniques estimated from the mean of the sample. In general, a variety of they discuss to zoom in or peel away layers of data would, in all different central limit bounds can be applied straightforwardly to likelihood, trigger new queries. these sampling problems; different properties of the data may allow tighter bounds, depending on how the underlying data is 4.1.2 Tag Clouds distributed. We may therefore expect that an approximate, Tag Clouds are a common visualization that does not hinge on incremental operation should return both a value, and a precision [32]. As there are only so many possible sizes for text, a probability distribution function (such as 95% confidence small uncertainty range makes little difference to the tags. It may bounds). be possible to render the most frequent words in a visualization using the constraints suggested by ManiWordle [15]. (As Kosara 3.5 Sketch Estimators shows, however, adding blur to text may render it unreadable, A different approach to trading speed for accuracy is through rather than indicating—as one might hope—that the value database “sketch estimators.” Database sketches attempt to rapidly associated with the word is uncertain [16]. Other types of aggregate data by keeping summaries that are smaller than the annotations might help indicate uncertainty, however.) number of items. Sketches maintain probabilistic aggregations of values, which can be queried rapidly. Ruso and Dobra [23] 4.2 Uncertainty Visualization compares several different sketch estimators, and provides their In addition to portraying the estimated value, it is desirable for the statistical properties, including evaluating the quality of the visualization to show the range of possible values or estimates. As estimators that they produce. noted above, there seems to be a natural match between some forms of ‘uncertainty visualization’ and the approximate values 4 VISUALIZING AGGREGATE AND INCOMPLETE DATA with ranges that these estimation techniques produce. The term We have largely discussed the techniques that might be used to ‘uncertainty’ has taken on many meanings within the field of power and drive an interactive aggregate visualization system. In information visualization; authors have used it to refer not only to this section, we turn from examining databases to visualization uncertain data values, but to the quality, provenance, and even the research. There has largely been little work linking approximate structure of data (summarized in [28]). A broad typology of both database queries with uncertainty visualization, although the two sources and types of uncertainty in geospatial data [31] provides seem like a logical obvious fit. Olston and Mackinlay are a additional detail. Zuk and Carpendale [35] analyze several dramatic exception: their work on bounded uncertainty explicitly uncertainty visualizations using frameworks established by Bertin, mentions incremental data updates as one likely scenario [20]. Tufte, and Ware, finding that standard rules of visualization were However, their work focuses specifically on visualization only sparingly used within uncertainty visualizations, techniques, and does not discuss database sampling issues. In this compromising reader’s abilities to understand the visualization. section, we discuss Infovis research on uncertainty, focusing in 4.2.1 Statistical and Quantitative Uncertainty particular on visualizations that are likely to be appropriate for approximate databases. Of this broad family of uncertainty, we are interested solely in quantitative uncertainty: places where we know a numerical 4.1 Types of Visualizations result, possibly within a degree of precision (that is, statistical uncertainty). In [30], the authors produce a model for maintaining Only certain visualization techniques would be appropriate to uncertainty information in a spreadsheet. They introduce three incremental visualizations. In this section, we discuss several forms of uncertainty: estimates which are known to be inaccurate visualizations that can or do not apply to large data visualizations. (but not by how much); intervals, in which a value is known to In Shneiderman’s discussion of “squeezing a billion points into a fall into a range; and probabilities, in which a value can be million pixels” [26], he distinguishes between “one point per expressed as a probability curve. These allow them to create pixel” techniques, which will require zooming, and aggregate approximate line graphs, using translucency for probability, visualizations. A scatterplot is an example of the former: a dotted lines for estimation, and filled regions for ranges (Figure 3, scatterplot of a billion points must plot (and overplot) a billion bottom). They also offer a 3D chart, which uses translucency at pixels. each point to represent probability. 4.1.1 Aggregate Visualizations Similarly, Olston and Mackinlay [20] render bounded and In contrast, aggregate visualizations count elements. Those same statistical uncertainty. They use error bars to indicate statistical billion points might be drawn as a two-dimensional histogram, ranges (as error bars indicate a ‘likely region and estimator’); they showing the number of points that occur within each region. This render bounded (such as 4.5 +/- 3) as “graphical fuzz”, greyed latter visualization can be imprecise without losing its meaning. regions. Their techniques work well for scatterplots and line A treemap is similarly a sort of histogram, with each cell as a charts; they are forced to compromise for stacked-bar charts and counted group-by operation. pie charts (Figure 3, top-left). Elmqvist and Fekete [7] suggest a broad spectrum of ideas for 4.2.2 Challenges in Quantitative Visualization of aggregate visualizations. While the paper refers to these as Uncertainty “hierarchical” visualization, their technique is to ensure that Several user studies of uncertainty visualization have suggested individual data points are aggregated together. They suggest that there are real challenges to making uncertain data easily visualizations that can be aggregated by sum, average, median, readable to users. Kosara [16] argues that while blur might help and other statistical measures. They suggest using hierarchical cue depth, it is difficult to compare different amounts of blur. clustering as a base techniques to modify well-known Wittenbrink et al test several different glyphs that can be used visualizations (such as scatter plots, parallel coordinates, and star to highlight uncertainty in vector fields [33]. Their research, glyphs) into aggregate visualizations by summarizing parts of which examines glyphs that show uncertainty in both angle and graphs. Many of their techniques are appropriate for the aggregate length, evaluates tradeoffs not raised by others. For example,
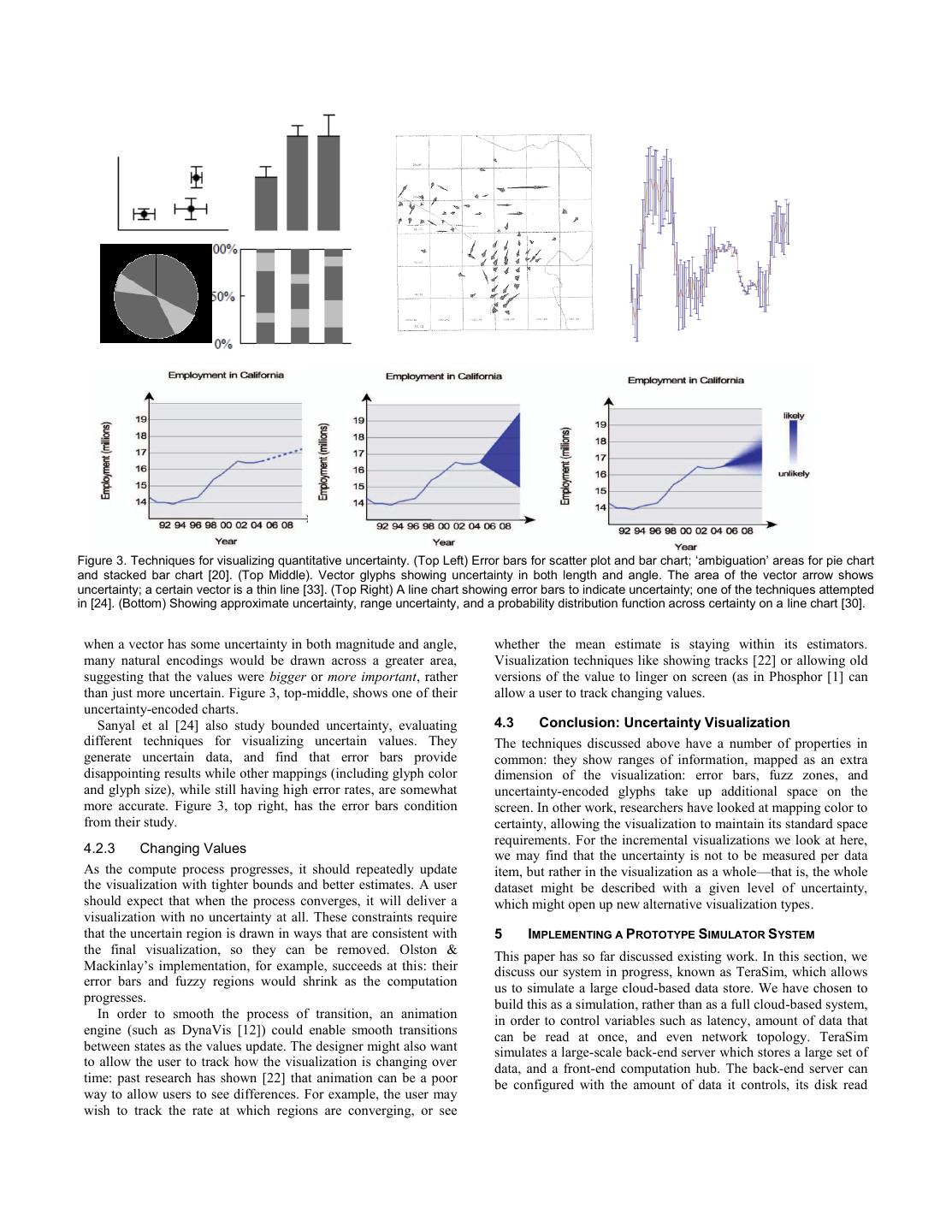
6 .Figure 3. Techniques for visualizing quantitative uncertainty. (Top Left) Error bars for scatter plot and bar chart; ‘ambiguation’ areas for pie chart and stacked bar chart [20]. (Top Middle). Vector glyphs showing uncertainty in both length and angle. The area of the vector arrow shows uncertainty; a certain vector is a thin line [33]. (Top Right) A line chart showing error bars to indicate uncertainty; one of the techniques attempted in [24]. (Bottom) Showing approximate uncertainty, range uncertainty, and a probability distribution function across certainty on a line chart [30]. when a vector has some uncertainty in both magnitude and angle, whether the mean estimate is staying within its estimators. many natural encodings would be drawn across a greater area, Visualization techniques like showing tracks [22] or allowing old suggesting that the values were bigger or more important, rather versions of the value to linger on screen (as in Phosphor [1] can than just more uncertain. Figure 3, top-middle, shows one of their allow a user to track changing values. uncertainty-encoded charts. Sanyal et al [24] also study bounded uncertainty, evaluating 4.3 Conclusion: Uncertainty Visualization different techniques for visualizing uncertain values. They The techniques discussed above have a number of properties in generate uncertain data, and find that error bars provide common: they show ranges of information, mapped as an extra disappointing results while other mappings (including glyph color dimension of the visualization: error bars, fuzz zones, and and glyph size), while still having high error rates, are somewhat uncertainty-encoded glyphs take up additional space on the more accurate. Figure 3, top right, has the error bars condition screen. In other work, researchers have looked at mapping color to from their study. certainty, allowing the visualization to maintain its standard space requirements. For the incremental visualizations we look at here, 4.2.3 Changing Values we may find that the uncertainty is not to be measured per data As the compute process progresses, it should repeatedly update item, but rather in the visualization as a whole—that is, the whole the visualization with tighter bounds and better estimates. A user dataset might be described with a given level of uncertainty, should expect that when the process converges, it will deliver a which might open up new alternative visualization types. visualization with no uncertainty at all. These constraints require that the uncertain region is drawn in ways that are consistent with 5 IMPLEMENTING A PROTOTYPE SIMULATOR SYSTEM the final visualization, so they can be removed. Olston & This paper has so far discussed existing work. In this section, we Mackinlay’s implementation, for example, succeeds at this: their discuss our system in progress, known as TeraSim, which allows error bars and fuzzy regions would shrink as the computation us to simulate a large cloud-based data store. We have chosen to progresses. build this as a simulation, rather than as a full cloud-based system, In order to smooth the process of transition, an animation in order to control variables such as latency, amount of data that engine (such as DynaVis [12]) could enable smooth transitions can be read at once, and even network topology. TeraSim between states as the values update. The designer might also want simulates a large-scale back-end server which stores a large set of to allow the user to track how the visualization is changing over data, and a front-end computation hub. The back-end server can time: past research has shown [22] that animation can be a poor be configured with the amount of data it controls, its disk read way to allow users to see differences. For example, the user may wish to track the rate at which regions are converging, or see
7 .speed (expressed as number of rows per second), and its Second, we have highlighted the major issues in the data communication latency. sampling literature, including the difficulty of getting a good We are using TeraSim to explore a variety of different random sample, and the challenges involved in join queries. visualization techniques over this data. Our goals are to explore Third, we have discussed some visualization tools that help possible visualizations of confidence levels and approximate indicate how the visualization field could connect the uncertainty- results; to better understand the database constraints needed to laden data produced by these approximate queries. support them; and to explore how users interact with changing Last, we have discussed TeraSim, a testbed for visualizing real- data. time results from dynamic queries across large data. In reality, TeraSim is implemented as a single application running over a single commodity database. The database contains ACKNOWLEDGEMENTS pre-sampled data, with a few millions of rows. The results that it My thanks to the many collaborators who have provided critical provides can be scaled up (simply by repeating values) to simulate feedback on this work, including Steven Drucker, John Platt, billions or more of rows. The front-end can issue queries to the Christian Konig, and the anonymous reviewers. Research on this database, which returns appropriate statistical properties: usually project was motivated by probing questions from Sean Boon and means, counts, and standard deviations. The front-end then Alex Gorev. Shankar Narayanan implemented the first steps combines these counts to generate its estimates and error bounds, toward TeraSim. and presents them to the user. The front-end iterates its queries to the back end, getting back increasingly-large estimates. REFERENCES TeraSim is designed to handle multi-dimensional histogram [1] P. Baudisch, D. Tan, M. Collomb, D. Robbins, K. Hinckley, M. queries of the form Agrawala, S. Zhao, and G. Ramos. Phosphor: explaining transitions in the user interface using afterglow effects. In Proceedings of the SELECT <G1, G2>, MEAN/SUM/COUNT (*) 19th Annual ACM Symposium on User Interface Software and FROM <TABLE> Technology (UIST '06). ACM, New York, NY, USA, 169-178. 2006. WHERE <Condition> [2] S. Card, G. Robertson, and J. Mackinlay. The Information GROUP BY <G1, G2> Visualizer, an Information Workspace. In Proceedings of the SIGCHI conference on Human factors in computing systems: where the condition is limited only on columns that are in the Reaching through technology (CHI '91). ACM, New York, NY, table and the group can take one or many columns. TeraSim USA, 181-186. 1991. cannot, however, handle join operations. [3] S. Chaudhuri and U. Dayal. An overview of data warehousing and We are in the process of extending the back-end so that the OLAP technology. SIGMOD Record. 26(1):65-74. March 1997. system can simulate a cloud of computers, rather than a single [4] S.-M. Chan, L. Xiao, J. Gerth, P. Hanarhan. Maintaining machine. At that point, each back-end machine will pass back not interactivity while exploring massive time series. In Proceedings of its own confidence bounds, but rather components that will allow IEEE VAST 2008: 59-66. 2008. the front-end to compute the confidence bounds. For example, the [5] F. Chang, J. Dean, S. Ghemawat, W. Hsieh, D. Wallach, M. SUM estimator is based on the sum of the entire back-end sample, Burrows, T. Chandra, A. Fikes, and R. Gruber. Bigtable: a multiplied out to match the size of the full dataset. Each back-end distributed storage system for structured data. In Proceedings of the replies with the sum of the back-end sample and their fraction of 7th USENIX Symposium on Operating Systems Design and the size; the system combines these across all of the machines to Implementation (OSDI '06), Vol. 7. USENIX Association, Berkeley, generate a single estimator. Similarly, the error bounds are CA, USA, 15-15. 2006. computed based on the standard deviation of the sample; each [6] T. Condie, N. Conway, P. Alvaro, J. M. Hellerstein, K. Elmeleegy, simulated machine will compute a partial result, and the front-end and R. Sears. MapReduce online. In Proceedings of the 7th USENIX conference on Networked systems design and implementation will combine them. (NSDI'10). USENIX Association, Berkeley, CA, USA, 21-21. 2010. 5.1 Passing Incremental Data [7] N. Elmqvist and J.-D. Fekete. Hierarchical Aggregation for Information Visualization: Overview, Techniques, and Design In our current implementation, TeraSim passes entire histograms Guidelines. IEEE Transactions on Visualization and Computer at a time. Each server computes its histogram and passes it to the Graphics 16(3):439-454. May 2010. front-end; the front-end, in turn, replaces its current histogram and [8] D. Fisher. Hotmap: Looking at Geographic Attention. IEEE re-renders. As we experiment with more (simulated) back-end Transactions on Visualization and Computer Graphics 13(6): 1184- servers and more data, we are beginning to encounter times when 1191. November 2007. passing the entire histogram for a dataset gets large (such as when [9] P. Haas, J. Hellerstein. Ripple Joins for Online Aggregation. In we group on vocabulary within a document.) We are designing a Proceedings of ACM SIGMOD International Conference on system for with passing incremental histograms: tables that Management of Data. 1999. represent only the difference from the previous data. [10] P. Haas. The Need for Speed: Speeding Up DB2 Using Sampling. While TeraSim is in early stages yet, we are finding it a robust IDUG Solutions Journal, 10:32–34. 2003. platform to explore several different types of data, and to motivate [11] J. Hellerstein, R. Avnur, A. Chou, C. Olston, V. Raman, T. Roth, C. further research on building incremental and scalable back-ends. Hidber, P. Haas. Interactive Data Analysis with CONTROL. IEEE Computer, 32(8). August, 1999. 6 CONCLUSION [12] J. Heer and G. Robertson. Animated Transitions in Statistical Data In this paper, we have contributed four interrelated ideas: Graphics. IEEE Transactions on Visualization and Computer Graphics 13(6): 1240-1247. November 2007. First, we have argued for linking incremental data querying [13] C. Jermaine, A. Dobra, S. Arumugam, S. Joshi, and A. Pol. The techniques to visualizations. We have shown applications and Sort-Merge-Shrink Join. ACM Transactions on Database Systems uses where rapid, less-accurate results are more valuable than 31(4): 1382-1416. December 2006. slow, more-accurate results.
8 .[14] S. Joshi and C. Jermaine. Materialized Sample Views for Database IS&T Conference on Electronic Imaging, Visualization and Data Approximation. IEEE Transactions on Knowledge and Data Analysis 2005, 5669: 146-157. 2005. Engineering. 20(3): 337-351. March 2008. [32] F. Viegas, M. Wattenberg, and J. Feinberg. Participatory [15] K. Koh, B. Lee, B. Kim, and J. Seo. 2010. ManiWordle: Providing Visualization with Wordle. IEEE Transactions on Visualization and Flexible Control over Wordle. IEEE Transactions on Visualization Computer Graphics 15(6):1137-1144. November 2009. and Computer Graphics 16(6): 1190-1197. November 2010. [33] C. Wittenbrink, A. Pang, and S. Lodha. Glyphs for Visualizing [16] R. Kosara, S. Miksch, and H. Hauser. Semantic Depth of Field. In Uncertainty in Vector Fields. IEEE Transactions on Visualization Proceedings of the IEEE Symposium on Information Visualization and Computer Graphics. 2(3):266-279. September 1996. 2001 (INFOVIS'01). IEEE Computer Society. 2001. [34] Y. Yu, M. Isard, D. Fetterly, M. Budiu, U. Erlingsson, P. Kumar [17] G. Luo, C. Ellmann, P. Haas, and J. Naughton. A Scalable Hash Gunda, and J. Currey. DryadLINQ: a system for general-purpose Ripple Join Algorithm. In Proceedings of the 2002 ACM SIGMOD distributed data-parallel computing using a high-level language. In International Conference on Management of Data (SIGMOD '02). Proceedings of the 8th USENIX Conference on Operating Systems ACM, New York, NY, USA. 2002. Design and Implementation (OSDI'08). USENIX Association, [18] S. Melnik, A. Gubarev, J. Long, G. Romer, S. Shivakumar, M. Berkeley, CA, USA, 1-14. 2008. Tolton, and T. Vassilakis. Dremel: interactive analysis of web-scale [35] T. Zuk and S. Carpendale. Visualization of Uncertainty and datasets. In Proceedings of the VLDB Endowment. 3(1-2):330-339. Reasoning. In Proceedings of the 8th international symposium on September 2010. Smart Graphics (SG '07). Springer-Verlag, Berlin, Heidelberg. 2007. [19] F. Olken and D. Rotem. 1990. Random sampling from database files: a survey. In Proceedings of the 5th international conference on Statistical and Scientific Database Management (SSDBM'1990), Zbigniew Michalewicz (Ed.). Springer-Verlag, London, UK, 92-111. 1990. [20] C. Olston and Mackinlay, J. Visualizing data with bounded uncertainty. In Proceedings of IEEE Symposium on Information Visualization, pp. 37-40. 2002 [21] R. Pike, S. Dorward, R. Griesemer, and S. Quinlan. Interpreting the data: Parallel analysis with Sawzall. Scientific Programming Journal. 13(4): 277-298. October 2005. [22] G. Robertson, R. Fernandez, D. Fisher, B. Lee, and J. Stasko, Effectiveness of Animation in Trend Visualization. IEEE Transactions on Visualization and Computer Graphics. 14(6):1325- 1332. November 2008 [23] F. Rusu and A. Dobra. Statistical analysis of sketch estimators. In Proceedings of the 2007 ACM SIGMOD International Conference on Management of Data (SIGMOD '07). ACM, New York, NY, USA, 187-198. 2007. [24] J. Sanyal, S. Zhang, G. Bhattacharya, P. Amburn, and R. Moorhead. 2009. A User Study to Compare Four Uncertainty Visualization Methods for 1D and 2D Datasets. IEEE Transactions on Visualization and Computer Graphics 15(6): 1209-1218. November 2009. [25] S. Seow. Designing and Engineering Time: the Psychology of Timer Perception in Software. Boston:Pearson Education. 2008 [26] B. Shneiderman: Extreme visualization: squeezing a billion records into a million pixels. In Proceedings of the 2007 ACM SIGMOD International Conference on Management of Data (SIGMOD '07). 3- 12. 2007. [27] W. Simonson and W. Alsbrooks. A DBMS for the U. S. Bureau of the Census. In Proceedings of the 1st International Conference on Very Large Data Bases (VLDB '75). ACM, New York, NY, USA, 496-498. 1975. [28] M. Skeels, B. Lee, G. Smith, and G. Robertson. Revealing Uncertainty for Information Visualization. In Proceedings of the Working Conference on Advanced Visual Interfaces. ACM, New York, NY, USA. 2008, 376-379 [29] G. Smith, M. Czerwinski, B. Meyers, D. Robbins, G. Robertson, and D. Tan. FacetMap: A Scalable Search and Browse Visualization. IEEE Transactions on Visualization and Computer Graphics 12(5): 797-804. September 2006. [30] A. Streit, B. Pham, and R. Brown. A Spreadsheet Approach to Facilitate Visualization of Uncertainty in Information. IEEE Transactions on Visualization and Computer Graphics 14(1): 61-72. January 2008. [31] J. Thomson, E. Hetzler, A. MacEachren, M. Gahegan and M. Pavel, A typology for visualizing uncertainty. In Proceedings of SPIE &