GraphLab: A New Framework For Parallel Machine Learning

1 . GraphLab: A New Framework For Parallel Machine Learning Yucheng Low Joseph Gonzalez Aapo Kyrola Carnegie Mellon University Carnegie Mellon University Carnegie Mellon University ylow@cs.cmu.edu jegonzal@cs.cmu.edu akyrola@cs.cmu.edu Danny Bickson Carlos Guestrin Joseph M. Hellerstein Carnegie Mellon University Carnegie Mellon University UC Berkeley bickson@cs.cmu.edu guestrin@cs.cmu.edu hellerstein@cs.berkeley.edu Abstract data representation. Consequently, many ML experts have turned to high-level abstractions, which dramatically sim- plify the design and implementation of a restricted class of Designing and implementing efficient, provably parallel algorithms. For example, the MapReduce abstrac- correct parallel machine learning (ML) algo- tion [Dean and Ghemawat, 2004] has been successfully ap- rithms is challenging. Existing high-level par- plied to a broad range of ML applications [Chu et al., 2006, allel abstractions like MapReduce are insuf- Wolfe et al., 2008, Panda et al., 2009, Ye et al., 2009]. ficiently expressive while low-level tools like MPI and Pthreads leave ML experts repeatedly However, by restricting our focus to ML algorithms that solving the same design challenges. By tar- are naturally expressed in MapReduce, we are often forced geting common patterns in ML, we developed to make overly simplifying assumptions. Alternatively, by GraphLab, which improves upon abstractions coercing efficient sequential ML algorithms to satisfy the like MapReduce by compactly expressing asyn- restrictions imposed by MapReduce, we often produce in- chronous iterative algorithms with sparse com- efficient parallel algorithms that require many processors putational dependencies while ensuring data con- to be competitive with comparable sequential methods. sistency and achieving a high degree of parallel In this paper we propose GraphLab, a new parallel frame- performance. We demonstrate the expressiveness work for ML which exploits the sparse structure and com- of the GraphLab framework by designing and mon computational patterns of ML algorithms. GraphLab implementing parallel versions of belief propaga- enables ML experts to easily design and implement effi- tion, Gibbs sampling, Co-EM, Lasso and Com- cient scalable parallel algorithms by composing problem pressed Sensing. We show that using GraphLab specific computation, data-dependencies, and scheduling. we can achieve excellent parallel performance on We provide an efficient shared-memory implementation1 large scale real-world problems. of GraphLab and use it to build parallel versions of four popular ML algorithms. We focus on the shared-memory multiprocessor setting because it is both ubiquitous and has 1 INTRODUCTION few effective high-level abstractions. We evaluate the algo- Exponential gains in hardware technology have enabled so- rithms on a 16-processor system and demonstrate state-of- phisticated machine learning (ML) techniques to be applied the-art performance. Our main contributions include: to increasingly challenging real-world problems. However, recent developments in computer architecture have shifted • A graph-based data model which simultaneously rep- the focus away from frequency scaling and towards paral- resents data and computational dependencies. lel scaling, threatening the future of sequential ML algo- • A set of concurrent access models which provide a rithms. In order to benefit from future trends in processor range of sequential-consistency guarantees. technology and to be able to apply rich structured models • A sophisticated modular scheduling mechanism. to rapidly scaling real-world problems, the ML community • An aggregation framework to manage global state. must directly confront the challenges of parallelism. • GraphLab implementations and experimental evalua- tions of parameter learning and inference in graphi- However, designing and implementing efficient and prov- cal models, Gibbs sampling, CoEM, Lasso and com- ably correct parallel algorithms is extremely challenging. pressed sensing on real-world problems. While low level abstractions like MPI and Pthreads pro- vide powerful, expressive primitives, they force the user 1 The C++ reference implementation of the GraphLab is avail- to address hardware issues and the challenges of parallel able at http://select.cs.cmu.edu/code. 

2 .2 EXISTING FRAMEWORKS assumes that processors do not fail and all data is stored in shared-memory. As a consequence, GraphLab does not in- There are several existing frameworks for designing and cur the unnecessary disk overhead associated with MapRe- implementing parallel ML algorithms. Because GraphLab duce in the multi-core setting. generalizes these ideas and addresses several of their criti- cal limitations we briefly review these frameworks. 2.2 DAG ABSTRACTION 2.1 MAP-REDUCE ABSTRACTION In the DAG abstraction, parallel computation is represented as a directed acyclic graph with data flowing along edges A program implemented in the MapReduce framework between vertices. Vertices correspond to functions which consists of a Map operation and a Reduce operation. The receive information on inbound edges and output results Map operation is a function which is applied independently to outbound edges. Implementations of this abstraction in- and in parallel to each datum (e.g., webpage) in a large data clude Dryad [Isard et al., 2007] and Pig Latin [Olston et al., set (e.g., computing the word-count). The Reduce oper- 2008]. ation is an aggregation function which combines the Map outputs (e.g., computing the total word count). MapReduce While the DAG abstraction permits rich computational de- performs optimally only when the algorithm is embarrass- pendencies it does not naturally express iterative algo- ingly parallel and can be decomposed into a large num- rithms since the structure of the dataflow graph depends on ber of independent computations. The MapReduce frame- the number of iterations (which must therefore be known work expresses the class of ML algorithms which fit the prior to running the program). The DAG abstraction also Statistical-Query model [Chu et al., 2006] as well as prob- cannot express dynamically prioritized computation. lems where feature extraction dominates the run-time. 2.3 SYSTOLIC ABSTRACTION The MapReduce abstraction fails when there are computa- The Systolic abstraction [Kung and Leiserson, 1980] (and tional dependencies in the data. For example, MapReduce the closely related Dataflow abstraction) extends the DAG can be used to extract features from a massive collection of framework to the iterative setting. Just as in the DAG Ab- images but cannot represent computation that depends on straction, the Systolic abstraction forces the computation to small overlapping subsets of images. This critical limita- be decomposed into small atomic components with limited tion makes it difficult to represent algorithms that operate communication between the components. The Systolic ab- on structured models. As a consequence, when confronted straction uses a directed graph G = (V, E) which is not with large scale problems, we often abandon rich struc- necessarily acyclic) where each vertex represents a proces- tured models in favor of overly simplistic methods that are sor, and each edge represents a communication link. In amenable to the MapReduce abstraction. a single iteration, each processor reads all incoming mes- Many ML algorithms iteratively transform parameters dur- sages from the in-edges, performs some computation, and ing both learning and inference. For example, algorithms writes messages to the out-edges. A barrier synchroniza- like Belief Propagation (BP), EM, gradient descent, and tion is performed between each iteration, ensuring all pro- even Gibbs sampling, iteratively refine a set of parameters cessors compute and communicate in lockstep. until some termination condition is achieved. While the While the Systolic framework can express iterative com- MapReduce abstraction can be invoked iteratively, it does putation, it is unable to express the wide variety of update not provide a mechanism to directly encode iterative com- schedules used in ML algorithms. For example, while gra- putation. As a consequence, it is not possible to express dient descent may be run within the Systolic abstraction us- sophisticated scheduling, automatically assess termination, ing a Jacobi schedule it is not possible to implement coor- or even leverage basic data persistence. dinate descent which requires the more sequential Gauss- The popular implementations of the MapReduce abstrac- Seidel schedule. The Systolic abstraction also cannot tion are targeted at large data-center applications and there- express the dynamic and specialized structured schedules fore optimized to address node-failure and disk-centric par- which were shown by Gonzalez et al. [2009a,b] to dramat- allelism. The overhead associated with the fault-tolerant, ically improve the performance of algorithms like BP. disk-centric approach is unnecessarily costly when applied to the typical cluster and multi-core settings encountered 3 THE GRAPHLAB ABSTRACTION in ML research. Nonetheless, MapReduce is used in small By targeting common patterns in ML, like sparse data clusters and even multi-core settings [Chu et al., 2006]. The dependencies and asynchronous iterative computation, GraphLab implementation2 described in this paper does not GraphLab achieves a balance between low-level and address fault-tolerance or parallel disk access and instead high-level abstractions. Unlike many low-level abstrac- 2 The GraphLab abstraction is intended for both the multicore tions (e.g., MPI, PThreads), GraphLab insulates users and cluster settings and a distributed, fault-tolerant implementa- from the complexities of synchronization, data races and tion is ongoing research. deadlocks by providing a high level data representation 

3 .through the data graph and automatically maintained data- Algorithm 1: Sync Algorithm on k consistency guarantees through configurable consistency (0) t ← rk models. Unlike many high-level abstractions (i.e., MapRe- foreach v ∈ V do duce), GraphLab can express complex computational de- t ← Foldk (Dv , t) pendencies using the data graph and provides sophisti- T [k] ← Applyk (t) cated scheduling primitives which can express iterative parallel algorithms with dynamic scheduling. To aid in the presentation of the GraphLab framework we of computation. For every vertex v, we define Sv as the use Loopy Belief Propagation (BP) [Pearl, 1988] on pair- neighborhood of v which consists of v, its adjacent edges wise Markov Random Fields (MRF) as a running example. (both inbound and outbound) and its neighboring vertices A pairwise MRF is an undirected graph over random vari- as shown in Fig. 1(a). We define DSv as the data cor- ables where edges represent interactions between variables. responding to the neighborhood Sv . In addition to DSv , Loopy BP is an approximate inference algorithm which es- update functions also have read-only access, to the shared timates the marginal distributions by iteratively recomput- data table T. We define the application of the update func- ing parameters (messages) associated with each edge until tion f to the vertex v as the state mutating computation: some convergence condition is achieved. DSv ← f (DSv , T). 3.1 DATA MODEL We refer to the neighborhood Sv as the scope of v because The GraphLab data model consists of two parts: a directed Sv defines the extent of the graph that can be accessed by data graph and a shared data table. The data graph f when applied to v. For notational simplicity, we denote G = (V, E) encodes both the problem specific sparse com- f (DSv , T) as f (v). A GraphLab program may consist of putational structure and directly modifiable program state. multiple update functions and it is up to the scheduling The user can associate arbitrary blocks of data (or param- model (see Sec. 3.4) to determine which update functions eters) with each vertex and directed edge in G. We denote are applied to which vertices and in which parallel order. the data associated with vertex v by Dv , and the data asso- ciated with edge (u → v) by Du→v . In addition, we use 3.2.2 Sync Mechanism (u → ∗) to represent the set of all outbound edges from u and (∗ → v) for inbound edges at v. To support glob- The sync mechanism aggregates data across all vertices in ally shared state, GraphLab provides a shared data table the graph in a manner analogous to the Fold and Reduce (SDT) which is an associative map, T [Key] → Value, be- operations in functional programming. The result of the tween keys and arbitrary blocks of data. sync operation is associated with a particular entry in the In the Loopy BP, the data graph is the pairwise MRF, with Shared Data Table (SDT). The user provides a key k, a fold the vertex data Dv to storing the node potentials and the function (Eq. (3.1)), an apply function (Eq. (3.3)) as well (0) directed edge data Du→v storing the BP messages. If as an initial value rk to the SDT and an optional merge the MRF is sparse then the data graph is also sparse and function used to construct parallel tree reductions. GraphLab will achieve a high degree of parallelism. The (i+1) (i) SDT can be used to store shared hyper-parameters and the rk ← Foldk Dv , rk (3.1) global convergence progress. rkl ← Mergek rki , rkj (3.2) 3.2 USER DEFINED COMPUTATION (|V |) T [k] ← Applyk (rk ) (3.3) Computation in GraphLab can be performed either through an update function which defines the local computation, When the sync mechanism is invoked, the algorithm in or through the sync mechanism which defines global ag- Alg. 1 uses the Foldk function to sequentially aggregate gregation. The Update Function is analogous to the Map in data across all vertices. The Foldk function obeys the same MapReduce, but unlike in MapReduce, update unctions are consistency rules (described in Sec. 3.3) as update func- permitted to access and modify overlapping contexts in the tions and is therefore able to modify the vertex data. If graph. The sync mechanism is analogous to the Reduce the Mergek function is provided a parallel tree reduction is operation, but unlike in MapReduce, the sync mechanism used to combine the results of multiple parallel folds. The runs concurrently with the update functions. Applyk then finalizes the resulting value (e.g., rescaling) before it is written back to the SDT with key k. 3.2.1 Update Functions The sync mechanism can be set to run periodically in the A GraphLab update function is a stateless user-defined background while the GraphLab engine is actively apply- function which operates on the data associated with small ing update functions or on demand triggered by update neighborhoods in the graph and represents the core element functions or user code. If the sync mechanism is executed 

4 . Scopev The full consistency model ensures that during the exe- Data Data Data Data Data Data Data Data Data cution of f (v) no other function will read or modify data Data Data v Data Data within Sv . Therefore, parallel execution may only occur on vertices that do not share a common neighbor. The slightly (a) Scope weaker edge consistency model ensures that during the ex- ecution of f (v) no other function will read or modify any of the data on v or any of the edges adjacent to v. Under the edge consistency model, parallel execution may only Data Data Data Data occur on non-adjacent vertices. Finally, the weakest vertex Data Data Data Data Data Data Data Data Data consistency model only ensures that during the execution of f (v) no other function will be applied to v. The vertex consistency model is therefore prone to race conditions and (b) Consistency Models should only be used when reads and writes to adjacent data can be done safely (In particular repeated reads may return Figure 1: (a) The scope, Sv , of vertex v consists of all the data at different results). However, by permitting update functions the vertex v, its inbound and outbound edges, and its neighboring to be applied simultaneously to neighboring vertices, the vertices. The update function f when applied to the vertex v can vertex consistency model permits maximum parallelism. read and modify any data within Sv . (b). We illustrate the 3 data consistency models by drawing their exclusion sets as a ring Choosing the right consistency model has direct implica- where no two update functions may be executed simultaneously tions to program correctness. One method to prove correct- if their exclusions sets (rings) overlap. ness of a parallel algorithm is to show that it is equivalent to a correct sequential algorithm. To capture the relation in the background, the resulting aggregated value may not between sequential and parallel execution of a program we be globally consistent. Nonetheless, many ML applications introduce the concept of sequential consistency: are robust to approximate global statistics. Definition 3.1 (Sequential Consistency). A GraphLab pro- In the context of the Loopy BP example, the update func- gram is sequentially consistent if for every parallel execu- tion is the BP message update in which each vertex recom- tion, there exists a sequential execution of update functions putes its outbound messages by integrating the inbound that produces an equivalent result. messages. The sync mechanism is used to monitor the The sequential consistency property is typically a sufficient global convergence criterion (for instance, average change condition to extend algorithmic correctness from the se- or residual in the beliefs). The Foldk function accumulates quential setting to the parallel setting. In particular, if the the residual at the vertex, and the Applyk function divides algorithm is correct under any sequential execution of up- the final answer by the number of vertices. To monitor date functions, then the parallel algorithm is also correct if progress, we let GraphLab run the sync mechanism as a sequential consistency is satisfied. periodic background process. Proposition 3.1. GraphLab guarantees sequential consis- 3.3 DATA CONSISTENCY tency under the following three conditions: 1. The full consistency model is used Since scopes may overlap, the simultaneous execution of 2. The edge consistency model is used and update func- two update functions can lead to race-conditions resulting tions do not modify data in adjacent vertices. in data inconsistency and even corruption. For example, 3. The vertex consistency model is used and update func- two function applications to neighboring vertices could si- tions only access local vertex data. multaneously try to modify data on a shared edge resulting in a corrupted value. Alternatively, a function trying to nor- In the Loopy BP example the update function only needs to malize the parameters on a set of edges may compute the read and modify data on the adjacent edges. Therefore the sum only to find that the edge values have changed. edge consistency model ensures sequential consistency. GraphLab provides a choice of three data consistency mod- 3.4 SCHEDULING els which enable the user to balance performance and data The GraphLab update schedule describes the order in consistency. The choice of data consistency model deter- which update functions are applied to vertices and is rep- mines the extent to which overlapping scopes can be exe- resented by a parallel data-structure called the scheduler. cuted simultaneously. We illustrate each of these models The scheduler abstractly represents a dynamic list of tasks in Fig. 1(b) by drawing their corresponding exclusion sets. (vertex-function pairs) which are to be executed by the GraphLab guarantees that update functions never simulta- GraphLab engine. neously share overlapping exclusion sets. Therefore larger exclusion sets lead to reduced parallelism by delaying the Because constructing a scheduler requires reasoning execution of update functions on nearby vertices. about the complexities of parallel algorithm design, the 

5 .GraphLab framework provides a collection of base sched- v1 v1 ules. To represent Jacobi style algorithms (e.g., gradi- v3 v1 v3 v3 ent descent) GraphLab provides a synchronous sched- v2 v2 v2 v4 v4 uler which ensures that all vertices are updated simulta- v5 v5 v5 Update2 Update2 neously. To represent Gauss-Seidel style algorithms (e.g., v4 Update1 Update1 Gibbs sampling, coordinate descent), GraphLab provides a Data Graph Desired Execution Sequence Execution Plan round-robin scheduler which updates all vertices sequen- tially using the most recently available data. Figure 2: A simple example of the set scheduler planning pro- Many ML algorithms (e.g., Lasso, CoEM, Residual BP) re- cess. Given the data graph, and a desired sequence of execution quire more control over the tasks that are created and the where v1 , v2 and v5 are first run in parallel, then followed by v3 and v4 . If the edge consistency model is used, we observe that the order in which they are executed. Therefore, GraphLab execution of v3 depends on the state of v1 , v2 and v5 , but the v4 provides a collection of task schedulers which permit up- only depends on the state of v5 . The dependencies are encoded in date functions to add and reorder tasks. GraphLab pro- the execution plan on the right. The resulting plan allows v4 to be vides two classes of task schedulers. The FIFO sched- immediately executed after v5 without waiting for v1 and v2 . ulers only permit task creation but do not permit task re- ordering. The prioritized schedules permit task reordering Data Dependency Graph CPU 1 at the cost of increased overhead. For both types of task Data Data scheduler GraphLab also provide relaxed versions which CPU 2 Data Data Data increase performance at the expense of reduced control: CPU 3 Data Data Data Strict Order Relaxed Order Update1(v1) Data Data FIFO Single Queue Multi Queue / Partitioned Update2(v5) Execute Update Prioritized Priority Queue Approx. Priority Queue Update1(v3) Shared Data Table Update1(v9) In addition GraphLab provides the splash scheduler based … Data Data Data Data 1 2 3 4 on the loopy BP schedule proposed by Gonzalez et al. Scheduler [2009a] which executes tasks along spanning trees. Figure 3: A summary of the GraphLab framework. The user pro- In the Loopy BP example, different choices of scheduling vides a graph representing the computational data dependencies, leads to different BP algorithms. Using the Synchronous as well as a SDT containing read only data. The user also picks a scheduler corresponds to the classical implementation of scheduling method or defines a custom schedule, which provides BP and using priority scheduler corresponds to Residual a stream of update tasks in the form of (vertex, function) pairs to the processors. BP [Elidan et al., 2006]. The set scheduler compiles an execution plan by rewrit- 3.4.1 Set Scheduler ing the execution sequence as a Directed Acyclic Graph Because scheduling is important to parallel algorithm de- (DAG), where each vertex in the DAG represents an update sign, GraphLab provides a scheduler construction frame- task in the execution sequence and edges represent execu- work called the set scheduler which enables users to safely tion dependencies. Fig. 2 provides an example of this pro- and easily compose custom update schedules. To use the cess. The DAG imposes a partial ordering over tasks which set scheduler the user specifies a sequence of vertex set can be compiled into a parallel execution schedule using and update function pairs ((S1 , f1 ), (S2 , f2 ) · · · (Sk , fk )), the greedy algorithm described by Graham [1966]. where Si ⊆ V and fi is an update function. This sequence 3.5 TERMINATION ASSESSMENT implies the following execution semantics: Efficient parallel termination assessment can be challeng- for i = 1 · · · k do ing. The standard termination conditions used in many it- Execute fi on all vertices in Si in parallel. erative ML algorithms require reasoning about the global Wait for all updates to complete state. The GraphLab framework provides two methods The amount of parallelism depends on the size of each set; for termination assessment. The first method relies on the procedure is highly sequential if the set sizes are small. the scheduler which signals termination when there are no Executing the schedule in the manner described above can remaining tasks. This method works for algorithms like lead to the majority of the processors waiting for a few pro- Residual BP, which use task schedulers and stop produc- cessors to complete the current set. However, by leveraging ing new tasks when they converge. The second termination the causal data dependencies encoded in the graph structure method relies on user provided termination functions which we are able to construct an execution plan which identifies examine the SDT and signal when the algorithm has con- tasks in future sets that can be executed early while still verged. Algorithms, like parameter learning, which rely on producing an equivalent result. global statistics use this method. 

6 .3.6 SUMMARY AND IMPLEMENTATION Algorithm 2: BP update function A GraphLab program is composed of the following parts: BPUpdate(Dv , D∗→v , Dv→∗ ∈ Sv ) begin Compute the local belief b(xv ) using {D∗→v Dv } 1. A data graph which represents the data and compu- foreach (v → t) ∈ (v → ∗) do tational dependencies. Update mv→t (xt ) using {D∗→v , Dv } and λaxis(vt) 2. Update functions which describe local computation from the SDT. ˛˛ ˛˛ 3. A Sync mechanism for aggregating global state. residual ← ˛˛mv→t (xt ) − moldv→t (xt ) ˛˛ 1 if residual > Termination Bound then 4. A data consistency model (i.e., Fully Consistent, AddTask(t, residual) Edge Consistent or Vertex Consistent), which deter- end mines the extent to which computation can overlap. end 5. Scheduling primitives which express the order of end computation and may depend dynamically on the data. We implemented an optimized version of the GraphLab Algorithm 3: Parameter Learning Sync framework in C++ using PThreads. The resulting Fold(acc, vertex) begin GraphLab API is available under the LGPL license at Return acc + image statistics on vertex http://select.cs.cmu.edu/code. The data con- end sistency models were implemented using race-free and Apply(acc) begin Apply gradient step to λ using acc and return λ deadlock-free ordered locking protocols. To attain max- end imum performance we addressed issues related to paral- lel memory allocation, concurrent random number gener- ation, and cache efficiency. Since mutex collisions can be costly, lock-free data structures and atomic operations were local iterative computation and global aggregation as well used whenever possible. To achieve the same level of per- as several different computation schedules. formance for parallel learning system, the ML community We begin by using the GraphLab data-graph to build a large would have to repeatedly overcome many of the same time (256x64x64) three dimensional MRF in which each ver- consuming systems challenges needed to build GraphLab. tex corresponds to a voxel in the original image. We con- The GraphLab API has the opportunity to be an interface nect neighboring voxels in the 6 axis aligned directions. between the ML and systems communities. Parallel ML We store the density observations and beliefs in the vertex algorithms built around the GraphLab API automatically data and the BP messages in the directed edge data. As benefit from developments in parallel data structures. As shared data we store three global edge parameters which new locking protocols and parallel scheduling primitives determine the smoothing (accomplished using a Laplace are incorporated into the GraphLab API, they become im- similarity potentials) in each dimension. Prior to learn- mediately available to the ML community. Systems experts ing the model parameters, we first use the GraphLab sync can more easily port ML algorithms to new parallel hard- mechanism to compute axis-aligned averages as a proxy ware by porting the GraphLab API. for “ground-truth” smoothed images along each dimension. We then performed simultaneous learning and inference 4 CASE STUDIES in GraphLab by using the background sync mechanism To demonstrate the expressiveness of the GraphLab ab- (Alg. 3) to aggregate inferred model statistics and apply a straction and illustrate the parallel performance gains it gradient descent procedure. To the best of our knowledge, provides, we implement four popular ML algorithms and this is the first time graphical model parameter learning and evaluate these algorithms on large real-world problems us- BP inference have been done concurrently. ing a 16-core computer with 4 AMD Opteron 8384 proces- sors and 64GB of RAM. Results: In Fig. 4(a) we plot the speedup of the parame- 4.1 MRF PARAMETER LEARNING ter learning algorithm, executing inference and learning se- quentially. We found that the Splash scheduler outperforms To demonstrate how the various components of the other scheduling techniques enabling a factor 15 speedup GraphLab framework can be assembled to build a com- on 16 cores. We then evaluated simultaneous parameter plete ML “pipeline,” we use GraphLab to solve a novel learning and inference by allowing the sync mechanism to three-dimensional retinal image denoising task. In this task run concurrently with inference (Fig. 4(b) and Fig. 4(c)). we begin with raw three-dimensional laser density esti- By running a background sync at the right frequency, we mates, then use GraphLab to generate composite statistics, found that we can further accelerate parameter learning learn parameters for a large three-dimensional grid pair- while only marginally affecting the learned parameters. In wise MRF, and then finally compute expectations for each Fig. 4(d) and Fig. 4(e) we plot examples of noisy and de- voxel using Loopy BP. Each of these tasks requires both noised cross sections respectively. 

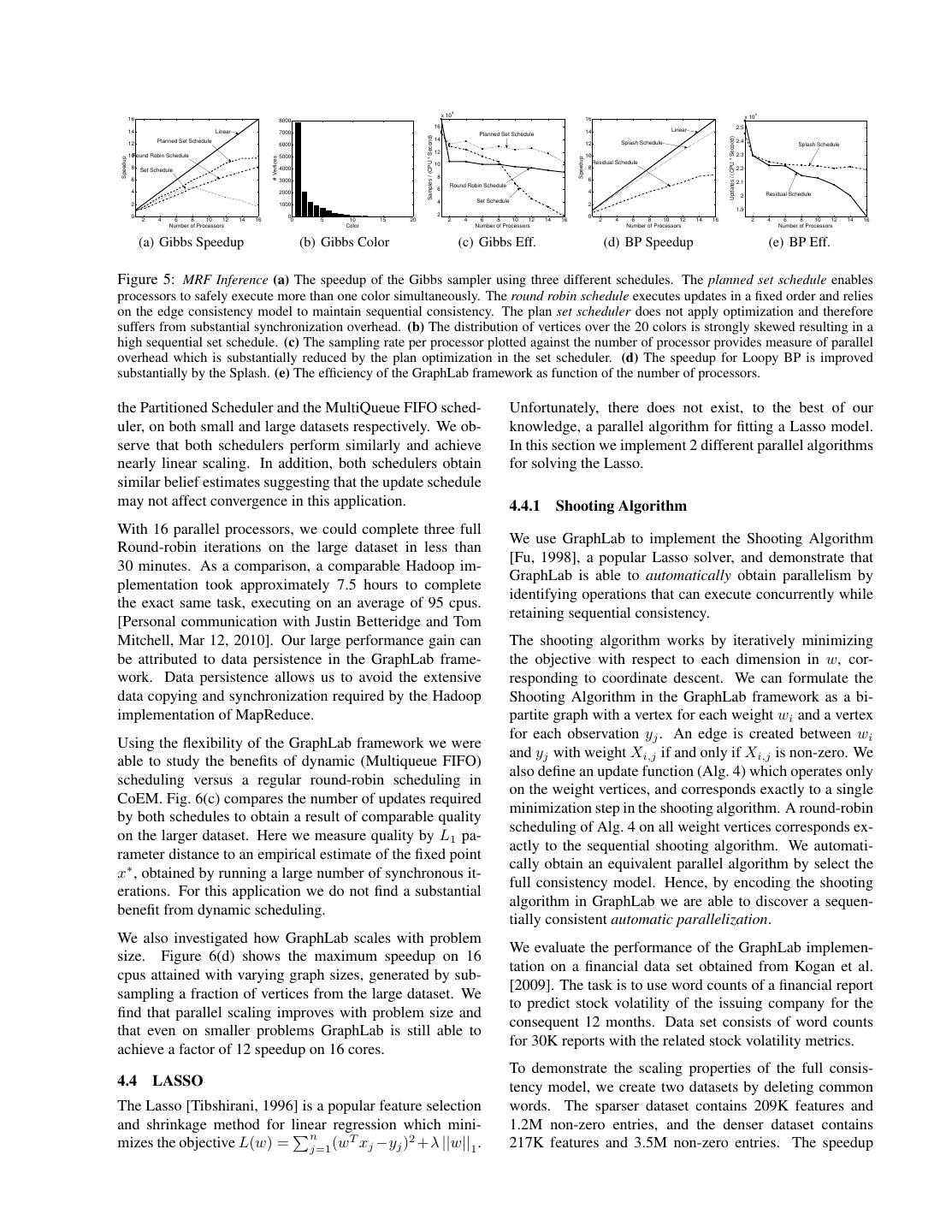
7 . 16 4 Linear 2000 14 3.5 Total Runtime (Seconds) Splash Schedule Average % deviation 12 3 Approx. Priority Schedule 1500 Average % deviation 10 2.5 Speedup Priority Schedule 8 Total Learning Runtime 2 1000 6 1.5 4 500 1 2 0.5 0 0 0 0 2 4 6 8 10 12 14 16 15 30 45 60 75 90 105 120 0 15 30 45 60 75 90 105 120 Number of Processors Sync Frequency (Seconds) Sync Frequency (Seconds) (a) Speedup (b) Bkgnd Sync. Runtime (c) Bkgnd Sync. Error (d) Original (e) Denoised Figure 4: Retinal Scan Denoising (a) Speedup relative to the best single processor runtime of parameter learning using priority, approx priority, and Splash schedules. (b) The total runtime in seconds of parameter learning and (c) the average percent deviation in learned parameters plotted against the time between gradient steps using the Splash schedule on 16 processors. (d,e) A slice of the original noisy image and the corresponding expected pixel values after parameter learning and denoising. 4.2 GIBBS SAMPLING number of colors (20) is needed and the vertex distribu- The Gibbs sampling algorithm is inherently sequential and tion over colors is heavily skewed. Consequently there is has frustrated efforts to build asymptotically consistent par- a strong sequential component to running the Gibbs sam- allel samplers. However, a standard result in parallel al- pler on this model. In contrast the Loopy BP speedup gorithms [Bertsekas and Tsitsiklis, 1989] is that for any demonstrates considerably better scaling with factor of 15 fixed length Gauss-Seidel schedule there exists an equiv- speedup on 16 processor. The larger cost per BP update alent parallel execution which can be derived from a col- in conjunction with the ability to run a fully asynchronous oring of the dependency graph. We can extract this form schedule enables Loopy BP to achieve relatively uniform of parallelism using the GraphLab framework. We first use update efficiency compared to Gibbs sampling. GraphLab to construct a greedy graph coloring on the MRF 4.3 CO-EM and then to execute an exact parallel Gibbs sampler. To illustrate how GraphLab scales in settings with large We implement the standard greedy graph coloring algo- structured models we designed and implemented a parallel rithm in GraphLab by writing an update function which version of Co-EM [Jones, Nigam and Ghani, 2000], a semi- examines the colors of the neighboring vertices of v, and supervised learning algorithm for named entity recognition sets v to the first unused color. We use the edge consis- (NER). Given a list of noun phrases (NP) (e.g., “big ap- tency model with the parallel coloring algorithm to ensure ple”), contexts (CT) (e.g., “citizen of ”), and co-occurence that the parallel execution retains the same guarantees as counts for each NP-CT pair in a training corpus, CoEM the sequential version. The parallel Gauss-Seidel schedule tries to estimate the probability (belief) that each entity (NP is then built using the GraphLab set scheduler (Sec. 3.4.1) or CT) belongs to a particular class (e.g., “country” or “per- and the coloring of the MRF. The resulting schedule con- son”). The CoEM update function is relatively fast, requir- sists of a sequence of vertex sets S1 to SC such that Si ing only a few floating operations, and therefore stresses contains all the vertices with color i. The vertex consis- the GraphLab implementation by requiring GraphLab to tency model is sufficient since the coloring ensures full se- manage massive amounts of fine-grained parallelism. quential consistency. The GraphLab graph for the CoEM algorithm is a bipar- To evaluate the GraphLab parallel Gibbs sampler we con- tite graph with each NP and CT represented as a vertex, sider the challenging task of marginal estimation on a fac- connected by edges with weights corresponding to the co- tor graph representing a protein-protein interaction network occurence counts. Each vertex stores the current estimate obtained from Elidan et al. [2006] by generating 10, 000 of the belief for the corresponding entity. The update func- samples. The resulting MRF has roughly 100K edges and tion for CoEM recomputes the local belief by taking a 14K vertices. As a baseline for comparison we also ran weighted average of the adjacent vertex beliefs. The adja- a GraphLab version of the highly optimized Splash Loopy cent vertices are rescheduled if the belief changes by more BP [Gonzalez et al., 2009b] algorithm. than some predefined threshold (10−5 ). We experimented with the following two NER datasets ob- Results: In Fig. 5 we present the speedup and efficiency tained from web-crawling data. results for Gibbs sampling and Loopy BP. Using the set schedule in conjunction with the planning optimization en- Name Classes Verts. Edges 1 CPU Runtime ables the Gibbs sampler to achieve a factor of 10 speedup small 1 0.2 mil. 20 mil. 40 min on 16 processors. The execution plan takes 0.05 seconds large 135 2 mil. 200 mil. 8 hours to compute, an immaterial fraction of the 16 processor run- ning time. Because of the structure of the MRF, a large We plot in Fig. 6(a) and Fig. 6(b) the speedup obtained by 

8 . 4 4 x 10 x 10 16 8000 16 16 2.5 14 Linear 7000 14 Linear Planned Set Schedule Samples / (CPU * Second) Updates / (CPU * Second) Planned Set Schedule 14 2.4 12 6000 12 Splash Schedule Splash Schedule 12 10Round Robin Schedule 5000 10 2.3 # Vertices Speedup Speedup 10 Residual Schedule 8 Set Schedule 4000 8 2.2 8 6 3000 6 2.1 Round Robin Schedule 4 6 4 2000 Residual Schedule 2 4 Set Schedule 2 1000 2 1.9 0 0 2 0 2 4 6 8 10 12 14 16 0 5 10 15 20 2 4 6 8 10 12 14 16 2 4 6 8 10 12 14 16 2 4 6 8 10 12 14 16 Number of Processors Color Number of Processors Number of Processors Number of Processors (a) Gibbs Speedup (b) Gibbs Color (c) Gibbs Eff. (d) BP Speedup (e) BP Eff. Figure 5: MRF Inference (a) The speedup of the Gibbs sampler using three different schedules. The planned set schedule enables processors to safely execute more than one color simultaneously. The round robin schedule executes updates in a fixed order and relies on the edge consistency model to maintain sequential consistency. The plan set scheduler does not apply optimization and therefore suffers from substantial synchronization overhead. (b) The distribution of vertices over the 20 colors is strongly skewed resulting in a high sequential set schedule. (c) The sampling rate per processor plotted against the number of processor provides measure of parallel overhead which is substantially reduced by the plan optimization in the set scheduler. (d) The speedup for Loopy BP is improved substantially by the Splash. (e) The efficiency of the GraphLab framework as function of the number of processors. the Partitioned Scheduler and the MultiQueue FIFO sched- Unfortunately, there does not exist, to the best of our uler, on both small and large datasets respectively. We ob- knowledge, a parallel algorithm for fitting a Lasso model. serve that both schedulers perform similarly and achieve In this section we implement 2 different parallel algorithms nearly linear scaling. In addition, both schedulers obtain for solving the Lasso. similar belief estimates suggesting that the update schedule may not affect convergence in this application. 4.4.1 Shooting Algorithm With 16 parallel processors, we could complete three full We use GraphLab to implement the Shooting Algorithm Round-robin iterations on the large dataset in less than [Fu, 1998], a popular Lasso solver, and demonstrate that 30 minutes. As a comparison, a comparable Hadoop im- GraphLab is able to automatically obtain parallelism by plementation took approximately 7.5 hours to complete identifying operations that can execute concurrently while the exact same task, executing on an average of 95 cpus. retaining sequential consistency. [Personal communication with Justin Betteridge and Tom Mitchell, Mar 12, 2010]. Our large performance gain can The shooting algorithm works by iteratively minimizing be attributed to data persistence in the GraphLab frame- the objective with respect to each dimension in w, cor- work. Data persistence allows us to avoid the extensive responding to coordinate descent. We can formulate the data copying and synchronization required by the Hadoop Shooting Algorithm in the GraphLab framework as a bi- implementation of MapReduce. partite graph with a vertex for each weight wi and a vertex for each observation yj . An edge is created between wi Using the flexibility of the GraphLab framework we were and yj with weight Xi,j if and only if Xi,j is non-zero. We able to study the benefits of dynamic (Multiqueue FIFO) also define an update function (Alg. 4) which operates only scheduling versus a regular round-robin scheduling in on the weight vertices, and corresponds exactly to a single CoEM. Fig. 6(c) compares the number of updates required minimization step in the shooting algorithm. A round-robin by both schedules to obtain a result of comparable quality scheduling of Alg. 4 on all weight vertices corresponds ex- on the larger dataset. Here we measure quality by L1 pa- actly to the sequential shooting algorithm. We automati- rameter distance to an empirical estimate of the fixed point cally obtain an equivalent parallel algorithm by select the x∗ , obtained by running a large number of synchronous it- full consistency model. Hence, by encoding the shooting erations. For this application we do not find a substantial algorithm in GraphLab we are able to discover a sequen- benefit from dynamic scheduling. tially consistent automatic parallelization. We also investigated how GraphLab scales with problem We evaluate the performance of the GraphLab implemen- size. Figure 6(d) shows the maximum speedup on 16 tation on a financial data set obtained from Kogan et al. cpus attained with varying graph sizes, generated by sub- [2009]. The task is to use word counts of a financial report sampling a fraction of vertices from the large dataset. We to predict stock volatility of the issuing company for the find that parallel scaling improves with problem size and consequent 12 months. Data set consists of word counts that even on smaller problems GraphLab is still able to for 30K reports with the related stock volatility metrics. achieve a factor of 12 speedup on 16 cores. To demonstrate the scaling properties of the full consis- 4.4 LASSO tency model, we create two datasets by deleting common The Lasso [Tibshirani, 1996] is a popular feature selection words. The sparser dataset contains 209K features and and shrinkage method for linear regression which mini- 1.2M non-zero entries, and the denser dataset contains n mizes the objective L(w) = j=1 (wT xj −yj )2 +λ ||w||1 . 217K features and 3.5M non-zero entries. The speedup 

9 . 16 16 16 Linear −6 14 Linear 14 MultiQueue FIFO Speedup with 16 cpus −7 14 12 MultiQueue FIFO 12 Partitioned Round robin Log(|x−x*|1) 10 10 −8 Speedup Speedup Partitioned 12 8 8 −9 6 6 −10 MultiQueue FIFO 10 4 4 −11 8 2 2 −12 0 0 0 2 4 6 6 2 4 6 8 10 12 14 16 2 4 6 8 10 12 14 16 0 20 40 60 80 100 Number of Processors Number of Processors Number of updates x 10 6 Single Processor Runtime (Seconds) (a) CoEM Speedup Small (b) CoEM Speedup Large (c) Convergence (d) Speedup with Problem Size Figure 6: CoEM Results (a,b) Speedup of MultiQueue FIFO and Partitioned Scheduler on both datasets. Speedup is measured relative to fastest running time on a single cpu. The large dataset achieves better scaling because the update function is slower. (c) Speed of convergence measured in number of updates for MultiQueue FIFO and Round Robin (equivalent to synchronized Jacobi schedule), (d) Speedup achieved with 16 cpus as the graph size is varied. Algorithm 4: Shooting Algorithm Algorithm 5: Compressed Sensing Outer Loop ShootingUpdate(Dwi , D∗→wi , Dwi →∗ ) begin while duality gap ≥ do Minimize the loss function with respect to wi Update edge and node data of the data graph. if wi changed by > then Use GraphLab to run GaBP on the graph Revise the residuals on all y s connected to wi Use Sync to compute duality gap Schedule all w s connected to neighboring y s Take a newton step end end end 4.5 Compressed Sensing 16 16 14 Linear 14 Linear To show how GraphLab can be used as a subcomponent of 12 12 Vertex Consistency a larger sequential algorithm, we implement a variation of Relative Speedup Relative Speedup Vertex Consistency 10 10 8 Full Consistency 8 Full Consistency the interior point algorithm proposed by Kim et al. [2007] 6 6 for the purposes of compressed sensing. The aim is to use 4 4 a sparse linear combination of basis functions to represent 2 2 0 0 the image, while minimizing the reconstruction error. Spar- 2 4 6 8 10 12 14 16 2 4 6 8 10 12 14 16 Number of Processors Number of Processors sity is achieved through the use of elastic net regularization. (a) Sparser Dataset Speedup (b) Denser Dataset Speedup The interior point method is a double loop algorithm where Figure 7: Shooting Algorithm (a) Speedup on the sparser dataset the sequential outer loop (Alg. 5) implements a Newton using vertex consistency and full consistency relative to the fastest method while the inner loop computes the Newton step by single processor runtime. (b) Speedup on the denser dataset using solving a sparse linear system using GraphLab. We used vertex consistency and full consistency relative to the fastest single Gaussian BP (GaBP) as a linear solver [Bickson, 2008] processor runtime. since it has a natural GraphLab representation. The GaBP GraphLab construction follows closely the BP example in Sec. 4.1, but represents potentials and messages analyti- curves are plotted in Fig. 7. We observed better scaling cally as Gaussian distributions. In addition, the outer loop (4x at 16 CPUs) on the sparser dataset than on the denser uses a Sync operation on the data graph to compute the du- dataset (2x at 16 CPUs). This demonstrates that ensuring ality gap and to terminate the algorithm when the gap falls full consistency on denser graphs inevitably increases con- below a predefined threshold. Because the graph structure tention resulting in reduced performance. is fixed across iterations, we can leverage data persistency in GraphLab, avoid both costly set up and tear down oper- Additionally, we experimented with relaxing the consis- ations and resume from the converged state of the previous tency model, and we discovered that the shooting algorithm iteration. still converges under the weakest vertex consistency guar- antees; obtaining solutions with only 0.5% higher loss on We evaluate the performance of this algorithm on a syn- the same termination criterion. The vertex consistent model thetic compressed sensing dataset constructed by apply- is much more parallel and we can achieve significantly bet- ing a random projection matrix to a wavelet transform of ter speedup, especially on the denser dataset. It remains an a 256 × 256 Lenna image (Fig. 8). Experimentally, we open question why the Shooting algorithm still functions achieved a factor of 8 speedup using 16 processors using under such weak guarantees. the round-robin scheduling. 

10 . 16 14 Acknowledgements 12 Linear 10 We thank Guy Blelloch and David O’Hallaron for their Speedup 8 guidance designing and implementing GraphLab. This 6 4 work is supported by ONR Young Investigator Pro- L1 Interior Point 2 gram grant N00014-08-1-0752, the ARO under MURI 0 2 4 6 8 10 12 Number of Processors 14 16 W911NF0810242, DARPA IPTO FA8750-09-1-0141, and (a) Speedup (b) Lenna (c) Lenna 50% the NSF under grants IIS-0803333 and NeTS-NBD CNS- 0721591. Joseph Gonzalez is supported by the AT&T Labs Figure 8: (a) Speedup of the Interior Point algorithm on the Fellowship Program. compressed sensing dataset, (b) Original 256x256 test image with 65,536 pixels, (c) Output of compressed sensing algorithm using References 32,768 random projections. J. Dean and S. Ghemawat. MapReduce: simplified data process- ing on large clusters. Commun. ACM, 51(1), 2004. C.T. Chu, S.K. Kim, Y.A. Lin, Y. Yu, G.R. Bradski, A.Y. Ng, and K. Olukotun. Map-reduce for machine learning on multicore. 5 CONCLUSIONS AND FUTURE WORK In NIPS, 2006. J. Wolfe, A. Haghighi, and D. Klein. Fully distributed EM for We identified several limitations in applying existing paral- very large datasets. In ICML. ACM, 2008. lel abstractions like MapReduce to Machine Learning (ML) B. Panda, J.S. Herbach, S. Basu, and R.J. Bayardo. Planet: problems. By targeting common patterns in ML, we devel- massively parallel learning of tree ensembles with mapreduce. Proc. VLDB Endow., 2(2), 2009. oped GraphLab, a new parallel abstraction which achieves J. Ye, J. Chow, J. Chen, and Z. Zheng. Stochastic gradient boosted a high level of usability, expressiveness and performance. distributed decision trees. In CIKM. ACM, 2009. Unlike existing parallel abstractions, GraphLab supports M. Isard, M. Budiu, Y. Yu, A. Birrell, and D. Fetterly. Dryad: the representation of structured data dependencies, iterative distributed data-parallel programs from sequential building computation, and flexible scheduling. blocks. SIGOPS Oper. Syst. Rev., 41(3), 2007. C. Olston, B. Reed, U. Srivastava, R. Kumar, and A. Tomkins. The GraphLab abstraction uses a data graph to encode Pig latin: A not-so-foreign language for data processing. SIG- the computational structure and data dependencies of the MOD, 2008. problem. GraphLab represents local computation in the H. T. Kung and C. E. Leiserson. Algorithms for VLSI processor form of update functions which transform the data on the arrays. Addison-Wesley, 1980. data graph. Because update functions can modify over- J. Gonzalez, Y. Low, and C. Guestrin. Residual splash for opti- lapping state, the GraphLab framework provides a set of mally parallelizing belief propagation. In AISTATS, 2009a. data consistency models which enable the user to specify J. Gonzalez, Y. Low, C. Guestrin, and D. O’Hallaron. Distributed the minimal consistency requirements of their application parallel inference on large factor graphs. In UAI, July 2009b. without having to build their own complex locking proto- J. Pearl. Probabilistic reasoning in intelligent systems: networks of plausible inference. 1988. cols. To manage sharing and aggregation of global state, G. Elidan, I. Mcgraw, and D. Koller. Residual belief propagation: GraphLab provides a powerful sync mechanism. Informed scheduling for asynchronous message passing. In To manage the scheduling of dynamic iterative parallel UAI, 2006. computation, the GraphLab abstraction provides a rich col- R. L. Graham. Bounds for certain multiprocessing anomalies. Bell System Technical Journal (BSTJ), 45:1563–1581, 1966. lection of parallel schedulers encompassing a wide range D. Bertsekas and J. Tsitsiklis. Parallel and Distributed Computa- of ML algorithms. GraphLab also provides a scheduler tion: Numerical Methods. Prentice-Hall, 1989. construction framework built around a sequence of vertex R. Jones. Learning to Extract Entities from Labeled and Unla- sets which can be used to compose custom schedules. beled Text. PhD thesis, Carnegie Mellon University. We developed an optimized shared memory implementa- K. Nigam and R. Ghani. Analyzing the effectiveness and applica- bility of co-training. In CIKM, 2000. tion GraphLab and we demonstrated its performance and R. Tibshirani. Regression shrinkage and selection via the lasso. J flexibility through a series of case studies. In each case ROY STAT SOC B, 58:267–288, 1996. study we designed and implemented a popular ML algo- Wenjiang J. Fu. Penalized regressions: The bridge versus the rithm and applied it to a large real-world dataset achieving lasso. J COMPUT GRAPH STAT, pages 397–416, 1998. state-of-the-art performance. S. Kogan, D. Levin, B.R. Routledge, J.S. Sagi, and N. A. Smith. Predicting risk from financial reports with regression. In Our ongoing research includes extending the GraphLab HLT/NAACL, 2009. framework to the distributed setting allowing for compu- Seung-Jean Kim, K. Koh, M. Lustig, S. Boyd, and D. Gorinevsky. tation on even larger datasets. While we believe GraphLab An interior-point method for large-scale 1-regularized least naturally extend to the distributed setting we face numer- squares. IEEE J SEL TOP SIGNAL PROC, 1, 2007. ous new challenges including efficient graph partitioning, D. Bickson. Gaussian Belief Propagation: Theory and Applica- load balancing, distributed locking, and fault tolerance. tion. PhD thesis, The Hebrew University of Jerusalem, 2008.