CrowdScreen: Algorithms for Filtering Data with Humans

1 . CrowdScreen: Algorithms for Filtering Data with Humans Aditya Parameswaran Hector Garcia-Molina Hyunjung Park Stanford University Stanford University Stanford University adityagp@cs.stanford.edu hector@cs.stanford.edu hyunjung@stanford.edu Neoklis Polyzotis Aditya Ramesh Jennifer Widom UC Santa Cruz Stanford University Stanford University alkis@cs.ucsc.edu aramesh1@stanford.edu widom@cs.stanford.edu ABSTRACT In this paper, we focus on one of these fundamental building Given a set of data items, we consider the problem of filtering them blocks, an algorithm to filter a set of data items. For example, we based on a set of properties that can be verified by humans. This may have a set of images, videos, or text, and we want to use hu- problem is commonplace in crowdsourcing applications, and yet, mans to decide if the items have particular properties. We use the to our knowledge, no one has considered the formal optimization term filter for each of the properties we wish to check. For instance, of this problem. (Typical solutions use heuristics to solve the prob- one filter could be “image shows a scientist,” and another could be lem.) We formally state a few different variants of this problem. “people in image are looking at camera.” If we apply both filters, We develop deterministic and probabilistic algorithms to optimize we should obtain images of scientists looking at the camera. The the expected cost (i.e., number of questions) and expected error. emphasis in this paper is on applying a single filter, however, we We experimentally show that our algorithms provide definite gains also provide extensions to conjunctions of filters. with respect to other strategies. Our algorithms can be applied in a At first sight, the problem of checking which of a set of items sat- variety of crowdsourcing scenarios and can form an integral part of isfy a filter seems trivial: Simply take each item in turn, and ask a any query processor that uses human computation. human a question: Does this item satisfy the filter? The solution is the subset of items that received a positive answer. Unfortunately, humans may make mistakes, so we may not get a desirable solu- 1. INTRODUCTION tion with such a simple strategy. We may instead show each item Crowdsourcing enables programmers to write procedures that to multiple people and somehow combine the answers, e.g., if 2 employ Human Computation [14] at a large scale in order to solve out of 3 vote yes, then we say the item satisfies the filter. But what problems that are hard to solve algorithmically, such as understand- is the right way to combine the votes? And how many questions ing text, sound, video and images. should we ask per item? Does it matter if humans are more likely Recently, there has been a lot of interest in the database research to make false positive mistakes, as opposed to false negatives? And community in using crowdsourcing within a database [4, 7, 8, 12, what if we know a priori that most items are very likely to satisfy 13]. The vision is to be able to pose declarative queries that not only the filter? How does this knowledge change our filtering approach? refer to stored data, but also to data computed on-demand from Furthermore, we may not have an unlimited budget or time to do humans. The goal is to design a query processor and optimizer our filtering. So how do we select a strategy that, for instance, min- that automatically decomposes the query into small unit tasks that imizes costs (e.g., total number of questions asked) while keeping are answerable by humans. These unit tasks could be as simple overall error below a desired threshold? as comparing two items, rating an item or answering a Boolean The problem of filtering with humans is, well, as old as human- question. ity itself, so not surprisingly there is a lot of prior work. Our work As part of the query processor, we require human-computation is reminiscent of statistical hypothesis testing [19]. While the un- versions of algorithmic building blocks, such as sorting, filtering, derlying model is similar to ours (our hypothesis is that an item searching, categorization or clustering, where the basic operations satisfies a filter), the fundamental difference with our work is in the are done by humans. For instance, humans may be asked to sort a optimization criteria: With hypothesis testing, one wishes to en- set of profile images by some desired property (such as beauty or sure that the decision on each item meets an error or cost bound. age), or to categorize a data set of videos into humor, action, drama In our case, on the other hand, we filter a large set of items, and and so on. The implementation of these building blocks poses a our bounds are on the overall error or cost. In Section 2 we argue new set of challenges, as it has to take into account mistakes in hu- that these optimization criteria are often desirable in crowdsourc- man input, monetary compensation for humans, and the inherently ing. Furthermore, in Section 7 we show that use of our criteria can high latency of human computation. lead to substantial cost savings over the traditional, more conserva- tive approach. Emerging crowdsourcing applications [4, 5] have implemented Permission to copy without fee all or part of this material is granted provided various types of filtering (e.g., majority voting), but have not stud- that the copies are not made or distributed for direct commercial advantage, ied how to implement optimal filtering strategies. Prior work on the VLDB copyright notice and the title of the publication and its date appear, using human feedback for information integration [9] (which we and notice is given that copying is by permission of the Very Large Data will show is worse than our algorithms) uses a heuristic approach to Base Endowment. To copy otherwise, or to republish, to post on servers solve the problem. Previous work has also looked at the problem of or to redistribute to lists, requires a fee and/or special permission from the publisher, ACM. deciding how and when to obtain labels for machine learning [17, VLDB ‘10, September 13-17, 2010, Singapore 11, 10], but not the problem of minimizing cost. We revisit related Copyright 2010 VLDB Endowment, ACM 000-0-00000-000-0/00/00. 

2 .work in more detail in Section 8. (We use two distinct probabilities of error because our experience Note that in addition to being useful for query optimization, fil- with Mechanical Turk indicates that the false positive rate and false tering is also of independent interest in human computation. For negative rate for a filter can be very different.) We can ask different example, detecting spam websites in a set of websites (a very com- humans the same question to get better accuracy, and we assume mon task on Mechanical Turk [1]) is also an instance of the single- that their errors are independent. (Thus we assume all humans are filter problem. Relevance judgments for search results [2], where able to answer the question with the same degree of accuracy.) the task is to determine whether a web-page is relevant or not for a A strategy is a computer algorithm that takes as input any one given web-search query, is another instance. item, asks one or more humans questions on that same item, and Our contributions are the following: eventually outputs either “Pass” or “Fail”. A Pass output repre- • We identify the interesting dimensions of the single filter sents a belief that the item satisfies the filter, while Fail represents problem, which in turn reveal which parameters of the prob- the opposite. Of course, a strategy can also make mistakes, and lem can be constrained or optimized in a meaningful manner our job will be to design good strategies, i.e., ones that “make few in Section 2. We formulate five different versions of the prob- mistakes without asking too many questions”. We will express this lem under constraints on these parameters. We also develop goal more formally later on. a novel grid-based visualization to reason about strategies for A strategy can be visualized by a two-dimensional grid like the the problems that we describe. one in Figure 1(a). The Y axis represents the number of YES an- • For deterministic strategies, in Section 3, we develop an al- swers obtained so far from humans, while the X axis is the number gorithm that designs an approximately optimal deterministic of NO answers so far. A grid point at (x, y) determines what the strategy (for the cases where we definitely want a determinis- strategy does after x NOs and y YESs have been received from hu- tic strategy due to simplicity of representation or not having mans: A blue grid point indicates that the strategy outputs Pass at to toss a random dice). this point, while a red point indicates a Fail decision. We call a point that is either blue or red a termination point. At a green point • For probabilistic strategies, in Section 4, we develop a lin- no decision is made and the strategy issues another question, and ear programming solution to produce the optimal probabilis- thus moves to either (x, y + 1) (if an additional YES is received) tic strategy. Our approach naturally generalizes to a setting or to (x + 1, y) (if a NO is received). We call green points continue where multiple possible answers may arise, instead of just points (i.e., we continue to ask questions.) Thus, the evaluation of two, for instance, colors: red, blue, green, and so on. an item starts at (0, 0) (no questions have been asked), and moves • We discuss how our techniques can be extended to the case through the grid until hitting either a blue or red grid point. Note of multiple filters in Section 6. that the black points are not reachable under any circumstances. • We show that our algorithms perform exceedingly well com- Our example in Figure 1(a) depicts a strategy that always asks a pared to standard statistics approaches as well as other naive fixed number of questions, in this case 4. Thus, the termination and heuristic approaches in Section 7. points are along the x + y = 4 line. Although we have described the strategy of Figure 1(a) as pro- 2. PRELIMINARIES cessing a sequence of YES/NO answers, it can also represent a sce- For the majority of this paper, we consider the single filter prob- nario where a batch of questions is asked at once. (In some systems lem, but we do generalize to multiple filters in Section 6. Also, we such as Mechanical Turk [1] it is more effective to issue batches of assume that our filters are “binary” (i.e., they simply return YES questions.) If a batch of questions is issued, the strategy describes or NO), rather than the “n-ary” filtering case, where the filters may what to do as each answer is received and processed. If a decision is return one out of a set of n disjoint alternatives. (This “n-ary” prob- reached before all answers are received, the outstanding questions lem is relevant when we are classifiying each item into exactly one can be canceled. If we process all answers and need more, we can out of a set of classes, e.g., assigning colors.) Our techniques gen- issue another batch of questions. (Note that we do not need to issue eralize directly to the “n-ary” filtering problem. another batch if we ask the maximum number of questions needed by the strategy in the first batch itself.) 2.1 Formal Definitions As a second example of a strategy, consider Figure 1(b). In this We are given a set of items D, where |D| = n. We introduce a strategy, we stop as soon as we get four YESs or four NOs. Thus, random variable V that controls whether an input item satisfies the the total number of questions will vary between 4 and 7. filter (V = 1) or not (V = 0). The selectivity of our filter, s, gives The astute reader will notice that both of our sample strategies us the probability that V = 1 (over all possible items). The selec- have a certain structure: The termination points (blue/red) form tivity may be estimated by sampling on a small number of items. an uninterrupted path, starting at the y axis and ending at the x (The sampling approach is commonly used by query optimizers to axis. All the points between this path and the origin are green, estimate the size of a selection operator.) and all points outside this area are white (cannot be reached). In However, we assume we cannot examine an item and determine Section 3.2 we will study strategies with these properties. with certainty whether that item satisfies the filter or not. The only Also note that the strategies of Figure 1(a) and 1(b) are deter- type of action we can perform on an item is to ask a human a ques- ministic, i.e., the output is the same for the same sequence of an- tion. The human can tell us YES (meaning that he thinks the item swers. In Section 4 we discuss probabilistic strategies where the satisfies the filter) or NO. The human can make mistakes, and in decision at each grid point is probabilistic. For instance, at a par- particular: ticular grid point we may continue asking questions with proba- bility 0.6, may determine Pass with probability 0.3 and Fail with • The false positive rate is: probability 0.1. Thus we represent each grid point by a triple like P r[answer is YES|V = 0] = e0 (0.6, 0.3, 0.1). For deterministic strategies, the only triple values allowed are (1, 0, 0) (green point), (0, 1, 0) (blue point) or (0, 0, 1) • The false negative rate is (red point). P r[answer is NO|V = 1] = e1 Note that our strategies are defined to be naturally uniform, i.e., 

3 . Figure 1: (a) Visualization of a Triangular Strategy (b) Visualization of a Rectangular Strategy (c) Error at Terminating Points vs. Overall Error the same strategy is applied to each item in the data set, and com- points (where Term(x, y) does not hold). plete, i.e., the strategy tells us what to do at each reachable point in • C is the expected cost across all termination points, i.e.,: the grid. In addition, we want our strategies to be terminating, i.e., the C= C(x, y) × [p0 (x, y) + p1 (x, y)] (3) strategy always terminates in a finite number of steps, no matter (x,y) what sequence of YES/NO answers are received to the questions Note that to evaluate our n items using the same strategy, we (a terminating strategy effectively corresponds to a closed shape will incur an expected cost of nC. around the origin). Note that the strategies in Figures 1(a) and 1(b) are terminating. We will enforce a termination constraint in our To illustrate these metrics, consider the simple deterministic strat- problem formulations in Section 2.3. egy in Figure 1(c), and assume that s = 0.5, e1 = 0.1, e0 = 0.2. We also want our strategies to be fully determined in advance, At each termination point (x, y) we show E(x, y). For example, so that we do not need to do any computation on the fly while the E(0, 2) = 0.05. This number can be interpreted as follows: In 5% answers are received. Thus, we present algorithms that compute of the cases where we end up terminating at (0, 2), an error will be complete strategies. made. In the remaining 95% of the cases a correct (Pass) decision will be made. To compute E(0, 2), we need the p0 and p1 values. 2.2 Metrics Since there is only a single way to get to (0, 2) (two consecutive YESs) the computation is simple: p0 (0, 2) is (1 − s) (V must be To determine which strategy is best, we study two types of met- 0) times twice e0 , i.e., 0.02 (thus, p0 (0, 2) = (1 − s) × e20 ). Simi- rics, involving error and cost. We start by defining two quantities, larly, p1 (0, 2) = s × (1 − e1 )2 = 0.5 × 0.9 × 0.9 = 0.405. Thus, given a strategy: E(0, 2) = 0.02/[0.02 + 0.405] = 0.05. When there are multiple • p1 (x, y) is the probability that the strategy reaches point (x, y) ways to get to a point (e.g., for (1, 1)) the p0 , p1 computation is and the item satisfies the filter (V = 1); and more complex, and will be discussed in Section 2.4. • p0 (x, y) is the probability that the strategy reaches point (x, y) The expected error E for this sample strategy is the error weighed and the item does not satisfy the filter (V = 0). by the probability of getting to each termination point. In this case, Below we give a simple example to illustrate these quantities, and it turns out that E = 0.115. Notice the difference between the in Section 2.4 we show how to compute them in general. Further- overall error E and the individual termination point errors: The more, let us say if a Pass decision is made at (x, y) then Pass(x, y) error at (1, 1) is quite high, but because it is not very likely that holds, and that if a Fail decision is made, then Fail(x, y) holds. If we end up at (1, 1), that error does not contribute as much to the either decision is made, we say that Term(x, y) holds. overall E. We can now define the following metrics: • E(x, y) (only of interest when Term(x, y) holds) is the prob- 2.3 The Problems ability of error given that the strategy terminated at (x, y). If Given input parameters s, e1 , and e0 , the search for a “good” or Pass(x, y), then an error is made if V = 0, so E(x, y) is “optimal” strategy can be formulated in a variety of ways. Since we p0 (x, y) divided by the probability that the strategy reached want to ensure that the strategy terminates, we enforce a threshold (x, y) (i.e., divided by p0 (x, y) + p1 (x, y)). The Fail(x, y) m on the maximum number of questions we can ask for any item case is analogous, so we get: (which is nothing but a maximum budget for any item that we want  to filter). p0 (x,y)  [p0 (x,y)+p1 (x,y)] if Pass(x, y)  We start with the problem we will focus on in this paper: p1 (x,y) E(x, y) = if Fail(x, y) (1) P ROBLEM 1 (C ORE ). Given an error threshold τ and a bud-  [p0 (x,y)+p1 (x,y)]  0 else get threshold per item m, find a strategy that minimizes C under the constraint E < τ and ∀(x, y) C(x, y) < m. • E is the expected error across all termination points. That is: An alternative would be to constrain the error at each termination E= E(x, y) × [p0 (x, y) + p1 (x, y)]. (2) point: (x,y) P ROBLEM 2 (C ORE : P ER -I TEM E RROR ). Given an error thresh- • C(x, y) (only of interest when Term(x, y) holds) is the num- old τ and a budget threshold per item m, find a strategy that mini- ber of questions used to reach a decision at (x, y), i.e., simply mizes C under the constraint ∀(x, y) E(x, y) < τ and C(x, y) < x + y. We consider C(x, y) to be zero at all non-termination m. 

4 .    p0 (x − 1, y)(1 − e0 ) + p0 (x, y − 1)e0 if ¬Term(x, y − 1) ∧ ¬Term(x − 1, y) p0 (x, y − 1)e0 if ¬Term(x, y − 1) ∧ Term(x − 1, y)  p0 (x, y) =  p0 (x − 1, y)(1 − e0 )  if Term(x, y − 1) ∧ ¬Term(x − 1, y)  0 if Term(x, y − 1) ∧ Term(x − 1, y)    p1 (x, y − 1)(1 − e1 ) + p1 (x − 1, y)e1 if ¬Term(x, y − 1) ∧ ¬Term(x − 1, y) p1 (x, y − 1)(1 − e1 ) if ¬Term(x, y − 1) ∧ Term(x − 1, y)  p1 (x, y) =   p1 (x − 1, y)e1 if Term(x, y − 1) ∧ ¬Term(x − 1, y)  0 if Term(x, y − 1) ∧ Term(x − 1, y) Figure 2: Recursive Equations for p0 and p1 In Problem 2 we ensure that the error is never above threshold, to (x, y) is the sum of two quantities: (a) the probability of the item even in very unlikely executions. This formulation may be pre- not satisfying the filter and getting to (x, y −1) and getting an extra ferred when errors are disastrous, e.g., if our filter is checking for YES, and (b) the probability of the item not satisfying the filter and patients with some disease, or for defective automobiles. However, getting to (x − 1, y) and getting an extra NO. The probability of in other cases we may be willing to tolerate uncertainty in some getting an extra YES given that the item does not satisfy the filter individual decisions (i.e., high E(x, y) at some points), in order is precisely e0 , and the probability of getting a NO is (1 − e0 ). We to reduce costs, as long as the overall error E is acceptable. For can write similar equations for p1 , as shown in the figure. instance, say we are filtering photographs that will be used by an Given values for p0 and p1 , we can use the definitions of Sec- internet shopping site. In some unlikely case, we may get 10 YES tion 2.1 to compute the errors and costs at each point, and the over- and 10 NO votes, which may mean we are not sure if the photo sat- all error and cost. Note that we do not have to compute the p values isfies the filter. In this case we may prefer to stop asking questions at all points, but only for the reachable points, as all other points to contain costs and make a decision, even though the error rate have zero error E(x, y) and cost C(x, y). at this point will be high no matter what we decide. In Section 7 we study the price one pays (number of questions) for adopting 3. DETERMINISTIC STRATEGIES the more conservative approach of Problem 2 under the same error This section develops algorithms that find effective deterministic threshold. strategies for Problem 1. Instead of minimizing the overall cost, one could minimize the maximum cost at any given point, as in the next problem: 3.1 The Paths Principle P ROBLEM 3 (M AXIMUM C OST ). Given an error threshold τ , Given a deterministic strategy, using Equations 1, 2, 3 and Fig- find a strategy that minimizes the maximum value of C(x, y) (over ure 2 given earlier, it is easy to see that the following theorem holds: all points), under the constraint E < τ . T HEOREM 3.1 (C OMPUTATION OF C OST AND E RROR ). The expected cost and error of a strategy can be computed in time pro- Another variation is to minimize error, given some constraint on portional to the number of reachable grid points. the number of questions. We specify two such variants next. In the first variant we have a maximum budget for each item we want to Based on the above theorem, we have a brute force algorithm to filter, while in the second variant we have an additional constraint find the best deterministic strategy, namely by examining strategies on the expected overall cost. corresponding to all possible assignments of Pass, Fail or Continue (i.e., continue asking questions) to each point in (0, 0) to (m, m). P ROBLEM 4 (E RROR ). Given a budget threshold per item m, (There are 3m such assignments.) Evaluating cost and error for find a strategy that minimizes E under the constraint ∀(x, y) C(x, y) < each strategy takes time O(m2 ) using the recursive equations. We m. select the one that satisfies the error threshold, and minimizes cost. We call this algorithm naive3. P ROBLEM 5 (E RROR - II). Given a budget threshold per item Note that some of these strategies are not terminating. However, m and a cost threshold α, find a strategy that minimizes E under termination can also be checked easily for each strategy considered the constraints ∀(x, y) C(x, y) < m and C < α. in time proportional to the number of reachable grid points in the strategy. (If the p0 and p1 values at all points on the line x + y = 2.4 Computing Probabilities at Grid Points m , for some m ≤ m is zero, then the strategy is terminating.) In this subsection we show how to compute the p0 and p1 values defined in the previous subsection. We focus on a deterministic T HEOREM 3.2 (B EST S TRATEGY: NAIVE 3). The naive3 al- strategy (probabilistic strategies are discussed in Section 4). gorithm finds the best strategy for Problem 1 in O(m2 3m ). We compute the p values recursively, starting at the origin. In particular, note that p0 (0, 0) is (1 − s) and p1 (0, 0) is s. (For We are able to reduce significantly the search space of the naive instance, p0 (0, 0) is the probability that the item does not satisfy algorithm by excluding the provably suboptimal strategies. Our the filter and the strategy visits the point (0, 0) — which it has to.) exclusion criterion is based on the following fundamental theorem. We can then derive the probability p0 and p1 for every other point T HEOREM 3.3 (PATHS P RINCIPLE ). Given s, e1 , e0 , for ev- in the grid as shown in Figure 2. (Recall that Term(x, y) means ery point (x, y), the function R(x, y) = p0 (x, y)/(p0 (x, y) + that (x, y) is a termination point, either Pass or Fail.) p1 (x, y)) is a function of (x, y), independent of the particular (de- To see how these equations work, let us consider the first case for terministic or probabilistic) strategy. p0 , where neither (x − 1, y) nor (x, y − 1) are termination points. Note that we can get to (x, y) in two ways, either from (x, y − 1) P ROOF. Consider a single sequence of x No answers and y Yes on getting an extra YES, or from (x − 1, y) on getting an extra NO. answers. The probability that an item satisfies the filter, and gets the Thus, the probability of an item not satisfying the filter and getting particular sequence of x No answers and y Yes answers is precisely 

5 . Figure 3: (a) A Shape (b) Triangular Strategy Corresponds to a Shape (c) Ladder Shape Pruning a = s × ex1 × (1 − e1 )y , while the probability that an item does not 3.2 Shapes and Ladders satisfy the filter and gets the same sequence is b = (1 − s) × ey0 × In practice, considering all 2m strategies is computationally fea- (1 − e0 )x . The choice of strategy may change the number of such sible only for very small m. In this section, we design algorithms paths to the point (x, y), however the fraction of p0 to p0 + p1 is that only consider a subset of these 2m strategies and thereby can still b/(a + b). (Note that each path precisely adds a to p1 and b to only provide an approximate solution to the problem (i.e., the ex- p0 . Thus, if there are r paths, p0 /(p0 + p1 ) = (r × b)/[r × (a + pected cost may be slightly greater than the expected cost of the b)] = b/(a + b).) It can be shown that the proof also generalizes to optimal solution). The subset of strategies that we are interested in probabilistic strategies. (In that case, r can be a fractional number are those that correspond to shapes. We will describe an efficient of paths.) way of obtaining the best strategy that corresponds to a shape. Intuitively, this theorem holds because the strategy only changes the number of paths leading to a point, but the characteristics of the Shapes: A shape is defined by a connected sequence of (horizontal point stay the same. or vertical) segments on the grid, beginning at a point on the y- Using the previous theorem, we have the result that in order to axis, and ending at a point on the x axis, along with a special point reduce the error, for every termination point (x, y), Passing or Fail- somewhere along the sequence of segments, called a decision point. ing is independent of strategy, but is based simply on R(x, y). We also assume that each segment intersects at most with two other lines, namely the ones preceding and following it in the sequence. T HEOREM 3.4 (F ILTERING I NDEPENDENT OF S TRATEGY ). As an example, consider the shape in Figure 3(a) (ignore the dashed For every optimal strategy, for every point (x, y), if Term(x, y) lines for now) This shape begins at (0, 4), has a sequence of 14 holds, then: segments, and ends at (4, 0). The decision point (not shown in the • If R(x, y) > 1/2, then Fail(x, y) figure) is (for example) at (5, 5). As seen in the figure, the segments are allowed to go in any direction (up/down or left/right). • If R(x, y) < 1/2, then Pass(x, y) Each shape corresponds to precisely one strategy, namely the one P ROOF. Given a strategy, let there be a point (x, y) for which defined as follows: Pass(x, y) holds, but R(x, y) > 1/2. Let the error be: • For each point in the sequence of segments starting at the point on the y axis, until and including the decision point, E = E0 + E(x, y)(p0 (x, y) + p1 (x, y)) we color the point blue (i.e., we designate the point as Pass). (We split the error into two parts, one dependent on other termi- In the figure, all points in the sequence of segments starting nating points, and one just dependent on (x, y).) Currently, since from (0, 4) until and including (5, 5) are colored blue. (x, y) is Pass, E(x, y) is p0 (x, y)/(p0 (x, y) + p1 (x, y)). Thus, • For each point in the sequence of segments starting at the E = E0 + p0 (x, y). If we change (x, y) to Fail, we get E = point after the decision point, until and including the point E0 + p1 (x, y), then E < E. Thus, by flipping (x, y) to Fail, on the x axis, we color the point red (i.e., we designate the we can only reduce the error. Similarly, if R(x, y) < 1/2 and point as Fail). In the figure, all points after (5, 5) on the Fail(x, y) holds, we can only reduce the error by flipping it to sequence of segments are colored red. Pass(x, y). • For all the points inside or on the shape that are reachable, Thus, we only need to consider 2m strategies, namely those where we color them green; else we color them white. (Some points for each point, we can either set it to be a continue point or a termi- colored blue or red previously may actually be unreachable nation point, and if it is a termination point, then using the previous and will be colored white in this step.) In the figure, some theorem, we can infer whether it should be Pass or Fail.1 The algo- of the blue points, such as (2, 5), (1, 5), (1, 6), . . ., (5, 5), rithm that considers all such 2m strategies is called naive2. Thus, and some of the red points (5, 4), . . ., (4, 3), and (4, 1) are we have the following theorem: colored white, while some of the unreachable points inside the shape, such as (3, 4) and (4, 4) are colored white as well. T HEOREM 3.5 (B EST S TRATEGY: NAIVE 2). The naive2 al- The reachable points inside the shape, like (1, 1) or (2, 3) are gorithm finds the best strategy for Problem 1 in O(m2 2m ). colored green. 1 Note that there is a subtle point here. When R(x, y) = 1/2 then The strategies that correspond to shapes form a large and diverse the point can either be a Pass or a Fail point, with equal effect. (It class of strategies. In particular, the triangular strategy and rect- will contribute the same amount of error either way.) For simplicity angular strategy both correspond to shapes. Consider Figure 3(b), we assume it to always return Pass if this holds. which depicts a shape corresponding to the triangular strategy of 

6 .Figure 1(a). (Again, ignore dashed lines in the figure.) The shape segments from (0, 4) to (4, 0) in Figure 3(b) is not a ladder because consists of eight connected segments, beginning at (0, 4) and end- the vertical segments go from a larger y value to a smaller y value, ing at (4, 0), each alternately going one unit to the right or down. while the segment (0-2)-(3,2) is a ladder. The decision point in this case is the point (3, 2). Note that all We define the set of ladder shapes to be those shapes that contain points in the segments leading up to (3, 2) are either blue or white a decision point and two ladders, i.e., the connected sequence of (unreachable), while all points in the segments after (3, 2) are red segments from the point on the y axis to the decision point forms or white. In this case, all the points on the interior of the shape are one ladder and the connected sequence of segments from the point continue points. on the x axis to the decision point forms the second ladder. Thus, The rectangular strategy of Figure 1(b) corresponds to the shape ladder shapes are a subset of the set of all shapes. Intuitively, ladder formed by two segments, one from (0, 4) to (4, 4) and one from shapes are the shapes that we would expect to be optimal: the shape (4, 4) to (4, 0). The point (4, 4) is the decision point. As yet is smaller at the sides (close to the x and y axis, where we are more another example, consider Figure 3(c). If we consider the shape certain whether the item satisfies the filter or not), and larger close corresponding to the solid lines, we have a segment from (0, 2) to the center (away from both the x and y axis, where we are more to (0, 5), another from (0, 5) to (2, 5), and so on until (6, 6) — uncertain about the item). which is the decision point. Then we have five segments from (6, As before, the strategy that corresponds to a ladder shape is the 6) to (0, 6). Once again, notice that some of the points before the one formed by coloring all the points in the “upper” ladder blue, decision point in the sequence of segments, such as (3, 4) and (2, 5) and all the points in the “lower” ladder red, then coloring all re- are unreachable, and some points after the decision point, like (6, maining reachable points inside the shape green, and coloring all 1) and (6, 2) are unreachable. The decision point is unreachable as unreachable points inside or on the boundary of the shape white. In well. In this case, all internal points are reachable (and thus colored the following, we provide a few examples of how we can convert green). any shape into a ladder shape such that the strategy corresponding As an example of a strategy that does not correspond to a shape, to the ladder shape has the same or lower cost than the strategy cor- if the strategy in Figure 3(c) had an additional terminating point, responding to the shape. Since the set of ladder shapes is a subset say Fail at point (1, 1), then it can never correspond to a shape. of all possible shapes, if we want to find the best strategy corre- Why shapes? One objection one may have to studying shapes is sponding to a shape, we can thus focus on ladder shapes instead of that the best strategy corresponding to shapes may be much worse all shapes. Thus, we have the following theorems: than the best strategy overall. T HEOREM 3.7 (T RANSFORMATION ). Any shape can be con- However, the properties that shapes obey make intuitive sense. verted into a ladder shape yielding lesser cost and the same error. First, note that the strategies that correspond to shapes only have We now describe some examples of how the conversion algorithm terminating points on the “boundary” of the strategy, and not on works. The algorithm along with an informal proof can be found in the interior. This makes sense because it is not worthwhile to have the appendix. The algorithm essentially prunes redundant portions a termination point inside the boundary of termination points, since of the shape to give a ladder shape. we might as well move the boundary earlier. Second, the strategies have a single decision point; this makes sense because it is not use- T HEOREM 3.8 (B EST S HAPE ). For problem 1, the best strat- ful to alternate between red and blue points on the boundary, since egy from the set of shapes has equal cost to the best strategy from the more YES answers we get relative to NO answers, the more the set of ladder shapes. likely the item should satisfy the filter, hence we should be able The above theorem gives us an algorithm, denoted ladder, which to improve the strategy by converting it to one with a single point considers a small subset of the set of all shapes, namely all the where the colors change. ladder shapes. Note that this algorithm is still worst-case expo- In addition, we found that over 100 iterations of the naive2 al- nential; however, as we will see in the experiments, this algorithm gorithm for random instances of the parameters s, e1 , e0 and m, by performs reasonably well in practice, and in particular, much better inspection all of the optimal strategies corresponded to shapes. In than naive2. addition, as we will see in the experiments, on varying parameters, Examples of Converting Shapes to Ladder Shapes: First, con- the best strategy given by naive2 is no better than the best strategy sider the triangular strategy shown in Figure 3(b). As it stands, corresponding to a shape. the shape (formed from the solid lines in the figure) is not a ladder Hence, we pose the following conjecture: shape, since the sequence of segments leading to the decision point C ONJECTURE 3.6. Given a problem, the best deterministic strat- (3, 2) from the point on the x axis as well as the point on the y egy is one that corresponds to a shape. axis don’t form ladders. While the ladder from the y axis has seg- ments that go “down” instead of “up”, the ladder from the x axis Proving this conjecture remains open. has segments that go “left” instead of “right”. In the strategy cor- Ladder Shapes: From all strategies that correspond to shapes, if responding to the shape, note that asking questions at points above we wanted to find the best strategy, we can prove that we only need the line y = 2 is redundant, because once we cross y = 2 (i.e., consider the subset of shapes that we call ladder shapes. A ladder 2 Yes answers), we will always reach a Pass point. Similarly, no- shape is formed out of two ladders connected at the decision point. tice that asking questions at points on the right of the line x = 3 We first define a ladder to be a connected sequence of (flat or ver- is redundant. Thus, we can convert this triangular strategy into a tical) segments connecting grid points, such that the flat lines go rectangular strategy with the same error and lower cost simply by “right”, i.e., from a smaller x value to a larger x value, and the ver- pruning the regions to the top and to the right of the decision point, tical lines go “up”, i.e., from a smaller y value to a larger y value. and having termination points earlier. Notice that this corresponds As an example, in Figure 3(c), the sequence of (dashed and solid) to the ladder shape formed by the two dashed ladders (one from (0, segments (0, 2)-(0, 3)-(3, 3)-(3, 6)-(6, 6) forms a ladder, while the 2) to (3, 2) and one from (3, 0) to (3, 2), with the decision point sequence of segments (0, 2)-(0, 5)-(2, 5)-(2, 3)-(3, 3)-(3, 6)-(6, 6) (3, 2)). Thus, the shape (giving the triangular strategy) can be con- is not a ladder because (2, 5) to (2, 3) goes from a larger y value verted into a ladder shape (giving a rectangular strategy) with lower to a smaller y value. As another example, the sequence of solid cost and the same error. 

7 . As another example, consider Figure 3(c). Here the solid blue 3. line represents a shape corresponding to the strategy formed by the E= E(x, y) × [p0 (x, y) + p1 (x, y)] (6) blue, green and red dots. The shape has 10 lines: (0, 2)-(0, 5)-(2, (x,y);x+y≤m 5)-(2, 3)-(3, 3)-(3, 6)-(6, 6) (which is also the decision point), (6, 6)-(6, 2) and so on. Now consider the shape corresponding to the C= C(x, y) × [p0 (x, y) + p1 (x, y)] (7) dashed blue line in the figure. (This shape is the same as the solid (x,y);x+y≤m shape, except for the portion (0, 3) to (3, 3) which bypasses the segment portions (0, 3)-(0, 5)-(2, 5)-(2, 3)-(3, 3), and the portion • The counterpart of the equations in Figure 2 is simpler since (5, 0) to (5, 1) which bypasses the segment portions (6, 0)-(6, 1)- we ask an additional question at (x, y − 1) with probability (5, 1)). Notice that this shape corresponds to a ladder shape (with a(x, y − 1) and at (x − 1, y) with probability a(x − 1, y). one ladder beginning at (0, 2) and ending at (6, 6), and another ∀(x, y); x + y ≤ m : beginning at (5, 0) and ending at (6, 6), with a decision point at p0 (x, y) = e0 · p0 (x, y − 1) · a(x, y − 1) (8) (6, 6)). This ladder shape corresponds to the strategy where there +(1 − e0 ) p0 (x − 1, y) · a(x − 1, y) is a blue point at (1, 3) and a red point at (5, 0). Notice that for the strategy that corresponds to the shape, asking questions at (1, ∀(x, y); x + y ≤ m : 3) and (1, 4) is redundant because the item will “Pass” no matter p1 (x, y) = e1 · p1 (x − 1, y) · a(x − 1, y) (9) what answers we get at (1, 3) and (1, 4). Thus, moving the segment +(1 − e1 ) p1 (x, y − 1) · a(x, y − 1) portion down to (1, 3) and to (5, 0) gives us a ladder shape that • In addition, we have the following constraints: corresponds to a strategy that asks fewer questions to obtain the same result. ∀(x, y); x + y = m : b(x, y) = 1 (10) As yet another example, consider Figure 3(a), in this case, the The constraint above forces the strategy to terminate at m shape corresponding to the solid lines in the figure (with decision questions. point (5, 5)), can be replaced by the ladder shape corresponding to the two ladders (0, 4)-(3, 4) and (3, 0)-(3, 4), with decision point ∀(x, y); x + y ≤ m : a(x, y) + b(x, y) = 1 (11) (3, 4). This constraint simply forces the probabilities of termination Thus, we have shown some examples of how we can convert and continuation at each point on the grid to add up to one. shapes into ladder shapes such that the strategy corresponding to the ladder shape has lower cost than the strategy corresponding to This program is not linear, due to constraints 6, 7, 8 and 9 (all of the shape. which involve a product of two variables). A key technical result of our work is that we can use the Paths Principle (Theorem 3.3) to transform the program into a linear program. 4. PROBABILISTIC STRATEGIES Transformed Program: We introduce a new pair of variables cP ath In this section, we consider probabilistic strategies. Recall that and tP ath to replace p0 , p1 , a, b for every point in the grid. The a probabilistic strategy is again represented in a grid, however, variable cP ath(x, y) corresponds to the (fractional) number of paths each point has a triple (r1 , r2 , r3 ) corresponding to the probability in the strategy from (0, 0) to (x, y) that continue onwards beyond of returning Pass (blue), Fail (red), or Continue asking questions (x, y), while tP ath(x, y) is the number of paths in the strategy that (green). terminate at (x, y). Thus, cP ath(x, y) + tP ath(x, y) represents Since the Paths Principle (Theorem 3.3) also holds for proba- the number of paths reaching (x, y). For instance cP ath(x, y) = 0 bilistic strategies, at least one of r1 or r2 must be 0 at each point implies that all paths reaching (x, y) terminate at (x, y). (x, y). We let a(x, y) = r3 be the probability that we continue to We let S1 (x, y) = s×ex1 ×(1−e1 )y (i.e., the probability that the ask questions at (x, y), and b(x, y) be 1 − a(x, y) = r1 + r2 . (This item satisfies the filter, and we get a given sequence of x no answers is the probability that the strategy terminates at that point.) and y yes answers), and S0 (x, y) = (1 − s) × ey0 × (1 − e0 )x (i.e., We can pose Problem 1 as a set of constraints, where the ob- the probability that the item does not satisfy the filter, and we get jective is to minimize the expected cost C, given a constraint that a given sequence of x no answers and y yes answers). Note that E < τ , along with some additional constraints, which are essen- R(x, y) = S0 (x, y)/(S0 (x, y) + S1 (x, y)). Note also that S0 and tially the counterparts of the equations described in Section 2. S1 are constants. • We have the probabilistic counterpart of Equation 1: The following relationships are immediate: ∀(x, y); x + y ≤ m : p0 (x, y) = S0 (x, y) × (cP ath(x, y) + tP ath(x, y)) (4) E(x, y) = b(x, y) × min(R(x, y), 1 − R(x, y)) (Recall that R(x, y) is defined in Theorem 3.3.) Note that p1 (x, y) = S1 (x, y) × (cP ath(x, y) + tP ath(x, y)) the error at a certain point is simply the probability that the These relationships hold because the probability of getting to a strategy terminates at that point, times the smaller of the two point when the item satisfies the filter (or not) is simply the total error probabilities R(x, y) and 1 − R(x, y) (since the Paths number of paths times the probability of a single path when the Principle tells us that we would always choose whichever of item satisfies the filter (or not). Pass or Fail has lower error probability). Note that R(x, y) Additionally, since the probability a is simply the fraction of is a constant, independent of the strategy. paths that continue beyond (x, y), we have: • The cost at a given point is simply the probability that the strategy terminates at that point times the total number of a(x, y) = cP ath(x, y)/(cP ath(x, y) + tP ath(x, y)) questions asked to get to the point. b(x, y) = tP ath(x, y)/(cP ath(x, y) + tP ath(x, y)) ∀(x, y); x + y ≤ m : C(x, y) = b(x, y) × (x + y) (5) Now we describe how to rewrite the equations in terms of cP ath • The error and cost equations stay the same as equations 2 and and tP ath. 

8 . • Constraints 4, 5, 6 and 7 transform into: T HEOREM 5.2. The best strategy for Problem 4 can be found in O(m2 ). E= tP ath(x, y) × min(S0 (x, y), S1 (x, y)) (x,y);x+y≤m (We can actually compute the best strategy in O(m) if binomial C= tP ath(x, y)(x + y)(S0 (x, y) + S1 (x, y)) expressions involving m can be computed in O(1) time.) Subsequently, we can solve Problem 3 by performing repeated (x,y);x+y≤m doubling of the maximum cost m, until we find a triangular shape (Recall that S0 , S1 are constants, so the constraints are lin- for which E < τ , followed by binary search between the two ear.) In other words, E is precisely the number of paths lead- thresholds m and m/2. Thus, we have the following theorem: ing to the point that terminate at that point, times the smaller of the two error probabilities. The cost C is simply the cost T HEOREM 5.3. The best strategy for Problem 4 can be found for all paths terminating at (x, y) (each such path has proba- in O(m2 log m). bility S0 + S1 ). (We can actually compute the best strategy in O(m log m) if bino- • Constraints 8 and 9 transform into: mial expressions involving m can be computed in O(1) time.) ∀(x, y); x + y ≤ m : cP ath(x, y) + tP ath(x, y) = cP ath(x, y − 1) + cP ath(x − 1, y) 5.3 Problem 5 For Problem 5, we can use the same linear programming formu- In other words, the number of paths into (x, y) are precisely lation as in Section 2.4, except that we constrain C and minimize those that come from (x, y − 1) and (x − 1, y) E. We thus have the following: • We replace constraint 10 with the following, which implies T HEOREM 5.4. The best probabilistic strategy for Problem 5 that no paths go beyond x + y = m. can be found in O(m4 ). ∀(x, y); x + y = m : cP ath(x, y) = 0 • We also have the constraint that there is a single path to 6. MULTIPLE FILTERS (0, 0), i.e. Now, we consider the case when we have independent filters f1 , f2 , . . . , fk , with independent selectivities s1 , s2 , . . . , sk , and cP ath(0, 0) + tP ath(0, 0) = 1 independent error rates e10 , e11 , e20 , e21 , . . . , ek0 , ek1 , where ei0 is the probability that a human answers YES when the item actu- No additional constraints exist. ally does not pass the ith filter, and ei1 is the probability that the Since linear programs can be solved in time quadratic in the human answers NO when the item actually does pass the ith filter. number of variables and constraints, we have the following theo- Note that the multiple filters problem is much harder than the single rem: filter one, since a strategy not only must decide when to continue T HEOREM 4.1 (B EST P ROBABILISTIC S TRATEGY ). The best asking questions, but must also now decide which question to ask probabilistic strategy for Problem 1 can be found in O(m4 ). next (i.e., for what filter). The problem becomes even harder when We denote the algorithm corresponding to the linear program above the filters are correlated, however, we leave it for future work. as linear. We can visualize the multiple filters case as a 2k dimensional grid, where each point (x10 , x11 , x20 , x21 , . . . , xk0 , xk1 ) corre- sponds to the number of NO and YES answers received from hu- 5. OTHER FORMULATIONS mans for each of the filters. (xi0 indicates the number of NO an- 5.1 Problem 2 swers for the ith filter, and xi1 indicates the number of YES an- swers for the ith filter.) For Problem 2, we can show that we simply need to compute In its most general form, the multiple filters problem allows us, R(x, y) for every point in (0, 0) to (m, m), bottom up, and for at any point on this 2k-dimensional grid, to ask a question corre- every point where we find that min(R(x, y), 1 − R(x, y)) < τ , we sponding to any of the k filters. Thus, each point can correspond to make the point a terminating point, returning Fail if R(x, y) ≤ 0.5 “Pass”, “Fail”, or “Ask ith Filter”, where i can be one from 1 . . . k. and Fail otherwise. Using a general form of the Paths Principle (Theorem 3.3), if a In fact, we can actually terminate earlier if we find that p0 and point is a terminating point, we can infer whether it should be a p1 are 0 for all points (x, y) : x + y = m at some m < m. In this Pass or a Fail point. case, we do not need to proceed beyond points along x + y = m . We can in fact represent the problem as a linear program, gener- Note that a feasible strategy that terminates and satisfies E(x, y) < alizing the linear program in Section 4. The counterpart of the vari- τ for every terminating point may not exist. ables tP ath and cP ath are tP ath and cP ath1 , . . . , cP athk , rep- Thus, we have the following theorem: resenting respectively, the number of paths terminating at a given T HEOREM 5.1. The best strategy for Problem 2 can be found point and the number of paths continuing in the direction of each in O(m2 ). of the k filters. Similarly, the total number of paths coming into a point is simply the paths coming in from each of the k directions. 5.2 Problems 3 and 4 T HEOREM 6.1. The best probabilistic strategy for the multiple We begin by considering Problem 4 first. This problem formu- filters version of Problem 5 can be found in O(m4k ). lation is identical to Maximum A-Posteriori (MAP) estimation. In this case we simply ask all m questions (since there is no gain to This algorithm is exponential in the number of filters k, which may asking fewer than m questions). We can estimate the p0 and p1 at not be very large. However, any algorithm whose output is a strat- all points along x + y = m for this triangular strategy. If p0 > p1 , egy using our visualization would need Ω(m2k ), since we need to we return Fail at that point and Pass otherwise. We can then esti- provide a decision for each point in the 2k dimensional cube of size mate the error E over all the terminating points. m2k . It remains to be seen if we can find an optimal or approxi- Thus, we have the following theorem: mately optimal strategy whose representation is smaller. 

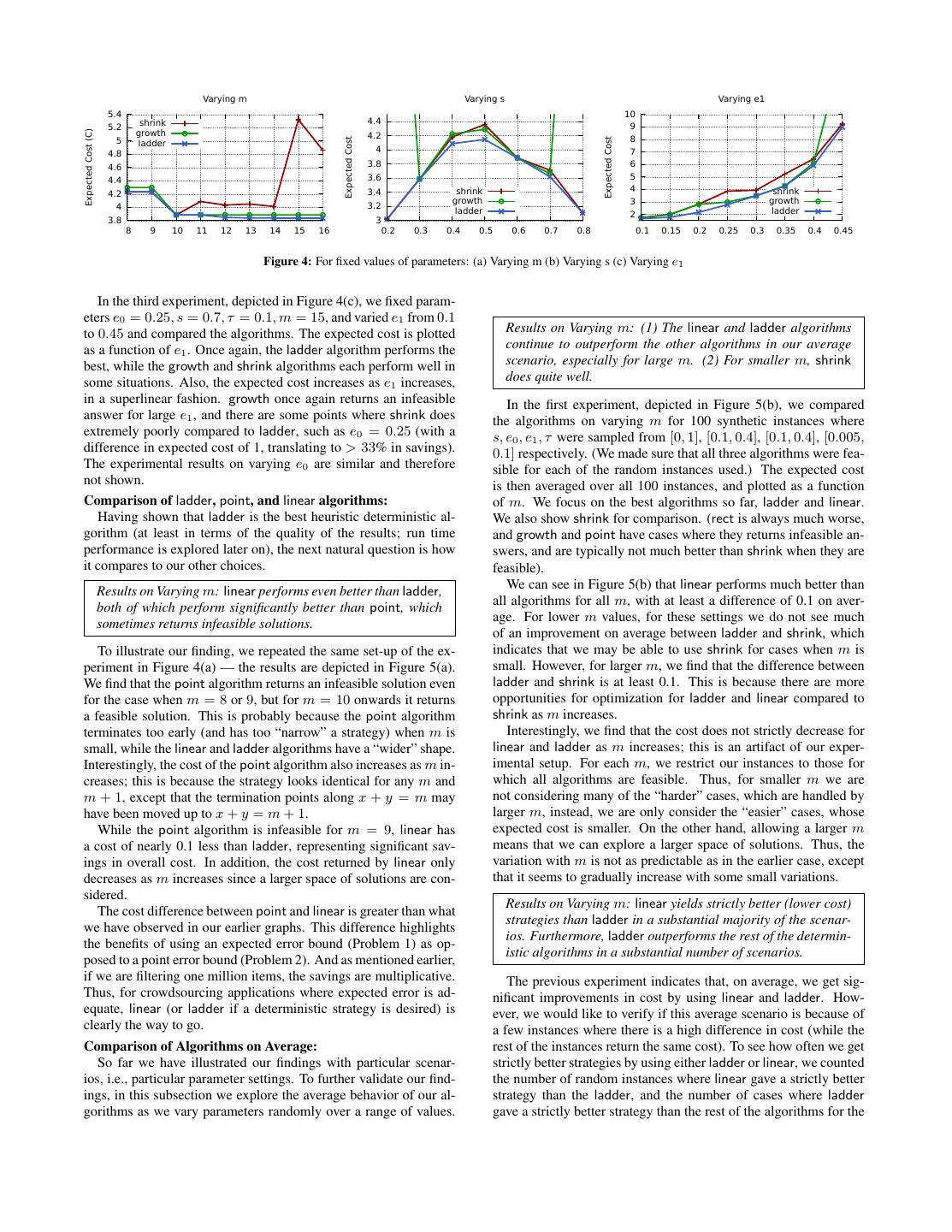
9 .7. EXPERIMENTS rithms return an infeasible solution (i.e., where the error constraint The goal of our experiments is to study the runtime and expected is violated). It can be shown that for all algorithms except growth cost and errors of our algorithms with respect to other naive and and point, either all algorithms return feasible solutions or none approximate algorithms. We continue to focus on Problem 1. of them do. Algorithms growth and point, in addition to failing In our experiments we explored wide ranges of values for our whenever other algorithms fail, also fail in some other cases. parameters m, e0 , e1 , τ, s. In some cases we manually selected the Comparison of Heuristic Deterministic Algorithms: values, to study scenarios that interested us or to study extreme Results on Varying m: ladder results in large cost savings cases in the parameter space. In other cases, we synthetically gener- compared to other heuristic deterministic algorithms, and fur- ated random instances of the parameter values (over given ranges), thermore its cost decreases as m increases to explore the average behavior. Since we do not have space to report all of our results, we only report some representative ones, Figure 4(a) presents the results of an experiment that supports and we explain how they support the findings that we state in boxes this finding. In this scenario, the parameters are s = 0.6, e0 = below. 0.2, e1 = 0.25, τ = 0.05, and m (horizontal axis) is varied from 8 to 16. The vertical axis shows the expected cost C returned by Algorithms: the strategy found by the heuristic deterministic algorithms. For We experimented with the following exact deterministic algo- instance, when m is 14, the cost for ladder is about 3.85 (i.e., we rithms: need around 3.85 questions on average to get the desired expected • naive3: The naive algorithm that considers all 3m strategies. error), growth is about 3.9 and shrink is about 4. The plot for rect • naive2: The naive algorithm that considers all 2m strategies is not shown, but rect is a straight line at about 5.6. (after pruning strategies that violate the Paths Principle). Note that even these small differences in expected cost can re- sult in major cost savings overall. If there are a million items that We also experimented with the following heuristic deterministic need to be filtered, where each question costs 10 cents and m is 14, algorithms: the ladder algorithm results in at least 0.05 ∗ 106 ∗ 0.1 = $5000 • ladder: This algorithm returns the best strategy correspond- of savings over the shrink and growth algorithm, and a whopping ing to a ladder shape. This algorithm always returns a better $100000 of savings over the rect algorithm. deterministic strategy than the heuristic proposed in [9], as While at first one might think that increasing the question limit we will see in Section 8. m will increase the overall cost, observe that in reality the oppo- • growth: This greedy algorithm “grows” a strategy until the site is true for the ladder and rect algorithms. The reason is that constraints are met. It begins with the null strategy at (0, 0) as m increases, the number of shapes available for consideration (i.e., terminate and return Pass or Fail). Then, the algorithm strictly increases, giving the optimizer more choices. The same “pushes the boundary ahead”. In other words, in each itera- cannot be said of the shrink and growth algorithms, since these are tion, the algorithm in turn considers moving each termination both heuristic greedy search algorithms that can get stuck in local point (x, y) to (x + 1, y) and (x, y + 1) and computes the minima. For instance, the cost for shrink increases as m goes from ratio of change in cost to change in error. The algorithm de- 10 to 11, and once again from 14 to 15 in the experiment above. cides to move the termination point that yields the smallest Note also that none of the algorithms give a feasible solution when increase in this ratio. This “pushing” continues until the error m < 8 for the set of constraints. constraint is satisfied. As mentioned earlier, space constraints prevent us from includ- • shrink: This greedy algorithm “shrinks” a strategy until the ing multiple results per finding. The extensive additional experi- cost cannot be decreased any longer. It begins with the tri- ments we performed support all of our findings. angular strategy that asks all m questions, and “pushes the Results on Varying s: growth sometimes gets stuck in local boundary in”. In other words, in each iteration, the algorithm minima; if not, shrink and growth outperform rect. for each terminating point (x, y) in turn, considers adding a terminating point at (x, y −1) or (x−1, y) and computes the Our second experiment, depicted in Figure 4(b), illustrates this ratio of the change in cost to change in error. The algorithm finding. We fixed parameters e0 = 0.2, e1 = 0.25, τ = 0.05, m = decides to add a terminating point that yields the largest in- 10, and varied s from 0.2 to 0.8 and compared the same algorithms crease in this ratio. The “shrinking” continues as long as the as before. The expected cost is plotted as a function of s. For in- error constraint is satisfied. stance, when s is 0.5, the cost for ladder is about 4.15, growth is • rect: This algorithm tries all rectangular strategies that fit in about 4.28, rect (not depicted in figure) is about 5.68 and shrink (m, m). is about 4.35. Once again, ladder performs the best. As expected, In addition, we have the optimal probabilistic algorithm: the cost increases when s is close to 0.5 since that situation is the most uncertain (and therefore we need to ask more questions). Ad- • linear: This algorithm returns the strategy computed by the ditionally, when s < 0.3 or s > 0.7, growth gives an infeasible linear program in Section 4. answer (i.e., it gives a strategy that does not satisfy the constraint Also, we compared our algorithms against the best algorithm for on error) — depicted in the graph as the cost being set to ∞. Since Problem 2. the growth strategy does a local search around the origin, it can get • point: This algorithm ensures that at every termination point, stuck in an infeasible local minimum where the error can no longer E(x, y) < τ . Thus, this algorithm is optimal for Problem 2. be reduced by growing the strategy. The algorithm rect is much When the algorithm cannot find a feasible solution for Prob- worse than the other algorithms with an additional expected cost of lem 2, we modify the solution to ensure that at least the cost at least 1 over the other algorithms. However, it does give a feasible constraint C(x, y) < m is satisfied. That is, for an infeasi- solution when growth does not. ble solution, we add termination points along the boundary x + y = m, if those points are reachable. Results on Varying e1 : Cost increases superlinearly as e1 in- creases for all algorithms. Note that there may be parameters for which some of the algo- 

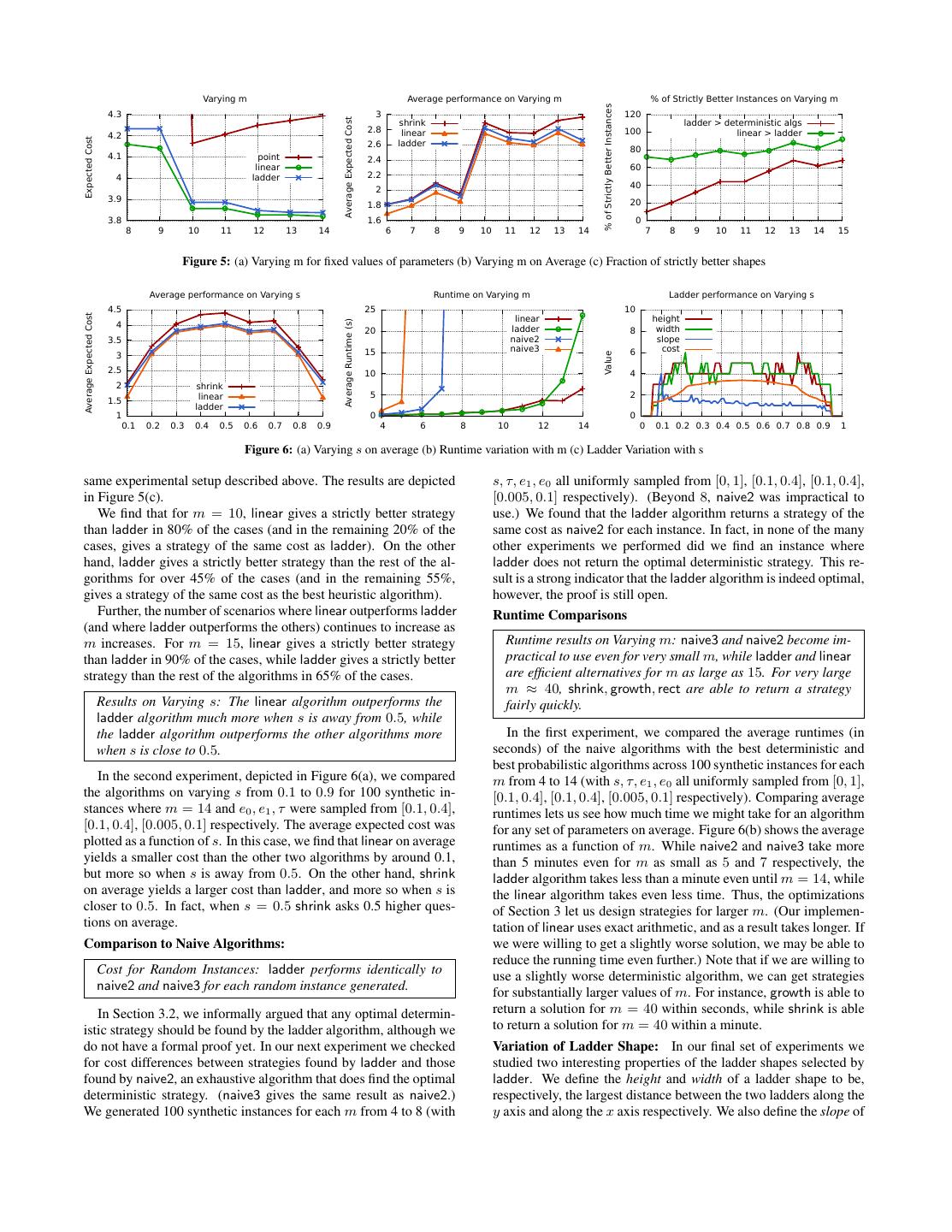
10 . Varying m Varying s Varying e1 5.4 10 shrink 4.4 5.2 9 Expected Cost (C) growth 4.2 5 8 Expected Cost Expected Cost ladder 4 7 4.8 4.6 3.8 6 4.4 3.6 5 3.4 shrink 4 shrink 4.2 growth 3 growth 4 3.2 ladder 2 ladder 3.8 3 8 9 10 11 12 13 14 15 16 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.1 0.15 0.2 0.25 0.3 0.35 0.4 0.45 Figure 4: For fixed values of parameters: (a) Varying m (b) Varying s (c) Varying e1 In the third experiment, depicted in Figure 4(c), we fixed param- eters e0 = 0.25, s = 0.7, τ = 0.1, m = 15, and varied e1 from 0.1 to 0.45 and compared the algorithms. The expected cost is plotted Results on Varying m: (1) The linear and ladder algorithms as a function of e1 . Once again, the ladder algorithm performs the continue to outperform the other algorithms in our average best, while the growth and shrink algorithms each perform well in scenario, especially for large m. (2) For smaller m, shrink some situations. Also, the expected cost increases as e1 increases, does quite well. in a superlinear fashion. growth once again returns an infeasible In the first experiment, depicted in Figure 5(b), we compared answer for large e1 , and there are some points where shrink does the algorithms on varying m for 100 synthetic instances where extremely poorly compared to ladder, such as e0 = 0.25 (with a s, e0 , e1 , τ were sampled from [0, 1], [0.1, 0.4], [0.1, 0.4], [0.005, difference in expected cost of 1, translating to > 33% in savings). 0.1] respectively. (We made sure that all three algorithms were fea- The experimental results on varying e0 are similar and therefore sible for each of the random instances used.) The expected cost not shown. is then averaged over all 100 instances, and plotted as a function Comparison of ladder, point, and linear algorithms: of m. We focus on the best algorithms so far, ladder and linear. Having shown that ladder is the best heuristic deterministic al- We also show shrink for comparison. (rect is always much worse, gorithm (at least in terms of the quality of the results; run time and growth and point have cases where they returns infeasible an- performance is explored later on), the next natural question is how swers, and are typically not much better than shrink when they are it compares to our other choices. feasible). Results on Varying m: linear performs even better than ladder, We can see in Figure 5(b) that linear performs much better than both of which perform significantly better than point, which all algorithms for all m, with at least a difference of 0.1 on aver- sometimes returns infeasible solutions. age. For lower m values, for these settings we do not see much of an improvement on average between ladder and shrink, which To illustrate our finding, we repeated the same set-up of the ex- indicates that we may be able to use shrink for cases when m is periment in Figure 4(a) — the results are depicted in Figure 5(a). small. However, for larger m, we find that the difference between We find that the point algorithm returns an infeasible solution even ladder and shrink is at least 0.1. This is because there are more for the case when m = 8 or 9, but for m = 10 onwards it returns opportunities for optimization for ladder and linear compared to a feasible solution. This is probably because the point algorithm shrink as m increases. terminates too early (and has too “narrow” a strategy) when m is Interestingly, we find that the cost does not strictly decrease for small, while the linear and ladder algorithms have a “wider” shape. linear and ladder as m increases; this is an artifact of our exper- Interestingly, the cost of the point algorithm also increases as m in- imental setup. For each m, we restrict our instances to those for creases; this is because the strategy looks identical for any m and which all algorithms are feasible. Thus, for smaller m we are m + 1, except that the termination points along x + y = m may not considering many of the “harder” cases, which are handled by have been moved up to x + y = m + 1. larger m, instead, we are only consider the “easier” cases, whose While the point algorithm is infeasible for m = 9, linear has expected cost is smaller. On the other hand, allowing a larger m a cost of nearly 0.1 less than ladder, representing significant sav- means that we can explore a larger space of solutions. Thus, the ings in overall cost. In addition, the cost returned by linear only variation with m is not as predictable as in the earlier case, except decreases as m increases since a larger space of solutions are con- that it seems to gradually increase with some small variations. sidered. Results on Varying m: linear yields strictly better (lower cost) The cost difference between point and linear is greater than what strategies than ladder in a substantial majority of the scenar- we have observed in our earlier graphs. This difference highlights ios. Furthermore, ladder outperforms the rest of the determin- the benefits of using an expected error bound (Problem 1) as op- istic algorithms in a substantial number of scenarios. posed to a point error bound (Problem 2). And as mentioned earlier, if we are filtering one million items, the savings are multiplicative. The previous experiment indicates that, on average, we get sig- Thus, for crowdsourcing applications where expected error is ad- nificant improvements in cost by using linear and ladder. How- equate, linear (or ladder if a deterministic strategy is desired) is ever, we would like to verify if this average scenario is because of clearly the way to go. a few instances where there is a high difference in cost (while the Comparison of Algorithms on Average: rest of the instances return the same cost). To see how often we get So far we have illustrated our findings with particular scenar- strictly better strategies by using either ladder or linear, we counted ios, i.e., particular parameter settings. To further validate our find- the number of random instances where linear gave a strictly better ings, in this subsection we explore the average behavior of our al- strategy than the ladder, and the number of cases where ladder gorithms as we vary parameters randomly over a range of values. gave a strictly better strategy than the rest of the algorithms for the 

11 . Varying m Average performance on Varying m % of Strictly Better Instances on Varying m % of Strictly Better Instances 4.3 3 120 Average Expected Cost shrink ladder > deterministic algs 2.8 linear 100 linear > ladder 4.2 Expected Cost 2.6 ladder 80 4.1 point 2.4 linear 60 4 ladder 2.2 40 2 3.9 20 1.8 3.8 1.6 0 8 9 10 11 12 13 14 6 7 8 9 10 11 12 13 14 7 8 9 10 11 12 13 14 15 Figure 5: (a) Varying m for fixed values of parameters (b) Varying m on Average (c) Fraction of strictly better shapes Average performance on Varying s Runtime on Varying m Ladder performance on Varying s 4.5 25 10 Average Expected Cost linear height Average Runtime (s) 4 ladder width 20 8 3.5 naive2 slope 15 naive3 6 cost 3 Value 2.5 10 4 2 shrink linear 5 2 1.5 ladder 1 0 0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 4 6 8 10 12 14 0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1 Figure 6: (a) Varying s on average (b) Runtime variation with m (c) Ladder Variation with s same experimental setup described above. The results are depicted s, τ, e1 , e0 all uniformly sampled from [0, 1], [0.1, 0.4], [0.1, 0.4], in Figure 5(c). [0.005, 0.1] respectively). (Beyond 8, naive2 was impractical to We find that for m = 10, linear gives a strictly better strategy use.) We found that the ladder algorithm returns a strategy of the than ladder in 80% of the cases (and in the remaining 20% of the same cost as naive2 for each instance. In fact, in none of the many cases, gives a strategy of the same cost as ladder). On the other other experiments we performed did we find an instance where hand, ladder gives a strictly better strategy than the rest of the al- ladder does not return the optimal deterministic strategy. This re- gorithms for over 45% of the cases (and in the remaining 55%, sult is a strong indicator that the ladder algorithm is indeed optimal, gives a strategy of the same cost as the best heuristic algorithm). however, the proof is still open. Further, the number of scenarios where linear outperforms ladder Runtime Comparisons (and where ladder outperforms the others) continues to increase as m increases. For m = 15, linear gives a strictly better strategy Runtime results on Varying m: naive3 and naive2 become im- than ladder in 90% of the cases, while ladder gives a strictly better practical to use even for very small m, while ladder and linear strategy than the rest of the algorithms in 65% of the cases. are efficient alternatives for m as large as 15. For very large m ≈ 40, shrink, growth, rect are able to return a strategy Results on Varying s: The linear algorithm outperforms the fairly quickly. ladder algorithm much more when s is away from 0.5, while the ladder algorithm outperforms the other algorithms more In the first experiment, we compared the average runtimes (in when s is close to 0.5. seconds) of the naive algorithms with the best deterministic and best probabilistic algorithms across 100 synthetic instances for each In the second experiment, depicted in Figure 6(a), we compared m from 4 to 14 (with s, τ, e1 , e0 all uniformly sampled from [0, 1], the algorithms on varying s from 0.1 to 0.9 for 100 synthetic in- [0.1, 0.4], [0.1, 0.4], [0.005, 0.1] respectively). Comparing average stances where m = 14 and e0 , e1 , τ were sampled from [0.1, 0.4], runtimes lets us see how much time we might take for an algorithm [0.1, 0.4], [0.005, 0.1] respectively. The average expected cost was for any set of parameters on average. Figure 6(b) shows the average plotted as a function of s. In this case, we find that linear on average runtimes as a function of m. While naive2 and naive3 take more yields a smaller cost than the other two algorithms by around 0.1, than 5 minutes even for m as small as 5 and 7 respectively, the but more so when s is away from 0.5. On the other hand, shrink ladder algorithm takes less than a minute even until m = 14, while on average yields a larger cost than ladder, and more so when s is the linear algorithm takes even less time. Thus, the optimizations closer to 0.5. In fact, when s = 0.5 shrink asks 0.5 higher ques- of Section 3 let us design strategies for larger m. (Our implemen- tions on average. tation of linear uses exact arithmetic, and as a result takes longer. If Comparison to Naive Algorithms: we were willing to get a slightly worse solution, we may be able to reduce the running time even further.) Note that if we are willing to Cost for Random Instances: ladder performs identically to use a slightly worse deterministic algorithm, we can get strategies naive2 and naive3 for each random instance generated. for substantially larger values of m. For instance, growth is able to In Section 3.2, we informally argued that any optimal determin- return a solution for m = 40 within seconds, while shrink is able istic strategy should be found by the ladder algorithm, although we to return a solution for m = 40 within a minute. do not have a formal proof yet. In our next experiment we checked Variation of Ladder Shape: In our final set of experiments we for cost differences between strategies found by ladder and those studied two interesting properties of the ladder shapes selected by found by naive2, an exhaustive algorithm that does find the optimal ladder. We define the height and width of a ladder shape to be, deterministic strategy. (naive3 gives the same result as naive2.) respectively, the largest distance between the two ladders along the We generated 100 synthetic instances for each m from 4 to 8 (with y axis and along the x axis respectively. We also define the slope of 

12 .a ladder shape to be the ratio of the y coordinate to the x coordinate most “informed” worker is asked for a label on the fly on the most of the decision point. Since there is no counterpart to ladders and uncertain item [10, 11], and the accuracy of the worker is learned decision points in the strategies output by linear, we cannot study as labels are obtained. Other work [18, 6] considers a setting where them in this way. the worker’s labels are provided beforehand, and the goal is to infer the labels of items and the accuracy of different workers. Results on Varying s: The optimal ladder shape for ladder has None of the previous studies deal with the problem of optimizing a decision point closer to the y axis (larger slope) when s is the number of questions asked to the crowd. In large-scale human small and closer to the x axis (smaller slope) when s is large. computation, especially in marketplaces such as Mechanical Turk, In addition, the closer s is to 0.5, the further away the decision this metric is the most critical cost factor that needs to be optimized. point of the ladder shape is from the origin. In our work so far we have not taken into account knowledge of or We fix e1 = 0.2, e0 = 0.2, τ = 0.05, m = 12, and vary s in discrepancies in worker accuracies, assuming a rapidly changing increments of 0.005 from 0 until 1. The results are depicted in Fig- and replaceable worker pool (as in Mechanical Turk). As future ure 6(c). We find that the slope of the optimal ladder shape moves work we will explore incorporating worker accuracy into our theory from 4 all the way down to 0 gradually as we increase s. (Note that and algorithms. we set slope = 0 when the strategy is simply a terminating point Filtering Applications: Several practical applications have used at the origin.) This result can be explained as follows: When s is heuristic strategies for filtering, typically a majority vote over a very small, it is unlikely that we will get any YES answers, so more fixed number of workers, in the context of sentiment analysis and questions need to be asked to verify that an item actually passes the NLP tasks [15], categorization of URLs [3], search result evalua- filter, but not when the item does not pass the filter. On the other tion [2], and evaluation of competing translations [20]. In fact, for hand, when s is large, it is unlikely that we will get any NO an- all these strategies (which correspond to the triangular strategy de- swers, so more questions are needed to ascertain whether an item scribed earlier), we can replace them with an equivalent rectangular fails the filter. Note that cost increases until 0.5 and then decreases, strategy with much lower cost and the same answers. If the ladder as expected. Height and width are mirror images of each other or linear algorithms are used, the cost can be reduced even further. across x = 0.5: this is expected since e0 = e1 , thus the best shape Statistical Hypothesis Testing: Our problem is also related to the for s is the best shape for 1 − s. field of Statistical Hypothesis Testing [19]. This field is concerned with the problem of trying to estimate whether a certain hypoth- 8. RELATED WORK esis is true or not given the observed data. One such method of The work related to our paper falls under four categories: crowd- estimation is to compute the LR (Likelihood Ratio), i.e., the ratio sourced schema matching, active learning, filtering applications, of the probability that a given hypothesis is true given the data to and statistical hypothesis testing. the probability that an alternative hypothesis is true given the same data. Subsequently the LR is checked to see if it is statistically sig- Crowdsourced schema matching: Recent work by McCann et. nificant. In our case, our two hypotheses (for a given data item) al. [9] has considered the problem of using crowdsourcing for schema are simply whether or not the item satisfies the filter. Unlike typi- matching. The core of the problem is similar: the crowd provides cal applications of hypothesis testing, where the goal is to estimate noisy answers, and the goal is to determine whether a match is true the parameters of some distribution, here the distribution is pro- or not. The strategy used is the following: ask at least v1 ques- vided to us (i.e., that the item satisfies the filter with probability s). tions, and stop either when the difference between the number of For Problem 2, in fact, our algorithm computes the LR to see if it is YES and NO answers reaches a certain threshold δ, or when the greater than the threshold (τ ) for all reachable points. However, the total number of questions asked is v2 . The authors prove prob- hypothesis testing techniques do not help us address the problem of abilistic bounds on the maximum error from this strategy, under minimizing overall cost while testing a large set of data items. specific assumptions for the performance of human workers. The proposed strategy can be mapped to a shape in our framework. In fact, we can convert the shape into a ladder shape (as described in 9. CONCLUSION Section 3.2), and obtain a new strategy that asks fewer questions We studied the problem of optimizing filtering of data using hu- while providing the same error guarantees. Moreover, since [9] mans. Our optimal and heuristic algorithms efficiently find fil- does not optimize for the number of questions, our cost-optimized tering strategies that result in significant cost savings relative to algorithms can provide even further improvements. commonly-used strategies in crowdsourcing applications. Active Learning: The field of active learning [16] addresses the We focused our presentation primarily on the single-filter prob- problem of actively selecting training data to ask an “oracle” (for lem. Our current solution to the multiple-filters problem is opti- instance, the oracle could be an expert user) that would help train mal, but has a large blow-up in representation; we hope to find a a classifier with the least error. Our metric for error (i.e., expected more compact representation. Other future work includes incorpo- error) is the same as the 0-1 loss used in machine learning. rating human accuracy, handling correlations between filters in the Typical papers studying active learning do not assume that the multiple-filters case, extending our techniques for the categoriza- oracle makes mistakes, and in any case, repeating the same question tion and clustering problems, and attempting to resolve the open to the oracle would typically not help. However, there are some question of whether shapes are optimal for deterministic strategies. papers that do consider the case when many interchangeable noisy humans can be used as oracles, and we discuss them next. 10. REFERENCES [1] Mechanical Turk. http://mturk.com. Sheng et. al. [17] consider the problem of obtaining labels for [2] Omar Alonso, Daniel E. Rose, and Benjamin Stewart. training data in the context of machine learning. Specifically, the Crowdsourcing for relevance evaluation. SIGIR Forum, 42, 2008. problem is whether to ask for another label for an existing data [3] E. Bakshy et. al. Everyone’s an influencer: quantifying influence on item or whether to acquire more data items, in order to maximize twitter. In WSDM, 2011. the utility of the training data set for the machine learning algo- [4] M. J. Franklin, D. Kossmann, T. Kraska, S. Ramesh, and R. Xin. rithm. Similar work has considered a pool of workers where the Crowddb: answering queries with crowdsourcing. In SIGMOD, 2011. 

13 . [5] G. Little et. al. Turkit: tools for iterative tasks on mechanical turk. In sect the shape. (The decision point may need to be moved if it is HCOMP, 2009. unreachable.) After this procedure, we may assume that the x-path [6] J. Whitehill et. al. Whose vote should count more: Optimal now has segments that go right, upwards or to the left, while the integration of labels from labelers of unknown expertise. In NIPS. y-path now has segments that go right, upwards and downwards. 2009. (Essentially all that we are saying is that for every shape with these [7] A. Marcus, E. Wu, D. Karger, S. Madden, and R. Miller. Crowdsourced databases: Query processing with people. In CIDR, unreachable portions, there is another shape without it, with same 2011. cost.) This also means that for a given y value there is a single point [8] A. Marcus, E. Wu, D. Karger, S. Madden, and R. Miller. on the x-path, and for a given x value, there is a single point on the Demonstration of qurk: a query processor for human operators. In y-path. SIGMOD, 2011. Step 2: Pruning Redundant Regions: We now convert both x- [9] Robert McCann, Warren Shen, and AnHai Doan. Matching schemas in online communities: A web 2.0 approach. In ICDE ’08. path and y-path into ladders. We describe our algorithm for the [10] P. Donmez et. al. Efficiently learning the accuracy of labeling sources x-path, the algorithm for the y-path follows similarly. (As we de- for selective sampling. In KDD, 2009. scribe the algorithm, we also provide an informal explanation as to [11] P. Perona P. Welinder. Online crowdsourcing: rating annotators and why it works.) The algorithm is essentially a scan along the x axis obtaining cost-effective labels. In CVPR, 2010. that incrementally builds the ladder. [12] A. Parameswaran, A. Das Sarma, H. Garcia-Molina, N. Polyzotis, We begin at x = 0, and scan the points corresponding to the x- and J. Widom. Human-assisted graph search: it’s okay to ask path for the given x coordinate. For some x = xi , we may find that questions. Proc. VLDB Endow., 4:267–278, February 2011. there are some points along the x-path that have the x coordinate [13] A. Parameswaran and N. Polyzotis. Answering queries using set to xi . Find one such point which has the largest such y (say yi ). humans, algorithms and databases. In CIDR, 2011. Now, we add the portion (xi , 0) − (xi , yi ) to the ladder. We can [14] Alexander J. Quinn and Benjamin B. Bederson. Human computation: do this because no matter what answers we get to the questions to a survey and taxonomy of a growing field. In CHI, 2011. [15] R. Snow et. al. Cheap and fast—but is it good?: evaluating the right of (xi , 0), with a y coordinate less than yi , we will always non-expert annotations for natural language tasks. In EMNLP, 2008. end at a Fail terminating point. Now, we ignore the x-path portion [16] Burr Settles. Active learning literature survey. Computer Sciences below y = yi . (We can effectively assume that we moved the x Technical Report 1648, University of Wisconsin–Madison, 2009. axis to y = yi (and the origin to (xi , yi )). We now repeat the same [17] V. S. Sheng, F. Provost, and P. Ipeirotis. Get another label? procedure. Let us say the next x coordinate for which we find an improving data quality and data mining using multiple, noisy x-path point is x = xj . We add (xi , yi ) − (xj , yi ) to the ladder. labelers. In SIGKDD, pages 614–622, 2008. Let the point on x-path with the largest y value at xj be yj . We [18] V. Raykar et. al. Supervised learning from multiple experts: whom to then add (xj , yi ) − (xj , yj ) to the ladder. Subsequently, we ignore trust when everyone lies a bit. In ICML, 2009. all x-path points below yj . [19] Larry Wasserman. All of Statistics. Springer, 2003. In other words, for each x value, we always add a segment that [20] Omar F. Zaidan and Chris Callison-Burch. Feasibility of human-in-the-loop minimum error rate training. In EMNLP, 2009. connects the ladder to the ladder until x − 1, and optionally a seg- ment that goes from a smaller y value to a larger y value. We keep APPENDIX building the ladder until we hit the decision point. Note that the decision point is the point on the x-path with the largest y coordi- A. CONVERSION ALGORITHM nate, thus we will always hit it. In this manner, we maintain the Our algorithm proceeds in two steps: First, we prune unreach- invariant that all points to the right of the ladder being constructed able regions. Second, we prune redundant regions. are all points on x-path, and not on y-path. (Note that there cannot be any points on the y-path to the right of this ladder apart from Step 1: Pruning Unreachable Regions: We define y-path to be the decision point because otherwise we will violate the property the sequence of lines leading to the decision point from the point that the shape has no unreachable regions.) Thus, we ensure that if on the y axis in the shape (and including the decision point), and x- we ever reach a point on the lower ladder, we are sure to end at a path to be the sequence of lines leading to the decision point from x-path point and not an y-path point. the point on the x axis in the shape (and including the decision Similarly, we build the upper ladder corresponding to the y-path. point). We begin by pruning some of the the unreachable portions Here the invariant being maintained is that all points above this from the shape. Notice that if the x-path ever goes “down”, we can ladder must be y-path points. The decision point is then the point instead add a segment that goes “right” until we once again inter- on the y-path that has the largest x coordinate. The two ladders sect the shape. Additionally, if the y-path ever goes “left” we can meet at the decision point. instead add a segment that goes upwards until we once again inter-