Query by Output

1 . Query by Output Quoc Trung Tran Chee-Yong Chan Srinivasan Parthasarathy∗ National University of Singapore The Ohio State University {tqtrung, chancy}@comp.nus.edu.sg srini@cse.ohio-state.edu ABSTRACT 1. INTRODUCTION It has recently been asserted that the usability of a database A perennial challenge faced by many enterprises is the is as important as its capability. Understanding the database management of their increasingly large and complex databases schema, the hidden relationships among attributes in the which can contain hundreds and even thousands of tables data all play an important role in this context. Subscribing [10, 23]. The problem is exacerbated by the fact that the to this viewpoint, in this paper, we present a novel data- metadata and documentation for these databases are often driven approach, called Query By Output (QBO), which can incomplete or missing [11]. Several different approaches have enhance the usability of database systems. The central goal been proposed to address this important practical issue. One of QBO is as follows: given the output of some query Q example here is database structure mining where the goal on a database D, denoted by Q(D), we wish to construct an is to discover structural relationships among the database alternative query Q such that Q(D) and Q (D) are instance- tables [1, 11, 23]. Another example is intensional query an- equivalent. To generate instance-equivalent queries from swering where the goal is to augment query answers with Q(D), we devise a novel data classification-based technique additional information to help users understand the results that can handle the at-least-one semantics that is inherent in as well as relevant database content [15]. the query derivation. In addition to the basic framework, we In this paper, we present a novel data-driven approach design several optimization techniques to reduce processing called Query by Output (QBO). QBO aims to derive interest- overhead and introduce a set of criteria to rank order out- ing query-based characterizations of an input database table put queries by various notions of utility. Our framework is which can be the result of some query or materialized view. evaluated comprehensively on three real data sets and the In contrast to conventional querying which takes an input results show that the instance-equivalent queries we obtain query Q and computes its output, denoted by Q(D), w.r.t. are interesting and that the approach is scalable and robust an input database D, the basic idea of QBO is to take as to queries of different selectivities. input the output Q(D) of some query Q and compute a set of queries Q1 , · · · , Qn such that each Qi (D) is (approxi- mately) equivalent to Q(D). We say that two queries Q and Categories and Subject Descriptors Q are instance-equivalent w.r.t. a database D (denoted by H.2.4 [System]: Query processing; H.2.8 [Database Ap- Q ≡D Q ), if Q(D) and Q (D) are equivalent. plications]: Data mining Before we discuss the specific contributions of this paper, we briefly highlight some of the use-case scenarios of our proposal. General Terms QBO Applications. The most obvious application of QBO is Algorithms, Design in conventional database querying where Q is known. Con- sider the scenario when a user submits a query Q to be evalu- ated on a database D. Instead of simply returning the query Keywords result Q(D) to the user, the database system can also apply query by output, instance-equivalent queries, at-least-one QBO to compute additional useful information about Q and D semantics in the form of instance-equivalent queries. Besides provid- ∗ ing alternative characterizations (potential simplifications) This work was done when the author was on sabbatical at of Q(D), IEQs can also help users to better understand the the National University of Singapore (NUS) in 2008. database schema. Specifically, since many enterprise data schema are very complex and large, potentially involving hundreds and even thousands of relations [23], the part of the database schema that is referenced by the user’s query Permission to make digital or hard copies of all or part of this work for may be quite different from that referenced by an IEQ. The personal or classroom use is granted without fee provided that copies are not made or distributed for profit or commercial advantage and that copies discovery of this alternative “path” in the schema to generate bear this notice and the full citation on the first page. To copy otherwise, to an instance-equivalent query can aid the user’s understand- republish, to post on servers or to redistribute to lists, requires prior specific ing of the database schema or potentially help refine the permission and/or a fee. user’s initial query. SIGMOD’09, June 29–July 2, 2009, Providence, Rhode Island, USA. Another obvious application of QBO is that it can help Copyright 2009 ACM 978-1-60558-551-2/09/06 ...$5.00. 535 

2 .the user better understand the actual data housed within Theorem 1. Given an input query Q, we define QBOS the database. Unusual or surprising IEQs can be useful for to be the problem to find the output query Q where Q is a uncovering hidden relationships among the data. In several conjunctive query that involves only projection and selection instances simpler or easier to understand relationships may (with predicates in the form “Ai op c”, Ai is an attribute, be uncovered which can again aid in the understanding of c is constant and op ∈ {<, ≤, =, =, >, ≥}) such that (1): the data contained within the complex database and help Q (D) ≡D Q(D) and (2) the number of operators (AND, the user refine future queries posed to the database. OR and NOT) used in the selection condition is minimized. QBO may also have interesting applications in database se- Then QBOS is unlikely to be in P . curity where attackers who have some prior domain knowl- edge of the data may attempt to derive sensitive informa- Proof Sketch: We prove Theorem 1 by reducing the Min- tion. For example, if an attacker is aware of the existing imization Circuit Size Problem to QBOS . Details are given correlation structure in the data, they can easily use this in- in [20]. ✷ formation to formulate two or more separate queries which on paper look very different (e.g. using different selection Theorem 2. Given an input query Q, we define QBOG criteria) but in reality may be targeting the same set of tu- to be the problem to find an output query Q such that Q (D) ≡D ples in the database. Such sets or groups of queries can Q(D) and Q can contain arbitrary arithmetic expressions in potentially be used to reverse-engineer the privacy preserv- the select-clause. Then QBOG is PSPACE-hard. ing protocol in use. Subsequently, sensitive information can be gleaned. As a specific example, consider a protocol such Proof Sketch: We prove Theorem 2 by reducing the Inte- as -diversity [24] which relies on detecting how similar the ger Circuit Evaluation Problem to QBOG . Details are given current query is with a previous set of queries (history) an- in [20]. ✷ swered by the database, to determine if the current query Given the above results, in this paper, we consider re- can be answered without violating the privacy constraints. lational queries Q where the select-clause refer to only at- The notion of similarity used by such methods relies primar- tributes (and not to constants or arithmetic/aggregation/string ily on the selection attributes and thus such protocols will expressions) to ensure that Q can be derived efficiently from fail to recognize IEQs that use different selection attributes. Q(D). We also require that Q(D) = ∅ for the problem to be Privacy in such protocols will then be breached. Automat- interesting. ically recognizing such IEQs via the methods proposed in For simplicity, our approach considers only select-project- this paper and subsequently leveraging this information to join (SPJ) queries for Q where all the join predicates in Q enhance such protocols may provide more stringent protec- are foreign-key joins. Thus, our approach requires only very tion against such kinds of attacks. basic database integrity constraint information (i.e., primary Another important class of QBO applications is in scenar- and foreign key constraints). Based on the knowledge of ios where the input consists of Q(D) but not Q itself. Such the primary and foreign key constraints in the database, the scenarios are common in data analysis and exploration appli- database schema can be modeled as a schema graph, denoted cations where the information provided is often incomplete: by SG, where each node in SG represents a relation, and the data set Q(D), which is produced by some query/view each edge between two nodes represents a foreign-key join Q, is available but not the query/view [11]. The ability between the relations corresponding to the nodes. to reverse engineer Q from Q(D) then becomes important. For ease of presentation and without loss of generality, Annotating data with relevant metadata is essential in cu- we express each Q as a relational algebra expression. To rated databases [6]. Such reverse engineering is also useful keep our definitions and notations simple and without loss for generating concise query-based summaries of groups of of generality, we shall assume that there are no multiple tuples of interest to the user (e.g., dominant tuples selected instances of a relation in Q and Q . by skyline queries [4]). Running Example. In this paper, we use a database hous- Contributions. In this paper, we introduce the novel prob- ing baseball statistics1 for our running example as well as lem of QBO and propose a solution, TALOS, that models the in our experiments. Part of the schema is illustrated in QBO problem as a data classification task with a unique prop- Figure 1, where the key attribute names are shown in bold. erty that we term at-least-one semantics. To handle data The Master relation describes information about each player classification with this new semantics, we develop a new (identified by pID): the attributes name, country, weight, dynamic class labeling technique and also propose effective bats, and throws refer to his name, birth country, weight (in optimization techniques to efficiently compute IEQs. Our pounds), batting hand (left, right, or both), and throwing experimental evaluation of TALOS demonstrates its efficiency hand (left or right), respectively. The Batting relation pro- and effectiveness in generating interesting IEQs. vides the number of home runs (HR) of a player when he was playing for a team in a specific year and season (stint). 2. OVERVIEW OF OUR APPROACH The Team relation specifies the rank obtained by a team for a specified year. The QBO problem takes as inputs a database D, an op- tional query Q, and the query’s output Q(D) (w.r.t. D) Notations. Given a query Q, we use rel(Q) to denote and computes one or more IEQs Q , where Q and Q are the collection of relations involved in Q (i.e., relations in IEQs if Q(D) ≡D Q (D). We refer to Q as the input query, SQL’s from-clause); proj(Q) to denote the set of projected Q(D) as the input result, and Q as the output query. attributes in Q (i.e., attributes in SQL’s select-clause); and First, let us state the following theoretical results that we sel(Q) to denote the set of selection predicates in Q (i.e., have established for variants of the QBO problem. conditions in SQL’s where-clause). 1 http://baseball1.com/statistics/ 536 

3 . pID year stint team HR pID name country weight bats throws P1 2001 2 PIT 40 P1 A USA 85 L R P1 2003 2 ML1 50 team year rank P2 B USA 72 R R P2 2001 1 PIT 73 PIT 2001 7 P3 C USA 80 R L P2 2002 1 PIT 40 PIT 2002 4 P4 D Germany 72 L R P3 2004 2 CHA 35 CHA 2004 3 P5 E Japan 72 R R P4 2001 3 PIT 30 P5 2004 3 CHA 60 (a) Master (b) Batting (c) Team Figure 1: Running Example: Baseball Data Set D 2.1 Instance-Equivalent Queries (IEQs) Strong & weak IEQs. Consider two IEQs Q and Q (w.r.t. Our basic definition of instance-equivalent queries (IEQs) a database D); i.e., Q(D) ≡D Q (D). We say that Q and Q requires that the IEQs Q and Q produce the same output are strong IEQs if Q has a set of core relations S such that (w.r.t. some database D); i.e., Q(D) ≡D Q (D). The advan- (1) Q S is a core query of Q , and (2) QS (D) and Q S (D) tage of this simple definition is that it does not require the are equivalent. IEQs that are not strong are classified as knowledge of Q to derive Q , which is particularly useful for weak IEQs. QBO applications where Q is either missing or not provided. The strong IEQ definition essentially requires that both However, there is a potential “accuracy” tradeoff that arises Q and Q share a set of core relations such that Q(D) and from the simplicity of this weak form of equivalence: an IEQ Q (D) are projected from the same set of selected tuples may be “semantically” quite different from the input query from these core relations. Thus, in Example 1, Q1 and Q2 that produced Q(D) as the following example illustrates. are strong IEQs whereas Q1 and Q3 are weak IEQs. Note that in our definition of strong IEQ, we only impose Example 1. Consider the following three queries on the moderate restrictions on Q and Q (relative to the weak IEQ baseball database D in Figure 1: definition) so that the space of strong IEQs is not overly con- Q1 = πcountry (σbats=“R”∧throws=“R”(M aster)), strained and that the strong IEQs generated are hopefully Q2 = πcountry (σbats=“R”∧weight≤72 (M aster)), and both interesting as well as meaningful. Q3 = πcountry (σbats=“R”(M aster)). As in the case with weak IEQs, two strong IEQs can in- Observe that although all three queries produce the same volve different sets of relations. As an example, suppose output after projection ({USA,Japan}), only Q1 and Q2 se- query Q selects pairs of records from two core relations, Sup- lect the same set of tuples {P 2, P 5} from R. Specifically, if plier and Part, that are related via joining with a (non-core) we modify the queries by replacing the projection attribute Supply relation. Then it is possible for a strong IEQ Q to “country” with the key attribute “pID”, we have Q1 (D) = relate the same pair of core relations via a different relation- {P2,P5}, Q2 (D) = {P2,P5} and Q3 (D) = {P2,P3,P5}. ship (e.g., by joining with a different non-core Manufacture Thus, while all three queries are IEQs, we see that the equiv- relation). alence between Q1 and Q2 is actually “stronger” (compared We believe that each of the various notions of query equiv- to that between Q1 and Q3 ) in that both queries actually alence has useful applications in different contexts depending select the same set of relation tuples. ✷ on the available type of information about the input query and database. At one extreme, if both Q and the database However, if Q is provided as part of the input, then we integrity constraints are available, we can compute semanti- can define a stronger form of instance equivalence as sug- cally equivalent queries. At the other extreme, if only Q(D) gested by the above example. Intuitively, the stricter form and the database D are available, we can only compute weak of instance equivalence not only ensures that the instance- IEQs. Finally, if both Q and the database D are available, equivalent queries produce the same output (w.r.t. some we can compute both weak and strong IEQs. database D), but it also requires that their outputs be pro- Precise & approximate IEQs. It is also useful to per- jected from the same set of “core” tuples. We now formally mit some perturbation so as to include IEQs that are “close characterize weak and strong IEQs based on the concepts of enough” to the original. Perturbations could be in the form core relations and core queries. of extra records or missing records or a combination thereof. Core relations. Given a query Q, we say that S ⊆ rel(Q) Such generalizations are necessary in situations where there is a set of core relations of Q if S is a minimal set of relations are no precise IEQs and useful for cases where the computa- such that for every attribute Ri .A ∈ proj(Q), (1) Ri ∈ S or tional cost for finding precise IEQs is considered unaccept- (2) Q contains a chain of equality join predicates “Ri .A = ably high. Moreover, a precise IEQ Q might not always pro- · · · = Rj .B” such that Rj ∈ S. vide insightful characterizations of Q(D) as Q could be too Intuitively, a set of core relations of Q is a minimal set “detailed” with many join relations and/or selection predi- of relations in Q that “cover” all the projected attributes in cates. Q. As an example, if Q = πR1 .X σp (R1 × R2 × R3 ) where The imprecision of a weak IEQ Q of Q (w.r.t. D) can be p = (R1 .X = R3 .Y ) ∧ (R2 .Z = R3 .Z), then Q has two sets quantified by |Q(D)−Q (D)| + |Q (D)−Q(D)|; the impreci- of core relations, {R1 } and {R3 }. sion of a strong IEQ can be quantified similarly. Thus, Q is Core queries. Given a query Q where S ⊆ rel(Q), we use considered an approximate (strong/weak) IEQ of Q if its im- QS to denote the query that is derived from Q by replacing precision is positive; otherwise, Q is a precise (strong/weak) proj(Q) with the key attribute(s) of each relation in S. If S IEQ. is a set of core relations of Q, we refer to QS as a core query As the search space for IEQs can be very large, particu- of Q. larly with large complex database schema where each rela- 537 

4 .tion has foreign-key joins with other relations, users should πL (J1 ) ⊆ Q(D) and πL (J0 ) ∩ Q(D) = ∅. For the purpose of be able to restrict the search space by specifying hints/ pref- deriving sel(Q ), one simple approach to classify the tuples erences in the form of control parameters. Some examples in J is to label the tuples in J0 , which do not contribute include: (1) restricting Q to be conjunctive queries, (2) set- to the query’s result Q(D), as negative tuples, and label the ting an upper bound on the number of selection predicates tuples in J1 as positive tuples. in Q , (3) setting an upper bound on the number of relations Given the labeled tuples in J, the problem of finding a in Q , (4) specifying a specific set of relations to be included sel(Q ) can now be viewed as a data classification task to (excluded) in (from) Q , and (5) specifying a specific set of separate the positive and negative tuples in J: sel(Q ) is attributes to be included (excluded) in (from) the selection given by the selection conditions that specify the positive predicates in Q . In addition to these query-specific con- tuples. A natural solution is to examine if off-the-shelf data trols, some method-specific controls can also be applied on classifier can give us what we need. To determine what kind the IEQs search space; we discuss some of these in Section 4. of classifier to use, we must consider what we need to gener- We note although all the above user hints can be easily in- ate our desired IEQ Q . Clearly, the classifier should be effi- corporated into our proposed algorithms, we do not delve cient to construct and the output should be easy to interpret on these control knobs any further in the paper but instead and express using SQL; i.e., the output should be express- focus on the core problem of computing IEQs. ible in axis parallel cuts of the data space. These criteria rule out a number of classifier systems such as neural net- 2.2 TALOS: Conceptual Approach works, k-nearest neighbor classification, Bayesian classifiers, In this section, we give a conceptual overview of our ap- and support vector machines [16]. Rule based classifiers or proach, named TALOS (for Tree-based classifier with At Least decision trees (a form of rule-based classifier) are a natural One Semantics), for the QBO problem. solution in this context. TALOS uses decision tree classifier Given an input result Q(D), to generate a SPJ Q that for generating sel(Q ). is an IEQ of Q, we need to basically determine the three We now briefly describe how a simple binary decision tree components of Q : rel(Q ), sel(Q ), and proj(Q ). Clearly, is constructed to classify a set of data records D. For ex- if rel(Q ) contains a set of core relations of Q, then proj(Q ) pository simplicity, assume that all the attributes in D have can be trivially derived from these core relations2 . Thus, the numerical domains. A decision tree DT is constructed in a possibilities for Q depends mainly on the options for both top-down manner. Each leaf node N in the tree is associ- rel(Q ) and sel(Q ). Between these two components, enu- ated with a subset of the data records, denoted by DN , such merating different rel(Q ) is the easier task as rel(Q ) can that D is partitioned among all the leaf nodes. Initially, DT be obtained by choosing a subgraph G of the schema graph has only a single leaf node (i.e., its root node) which is as- SG such that G contains a set of core relations of Q: rel(Q ) sociated with all the records in D. Leaf nodes are classified is then given by all the relations represented in G. Note that into pure and non-pure nodes depending on a given good- it is not necessary for rel(Q) ⊆ rel(Q ) as Q may contain ness criterion. Common goodness criteria include entropy, some relations that are not core relations. The reason for ex- classification error and the Gini index [16]. At each iteration ploring different possibilities for rel(Q ) is to find interesting of the algorithm, the algorithm examines each non-pure leaf alternative characterizations of Q(D) that involve different node N and computes the best split for N that creates two join paths or selection conditions from those in Q. TALOS child nodes, N1 and N2 , for N . Each split is computed as a enumerates different schema subgraphs by starting out with function of an attribute A and a split value v associated with minimal subgraphs that contain a set of core relations of Q the attribute. Whenever a node N is split (w.r.t. attribute and then incrementally expanding the minimal subgraphs to A and split value v), the records in DN are partitioned be- generate larger, more complex subgraphs. tween DN1 and DN2 such that a tuple t ∈ DN is distributed We now come to most critical and challenging part of our into DN1 if t.A ≤ v; and DN2 , otherwise. solution which is how to generate “good” sel(Q )’s such that A popular goodness criterion for splitting, the Gini index, each sel(Q ) is not only succinct (without too many con- is computed as follows. For a data set S with k distinct ditions) and insightful but also minimizes the imprecision classes, its Gini index is Gini(S) = 1 − kj=1 (fj2 ) where between Q(D) and Q (D) if Q is an approximate IEQ. We fj denote the fraction of records in S belonging to class j. propose to formulate this problem as a data classification Thus, if S is split into two subsets S1 , S2 , then the Gini task as follows. index of the split is given by Consider the relation J that is computed by joining all |S1 | Gini(S1 ) + |S2 | Gini(S2 ) the relations in rel(Q ) based on the foreign-key joins rep- Gini(S1 , S2 ) = , |S1 | + |S2 | resented in G. Without loss of generality, let us suppose that we are looking for weak IEQs Q . Let L denote the where |Si | denote the number of records in Si . The general ordered listing of the attributes in proj(Q ) such that that objective is to pick the splitting attribute whose best split- the schema of πL (J) and Q(D) are equivalent3 . J can be ting value reduces the Gini index the most (the goal is to partitioned into two disjoint subsets, J = J0 ∪ J1 , such that reduce Gini to 0 resulting in all pure leaf nodes). Example 2. To illustrate how decision tree classifier can 2 Note that even though the definition of a weak IEQ Q of Q be applied to derive IEQs, consider the following query on does not require the queries to share a set of core relations, the baseball database D: Q4 = πname (σbats=“R”∧throws=“R” we find this restriction to be a reasonable and effective way M aster). Note that Q4 (D) = {B, E}. Suppose that the to obtain “good” IEQs. 3 If the search is for strong IEQs, then the discussion remains schema subgraph G considered contains both Master and the same except that L is the ordered listing of the key Batting; i.e., rel(Q4 ) = {Master, Batting}. The output of attributes of a set of core relations S of Q, and we replace J = Master pID Batting is shown in Figure 2(a). Us- Q(D) by QS (D). ing ti to denote the ith tuple in J, J is partitioned into 538 

5 . pID name country weight bats throws year team stint HR P1 A USA 85 L R 2001 PIT 2 40 P1 A USA 85 L R 2003 ML1 2 50 P2 B USA 72 R R 2001 PIT 1 73 P2 B USA 72 R R 2002 PIT 1 40 P3 C USA 80 R L 2004 CHA 2 35 P4 D Germany 72 L R 2001 PIT 3 30 P5 E Japan 72 R R 2004 CHA 3 60 (a) J = Master pID Batting N1 stint ” 1 stint > 1 N1 N2 N3 HR ” 50 HR > 50 { t3, t4 } HR ” 50 HR > 50 N2 N3 N2 N3 { t1, t2, t5, t6 } { t7 } { t1, t2, t4, t5, t6 } { t3, t7 } DT1 DT2 (b) Decision trees DT1 and DT2 Figure 2: Example of deriving IEQs for Q4 = πname (σbats=“R”∧throws=“R” M aster) on D J0 = {t1 , t2 , t5 , t6 } and J1 = {t3 , t4 , t7 }. Figure 2(b) shows tuple depending on whether there is any freedom to label two example decision trees, DT1 and DT2 , constructed from the tuple. A tuple t ∈ J is a bound tuple if either (1) t ∈ J0 J. Each decision tree partitions the tuples in J into differ- in which case t must be labeled negative, or (2) t is the only ent subsets (represented by the leaf nodes) by applying differ- tuple in some subset Pi , in which case t must certainly be ent sequences of attribute selection conditions. By labeling included in J1 and be labeled positive; otherwise, t is a free all tuples in J1 as positive, the IEQ derived from DT1 is tuple (i.e., t is in some subset Pi that contains more than given by Q4 = πname (σstint≤1∨(stint>1∧HR>50) (M aster one tuple). Batting)). More details are described in Section 4.1. ✷ In contrast to conventional classification problem where each record in the input data comes with a well defined 2.3 TALOS: Challenges class label, the classification problem formulated for QBO has There are two key challenges in adapting decision tree the unique characteristic where there is some flexibility in classifier for the QBO problem. the class label assignment. We refer to this property as at- At Least One Semantics. The first challenge concerns least-one semantics. To the best of our knowledge, we are the issue of how to assign class labels in a flexible manner not aware of any work that has addressed this variant of the without over constraining the classification problem and lim- classification problem. iting its effectiveness. Contrary to the impression given by An obvious approach to solve the at-least-one semantics the above simple class labeling scheme, the task of assigning variant is to map the problem into the traditional variant class labels to J is actually a rather intricate problem due by first applying some arbitrary class label assignment that to the fact that multiple tuples in J1 can be projected to the is consistent with the at-least-one semantics. In our exper- same tuple in πL (J1 ). Recall that in the simple class label- imental study, we compare against two such static labeling ing scheme described, a tuple t is labeled positive iff t ∈ J1 . schemes, namely, NI, which labels all free tuples as positive, However, note that it is possible to label only a subset of and RD, which labels a random non-empty subset of free tu- tuples J1 ⊆ J1 as positive (with tuples in J − J1 labeled ples in each Pi as positive4 . However, such static labeling as negative) and yet achieve πL (J1 ) = πL (J1 ) (without af- schemes do not exploit the flexible class labeling opportuni- fecting the imprecision of Q ). In other words, the simple ties to optimize the classification task. To avoid the limita- scheme of labeling all tuples in J1 as positive is just one tions of the static scheme, TALOS employs a novel dynamic (extreme) option out of many other possibilities. class labeling scheme to compute optimal node splits for de- We now discuss more precisely the various possibilities cision tree construction without having to enumerate an ex- of labeling positive tuples in J to derive different sel(Q ). ponential number of combinations of class labeling schemes Let πL (J1 ) = {t1 , · · · , tk }. Then J1 can be partitioned into for the free tuples. k subsets, J1 = P1 ∪ · · · ∪ Pk , where each Pi = {t ∈ J1 | the projection of t on L is ti }. Thus, each Pi represents Example 3. Continuing with Example 2, J1 is partitioned the subset of tuples in J1 that project to the same tuple in into two subsets: P1 = {t3 , t4 } and P2 = {t7 }, where P1 and πL (J1 ). Define J1 to be a subset of tuples of J1 such that it P2 contribute to the outputs “B” and “E”, respectively. The consists of at least one tuple from each subset Pi . Clearly, tuples in J0 and P2 are bound tuples, while the tuples in P1 πL (J1 ) = πL (J1 ), and there is a total of ki=1 (2|Pi | − 1) are free tuples. To derive an IEQ, at least one of the free possibilities for J1 . For a given J1 , we can derive sel(Q ) tuples in P1 must be labeled positive. If t3 is labeled positive using a data classifier based on labeling the tuples in J1 as and t4 is labeled negative, DT2 in Figure 2(b) is a simpler positive and the remaining tuples in J1 − J1 as negative. 4 We also experimented with a scheme that randomly labels Based on the above discussion on labeling tuples, each only one free tuple for each subset as positive, but the results tuple in J can be classified as either a bound tuple or free are worse than NI and RD. 539 

6 .decision tree constructed by partitioning J based on a selec- Based on conditions (A1) and (A2), it can be shown that tion predicate on attribute HR. The IEQ derived from DT2 the optimal value of Gini(S1 , S2 ) can be determined by con- is Q4 = πname σHR>50 (M aster Batting). ✷ sidering only five combinations of f1 and f2 values as indi- cated by the second and third columns in Table 1. The proof of this result is given elsewhere [20]. These five cases cor- Performance Issues. The second challenge concerns the respond to different combinations of whether the number of performance issue of how to efficiently generate candidates positive or negative tuples is being maximized in each of S1 for rel(Q ) and optimize the computation of the single in- and S2 : case C1 maximizes the number of positive tuples in put table J required for the classification task. To improve both S1 and S2 ; case C2 maximizes the number of positive performance, TALOS exploits join indices to avoid a costly tuples in S1 and maximizes the number of negative tuples explicit computation of J and constructs mapping tables to in S2 ; case C3 maximizes the number of negative tuples in optimize decision tree construction. S1 and maximizes the number of positive tuples in S2 ; and cases C4 and C5 maximize the number of negative tuples in 3. HANDLING AT-LEAST-ONE SEMANTICS both S1 and S2 . The optimal value of Gini(S1 , S2 ) is given by the minimum of the Gini index values derived from the In this section, we address the first challenge of TALOS above five cases. and present a novel approach for classifying data with the at-least-one semantics. 3.2 Updating Labels & Propagating Constraints 3.1 Computing Optimal Node Splits Once the optimal Gini(S1 , S2 ) index is determined for a The main challenge for classification with the at-least-one given node split, we need to update the split of S by con- semantics is how to optimize the node splits given the pres- verting the free tuples in S1 and S2 to bound tuples with ence of free tuples which offer flexibility in the class label either positive/negative class labels. The details of this up- assignment. We present a novel approach that computes dating depends on which of the five cases the optimal Gini the optimal node split without having to explicitly enumer- value was derived from, and is summarized by the last four ate all possible class label assignments to the free tuples. columns in Table 1. The idea is based on exploiting the flexibility offered by the For case C1, which is the simplest case, all the free tuples at-least-one semantics. in S1 and S2 will be converted to positive tuples. However, Let us consider an initial set of tuples S that has been for the remaining cases, which involve maximizing the num- split into two subsets, S1 and S2 , based on a value v of a ber of negative tuples in S1 or S2 , some of the free tuples may numeric attribute A (the same principle applies to categor- not be converted to bound tuples. Instead, the maximiza- ical attributes as well); i.e., a tuple t ∈ S belongs to S1 tion of negative tuples in S1 or S2 is achieved by propagating iff t.A ≤ v. The key question is how to compute the op- another type of constraints, referred to as “exactly-one” con- timal Gini index of this split without having to enumerate straints, to some subsets of tuples in S1 or S2 . Similar to all possible class label assignments for the free tuples in S the principle of at-least-one constraints, the idea here is to such that the at-least-one semantics is satisfied. Without make use of constraints to optimize the Gini index values for loss of generality, suppose that the set of free tuples in S subsequent node splits without having to explicitly enumer- is partitioned (as described in Section 2.3) into m subsets, ate all possible class label assignments. Thus, in Table 1, P1 , · · · , Pm , where each |Pi | > 1. the fourth and fifth columns specify which free tuples are Let ni,j denote the number of tuples in Pi ∩ Sj , and fj to be converted to bound tuples with positive and negative denote the number of free tuples in Sj to be labeled positive labels, respectively; where an ‘-’ entry means that no free to minimize Gini(S1 , S2 ), where i ∈ [1, m], j ∈ {1, 2}. We tuples are to be converted to bound tuples. The sixth and classify Pi , i ∈ [1, m], as a SP1 -set (resp. SP2 -set) if Pi is seventh columns specify what subsets of tuples in S1 and completely contained in S1 (resp. S2 ); otherwise, Pi is a S2 , respectively, are required to satisfy the exactly-one con- SP12 -set (i.e., ni,1 > 0 and ni,2 > 0). straint; where an ‘-’ entry column means that no constraints To satisfy the at-least-one semantics, we need to ensure are propagated to S1 or S2 . that at least one free tuple in each Pi , i ∈ [1, m], is labeled We now define the exactly-one constraint and explain why positive. Let Tj , j ∈ {1, 2}, denote the minimum number it is necessary. An exactly-one constraint on a set of free of free tuples in Sj that must be labeled positive to ensure tuples S requires that exactly one free tuple in S must be- this. Observe that for a specific Pi , i ∈ [1, m], if Pi a SP1 -set come labeled as positive with the remaining free tuples in S (resp. SP2 -set), then we must have T1 ≥ 1 (resp. T2 ≥ 1). labeled as negative. Consider case C2, which is to maximize Thus, Tj is equal to the number of SPj -sets. More precisely, the number of positive (resp. negative) tuples in S1 (resp. Tj = m S2 ). The maximization of the number of positive tuples in i=1 max{0, 1 − ni,3−j }, j ∈ {1, 2}. Thus, f1 and f2 must satisfy the following two conditions: S1 is easy to achieve since by converting all the free tuples in S1 to positive, the at-least-one constraints on the SP1 - m (A1) Tj ≤ fj ≤ i=1 ni,j , j ∈ {1, 2}; and sets and SP12 -sets are also satisfied. Consequently, for each SP12 -set Pi , all the free tuples in Pi ∩ S2 can be converted (A2) f1 + f2 ≥ m. to negative tuples (to maximize the number of negative tu- ples in S2 ) without violating the at-least-one constraint on Condition (A1) specifies the possible number of free tuples to Pi . However, for a SP2 -set Pi , to maximize the number be labeled positive for each Sj , while condition (A2) specifies of negative tuples in Pi while satisfying the at-least-one se- the minimum combined number of tuples in S to be labeled mantics translates to an exactly-one constraint on Pi . Thus, positive in order that the at-least-one semantics is satisfied for case C2, an exactly-one constraint is propagated to each for each Pi . SP2 -set in S2 , and no constraints are propagated to S1 . A 540 

7 . Number of free tuples Exactly-One to be labeled positive Labeling of free tuples Constraint Propagation Case f1 f2 positive negative S1 S2 m m C1 n i=1 i,1 i=1 ni,2 S1 ∪ S2 - - - m C2 i=1 n i,1 T2 S1 SP12 -sets in S2 - SP2 -sets m C3 T1 i=1 ni,2 S2 SP12 -sets in S1 SP1 -sets - C4 T1 m − T1 - SP12 -sets in S1 SP1 -sets All subsets C5 m − T2 T2 - SP12 -sets in S2 All subsets SP2 -sets Table 1: Optimizing Node Splits similar reasoning applies to cases C3 to C5. Thus, while 4.1 Classifying Data in TALOS the at-least-one constraint is applied to each subset of free We first give an overview of SLIQ [13], a well-known deci- tuples Pi in the initial node split, the exactly-one constraint sion tree classifier, that we have chosen to adapt for TALOS. is applied to each Pi for subsequent node splits. This sec- We then describe the extensions required by TALOS to han- ond variant of the node split problem can be optimized by dle data classfication in the presence of free tuples. Finally, techniques similar to what we have explained so far for the we present a non-optimized, naive variant of TALOS. It is im- first variant. In particular, the first condition (A1) for f1 portant to emphasize that our approach is orthogonal to the and f2 remains unchanged, but the second condition (A2) choice of the decision tree technique. becomes f1 + f2 = m. Consequently, the optimization of the Overview of SLIQ. To optimize the decision tree construc- Gini index value becomes simpler and only needs to consider tion on a set of data records D, SLIQ uses two key data cases C4 and C5. structures. First, a sorted attribute list, denoted by ALi , Example 4. To illustrate how class labels are updated is pre-computed for each attribute Ai in D. Each ALi can and how constraints are propagated during a node split, con- be thought of as a two-column table (val, row), of the same sider the following query on the baseball database D: Q5 = cardinality as D, that is sorted in non-descending order of πstint (σcountry=“USA” M aster pID Batting). Suppose that val. Each record r = (v, i) in ALi corresponds to the ith the weak-IEQ Q5 being considered has rel(Q5 ) = {M aster, tuple t in D, and v = t.Ai . The sorted attribute lists are Batting}. Let J = M aster pID Batting (shown in Fig- used to speed up the computation of optimal node splits. To ure 2(a)). Since Q5 (D) = {1, 2}, we have J0 = {t6 , t7 }, determine the optimal node split w.r.t. Ai requires a single P1 = {t1 , t2 , t5 } (corresponding to stint = 2) and P2 = sequential scan of ALi . {t3 , t4 } (corresponding to stint = 1). The tuples in J0 are Second, a main-memory array called class list, denoted labeled negative, while the tuples in P1 and P2 are all free by CL, is maintained for D. This is a two-column table tuples. (nid, cid) with one record per tuple in D. The ith entry in Suppose that the splitting attribute considered is “weight”, CL, denoted by CL[i], corresponds to the ith tuple t in D, and the optimal splitting value for “weight” is 72. The Gini(S1 , where CL[i].nid is the identifier of leaf node N , t ∈ DN , and S2 ) values computed (w.r.t. “weight = 72”) for the five CL[i].cid refers to the class label of t. CL is used to keep cases, C1 to C5, are 0.29, 0.48, 0.21, 0.4 and 0.4, respec- track of the tuples location (i.e., in which leaf nodes) as leaf tively. Thus, the optimal value of Gini(S1 , S2 ) is 0.21 (due nodes are split. to case C3). We then split tuples with weight ≤ 72 (i.e., Class List Extension. In order to support data classifi- {t3 , t4 , t6 , t7 }) into S1 and tuples with weight > 72 (i.e., cation with free tuples, where their class labels are assigned {t1 , t2 , t5 }) into S2 . Thus, P1 is a SP2 -set while P2 is a SP1 - dynamically, we need to extend SLIQ with the following mod- set. Since the optimal Gini index computed is due to case ification. The class list table CL(nid, cid, sid) is extended C3 (i.e., maximizing negative tuples in S1 and maximizing with an additional column “sid”, which represents a subset positive tuples in S2 ), all the free tuples in S2 (i.e., t1 , t2 identifier, to indicate which subset (i.e., Pi ) a tuple belongs and t5 ) are labeled positive, and an exactly-one constraint is to. This additional information is needed to determine the propagated to the set of tuples P2 ∩ S1 (i.e., {t3 , t4 }). ✷ optimal Gini index values as discussed in the previous sec- In summary, TALOS is able to efficiently compute the opti- tion. Consider a tuple t which is the ith tuple in D. The mal Gini index value for each attribute split value considered cid and sid values in CL are maintained as follows: if t be- without enumerating an exponential number of class label longs to J0 , then CL[i].cid = 0 and CL[i].sid = 0; if t is a assignments for the free tuples. bound tuple in Pj , then CL[i].cid = 1 and CL[i].sid = j; otherwise, if t is a free tuple in Pj , then CL[i].cid = −1 and CL[i].sid = j. 4. OPTIMIZING PERFORMANCE In this section, we first explain how TALOS adapts a well- Example 5. Figure 3 shows some data structures cre- known decision tree classifier for performing data classifica- ated for computing IEQs for Q4 (D). Figure 3(a) shows the tion in the presence of free tuples where their class labels attribute list created for attribute Master.name; and Fig- are not fixed. We then explain the performance challenges ure 3(d) shows the initial class list created for Jhub , where of deriving Q when rel(Q ) involves multiple relations and all the records are in a single leaf node (with nid value of 1). present optimization techniques to address these issues. For ✷ ease of presentation and without loss of generality, the dis- cussion here assumes weak IEQs. Naive TALOS. Before presenting the optimizations for TA- 541 

8 . rM rB rT nid cid sid val row rM S rJ 1 0 0 1 1 1 A 1 1 {1} 2 3 1 1 -1 1 B 2 2 {2, 3} 2 4 2 1 -1 1 C 3 3 {4} 3 5 3 1 0 0 D 4 4 {5} 4 6 1 1 0 0 E 5 5 {6} 5 7 3 1 1 2 (a) ALname (b) Jhub (c) MM aster (d) CL Figure 3: Example data structures for Q4 (D) LOS in the next section, let us first describe a non-optimized, Based on the foreign-key join relationships represented naive variant of TALOS (denoted by TALOS-). Suppose that in the schema subgraph G, TALOS computes the join of all we are considering an IEQ Q where rel(Q ) = {R1 , · · · , Rn }, the appropriate join indices for rel(Q ) to derive a relation, n > 1, that is derived from some schema subgraph G. First, called the hub table, denoted by Jhub . Computing Jhub is TALOS- joins all the relations in rel(Q ) (based on the foreign- much more efficient than computing J since there are fewer key joins represented in G) to obtain a single relation J. number of join operations (i.e., number of relevant join in- Next, TALOS- computes attribute lists for the attributes in dices) and each join attribute is a single integer-valued col- J and a class list for J. TALOS- is now ready to construct umn. a decision tree DT to derive the IEQ Q with these struc- tures. DT is initialized with a single leaf node consisting of Example 6. Consider again query Q4 introduced in Ex- the records in J, which is then refined iteratively by split- ample 2. Suppose that we are computing IEQ Q4 with rel(Q4 ) ting the leaf nodes in DT . TALOS- terminates the splitting = {Master, Batting, Team}. Figure 3(b) shows the hub of a leaf node when (1) its tuples are either all labeled pos- table, Jhub , produced by joining two join indices: one for itive or all labeled negative; or (2) its tuples have the same Master pID Batting and the other for Batting team,year attribute values w.r.t. all the splitting attributes. Finally, Team. Here, rM , rB , and rT refer to the row identifiers for TALOS- classifies each leaf node in DT as positive or negative M aster, Batting, and T eam relations, respectively. ✷ as follows: a leaf node is classified as positive if and only if (1) all its tuples are labeled positive, or (2) the ratio of the Mapping Tables. Instead of computing and operating on number of its positive tuples to the number of its negative large attribute lists (each with cardinality equal to |J|) as tuples is no smaller than a threshold value given by τ . In in the naive approach, TALOS operates over the smaller pre- our experiments, we set τ = 1. sel(Q ) is then derived from computed attribute lists ALi for the base relations in rel(Q ) the collection of positive leaf nodes in DT as follows. Each together with small mapping tables to link the pre-computed set of tuples in a positive leaf node is specified by a selection attribute lists to the hub table. In this way, TALOS only predicate that is a conjunction of the predicates along the needs to pre-compute once the attribute lists for all the base path from the root node to that leaf node, and the set of relations, thereby avoiding the overhead of computing many tuples in a collection of positive leaf nodes is specified by a large attribute lists for different rel(Q ) considered. selection predicate that is a disjunction of the selection pred- Each mapping table, denoted by Mi , is created for each icate for each selected leaf node. In the event that all the Ri ∈ rel(Q ) that links each record r in Ri to the set of leaf nodes in DT are classified as negative, the computation records in Jhub that are related to r. Specifically, for each of Q is not successful (i.e., there is no IEQ for rel(Q )) and record r in Ri , there is one record in Mi of the form (j, S), we refer to Q as a pruned IEQ. where j is the row identifier of r, and S is a set of row identifiers representing the set of records in Jhub that are created from r. 4.2 Optimizations The naive TALOS described in the previous section suf- Example 7. Figure 3(c) shows the mapping table MM aster fers from two drawbacks. First, the overhead of computing that links the Master relation in Figure 1 and Jhub in Fig- J can be high especially if there are many large relations ure 3(b). The record (2, {2, 3}) in MM aster indicates that in rel(Q ). Second, since the cardinality of J can be much the second tuple in Master relation (with pID of P 2), con- larger than the cardinality of each of the relations in rel(Q ), tributed two tuples, located in the second and third rows, in building decision trees directly using J entails the compu- Jhub . ✷ tation and scanning of correspondingly large attribute lists which further increases the computation cost. In the rest of Computing Class List. We now explain how TALOS can this section, we present the optimization techniques used by efficiently compute the class list CL for J (without having TALOS to address the above performance issues. explicitly computed J) by using the attribute lists, hub ta- Join Indices & Hub Table. To avoid the overhead of ble, and mapping tables. The key task in computing CL is computing J from rel(Q ), TALOS exploits pre-computed join to partition the records in J into subsets (J0 , P1 , P2 , etc.), as indices [21] which is a well-known technique for optimizing described in the previous section. For simplicity and with- joins. For each pair of relations, R and R , in the database out loss of generality, assume that the schema of Q(D) has schema that are related by a foreign-key join, its join index, n attributes A1 , · · · , An , where each Ai is an attribute of re- denoted by IR,R , is a set of pairs of row identifiers referring lation Ri . TALOS first initializes CL with one entry for each to a record in each of R and R that are related by the record in Jhub with the following default values: nid = 1, foreign-key join. cid = 0, and sid = 0. For each record rk that is accessed 542 

9 . est by a sequential scan of Q(D), TALOS examines the value vi troduce a second variant, denoted by Fm , which relies on of each attribute Ai of rk . For each vi , TALOS first retrieves estimating pa , pb , and pc using existing data probabilistic the set of row identifiers RIvi of records in Ri that have a models (as opposed to using the actual values from the data est value of vi for attribute Ri .Ai by performing a binary search set). Fm captures how the equivalence of queries is af- est on the attribute list for Ri .Ai . With this set of row identi- fected by database updates, and the IEQ with high Fm is est fiers RIvi , TALOS probes the mapping table Mi to retrieve preferable to another IEQ with low Fm . For simplicity, we est the set of row identifiers JIvi of the records in Jhub that are use a simple independent model [20] to estimate Fm ; other related to the records referenced by RIvi . The intersection techniques such as the Bayesian model by Getoor and oth- of the JIvi ’s for all the attribute values of rk , denoted by ers [8] can be applied too. The second variant has the benefit Pk , represents the set of records in J that can generate rk . that estimates which are computed from a global distribu- TALOS updates the entries in CL corresponding to the row tion model may more accurately reflect the true relevance of identifiers in Pk as follows: (1) the sid value of each entry the IEQs than one computed directly from the data. This of is set to k (i.e., all the entries belong to the same subset course pre-supposes that future updates follow the existing corresponding to record rk ); and (2) the cid value of each data distribution. entry is set to 1 (i.e., tuple is labeled positive) if |Pk | = 1; otherwise, it is set to −1 (i.e., it is a free tuple). 6. EXPERIMENTAL STUDY Example 8. We illustrate how TALOS creates CL for query In this section, we evaluate the performance of the pro- Q4 , which is shown in Figure 3(d). Initially, each row in posed approaches for computing IEQs and study the rele- CL is initialized with sid = 0 and cid = 0. TALOS then ac- vance of the results returned. The algorithms being com- cess each record of Q4 (D) sequentially. For the first record pared include our proposed TALOS approach, which is based (with name = “B’), TALOS searches ALname and obtains on a dynamic assignment of class labels for free tuples, and RIB = {2}. It then probes MM aster with the row identi- two static class labeling techniques: NI labels all the free tu- fer in RIB and obtains JIB = {2, 3}. Since Q4 (D) con- ples as positive, and RD labels a random number of at least tains only one attribute, we have P1 = {2, 3}. The second one free tuple in each subset as positive. We also examined and the third rows in CL are then updated with sid = 1 the effectiveness of our proposed optimizations by compar- and cid = −1. Similarly, for the second record in Q4 (D) ing against a non-optimized naive variant of TALOS (denoted (with name = “E”), TALOS searches ALname and obtains by TALOS-) described in Section 4.1. RIE = {5}, and derives JIE = {6} and P2 = {6}. The The database system used for the experiments is MySQL sixth row in CL is then updated with sid = 2 and cid = 1. Server 5.0.51; and all algorithms are coded using C++ and ✷ compiled and optimized with gcc. Our experiments are con- ducted on dual core 2.33GHz machine with 3.25GB RAM, running Linux. The experimental result timings reported 5. RANKING IEQS are averaged over 5 runs with caching effects removed. In this section, we describe the ranking criteria we adopt to prioritize results presented to the user. Specifically, we 6.1 Data sets & Queries consider a metric based on the Minimum Description Length We use three real data sets: one small size (Adult), one (MDL) principle [18], and two metrics based on the F-measure medium size (Baseball) and one large data set (TPC-H). All [22]. the test queries are given in Table 2, where sf refers to the Minimum Description Length (MDL). The MDL prin- selectivity factor of a query. ciple argues that all else being equal, the best model is Adult. The Adult data set, from the UCI Machine Learn- the one that minimizes the sum of the cost of describing ing Repository5 , is a single-relation data set that has been the data given the model and the cost of describing the used in many classification works. We use this data set to il- model itself. If M is a model that encodes the data D, lustrate the utility of the IEQs for the simple case when both then the total cost of the encoding, cost(M, D), is defined the input query Q as well as the output IEQ Q involve only as: cost(M, D) = cost(D|M ) + cost(M ), where cost(M ) is one relation. The four test queries for this data set are A1 , the cost to encode the model (i.e., the decision tree in our A2 , A3 and A4 6 . The first three queries have different selec- case) and cost(D|M ) is the cost to encode the data given the tivities: low (A1 ), medium (A2 ) and very high (A3 ). Query model. We can rely on succinct tree-based representations A4 is used to illustrate how TALOS handles skyline queries to compute cost(M ). The data encoding cost, cost(D|M ), [4]. is calculated as the sum of classification errors. The details In addition, we also run three sets of workload queries with of the encoding computations are given elsewhere [13]. varying selectivities (low, medium, high) shown in Table 3. F-measure. We now present two useful metrics based on Each workload set Wi consists of five queries denoted by Wi1 the popular F-measure. The first variant follows the stan- to Wi5 . The average selectivity factor of the queries in W1 , dard definition of F-measure: the F-measure for two IEQs W2 , and W3 are, respectively, 0.85, 0.43, and 0.05. Q and Q is defined as Fm = 2×|pa2×|p a| |+|pb |+|pc | , where pa = Baseball. The baseball data set is a more complex, multi- Q(D)∩Q (D), pb = Q (D)−Q(D), and pc = Q(D)−Q (D). relation database that contains Batting, Pitching, and Field- We denote this variant as F-measure in our experimental ing statistics for Major League Baseball from 1871 through study. 5 http://archive.ics.uci.edu/ml/datasets/Adult Observe that the first variant is useful only for approx- 6 We use gain, ms, edu, loss, nc, hpw, and rs, respectively, imate IEQs, and is not able to distinguish among precise as abbreviations for capital-gain, marital-status, education, IEQs as this metric gives identical values for precise IEQs capital-loss, native-country, hours-per-week, and relation- since pb and pc are empty. To rank precise IEQs, we in- ship. 543 

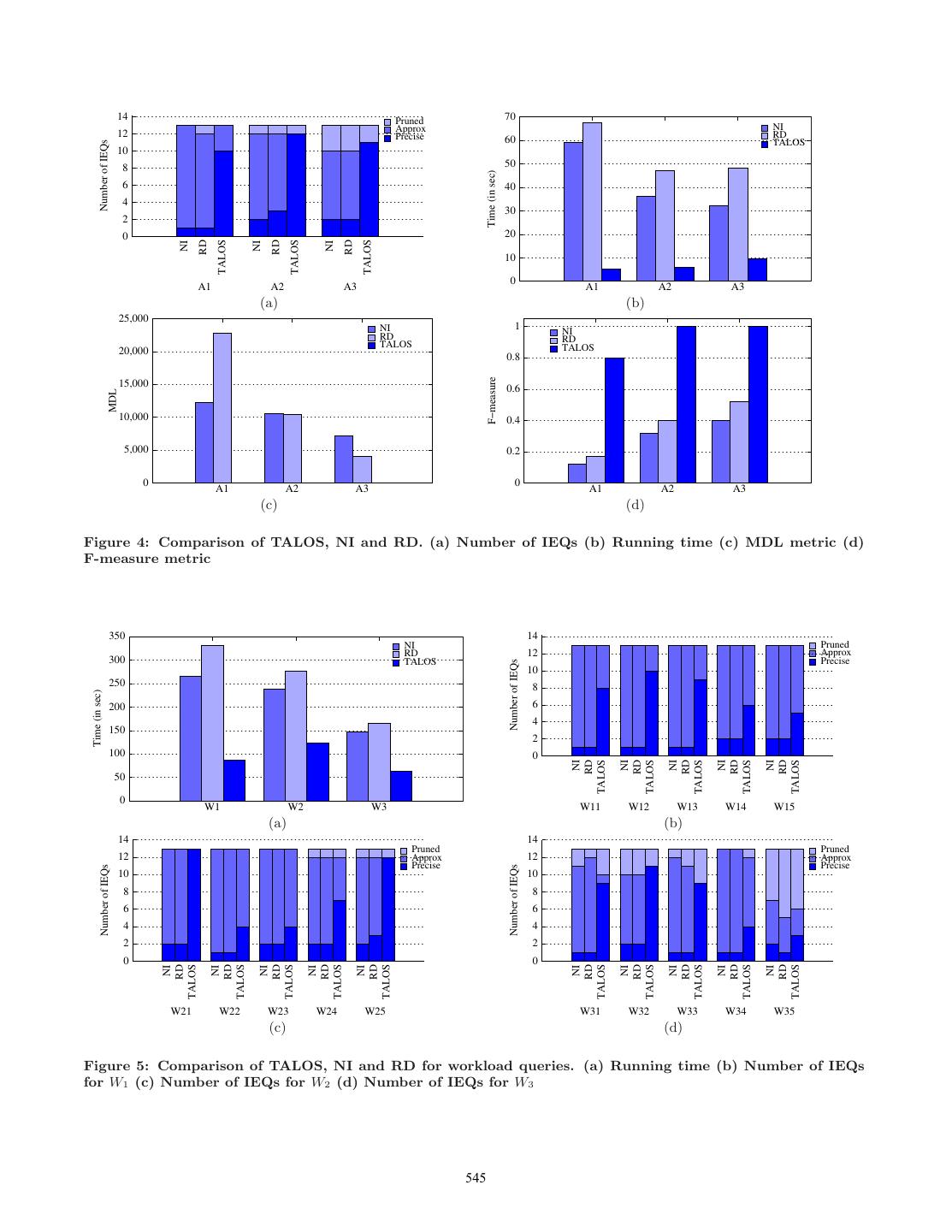
10 . Query sf Average height Average size A1 πnc (σocc=“Armed-Force” adult) 0.91 Query NI RD TALOS NI RD TALOS A2 πedu (σms=“Married-AF”∧race=“Asian” adult) 0.17 A1 14.9 19.8 2.1 5304 9360 4.7 A3 πedu,occ (σms=“Never-married”∧64≤age≤68 0.06 A2 13.4 20.1 3.2 4769 4966 6.9 σrace=“White”∧gain>500∧sex=“F” adult) A3 16.1 21.8 6.5 3224 2970 19.2 A4 πid (σSKY -LIN E(gain M AX,age M IN ) adult) 0.06 B1 πname (σteam=“ARI”∧year=2006∧HR>10 0.0004 (M aster Batting)) B2 πname (σsum(HR)>600 ) (M aster Batting) 0.001 Table 4: Comparison of decision trees for NI, RD, B3 πname (σSKY -LIN E(HR M AX,SO M IN ) 0.002 and TALOS (M aster Batting)) B4 πname,year,rank (σteam=“CIN”∧1982<year<1988 0.0004 (M anager T eam)) T1 πmf gr (σbrand=“Brand#32”(part)) 0.2 LOS outperforms NI and RD in terms of both the total number T2 πname (σprice>500,000∧priority=“Urgent” 0.0004 (customer order)) of (precise and approximate) IEQs computed7 as well as the running time. In particular, observe that the number of pre- Table 2: Test queries for experiments cise IEQs from TALOS is consistently larger than that from NI and RD. This is due to the flexibility of TALOS’s dynamic Query sf assignment of class labels for free tuples which increase its W11 πms (σ19≤age≤22∧edu=“Bachelors” adult) 0.79 opportunities to derive precise IEQs. In contrast, the static W12 πnc (σocc=“Armed-Force” adult) 0.91 class label assignment schemes of NI and RD are too restric- W13 πocc,ms (σnc=“Phillipines”∧30≤age≤40 adult) 0.83 tive and are not effective for generating precise IEQs. W14 πedu,age (σwc=“Private”∧race=“Asian” adult) 0.82 W15 πocc,edu (σgain>9999 adult) 0.89 In addition, TALOS is also more efficient than NI and RD in W21 πedu (σ23≤age≤24∧nc=“Germany” adult) 0.53 terms of the running time. The reason for this is due to the W22 πage,wc,edu (σhpw≤19∧race=“White” adult) 0.64 flexibility of TALOS’s dynamic labeling scheme for free tuples W23 πedu,age,ms (σwc=“Private”∧race=“Asian” adult) 0.61 W24 πedu,age (σms=“Separated”∧wc=“State-gov” 0.2 which results in decision trees that are smaller than those σrace=“White” adult) constructed by NI and RD. Table 4 compares the decision W25 πedu (σms=“Married-AF”∧race=“Asian” adult) 0.17 trees constructed by TALOS, NI, and RD in terms of their aver- W31 πage (σms=“Divorced”∧wc=“State”∧age>70 adult) 0.002 W32 πocc,edu (σms=“NM”∧64≤age≤68∧race=“White” 0.06 age height and average size (i.e., number of nodes). Observe σgain>2000∧sex=“F” adult) that the decision trees constructed by TALOS are significantly W33 πage,wc,edu (σhpw≤19∧race=“White”∧nc=“England” 0.01 more compact than that by NI and RD. adult) Figures 4(c) and (d) compare the quality of the IEQs W34 πedu,age,gain (σms=“Married-civ”∧race“Asian” 0.17 σ30≤age≤37 adult) generated by the three algorithms using the MDL and F- W35 πedu,gain (σgain>5000∧nc=“Vietnam” adult) 0.0008 measure metrics, respectively. The results show that TALOS produces much better quality IEQs than both NI and RD: Table 3: Workload query sets (W1 , W2 , W3 ) for Adult while the average value of the MDL metric for TALOS is ex- tremely low (under 60), the corresponding values of both NI and RD are in the range of [4000, 22000]. For the F-measure 2006 created by Sean Lahman. There are 16, 639 records of metric, the average value for TALOS is nearly 1 (larger than baseball players, 88, 686 records in Batting, 37, 598 records 0.8), whereas the values for NI and RD are only around 0.3 in P itching, 128, 426 records F ielding and other auxiliary and 0.4, respectively. relations (AwardsPlayer, Allstar, Team, Managers, etc.). Figure 5 compares the three algorithms for the three sets The queries used for this data set (B1 , B2 , B3 , B4 ) are of workload queries, W1 , W2 , and W3 , on the Adult data set. common queries that mainly relate to baseball players’ per- As the results in Figure 5(a) show, TALOS again outperforms formance. both NI and RD in terms of running time. For both low and TPC-H. To evaluate the scalability of our approach, we medium selectivity query workload (i.e., W1 and W2 ), the use the TPC-H data set (with a scaling factor of 1) and two results in Figures 5(b) and (c) show TALOS is able to find test queries, T1 and T2 . many more precise IEQs for all queries compared to NI and RD. The reason for this is because such queries have a larger 6.2 Comparing TALOS, NI, and RD number of free tuples which gives TALOS more flexibility to derive precise IEQs. Figure 5(d) shows the comparison for In this section, we compare TALOS against the two static the high selectivity query workload (i.e., W3 ). As the num- class-labeling schemes, NI and RD, in terms of their efficiency ber of free tuples is smaller for highly selective queries, the as well as the quality of the generated IEQs. flexibility for TALOS becomes reduced, but TALOS still obtains Figures 4(a) and (b) compare the performance of the three about 1.5 to 9 times larger number of precise IEQs compared algorithms in terms of the number of weak IEQs generated to NI and RD. and their running times, respectively, using the queries A1 Our comparison results for the Baseball data set (not to A4 . Note that Figure 4 only compares the performance shown) also demonstrate similar trends with TALOS outper- for weak IEQs because as the Adult data set is a single- forming NI and RD in both the running time as well as the relation database, all the tuples are necessarily bound when number and quality of IEQs generated. computing strong IEQs. Thus, the performance results for strong IEQs are the same for all algorithms and are therefore 7 omitted. Similarly, the results for query A4 are also omitted For clarity, we have also indicated in Figure 4(a) the num- ber of pruned IEQs (defined in Section 4.1) computed by from the graphs because it happens that all the tuples are each algorithm. Since the number of decision trees consid- bound for query A4 ; hence, the performance results are again ered by all three algorithms are the same, the sum of the the same for all three algorithms. number of precise, approximate, and pruned IEQs gener- The results in Figures 4(a) and (b) clearly show that TA- ated by all the algorithms are the same. 544 

11 . 14 Pruned 70 Approx NI 12 Precise RD 60 TALOS Number of IEQs 10 8 50 Time (in sec) 6 40 4 30 2 0 20 NI RD TALOS NI RD TALOS NI RD TALOS 10 0 A1 A2 A3 A1 A2 A3 (a) (b) 25,000 NI 1 NI RD RD TALOS TALOS 20,000 0.8 F−measure 15,000 0.6 MDL 10,000 0.4 5,000 0.2 0 0 A1 A2 A3 A1 A2 A3 (c) (d) Figure 4: Comparison of TALOS, NI and RD. (a) Number of IEQs (b) Running time (c) MDL metric (d) F-measure metric 350 14 NI Pruned RD 12 Approx 300 TALOS Precise Number of IEQs 10 250 8 Time (in sec) 200 6 4 150 2 100 0 NI RD TALOS NI RD TALOS NI RD TALOS NI RD TALOS NI RD TALOS 50 0 W1 W2 W3 W11 W12 W13 W14 W15 (a) (b) 14 14 Pruned Pruned 12 Approx 12 Approx Precise Precise Number of IEQs Number of IEQs 10 10 8 8 6 6 4 4 2 2 0 0 NI RD TALOS NI RD TALOS NI RD TALOS NI RD TALOS NI RD TALOS NI RD TALOS NI RD TALOS NI RD TALOS NI RD TALOS NI RD TALOS W21 W22 W23 W24 W25 W31 W32 W33 W34 W35 (c) (d) Figure 5: Comparison of TALOS, NI and RD for workload queries. (a) Running time (b) Number of IEQs for W1 (c) Number of IEQs for W2 (d) Number of IEQs for W3 545 

12 . est 400 Q IEQ Fm TALOS A1,1 σgain>7298∧ms=“Married-AF” (adult) 0.63 350 TALOS− A1,2 σedu=“Preschool”∧race=“Eskimo” (adult) 0.25 300 A1,3 σloss>3770 (adult) 0.24 A2,1 σloss>3683∧edu num>10 (adult) 0.07 Time (in sec) 250 A2,2 σage≤24∧nc=“Hungary” (adult) 0.06 A3,1 σp1 ∨p2 (adult) 0.004 200 p1 = (age ≤ 85 ∧ hpw ≤ 1 ∧ edu > 13) 150 p2 = (age > 85∧edu = “Master”∧hpw ≤ 40) 100 Table 5: Weak IEQs on Adult 50 0 B1 B2 B3 T1 T2 and 7, the F-measure metric values are shown in terms of their |pa |, |pb | and |pc | values; a IEQ is precise iff |pb | = 0 Figure 6: Comparison of TALOS and TALOS- and |pc | = 0. We use Xi,j to denote an IEQ for a query Xi , X ∈ {A, B, T }. 6.3 Effectiveness of Optimizations Adult. In query A1 , we want to know the native country of people whose occupation is in the Armed Force. The query Figure 6 examines the effectiveness of the optimizations by result is “U.S”. From the weak IEQs, we learn that the people comparing the running times of TALOS and TALOS- on both who is married to some one in the Armed Force and have the Baseball and TPC-H data sets. Note that the num- high capital gain (A1,1 ) have the same native country “U.S”; ber and quality of IEQs produced by TALOS and TALOS- are or people with high capital loss (> 3770) also have “U.S” as the same as these qualities are independent of the optimiza- their native country (A1,3 ). tions. The results show that TALOS is about 2 times faster In query A2 , we want to know the education level of than TALOS-. The reason is that the attribute lists accessed Asians who have a spouse working in the Air Force. The by TALOS, which correspond to the base relations, are much result shows that they all have bachelor degrees. From smaller than the attribute lists accessed by TALOS-, which the weak IEQs, we know that Hungarians who are younger are based one J. For example, for query T1 , the attribute than 25 also have the same education level (A2,2 ). For the list constructed by TALOS- for attribute “container” in part strong IEQs, we have some interesting characterizations: relation is 4 times larger than that constructed by TALOS; A2,3 shows that these Asians are from Philippines, while and for query T2 , the attribute list constructed by TALOS- A2,4 shows that these Asians are wives whose age are at for attribute “acctbal” in customer relation is 10 times larger most 30 and work more than 52 hours per week. Such alter- than that constructed by TALOS. In addition, the computa- native queries provide more insights about query A2 on the tion of Jhub by TALOS using join indices is also more efficient Adult data set. than the computation of J by TALOS-. In query A3 , we want to find the occupation and educa- For the queries B1 , B2 , and B3 on the Baseball data set, tion of white females who are never married with age in the the number of IEQs (both precise and approximate) gener- range [64, 68], and have capital gain > 500. The query result ated by TALOS is in the range [50, 80] with an average running has 5 records. The strong IEQ A3,2 provides more insights time of about 80 seconds. Thus, it takes TALOS about 1.2 about this group of people: those in the age range [64, 66] seconds to generate one IEQ which is reasonable. Note that are highly educated, whereas the others in the age range the comparison for query B4 is omitted because while TALOS [67, 68] have high capital gains. takes only 37.6 seconds to complete, the running time by Query A4 is a skyline query looking for people with maxi- TALOS- exceeds 15 minutes. mal capital gain and minimal age. The query result includes For the queries T1 and T2 on the TPC-H data set, TALOS four people. Both strong and weak IEQs return the same takes 34.34 seconds to compute six precise IEQs for T1 , and IEQs for this query. Interestingly, the precise IEQ A4,1 pro- takes 200 seconds to compute one precise and one approxi- vides a simplification of A4 : the people selected by this sky- mate IEQs. T2 is more costly to evaluate than T1 because line query are (1) very young (age ≤ 17) and have capital the decision trees constructed for T2 are larger and more gain in the range 1055 − 27828, or (2) have very high capital complex: the average height and size of the decision trees gain (> 27828), work in the protective service, and whose for T2 are, respectively, 2 and 4 times, larger than those for race is classified as “others”. T1 . Overall, even for the large TPC-H data set, the running time for TALOS is still reasonable. Baseball. In query B1 , we want to find all players who belong to team “ARI” in 2006 and have a high performance 6.4 Strong and Weak IEQs (HR > 10). The result includes 7 players. From the IEQ In this section, we discuss some of the IEQs generated B1,1 , we know more information about these players’ perfor- by TALOS for the various queries. The sample of weak and mance (G, RBI, etc.), and their personal information (e.g., strong IEQs generated from Adult data set are shown in birth year). In addition, from IEQ B1,2 , we also know that Tables 5 and 6, respectively. Tables 7 show sample weak one player in this group got an award when he played in IEQs generated from Baseball and TPC-H data sets, re- “NL” league. spectively8 . For each IEQ, we also show its value for the In query B2 , we want to find the set of high performance F-measure or Fm est metric; the latter is used only in Table 5 players who have very high total home runs (> 600). There as all the IEQs shown in this table are precise. In Tables 6 are four players with these characteristics. The IEQ B2,1 indicates that some of these players play for “ATL” or “NY1” 8 The weak IEQs shown in Table 7 actually turn out to be team. The IEQ B2,2 indicates one player in this group is strong IEQs as well for the queries B1 to B4 . highly paid and has a left throwing hand. 546 

13 . Q IEQ |pa | |pb | |pc | this manufacturer also supplies some parts at a high price, A1,4 σp1 (adult) 1 1 13 p1 = (48 < hpw ≤ 50 ∧ race = where their available quantity is in the range [332, 1527]. “Eskimo”,“Asian” ∧ 6849 < gain ≤ 7298 ∧ The IEQ T1,2 indicates that this manufacturer also supplies loss ≤ 0 ∧ edu num > 14) others products in the container named “SM bag” with an A2,3 σms=“Married-AF”∧nc=“Philippines” (adult) 1 0 0 A2,4 σrace=“Asian”∧rs=“Wife”∧hpw>52∧age≤30 1 0 0 available quantity of at most one. (adult) A3,2 σp1 ∨p2 (adult) 5 0 0 p1 = (63 < age ≤ 66 ∧ edu > 15 ∧ ms = 7. RELATED WORK “NM”) p2 = (66 < age ≤ 68 ∧ ms = “NM” ∧ gain > Although the title of our paper is inspired by Zloof’s in- 2993) fluential work on Query by Example (QBE) [25], the problem A4,1 σp1 ∨p2 (adult) 4 0 0 addressed by QBE, which is on providing a more intuitive p1 = (1055 < gain ≤ 27828 ∧ age ≤ 17) form-based interface for database querying, is completely p2 = (gain > 27828 ∧ occ = P ∧ race = O) different from QBO. There are several recent work [2, 3, 5, 14] that share the Table 6: Strong IEQs on Adult same broad principle of “reverse query processing” as QBO but differ totally in the problem objectives and techniques. Q IEQ |pa | |pb | |pc | Binnig et al. [2, 3] addressed the problem of generating test B1,1 σp1 ∨p2 (M aster Batting) 7 0 0 p1 = (team = “ARI” ∧ G ≤ 156 ∧ 70 < databases: given a query Q and a desired result R, generate RBI ≤ 79 ∧ year > 1975) a database D such that Q(D) = R. Bruno et al. [5] and p2 = (team = “ARI” ∧ G > 156 ∧ BB ≤ 78) Mishra et al. [14] examined the problem of generating test B1,2 σlg=“NL”∧year=12∧71<height≤72∧nc=“D.R” 1 0 6 (M aster AwardsP layer) queries to meet certain cardinality constraints: given a query B2,1 σp1 ∨p2 (M aster Batting) 4 0 0 Q, a database D, and a set of target cardinality constraints p1 = (BB ≤ 162 ∧ HR > 46 ∧ team ∈ on intermediate subexpression in Q’s evaluation plan, mod- {“ATL”, “NY1”} ∧ RBI ≤ 127) ify Q to generate a new query Q such that the evaluation p2 = (BB > 162) B2,2 σsalary>21680700∧throws=“L” (M aster 1 0 3 plan of Q on D satisfies the cardinality constraints. Salaries) An area that is related and complementary to QBO is in- B3,1 σ(team=“WS2”∧R≤4)∨(team=“NYA”∧state=“LA”) 2 0 33 tensional query answering (IQA) or cooperative answering, (M aster M anager) B3,2 σp1 ∨p2 ) (M aster Salaries) 2 0 33 where for a given Q, the goal of IQA is to augment the p1 = (height ≤ 78 ∧ weight > 229 ∧ query’s answer Q(D) with additional “intensional” informa- country = “DR” ∧ 180000 < salary < tion in the form of a semantically equivalent query9 that 195000) p2 = (height > 78∧state = “GA”∧salary < is derived from the database integrity constraints [7, 15]. 302500) While semantic equivalence is stronger than instance equiv- B4,1 σ21<L≤22∧SB≤0∧67<W ≤70 (M ananger 1 0 5 alence and can be computed in a data-independent manner M aster Batting T eam) using only integrity constraints (ICs), there are several ad- T1,1 σprice>2096.99∧331<avaiqty≤1527 (part) 1 0 0 T1,2 σavaiqty≤1∧container=“SM bag” (part 1 0 0 vantages of adopting instance equivalence for QBO. First, in part supp) practice, many data semantics are not explicitly captured using ICs in the database for various reasons [9]; hence, Table 7: Weak IEQs on Baseball and TPCH the effectiveness of IQA could be limited for QBO. Second, even when the ICs in the database are complete, it can be very difficult to derive semantically equivalent queries for Query B3 is a skyline query that looks for players with complex queries (e.g., skyline queries that select dominant maximal number of home runs (HR) and minimal number objects). By being data-specific, IEQs can often provide in- of strike outs (SO). The result has 35 players. The IEQs pro- sightful and surprising characterizations of the input query vide different characterizations of these players. Query B3,1 and its result. Third, as IQA requires the input query Q to indicates that two players in this group are also the man- be known, IQA therefore cannot be applied to QBO applica- agers of “WS2” and “NYA” teams; while query B3,2 indicates tions where only Q(D) (but not Q) is available. Thus, we that two players in this group are averagely paid. view IQA and our proposed data-driven approach to com- Query B4 is an interesting query that involves multiple pute IEQs as complementary techniques for QBO. core relations. This query asks for the managers of team More recently, an interesting direction of using Pr´ecis queries “CIN” from 1983 to 1988, the year they managed the team [12, 19] has been proposed. The idea is to augment a user’s as well as the rank that the team gained. There are 3 man- query result with other related information (e.g., relevant agers in the result. In this query, we note that TALOS found tuples from other relations) and also allow the results to alternative join-paths to link the two core relations, Man- be personalized based on user-specified or domain require- ager and Team. The first alternative join-path (shown by ments. The objectives of this work is orthogonal to QBO; and B4,1 ) involves Manager, Master, Batting, and Team. The as in IQA, it is a query-driven approach that requires the second alternative join-path (not shown) involves Manager, input query to be known. Master, Fielding, and Team. The IEQ B4,1 reveals the in- In the data mining literature, a somewhat related problem teresting observation that there is one manger who is also to ours is the problem of redescription mining introduced by a player in the same year that he managed the team with Ramakrishnan [17]. The goal in redescription mining is to some additional information about this manager-player. find different subsets of data that afford multiple descrip- tions across multiple vocabularies covering the same data TPC-H. Query T1 retrieves the manufacturers who supply products of brand “brand#32”. The result includes one man- 9 Two queries Q and Q are semantically equivalent if for ufacturer “Manufacturer#1”. The IEQ T1,1 indicates that every valid database D, Q(D) ≡ Q (D). 547 

14 .set. At an abstract level, our work is different from these [5] N. Bruno, S. Chaudhuri, and D. Thomas. Generating methods in several ways. First, we are concerned with a queries with cardinality constraints for dbms testing. fixed subset of the data (the output of the query). Second, IEEE TKDE, 18(12):1721–1725, 2006. none of the approaches for redescription mining account for [6] P. Buneman, J. Cheney, W.-C. Tan, and structural (relational) information in the data (something S. Vansummeren. Curated databases. In PODS, pages we explicitly address). Third, redescription mining as it was 1–12, 2008. originally posited requires multiple independent vocabulary [7] T. Gaasterl, P. Godfrey, and J. Minker. An overview descriptions to be identified. We do not have this require- of cooperative answering. Journal of Intelligent ment as we are simply interested in alternative query for- Information Systems, (2):123–157, 1992. mulations within an SQL context. Finally, the notion of [8] L. Getoor, B. Taskar, and D. Koller. Selectivity “at-least-one” semantics described in our work is something estimation using probabilistic models. In SIGMOD, redescription mining is not concerned with as it is an artifact pages 461–472, 2001. of the SQL context of our work. [9] P. Godfrey, J. Gryz, and C. Zuzarte. Exploiting constraint-like data characterizations in query 8. CONCLUSION optimization. In SIGMOD, pages 582–592, 2001. [10] H. V. Jagadish, A. Chapman, A. Elkiss, In this work, we have introduced a new data-driven ap- M. Jayapandian, Y. Li, A. Nandi, and C. Yu. Making proach called query by output (QBO) targeted at improving database systems usable. In SIGMOD, pages 13–24, the usability of database management systems. The goal of 2007. QBO is to discover instance-equivalent queries. Such queries can shed light on hidden relationships within the data, pro- [11] T. Johnson, A. Marathe, and T. Dasu. Database vide useful information on the relational schema as well as exploration and bellman. 26(3):34–39, 2003. potentially summarize the original query. [12] G. Koutrika, A. Simitsis, and Y. Ioannidis. Pr´ecis: The We have developed an efficient system called TALOS for essence of a query answer. In ICDE, page 69, 2006. QBO, and our experimental results on several real database [13] M. Mehta, R. Agrawal, and J. Rissanen. SLIQ: A fast workloads of varying complexity highlight the benefits of our scalable classifier for data mining. In EDBT, pages approach. 18–32, 1996. Although our discussions focus primarily on QBO where [14] C. Mishra, N. Koudas, and C. Zuzarte. Generating Q is known (to identify core relations), extending to the targeted queries for database testing. In SIGMOD, case without Q is feasible too: it requires an additional pre- pages 499–510, 2008. processing phase to map each column of Q(D) to a set of [15] A. Motro. Intensional answers to database queries. relation attributes by comparing the column contents. In IEEE TKDE, 6(3):444–454, 1994. addition, our approach also could be adapted to handle du- [16] M. P.N. Tan and V.Kumar. Introduction to Data plicates in Q(D) by using the at-least-k semantics instead Mining. Addison-Wesley, 2006. of at-least-one semantics. [17] N. Ramakrishnan, D. Kumar, B. Mishra, M. Potts, As part of our future work, we plan to explore a hybrid and R. F. Helm. Turning cartwheels: An alternating approach that includes an off-line phase to mine for soft algorithm for mining redescriptions. In KDD, pages constraints in the database and an online phase that exploits 266–275, 2004. both the database contents as well as mined constraints. [18] J. Rissanen. Modeling by shortest data description. Another interesting direction to be explored is to increase Automatica, 14:465–471, 1978. the expressiveness of IEQs (e.g., SPJ + union queries). [19] A. Simitsis, G. Koutrika, and Y. E. Ioannidis. Generalized pr´ecis queries for logical database subset 9. ACKNOWLEDGMENTS creation. In ICDE, pages 1382–1386, 2007. We would like to thank the anonymous reviewers for their [20] Q. T. Tran, C.-Y. Chan, and S. Parthasarathy. Query constructive suggestions to improve the paper’s presenta- by output. Technical Report TRA4/09, National tion. The third author would also like to acknowledge the University of Singapore - School of Computing, April following NSF grants: IIS-0347662 (CAREER) and CCF- 2009. 0702587. [21] P. Valduriez. Join indices. ACM Trans. Database Syst., 12(2):218–246, 1987. [22] C. J. van Rijsbergen. Information Retireval. 10. REFERENCES Butterworth, 1979. [23] W. Wu, B. Reinwald, Y. Sismanis, and R. Manjrekar. [1] P. Andritsos, R. J. Miller, and P. Tsaparas. Discovering topical structures of databases. In Information-theoretic tools for mining database SIGMOD, pages 1019–1030, 2008. structure from large data sets. In SIGMOD, pages 731–742, 2004. [24] X. Xiao and Y. Tao. Output perturbation with query relaxation. Proc. VLDB Endow., 1(1):857–869, 2008. [2] C. Binnig, D. Kossmann, and E. Lo. Reverse query processing. In ICDE, pages 506–515, 2007. [25] M. M. Zloof. Query by example. In AFIPS NCC, ¨ pages 431–438, 1975. [3] C. Binnig, D. Kossmann, E. Lo, and M. T. Ozsu. QAGen: generating query-aware test databases. In SIGMOD, pages 341–352, 2007. [4] S. Borzsonyi, D. Kossmann, and K. Stocker. The skyline operator. In ICDE, pages 421–430, 2001. 548