So Who Won?Dynamic Max Discovery with the Crowd

1 . So Who Won? Dynamic Max Discovery with the Crowd Stephen Guo Aditya Parameswaran Hector Garcia-Molina Stanford University Stanford University Stanford University Stanford, CA, USA Stanford, CA, USA Stanford, CA, USA sdguo@cs.stanford.edu adityagp@cs.stanford.edu hector@cs.stanford.edu ABSTRACT zon’s Mechanical Turk (mturk.com) can be used by the database We consider a crowdsourcing database system that may cleanse, system to find human workers and perform the tasks, although populate, or filter its data by using human workers. Just like a con- there are many other companies now offering services in this space ventional DB system, such a crowdsourcing DB system requires (CrowdFlower crowdflower.com, uTest utest.com, Microtask mi- data manipulation functions such as select, aggregate, maximum, crotask.com, Tagasauris tagasauris.com). average, and so on, except that now it must rely on human oper- Just like a conventional database system, a crowdsourcing database ators (that for example compare two objects) with very different system will need to perform data processing functions like selects latency, cost and accuracy characteristics. In this paper, we focus and aggregates, except that now these functions may involve inter- on one such function, maximum, that finds the highest ranked object acting with humans. For example, to add a field “average movie rat- or tuple in a set. In particularm we study two problems: given a set ing” to movie tuples involves an aggregate over the user inputs. Se- of votes (pairwise comparisons among objects), how do we select lecting “horror movies” may involve asking humans what movies the maximum? And how do we improve our estimate by requesting are “horror movies.” The underlying operations (e.g., ask a human additional votes? We show that in a crowdsourcing DB system, the if a given movie is a “horror movie” or ask a human which of two optimal solution to both problems is NP-Hard. We then provide cameras is best) have very different latency, cost and accuracy char- heuristic functions to select the maximum given evidence, and to acteristics than in a traditional database system. Thus, we need to select additional votes. We experimentally evaluate our functions develop effective strategies for performing such fundamental data to highlight their strengths and weaknesses. processing functions. In particular, in this paper we focus on the Max (Maximum) func- tion: The database has a set of objects (e.g., maps, photographs, 1. INTRODUCTION Facebook profiles), where conceptually each object has an intrinsic A crowdsourcing database system uses people to perform data “quality” measure (e.g., how useful is a map for a specific human- cleansing, collection or filtering tasks that are difficult for comput- itarian mission, how well does a photo describe a given restaurant, ers to perform. For example, suppose that a large collection of maps how likely is it that a given Facebook profile is the actual profile of is being loaded into the database, and we would like to add data Lady Gaga). Of the set of objects, we want to find the one with the fields to identify “features” of interest such as washed out roads, largest quality measure. While there are many possible underlying dangerous curves, intersections with dirt roads or tracks not on the types of human operators, in this paper we focus on a pairwise op- maps, accidents, possible shelter, and so on. Such features are very erator: a human is asked to compare two objects and returns the one hard for image analysis software to identify, but could be identified object he thinks is of higher quality. We call this type of pairwise relatively easily by people who live in the area, who visited the area comparison a vote. recently, or who are shown satellite images of the area. A crowd- If we ask two humans to compare the same pair of objects they sourcing database system issues tasks to people (e.g., tag features may give us different answers, either because they makes mistakes on this map, compare the quality of one map as compared to an- or because their notion of quality is subjective. Either way, the other), collects the answers, and verifies the answers (e.g., by ask- crowdsourcing algorithm may need to submit the same vote to mul- ing other people to check identified features). We focus on crowd- tiple humans to increase the likelihood that its final answer is cor- sourcing systems where people are paid for their work, although in rect (i.e. that the reported max is indeed the object with the highest others they volunteer their work (e.g., in the Christmas Bird Count, quality measure). Of course, executing more votes increases the http://birds.audubon.org/christmas-bird-count, volunteers identify cost of the algorithm, either in running time and/or in monetary birds across the US), while in other systems the tasks are pre- compensation given to the humans for their work. sented as games that people do for fun (e.g., gwap.com). Ama- There are two types of algorithms for the Max Problem: struc- tured and unstructured. With a structured approach, a regular pat- tern of votes is set up in advance, as in a tournament. For example, if we have 8 objects to consider, we can first compare 1 to 2, 3 to 4, 5 to 6 and 7 to 8. After we get all results, we compare the 1-2 Permission to make digital or hard copies of all or part of this work for winner to the 3-4 winner and the 5-6 winner to the 7-8 winner. In personal or classroom use is granted without fee provided that copies are the third stage, we compare the two winners to obtain the overall not made or distributed for profit or commercial advantage and that copies winner, which is declared the max. If we are concerned about vot- bear this notice and the full citation on the first page. To copy otherwise, to republish, to post on servers or to redistribute to lists, requires prior specific ing errors, we can repeat each vote an odd number of times and use permission and/or a fee. the consensus result. For instance, three humans can be asked to do Copyright 20XX ACM X-XXXXX-XX-X/XX/XX ...$10.00. 

2 .the 1-2 comparison, and the winner of this comparison is the object ment Problem, some of which are adapted from solutions for that wins in 2 or 3 of the individual votes. sorting with noisy comparisons. For small problem settings, While structured approaches are very effective in predictable en- we compare the heuristic solutions to those provided by ML. vironments (such as in a sports tournament), they are much harder When there is only a small number of votes available, we to implement in a crowdsourcing database system, where humans show that one of our methods, a novel algorithm based on may simply not respond to a vote, or may take an unacceptably long PageRank, is the best heuristic. time to respond. In our 8-object example, for instance, after asking • We provide the first formal definition of the Next Votes Prob- for the first 4 votes, and waiting for 10 minutes, we may have only lem, and again, propose a formulation based on ML. We the answers to the 1-2 and 5-6 comparisons. We could then re-issue show that selecting optimal additional votes is NP-Hard, while the 3-4 and 7-8 comparisons and just wait, but perhaps we should computation of the probabilities involved is #P-Hard. also try comparing the winner of 1-2 with the winner of 5-6 (which • We propose four novel heuristics for the Next Votes Prob- was not in our original plan). lem. We experimentally evaluate the heuristics, and when The point is that even if we start with a structured plan in mind, feasible, compare them to the ML formulation. because of incomplete votes we will likely be faced with an un- structured scenario: some subset of the possible votes have com- 2. JUDGMENT PROBLEM pleted (some with varying numbers of repetitions), and we have to answer one or both of the following questions: 2.1 Problem Setup • Judgment Problem: what is our current best estimate for the Objects and Permutations: We are given a set O of n objects overall max winner? {o1 , ..., on }, where each object oi is associated with a latent quality • Next Votes Problem: if we want to invoke more votes, which ci , with no two c’s being the same. If ci > cj , we say that oi are the most effective ones to invoke, given the current stand- is greater than oj . Let π denote a permutation function, e.g., a ing of results? bijection from N to N , where N = {1, ..., n}. We use π(i) to In this paper we focus precisely on these two problems, in an un- denote the rank, or index, of object oi in permutation π, and π −1 (i) structured setting that is much more likely to occur in a crowdsourc- to denote the object index of the ith position in permutation π. If ing database system. Both of these problems are quite challenging π(i) < π(j), we say that oi is ranked higher than oj in permutation because there may be many objects in the database, and because π. Since no two objects have the same quality, there exists a true there are many possible votes to invoke. An additional challenge permutation π ∗ such that for any pair (i, j), if π ∗ (i) < π ∗ (j), then is contradictory evidence. For instance, say we have three objects, cπ∗ (i) > cπ∗ (j) . Note that throughout this paper, we use the terms and one vote told us 1 was better than 2, another vote told us that permutation and ranking interchangeably. 2 was better than 3, and a third one told us that 3 was better and 1. What is the most likely max in a scenario like this one where evi- Voting: We wish to develop an algorithm to find the maximum dence is in conflict? Should we just ignore “conflicting” evidence, (greatest) object in set O, i.e., to find π ∗−1 (1). The only type of op- but how exactly do we do this? Yet another challenge is the lack of eration or information available to an algorithm is a pairwise vote: evidence for some objects. For example, say our evidence is that in a vote, a human worker is shown two objects oi and oj , and 1 is better than objects 2, 3 and 4. However, there are two addi- is asked to indicate the greater object. We assume that all work- tional objects, 5 and 6, for which there is no data. If we can invoke ers vote correctly with probability p (0.5 < p ≤ 1), where p is a one more vote, should we compare the current favorite, object 1, quantity indicating average worker accuracy. We also assume p is against another object to verify that it is the max, or should we at unaffected by worker identities, object values, or worker behavior. least try comparing 5 and 6, for which we have no information? In other words, each vote can be viewed as a independent Bernoulli The Judgment Problem draws its roots from the historical paired trial with success probability p. Note that in general the value p is comparisons problem, wherein the goal is to find the best rank- not available to the algorithm, but we may use it for evaluating ing of objects when noisy evidence is provided [20, 29, 12]. The the algorithm. However, for reference we do study two algorithms problem is also related to the Winner Determination problem in the where p is known. economic and social choice literature [6], wherein the goal is to find Goals: No matter how the algorithm decides to issue vote requests the best object via a voting rule: either by finding a “good” rank- to workers, at the end it must select what it thinks is the maximum ing of objects and then returning the best object(s) in that ranking, object based on the evidence, i.e., based on the votes completed or by scoring each object and returning the best scoring object(s). so far. We start by focusing on this Judgment Problem, which we As we will see in Section 2, our solution to the Judgment Problem define as follows: differs from both of these approaches. As far as we know, no coun- P ROBLEM 1 (J UDGMENT ). Given W , predict the maxi- terpart of the Next Votes problem exists in the literature. We survey mum object in O, π ∗−1 (1). related work in more detail in Section 4. In summary, our contributions are as follows: In Section 3, we then address the other important problem, i.e., • We formalize the Max Problem for a crowdsourcing database how to request additional votes (in case the algorithm decides it is system, with its two subproblems, the Judgment and the Next not done yet). In general, a solution to the Judgment Problem is Votes problems. based upon a scoring function s. The scoring function first com- • We propose a Maximum Likelihood (ML) formulation of putes a score s(i) for each object oi , with the score s(i) represent- the Judgment Problem, which finds the object that is prob- ing the “confidence” that object oi is the true maximum. As we abilistically the most likely to be the maximum. We show will see, for some strategies scores are actual probabilities, for oth- that computing the Maximum Likelihood object is NP-Hard, ers they are heuristic estimates. Then, the strategy selects the object while computation of the probabilities involved is #P-Hard. with the largest score as its answer. To the best of our knowledge, our ML formulation is the first Representation: We represent the evidence obtained as an n × n formal definition and analysis of the Judgment Problem. vote matrix W , with wij being the number of votes for oj being • We propose and evaluate four different heuristics for the Judg- greater than oi . Note that wii = 0 for all i. No other assumptions 

3 . Since we know the values of both p and W , we can derive a for- mula for P (πd |W ) in Equation 1. In particular, the most likely permutation(s), is simply: arg max P (πd |W ) (4) d 0 1 The permutations optimizing Equation 4 are also known as Kemeny 0 2 0 0 permutations or Kemeny rankings [9]. B 0 0 2 3 C W =B C For example, consider the matrix W of Figure 1. We do not show @ 0 1 0 1 A the computations here, but it turns out that the two most probable 0 0 1 0 permutations of the objects are (D, C, B, A) and (C, D, B, A), with all other permutations having lower probability. This result Figure 1: How should these objects be ranked? Vote matrix (left) and roughly matches our intuition, since object A was never voted to equivalent graph representation (right). Arc weights indicate number of votes. be greater than any of the other objects, and C and D have more votes in favor over B. are made about the structure of matrix W . The evidence can also We can derive the formula for the probability that a given object be viewed as a directed weighted graph Gv = (V, A), with the oj has a given rank k. Let π −1 (i) denote the position of object vertices being the objects and the arcs representing the vote out- i in the permutation associated with random variable π. We are comes. For each pair (i, j), if wij > 0, arc (i, j) with weight interested in the probability P (π −1 (k) = j|W ). Since the event wij is present in A. For example, Figure 1 displays a sample vote (π = πd ) is disjoint for different permutations πd , we have: matrix and equivalent graph representation. In this example, ob- X ject 1 is called A, object 2 is B, and so on. For instance, there is P (π −1 (k) = j|W ) = P (πd |W ) an arc from vertex (object) B to vertex C with weight 2 because −1 d:πd (k)=j w2,3 = 2, and there is a reverse arc from C to B with weight 1 because w3,2 = 1. If there are no votes (wij = 0, as from B to A), Substituting for P (πd |W ) using Equation 1 and simplifying, we we can either say that there is no arc, or that the arc has weight 0. have: X P (W |πd ) 2.2 Maximum Likelihood −1 d:πd (k)=j Preliminaries: We first present a Maximum Likelihood (ML) for- P (π −1 (k) = j|W ) = X (5) mulation of the Judgment Problem. We directly compute the object P (W |πl ) that has the highest probability of being the maximum object in O, l given vote matrix W . Assuming that average worker accuracy p Since we are interested in the object oj with the highest proba- is known, the ML formulation we present is the optimal feasible bility of being rank 1, e.g., P (π −1 (1) = j|W ), we now have the solution to the Judgment Problem. Maximum Likelihood formulation to the Judgment Problem: Let π be a random variable over the set of all n! possible permu- tations, where we assume a-priori that each permutation is equally ML F ORMULATION 1 (J UDGMENT ). Given W and p, likely to be observed. We denote the probability of a given permu- determine: arg maxj P (π −1 (1) = j|W ). tation πd given the vote matrix W as P (π = πd |W ). For the ease of exposition, we adopt the shorthand P (πd |W ) instead of writing P (π = πd |W ). To derive the formula for P (πd |W ), we first apply In the example graph of Figure 1, while C and D both have Bayes’ theorem, Kemeny permutations where they are the greatest objects, D is the more likely max over a large range of p values. For instance, P (W |πd )P (πd ) P (W |πd )P (πd ) for p = 0.75, P (π −1 (1) = C|W ) = 0.36 while P (π −1 (1) = P (πd |W ) = = X (1) P (W ) P (W |πj )P (πj ) D|W ) = 0.54. This also matches our intuition, since C has one j vote where it is less than B, while D is never voted to be less than either A or B. From our assumption that the prior probabilities of all permutations 1 Maximum Likelihood Strategy: Equation 5 implies that we only are equal, P (πd ) = n! . need to compute P (W |πd ) for each possible permutation πd , us- Now consider P (W |πd ). Given a permutation πd , for each un- ing Equation 3, in order to determine P (π −1 (k) = j|W ) for all ordered pair {i, j}, the probability fπd (i, j) of observing wij and values j and k. In other words, by doing a single pass through all wji is the binomial distribution probability mass function (p.m.f.): permutations, we can compute the probability that any object oj ( `w +w ´ w has a rank k, given the vote matrix W . ij ji p ji (1 − p)wij if πd (i) < πd (j) We call this exhaustive computation of probabilities the Max- fπd (i, j) = `w w+w ij imum Likelihood Strategy and use it as a baseline in our experi- ´ w ij wji ji p ij (1 − p)wji if πd (j) < πd (i) ments. Note that the ML strategy is the optimal feasible solution (2) to the Judgment Problem. The pseudocode for this strategy is dis- Note that if both wij and wji are equal to 0, then fπd (i, j) = played in Strategy 1. The strategy utilizes a ML scoring function, 1. Now, given a permutation πd , observing the votes involving an unordered pair {i, j} is conditionally independent of observ- which computes the score of each object as s(j) = P (π −1 (1) = j|W ). The predicted max is then the object with the highest score. ing the votes involving any other unordered pair. Using this fact, Note that the strategy can be easily adapted to compute the maxi- P (W |πd ), the probability of observing all votes given a permuta- mum likelihood of arbitrary ranks (not just first) over the set of all tion πd is simply: Y possible permutations. P (W |πd ) = fπd (i, j) (3) i,j:i<j 2.3 Computational Complexity 

4 .Maximum Likelihood Permutations: We begin by considering graph like Figure 1. In particular, we view weighted arcs as mul- the complexity of computing Equation 4. The problem has been tiple arcs. For instance, if there is an arc from vertex A to B with shown to be NP-Hard [31]. We briefly describe the result, before weight 3, we can instead view it as 3 separate edges from A to B. moving on to the Judgment Problem. We use this alternate representation in our proof. Consider Equation 3. Let ψ(πd , W ) denote the number ofX votes An arc i → j respects a permutation if the permutation has oj in W that agree with permutation πd , e.g. ψ(πd , W ) = wij .ranked higher than oi (and does not if the permutation has oi ranked ij:πd (j)<πd (i) higher than oj ). A Kemeny permutation is simply a permutation Let T (W ) denote the total number of votes in W , e.g. T = ||W ||1 . of the vertices (objects), such that the number of arcs that do not Equation 3 can be rewritten as: respect the permutation is minimum. There may be many such permutations, but there always is at least one such permutation. P (W |πd ) = Zpψ(πd ,W ) (1 − p)T (W )−ψ(πd ,W ) (6) The starting vertex (rank 1 object) in any of these permutations is x a−x a Kemeny winner. It can be shown that finding a Kemeny winner In this expression, Z is a constant. Note that p (1 − p) is an is NP-Hard (using a reduction from the feedback arc set problem, increasing function with respect to x, for 0.5 < p < 1 and constant similar to the proof in Hudry et al. [17]). a. Therefore, maximizing P (W |πd ) is equivalent to maximiz- We now reduce the Kemeny winner determination problem to ing ψ(πd , W ). This implies that computing arg maxi ψ(πi , W ) is one of finding the maximum object. Consider a directed weighted equivalent to computing the most likely permutation(s), arg maxi P (πi |W ). graph G, where we wish to find a Kemeny winner. We show that ψ(·) is known as the Kemeny metric, and has been well studied in with a suitable probability p, which we set, the maximum object the economic and social choice literature [19]. Referring to the (i.e., the solution to the Judgment Problem) in G is a Kemeny win- example in Figure 1, the Kemeny metric is maximized by two per- ner. As before, the probability that a certain object oj is the maxi- mutations of the objects, (D, C, B, A) or (C, D, B, A). For both mum object is the right hand side of Equation 5 with k set to 1. The these permutations, the Kemeny metric is equal to 2+2+1+3 = 8. denominator can be ignored since it is a constant for all j. We set We next show that maximizing the Kemeny metric is equivalent to worker accuracy p to be very close to 1. In particular, we choose a solving a classical NP-Hard problem. value p such that 1−p p < n!1 . Consider the directed graph Gv = (V, A) representing the votes Now, consider all permutations πd that areX not Kemeny permuta- of W (Figure 1 is an example). The minimum feedback arc set of ′ ′ tions. In this case, it can be shown that P (W |πd ) < Gv is the smallest weight set of arcs A ⊆ A such that (V, A\A ) is d:πd is not Kemeny acyclic. Equivalently, the problem can also be seen as maximizing ′ P (W |πs ) for any Kemeny permutation πs . Thus, the object oj that the weight of acyclic graph (V, A\A ). maximizes Equation 5 (for k = 1) has to be one that is a Kemeny Now, supposing we have a method to solve for the minimum winner. feedback arc set, consider a topological ordering πt of the vertices X To see why P (W |πd ) < P (W |πs ) for a Ke- in the resulting acyclic graph. Referring back to Equation 6, the d:πd is not Kemeny permutation πt maximizes the Kemeny metric pψ(π,W ) . Therefore, meny permutation πs , notice that the left hand side is at most n! × solving the minimum feedback arc set problem for Gv is equivalent ′ ′ P (W |πd ) where πd is the permutation (not Kemeny) that has the to our original problem of finding the most likely permutation given least number of arcs that do not respect the permutation. Note that a set of votes. Referring back to our example in Figure 1, the mini- ′ P (W |πd ) is at most P (W |πs )× 1−p , since this permutation has at mum feedback arc set is 2, equivalent to cutting arc (C, B) and one p least one more mistake as compared to any Kemeny permutation. of arcs (C, D) or (D, C). Therefore, we have shown that, for a suitable p, the maximum Finding the minimum feedback arc set in a directed graph is a object in G is a Kemeny winner. Thus, we have a reduction from classical NP-Hard problem, implying that the problem of finding the Kemeny winner problem to the Judgement problem. Since find- the ML permutation given a set of votes is NP-Hard as well. ing a Kemeny winner is NP-Hard, this implies that finding the max- T HEOREM 1. (Hardness of Maximum Likelihood Permutation) [31] imum object in G is NP-Hard. Finding the Maximum Likelihood permutation given evidence is NP-Hard. #P-Hardness of Probability Computations: In addition to being NP-Hard to find the maximum object, we can show that evaluating Hardness of the Judgment Problem: In Section 2.2, we presented the numerator of the right hand side of Equation 5 (with k = 1) is a formulation for the Judgment Problem based on ML for finding #P-Hard, in other words: computing P (π −1 (1) = j, W ) is #P- the object most likely to be the max (maximum) object in O. Un- Hard. fortunately, the strategy based on that formulation was computa- We use a reduction from the problem of counting the number tionally infeasible, as it required computation across all n! permu- of linear extensions in a directed acyclic graph (DAG), which is tations of the objects in O. We now show that the optimal solution known to be #P-Hard. to the problem of finding the maximum object is in fact NP-Hard using a reduction from the problem of determining Kemeny win- ners [17]. (Hudry et al. [17] actually show that determining Slater T HEOREM 3. (#P-Hardness of Probability Computation) Com- winners in tournaments is NP-Hard, but their proof also holds for puting P (π −1 (1) = j, W ) is #P-Hard. Kemeny winners. We will describe the Kemeny winner problem P ROOF. A linear extension is a permutation of the vertices, such below.) Our results and proof are novel. that all arcs in the graph respect the permutation (i.e., a linear ex- tension is the same as a Kemeny permutation for a DAG). T HEOREM 2. (Hardness of the Judgment Problem) Finding the Consider a DAG G = (V, A). We add an additional vertex x maximum object given evidence is NP-Hard. such that there is an arc from each of the vertices in G to x, giv- P ROOF. We first describe the Kemeny winner problem. In this ing a new graph G′ = (V ′ , A′ ). We now show that computing proof, we use an alternate (but equivalent) view of a directed weighted P (π −1 (1) = x, W ) in G′ can be used to compute the number of 

5 .linear extensions in G. Notice that: Given vote matrix W , we construct a complete graph between all ′ |A | objects where arc weights lji are equal to P (π(i) < π(j)|wij , wji ). P (π −1 (1) = x, W ) = X ai pi (1 − p)|A |−i ′ lji reflects the probability that oi is greater than oj given the local i=0 evidence wij and wji . It is important to note that this method is a ′ heuristic, e.g., we compute P (π(i) < π(j)|wij , wji ), rather than |A | |A′ | X 1 − p |A′ |−i P (π(i) < π(j)|W ), which requires full enumeration over all n! =p × ai ( ) (7) permutations. i=0 p How do we compute arc weight P (π(i) < π(j)|wij , wji )? where ai is the number of permutations where there are i arcs that respect the permutation. Clearly, the number that we wish to de- P (π(i) < π(j)|wij , wji ) = termine is a|A′ | , since that is the number of permutations that cor- P (wij , wji |π(i) < π(j))P (π(i) < π(j)) respond to linear extensions. Equation 7 is a polynomial of degree P (wij , wji ) |A′ | in 1−p p , thus, we may simply choose |A′ | + 1 different values (8) 1−p of p , generate |A′ | + 1 different graphs G′ , and use the probabil- Assuming that a priori all permutations π are equally likely, P (π(i) < ity computation in Equation 7 to create a set of |A′ | + 1 equations π(j)) = P (π(j) < π(i)) by symmetry. Using Equation 8 to involving the ai coefficients. We may then derive the value of a|A| find expressions for P (π(i) < π(j)|wij , wji ) and P (π(i) > using Lagrange’s interpolation formula. π(j)|wij , wji ), we can derive the following: Since vertex x is the only maximum vertex in G′ , by comput- ing P (π −1 (1) = x, W ) in G′ , we count the number of linear P (π(i) < π(j)|wij , wji ) P (wij , wji |π(i) < π(j)) = (9) extensions in DAG G. Since counting the number of linear ex- P (π(i) > π(j)|wij , wji ) P (wij , wji |π(i) > π(j)) tensions in a DAG is #P-Hard, this implies that the computation of P (π −1 (1) = x, W ) in G′ is #P-Hard, which implies that the com- Since P (π(i) < π(j)|wij , wji )+P (π(j) < π(i)|wij , wji ) = 1, putation of P (π −1 (k) = j, W ) for directed graph Gv (associated we can simplify Equation 9 to get the following expression: with vote matrix W ) is #P-Hard. P (π(i) < π(j)|wij , wji ) = P (wij , wji |π(i) < π(j)) (10) Strategy 1 Maximum Likelihood P (wij , wji |π(i) < π(j)) + P (wij , wji |π(i) > π(j)) Require: n objects, probability p, vote matrix W Using Equation 2, P (wij , wji |π(i) < π(j)) and P (wij , wji |π(i) < Ensure: ans = maximum likelihood maximum object π(j)) can be computed directly from the binomial distribution p.m.f. s[·] ← 0 {s[i] is used to accumulate the probability that i is the Therefore, we can compute the arc weight lji = P (π(i) < π(j)|wij , wji ) maximum object} needed for the Indegree scoring function. It should be clear that for each permutation π of n objects do lij + lji = 1. Also, if wij and wji are both equal to zero, then both prob ← 1 {prob is the probability of permutation π given lij and lji are computed to be 0.5. vote matrix W } for each tuple (i, j) : i < j do Strategy 2 Indegree if π(i) < π(j) then` prob ← prob × wijw+w ji p ji (1 − p)wij ´ w Require: n objects, probability p, vote matrix W ij Ensure: ans = predicted maximum object else s[·] ← 0 prob ← prob × wijw+w ´ w p ij (1 − p)wji ` ji ji for i : 1 . . . n do end if for j : 1 . . . n, j = i do end for s[i] ← s[i] + lji {lji = P (π(i) < π(j)|wij , wji )} s[π −1 (1)] ← s[π −1 (1)] + prob end for end for end for ans ← argmaxi s[i] ans ← argmaxi s[i] The Indegree scoring function, displayed in Strategy 2, computes 2.4 Heuristic Strategies P the score of object oj as: s(j) = i lij . Intuitively, vertices with The ML scoring function is computationally inefficient and also higher scores correspond to objects which have compared favorably requires prior knowledge of p, the average worker accuracy, which to other objects, and hence should be ranked higher. The predicted is not available to us in real-world scenarios. We next investigate ranking has been shown to be a constant factor approximation to the performance and efficiency of four heuristic strategies, each of the feedback arc set for directed graphs where all arcs (i, j) are which runs in polynomial time. The heuristics we present, exclud- present and lij + lji = 1 [11]. The running time of this heuristic is ing the Indegree heuristic, do not require explicit knowledge of the dominated by the time to do the final sort of the scores. worker accuracy p. Let us walk through the example graph in Figure 1. First, for Indegree Strategy: The first heuristic we consider is an Indegree those pairs of vertices that do not have any votes between them, scoring function proposed by Coppersmith et al. [11] to approx- we have lAC = 0.5, lCA = 0.5, lAD = 0.5, and lDA = 0.5. By imate the optimal feedback arc set in a directed weighted graph symmetry, lCD = 0.5 and lDC = 0.5. Given a value of p, we where arc weights lij , lji satisfy lij + lji = 1 for each pair of use Equation 10 to compute the rest of the arc weights. For p = vertices i and j. In this section, we describe how to transform our 0.55, we have lAB = 0.599, lBA = 0.401, lBC = 0.55, lCB = vote matrix W to a graph where this Indegree scoring function can 0.45, lBD = 0.646, and lDB = 0.354. With these computed arc be applied. Let π(i) denote the rank, or index, of object oi in the weights, we obtain the scores: s(A) = 1.401, s(B) = 1.403, s(C) = permutation associated with random variable π. 1.55, and s(D) = 1.65, generating a predicted ranking of (D, C, B, A), 

6 .with object D being the predicted maximum object. Note that if p s(C) = 3 − 2 + 3 = 4, and s(D) = 4 − 1 + 3 = 6. The predicted is larger, e.g. p = 0.95, the Indegree heuristic predicts the same ranking is then (D, C, B, A), with object D being the predicted ranking. maximum object. Local Strategy: The Indegree heuristic is simple to compute, but PageRank Strategy: Both the Indegree and Local heuristics use only takes into account local evidence. That is, the score of object only information one or two steps away to make inferences about oi only depends on the votes that include oi directly. We now con- the objects of O. We next consider a global heuristic scoring func- sider a Local scoring function, adapted from a heuristic proposed tion inspired by the PageRank [26] algorithm. The general idea be- by David [13], which considers evidence two steps away from oi . hind using a PageRank-like procedure is to utilize the votes in W as This method was originally proposed to rank objects in incomplete a way for objects to transfer “strength” between each other. The use tournaments with ties. We adapted the scoring function to our set- of PageRank to predict the maximum has been previously consid- ting, where there can be multiple comparisons between objects, and ered [5] in the literature. Our contribution is a modified PageRank there are no ties in comparisons. to predict the maximum object in O, which in particular, can handle This heuristic is based P on the notion of wins and losses, P defined directed cycles in the directed graph representing W . as follows: wins(i) = j w ji and losses(i) = i wij . For Consider again the directed graph Gv representing the votes of instance, in Figure 1, vertex B has 3 wins and 5 losses. + W (Figure 1 is an example). Let + P d (i) to + denote the outdegree of The score s(i) has three components. The first is simply wins(i)− vertex i in Gv , e.g. d (i) = j wij . If d (i) = 0, we say that i losses(i), reflecting the net number of votes in favor of oi . For is a sink vertex. vertex B, this first component would be 3 − 5 = −2. Since this Let prt (i) represent the PageRank of vertex i in iteration t. We first component does not reflect the “strength” of the objects oi was initialize each vertex to have the same initial PageRank, e.g., pr0 (·) = compared against, we next add a “reward”: for each oj such that 1 n . In each iteration t + 1, we apply the following update equation wji > wij (i has net wins over j), we add wins(j) to the score to each vertex i: of oi . In our example, B only has net wins over A, so we reward X wji B with wins(A) (which in this case is zero). On the other hand, prt+1 (i) = prt (j) (12) d+ (j) since C beat out B, then C gets a reward of wins(B) = 3 added j to its score. Finally, we “penalize” s(i) by subtracting losses(j) For each iteration, each vertex j transfers all its PageRank (from for each oj that overall beat oi . In our example, we subtract from the previous iteration) proportionally to the other vertices i whom s(B) both losses(C) = 2 and losses(D) = 1. Thus, the final workers have indicated may be greater than j, where the propor- score s(B) is −2 plus the reward minus the penalty, i.e., s(B) = w tion of j’s PageRank transferred to i is equal to d+ji . Intuitively, (j) −2 + 0 − 3 = −5. prt (i) can be thought as a proxy for the probability that object oi More formally, score s(i) is defined as follows: X is the maximum object in O (during iteration t). s(i) = wins(i) − losses(i) + [1(wji > wij )wins(j)] What happens to the PageRank vector after performing many j update iterations using Equation 12? Considering the strongly con- X nected components (SCCs) of Gv , let us define a terminal SCC to − [1(wij > wji )losses(j)] (11) be a SCC whose vertices do not have arcs transitioning out of the j SCC. After a sufficient number of iterations, the PageRank prob- ability mass in Gv becomes concentrated in the terminal SCCs Strategy 3 Local of Gv , with all other vertices outside of these SCCs having zero Require: n objects, vote matrix W PageRank [4]. In the context of our problem, these terminal SCCs Ensure: ans = predicted maximum object can be thought of as sets of objects which are ambiguous to order. wins[·], losses[·], s[·] ← 0 {objects are ranked by s[·]} Our proposed PageRank algorithm is described in Strategy 4. for each tuple (i, j) : do How is our strategy different from the standard PageRank algo- wins[j] ← wins[j] + wij rithm? The original PageRank update equation is: losses[i] ← losses[i] + wij 1−d X wji end for prt+1 (i) = +d prt (j)) n j d+ (j) for i : 1 . . . n do s[i] ← wins[i] − losses[i] {add wins − losses to s} Comparing the original equation and Equation 12, the primary dif- for j : 1 . . . n, j = i do ference is that we use a damping factor d = 1, e.g. we remove jump if wij < wji then probabilities. PageRank was designed to model the behavior of a s[i] ← s[i] + wins[j] {add reward} random surfer traversing the web, while for the problem of ranking else if wij > wji then objects, we do not need to model a random jump vector. s[i] ← s[i] − losses[j] {subtract penalty} A second difference between our modified PageRank and the end if original PageRank is that prior to performing any update iterations, end for for each sink vertex i, we set wii equal to 1 in W . In our set- end for ting, sinks correspond to objects which may be the maximum object ans ← argmaxi s[i] (e.g., no worker voted that oi is less than another object). By set- ting wii to 1 initially, from one iteration to the next, the PageRank Having computed s(·), we sort all objects by decreasing order in sink i remains in sink i. This allows PageRank to accumulate of s. The resulting permutation is our predicted ranking, with the in sinks. Contrast this with the standard PageRank methodology, vertex having largest s being our predicted maximum object. An where when a random surfer reaches a sink, it is assumed that (s)he implementation of the method is displayed in Strategy 3. transitions to all other vertices with equal probability. To complete the example of Figure 1, Strategy 3 computes the Finally, a caveat to our PageRank strategy is that the PageRank following scores: s(A) = 0−2−5 = −7, s(B) = 3−5−3 = −5, vector (pr(·) in Strategy 4) may not converge for some vertices 

7 .Strategy 4 PageRank Heuristic Prediction Require: n objects, vote matrix W , K iterations ML (D, C, B, A) and (C, D, B, A) Ensure: ans = predicted maximum object Indegree (D, C, B, A) construct Gv = (V, A) from W Local (D, C, B, A) compute d+ [·] for each vertex {compute all outdegrees} for i : 1 . . . n do PageRank Maximum object = C if d+ [i] == 0 then Iterative (C, D, B, A), (C, D, A, B), (D, C, B, A), or wii ← 1 (D, C, A, B) end if end for Table 1: Predictions using each heuristic for Figure 1. 1 pr0 [·] ← n {pr0 is the PageRank vector in iteration 0} for k : 1 . . . K do ject C to be the maximum object in O. for i : 1 . . . n do Iterative Strategy: We next propose an Iterative heuristic strategy for j : 1 . . . n, j = i do to determine the maximum object in O. The general framework is w prk [i] ← prk [i] + d+ji [j] prk−1 [j] the following: end for 1. Place all objects in a set. end for 2. Rank the objects in the set by a scoring metric. end for compute period[·] of each vertex using final iterations of pr[·] 3. Remove the lower ranked objects from the set. for i : 1 . . . n do 4. Repeat steps 3 and 4 until only one object remains. s[i] ← 0 {s[·] is a vector storing average PageRank} There are two parameters we can vary in this framework: the for j : 0 . . . period[i] − 1 do scoring metric and the number of objects eliminated each itera- s[i] ← s[i] + prK−j [i] tion. Let us define the dif (i) metric of object oi to be equal to end for wins(i) − losses(i). An implementation of the Iterative strategy s[i] s[i] ← period[i] using the dif metric is displayed in Strategy 5. In our particular im- end for plementation, we emphasize computational efficiency and remove ans ← argmaxi s[i] half of the remaining objects each iteration. The Iterative strat- egy relies upon the elimination of lower ranked objects before re- ranking higher ranked objects. With each iteration, as more objects in terminal SCCs. To handle the oscillating PageRank in terminal are removed, the dif s of the higher ranked objects separate from SCCs, we execute our PageRank update equation (Equation 12) for the dif s of the lower ranked objects. Basically, by removing lower a large number of iterations, denoted as K in Strategy 4. Then, we ranked objects, the strategy is able to more accurately rank the re- examine the final iterations, say final 10%, of the PageRank vector maining set of objects. The strategy can be thought of as iteratively to empirically determine the period of each vertex, where we de- narrowing in on the maximum object. fine the period as the number of iterations for the PageRank value It is important to note that other scoring metrics can be used with of a vertex to return to its current value. In practice, we find that this Iterative strategy as well. For example, by iteratively ranking running PageRank for K iterations, where K = O(n), is sufficient with the Local heuristic, we were able to achieve (slightly) better to detect the period of nearly all vertices in terminal SCCs. For performance than the simple dif metric. Our method is similar to example, consider a graph among 3 objects A, B, C with 3 arcs: the Greedy Order algorithm proposed by Cohen et al. [7], who con- (A, B), (B, C), and (C, B). All vertices initially have 31 PageR- sidered a problem related to feedback arc set. Our strategy differs ank probability. After 1 iteration, the PageRank vector is (0, 32 , 13 ). in that it is more general (e.g., it can utilize multiple metrics), and After 2 iterations, the PageRank vector is (0, 13 , 32 ). And so on. In our strategy can be optimized (e.g., if we eliminate half of the ob- this example, object B and C each have periods of 2. jects each iteration, we require only a logarithmic number of sorts, With the periods computed for each vertex, we compute an av- as opposed to a linear number). erage PageRank value for each vertex over its period. This aver- The Iterative strategy can also be viewed as a scoring function age PageRank is used as the scoring function s(·) for this strat- s(·), like the prior heuristics we have examined. Denoted as s[·] egy. After the termination of PageRank, we sort the vertices by in Strategy 5, we can assign each object a score equal to the it- decreasing order of s(·), and predict that the vertex with maximum eration number in which it was removed from set T . Using this average PageRank corresponds to the maximum object in O. Note scoring function s(·), the predicted maximum object is then simply that our PageRank heuristic is primarily intended to predict a maxi- argmaxi s(i). mum object, not to predict a ranking of all objects (as many objects Returning to the example graph in Figure 1, the Iterative heuris- will end up with no PageRank). However, for completeness, when tic first computes the dif metric for each object: dif (A) = −2, evaluating PageRank in later experiments, we still do consider the dif (B) = −2, dif (C) = 1 and dif (D) = 3. The objects are predicted ranking induced by PageRank. The details of our imple- then placed in a set and sorted by dif . In the first iteration, objects mentation are displayed in Strategy 4. A and B are assigned ranks 3 and 4 and removed from the set. To illustrate our PageRank heuristic, consider again the example Then, dif is recomputed among all remaining objects in the set, in Figure 1. There are 2 SCCs in the graph: (A) and (B, C, D), dif (C) = 0 and dif (D) = 0. In the second iteration, either object with (B, C, D) being a terminal SCC. Each of the 4 vertices is ini- C or D is removed and assigned rank 2. In the third iteration, the tialized with 0.25 PageRank. After the first iteration, the PageRank remaining object is removed and assigned rank 1. Therefore, the vector is (0, 0.375, 0.35, 0.275). After the second iteration, the predicted ranking of the Iterative heuristic is equally likely to be PageRank vector is (0, 0.375, 0.35, 0.275). After ~20 iterations, (C, D, B, A), (C, D, A, B), (D, C, B, A), or (D, C, A, B), with the PageRank vector oscillates around (0, 0.217, 0.435, 0.348). With the predicted maximum object of the heuristic being object C or D a sufficiently large number of iterations and an appropriately cho- with equal probability. sen convergence threshold, the heuristic determines a period of To summarize, Table 1 displays the predictions for ML and our 1 for both SCCs and computes an average PageRank vector of four heuristics for the example displayed in Figure 1. How can we (0, 0.217, 0.435, 0.348). The PageRank heuristic then predicts ob- determine which heuristic strategy is superior to the others? 

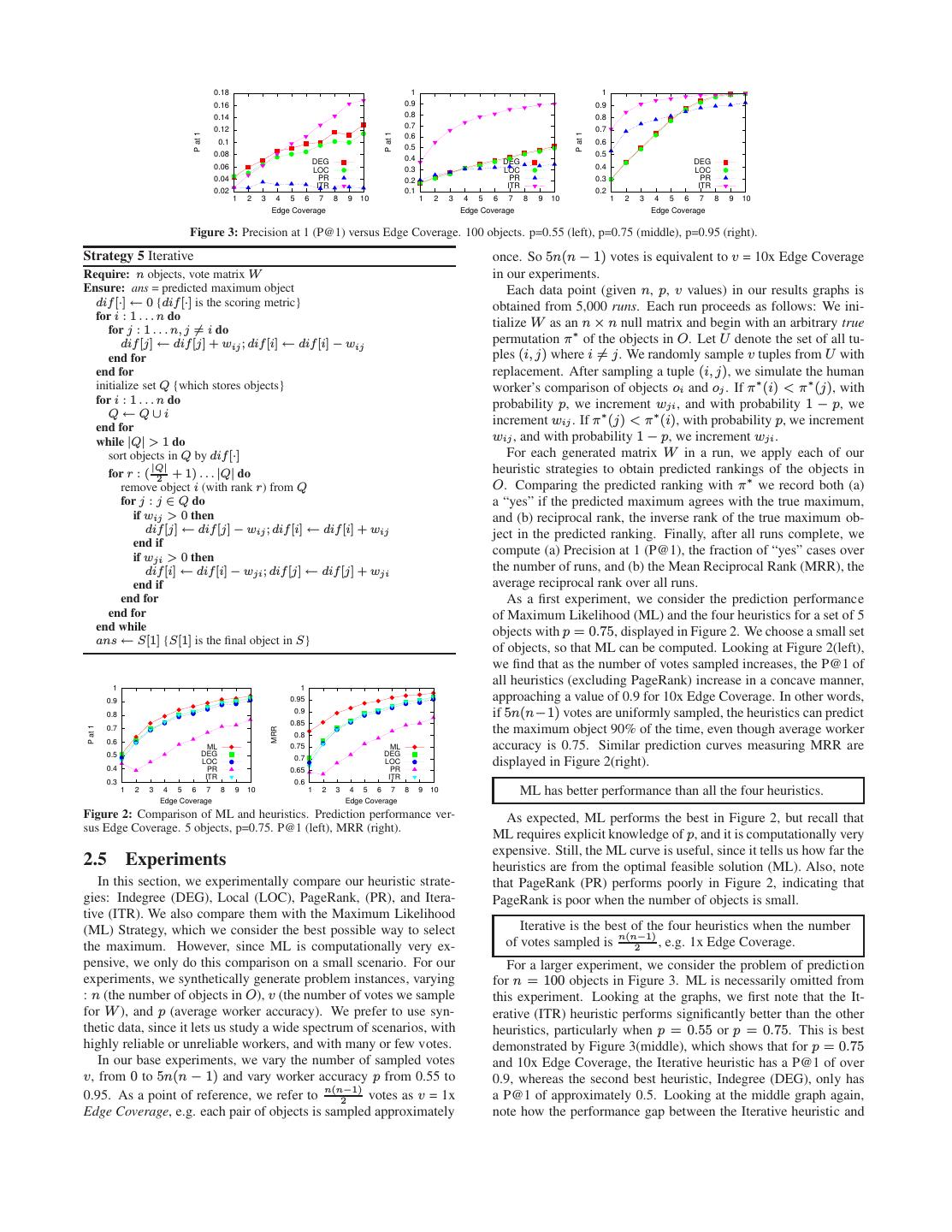
8 . 0.18 1 1 0.16 0.9 0.9 0.14 0.8 0.8 0.7 0.12 0.7 P at 1 P at 1 P at 1 0.6 0.1 0.6 0.5 0.08 0.5 DEG 0.4 DEG DEG 0.06 LOC 0.3 LOC 0.4 LOC 0.04 PR 0.2 PR 0.3 PR ITR ITR ITR 0.02 0.1 0.2 1 2 3 4 5 6 7 8 9 10 1 2 3 4 5 6 7 8 9 10 1 2 3 4 5 6 7 8 9 10 Edge Coverage Edge Coverage Edge Coverage Figure 3: Precision at 1 (P@1) versus Edge Coverage. 100 objects. p=0.55 (left), p=0.75 (middle), p=0.95 (right). Strategy 5 Iterative once. So 5n(n − 1) votes is equivalent to v = 10x Edge Coverage Require: n objects, vote matrix W in our experiments. Ensure: ans = predicted maximum object Each data point (given n, p, v values) in our results graphs is dif [·] ← 0 {dif [·] is the scoring metric} obtained from 5,000 runs. Each run proceeds as follows: We ini- for i : 1 . . . n do tialize W as an n × n null matrix and begin with an arbitrary true for j : 1 . . . n, j = i do dif [j] ← dif [j] + wij ; dif [i] ← dif [i] − wij permutation π ∗ of the objects in O. Let U denote the set of all tu- end for ples (i, j) where i = j. We randomly sample v tuples from U with end for replacement. After sampling a tuple (i, j), we simulate the human initialize set Q {which stores objects} worker’s comparison of objects oi and oj . If π ∗ (i) < π ∗ (j), with for i : 1 . . . n do probability p, we increment wji , and with probability 1 − p, we Q ←Q∪i increment wij . If π ∗ (j) < π ∗ (i), with probability p, we increment end for while |Q| > 1 do wij , and with probability 1 − p, we increment wji . sort objects in Q by dif [·] For each generated matrix W in a run, we apply each of our |Q| for r : ( 2 + 1) . . . |Q| do heuristic strategies to obtain predicted rankings of the objects in remove object i (with rank r) from Q O. Comparing the predicted ranking with π ∗ we record both (a) for j : j ∈ Q do a “yes” if the predicted maximum agrees with the true maximum, if wij > 0 then and (b) reciprocal rank, the inverse rank of the true maximum ob- dif [j] ← dif [j] − wij ; dif [i] ← dif [i] + wij ject in the predicted ranking. Finally, after all runs complete, we end if if wji > 0 then compute (a) Precision at 1 (P@1), the fraction of “yes” cases over dif [i] ← dif [i] − wji ; dif [j] ← dif [j] + wji the number of runs, and (b) the Mean Reciprocal Rank (MRR), the end if average reciprocal rank over all runs. end for As a first experiment, we consider the prediction performance end for of Maximum Likelihood (ML) and the four heuristics for a set of 5 end while objects with p = 0.75, displayed in Figure 2. We choose a small set ans ← S[1] {S[1] is the final object in S} of objects, so that ML can be computed. Looking at Figure 2(left), we find that as the number of votes sampled increases, the P@1 of 1 1 all heuristics (excluding PageRank) increase in a concave manner, 0.9 0.95 approaching a value of 0.9 for 10x Edge Coverage. In other words, 0.8 0.9 if 5n(n−1) votes are uniformly sampled, the heuristics can predict 0.85 the maximum object 90% of the time, even though average worker P at 1 0.7 MRR 0.8 0.6 ML 0.75 ML accuracy is 0.75. Similar prediction curves measuring MRR are 0.5 DEG DEG 0.7 0.4 LOC PR 0.65 LOC PR displayed in Figure 2(right). ITR ITR 0.3 0.6 1 2 3 4 5 6 7 8 9 10 1 2 3 4 5 6 7 8 9 10 ML has better performance than all the four heuristics. Edge Coverage Edge Coverage Figure 2: Comparison of ML and heuristics. Prediction performance ver- As expected, ML performs the best in Figure 2, but recall that sus Edge Coverage. 5 objects, p=0.75. P@1 (left), MRR (right). ML requires explicit knowledge of p, and it is computationally very expensive. Still, the ML curve is useful, since it tells us how far the 2.5 Experiments heuristics are from the optimal feasible solution (ML). Also, note In this section, we experimentally compare our heuristic strate- that PageRank (PR) performs poorly in Figure 2, indicating that gies: Indegree (DEG), Local (LOC), PageRank, (PR), and Itera- PageRank is poor when the number of objects is small. tive (ITR). We also compare them with the Maximum Likelihood (ML) Strategy, which we consider the best possible way to select Iterative is the best of the four heuristics when the number the maximum. However, since ML is computationally very ex- of votes sampled is n(n−1)2 , e.g. 1x Edge Coverage. pensive, we only do this comparison on a small scenario. For our For a larger experiment, we consider the problem of prediction experiments, we synthetically generate problem instances, varying for n = 100 objects in Figure 3. ML is necessarily omitted from : n (the number of objects in O), v (the number of votes we sample this experiment. Looking at the graphs, we first note that the It- for W ), and p (average worker accuracy). We prefer to use syn- erative (ITR) heuristic performs significantly better than the other thetic data, since it lets us study a wide spectrum of scenarios, with heuristics, particularly when p = 0.55 or p = 0.75. This is best highly reliable or unreliable workers, and with many or few votes. demonstrated by Figure 3(middle), which shows that for p = 0.75 In our base experiments, we vary the number of sampled votes and 10x Edge Coverage, the Iterative heuristic has a P@1 of over v, from 0 to 5n(n − 1) and vary worker accuracy p from 0.55 to 0.9, whereas the second best heuristic, Indegree (DEG), only has 0.95. As a point of reference, we refer to n(n−1) 2 votes as v = 1x a P@1 of approximately 0.5. Looking at the middle graph again, Edge Coverage, e.g. each pair of objects is sampled approximately note how the performance gap between the Iterative heuristic and 

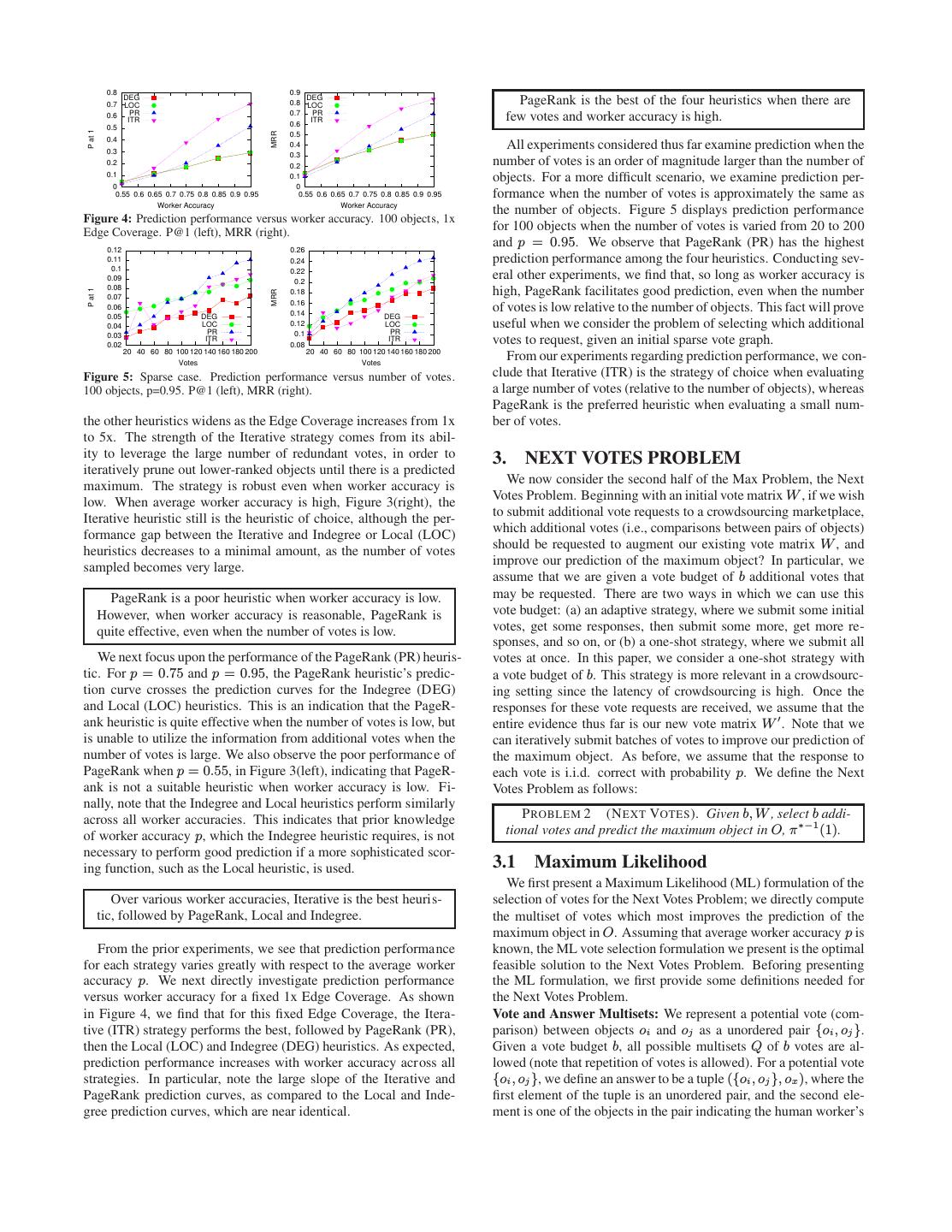
9 . 0.8 0.9 DEG DEG 0.7 LOC 0.8 LOC PageRank is the best of the four heuristics when there are PR 0.7 PR 0.6 ITR 0.6 ITR few votes and worker accuracy is high. 0.5 P at 1 MRR 0.5 0.4 0.3 0.4 All experiments considered thus far examine prediction when the 0.3 0.2 0.2 number of votes is an order of magnitude larger than the number of 0.1 0.1 objects. For a more difficult scenario, we examine prediction per- 0 0 0.55 0.6 0.65 0.7 0.75 0.8 0.85 0.9 0.95 0.55 0.6 0.65 0.7 0.75 0.8 0.85 0.9 0.95 formance when the number of votes is approximately the same as Worker Accuracy Worker Accuracy the number of objects. Figure 5 displays prediction performance Figure 4: Prediction performance versus worker accuracy. 100 objects, 1x Edge Coverage. P@1 (left), MRR (right). for 100 objects when the number of votes is varied from 20 to 200 0.12 0.26 and p = 0.95. We observe that PageRank (PR) has the highest 0.11 0.24 prediction performance among the four heuristics. Conducting sev- 0.1 0.22 0.09 0.2 eral other experiments, we find that, so long as worker accuracy is 0.08 high, PageRank facilitates good prediction, even when the number P at 1 MRR 0.18 0.07 0.16 0.06 0.14 of votes is low relative to the number of objects. This fact will prove 0.05 DEG DEG 0.04 LOC PR 0.12 LOC PR useful when we consider the problem of selecting which additional 0.03 0.1 0.02 ITR 0.08 ITR votes to request, given an initial sparse vote graph. 20 40 60 80 100 120 140 160 180 200 20 40 60 80 100 120 140 160 180 200 Votes Votes From our experiments regarding prediction performance, we con- Figure 5: Sparse case. Prediction performance versus number of votes. clude that Iterative (ITR) is the strategy of choice when evaluating 100 objects, p=0.95. P@1 (left), MRR (right). a large number of votes (relative to the number of objects), whereas PageRank is the preferred heuristic when evaluating a small num- the other heuristics widens as the Edge Coverage increases from 1x ber of votes. to 5x. The strength of the Iterative strategy comes from its abil- ity to leverage the large number of redundant votes, in order to 3. NEXT VOTES PROBLEM iteratively prune out lower-ranked objects until there is a predicted maximum. The strategy is robust even when worker accuracy is We now consider the second half of the Max Problem, the Next low. When average worker accuracy is high, Figure 3(right), the Votes Problem. Beginning with an initial vote matrix W , if we wish Iterative heuristic still is the heuristic of choice, although the per- to submit additional vote requests to a crowdsourcing marketplace, formance gap between the Iterative and Indegree or Local (LOC) which additional votes (i.e., comparisons between pairs of objects) heuristics decreases to a minimal amount, as the number of votes should be requested to augment our existing vote matrix W , and sampled becomes very large. improve our prediction of the maximum object? In particular, we assume that we are given a vote budget of b additional votes that PageRank is a poor heuristic when worker accuracy is low. may be requested. There are two ways in which we can use this However, when worker accuracy is reasonable, PageRank is vote budget: (a) an adaptive strategy, where we submit some initial quite effective, even when the number of votes is low. votes, get some responses, then submit some more, get more re- sponses, and so on, or (b) a one-shot strategy, where we submit all We next focus upon the performance of the PageRank (PR) heuris- votes at once. In this paper, we consider a one-shot strategy with tic. For p = 0.75 and p = 0.95, the PageRank heuristic’s predic- a vote budget of b. This strategy is more relevant in a crowdsourc- tion curve crosses the prediction curves for the Indegree (DEG) ing setting since the latency of crowdsourcing is high. Once the and Local (LOC) heuristics. This is an indication that the PageR- responses for these vote requests are received, we assume that the ank heuristic is quite effective when the number of votes is low, but entire evidence thus far is our new vote matrix W ′ . Note that we is unable to utilize the information from additional votes when the can iteratively submit batches of votes to improve our prediction of number of votes is large. We also observe the poor performance of the maximum object. As before, we assume that the response to PageRank when p = 0.55, in Figure 3(left), indicating that PageR- each vote is i.i.d. correct with probability p. We define the Next ank is not a suitable heuristic when worker accuracy is low. Fi- Votes Problem as follows: nally, note that the Indegree and Local heuristics perform similarly across all worker accuracies. This indicates that prior knowledge P ROBLEM 2 (N EXT VOTES ). Given b, W , select b addi- of worker accuracy p, which the Indegree heuristic requires, is not tional votes and predict the maximum object in O, π ∗−1 (1). necessary to perform good prediction if a more sophisticated scor- ing function, such as the Local heuristic, is used. 3.1 Maximum Likelihood We first present a Maximum Likelihood (ML) formulation of the Over various worker accuracies, Iterative is the best heuris- selection of votes for the Next Votes Problem; we directly compute tic, followed by PageRank, Local and Indegree. the multiset of votes which most improves the prediction of the maximum object in O. Assuming that average worker accuracy p is From the prior experiments, we see that prediction performance known, the ML vote selection formulation we present is the optimal for each strategy varies greatly with respect to the average worker feasible solution to the Next Votes Problem. Beforing presenting accuracy p. We next directly investigate prediction performance the ML formulation, we first provide some definitions needed for versus worker accuracy for a fixed 1x Edge Coverage. As shown the Next Votes Problem. in Figure 4, we find that for this fixed Edge Coverage, the Itera- Vote and Answer Multisets: We represent a potential vote (com- tive (ITR) strategy performs the best, followed by PageRank (PR), parison) between objects oi and oj as a unordered pair {oi , oj }. then the Local (LOC) and Indegree (DEG) heuristics. As expected, Given a vote budget b, all possible multisets Q of b votes are al- prediction performance increases with worker accuracy across all lowed (note that repetition of votes is allowed). For a potential vote strategies. In particular, note the large slope of the Iterative and {oi , oj }, we define an answer to be a tuple ({oi , oj }, ox ), where the PageRank prediction curves, as compared to the Local and Inde- first element of the tuple is an unordered pair, and the second ele- gree prediction curves, which are near identical. ment is one of the objects in the pair indicating the human worker’s 

10 .answer (e.g., x = i if the worker states that oi is greater than oj , or the highest score. Although this strategy is the optimal feasible so- x = j otherwise). lution to the Next Votes Problem, it is also computationally infea- For each vote multiset Q, we define an answer multiset a of Q to sible, since a single iteration of ML itself requires enumeration of be a multiset of answer tuples, where there is a one-to-one mapping all n! permutations of the objects in O. Additionally, knowledge from each unordered pair in Q to an answer tuple in a. Note that of worker accuracy p is required for ML vote selection. This leads each vote is answered (independently) with probability p. As an us to develop our own vote selection and evaluation framework en- example, if Q = {{oi , oj }, {ok , ol }}, a possible answer multiset a abling more efficient heuristics. that could be received from the workers is {({oi , oj }, oi ), ({ok , ol }, ok )}. Note that for a multiset of b votes, there are 2b pos- 3.2 Computational Complexity sible answer multisets. Let A(Q) denote the multiset of all possible As in the Judgment Problem, the Next Votes Problem also turns answer multisets of Q. out to be NP-Hard, while the computation of the probabilities in- Having defined vote and answer multisets, we next consider the volved also turns out to be #P-Hard. While the proofs use reduc- probability of receiving an answer multiset given W , then explain tions from similar problems, the details are quite different. how to compute the confidence of the maximum object having re- Hardness of the Next Votes Problem: We first show that the ML ceived an answer multiset, before finally presenting the ML vote formulation for the Next Votes Problem is NP-Hard, implying that selection strategy. finding the optimal set of next votes to request is intractable. Probabilities of Multisets and Confidences: Suppose that we T HEOREM 4 (H ARDNESS P OF N EXT VOTES ). Finding the vote submitted vote multiset Q and received answer multiset a from the multiset Q that maximizes a∈A(Q) maxi P (π −1 (1) = i, a∧W ) crowdsourcing marketplace. Let P (a|W ) denote the probability of observing an answer multiset a for Q, given initial vote matrix W . is NP-Hard, even for a single vote. We have the following: P ROOF. (Sketch) Our proof for the Next Votes problem uses a reduction from the same NP-Hard problem described in Sec- P (a ∧ W ) P (a|W ) = (13) tion 2.3, i.e., determining Kemeny winners. P (W ) We are given a graph G where we wish to find a Kemeny winner. where a∧W is the new vote matrix formed by combining the votes We add an extra vertex v to this graph to create a new graph, G′ , of a and W . where v does not have any incoming or outgoing arcs. By defini- Our estimate for how well we are able to predict the maximum tion, v is a Kemeny winner in G′ , since trivially, v can be placed object in O is then the probability of the maximum object, given anywhere in the permutation without changing the number of arcs the votes of our new vote matrix, i.e., a ∧ W . We denote this value that are respected. Therefore, there are at least two Kemeny win- by Pmax (a ∧ W ), i.e., this value is our confidence in the maximum ners in G′ . Recall, however, that our goal is to return a Kemeny object. The computation, based upon Equation 5, is the following: winner in G′ , not in G. Now, consider the solution to the Next Votes problem on G′ , Pmax (a ∧ W ) = max P (π −1 (1) = i|a ∧ W ) where an additional vote is requested. We need to show that the i two vertices returned by the Next Votes problem are both Kemeny This simplifies to give: winners in G. Let the two vertices be x, y. As before, recall that maxi P (π −1 (1) = i, a ∧ W ) X Pmax (a ∧ W ) = (14) P (π −1 (1) = i, a ∧ W ) = P (π)P (W ∧ a|π) P (a ∧ W ) π:i wins Maximum Likelihood Strategy: We can now define the Maxi- Ignoring P (π), which is a constant, we have two terms: mum Likelihood formulation of the Next Votes Problem. We wish X X to find the multiset Q of b votes such that, on average over all pos- F = max P (W ∧ x > y|π)+max P (W ∧ y > x|π) i i π:i wins π:i wins sible answer multisets for Q (and weighted by the probability of those answer multisets), our confidence in the prediction of the Now consider Kemeny permutations of W . Let the set of Kemeny maximum object is greatest. winners be S, and let the number of Kemeny permutations begin- In other words, we want to find the multiset that maximizes: ning with each of the winners be s1 ≥ s2 ≥ . . . sn . We also let X the probability p be very close to 1 so that only Kemeny permuta- P (a|W ) × Pmax (a ∧ W ) tions form part of F . If we choose two Kemeny winners as x and a∈A(Q) y, the expression F can be as large as (s1 + s2 ) × P , where P is which, on using Equations 13 and 14, simplifies to: the probability corresponding to one Kemeny permutation. On the other hand, if both of x and y are not Kemeny winners, then we can 1 X show that F < (s1 + s2 ) × P (since the constraint of x < y and × max P (π −1 (1) = i, a ∧ W ) P (W ) i y > x eliminates some non-zero number of permutations from the a∈A(Q) right hand side of the expression.) Now it remains to be seen if x Since P (W ) is a constant, independent of Q, we have: may be a Kemeny winner while y is not. Clearly, the first term can ML F ORMULATION 2 (N EXT VOTES ). Given b, W , be as big as s1 P . It remains to be seen if the second term can be find the vote multiset Q, |Q| = b, that maximizes s2 P . Note that since x is Kemeny, enforcing that y > x is going to X discount all permutations where max > x > y. Thus the second max P (π −1 (1) = i, a ∧ W ) (15) term cannot be as big as s2 P . Thus both the vertices returned by i a∈A(Q) the Next Votes problem are Kemeny winners. Thus, the Kemeny winner determination problem on G can be reduced to the Next Let score(Q) be the value in Equation 15. We now have an ex- Votes (with one vote) problem on G′ . haustive strategy to determine the best multiset Q: compute score(·) for all possible multisets of size b, and then choose the multiset with 

11 . Algorithm 6 General Vote Selection Framework Require: n objects, vote matrix W , budget b Ensure: ans = predicted maximum object compute score s[·] for all objects using function s {Step 1} initialize multiset Q {of votes to request} sort all objects by s[·], store object indices in index[·] select b votes for Q using a vote selection strategy {Step 2} submit batch Q update W with new votes from workers compute final score f [·] for all objects using function f {Step 3} Figure 6: How should we select additional votes to request? ans ← argmaxi f [i] #P-Hardness of Probability Computations: We next show that computing Equation 15 is #P-Hard. of b votes? Since ML vote selection is computationally infeasible, P T HEOREM 5 (#P-H −1 ARDNESS OF N EXT VOTES ). Computing we consider four efficient polynomial-time vote selection strate- a∈A(Q) maxi P (π (1) = i, a ∧ W ) is #P-Hard, even for a Q with a single vote. gies: Paired, Max, Greedy, and Complete Tournament strategies. For ease of explanation, we use the graph in Figure 6 as an ex- P ROOF. (Sketch) Our proof uses a reduction from the #P-Hard ample. Before executing a vote selection strategy, we assume that problem of counting linear extensions in a DAG. Consider a DAG each object has been scored by a scoring function in Step 1 of the G = (V, A). We now add two additional vertices, x and y, such framework, denoted by s[·] in Algorithm 6. As a running example that there is an arc from each of the vertices in G to x and to y to explain our strategies, we assume that our PageRank heuristic giving a new graph G′ = (V ′ , A ′ P). (Section 2.4) is used as the scoring function in Step 1: object A Consider the computation of a∈A(Q) maxi P (π −1 (1) = i, a∧ has score 0.5, objects B and E each have score 0.25, and objects W ) for Q = {{x, y}} for G′ ,P P which simplifies to: maxi π:i wins C, D, and F have score 0. Without loss of generality, assume that P (W ∧ (x > y)|π) + maxi π:i wins P (W ∧ (y > x)|π). the final rank order of the objects, before next vote selection, is The first of these two terms is maximized when x is the maxi- (A, B, E, C, D, F ). mum, and the second term is maximized when y is the maximum. Both terms are identical, since x and P y are identical, so we focus on Strategy 7 Paired Vote Selection only one of the terms. Let F (p) = π:x wins P (W ∧ x > y|π). Using a calculation similar to that used to derive Equation 7, we Require: n objects, budget b, vote multiset Q, scores s[·], sorted ′ P|A′ | ′ object indices index[·] have: F (p) = p|A | × i=0 ai ( 1−p p )|A |−i . We are interested in Ensure: Q = selected b votes a|A′ | , the number of permutations that correspond to linear exten- for i : 1 . . . b do sions. Once again, by repeating the trick in Theorem 3, we may Q ← Q ∪ (index[2i − 1], index[2i]) {index[1] has largest use multiple values for p to generate different graphs G′ , and use score s} the probability computation to derive many equations F (p) corre- end for sponding to different p, and then derive the value of a|A′ | using Lagrange’s interpolation. Therefore, counting the number of linear extensions in G can The first strategy we consider is Paired vote selection (PAIR), be reduced to a polynomial number of instances of computing the displayed in Strategy 7. In this strategy, pairs of objects are se- probability expression corresponding to the Next Votes problem. lected greedily, such that no object is included in more than one of the selected pairs. For example, with a budget of b = 2, the strat- 3.3 Selection and Evaluation of Additional Votes egy asks human workers to compare the rank 1 and rank 2 objects, We next present a general framework to select and evaluate ad- and the rank 3 and rank 4 objects, where rank is determined by the ditional votes for the Next Votes Problem. Our approach is the scoring function from Step 1 in Algorithm 6. The idea behind this following: strategy is to restrict each object to be involved in at most one of 1. score all objects with a scoring function s using initial vote the additional votes, thus distributing the b votes among the largest matrix W possible set of objects. This can be anticipated to perform well 2. select a batch of b votes to request when there are many objects with similar scores, e.g., when there ′ 3. evaluate the new matrix W (initial votes in W and addi- are many objects in the initial vote graph Gv which have equally tional b votes) with a scoring function f to predict the maxi- high chances of being the maximum object. Considering the exam- mum object in O. ple in Figure 6, for b = 2, this strategy requests the votes (A, B) This framework is displayed in more detail in Algorithm 6. In and (E, C). Step 1, we use a scoring function s(·) to score each object, and in Step 3, we use a scoring function f (·) to evaluate the new matrix Strategy 8 Max Vote Selection ′ W to predict the maximum object in O. We briefly discuss the Require: n objects, budget b, vote multiset Q, scores s[·], sorted choice of these scoring functions when presenting experimental re- object indices index[·] sults later in Section 3.4. For now, we assume the use of a scoring Ensure: Q = selected b votes function in Step 1 which scores objects proportional to the proba- for i : 2 . . . (b + 1) do bility that they are the maximum object in O. It is important to note Q ← Q ∪ (index[1], index[i]) {index[1] has largest score that our general framework assumes no knowledge of worker accu- s} racy p, unlike in ML vote selection. We next focus our attention end for upon how to select b additional votes (Step 2). Heuristic Vote Selection Strategies: How should we select pairs The second strategy we consider is Max vote selection (MAX), of objects for human workers to compare, when given a vote budget displayed in Strategy 8. In this strategy, human workers are asked 

12 .to compare the top-ranked object against other objects greedily. For 1 ML-ML example, with a budget of b = 2, this strategy asks human workers ML-PR 0.8 RAND to compare the rank 1 and rank 2 objects, and the rank 1 and rank PAIR GREEDY 3 objects, where rank is determined by the scoring function in Step COMPLETE Precision at 1 0.6 MAX 1 in Algorithm 6. Considering again the example in Figure 6, for b = 2, this strategy requests the votes (A, B) and (A, E). 0.4 Strategy 9 Greedy Vote Selection 0.2 Require: n objects, budget b, vote multiset Q, scores s[·], sorted object indices index[·] 0 50 100 150 200 Ensure: Q = selected b votes Initial Num Votes initialize priority queue S {storing unordered object pairs} Figure 7: Precision at 1 versus number of initial votes. 1 additional vote, 7 for i : 1 . . . b do objects, p=0.75. for j : (i + 1) . . . b do insert object pair (i, j) into S with priority (s[i] × s[j]) we construct a single round-robin tournament among the K objects end for with the highest scores from Step 1 of Algorithm 6, where K is end for the largest number such that K∗(K+1)2 ≤ b. In a single round- for i : 1 . . . b do robin tournament, each of the K objects is compared against every Remove highest priority object pair (x, y) from S Q ← Q ∪ (x, y) other exactly once. For the remaining r = b − K∗(K+1) 2 votes, we consider all object pairs containing the (K + 1)st (largest scoring) end for object and one of the first K objects, and weight each of these K object pairs by the product of the scores of the two objects (as we The third strategy we consider is Greedy vote selection (GREEDY), did with Greedy vote selection). We then select the r object pairs displayed in Strategy 9. In this strategy, all possible comparisons with highest weight. (unordered object pairs) are weighted by the product of the scores The idea behind the Complete Tournament strategy is that a round- of the two objects, where the scores are determined in Step 1 of robin tournament will likely determine the largest object among the Algorithm 6. In other words, a distribution is constructed across set of K objects. If the set of K objects contains the true max, this all possible object pairs, with higher weights assigned to object strategy can be anticipated to perform well. Regarding the selection pairs involving high scoring objects (which are more likely to be the of the remaining votes, the strategy can be thought of as augment- maximum object in O). After weighting all possible object pairs, ing the K object tournament to become an incomplete K +1 object this strategy submits the b highest weight pairs for human compar- tournament, where the remaining votes are selected greedily to best ison. Considering the example in Figure 6, object pairs (A, B) and determine if the (K +1)st object can possibly be the maximum ob- (A, E) has weight 0.125, (B, E) has weight 0.0625, and all other ject in O. Considering the example in Figure 6, for b = 2, there is a pairs have weight 0. For a budget b = 2, this strategy requests the 2-object tournament among objects A and B and vote (A, B) is re- votes (A, B) and (A, E). quested. Then, for the remaining vote, the strategy greedily scores Strategy 10 Complete (Round-Robin) Vote Selection object pairs which contain both the next highest ranked object not in the tournament, object E, and one of the initial 2 objects. Object Require: n objects, budget b, vote multiset Q, scores s[·], sorted pair (A, E) will be scored 0.125 and (B, E) will be scored 0.0625, object indices index[·] so the second vote requested is (A, E). Ensure: Q = selected b votes K ← 0 {K is the size of the round-robin tournament} while K∗(K+1) ≤ b do 3.4 Experiments 2 K ←K+1 Which of our four vote selection heuristics (PAIR, MAX, GREEDY, end while or COMPLETE) is the best strategy? We now describe a set of ex- K ←K−1 periments measuring the prediction performance of our heuristics for i : 1 . . . K do for various sets of parameters. When evaluating our vote selec- for j : (i + 1) . . . K do tion strategies, we utilized a uniform vote sampling procedure, de- Q ← Q ∪ (index[i], index[j]) {index[1] has largest score scribed previously in Section 2.5, to generate an initial vote matrix s} W . Then, in Step 1 of our vote selection framework (Algorithm 6), end for we adopted our PageRank heuristic (Section 2.4) as our scoring end for function s(·) to score each object in O. In Step 2, we executed initialize priority queue S {storing unordered object pairs} each of our vote selection strategies using these scores. In Step for i : 1 . . . K do 3, we used our PageRank heuristic as our scoring function f (·) to ′ insert object pair (i, K + 1) into S with priority (s[i] × s[K + score each object in the new matrix W (composed of both the ini- 1]) tial votes in vote matrix W and the b requested additional votes), end for and generate final predictions for the maximum object in O. Note for i : 1 . . . (b − K∗(K+1) 2 ) do that we performed several experiments contrasting prediction per- Remove highest priority object pair (x, y) from S formance of PageRank versus other possible scoring functions and Q ← Q ∪ (x, y) {select remaining votes greedily} found PageRank to be superior to the other functions. Hence, we end for selected PageRank as the scoring function for both Step 1 and Step 3 of our vote selection framework. The fourth strategy we consider is Complete Tournament vote selection (COMPLETE), displayed in Strategy 10. In this strategy, 

13 . 0.4 0.7 1.8 1.6 RAND RAND RAND RAND PAIR 0.6 PAIR 1.6 PAIR 1.4 PAIR 0.35 1.4 GREEDY 0.5 GREEDY MAX 1.2 MAX COMPLETE COMPLETE 1.2 GREEDY GREEDY Gain (P at 1) Gain (P at 1) Gain (P at 1) 0.3 1 MAX 0.4 MAX 1 COMPLETE COMPLETE P at 1 0.8 0.25 0.3 0.8 0.6 0.2 0.6 0.2 0.4 0.4 0.1 0.2 0.15 0.2 0 0 0 0.1 -0.1 -0.2 -0.2 0 5 10 15 20 0 2 4 6 8 10 12 14 16 18 20 20 40 60 80 100 120 140 160 180 200 20 40 60 80 100 120 140 160 180 200 Num Additional Votes Vote Number Initial Num Votes Initial Num Votes Figure 8: Precision at 1 versus number of additional votes (left). Incremen- 2.5 RAND 4 RAND tal Gain (P@1) of each vote relative to a 0 additional votes baseline (right). 2 PAIR MAX 3.5 PAIR MAX 3 100 objects, p=0.95, 200 initial votes. GREEDY GREEDY Gain (P at 1) Gain (P at 1) 0.3 0.4 1.5 COMPLETE 2.5 COMPLETE RAND RAND 2 PAIR 0.35 PAIR 0.25 1 1.5 GREEDY 0.3 GREEDY 0.2 COMPLETE COMPLETE 1 MAX 0.25 MAX 0.5 P at 1 P at 1 0.5 0.15 0.2 0 0 0.15 20 40 60 80 100 120 140 160 180 200 20 40 60 80 100 120 140 160 180 200 0.1 0.1 Initial Num Votes Initial Num Votes 0.05 0.05 Figure 10: Gain (P@1) relative to a 0 additional votes baseline vs number 0 0 0.5 0.6 0.7 0.8 0.9 1 0.5 0.6 0.7 0.8 0.9 1 of initial votes. 100 objects. 5 add. votes and p=0.75 (top left), 15 add. Worker Accuracy Worker Accuracy votes and p=0.75 (top right), 5 add. votes and p=0.95 (bottom left), 15 add. Figure 9: Precision at 1 versus worker accuracy. 100 objects, 100 initial votes and p=0.95 (bottom right). votes. 5 additional votes (left), 15 additional votes (right) general trends that can be observed in these figures. • ML vote selection outperforms heuristic strategies when General observations regarding all strategies: results are evaluated with ML scoring. • As the number of additional votes increases, prediction • However, when ML vote selection is evaluated with performance increases. PageRank (e.g., like the heuristics), prediction perfor- • As the number of additional votes increases, the gain mances of all methods are similar. from additional votes decreases (though the decrease is For a first experiment, we compare the prediction performance not very dramatic). (Precision at 1) of our four vote selection heuristics (and random • As worker accuracy increases, prediction performance initial vote selection (RAND)) against the “optimal” strategy, i.e., increases. the Maximum Likelihood (ML) vote selection procedure described • As worker accuracy increases, the gain from additional in Section 3.1. Recall that ML can be used in two places: when votes increases. selecting additional votes (as in Section 3.1), and when predicting We only explain the graph in Figure 8(right), since the others the max given the initial plus additional votes (e.g., ML evaluation are self-explanatory. In this graph, the vertical axis shows the in- in Section 2.2). We use ML-ML to refer to using ML for both tasks, cremental P@1 gain at k additional votes, defined as (P@1 with k this gives the best possible strategy. To gain additional insights, we additional votes - P@1 with k − 1 additional votes) / (P@1 with also consider ML-PR, a strategy where ML is used to select the ad- 0 additional votes). As we can see, the information provided by ditional votes, and PageRank is used to select the winner. Since ML additional votes is more valuable when there are fewer initial votes is computationally very expensive, for this experiment we consider (second bullet above). a small problem: select one additional vote given a set of 50 (2.5x Edge Coverage) to 200 initial votes (10x Edge Coverage) among a The Complete Tournament and Greedy strategies are signif- set of 7 objects, p = 0.75. icantly better than the Max and Paired strategies. Our experimental results are displayed in Figure 7. First, as ex- pected, ML-ML has the best performance. Clearly, ML-ML is do- We can also use Figures 8, 9 and 10 to compare our heuristics. ing a better job at selecting the additional vote and in selecting the First, notice that the difference between heuristics can be very sig- winner. Of course, keep in mind that ML-ML is not feasible in most nificant. For instance, in Figure 10(bottom left) we see that the scenarios, and it also requires knowledge of the worker accuracy p. Paired (PAIR) strategy provides a 0.7x P@1 gain for 5 additional Nevertheless, the gap between ML-ML and the other strategies in- votes (100 initial votes, p = 0.95), while the Complete Tournament dicates there is potential room for future improvement beyond the (COMPLETE) strategy provides a 1.5x P@1 gain, where we mea- heuristics we have developed. sure P@1 gain as (P@1 with k votes - P@1 with 0 votes) / (P@1 Second, we observe in Figure 7 that all other strategies, includ- with 0 votes). Second, we observe that the Complete Tournament ing ML-PR, perform similarly. The relative performance of ML-PR and Greedy (GREEDY) vote selection strategies consistently out- indicates that the gain achieved by ML-ML is due to its better pre- perform the Max (MAX) and Paired strategies in all scenarios. In diction of the winner, as opposed to its choice for the next vote. particular, the performance gap between the Complete Tournament In hindsight, this result is not surprising, since the selection of a or Greedy strategies and the Max or Paired strategies is greater single vote cannot be expected to have a large impact. (We will when selecting 15 additional votes, as compared to when selecting observe larger impacts when we select multiple additional votes.) 5 additional votes. This indicates that when a larger vote budget The results also demonstrate that our vote selection heuristics show b is available for additional votes, the additional votes will be bet- promise, since they seem to be doing equally well as ML, and since ter utilized by the more sophisticated strategies (Complete Tour- they often perform slightly better than RAND, at least for the se- nament and Greedy) as compared to the simpler strategies (Max lection of a single next vote. and Paired). Also, note in Figure 8(left) that the prediction perfor- To evaluate our heuristics in larger scenarios, we conducted a mances of the Complete Tournament and Greedy strategies steadily series of experiments, and the results of some of those are summa- improve with additional votes, while the Max and Paired strategies rized in Figures 8, 9 and 10. To begin, we summarize some of the taper off. 

14 . 4 4 0.35 RAND RAND 5 OBJ 3.5 PAIR 3.5 PAIR 0.3 10 OBJ 3 MAX 3 MAX 20 OBJ GREEDY GREEDY 0.25 Gain (P at 1) Gain (P at 1) 2.5 COMPLETE 2.5 COMPLETE P at 1 0.2 2 2 0.15 1.5 1.5 1 1 0.1 0.5 0.5 0.05 0 0 0 20 40 60 80 100 120 140 160 180 200 20 40 60 80 100 120 140 160 180 200 20 40 60 80 100 120 140 160 180 200 Initial Num Votes Initial Num Votes Initial Num Votes 3.5 RAND 5 RAND Figure 12: Variations of the Complete Tournament strategy, 10 additional 4.5 3 PAIR MAX 4 PAIR MAX votes. 5 OBJ = compare 5 objects 4 times each. 10 OBJ = compare 10 ob- 2.5 GREEDY 3.5 GREEDY jects 2 times each. 20 OBJ = compare 20 objects 1 time each. 100 objects, Gain (P at 1) Gain (P at 1) COMPLETE 3 COMPLETE 2 2.5 p=0.95. 1.5 2 1 1.5 1 ment strategy select fewer top objects and propose more redundant 0.5 0.5 votes, or should it select more objects and ask fewer votes per pair? 0 0 20 40 60 80 100 120 140 160 180 200 20 40 60 80 100 120 140 160 180 200 For instance, the Complete Tournmament strategy could select the Initial Num Votes Initial Num Votes top three objects and submit four votes for each pair, for a total of Figure 11: Objects are divided into k initial object types. Gain (P@1) 12 additional votes. Or it could select the top 4 objects, and for relative to a 0 additional votes baseline vs number of initial votes. 100 objects, p=0.95, 15 additional votes. 1 type (top left), 5 types (top right), 10 each of the possible 6 comparisons, request 2 votes (for the same types (bottom left), 20 types (bottom right). 12 total additional votes). What is the best approach? Figure 12 displays the Precision at 1 of the Complete Tourna- Given only votes between objects of the same type: ment strategy for 10 additional votes, where the votes are uniformly • The value of additional votes is greater when it is more and randomly distributed among the 5, 10, or 20 objects in O with difficult to predict the maximum object. highest score (as provided in Step 1 of Algorithm 6). We find that • The Complete Tournament strategy is the best strategy. distributing the 10 votes among 5 objects, where each object is compared against every other, leads to the best prediction perfor- In our scenarios so far, the Complete Tournament and Greedy mance. That is, we do not observe any benefit for distributing votes strategies perform similarly. To differentiate between the two, we among a larger set of objects when using the Complete Tourna- explored different ways in which the initial votes could be gen- ment strategy. The strategy performs well only when additional erated. (Recall that up to this point we have been randomly se- votes provide the ability to rank the objects in a set. Assuming that lecting the pairs of objects that are compared by the initial votes.) votes are distributed randomly among object pairs, the Complete We next discuss one of these possible different vote generation Tournament strategy is able to order the set only when most objects schemes. Suppose that our objects are of different types (e.g., soft- in the set are compared against each other. Note that Figure 12 is cover books, hardcover books, e-books, etc.), and for some reason only an illustration of the interaction between the number of top initial votes between objects of the same type are much more likely objects selected and the redundancy of votes. The results will vary than across types. For example, it is more likely that two e-books depending upon worker accuracy and the vote budget b. have been compared, rather than one e-book and one hard-cover book. (The situation is analogous to sporting events, where intra- league games are more likely than inter-league games.) 4. RELATED WORK For our experiment, we consider an extreme instance where there As far as we know, we are the first to address the Next Votes are no initial votes involving objects of different types. In partic- Problem, and there is no relevant literature that directly addresses ular, we divide our set O of n objects into k disjoint object types. this problem. Thus, in this section, we review work related to the When votes are sampled for the initial vote matrix W , sampling Judgment Problem. The algorithms and heuristics we presented for of votes is only permitted between objects of the same type. Keep the Judgment Problem are primarily drawn from three diverse topic in mind that predicting the maximum object in O is more diffi- areas: paired comparisons, social choice, and ranking. cult when there are more object types because each object type The Judgment Problem has its roots in the paired comparisons will likely have a leader (greatest object), each of these leaders will problem, first studied by statisticians decades ago [20, 12]. In the have on average similar probabilities of being the maximum object paired comparisons problem, given a set of pairwise observations (since object type groups are likely of similar size), and the ini- regarding a set of objects, it is desired to obtain a ranking of the tial vote matrix W provides no information regarding comparisons objects. In contrast, in the Judgment Problem, we are interested in between these leaders. predicting the maximum object. We perform experiments for different values of k (e.g., differ- The Judgment Problem also draws upon classical work in the ent numbers of initial object types), Figure 11 displays Precision economic and social choice literature regarding Winner Determi- at 1 gain relative to a 0 additional votes baseline. We observe that nation in elections [25, 31]. Numerous voting rules have been used the P@1 gain increases for the Complete Tournament and Greedy (Borda, Condorcet, Dodgson, etc.) to determine winners in elec- strategies as k increases, implying that the value of additional votes tions [28]. The voting rules most closely related to our work are is greater when it is more difficult to predict the maximum object the Kemeny rule [19] and Slater rule [29]. A Kemeny permutation from the initial vote matrix. That is, in the harder problem instances minimizes the total number of pairwise inconsistencies among all (larger k), the additional votes play a more critical role in compar- votes, whereas a Slater permutation minimizes the total number of ing the object type leaders. More importantly, the Complete Tour- pairwise inconsistencies in the majority-vote graph [6]. An object nament strategy outperforms the Greedy strategy (and the others is considered a Kemeny winner or Slater winner if it is the greatest too) in this more challenging scenario. object in a Kemeny permutation or Slater permutation. Finally, we conduct a more in-depth study of the Complete Tour- We believe our ML formulation is more principled than these nament vote selection strategy and examine the benefit of vote re- voting rules, since ML aggregates information across all possible dundancy. Given a limited budget, should the Complete Tourna- permutations. For example, in the graph of Figure 1, while C and 

15 .D are both admissible solutions for the Kemeny rule, ML returns 6. REFERENCES D as an answer, since D has almost one and a half more times [1] N. Ailon et al. Aggregating inconsistent information: ranking the probability of being the maximum object compared to C. No and clustering. JACM, 55(5), 2008. prior work about the Judgment Problem, to our knowledge, uses [2] M. Ajtai et al. Sorting and selection with imprecise the same approach as our ML formulation. comparisons. Automata, Languages and Programming, 2009. [3] O. Alonso et al. Crowdsourcing for relevance evaluation. In In the recent social choice literature, the research most closely SIGIR Forum, 2008. related to ours has been work by Conitzer et al. regarding Kemeny [4] P. Boldi et al. PageRank as a function of the damping factor. permutations and Maximum Likelihood [9, 10]. Conitzer has stud- In WWW, 2005. ied various voting rules and determined for which of them there ex- [5] F. Brandt et al. PageRank as a weak tournament solution. In ist voter error models where the rules are ML estimators [8]. In our WINE, 2007. [6] Y. Chevaleyre et al. A short introduction to computational study, we focused upon the opposite question: for a specific voter social choice. In SOFSEM, 2007. error model, we presented both Maximum Likelihood, as well as [7] W. Cohen et al. Learning to order things. Journal of Artificial heuristic solutions, to predict the winner. Intelligence Research, 10:243–270, 1999. Our work is also related to research in the theory community [8] V. Conitzer et al. Common voting rules as maximum regarding ranking in the presence of errors [21, 1] and noisy com- likelihood estimators. In UAI, 2005. [9] V. Conitzer et al. Improved bounds for computing kemeny putation [14, 2]. Both Kenyon et al. and Ailon et al. present ran- rankings. In AAAI, 2006. domized polynomial-time algorithms for feedback arc set in tour- [10] V. Conitzer et al. Preference functions that score rankings nament graphs. Their algorithms are intended to approximate the and maximum likelihood estimation. In IJCAI, 2009. optimal permutation, whereas we seek to predict the optimal win- [11] D. Coppersmith et al. Ordering by weighted number of wins ner. Feige et al. and Ajtai et al. present algorithms to solve a va- gives a good ranking for weighted tournaments. In SODA, 2006. riety of problems, including the Max Problem, but their scenarios [12] H.A. David. The method of paired comparisons. 1963. involve different comparison models or error models than ours. [13] H.A. David. Ranking from unbalanced paired-comparison More generally, in the last several years, there has been a sig- data. Biometrika, 74(2):432–436, 1987. nificant amount of work regarding crowdsourcing systems, both [14] U. Feige et al. Computing with noisy information. SIAM J. inside [15, 16] and outside [22, 23] the database community. Of Comput., 23(5):1001–1018, 1994. [15] M. Franklin et al. CrowdDB: answering queries with note is recent work by Tamuz et al. [30] on a crowdsourcing sys- crowdsourcing. In SIGMOD, 2011. tem that learns a similarity matrix across objects, while adaptively [16] P. Heymann et al. Turkalytics: analytics for human requesting votes. Not as much work has been done regarding gen- computation. In WWW, 2011. eral crowdsourcing algorithms [24, 27]. Instead, most algorithmic [17] O. Hudry. On the complexity of Slater’s problems. European work in crowdsourcing has focused upon quality control [3, 18]. Journal of Operational Research, 203(1):216–221, 2010. [18] P. Ipeirotis et al. Quality management on amazon mechanical turk. In KDD Workshop on Human Computation, 2010. 5. CONCLUSION [19] J. Kemeny. Mathematics without numbers. Daedalus, 1959. [20] M.G. Kendall et al. On the method of paired comparisons. In a conventional database system, finding the maximum ele- Biometrika, 31(3/4):324–345, 1940. ment in a set is a relatively simple procedure. It is thus some- [21] C. Kenyon-Mathieu et al. How to rank with few errors. In what surprising that in a crowdsourcing database system, finding STOC, 2007. the maximum is quite challenging, and there are many issues to [22] A. Kittur et al. Crowdsourcing user studies with mechanical consider. The main reason for the complexity, as we have seen, is turk. In CHI, 2008. [23] G. Little et al. TurKit: human computation algorithms on that our underlying comparison operation may give an incorrect an- mechanical turk. In UIST, 2010. swer, or it may even not complete. Thus, we need to decide which [24] A. Marcus et al. Human-powered sorts and joins. PVLDB, is the “most likely” max (Judgment Problem), and which additional 2011. votes to request to improve our answer (Next Votes Problem). [25] H. Moulin. Choosing from a tournament. Social Choice and Our results show that solving either one of these problems op- Welfare, 3(4):271–291, 1986. [26] L. Page et al. The PageRank citation ranking: Bringing order timally is very hard, but fortunately we have proposed effective to the web. Technical Report, 1998. heuristics that do well. There is a gap between the optimal solution [27] A. Parameswaran et al. Human-assisted graph search: it’s and what our heuristics find (as seen for example in Figure 7), but okay to ask questions. PVLDB, 2011. we believe that it will be very hard to close this gap without incur- [28] D. Saari. Basic geometry of voting. 1995. ring high computational costs. Among the heuristics, we observed [29] P. Slater. Inconsistencies in a schedule of paired significant differences in their predictive ability, indicating that it comparisons. Biometrika, 48(3/4):303–312, 1961. [30] O. Tamuz et al. Adaptively learning the crowd kernel. In is very important to carefully select a good heuristic. Our results ICML, 2011. indicate that in many cases (but not all) our proposed PageRank [31] P. Young. Optimal voting rules. J. Econ. Perspectives, 1995. heuristic is the best for the Judgment Problem, while the Complete Tournament heuristic is the best for the Next Votes Problem. Our results are based on a relatively simple model where object comparisons are pairwise, and worker errors are independent. Of course, in a real crowdsourced database system these assumptions may not hold. Yet we believe it is important to know that even with the simple model, the optimal strategies for the Judgment Problem and Next Votes Problem are NP-Hard. Furthermore, our heuristics can be used even in more complex scenarios, since they do not de- pend on the evaluation model. Even though they can be used when the model assumptions do not hold, we believe it is important to un- derstand how the heuristics perform in the more tractable scenario we have considered here.