BlinkDB: Queries with Bounded Errors and Bounded Response Times

1 . BlinkDB: Queries with Bounded Errors and Bounded Response Times on Very Large Data Sameer Agarwal† , Barzan Mozafari○ , Aurojit Panda† , Henry Milner† , Samuel Madden○ , Ion Stoica∗† †University of California, Berkeley ○ Massachusetts Institute of Technology ∗ Conviva Inc. {sameerag, apanda, henrym, istoica}@cs.berkeley.edu, {barzan, madden}@csail.mit.edu Abstract cessing of large amounts of data by trading result accuracy In this paper, we present BlinkDB, a massively parallel, ap- for response time and space. These techniques include sam- proximate query engine for running interactive SQL queries pling [10, 14], sketches [12], and on-line aggregation [15]. To on large volumes of data. BlinkDB allows users to trade- illustrate the utility of such techniques, consider the following off query accuracy for response time, enabling interactive simple query that computes the average SessionTime over queries over massive data by running queries on data samples all users originating in New York: and presenting results annotated with meaningful error bars. SELECT AVG(SessionTime) To achieve this, BlinkDB uses two key ideas: (1) an adaptive FROM Sessions optimization framework that builds and maintains a set of WHERE City = ‘New York’ multi-dimensional stratified samples from original data over time, and (2) a dynamic sample selection strategy that selects Suppose the Sessions table contains 100 million tuples for an appropriately sized sample based on a query’s accuracy or New York, and cannot fit in memory. In that case, the above response time requirements. We evaluate BlinkDB against the query may take a long time to execute, since disk reads are ex- well-known TPC-H benchmarks and a real-world analytic pensive, and such a query would need multiple disk accesses workload derived from Conviva Inc., a company that man- to stream through all the tuples. Suppose we instead exe- ages video distribution over the Internet. Our experiments cuted the same query on a sample containing only 10, 000 on a 100 node cluster show that BlinkDB can answer queries New York tuples, such that the entire sample fits in mem- on up to 17 TBs of data in less than 2 seconds (over 200× faster ory. This would be orders of magnitude faster, while still pro- than Hive), within an error of 2-10%. viding an approximate result within a few percent of the ac- tual value, an accuracy good enough for many practical pur- poses. Using sampling theory we could even provide confi- 1. Introduction dence bounds on the accuracy of the answer [16]. Modern data analytics applications involve computing aggre- Previously described approximation techniques make dif- gates over a large number of records to roll-up web clicks, ferent trade-offs between efficiency and the generality of the online transactions, content downloads, and other features queries they support. At one end of the spectrum, exist- along a variety of different dimensions, including demo- ing sampling and sketch based solutions exhibit low space graphics, content type, region, and so on. Traditionally, such and time complexity, but typically make strong assumptions queries have been executed using sequential scans over a about the query workload (e.g., they assume they know the large fraction of a database. Increasingly, new applications set of tuples accessed by future queries and aggregation func- demand near real-time response rates. Examples may include tions used in queries). As an example, if we know all future applications that (i) update ads on a website based on trends queries are on large cities, we could simply maintain random in social networks like Facebook and Twitter, or (ii) deter- samples that omit data about smaller cities. mine the subset of users experiencing poor performance At the other end of the spectrum, systems like online based on their service provider and/or geographic location. aggregation (OLA) [15] make fewer assumptions about the Over the past two decades a large number of approxima- query workload, at the expense of highly variable perfor- tion techniques have been proposed, which allow for fast pro- mance. Using OLA, the above query will likely finish much faster for sessions in New York (i.e., the user might be satisfied with the result accuracy, once the query sees the Permission to make digital or hard copies of all or part of this work for personal first 10, 000 sessions from New York) than for sessions in or classroom use is granted without fee provided that copies are not made or distributed for profit or commercial advantage and that copies bear this notice Galena, IL, a town with fewer than 4, 000 people. In fact, and the full citation on the first page. To copy otherwise, to republish, to post for such a small town, OLA may need to read the entire table on servers or to redistribute to lists, requires prior specific permission and/or a fee. to compute a result with satisfactory error bounds. Eurosys’13 April 15-17, 2013, Prague, Czech Republic In this paper, we argue that none of the previous solutions Copyright © 2013 ACM 978-1-4503-1994-2/13/04. . . $15.00 are a good fit for today’s big data analytics workloads. OLA 29 

2 .provides relatively poor performance for queries on rare tu- We implemented BlinkDB1 on top of Hive/Hadoop [22] ples, while sampling and sketches make strong assumptions (as well as Shark [13], an optimized Hive/Hadoop framework about the predictability of workloads or substantially limit that caches input/ intermediate data). Our implementation the types of queries they can execute. requires minimal changes to the underlying query processing To this end, we propose BlinkDB, a distributed sampling- system. We validate its effectiveness on a 100 node cluster, us- based approximate query processing system that strives to ing both the TPC-H benchmarks and a real-world workload achieve a better balance between efficiency and generality for derived from Conviva. Our experiments show that BlinkDB analytics workloads. BlinkDB allows users to pose SQL-based can answer a range of queries within 2 seconds on 17 TB of aggregation queries over stored data, along with response data within 90-98% accuracy, which is two orders of magni- time or error bound constraints. As a result, queries over mul- tude faster than running the same queries on Hive/Hadoop. tiple terabytes of data can be answered in seconds, accom- In summary, we make the following contributions: panied by meaningful error bounds relative to the answer • We use a column-set based optimization framework to that would be obtained if the query ran on the full data. In compute a set of stratified samples (in contrast to ap- contrast to most existing approximate query solutions (e.g., proaches like AQUA [6] and STRAT [10], which compute [10]), BlinkDB supports more general queries as it makes no only a single sample per table). Our optimization takes assumptions about the attribute values in the WHERE, GROUP into account: (i) the frequency of rare subgroups in the BY, and HAVING clauses, or the distribution of the values used data, (ii) the column sets in the past queries, and (iii) the by aggregation functions. Instead, BlinkDB only assumes that storage overhead of each sample. (§4) the sets of columns used by queries in WHERE, GROUP BY, • We create error-latency profiles (ELPs) for each query at and HAVING clauses are stable over time. We call these sets runtime to estimate its error or response time on each of columns “query column sets” or QCSs in this paper. available sample. This heuristic is then used to select the BlinkDB consists of two main modules: (i) Sample Cre- most appropriate sample to meet the query’s response ation and (ii) Sample Selection. The sample creation module time or accuracy requirements. (§5) creates stratified samples on the most frequently used QCSs to • We show how to integrate our approach into an existing ensure efficient execution for queries on rare values. By strat- parallel query processing framework (Hive) with minimal ified, we mean that rare subgroups (e.g., Galena, IL) are changes. We demonstrate that by combining these ideas over-represented relative to a uniformly random sample. This together, BlinkDB provides bounded error and latency for ensures that we can answer queries about any subgroup, re- a wide range of real-world SQL queries, and it is robust to gardless of its representation in the underlying data. variations in the query workload. (§6) We formulate the problem of sample creation as an opti- mization problem. Given a collection of past QCS and their historical frequencies, we choose a collection of stratified 2. Background samples with total storage costs below some user configurable Any sampling based query processor, including BlinkDB, storage threshold. These samples are designed to efficiently must decide what types of samples to create. The sample cre- answer queries with the same QCSs as past queries, and to ation process must make some assumptions about the nature provide good coverage for future queries over similar QCS. of the future query workload. One common assumption is If the distribution of QCSs is stable over time, our approach that future queries will be similar to historical queries. While creates samples that are neither over- nor under-specialized this assumption is broadly justified, it is necessary to be pre- for the query workload. We show that in real-world work- cise about the meaning of “similarity” when building a work- loads from Facebook Inc. and Conviva Inc., QCSs do re-occur load model. A model that assumes the wrong kind of sim- frequently and that stratified samples built using historical ilarity will lead to a system that “over-fits” to past queries patterns of QCS usage continue to perform well for future and produces samples that are ineffective at handling future queries. This is in contrast to previous optimization-based workloads. This choice of model of past workloads is one of sampling systems that assume complete knowledge of the tu- the key differences between BlinkDB and prior work. In the ples accessed by queries at optimization time. rest of this section, we present a taxonomy of workload mod- Based on a query’s error/response time constraints, the els, discuss our approach, and show that it is reasonable using sample selection module dynamically picks a sample on experimental evidence from a production system. which to run the query. It does so by running the query on multiple smaller sub-samples (which could potentially be 2.1 Workload Taxonomy stratified across a range of dimensions) to quickly estimate Offline sample creation, caching, and virtually any other type query selectivity and choosing the best sample to satisfy spec- of database optimization assumes a target workload that can ified response time and error bounds. It uses an Error-Latency be used to predict future queries. Such a model can either Profile heuristic to efficiently choose the sample that will best be trained on past data, or based on information provided by satisfy the user-specified error or time bounds. 1 http://blinkdb.org 30 

3 .users. This can range from an ad-hoc model, which makes no not lend itself to any “intelligent” sampling, leaving one with assumptions about future queries, to a model which assumes no choice but to uniformly sample data. This model is used by that all future queries are known a priori. As shown in Fig. 1, On-Line Aggregation (OLA) [15], which relies on streaming we classify possible approaches into one of four categories: data in random order. While the unpredictable query model is the most flexible Low flexibility / Flexibility High flexibility / one, it provides little opportunity for an approximate query Efficiency High Efficiency Low Efficiency processing system to efficiently sample the data. Further- Predictable     Predictable     Predictable     Unpredictable     more, prior work [11, 19] has argued that OLA performance’s Queries   Query   Predicates   Query   Column  Sets   Queries   on large clusters (the environment on which BlinkDB is in- tended to run) falls short. In particular, accessing individual Figure 1. Taxonomy of workload models. rows randomly imposes significant scheduling and commu- nication overheads, while accessing data at the HDFS block2 1. Predictable Queries: At the most restrictive end of the level may skew the results. spectrum, one can assume that all future queries are known in As a result, we use the model of predictable QCSs. As we advance, and use data structures specially designed for these will show, this model provides enough information to enable queries. Traditional databases use such a model for lossless efficient pre-computation of samples, and it leads to samples synopsis [12] which can provide extremely fast responses for that generalize well to future workloads in our experiments. certain queries, but cannot be used for any other queries. Intuitively, such a model also seems to fit in with the types Prior work in approximate databases has also proposed using of exploratory queries that are commonly executed on large lossy sketches (including wavelets and histograms) [14]. scale analytical clusters. As an example, consider the oper- 2. Predictable Query Predicates: A slightly more flexi- ator of a video site who wishes to understand what types ble model is one that assumes that the frequencies of group of videos are popular in a given region. Such a study may and filter predicates — both the columns and the values in require looking at data from thousands of videos and hun- WHERE, GROUP BY, and HAVING clauses — do not change dreds of geographic regions. While this study could result in a over time. For example, if 5% of past queries include only very large number of distinct queries, most will use only two the filter WHERE City = ‘New York’ and no other group columns, video title and viewer location, for grouping and or filter predicates, then this model predicts that 5% of future filtering. Next, we present empirical evidence based on real queries will also include only this filter. Under this model, world query traces from Facebook Inc. and Conviva Inc. to it is possible to predict future filter predicates by observing support our claims. a prior workload. This model is employed by materialized views in traditional databases. Approximate databases, such 2.2 Query Patterns in a Production Cluster as STRAT [10] and SciBORQ [21], have similarly relied on To empirically test the validity of the predictable QCS model prior queries to determine the tuples that are likely to be used we analyze a trace of 18, 096 queries from 30 days of queries in future queries, and to create samples containing them. from Conviva and a trace of 69, 438 queries constituting a 3. Predictable QCSs: Even greater flexibility is provided random, but representative, fraction of 7 days’ workload from by assuming a model where the frequency of the sets of Facebook to determine the frequency of QCSs. columns used for grouping and filtering does not change over Fig. 2(a) shows the distribution of QCSs across all queries time, but the exact values that are of interest in those columns for both workloads. Surprisingly, over 90% of queries are cov- are unpredictable. We term the columns used for grouping ered by 10% and 20% of unique QCSs in the traces from Con- and filtering in a query the query column set, or QCS, for the viva and Facebook respectively. Only 182 unique QCSs cover query. For example, if 5% of prior queries grouped or filtered all queries in the Conviva trace and 455 unique QCSs span all on the QCS {City}, this model assumes that 5% of future the queries in the Facebook trace. Furthermore, if we remove queries will also group or filter on this QCS, though the par- the QCSs that appear in less than 10 queries, we end up with ticular predicate may vary. This model can be used to decide only 108 and 211 QCSs covering 17, 437 queries and 68, 785 the columns on which building indices would optimize data queries from Conviva and Facebook workloads, respectively. access. Prior work [20] has shown that a similar model can This suggests that, for real-world production workloads, be used to improve caching performance in OLAP systems. QCSs represent an excellent model of future queries. AQUA [4], an approximate query database based on sam- Fig. 2(b) shows the number of unique QCSs versus the pling, uses the QCS model. (See §8 for a comparison between queries arriving in the system. We define unique QCSs as AQUA and BlinkDB). QCSs that appear in more than 10 queries. For the Con- 4. Unpredictable Queries: Finally, the most general viva trace, after only 6% of queries we already see close to model assumes that queries are unpredictable. Given this as- 60% of all QCSs, and after 30% of queries have arrived, we sumption, traditional databases can do little more than just see almost all QCSs — 100 out of 108. Similarly, for the Face- rely on query optimizers which operate at the level of a single query. In approximate databases, this workload model does 2 Typically, these blocks are 64 − 1024 MB in size. 31 

4 . 1 100 1 Fraction of Join Queries (CDF) Fraction of Queries (CDF) 0.9 90 0.9 Templates Seen (%) 0.8 80 0.8 70 New Unique 0.7 0.7 60 0.6 0.6 50 0.5 0.5 40 0.4 0.4 30 0.3 20 0.3 0.2 Conviva Queries (2 Years) 10 Conviva Queries (2 Years) 0.2 Facebook Queries (1 week) Facebook Queries (1 week) 0.1 0 Facebook Queries (1 Week) 0.1 0 20 40 60 80 100 0 20 40 60 80 100 0.001 0.01 0.1 1 10 100 1000 10000 100000 1e+06 Unique Query Templates (%) Incoming Queries (%) Size of Dimension Table(s) (GB) (a) QCS Distribution (b) QCS Stability (c) Dimension table size CDF Figure 2. 2(a) and 2(b) show the distribution and stability of QCSs respectively across all queries in the Conviva and Face- book traces. 2(c) shows the distribution of join queries with respect to the size of dimension tables. book trace, after 12% of queries, we see close to 60% of all 3.1 Supported Queries QCSs, and after only 40% queries, we see almost all QCSs — BlinkDB supports a slightly constrained set of SQL-style 190 out of 211. This shows that QCSs are relatively stable over declarative queries, imposing constraints that are similar to time, which suggests that the past history is a good predictor prior work [10]. In particular, BlinkDB can currently provide for the future workload. approximate results for standard SQL aggregate queries in- volving COUNT, AVG, SUM and QUANTILE. Queries involv- 3. System Overview ing these operations can be annotated with either an error bound, or a time constraint. Based on these constraints, the ' SELECT COUNT(*)! system selects an appropriate sample, of an appropriate size, FROM TABLE! WHERE (city=“NY”)! LIMIT 1s;! Sample'Selection' Result:( 1,101,822(±(2,105&& as explained in §5. HiveQL/SQL' Shark' (95%(confidence)( As an example, let us consider querying a table Query' Sessions, with five columns, SessionID, Genre, OS, City, and URL, to determine the number of sessions Sample'Creation'&' Maintenance' TABLE' in which users viewed content in the “western” genre, grouped by OS. The query: Original'' Data' SELECT COUNT(*) Distributed' Distributed' Filesystem' Cache' FROM Sessions WHERE Genre = ‘western’ Figure 3. BlinkDB architecture. GROUP BY OS ERROR WITHIN 10% AT CONFIDENCE 95% Fig. 3 shows the overall architecture of BlinkDB. BlinkDB extends the Apache Hive framework [22] by adding two ma- will return the count for each GROUP BY key, with each count jor components to it: (1) an offline sampling module that cre- having relative error of at most ±10% at a 95% confidence ates and maintains samples over time, and (2) a run-time level. Alternatively, a query of the form: sample selection module that creates an Error-Latency Pro- SELECT COUNT(*) file (ELP) for queries. To decide on the samples to create, we FROM Sessions use the QCSs that appear in queries (we present a more pre- WHERE Genre = ‘western’ cise formulation of this mechanism in §4.) Once this choice GROUP BY OS is made, we rely on distributed reservoir sampling3 [23] or bi- WITHIN 5 SECONDS nomial sampling techniques to create a range of uniform and stratified samples across a number of dimensions. will return the most accurate results for each GROUP BY key At run-time, we employ ELP to decide the sample to run in 5 seconds, along with a 95% confidence interval for the the query. The ELP characterizes the rate at which the error relative error of each result. (or response time) decreases (or increases) as the size of the While BlinkDB does not currently support arbitrary joins sample on which the query operates increases. This is used and nested SQL queries, we find that this is usually not a hin- to select a sample that best satisfies the user’s constraints. We drance. This is because any query involving nested queries or describe ELP in detail in §5. BlinkDB also augments the query joins can be flattened to run on the underlying data. How- parser, optimizer, and a number of aggregation operators to ever, we do provide support for joins in some settings which allow queries to specify bounds on error, or execution time. are commonly used in distributed data warehouses. In par- ticular, BlinkDB can support joining a large, sampled fact 3 Reservoir sampling is a family of randomized algorithms for creating fixed- table, with smaller tables that are small enough to fit in the sized random samples from streaming data. main memory of any single node in the cluster. This is one 32 

5 . Notation Description does not work well for a queries on filtered or grouped subsets T fact (original) table of the table. When members of a particular subset are rare, Q a query a larger sample will be required to produce high-confidence t a time bound for query Q estimates on that subset. A uniform sample may not contain e an error bound for query Q any members of the subset at all, leading to a missing row in n the estimated number of rows that can be the final output of the query. The standard approach to solv- accessed in time t ing this problem is stratified sampling [16], which ensures that ϕ the QCS for Q, a set of columns in T rare subgroups are sufficiently represented. Next, we describe x a ∣ϕ∣-tuple of values for a column set ϕ, for the use of stratified sampling in BlinkDB. example (Berkeley, CA) for ϕ =(City, State) D(ϕ) the set of all unique x-values for ϕ in T 4.1.1 Optimizing a stratified sample for a single query Tx , S x the rows in T (or a subset S ⊆ T) having the values x on ϕ (ϕ is implicit) First, consider the smaller problem of optimizing a stratified S(ϕ, K) stratified sample associated with ϕ, where sample for a single query. We are given a query Q specifying frequency of every group x in ϕ is capped by K a table T, a QCS ϕ, and either a response time bound t or ∆(ϕ, M) the number of groups in T under ϕ having an error bound e. A time bound t determines the maximum size less than M — a measure of sparsity of T sample size on which we can operate, n; n is also the opti- Table 1. Notation in §4.1 mal sample size, since larger samples produce better statisti- cal results. Similarly, given an error bound e, it is possible to of the most commonly used form of joins in distributed data calculate the minimum sample size that will satisfy the error warehouses. For instance, Fig. 2(c) shows the distribution of bound, and any larger sample would be suboptimal because the size of dimension tables (i.e., all tables except the largest) it would take longer than necessary. In general n is monoton- across all queries in a week’s trace from Facebook. We ob- ically increasing in t (or monotonically decreasing in e) but serve that 70% of the queries involve dimension tables that are will also depend on Q and on the resources available in the less than 100 GB in size. These dimension tables can be easily cluster to process Q. We will show later in §5 how we estimate cached in the cluster memory, assuming a cluster consisting n at runtime using an Error-Latency Profile. of hundreds or thousands of nodes, where each node has at Among the rows in T, let D(ϕ) be the set of unique values least 32 GB RAM. It would also be straightforward to extend x on the columns in ϕ. For each value x there is a set of rows BlinkDB to deal with foreign key joins between two sampled in T having that value, Tx = {r ∶ r ∈ T and r takes values x tables (or a self join on one sampled table) where both ta- on columns ϕ}. We will say that there are ∣D(ϕ)∣ “groups” Tx bles have a stratified sample on the set of columns used for of rows in T under ϕ. We would like to compute an aggregate joins. We are also working on extending our query model to value for each Tx (for example, a SUM). Since that is expensive, support more general queries, specifically focusing on more instead we will choose a sample S ⊆ T with ∣S∣ = n rows. complicated user defined functions, and on nested queries. For each group Tx there is a corresponding sample group S x ⊆ S that is a subset of Tx , which will be used instead of 4. Sample Creation Tx to calculate an aggregate. The aggregate calculation for each S x will be subject to error that will depend on its size. BlinkDB creates a set of samples to accurately and quickly an- The best sampling strategy will minimize some measure of swer queries. In this section, we describe the sample creation the expected error of the aggregate across all the S x , such as process in detail. First, in §4.1, we discuss the creation of a the worst expected error or the average expected error. stratified sample on a given set of columns. We show how a A standard approach is uniform sampling — sampling n query’s accuracy and response time depends on the availabil- rows from T with equal probability. It is important to un- ity of stratified samples for that query, and evaluate the stor- derstand why this is an imperfect solution for queries that age requirements of our stratified sampling strategy for vari- compute aggregates on groups. A uniform random sample ous data distributions. Stratified samples are useful, but carry allocates a random number of rows to each group. The size storage costs, so we can only build a limited number of them. of sample group S x has a hypergeometric distribution with n In §4.2 we formulate and solve an optimization problem to draws, population size ∣T∣, and ∣Tx ∣ possibilities for the group decide on the sets of columns on which we build samples. to be drawn. The expected size of S x is n ∣T∣T∣x ∣ , which is propor- 4.1 Stratified Samples tional to ∣Tx ∣. For small ∣Tx ∣, there is a chance that ∣S x ∣ is very small or even zero, so the uniform sampling scheme can miss In this section, we describe our techniques for constructing a some groups just by chance. There are 2 things going wrong: sample to target queries using a given QCS. Table 1 contains the notation used in the rest of this section. 1. The sample size assigned to a group depends on its size in Queries that do not filter or group data (for example, a SUM T. If we care about the error of each aggregate equally, it over an entire table) often produce accurate answers when is not clear why we should assign more samples to S x just run on uniform samples. However, uniform sampling often because ∣Tx ∣ is larger. 33 

6 .2. Choosing sample sizes at random introduces the possibil- allows the system to read more rows for each group that is ity of missing or severely under-representing groups. The actually selected. So in general we want access to a family of probability of missing a large group is vanishingly small, stratified samples (S n ), one for each possible value of n. but the probability of missing a small group is substantial. Fortunately, there is a simple method that requires main- taining only a single sample for the whole family (S n ). Ac- This problem has been studied before. Briefly, since error cording to our sampling strategy, for a single value of n, decreases at a decreasing rate as sample size increases, the the size of the sample for each group is deterministic and best choice simply assigns equal sample size to each groups. is monotonically increasing in n. In addition, it is not nec- In addition, the assignment of sample sizes is deterministic, essary that the samples in the family be selected indepen- not random. A detailed proof is given by Acharya et al. [4]. dently. So given any sample S n max , for any n ≤ n max there This leads to the following algorithm for sample selection: is an S n ⊆ S n max that is an optimal sample for n in the sense 1. Compute group counts: To each x ∈ of the previous section. Our sample storage technique, de- x 0 , ..., x∣D(ϕ)∣−1 , assign a count, forming a ∣D(ϕ)∣- scribed next, allows such subsets to be identified at runtime. vector of counts N n∗ . Compute N n∗ as follows: Let The rows of stratified sample S(ϕ, K) are stored sequen- N(n′ ) = (min(⌊ ∣D(ϕ)∣ n′ ⌋, ∣Tx 0 ∣), min(⌊ ∣D(ϕ)∣ n′ ⌋, ∣Tx 1 ∣, ...), tially according to the order of columns in ϕ. Fig. 5(a) shows the optimal count-vector for a total sample size n′ . Then an example of storage layout for S(ϕ, K). B i j denotes a data choose N n∗ = N(max{n′ ∶ ∣∣N(n′ )∣∣1 S(φ) ≤ n}). In words, our block in the underlying file system, e.g., HDFS. Records cor- V(φ) samples cap the count of each group at some value ⌊ ∣D(ϕ)∣ n′ ⌋. responding to consecutive values in ϕ are stored in the same In the future we will use the name K for the cap size ⌊ ∣D(ϕ)∣ ⌋. block, e.g., B 1 . If the records corresponding to a popular value ′ n 2. Take samples: For each x, sample N nx rows uniformly ∗ do not all fit in one block, they are spread across several at random without replacement from Tx , forming the sample contiguous blocks e.g., blocks B 41 , B 42 and B 43 contain rows S x . Note that when ∣Tx ∣ = N nx ∗ , our sample includes all the from S x . Storing consecutive records contiguously on the rows ofφTx , and there will be no sampling error for that group. disk significantly improves the execution times or range of the queries on the set of columns ϕ. When S x is spread over multiple blocks, each block con- tains a randomly ordered random subset from S x , and, by K K extension, from the original table. This makes it possible to efficiently run queries on smaller samples. Assume a query Q, that needs to read n rows in total to satisfy its error Figure 4. Example of a stratified sample associated with a set bounds or time execution constraints. Let n x be the num- of columns, ϕ. ber of rows read from S x to compute the answer. (Note n x ≤ max {K, ∣Tx ∣} and ∑x∈D(ϕ),x selected by Q n x = n.) Since the The entire sample S(ϕ, K) is the disjoint union of the S x . rows are distributed randomly among the blocks, it is enough Since a stratified sample on ϕ is completely determined by the for Q to read any subset of blocks comprising S x , as long as group-size cap K, we henceforth denote a sample by S(ϕ, K) these blocks contain at least n x records. Fig. 5(b) shows an ex- or simply S when there is no ambiguity. K determines the size ample where Q reads only blocks B 41 and B 42 , as these blocks and therefore the statistical properties of a stratified sample contain enough records to compute the required answer. for each group. Storage overhead. An important consideration is the over- For example, consider query Q grouping by QCS ϕ, and head of maintaining these samples, especially for heavy- assume we use S(ϕ, K) to answer Q. For each value x on ϕ, tailed distributions with many rare groups. Consider a table if ∣Tx ∣ ≤ K, the sample contains all rows from the original with 1 billion tuples and a column set with a Zipf distribution table, so we can provide an exact answer for this group. On with an exponent of 1.5. Then, it turns out that the storage the other hand, if ∣Tx ∣ > K, we answer Q based on K random required by sample S(ϕ, K) is only 2.4% of the original table rows in the original table. For the basic aggregate operators for K = 104 , 5.2% for K = 105 , and 11.4% for K = 106 . AVG, SUM, COUNT, and QUANTILE, K directly determines the These results are consistent with real-world data from error of Q’s result. In particular, these aggregate √ operators Conviva Inc., where for K = 105 , the overhead incurred for a have standard error inversely proportional to K [16]. sample on popular columns like city, customer, autonomous system number (ASN) is less than 10%. 4.1.2 Optimizing a set of stratified samples for all queries sharing a QCS 4.2 Optimization Framework Now we turn to the question of creating samples for a set We now describe the optimization framework to select sub- of queries that share a QCS ϕ but have different values of n. sets of columns on which to build sample families. Un- Recall that n, the number of rows we read to satisfy a query, like prior work which focuses on single-column stratified will vary according to user-specified error or time bounds. A samples [9] or on a single multi-dimensional (i.e., multi- WHERE query may also select only a subset of groups, which column) stratified sample [4], BlinkDB creates several multi- 34 

7 . K K B33 B43 B33 B43 K1 B22 B32 B42 B52 B22 B32 B42 B52 B21 B21 B1 B31 B41 B51 B6 B7 B8 B1 B31 B41 B51 B6 B7 B8 x x (a) (b) Figure 5. (a) Possible storage layout for stratified sample S(ϕ, K). dimensional stratified samples. As described above, each Given these three factors defined above, we now introduce stratified sample can potentially be used at runtime to im- our optimization formulation. Let the overall storage capacity prove query accuracy and latency, especially when the orig- budget (again in rows) be C. Our goal is to select β column inal table contains small groups for a particular column set. sets from among m possible QCSs, say ϕ i 1 , ⋯, ϕ i β , which can However, each stored sample has a storage cost equal to its best answer our queries, while satisfying: size, and the number of potential samples is exponential in the number of columns. As a result, we need to be careful β in choosing the set of column-sets on which to build strati- ∑ ∣S(ϕ i k , K)∣ ≤ C k=1 fied samples. We formulate the trade-off between storage cost and query accuracy/performance as an optimization prob- Specifically, in BlinkDB, we maximize the following mixed lem, described next. integer linear program (MILP) in which j indexes over all queries and i indexes over all possible column sets: 4.2.1 Problem Formulation The optimization problem takes three factors into account in G = ∑ p j ⋅ y j ⋅ ∆(q j , M) (1) determining the sets of columns on which stratified samples j should be built: the “sparsity” of the data, workload character- subject to istics, and the storage cost of samples. m ∑ ∣S(ϕ i , K)∣ ⋅ z i ≤ C (2) Sparsity of the data. A stratified sample on ϕ is useful when i=1 the original table T contains many small groups under ϕ. and Consider a QCS ϕ in table T. Recall that D(ϕ) denotes the set ∣D(ϕ i )∣ ∀ j ∶ yj ≤ max (z i min 1, ) (3) of all distinct values on columns ϕ in rows of T. We define a i∶ϕ i ⊆q j ∪i∶ϕ i ⊃q j ∣D(q j )∣ “sparsity” function ∆(ϕ, M) as the number of groups whose size in T is less than some number M 4 : where 0 ≤ y j ≤ 1 and z i ∈ {0, 1} are variables. Here, z i is a binary variable determining whether a sample ∆(ϕ, M) = ∣{x ∈ D(ϕ) ∶ ∣Tx ∣ < M}∣ family should be built or not, i.e., when z i = 1, we build a Workload. A stratified sample is only useful when it is bene- sample family on ϕ i ; otherwise, when z i = 0, we do not. ficial to actual queries. Under our model for queries, a query The goal function (1) aims to maximize the weighted sum has a QCS q j with some (unknown) probability p j - that is, of the coverage of the QCSs of the queries, q j . If we create a QCSs are drawn from a Multinomial (p 1 , p 2 , ...) distribution. stratified sample S(ϕ i , K), the coverage of this sample for q j The best estimate of p j is simply the frequency of queries with is defined as the probability that a given value x of columns q j QCS q j in past queries. is also present among the rows of S(ϕ i , K). If ϕ i ⊇ q j , then q j is covered exactly, but ϕ i ⊂ q j can also be useful by partially Storage cost. Storage is the main constraint against build- covering q j . At runtime, if no stratified sample is available that ing too many stratified samples, and against building strat- exactly covers the QCS for a query, a partially-covering QCS ified samples on large column sets that produce too many may be used instead. In particular, the uniform sample is a groups. Therefore, we must compute the storage cost of po- degenerate case with ϕ i = ∅; it is useful for many queries but tential samples and constrain total storage. To simplify the less useful than more targeted stratified samples. formulation, we assume a single value of K for all samples; Since the coverage probability is hard to compute in prac- a sample family ϕ either receives no samples or a full sam- tice, in this paper we approximate it by y j , which is deter- ple with K elements of Tx for each x ∈ D(ϕ). ∣S(ϕ, K)∣ is the mined by constraint (3). The y j value is in [0, 1], with 0 mean- storage cost (in rows) of building a stratified sample on a set ing no coverage, and 1 meaning full coverage. The intuition of columns ϕ. behind (3) is that when we build a stratified sample on a 4 Appropriate subset of columns ϕ i ⊆ q j , i.e. when z i = 1, we have par- values for M will be discussed later in this section. Alterna- tively, one could plug in different notions of sparsity of a distribution in our tially covered q j , too. We compute this coverage as the ra- formulation. tio of the number of unique values between the two sets, i.e., 35 

8 .∣D(ϕ i )∣/∣D(q j )∣. When ϕ i ⊂ q j , this ratio, and the true cov- BlinkDB to generate many different query plans for the same erage value, is at most 1. When ϕ i = q j , the number of unique query that may operate on different samples to satisfy the values in ϕ i and q j are the same, we are guaranteed to see all same error/response time constraints. In order to pick the the unique values of q j in the stratified sample over ϕ i and best possible plan, BlinkDB’s run-time dynamic sample selec- therefore the coverage will be 1. When ϕ i ⊃ q j , the coverage tion strategy involves executing the query on a small sample is also 1, so we cap the ratio ∣D(ϕ i )∣/∣D(q j )∣ at 1. (i.e., a subsample) of data of one or more samples and gath- Finally, we need to weigh the coverage of each set of ering statistics about the query’s selectivity, complexity and columns by their importance: a set of columns q j is more im- the underlying distribution of its inputs. Based on these re- portant to cover when: (i) it appears in more queries, which is sults and the available resources, BlinkDB extrapolates the re- represented by p j , or (ii) when there are more small groups sponse time and relative error with respect to sample sizes to under q j , which is represented by ∆(q j , M). Thus, the best construct an Error Latency Profile (ELP) of the query for each solution is when we maximize the sum of p j ⋅ y j ⋅ ∆(q j , M) sample, assuming different subset sizes. An ELP is a heuris- for all QCSs, as captured by our goal function (1). tic that enables quick evaluation of different query plans in The size of this optimization problem increases exponen- BlinkDB to pick the one that can best satisfy a query’s er- tially with the number of columns in T, which looks worry- ror/response time constraints. However, it should be noted ing. However, it is possible to solve these problems in prac- that depending on the distribution of underlying data and the tice by applying some simple optimizations, like considering complexity of the query, such an estimate might not always be only column sets that actually occurred in the past queries, accurate, in which case BlinkDB may need to read additional or eliminating column sets that are unrealistically large. data to meet the query’s error/response time constraints. Finally, we must return to two important constants we In the rest of this section, we detail our approach to query have left in our formulation, M and K. In practice we set execution, by first discussing our mechanism for selecting a M = K = 100000. Our experimental results in §7 show that set of appropriate samples (§5.1), and then picking an appro- the system performs quite well on the datasets we consider priate subset size from one of those samples by constructing using these parameter values. the Error Latency Profile for the query (§5.2). Finally, we dis- cuss how BlinkDB corrects the bias introduced by executing queries on stratified samples (§5.4). 5. BlinkDB Runtime In this section, we provide an overview of query execution in 5.1 Selecting the Sample BlinkDB and present our approach for online sample selec- Choosing an appropriate sample for a query primarily de- tion. Given a query Q, the goal is to select one (or more) sam- pends on the set of columns q j that occur in its WHERE and/or ple(s) at run-time that meet the specified time or error con- GROUP BY clauses and the physical distribution of data in the straints and then compute answers over them. Picking a sam- cluster (i.e., disk vs. memory). If BlinkDB finds one or more ple involves selecting either the uniform sample or one of the stratified samples on a set of columns ϕ i such that q j ⊆ ϕ i , we stratified samples (none of which may stratify on exactly the simply pick the ϕ i with the smallest number of columns, and QCS of Q), and then possibly executing the query on a subset run the query on S(ϕ i , K). However, if there is no stratified of tuples from the selected sample. The selection of a sample sample on a column set that is a superset of q j , we run Q in (i.e., uniform or stratified) depends on the set of columns in parallel on in-memory subsets of all samples currently main- Q’s clauses, the selectivity of its selection predicates, and the tained by the system. Then, out of these samples we select data placement and distribution. In turn, the size of the sam- those that have a high selectivity as compared to others, where ple subset on which we ultimately execute the query depends selectivity is defined as the ratio of (i) the number of rows se- on Q’s time/accuracy constraints, its computation complex- lected by Q, to (ii) the number of rows read by Q (i.e., num- ity, the physical distribution of data in the cluster, and avail- ber of rows in that sample). The intuition behind this choice able cluster resources (i.e., empty slots) at runtime. is that the response time of Q increases with the number of As with traditional query processing, accurately predict- rows it reads, while the error decreases with the number of ing the selectivity is hard, especially for complex WHERE and rows Q’s WHERE/GROUP BY clause selects. GROUP BY clauses. This problem is compounded by the fact that the underlying data distribution can change with the ar- 5.2 Selecting the Right Sample/Size rival of new data. Accurately estimating the query response Once a set of samples is decided, BlinkDB needs to select time is even harder, especially when the query is executed in a particular sample ϕ i and pick an appropriately sized sub- a distributed fashion. This is (in part) due to variations in ma- sample in that sample based on the query’s response time chine load, network throughput, as well as a variety of non- or error constraints. We accomplish this by constructing an deterministic (sometimes time-dependent) factors that can ELP for the query. The ELP characterizes the rate at which cause wide performance fluctuations. the error decreases (and the query response time increases) Furthermore, maintaining a large number of samples with increasing sample sizes, and is built simply by running (which are cached in memory to different extents), allows the query on smaller samples to estimate the selectivity and 36 

9 .project latency and error for larger samples. For a distributed example, the system has three stratified samples, one biased query, its runtime scales with sample size, with the scaling on date and country, one biased on date and the designated rate depending on the exact query structure (JOINS, GROUP media area for a video, and the last one biased on date and BYs etc.), physical placement of its inputs and the underlying ended flag. In this case it is not obvious which of these three data distribution [7]. The variation of error (or the variance samples would be preferable for answering the query. of the estimator) primarily depends on the variance of the In this case, BlinkDB constructs an ELP for each of these underlying data distribution and the actual number of tuples samples as shown in Figure 6. For many queries it is possi- processed in the sample, which in turn depends on the selec- ble that all of the samples can satisfy specified time or error tivity of a query’s predicates. bounds. For instance all three of the samples in our exam- ple can be used to answer this query with an error bound of Error Profile: An error profile is created for all queries with under 4%. However it is clear from the ELP that the sam- error constraints. If Q specifies an error (e.g., standard devia- ple biased on date and ended flag would take the short- tion) constraint, the BlinkDB error profile tries to predict the est time to find an answer within the required error bounds size of the smallest sample that satisfies Q’s error constraint. (perhaps because the data for this sample is cached), and Variance and confidence intervals for aggregate functions are BlinkDB would hence execute the query on that sample. estimated using standard closed-form formulas from statis- tics [16]. For all standard SQL aggregates, the variance is pro- 5.4 Bias Correction portional to ∼ 1/n, and thus the standard √ deviation (or the statistical error) is proportional to ∼ 1/ n, where n is the Running a query on a non-uniform sample introduces a cer- number of rows from a sample of size N that match Q’s filter tain amount of statistical bias in the final result since dif- predicates. Using this notation. the selectivity s q of the query ferent groups are picked at different frequencies. In particu- is the ratio n/N. lar while all the tuples matching a rare subgroup would be Let n i ,m be the number of rows selected by Q when run- included in the sample, more popular subgroups will only ning on a subset m of the stratified sample, S(ϕ i , K). Fur- have a small fraction of values represented. To correct for this thermore, BlinkDB estimates the query selectivity s q , sample bias, BlinkDB keeps track of the effective sampling rate for variance S n (for AVG/SUM) and the input data distribution f each group associated with each sample in a hidden column (for Quantiles) by running the query on a number of small as part of the sample table schema, and uses this to weight sample subsets. Using these parameter estimates, we calcu- different subgroups to produce an unbiased result. late the number of rows n = n i ,m required to meet Q’s error constraints using standard closed form statistical error esti- 6. Implementation mates [16]. Then, we run Q on S(ϕ i , K) until it reads n rows. Fig. 7 describes the entire BlinkDB ecosystem. BlinkDB is built Latency Profile: Similarly, a latency profile is created for all on top of the Hive Query Engine [22], supports both Hadoop queries with response time constraints. If Q specifies a re- MapReduce [2] and Spark [25] (via Shark [13]) at the execu- sponse time constraint, we select the sample on which to run tion layer and uses the Hadoop Distributed File System [1] at Q the same way as above. Again, let S(ϕ i , K) be the selected the storage layer. sample, and let n be the maximum number of rows that Q can Our implementation required changes in a few key com- read without exceeding its response time constraint. Then we ponents. We add a shim layer to the HiveQL parser to han- simply run Q until reading n rows from S(ϕ i , K). dle the BlinkDB Query Interface, which enables queries with The value of n depends on the physical placement of input response time and error bounds. Furthermore, the query in- data (disk vs. memory), the query structure and complexity, terface can detect data input, triggering the Sample Creation and the degree of parallelism (or the resources available to the and Maintenance module, which creates or updates the set of query). As a simplification, BlinkDB simply predicts n by as- random and multi-dimensional samples as described in §4. suming that latency scales linearly with input size, as is com- We further extend the HiveQL parser to implement a Sam- monly observed with a majority of I/O bounded queries in ple Selection module that re-writes the query and iteratively parallel distributed execution environments [8, 26]. To avoid assigns it an appropriately sized uniform or stratified sample non-linearities that may arise when running on very small as described in §5. We also add an Uncertainty Propagation in-memory samples, BlinkDB runs a few smaller samples un- module to modify all pre-existing aggregation functions with til performance seems to grow linearly and then estimates statistical closed forms to return errors bars and confidence the appropriate linear scaling constants (i.e., data processing intervals in addition to the result. rate(s), disk/memory I/O rates etc.) for the model. One concern with BlinkDB is that multiple queries might use the same sample, inducing correlation among the an- swers to those queries. For example, if by chance a sample 5.3 An Example has a higher-than-expected average value of an aggregation As an illustrative example consider a query which calculates column, then two queries that use that sample and aggre- average session time for “Galena, IL”. For the purposes of this gate on that column will both return high answers. This may 37 

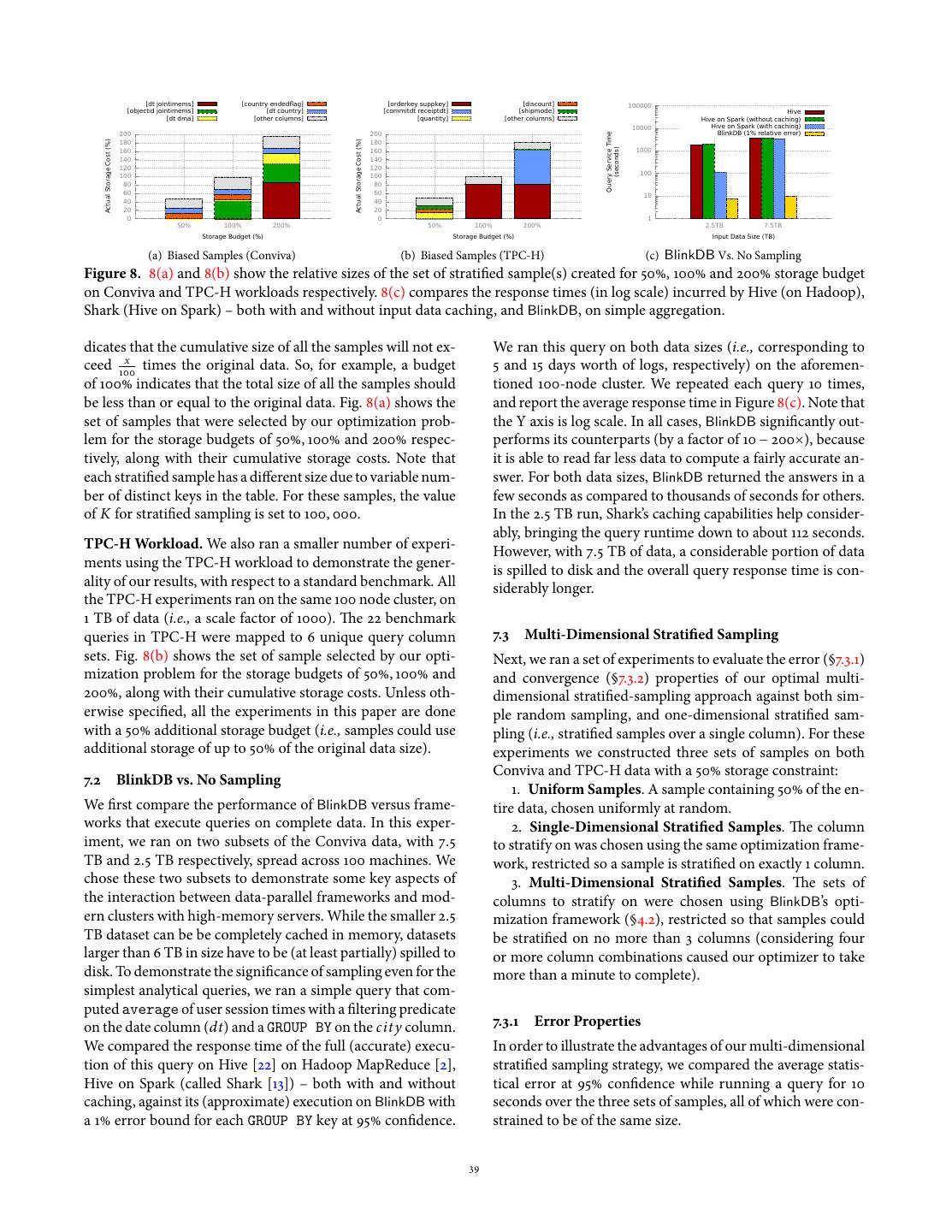
10 .                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                       (a) dt, country (b) (c) dt, ended              dt, dma flag             Figure 6. Error Latency Profiles for a variety of samples    when executing a query to calculate average session time in Galena.  (a) Shows the ELP for a sample biased on date and country, (b) is the ELP for a sample biased on date and designated media area (dma), and (c) is the ELP for a sample biased on date and the ended flag. BlinkDB  Query  Interface   the well-known TPC-H benchmark [3]. First, we compare Hive  Query  Engine   BlinkDB to query execution on full-sized datasets to demon- Uncertainty  Propagation   Sample  Selection   strate how even a small trade-off in the accuracy of final Shark   answers can result in orders-of-magnitude improvements in Hadoop   (Hive  on  Spark)   BlinkDB   MapReduce   Metastore   query response times. Second, we evaluate the accuracy and Spark   convergence properties of our optimal multi-dimensional Sample  Creation  and    Maintenance   stratified-sampling approach against both random sampling Hadoop  Distributed  File  System  (HDFS)   and single-column stratified-sampling approaches. Third, we Figure 7. BlinkDB’s Implementation Stack evaluate the effectiveness of our cost models and error pro- jections at meeting the user’s accuracy/response time re- introduce subtle inaccuracies in analysis based on multiple quirements. Finally, we demonstrate BlinkDB’s ability to scale queries. By contrast, in a system that creates a new sample gracefully with increasing cluster size. for each query, a high answer for the first query is not pre- dictive of a high answer for the second. However, as we have already discussed in §2, precomputing samples is essential for 7.1 Evaluation Setting performance in a distributed setting. We address correlation The Conviva and the TPC-H datasets were 17 TB and 1 TB among query results by periodically replacing the set of sam- (i.e., a scale factor of 1000) in size, respectively, and were both ples used. BlinkDB runs a low priority background task which stored across 100 Amazon EC2 extra large instances (each periodically (typically, daily) samples from the original data, with 8 CPU cores (2.66 GHz), 68.4 GB of RAM, and 800 creating new samples which are then used by the system. GB of disk). The cluster was configured to utilize 75 TB of An additional concern is that the workload might change distributed disk storage and 6 TB of distributed RAM cache. over time, and the sample types we compute are no longer Conviva Workload. The Conviva data represents informa- “optimal”. To alleviate this concern, BlinkDB keeps track of tion about video streams viewed by Internet users. We use statistical properties of the underlying data (e.g., variance query traces from their SQL-based ad-hoc querying system and percentiles) and periodically runs the sample creation which is used for problem diagnosis and data analytics on a module described in §4 to re-compute these properties and log of media accesses by Conviva users. These access logs are decide whether the set of samples needs to be changed. To 1.7 TB in size and constitute a small fraction of data collected reduce the churn caused due to this process, an operator can across 30 days. Based on their underlying data distribution, set a parameter to control the percentage of sample that can we generated a 17 TB dataset for our experiments and be changed at any single time. partitioned it across 100 nodes. The data consists of a single In BlinkDB, uniform samples are generally created in a large fact table with 104 columns, such as customer ID, few hundred seconds. This is because the time taken to create city, media URL, genre, date, time, user OS, them only depends on the disk/memory bandwidth and the browser type, request response time, etc. The 17 degree of parallelism. On the other hand, creating stratified TB dataset has about 5.5 billion rows and shares all the key samples on a set of columns takes anywhere between a 5 − characteristics of real-world production workloads observed 30 minutes depending on the number of unique values to at Facebook Inc. and Microsoft Corp. [7]. stratify on, which decides the number of reducers and the The raw query log consists of 19, 296 queries, from which amount of data shuffled. we selected different subsets for each of our experiments. We ran our optimization function on a sample of about 200 7. Evaluation queries representing 42 query column sets. We repeated the In this section, we evaluate BlinkDB’s performance on a 100 experiments with different storage budgets for the stratified node EC2 cluster using a workload from Conviva Inc. and samples– 50%, 100%, and 200%. A storage budget of x% in- 38 

11 . [dt jointimems] [country endedflag] [orderkey suppkey] [discount] 100000 [objectid jointimems] [dt country] [commitdt receiptdt] [shipmode] Hive [dt dma] [other columns] [quantity] [other columns] Hive on Spark (without caching) 10000 Hive on Spark (with caching) 200 200 BlinkDB (1% relative error) Query Service Time 180 180 Actual Storage Cost (%) Actual Storage Cost (%) (seconds) 160 160 1000 140 140 120 120 100 100 100 80 80 60 60 10 40 40 20 20 0 0 1 50% 100% 200% 50% 100% 200% 2.5TB 7.5TB Storage Budget (%) Storage Budget (%) Input Data Size (TB) (a) Biased Samples (Conviva) (b) Biased Samples (TPC-H) (c) BlinkDB Vs. No Sampling Figure 8. 8(a) and 8(b) show the relative sizes of the set of stratified sample(s) created for 50%, 100% and 200% storage budget on Conviva and TPC-H workloads respectively. 8(c) compares the response times (in log scale) incurred by Hive (on Hadoop), Shark (Hive on Spark) – both with and without input data caching, and BlinkDB, on simple aggregation. dicates that the cumulative size of all the samples will not ex- We ran this query on both data sizes (i.e., corresponding to ceed 100x times the original data. So, for example, a budget 5 and 15 days worth of logs, respectively) on the aforemen- of 100% indicates that the total size of all the samples should tioned 100-node cluster. We repeated each query 10 times, be less than or equal to the original data. Fig. 8(a) shows the and report the average response time in Figure 8(c). Note that set of samples that were selected by our optimization prob- the Y axis is log scale. In all cases, BlinkDB significantly out- lem for the storage budgets of 50%, 100% and 200% respec- performs its counterparts (by a factor of 10 − 200×), because tively, along with their cumulative storage costs. Note that it is able to read far less data to compute a fairly accurate an- each stratified sample has a different size due to variable num- swer. For both data sizes, BlinkDB returned the answers in a ber of distinct keys in the table. For these samples, the value few seconds as compared to thousands of seconds for others. of K for stratified sampling is set to 100, 000. In the 2.5 TB run, Shark’s caching capabilities help consider- ably, bringing the query runtime down to about 112 seconds. TPC-H Workload. We also ran a smaller number of experi- However, with 7.5 TB of data, a considerable portion of data ments using the TPC-H workload to demonstrate the gener- is spilled to disk and the overall query response time is con- ality of our results, with respect to a standard benchmark. All siderably longer. the TPC-H experiments ran on the same 100 node cluster, on 1 TB of data (i.e., a scale factor of 1000). The 22 benchmark queries in TPC-H were mapped to 6 unique query column 7.3 Multi-Dimensional Stratified Sampling sets. Fig. 8(b) shows the set of sample selected by our opti- Next, we ran a set of experiments to evaluate the error (§7.3.1) mization problem for the storage budgets of 50%, 100% and and convergence (§7.3.2) properties of our optimal multi- 200%, along with their cumulative storage costs. Unless oth- dimensional stratified-sampling approach against both sim- erwise specified, all the experiments in this paper are done ple random sampling, and one-dimensional stratified sam- with a 50% additional storage budget (i.e., samples could use pling (i.e., stratified samples over a single column). For these additional storage of up to 50% of the original data size). experiments we constructed three sets of samples on both Conviva and TPC-H data with a 50% storage constraint: 7.2 BlinkDB vs. No Sampling 1. Uniform Samples. A sample containing 50% of the en- We first compare the performance of BlinkDB versus frame- tire data, chosen uniformly at random. works that execute queries on complete data. In this exper- 2. Single-Dimensional Stratified Samples. The column iment, we ran on two subsets of the Conviva data, with 7.5 to stratify on was chosen using the same optimization frame- TB and 2.5 TB respectively, spread across 100 machines. We work, restricted so a sample is stratified on exactly 1 column. chose these two subsets to demonstrate some key aspects of 3. Multi-Dimensional Stratified Samples. The sets of the interaction between data-parallel frameworks and mod- columns to stratify on were chosen using BlinkDB’s opti- ern clusters with high-memory servers. While the smaller 2.5 mization framework (§4.2), restricted so that samples could TB dataset can be be completely cached in memory, datasets be stratified on no more than 3 columns (considering four larger than 6 TB in size have to be (at least partially) spilled to or more column combinations caused our optimizer to take disk. To demonstrate the significance of sampling even for the more than a minute to complete). simplest analytical queries, we ran a simple query that com- puted average of user session times with a filtering predicate on the date column (dt) and a GROUP BY on the cit y column. 7.3.1 Error Properties We compared the response time of the full (accurate) execu- In order to illustrate the advantages of our multi-dimensional tion of this query on Hive [22] on Hadoop MapReduce [2], stratified sampling strategy, we compared the average statis- Hive on Spark (called Shark [13]) – both with and without tical error at 95% confidence while running a query for 10 caching, against its (approximate) execution on BlinkDB with seconds over the three sets of samples, all of which were con- a 1% error bound for each GROUP BY key at 95% confidence. strained to be of the same size. 39 

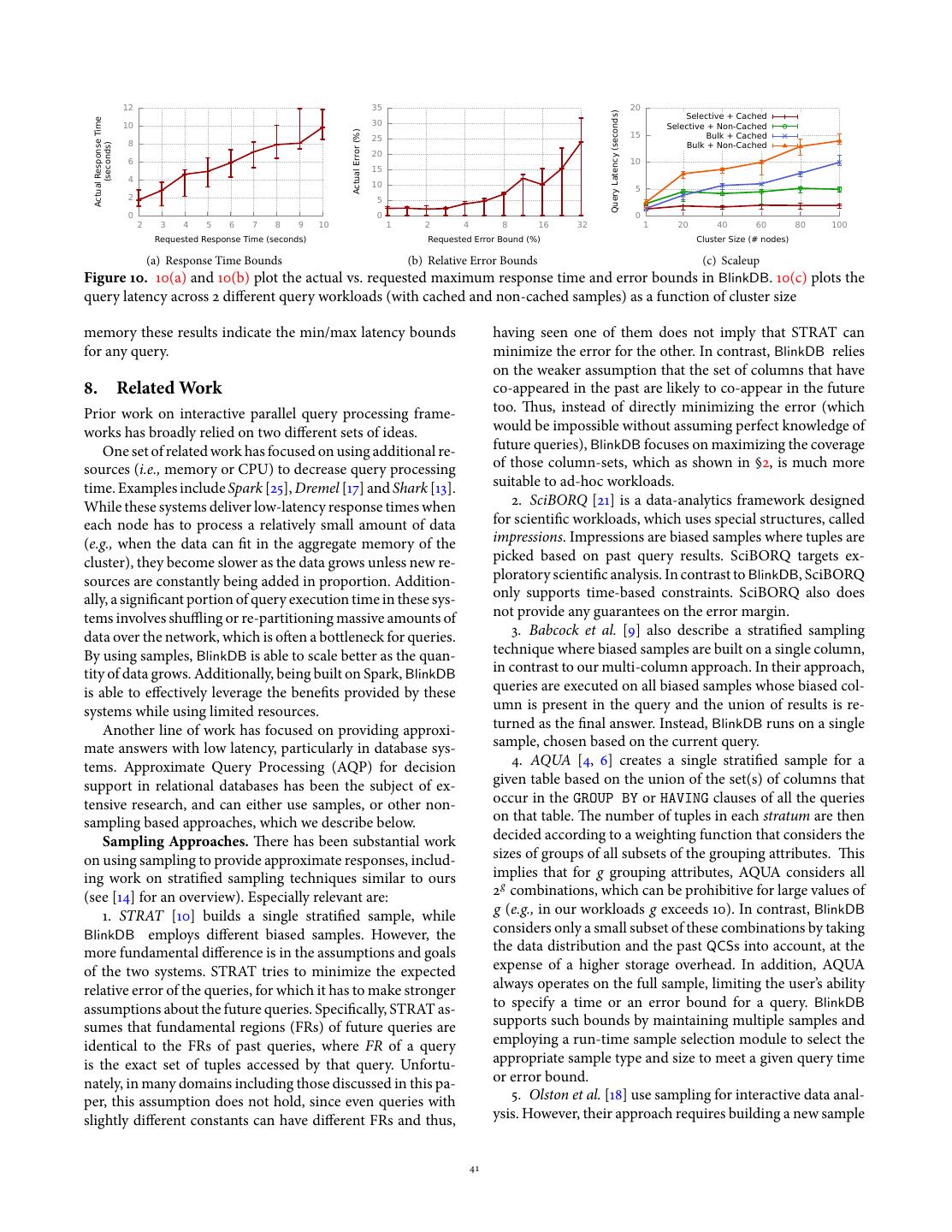
12 . 10 11 10000 Uniform Samples Uniform Samples Uniform Samples Statistical Error (%) Statistical Error (%) 9 10 Single Column Single Column Single Column 8 Multi-Column 9 Multi-Column 1000 Time (seconds) Multi-Column 7 8 6 7 100 5 6 4 5 10 3 4 1 2 3 1 2 QCS1 QCS2 QCS3 QCS4 QCS5 QCS1 QCS2 QCS3 QCS4 QCS5 QCS6 0.1 (16) (10) (1) (12) (1) (4) (6) (3) (7) (1) (1) 0 5 10 15 20 25 30 35 Unique QCS Unique QCS Statistical Error (%) (a) Error Comparison (Conviva) (b) Error Comparison (TPC-H) (c) Error Convergence (Conviva) Figure 9. 9(a) and 9(b) compare the average statistical error per QCS when running a query with fixed time budget of 10 seconds for various sets of samples. 9(c) compares the rates of error convergence with respect to time for various sets of samples. For our evaluation using Conviva’s data we used a set of 40 To test time-bounded queries, we picked a sample of 20 Con- of the most popular queries (with 5 unique QCSs) and 17 TB viva queries, and ran each of them 10 times, with a maximum of uncompressed data on 100 nodes. We ran a similar set of time bound from 1 to 10 seconds. Figure 10(a) shows the re- experiments on the standard TPC-H queries (with 6 unique sults run on the same 17 TB data set, where each bar repre- QCSs). The queries we chose were on the l ineitem table, and sents the minimum, maximum and average response times were modified to conform with HiveQL syntax. of the 20 queries, averaged over 10 runs. From these results In Figures 9(a), and 9(b), we report the average statisti- we can see that BlinkDB is able to accurately select a sample cal error in the results of each of these queries when they to satisfy a target response time. ran on the aforementioned sets of samples. The queries are Figure 10(b) shows results from the same set of queries, binned according to the set(s) of columns in their GROUP BY, also on the 17 TB data set, evaluating our ability to meet spec- WHERE and HAVING clauses (i.e., their QCSs) and the num- ified error constraints. In this case, we varied the requested bers in brackets indicate the number of queries which lie maximum error bound from 2% to 32% . The bars again repre- in each bin. Based on the storage constraints, BlinkDB’s op- sent the minimum, maximum and average errors across dif- timization framework had samples stratified on QCS1 and ferent runs of the queries. Note that the measured error is QCS2 for Conviva data and samples stratified on QCS1 , almost always at or less than the requested error. However, QCS2 and QCS4 for TPC-H data. For common QCSs, as we increase the error bound, the measured error becomes multi-dimensional samples produce smaller statistical errors closer to the bound. This is because at higher error rates the than either one-dimensional or random samples. The opti- sample size is quite small and error bounds are wider. mization framework attempts to minimize expected error, rather than per-query errors, and therefore for some specific QCS single-dimensional stratified samples behave better than 7.5 Scaling Up multi-dimensional samples. Overall, however, our optimiza- Finally, in order to evaluate the scalability properties of tion framework significantly improves performance versus BlinkDB as a function of cluster size, we created 2 different single column samples. sets of query workload suites consisting of 40 unique Con- viva queries each. The first set (marked as sel ective) consists 7.3.2 Convergence Properties of highly selective queries – i.e., those queries that only oper- We also ran experiments to demonstrate the convergence ate on a small fraction of input data. These queries occur fre- properties of multi-dimensional stratified samples used by quently in production workloads and consist of one or more BlinkDB. We use the same set of three samples as §7.3, taken highly selective WHERE clauses. The second set (marked as over 17 TB of Conviva data. Over this data, we ran multiple bul k) consists of those queries that are intended to crunch queries to calculate average session time huge amounts of data. While the former set’s input is gener- For a particular ISP’s customers in 5 US Cities and deter- ally striped across a small number of machines, the latter set mined the latency for achieving a particular error bound with of queries generally runs on data stored on a large number 95% confidence. Results from this experiment (Figure 9(c)) of machines, incurring a higher communication cost. Fig- show that error bars from running queries over multi- ure 10(c) plots the query latency for each of these workloads dimensional samples converge orders-of-magnitude faster as a function of cluster size. Each query operates on 100n GB than random sampling (i.e., Hadoop Online [11, 19]), and are of data (where n is the cluster size). So for a 10 node clus- significantly faster to converge than single-dimensional strat- ter, each query operates on 1 TB of data and for a 100 node ified samples. cluster each query operates on around 10 TB of data. Fur- ther, for each workload suite, we evaluate the query latency 7.4 Time/Accuracy Guarantees for the case when the required samples are completely cached In this set of experiments, we evaluate BlinkDB’s effectiveness in RAM or when they are stored entirely on disk. Since in re- at meeting different time/error bounds requested by the user. ality any sample will likely partially reside both on disk and in 40 

13 . 12 35 20 Query Latency (seconds) Selective + Cached Actual Response Time 10 30 Selective + Non-Cached Actual Error (%) 25 15 Bulk + Cached 8 Bulk + Non-Cached (seconds) 20 6 10 15 4 10 5 2 5 0 0 0 2 3 4 5 6 7 8 9 10 1 2 4 8 16 32 1 20 40 60 80 100 Requested Response Time (seconds) Requested Error Bound (%) Cluster Size (# nodes) (a) Response Time Bounds (b) Relative Error Bounds (c) Scaleup Figure 10. 10(a) and 10(b) plot the actual vs. requested maximum response time and error bounds in BlinkDB. 10(c) plots the query latency across 2 different query workloads (with cached and non-cached samples) as a function of cluster size memory these results indicate the min/max latency bounds having seen one of them does not imply that STRAT can for any query. minimize the error for the other. In contrast, BlinkDB relies on the weaker assumption that the set of columns that have 8. Related Work co-appeared in the past are likely to co-appear in the future Prior work on interactive parallel query processing frame- too. Thus, instead of directly minimizing the error (which works has broadly relied on two different sets of ideas. would be impossible without assuming perfect knowledge of One set of related work has focused on using additional re- future queries), BlinkDB focuses on maximizing the coverage sources (i.e., memory or CPU) to decrease query processing of those column-sets, which as shown in §2, is much more time. Examples include Spark [25], Dremel [17] and Shark [13]. suitable to ad-hoc workloads. While these systems deliver low-latency response times when 2. SciBORQ [21] is a data-analytics framework designed each node has to process a relatively small amount of data for scientific workloads, which uses special structures, called (e.g., when the data can fit in the aggregate memory of the impressions. Impressions are biased samples where tuples are cluster), they become slower as the data grows unless new re- picked based on past query results. SciBORQ targets ex- sources are constantly being added in proportion. Addition- ploratory scientific analysis. In contrast to BlinkDB, SciBORQ ally, a significant portion of query execution time in these sys- only supports time-based constraints. SciBORQ also does tems involves shuffling or re-partitioning massive amounts of not provide any guarantees on the error margin. data over the network, which is often a bottleneck for queries. 3. Babcock et al. [9] also describe a stratified sampling By using samples, BlinkDB is able to scale better as the quan- technique where biased samples are built on a single column, tity of data grows. Additionally, being built on Spark, BlinkDB in contrast to our multi-column approach. In their approach, is able to effectively leverage the benefits provided by these queries are executed on all biased samples whose biased col- systems while using limited resources. umn is present in the query and the union of results is re- Another line of work has focused on providing approxi- turned as the final answer. Instead, BlinkDB runs on a single mate answers with low latency, particularly in database sys- sample, chosen based on the current query. tems. Approximate Query Processing (AQP) for decision 4. AQUA [4, 6] creates a single stratified sample for a support in relational databases has been the subject of ex- given table based on the union of the set(s) of columns that tensive research, and can either use samples, or other non- occur in the GROUP BY or HAVING clauses of all the queries sampling based approaches, which we describe below. on that table. The number of tuples in each stratum are then Sampling Approaches. There has been substantial work decided according to a weighting function that considers the on using sampling to provide approximate responses, includ- sizes of groups of all subsets of the grouping attributes. This ing work on stratified sampling techniques similar to ours implies that for g grouping attributes, AQUA considers all (see [14] for an overview). Especially relevant are: 2 g combinations, which can be prohibitive for large values of 1. STRAT [10] builds a single stratified sample, while g (e.g., in our workloads g exceeds 10). In contrast, BlinkDB BlinkDB employs different biased samples. However, the considers only a small subset of these combinations by taking more fundamental difference is in the assumptions and goals the data distribution and the past QCSs into account, at the of the two systems. STRAT tries to minimize the expected expense of a higher storage overhead. In addition, AQUA relative error of the queries, for which it has to make stronger always operates on the full sample, limiting the user’s ability assumptions about the future queries. Specifically, STRAT as- to specify a time or an error bound for a query. BlinkDB sumes that fundamental regions (FRs) of future queries are supports such bounds by maintaining multiple samples and identical to the FRs of past queries, where FR of a query employing a run-time sample selection module to select the is the exact set of tuples accessed by that query. Unfortu- appropriate sample type and size to meet a given query time nately, in many domains including those discussed in this pa- or error bound. per, this assumption does not hold, since even queries with 5. Olston et al. [18] use sampling for interactive data anal- slightly different constants can have different FRs and thus, ysis. However, their approach requires building a new sample 41 

14 .for each query template, while BlinkDB shares stratified sam- chooses the best samples for satisfying query constraints. ples across column-sets. This both reduces our storage over- Evaluation results on real data sets and on deployments of head, and allows us to effectively answer queries for which up to 100 nodes demonstrate the effectiveness of BlinkDB at templates are not known a priori. handling a variety of queries with diverse error and time con- Online Aggregation. Online Aggregation (OLA) [15] and straints, allowing us to answer a range of queries within 2 sec- its successors [11, 19] proposed the idea of providing approx- onds on 17 TB of data with 90-98% accuracy. imate answers which are constantly refined during query ex- ecution. It provides users with an interface to stop execution Acknowledgements once they are satisfied with the current accuracy. As com- We are indebted to our shepherd Kim Keeton for her invaluable feedback and monly implemented, the main disadvantage of OLA systems suggestions that greatly improved this work. We are also grateful to Surajit is that they stream data in a random order, which imposes Chaudhuri, Michael Franklin, Phil Gibbons, Joe Hellerstein, and members a significant overhead in terms of I/O. Naturally, these ap- of the UC Berkeley AMP Lab for their detailed comments on the draft and proaches cannot exploit the workload characteristics in op- insightful discussions on this topic. This research is supported in part by NSF timizing the query execution. However, in principle, tech- CISE Expeditions award CCF-1139158, the DARPA XData Award FA8750- niques like online aggregation could be added to BlinkDB, 12-2-0331, and gifts from Qualcomm, Amazon Web Services, Google, SAP, to make it continuously refine the values of aggregates; such Blue Goji, Cisco, Clearstory Data, Cloudera, Ericsson, Facebook, General techniques are largely orthogonal to our ideas of optimally Electric, Hortonworks, Huawei, Intel, Microsoft, NetApp, Oracle, Quanta, selecting pre-computed, stratified samples. Samsung, Splunk, VMware and Yahoo!. Materialized Views, Data Cubes, Wavelets, Synopses, Sketches, Histograms. There has been a great deal of work References on “synopses” (e.g., wavelets, histograms, sketches, etc.) and [1] Apache Hadoop Distributed File System. http://hadoop.apache.org/ lossless summaries (e.g. materialized views, data cubes). In hdfs/. general, these techniques are tightly tied to specific classes of [2] Apache Hadoop Mapreduce Project. http://hadoop.apache.org/ mapreduce/. queries. For instance, Vitter and Wang [24] use Haar wavelets [3] TPC-H Query Processing Benchmarks. http://www.tpc.org/tpch/. to encode a data cube without reading the least significant [4] S. Acharya, P. B. Gibbons, and V. Poosala. Congressional samples for approximate answering of group-by queries. In ACM SIGMOD, May 2000. bits of SUM/COUNT aggregates in a flat query5 , but it is not [5] S. Acharya, P. B. Gibbons, V. Poosala, and S. Ramaswamy. Join synopses clear how to use the same encoding to answer joins, sub- for approximate query answering. In ACM SIGMOD, June 1999. [6] S. Acharya, P. B. Gibbons, V. Poosala, and S. Ramaswamy. The Aqua queries, or other complex expressions. Thus, these techniques approximate query answering system. ACM SIGMOD Record, 28(2), 1999. are most applicable6 when future queries are known in ad- [7] S. Agarwal, S. Kandula, N. Bruno, M.-C. Wu, I. Stoica, and J. Zhou. Re- optimizing Data Parallel Computing. In NSDI, 2012. vance (modulo constants or other minor details). Nonethe- [8] G. Ananthanarayanan, S. Kandula, A. G. Greenberg, et al. Reining in the less, these techniques are orthogonal to BlinkDB, as one could outliers in map-reduce clusters using mantri. In OSDI, pages 265–278, 2010. [9] B. Babcock, S. Chaudhuri, and G. Das. Dynamic sample selection for use different wavelets and synopses for common queries and approximate query processing. In VLDB, 2003. resort to stratified sampling when faced with ad-hoc queries [10] S. Chaudhuri, G. Das, and V. Narasayya. Optimized stratified sampling for approximate query processing. TODS, 2007. that cannot be supported by the current set of synopses. [11] T. Condie, N. Conway, P. Alvaro, J. M. Hellerstein, K. Elmeleegy, and For instance, the join-synopsis [5] can be incorporated into R. Sears. Mapreduce online. In NSDI, 2010. [12] G. Cormode. Sketch techniques for massive data. In Synposes for Massive BlinkDB whereby any join query involving multiple tables Data: Samples, Histograms, Wavelets and Sketches. 2011. would be conceptually rewritten as a query on a single join [13] C. Engle, A. Lupher, R. Xin, M. Zaharia, et al. Shark: Fast Data Analysis Using Coarse-grained Distributed Memory. In SIGMOD, 2012. synopsis relation. Thus, implementing such synopsis along- [14] M. Garofalakis and P. Gibbons. Approximate query processing: Taming the side the current set of stratified samples in BlinkDB may im- terabytes. In VLDB, 2001. Tutorial. [15] J. M. Hellerstein, P. J. Haas, and H. J. Wang. Online aggregation. In prove the performance for certain cases. Incorporating the SIGMOD, 1997. storage requirement of such synopses into our optimization [16] S. Lohr. Sampling: design and analysis. Thomson, 2009. [17] S. Melnik, A. Gubarev, J. J. Long, G. Romer, S. Shivakumar, M. Tolton, and formulation makes an interesting line of future work. T. Vassilakis. Dremel: interactive analysis of web-scale datasets. Commun. ACM, 54:114–123, June 2011. [18] C. Olston, E. Bortnikov, K. Elmeleegy, F. Junqueira, and B. Reed. Interactive 9. Conclusion analysis of web-scale data. In CIDR, 2009. [19] N. Pansare, V. R. Borkar, C. Jermaine, and T. Condie. Online Aggregation In this paper, we presented BlinkDB, a parallel, sampling- for Large MapReduce Jobs. PVLDB, 4(11):1135–1145, 2011. based approximate query engine that provides support for [20] C. Sapia. Promise: Predicting query behavior to enable predictive caching strategies for olap systems. DaWaK, pages 224–233. Springer-Verlag, 2000. ad-hoc queries with error and response time constraints. [21] L. Sidirourgos, M. L. Kersten, and P. A. Boncz. SciBORQ: Scientific data BlinkDB is based on two key ideas: (i) a multi-dimensional management with Bounds On Runtime and Quality. In CIDR’11, 2011. [22] A. Thusoo, J. S. Sarma, N. Jain, et al. Hive: a warehousing solution over a sampling strategy that builds and maintains a variety of sam- map-reduce framework. PVLDB, 2(2), 2009. ples, and (ii) a run-time dynamic sample selection strategy [23] S. Tirthapura and D. Woodruff. Optimal random sampling from dis- tributed streams revisited. Distributed Computing, pages 283–297, 2011. that uses parts of a sample to estimate query selectivity and [24] J. S. Vitter and M. Wang. Approximate computation of multidimensional aggregates of sparse data using wavelets. SIGMOD, 1999. 5A SQL statement without any nested sub-queries. [25] M. Zaharia et al. Resilient distributed datasets: A fault-tolerant abstraction for in-memory cluster computing. In NSDI, 2012. 6 Also,note that materialized views can be still too large for real-time pro- [26] M. Zaharia, A. Konwinski, A. D. Joseph, et al. Improving MapReduce cessing. Performance in Heterogeneous Environments. In OSDI, 2008. 42