1. So Who Won: Dynamic Max Discovery with the Crowd Assma Boughoula 

2. Mo=va=on Which ki?en is cutest? Which dog is largest? 

3. Problem Statement •  Set O of n objects {o1, …, on} •  Each oi has quality ci •  π : permuta=on or ranking of O •  If π(i) < π(j) then oi is ranked higher than oj and ci>cj •  W : n x n matrix of votes from workers •  Assump=ons: –  ci ≠ cj for all i ≠ j –  Workers can only compare a pair of objects •  Goal: arrive at the correct permuta=on π quickly and efficiently 

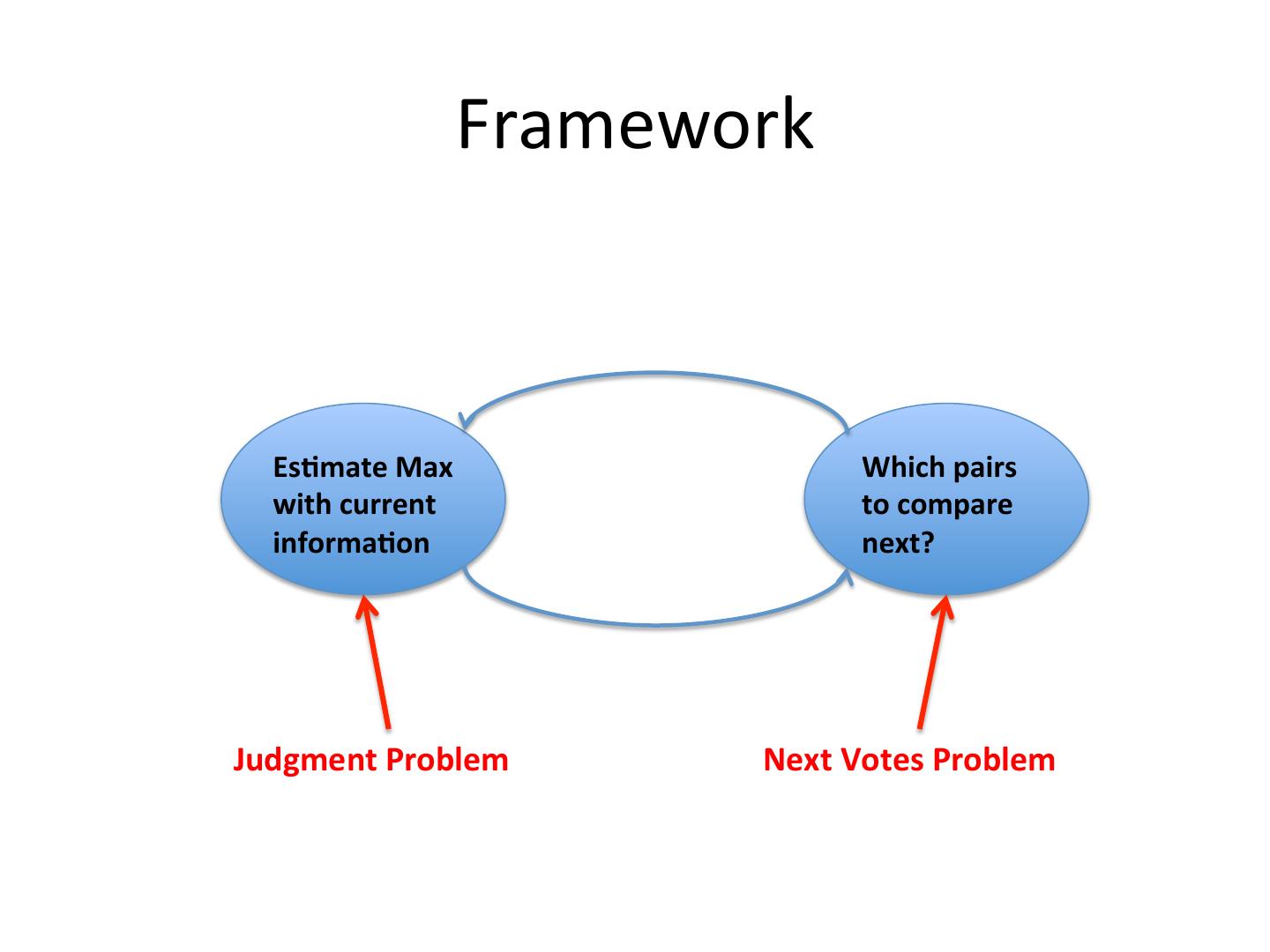
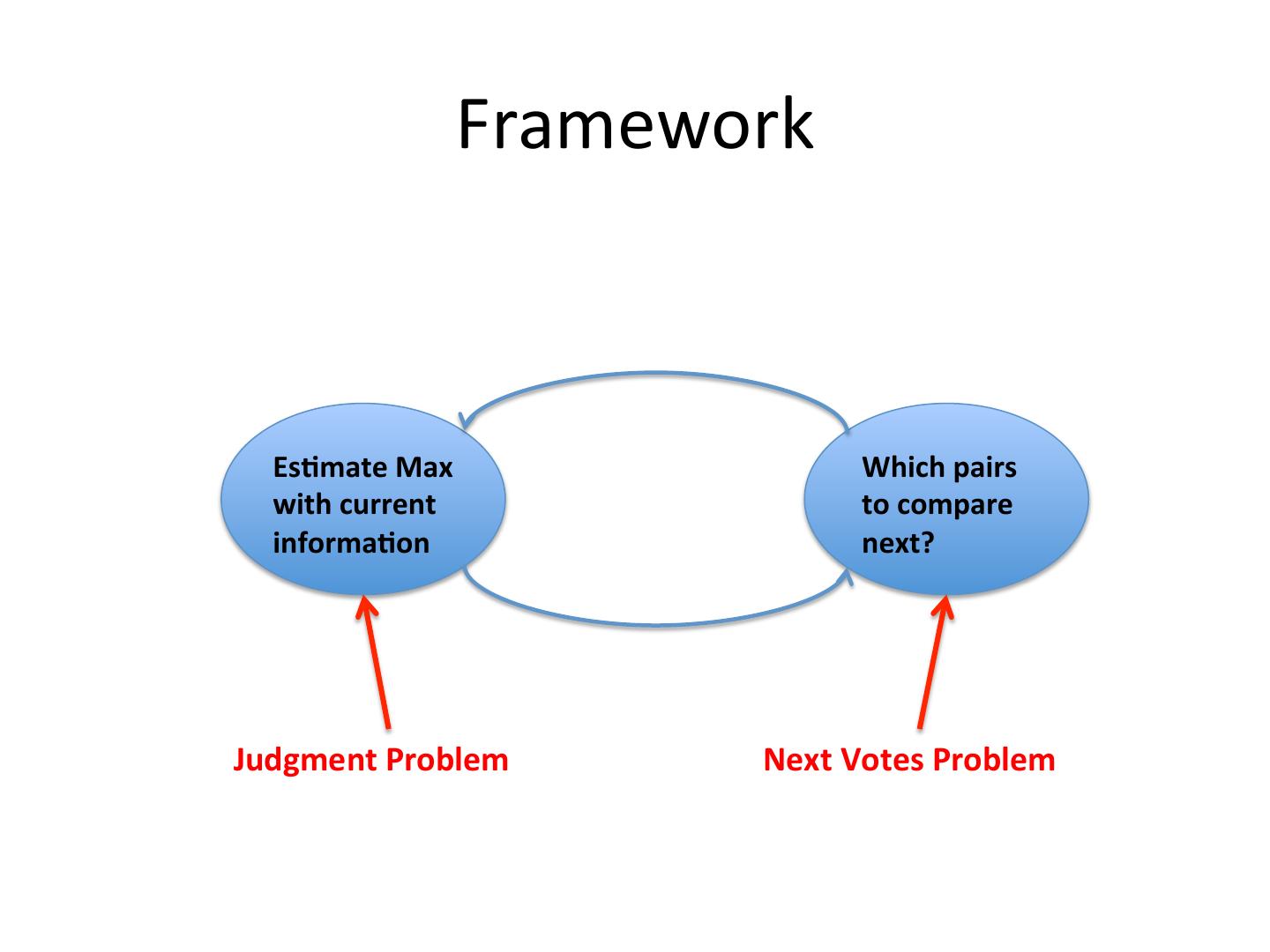
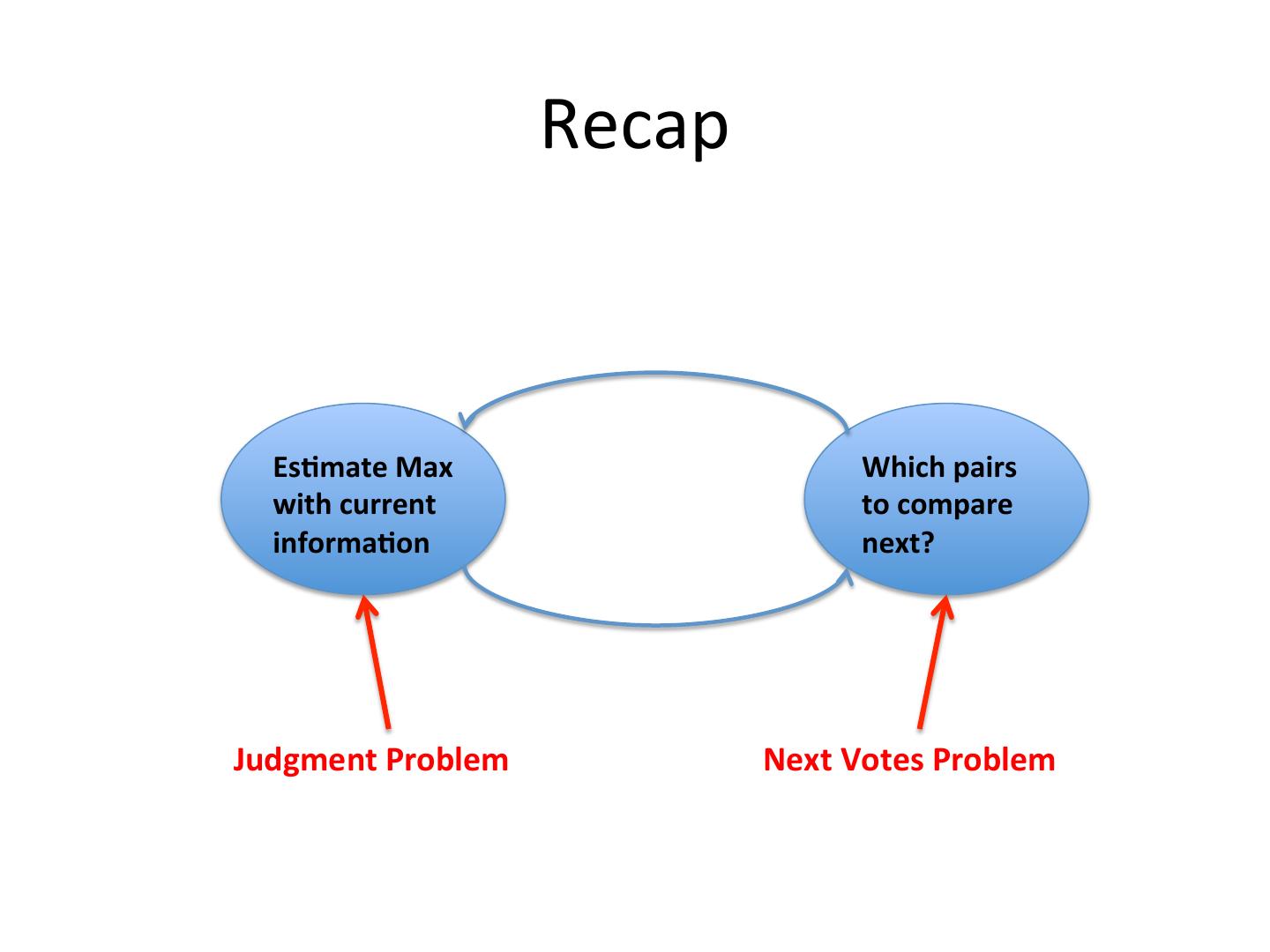
4. Framework •  Two sub-problems Es-mate Max Which pairs with current to compare informa-on next? 

5. Framework Es-mate Max Which pairs with current to compare informa-on next? Judgment Problem Next Votes Problem 

6. Outline •  Judgment Problem •  Next Votes Problem –  Maximum Likelihood –  Maximum Likelihood (ML) baseline (ML) baseline –  Heuris=c Strategies –  Heuris=c Vote •  Indegree Selec=on Strategies •  Local •  Paired •  PageRank •  Max •  Itera=ve •  Greedy •  Round Robin 

7.Judgment Problem A B C D A B C D 

8. Judgment Problem Maximum Likelihood •  Average worker accuracy p is known •  Calculate P(πd|W) for each permuta=on πd •  Choose most probable permuta=on In example: (D, C, B, A) (C, D, B, A) •  There are n! possible permuta=ons!!! Exhaus=ve, inefficient 

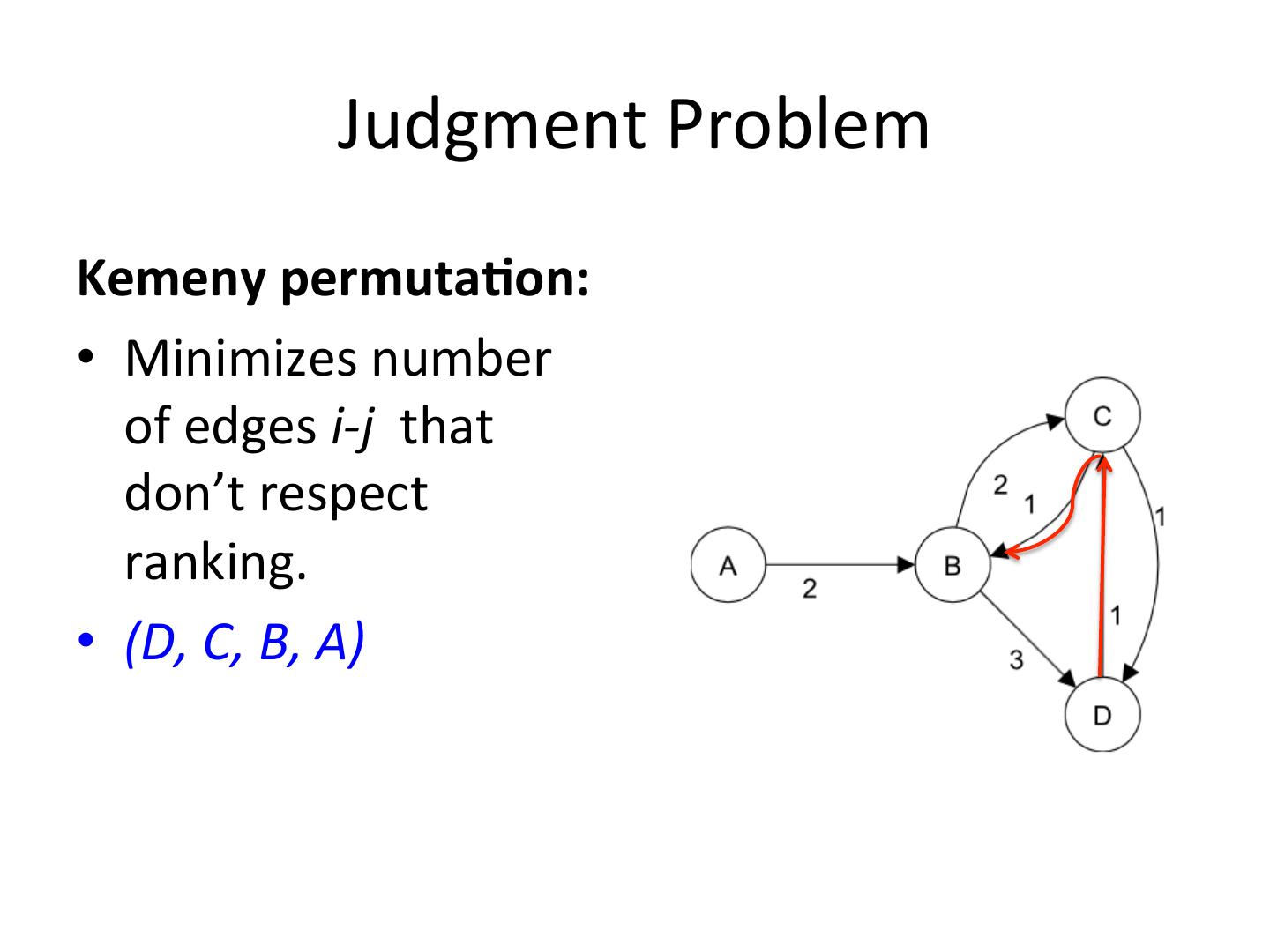
9. Judgment Problem Kemeny permuta-on: •  Minimizes number of edges i-j that don’t respect ranking. •  (D, C, B, A) 

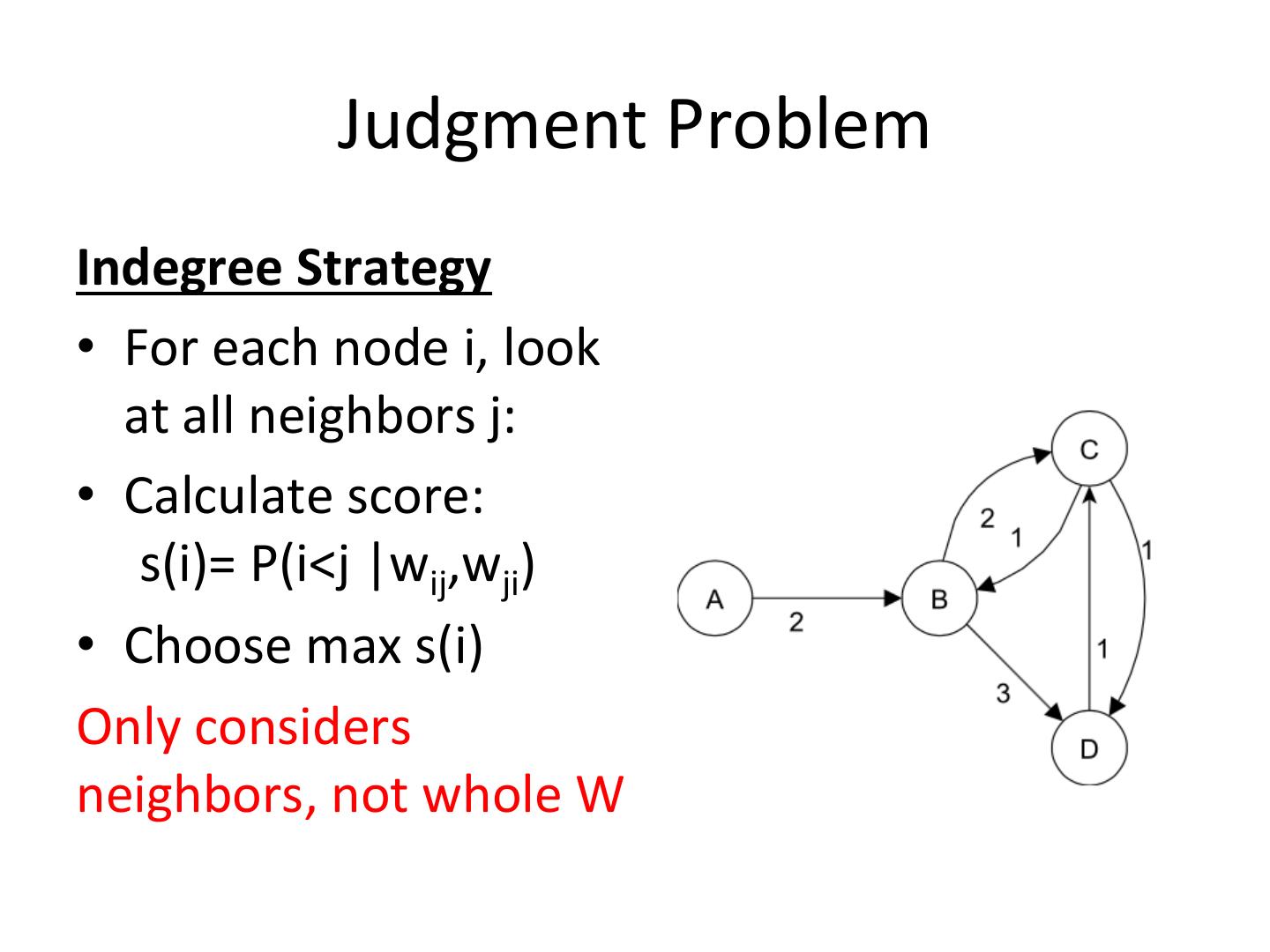
10. Judgment Problem Indegree Strategy •  For each node i, look at all neighbors j: •  Calculate score: s(i)= P(i<j |wij,wji) •  Choose max s(i) Only considers neighbors, not whole W 

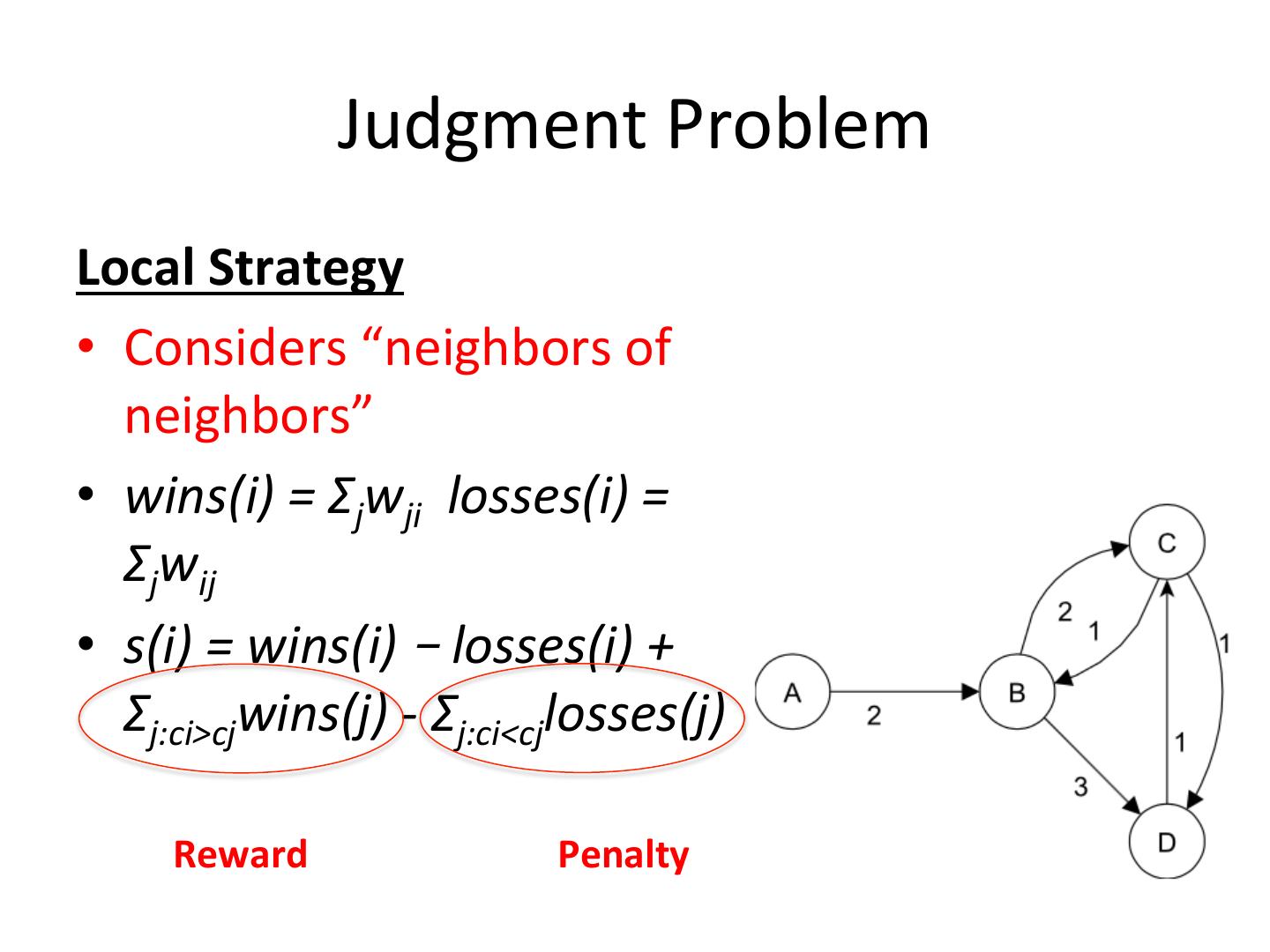
11. Judgment Problem Local Strategy •  Considers “neighbors of neighbors” •  wins(i) = Σjwji losses(i) = Σjwij •  s(i) = wins(i) – losses(i) + Σj:ci>cjwins(j) - Σj:ci<cjlosses(j) Reward Penalty 

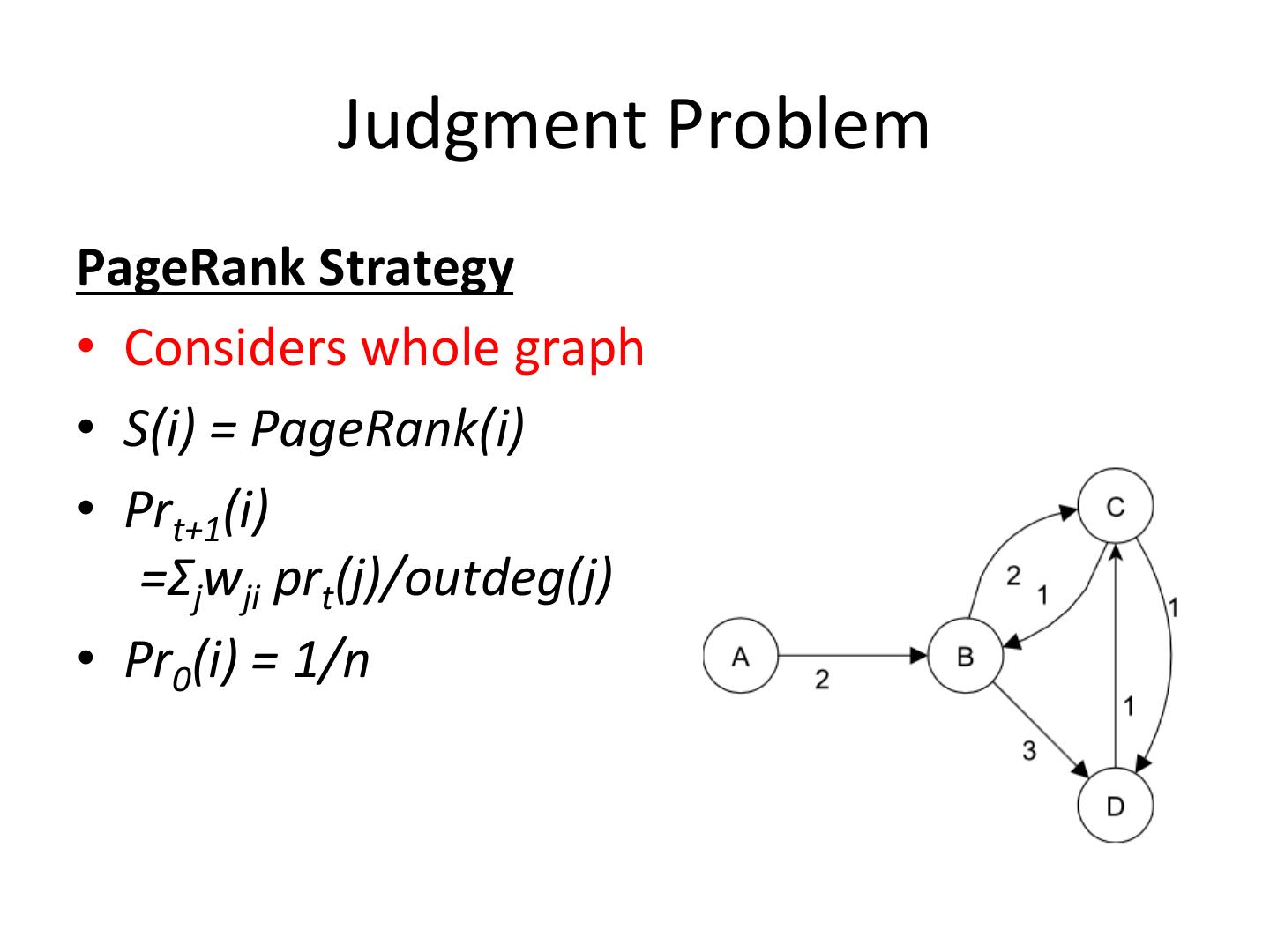
12. Judgment Problem PageRank Strategy •  Considers whole graph •  S(i) = PageRank(i) •  Prt+1(i) =Σjwji prt(j)/outdeg(j) •  Pr0(i) = 1/n 

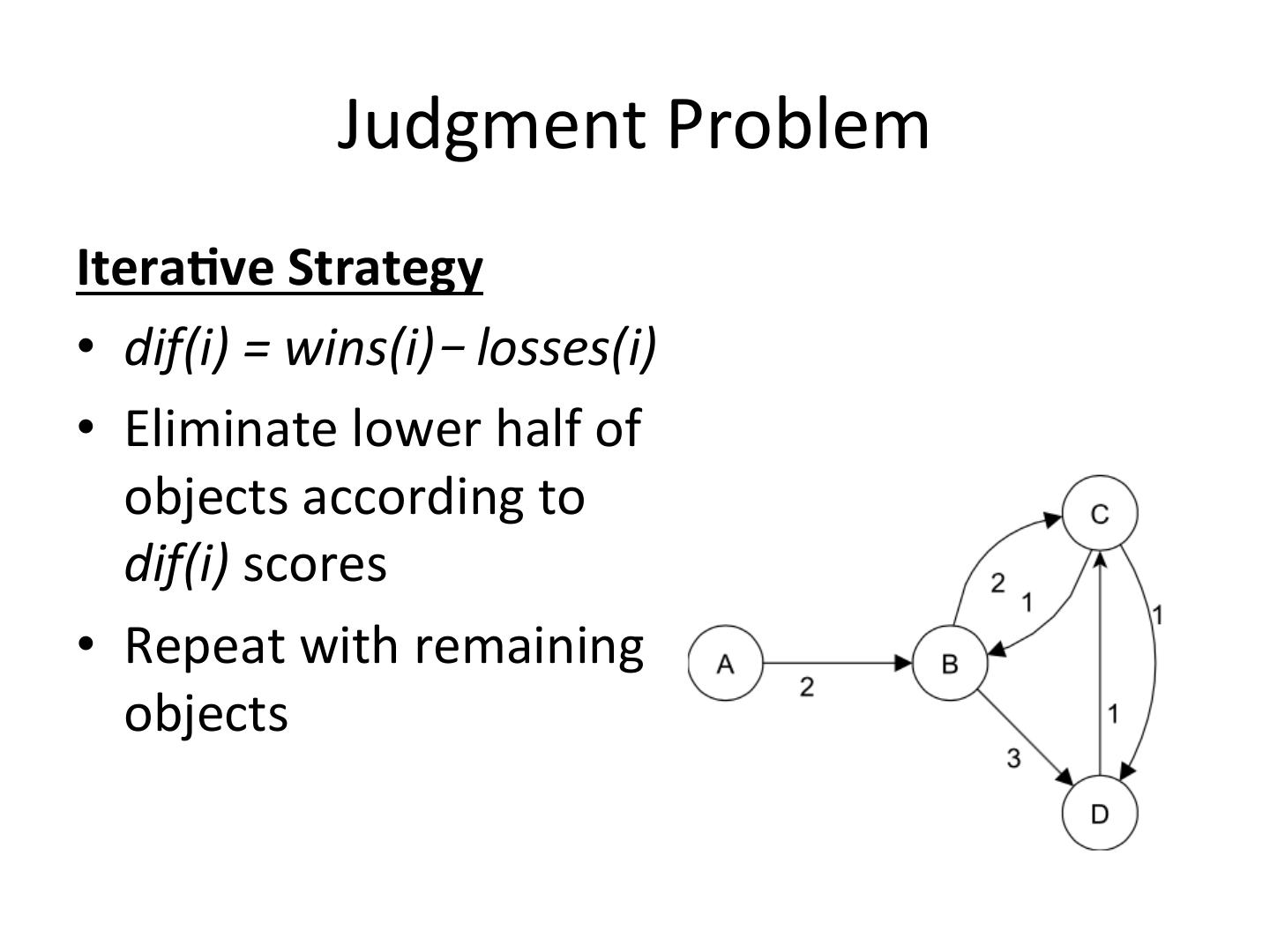
13. Judgment Problem Itera-ve Strategy •  dif(i) = wins(i)– losses(i) •  Eliminate lower half of objects according to dif(i) scores •  Repeat with remaining objects 

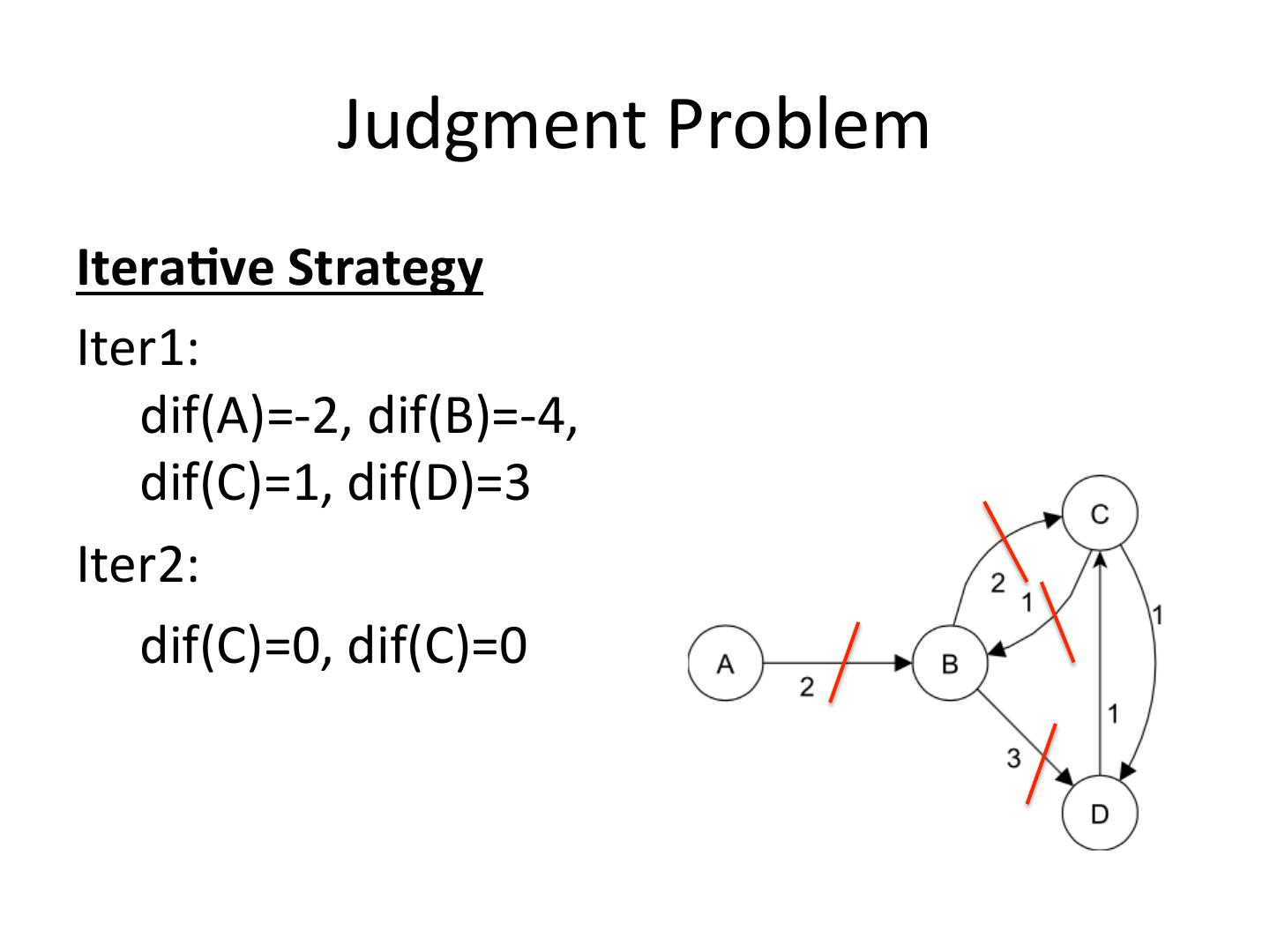
14. Judgment Problem Itera-ve Strategy Iter1: dif(A)=-2, dif(B)=-4, dif(C)=1, dif(D)=3 Iter2: dif(C)=0, dif(C)=0 

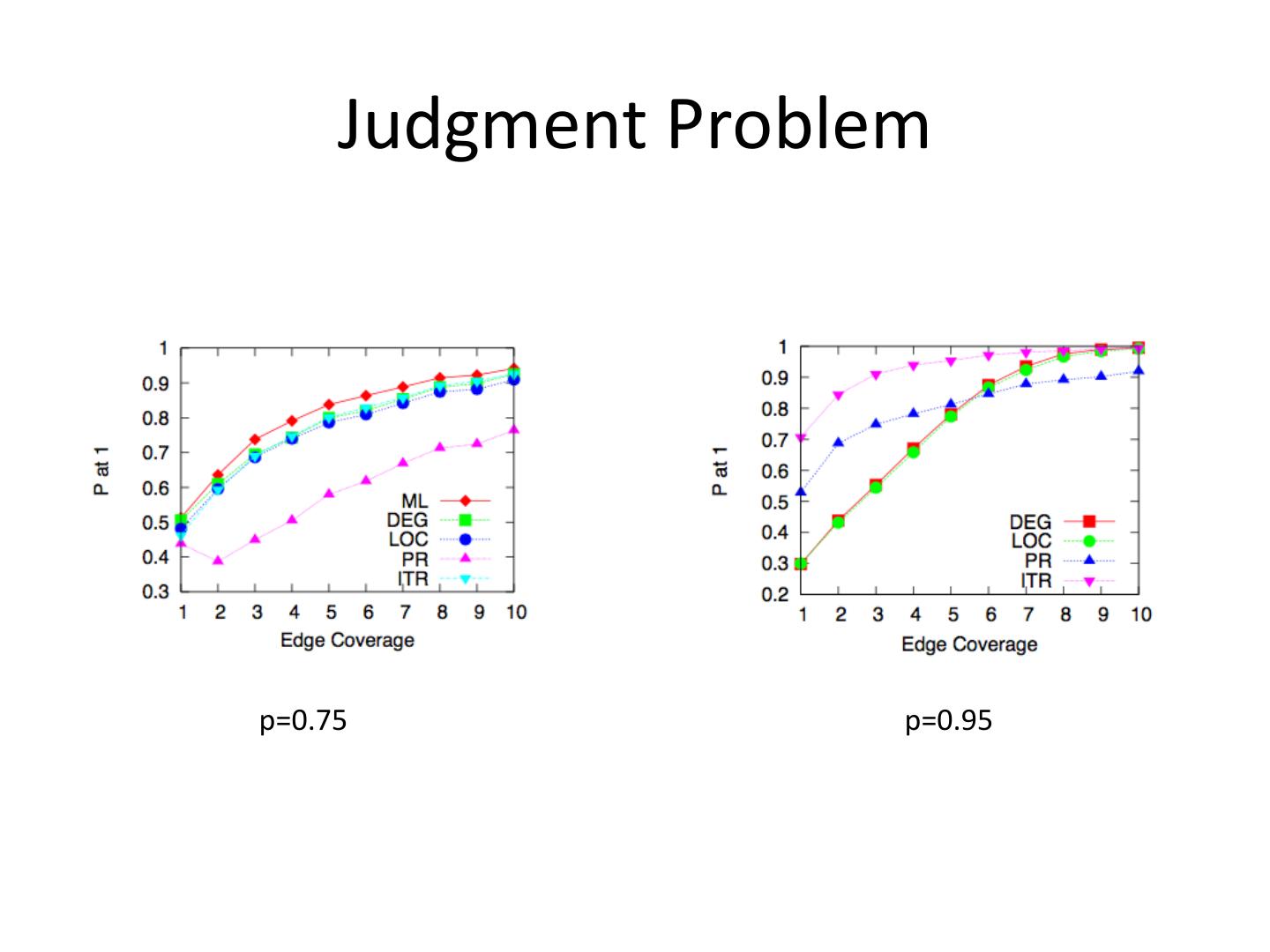
15. Judgment Problem p=0.75 p=0.95 

16. Framework Es-mate Max Which pairs with current to compare informa-on next? Judgment Problem Next Votes Problem 

17. Next Votes Problem Some Nota=on… •  Budget b = # votes to be requested •  Poten=al vote {oi, oj} •  Q = {{oi, oj},…} possible mul=set of b votes •  Answer tuple ({oi, oj}, ox) •  Answer mul=set a={({oi, oj}, ox),…} •  2b possible answer mul=sets for each Q !!! •  a∧W : updated W matrix 

18. Next Votes Problem Maximum Likelihood •  Look for Q such that a∧W increases our confidence when es=ma=ng the max the most. •  Choose Q that maximizes: ΣamaxiP(i is max, a∧W ) •  Assumes average worker accuracy p known 

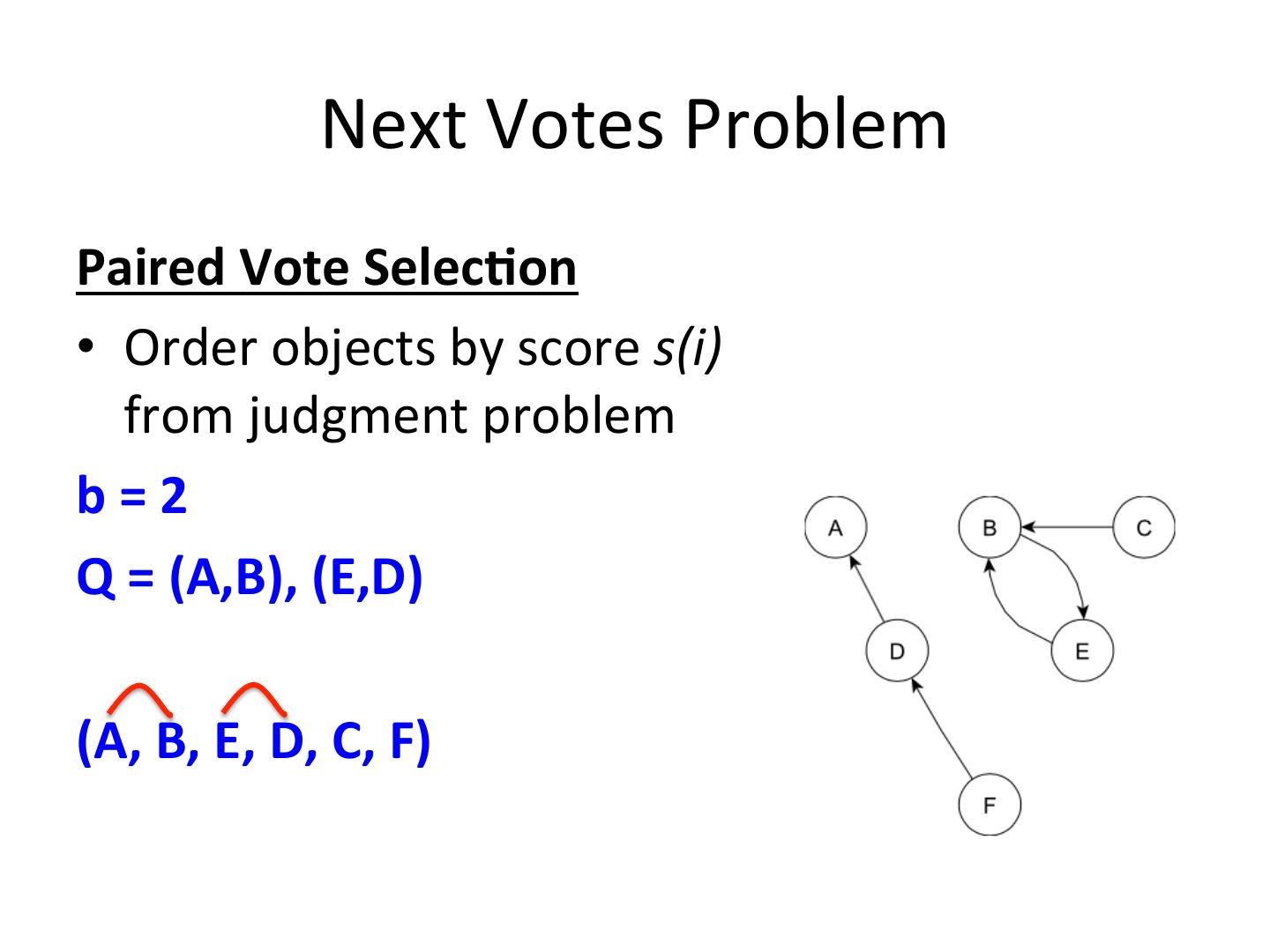
19. Next Votes Problem Paired Vote Selec-on •  Order objects by score s(i) from judgment problem b = 2 Q = (A,B), (E,D) (A, B, E, D, C, F) 

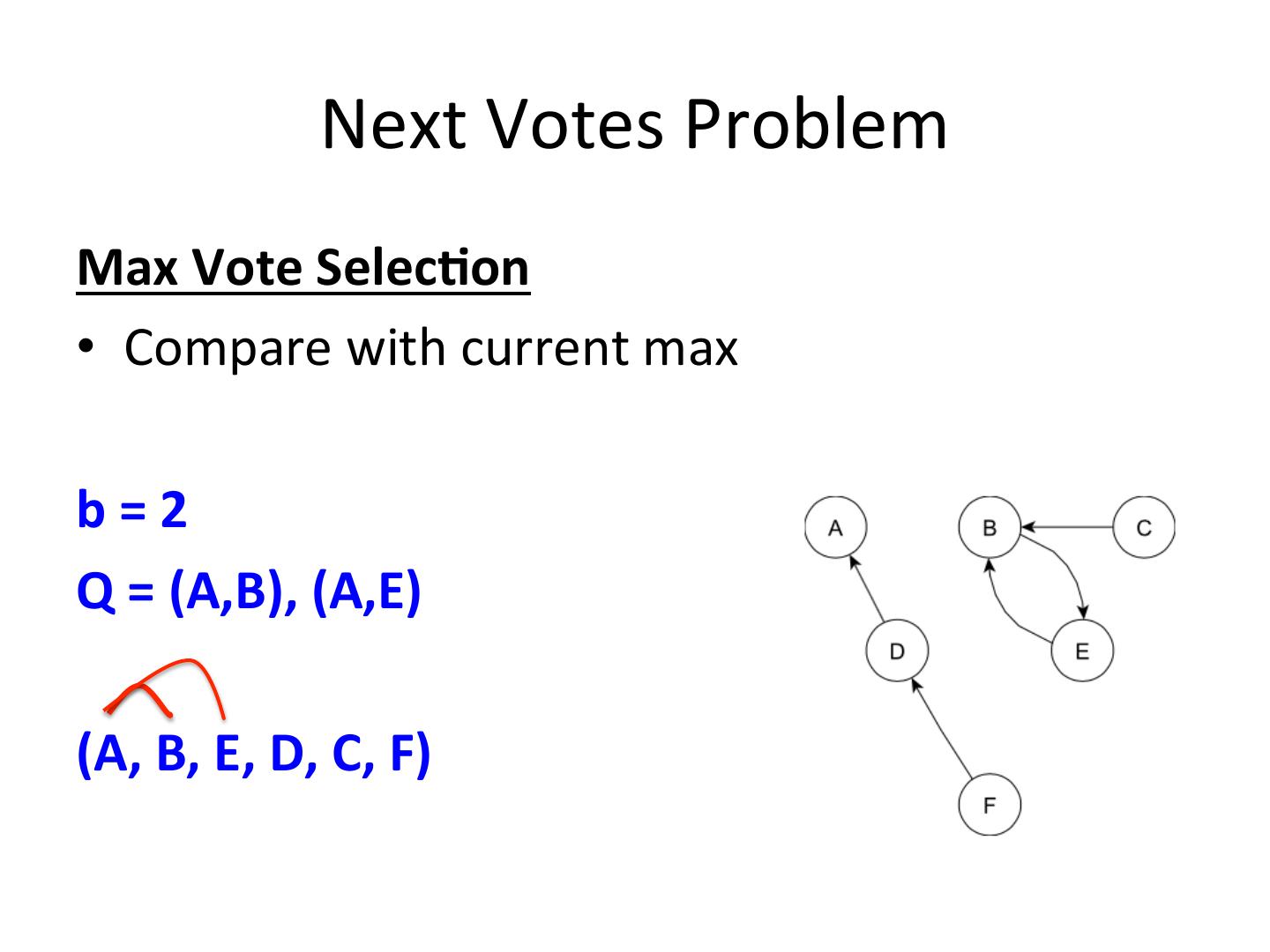
20. Next Votes Problem Max Vote Selec-on •  Compare with current max b = 2 Q = (A,B), (A,E) (A, B, E, D, C, F) 

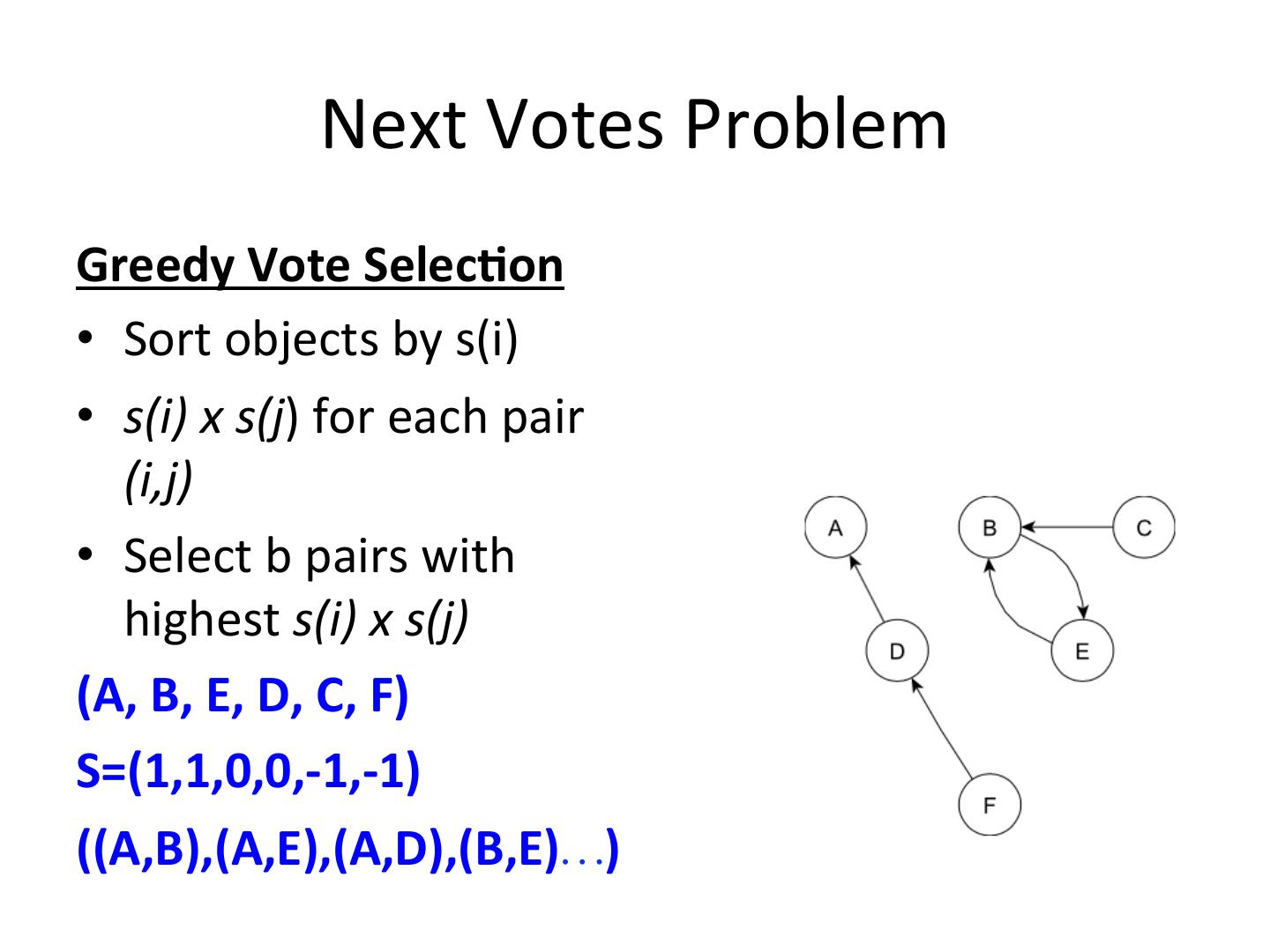
21. Next Votes Problem Greedy Vote Selec-on •  Sort objects by s(i) •  s(i) x s(j) for each pair (i,j) •  Select b pairs with highest s(i) x s(j) (A, B, E, D, C, F) S=(1,1,0,0,-1,-1) ((A,B),(A,E),(A,D),(B,E)…) 

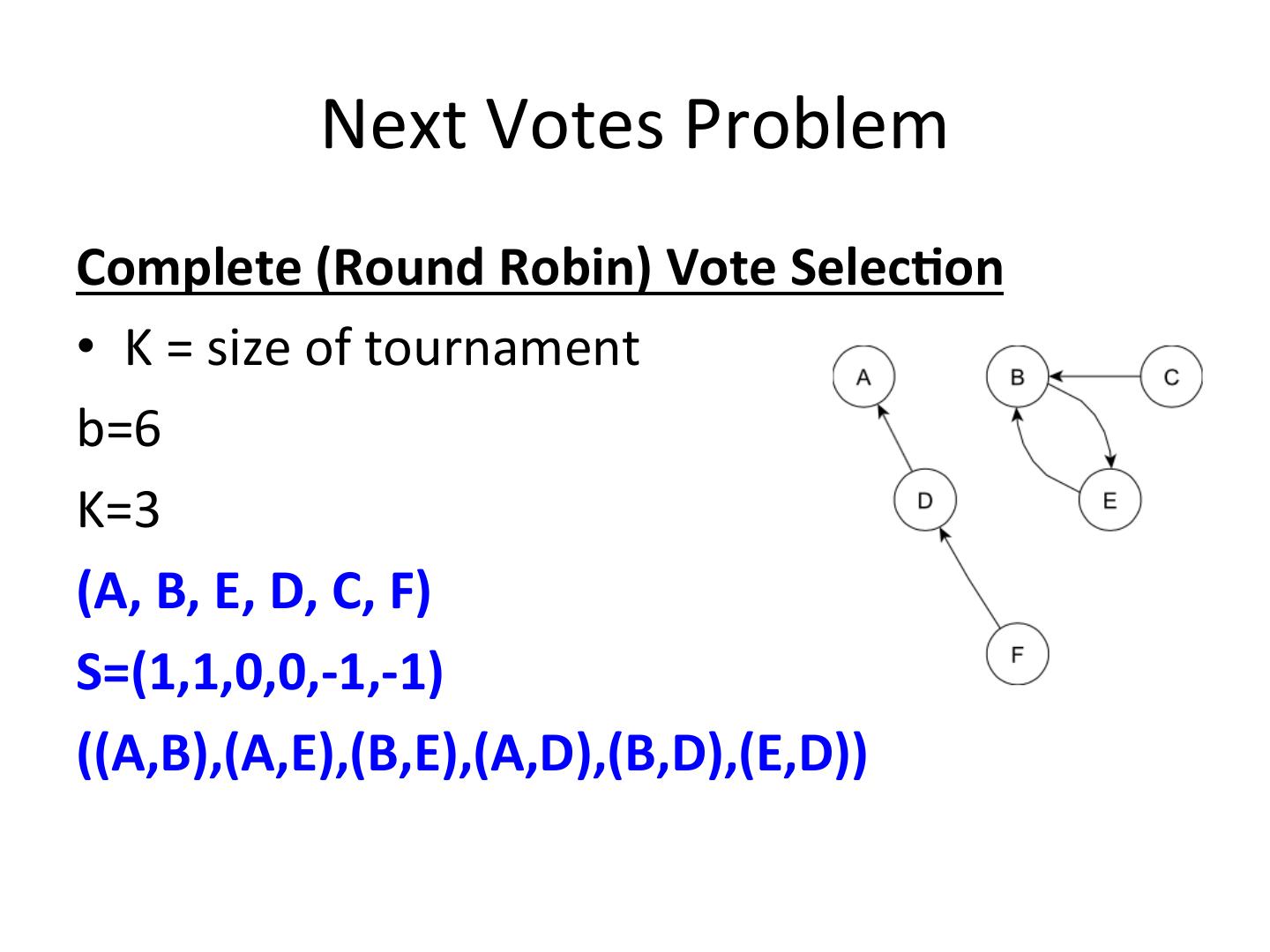
22. Next Votes Problem Complete (Round Robin) Vote Selec-on •  K = size of tournament b=6 K=3 (A, B, E, D, C, F) S=(1,1,0,0,-1,-1) ((A,B),(A,E),(B,E),(A,D),(B,D),(E,D)) 

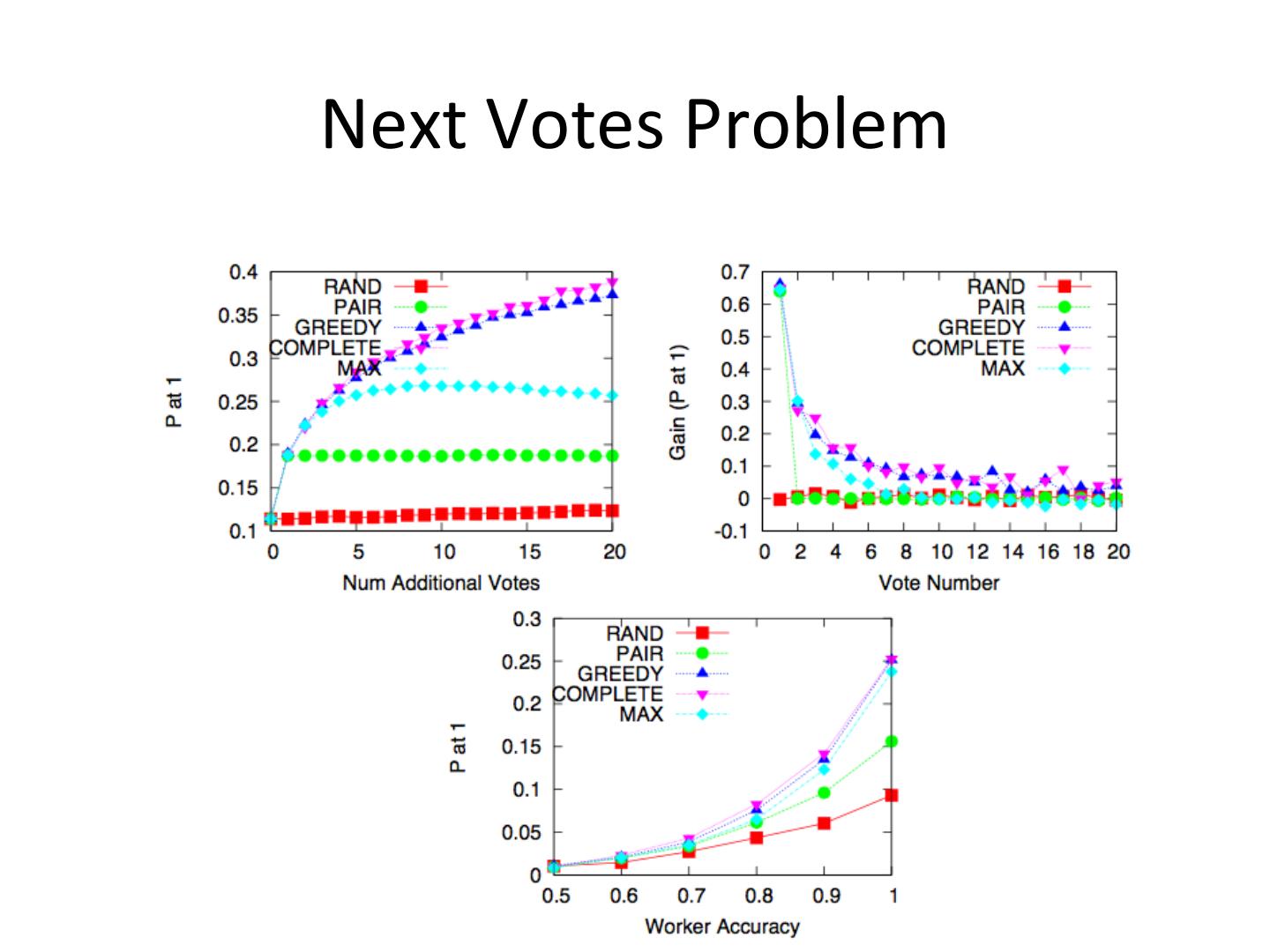
23.Next Votes Problem 

24. Recap Es-mate Max Which pairs with current to compare informa-on next? Judgment Problem Next Votes Problem 

25. Recap •  Judgment Problem •  Next Votes Problem –  Maximum Likelihood –  Maximum Likelihood (ML) baseline (ML) baseline –  Heuris=c Strategies –  Heuris=c Vote •  Indegree Selec=on Strategies •  Local •  Paired •  PageRank •  Max •  Itera-ve •  Greedy •  Round Robin