Sample + Seek：使用分布精度保证逼近聚合

1 .Sample + Seek: Approximating Aggregates with Distribution Precision Guarantee Bolin Ding Silu Huang * Surajit Chaudhuri Kaushik Chakrabarti Chi Wang { bolind , surajitc , kaushik , chiw }@microsoft.com shuang86@illinois.edu Microsoft Research University of Illinois * Work done while in Microsoft

2 .Outline Introduction Overview of Our Approach Main Technical Results Related Work Experiments Conclusion

3 .Outline Introduction Overview of Our Approach Main Technical Results Related Work Experiments Conclusion

4 .Motivation Interactive BI queries Aggregate queries with complicated and (maybe) selective predicates Large data size and response in seconds Answer with small error is fine General trend is enough for decision making Error exists in visualization anyway Error guarantee is important

5 .Problem Definition Aggregate queries on a simple table   SELECT FROM WHERE GROUP BY   Exact answer: Approximation:   Answer and Normalize Group by dimensions Measure attribute Aggregate function: count, sum, avg, count distinct Extensible to SPJ queries (with foreign key joins between fact and dim tables) Filter predicate: AND/OR of atomic predicates, atomic predicate can be equality or range predicate    

6 .Problem Definition: Error Guarantee Measuring error: Guarantee on the whole distribution Considering information gain in decision trees Semantics of the guarantee Total difference of the sector areas   Exact answer: Approximation:           Error

7 .Problem Definition: Goal of Our System Error bound (e.g., 5%) Give an answer with for any query Pre-built sample and index: query-independent, size sublinear or linear to the original data size Sublinear processing time Constant number of random I/ Os (if needed)   Exact answer: Approximation:          

8 .Problem Definition: Goal of Our System Error bound (e.g., 5%) Give an answer with for any query Pre-built sample and index: query-independent, size sublinear or linear to the original data size Sublinear processing time Constant number of random I/ Os (if needed)   Exact answer: Approximation:          

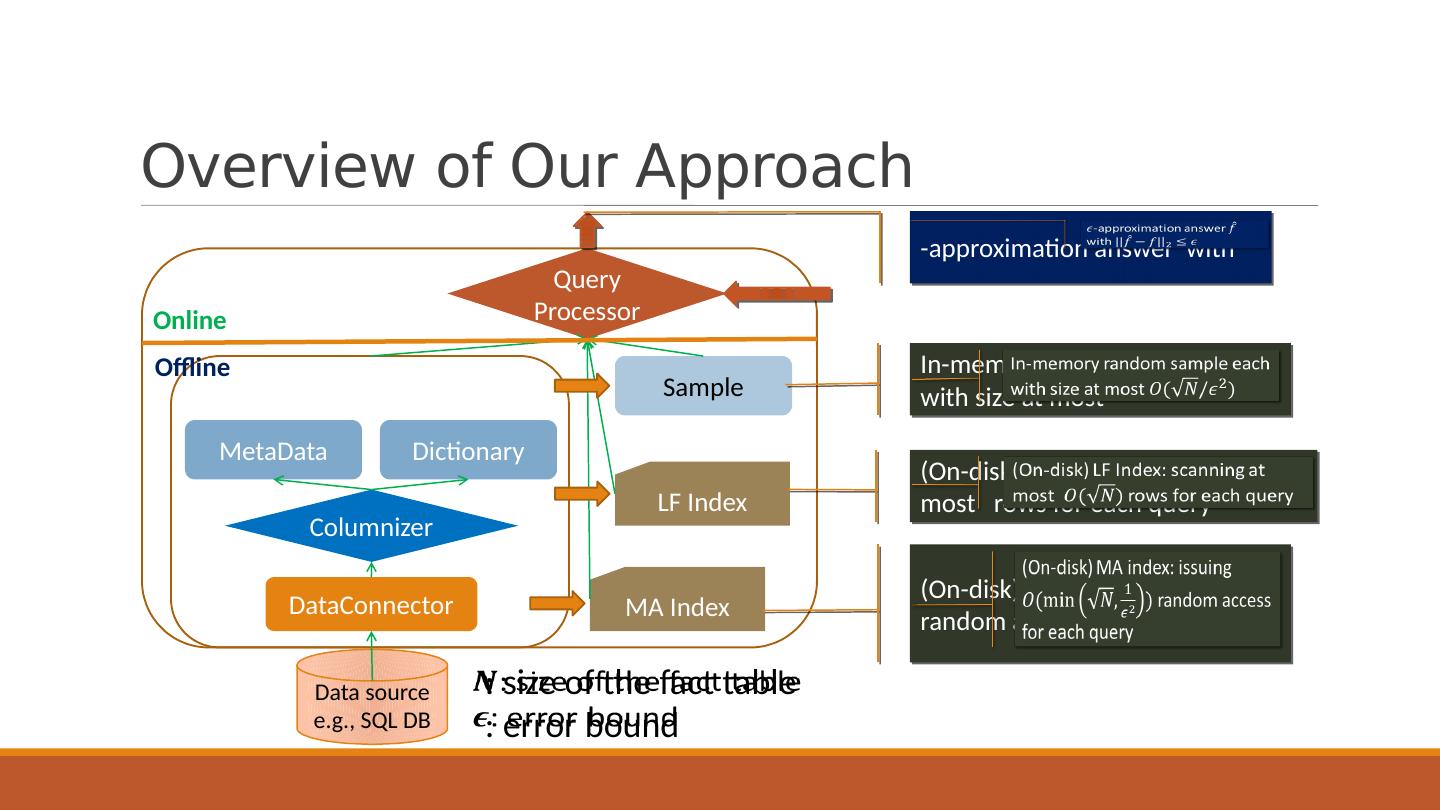
9 .Overview of Our Approach DataConnector Columnizer Sample LF Index MA Index MetaData Dictionary Query Processor Data source e.g., SQL DB In-memory random sample each with size at most   (On-disk) LF Index: scanning at most rows for each query   (On-disk) MA index: issuing random access for each query   -approximation answer with   Online Offline : size of the fact table : error bound  

10 .Overview of Our Approach DataConnector Columnizer Sample LF Index MA Index MetaData Dictionary Query Processor Data source e.g., SQL DB In-memory random sample each with size at most   (On-disk) LF Index: scanning at most rows for each query   (On-disk) MA index: issuing random access for each query   -approximation answer with   Online Offline : size of the fact table : error bound  

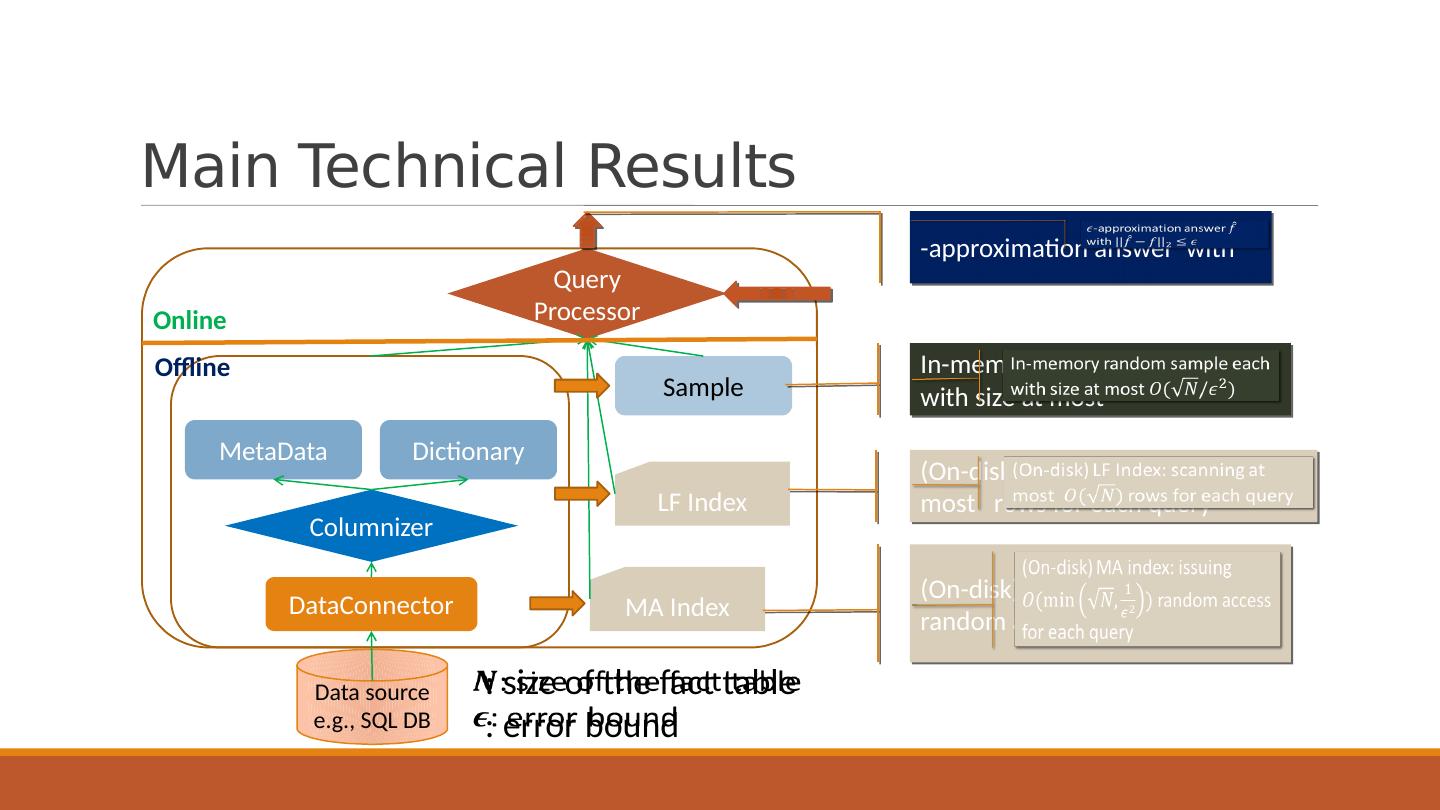
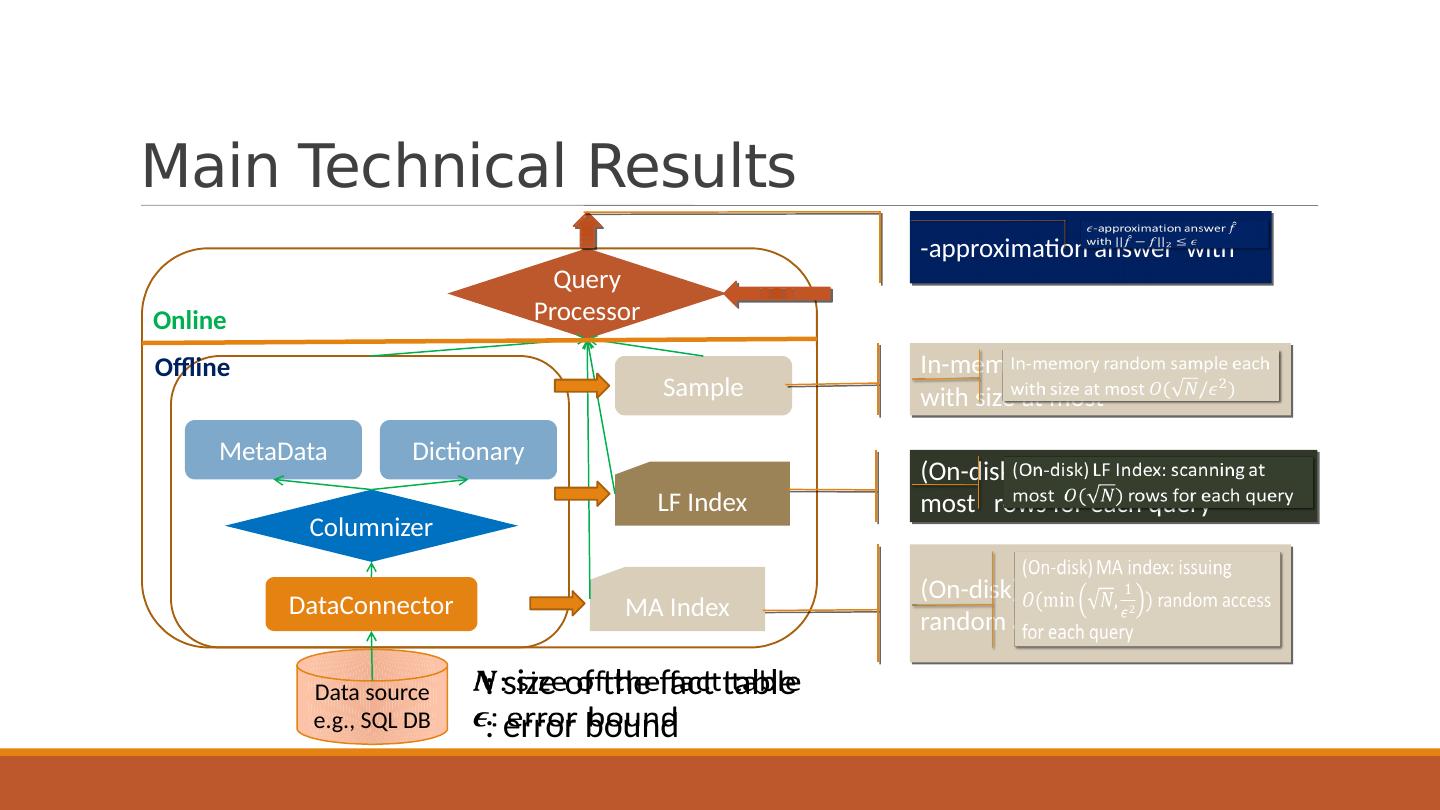
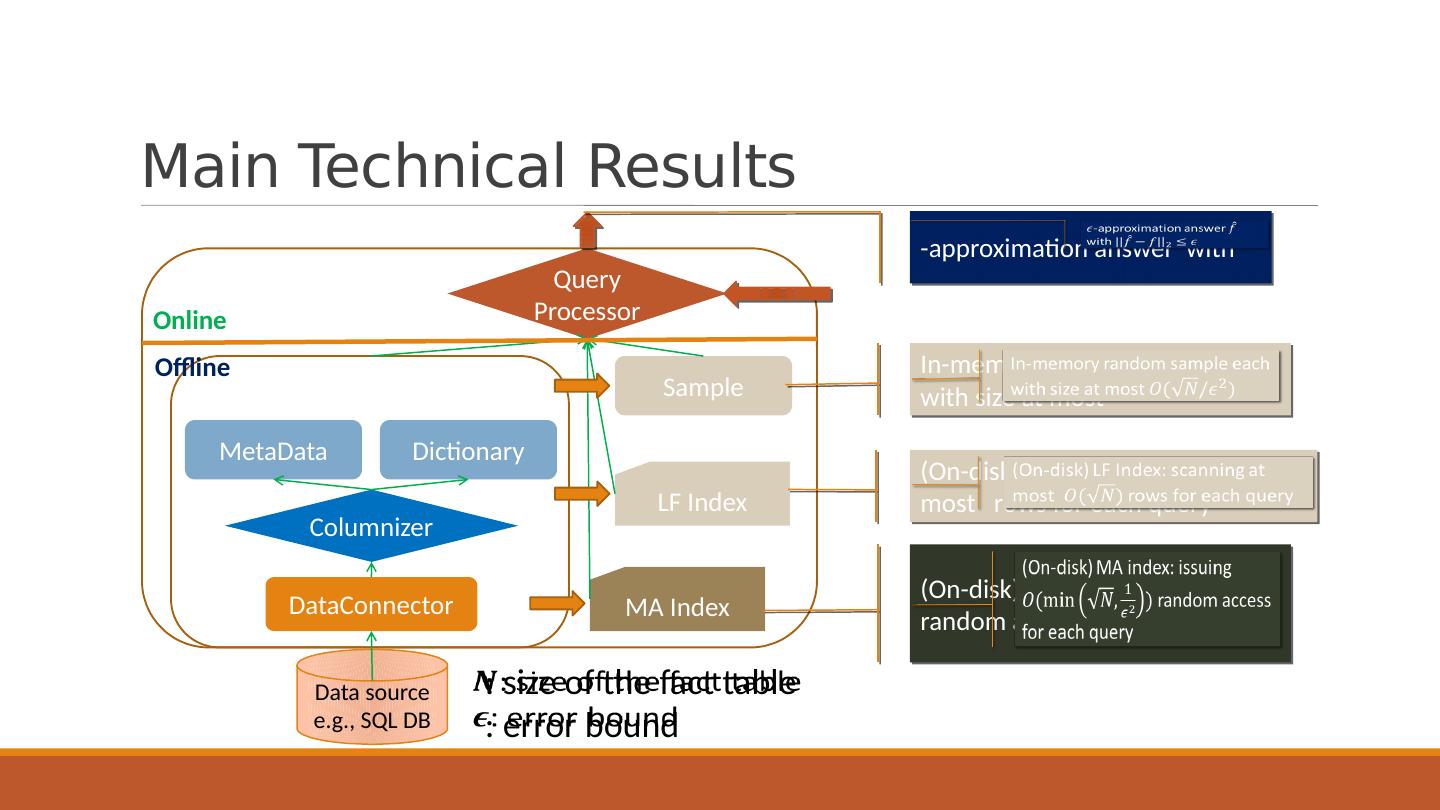
11 .Main Technical Results DataConnector Columnizer Sample LF Index MA Index MetaData Dictionary Query Processor Data source e.g., SQL DB (On-disk) LF Index: scanning at most rows for each query   (On-disk) MA index: issuing random access for each query   -approximation answer with   Online Offline In-memory random sample each with size at most   : size of the fact table : error bound  

12 .Sampling for COUNT Aggregates Simple uniform sampling ( offline ) Pick a random sample of size from table ( online ) Run the query on to get Lemma I (corollary from [Li et al. PODS15]) If the query has NO predicate, w.h.p ., we have   SELECT FROM WHERE GROUP BY  

13 .Sampling for COUNT Aggregates with Predicates Uniform sampling for queries predicates ( offline ) Pick a random sample of size from table with ( online ) Run the query on to get Lemma II (our new result) Selectivity of predicate : If , w.h.p ., we have For SUM, , where is the range of measure   SELECT FROM WHERE GROUP BY  

14 .Sampling for SUM Aggregates with Predicates Weighted sampling and HT-like estimator SUM( B ): SUM aggregate on dimension B ( offline ) Pick a random sample of size from table weighed on B ( online ) Run the query on with COUNT aggregate Lemma III (our new result) If , w .h.p., we have   SELECT FROM WHERE GROUP BY  

15 .Sampling for SUM Aggregates with Predicates Weighted sampling and HT-like estimator SUM( B ): SUM aggregate on dimension B ( offline ) Pick a random sample of size from table weighed on B ( online ) Run the query on with COUNT aggregate Lemma III (our new result) If , w .h.p., we have   SELECT FROM WHERE GROUP BY  

16 .When Sampling is Not Sufficient For low predicate selectivity Given query , rows satisfying :   Table with rows   Have NOT collected enough rows satisfying :   Global sample with rows  

17 .When Sampling is Not Sufficient For low predicate selectivity Given query , rows satisfying :   Table with rows   Solution : since is small we can access all the rows satisfying (with the help of LF index) what if there are rows and they are not stored sequentially?  

18 .When Sampling is Not Sufficient For low predicate selectivity Given query , rows satisfying :   Table with rows   Solution : since is small we can access all the rows satisfying (with the help of LF index) what if there are rows and they are not stored sequentially?  

19 .When Sampling is Not Sufficient For low predicate selectivity Given query , rows satisfying :   Table with rows   Solution : since is small we can access all the rows satisfying (with the help of MA index) what if there are rows and they are not stored sequentially? Get a -sample of row addresses   Per-column non-clustered index

20 .Augment Index with Approximate Measures Approximate weighted sampling SUM( B ): SUM aggregate on dimension B ( offline ) Attach an approximate measure M’ s.t. 1 M’ / M 2 to the index ( online ) Lookup for a random sample of size weighted on B’ ( online ) Issue I/ Os and run the query on with HT-like estimator (no predicate) Lemma VI (our new result) W.h.p., we have   SELECT FROM WHERE (very selective) GROUP BY  

21 .Augment Index with Approximate Measures Approximate weighted sampling SUM( B ): SUM aggregate on dimension B ( offline ) Attach an approximate measure M’ s.t. 1 M’ / M 2 to the index ( online ) Lookup for a random sample of size weighted on B’ ( online ) Issue I/ Os and run the query on with HT-like estimator (no predicate) Lemma VI (our new result) W.h.p., we have   SELECT FROM WHERE (very selective) GROUP BY  

22 .OLAP (data cube) and ColumnStore index Online aggregation Offline sampling (BlinkDB) Deterministic approximate query processing (DAQ) Related Work

23 .OLAP (data cube) and ColumnStore index Online aggregation Offline sampling (BlinkDB) Deterministic approximate query processing (DAQ) Related Work

24 .Experiments TPC-H schema (with eight tables - 300M rows in LINEITEM) Queries with 1-4 group-by dims, and 0-4 predicate dims 100 speedup for queries   Actual error is “always” smaller than the requested (consistent to the theoretical results)  

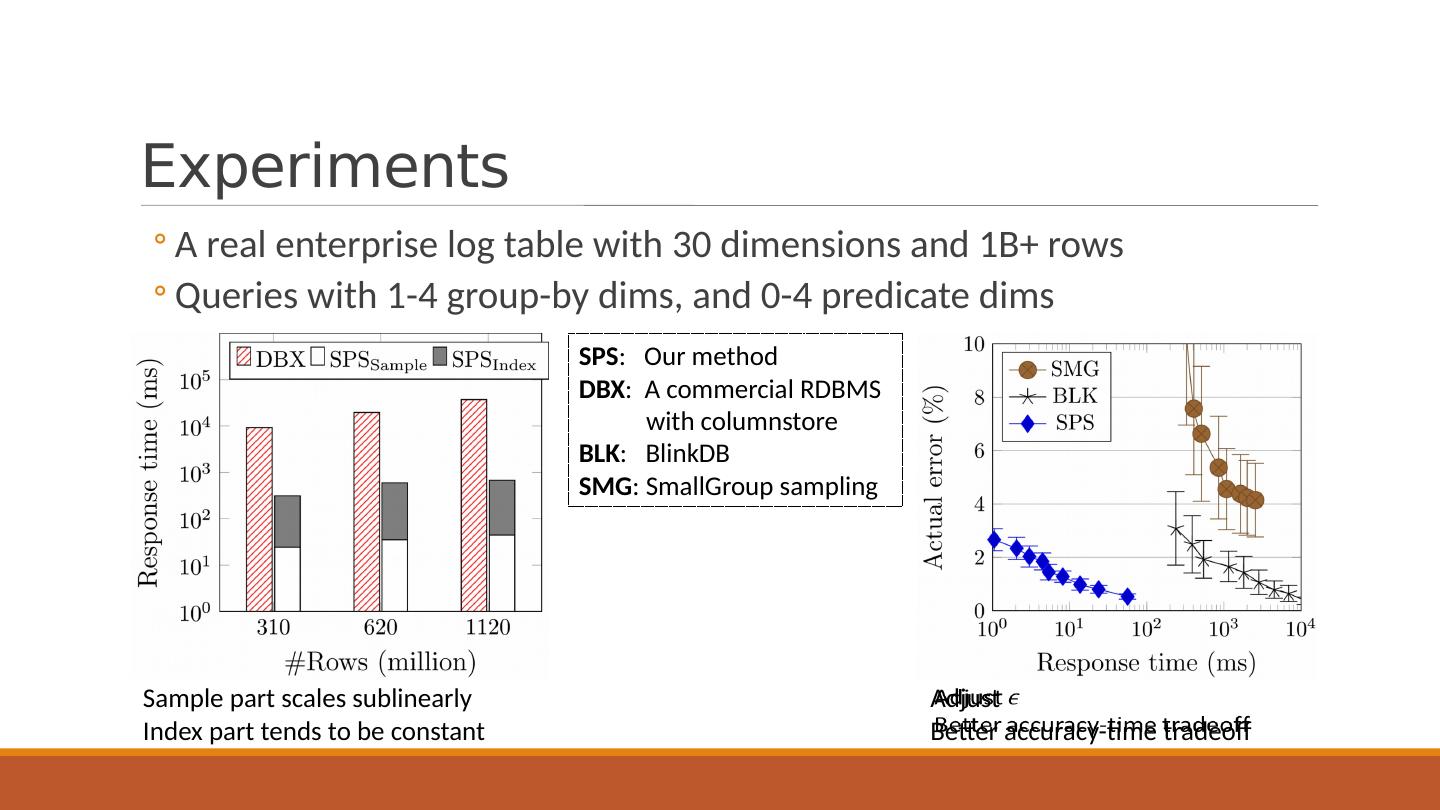
25 .Experiments A real enterprise log table with 30 dimensions and 1B+ rows Queries with 1-4 group-by dims, and 0-4 predicate dims SPS : Our method DBX : A commercial RDBMS with columnstore BLK : BlinkDB SMG : SmallGroup sampling Sample part scales sublinearly Index part tends to be constant Adjust Better accuracy-time tradeoff  

26 .Experiments A real enterprise log table with 30 dimensions and 1B+ rows Queries with 1-4 group-by dims, and 0-4 predicate dims SPS : Our method DBX : A commercial RDBMS with columnstore BLK : BlinkDB SMG : SmallGroup sampling Sample part scales sublinearly Index part tends to be constant Adjust Better accuracy-time tradeoff  

27 .Conclusion Time flies! Let’s process everything faster!

28 .

29 .When Sampling is Sufficient For high predicate selectivity Given query , rows satisfying :   Table with rows   Have collected enough rows satisfying :   Global sample with rows