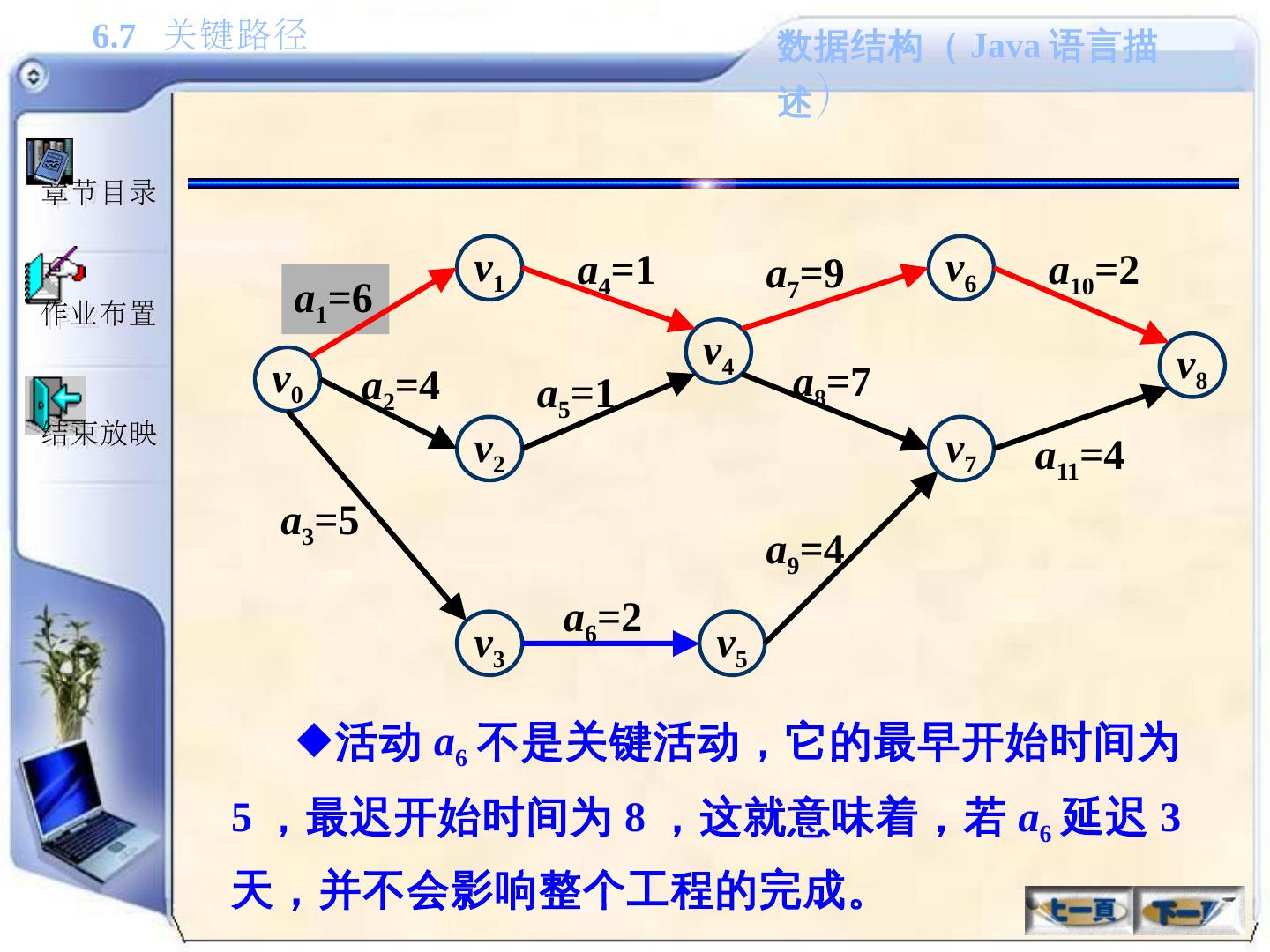
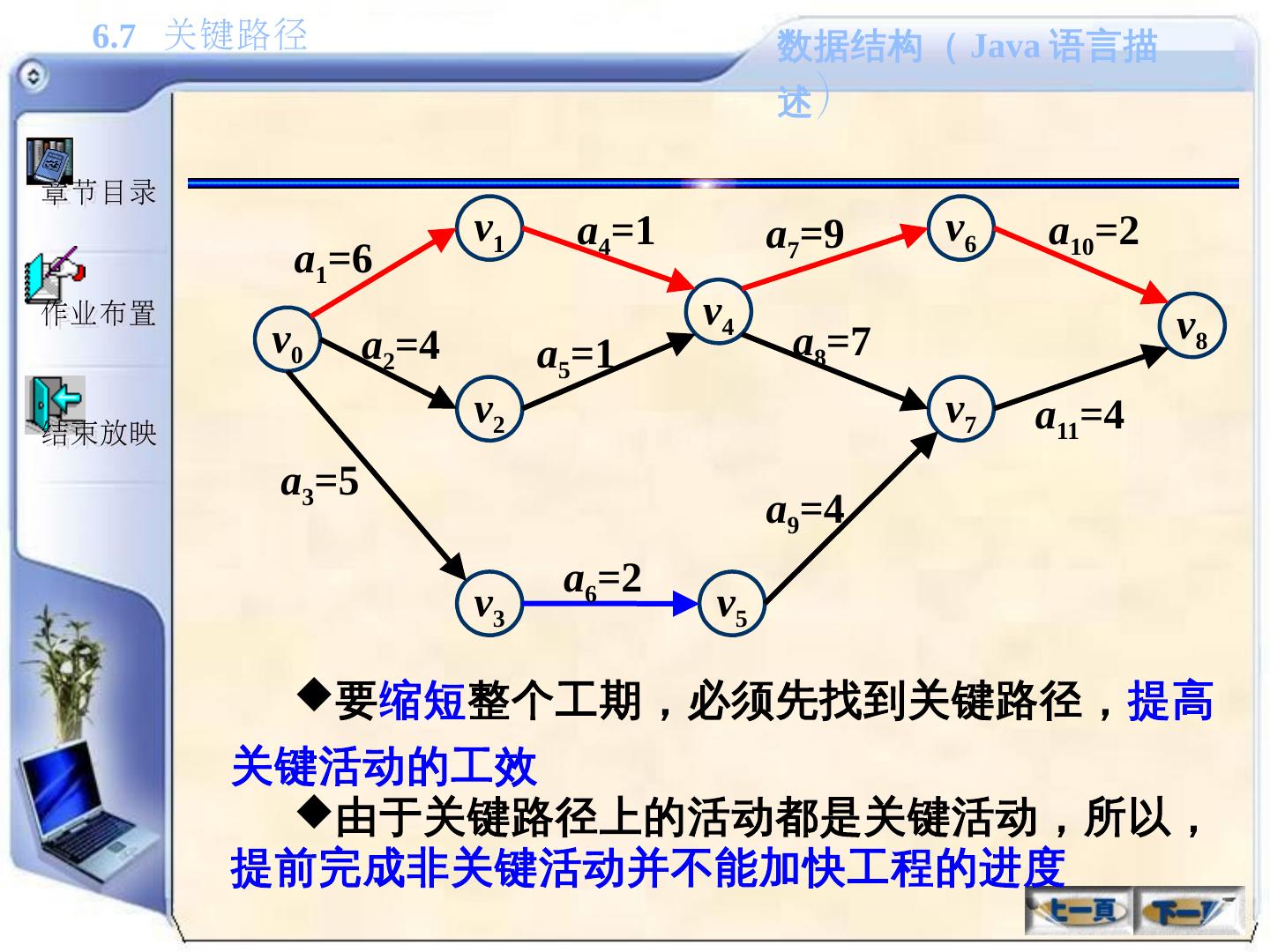
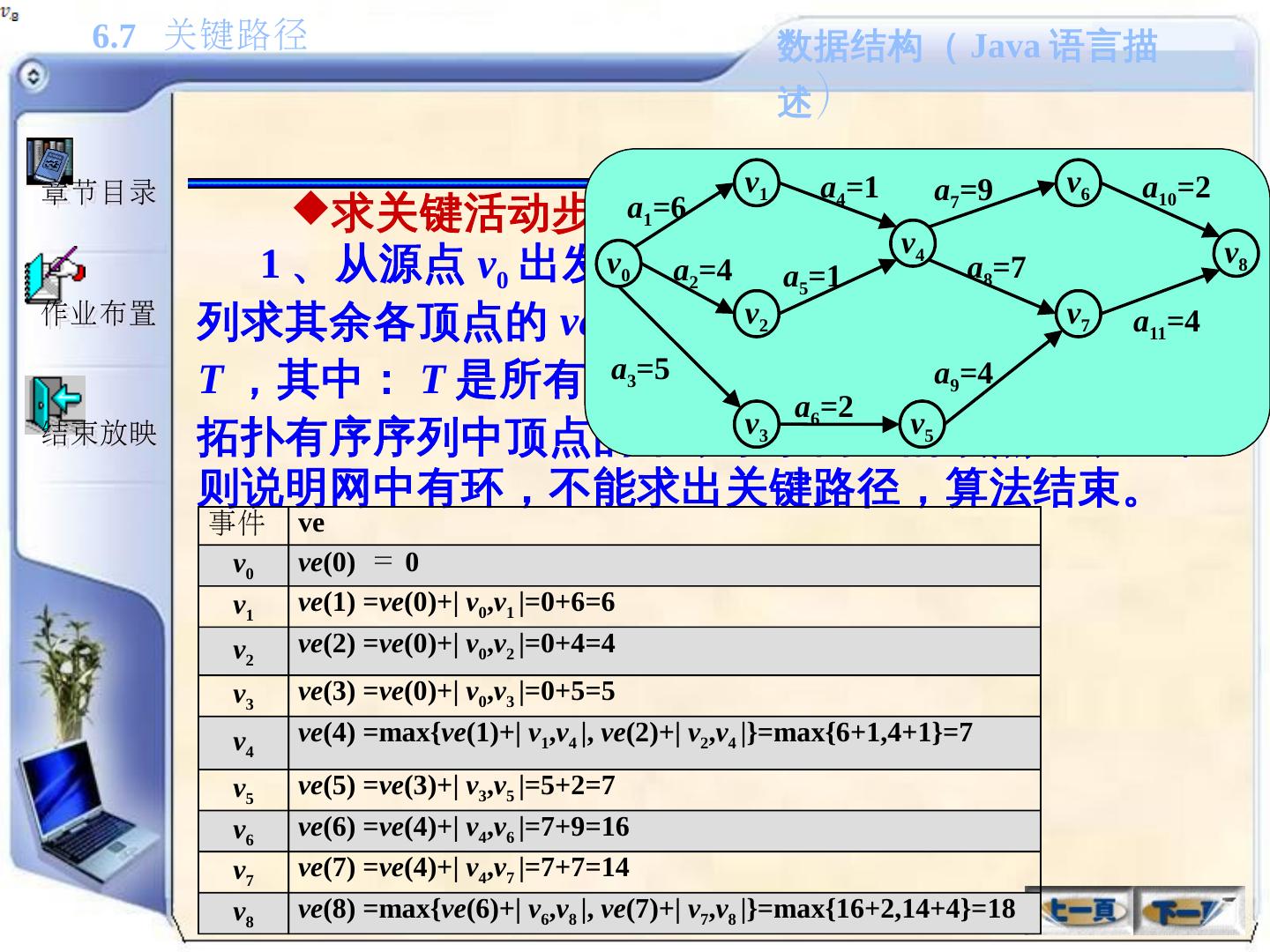
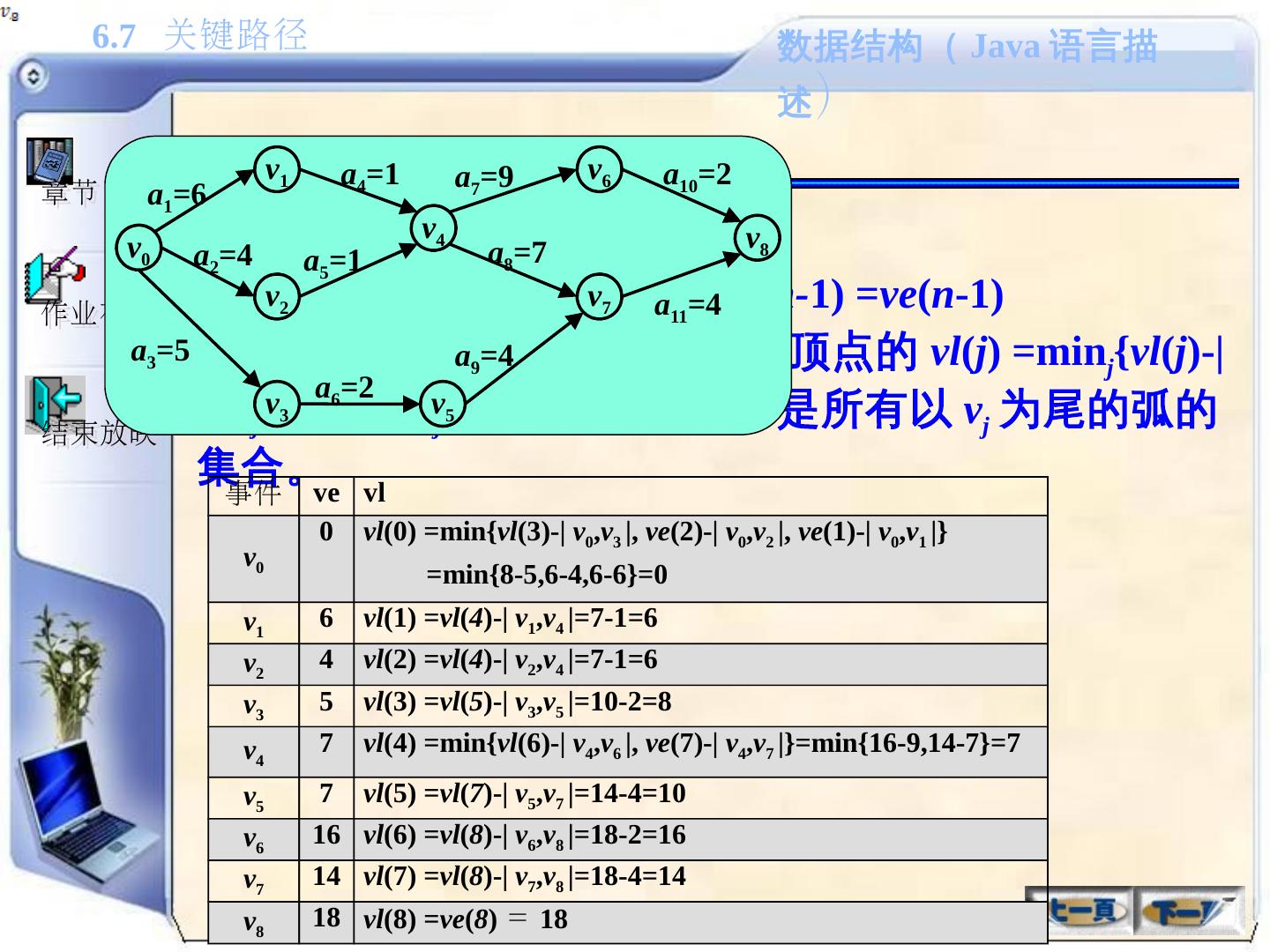
- 快召唤伙伴们来围观吧
- 微博 QQ QQ空间 贴吧
- 文档嵌入链接
- 复制
- 微信扫一扫分享
- 已成功复制到剪贴板
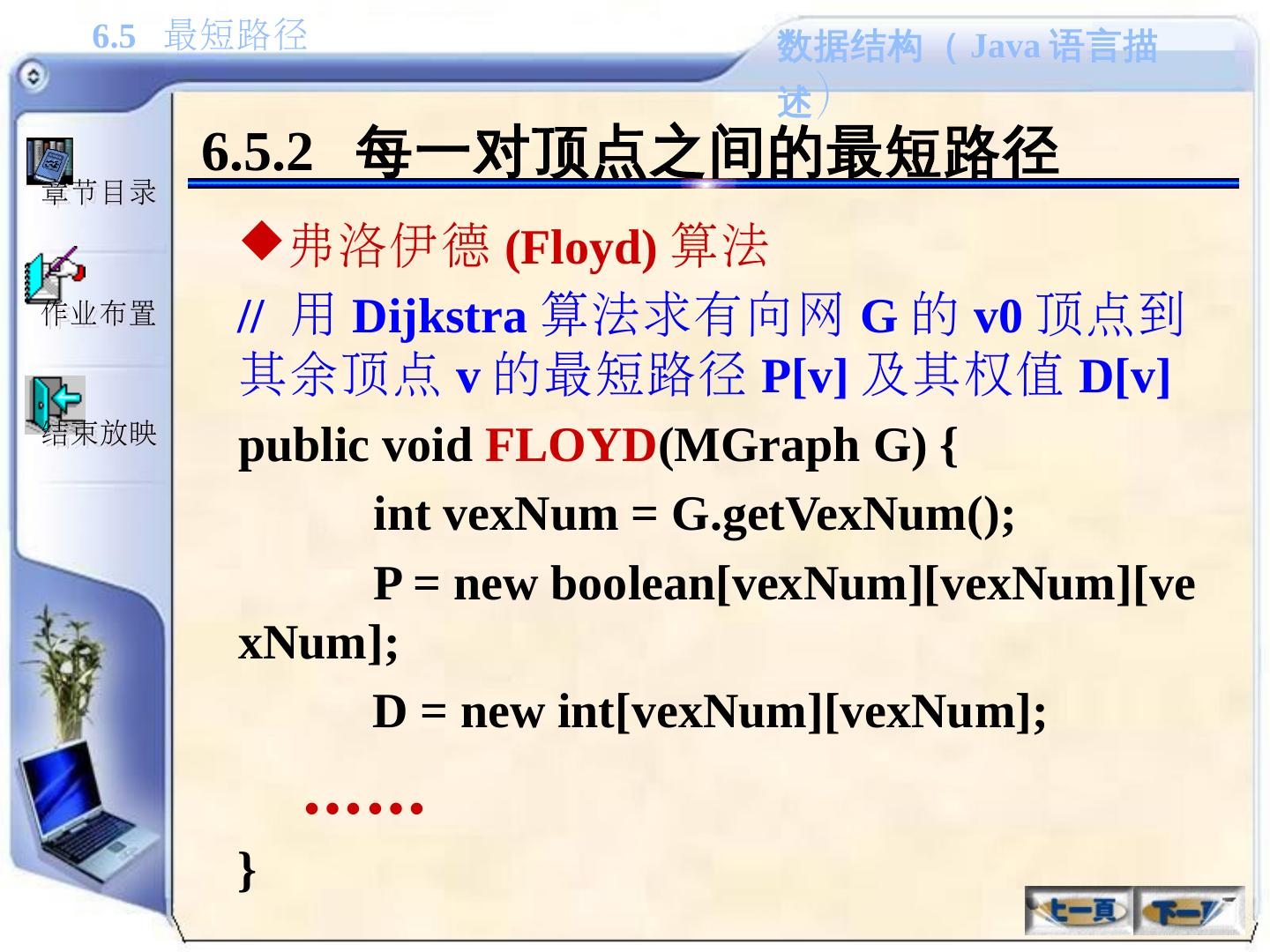
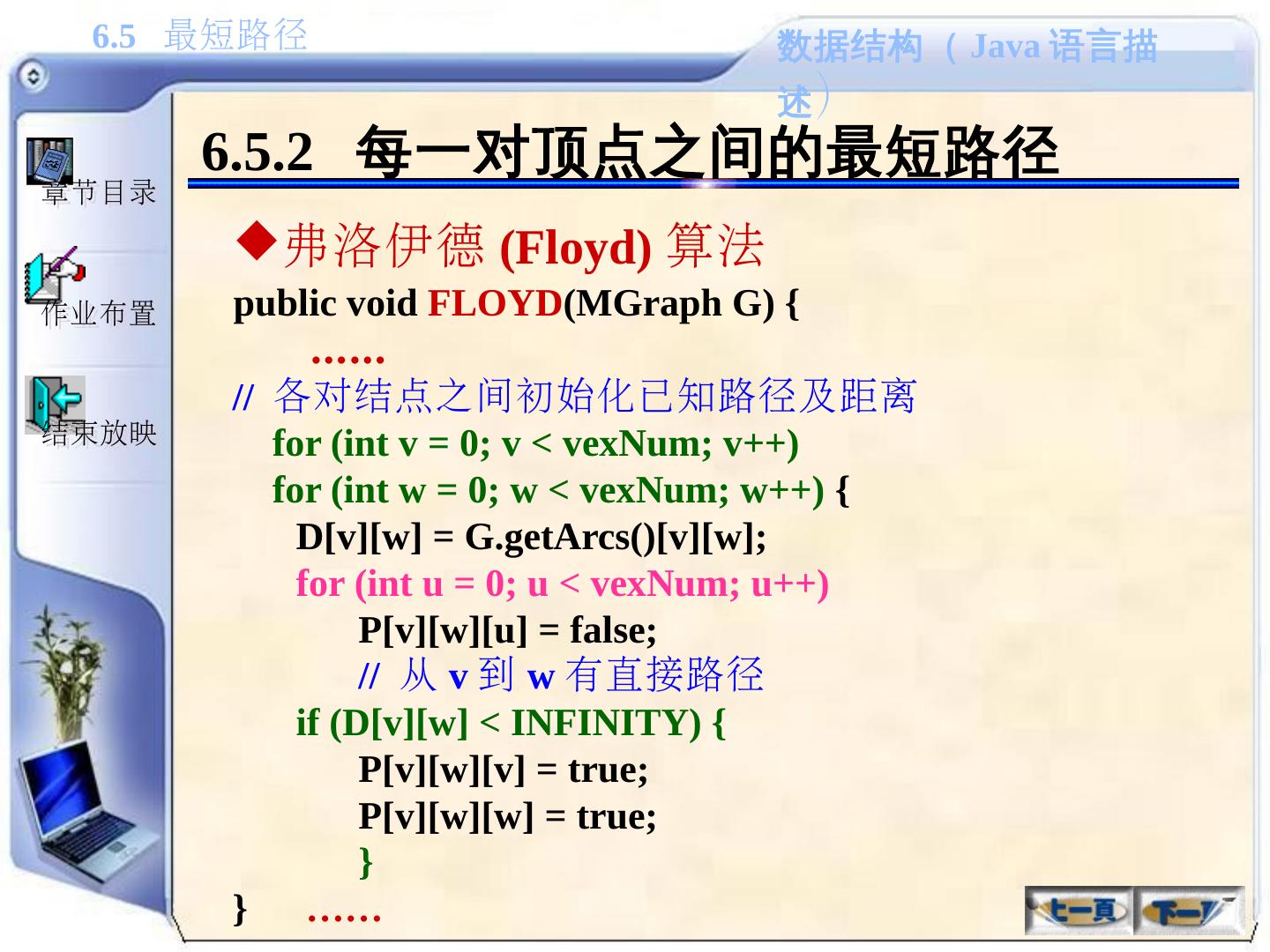
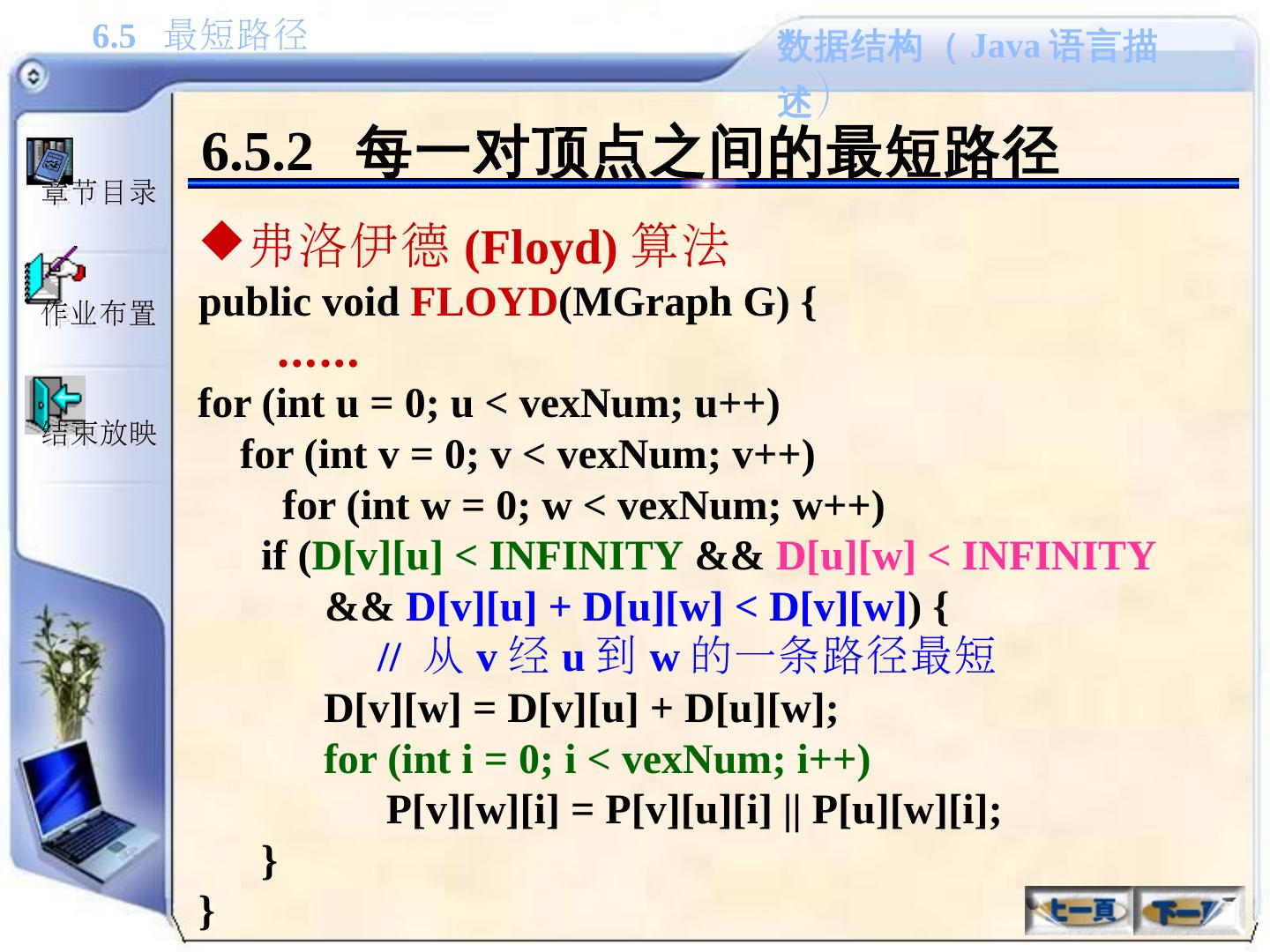
(Java语言描述) 6.5 最短路径作业布置结束放映章节目录教学内容6.1 ...
展开查看详情
1 .第六章 图
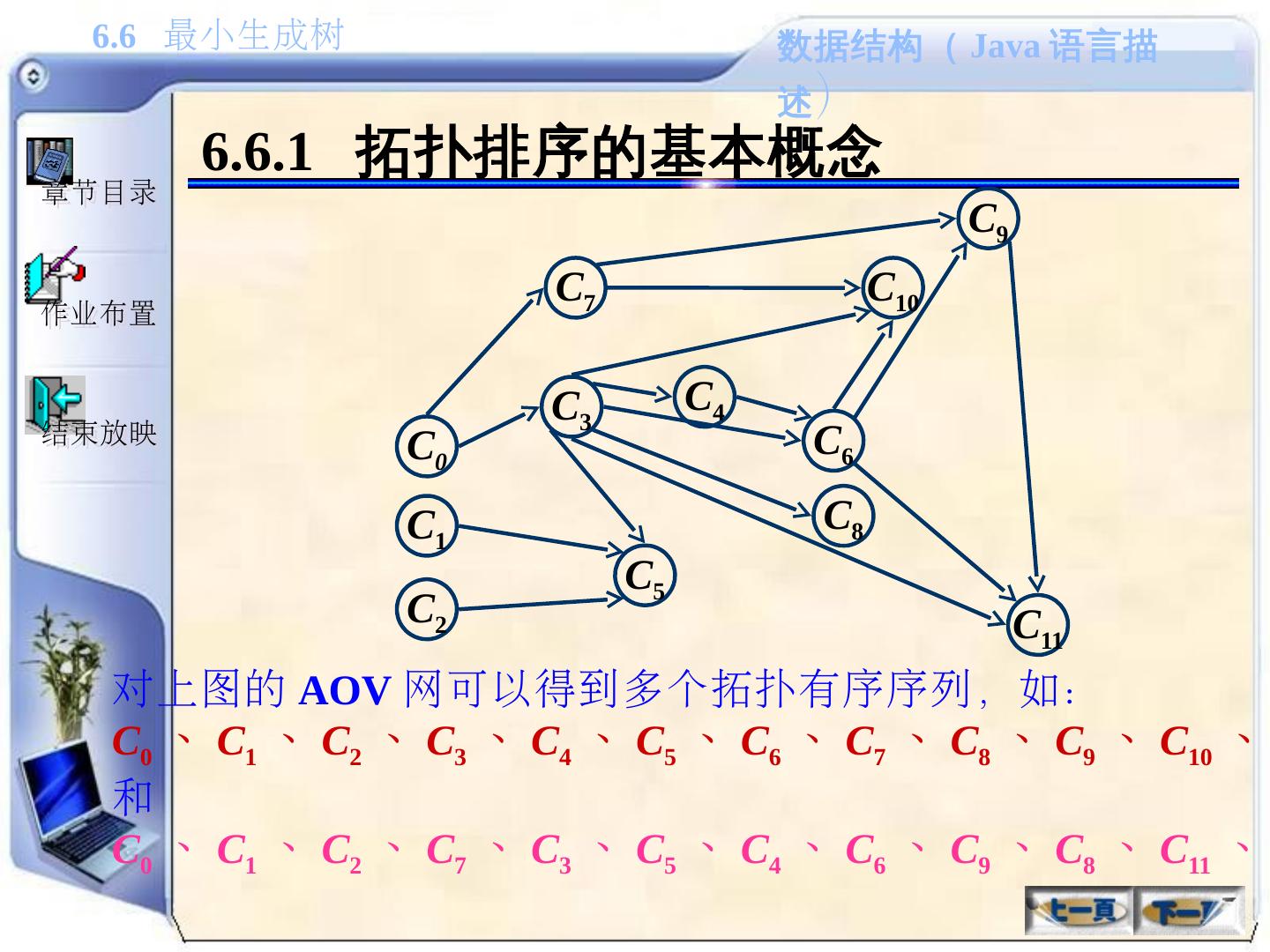
2 .教学内容 6.1 图的概述 6.2 图的存储结构 6.3 图的遍历 6.4 最小生成树 6.5 最短路径 6.6 拓扑排序 6.7 关键路径
3 .教学重点与难点 重点: 图的概念;图的存储结构;图的遍历;最小生成树;最短路径;拓扑排序;关键路径。 难点: 最小生成树;最短路径;关键路径;图 的应用
4 .学 习 指 南 图是较线性表和树更为复杂的数据结构, 因此和线性表、树不同,虽然在遍历图的同时可以对顶点或弧进行各种操作,但更多图的应用问题如求最小生成树等在图论的研究中都早已有了特定算法,在本章中主要是介绍它们在计算机中的具体实现。这些算法乍一看都比较难,应多对照具体图例的存储结构进行学习。而图遍历的两种搜索路径和树遍历的两种搜索路径极为相似,应将两者的算法对照学习以便提高学习的效益。
5 .学 习 指 南 图是较线性表和树更为复杂的数据结构, 因此和线性表、树不同,虽然在遍历图的同时可以对顶点或弧进行各种操作,但更多图的应用问题如求最小生成树等在图论的研究中都早已有了特定算法,在本章中主要是介绍它们在计算机中的具体实现。这些算法乍一看都比较难,应多对照具体图例的存储结构进行学习。而图遍历的两种搜索路径和树遍历的两种搜索路径极为相似,应将两者的算法对照学习以便提高学习的效益。
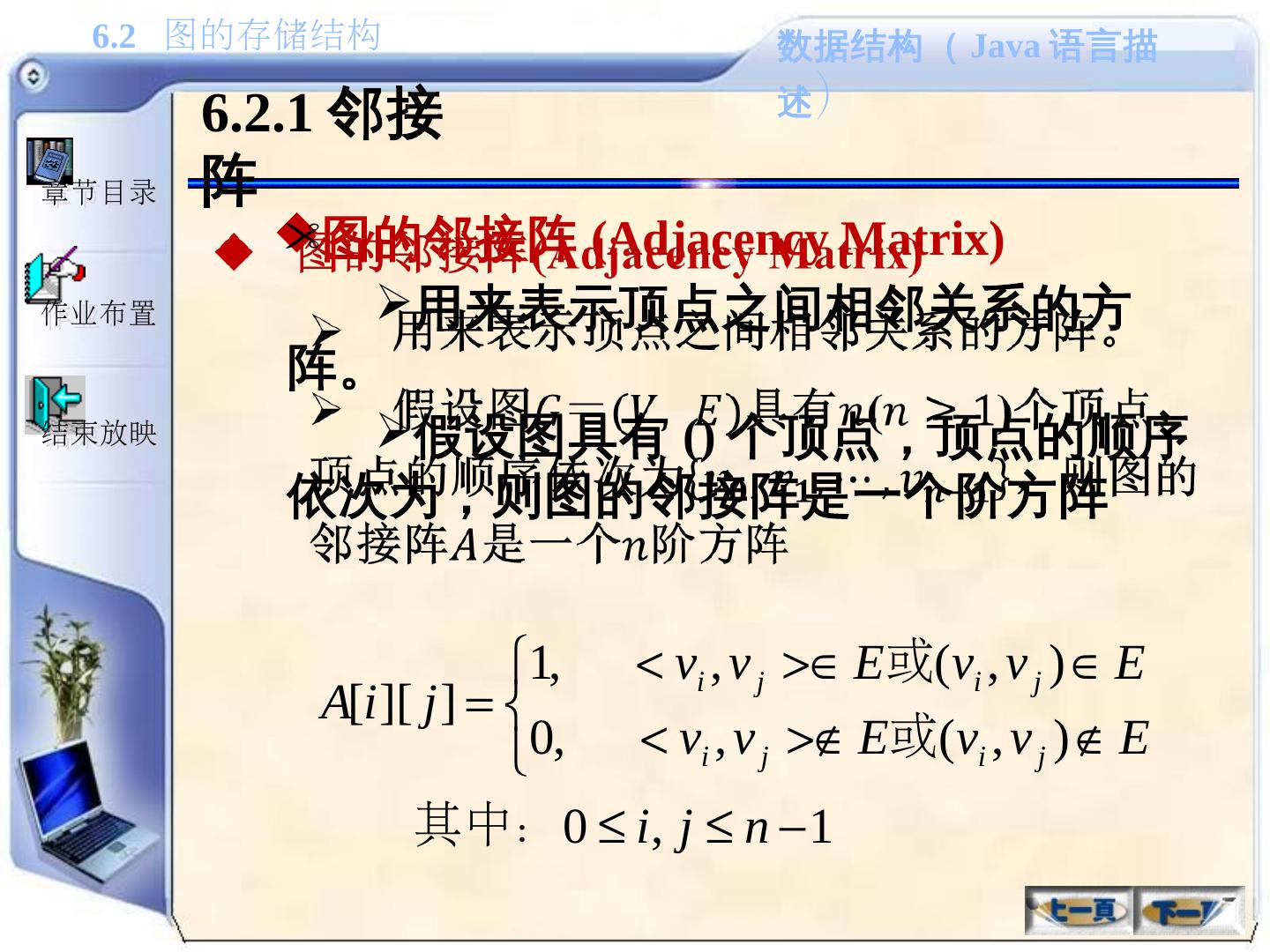
6 .6.1.1 图的基本概念 ---- 图 由顶点( Vertex )集和边 ( Edge )集组成, 记为 G =( V , E ) , 其中 V 是 有穷非空集 合,称为 顶点集 , v ∈ V 称为顶点。 E 是 有穷集 合,称为 边集 , e ∈ E 称为边 . E A C B D 例如 : G = ( V , E ) 其中 V ={A, B, C, D, E} E ={<A,B>, <A,E>, <B,C>, <C,D>, <D,B>, <D,A>, <E,C> } 零图: E 是空集, 此时图只有顶点没有边
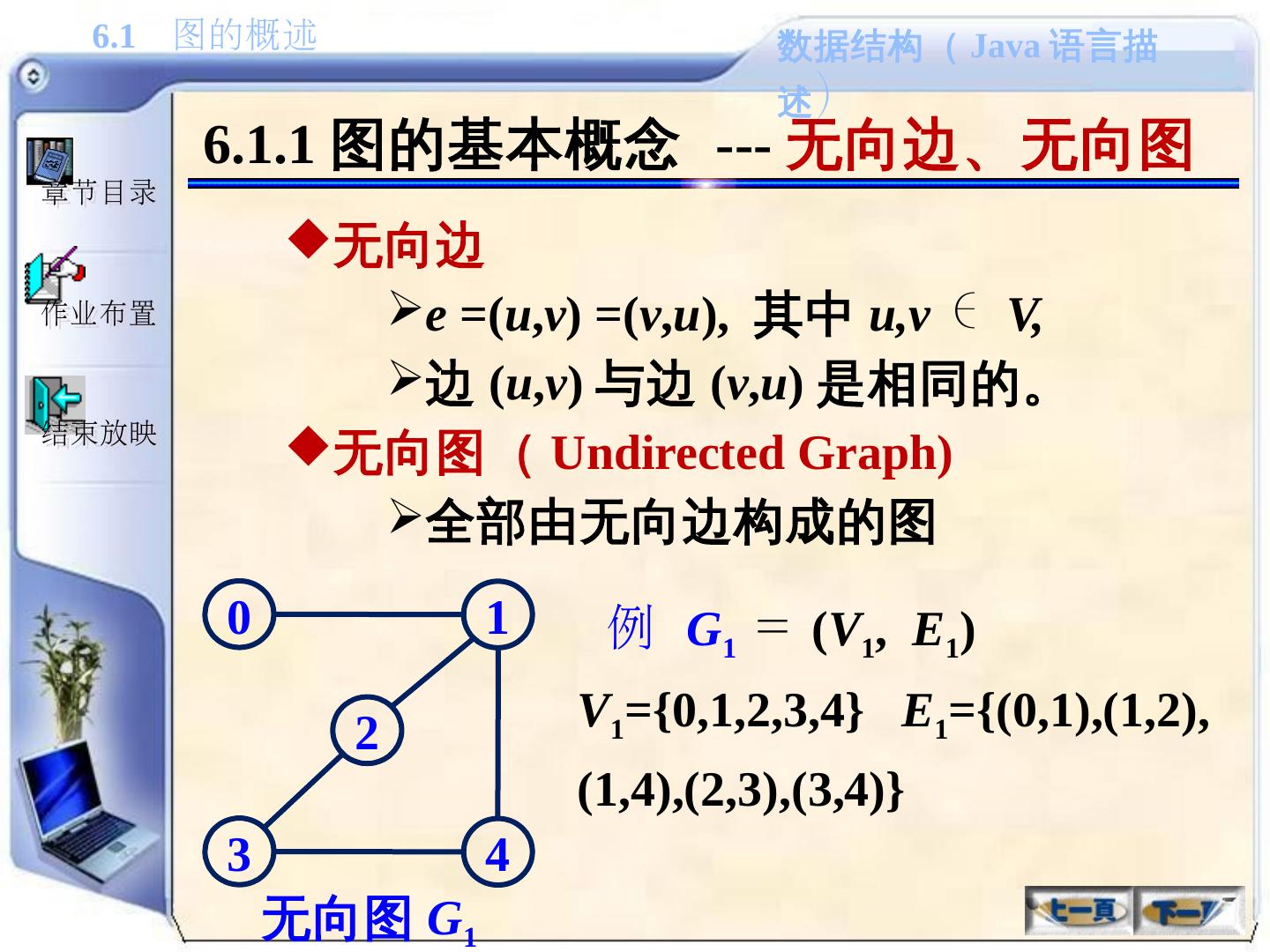
7 .6.1.1 图的基本概念 --- 无向边、无向图 无向边 e =( u , v ) =( v , u ), 其中 u,v ∈ V, 边 ( u , v ) 与边 ( v , u ) 是相同的。 无向图( Undirected Graph) 全部由无向边构成的图 0 1 3 4 2 无向图 G 1 例 G 1 = ( V 1 , E 1 ) V 1 ={0,1,2,3,4} E 1 ={(0,1),(1,2),(1,4),(2,3),(3,4)}
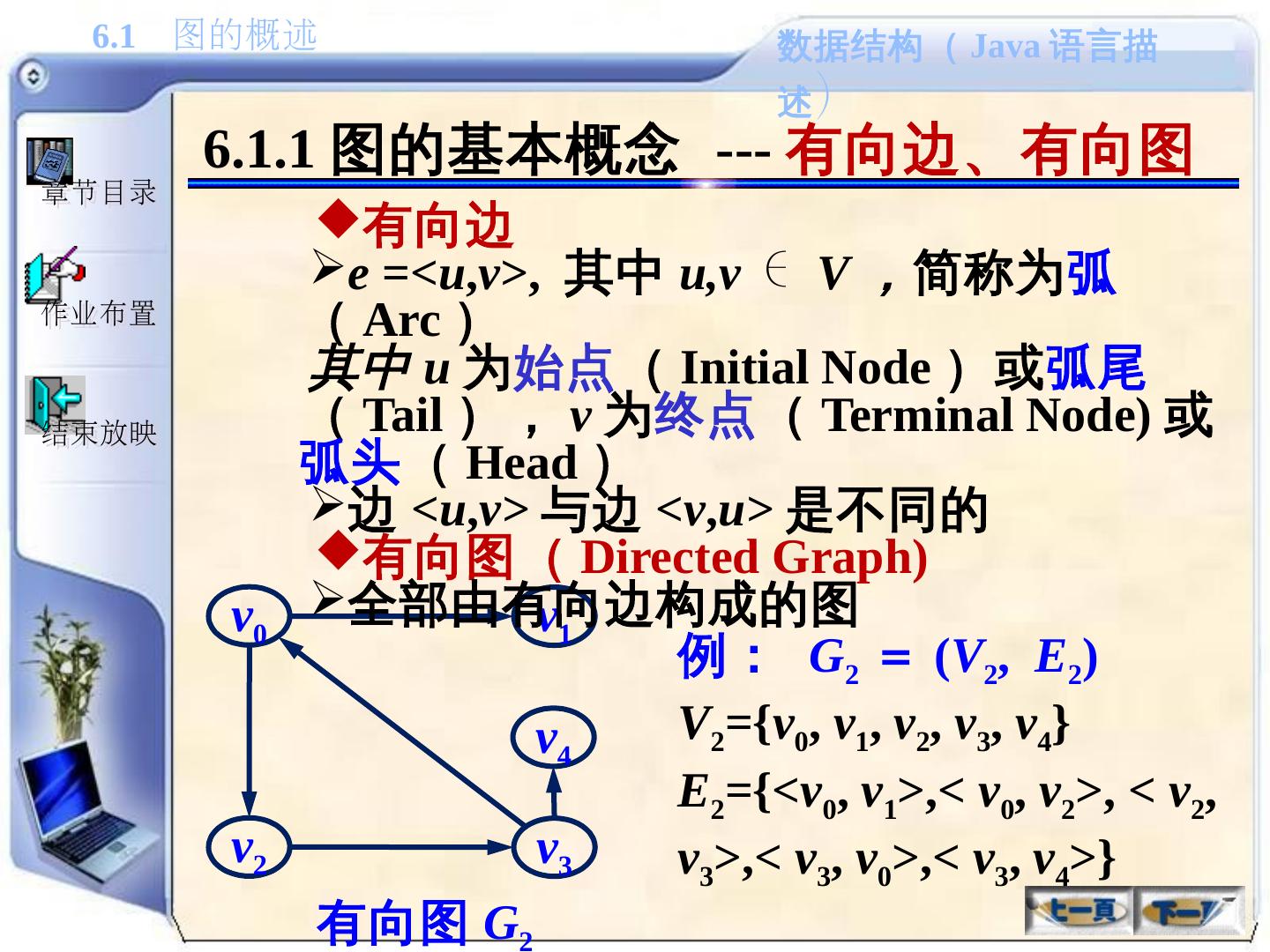
8 .6.1.1 图的基本概念 --- 有向边、有向图 例: G 2 = ( V 2 , E 2 ) V 2 ={ v 0 , v 1 , v 2 , v 3 , v 4 } E 2 ={< v 0 , v 1 >,< v 0 , v 2 >, < v 2 , v 3 >,< v 3 , v 0 >,< v 3 , v 4 >} v 0 v 1 v 2 v 3 v 4 有向图 G 2 有向边 e =< u , v> , 其中 u,v ∈ V , 简称为 弧 ( Arc ) 其中 u 为 始点 ( Initial Node )或 弧尾 ( Tail ), v 为 终点 ( Terminal Node) 或 弧头 ( Head ) 边 < u , v> 与边 < v , u> 是不同的 有向图( Directed Graph) 全部由有向边构成的图
9 .6.1.1 图的基本概念 --- 权、网 A B E F D C 2 10 2 7 5 5 无向网 G 3 A B C D 1 4 7 6 4 有向网 G 4
10 .6.1.1 图的基本概念 --- 权、网 权( Weight ) : 在一个图中,每条边可以标上 具有某种含义的数值 ,此数值称为该边上的权 通常权是一个 非负实数 权可以表示从一个顶点到另一个顶点的距离、时间或代价等含义 网( Network) 边上标识权的图称为 网
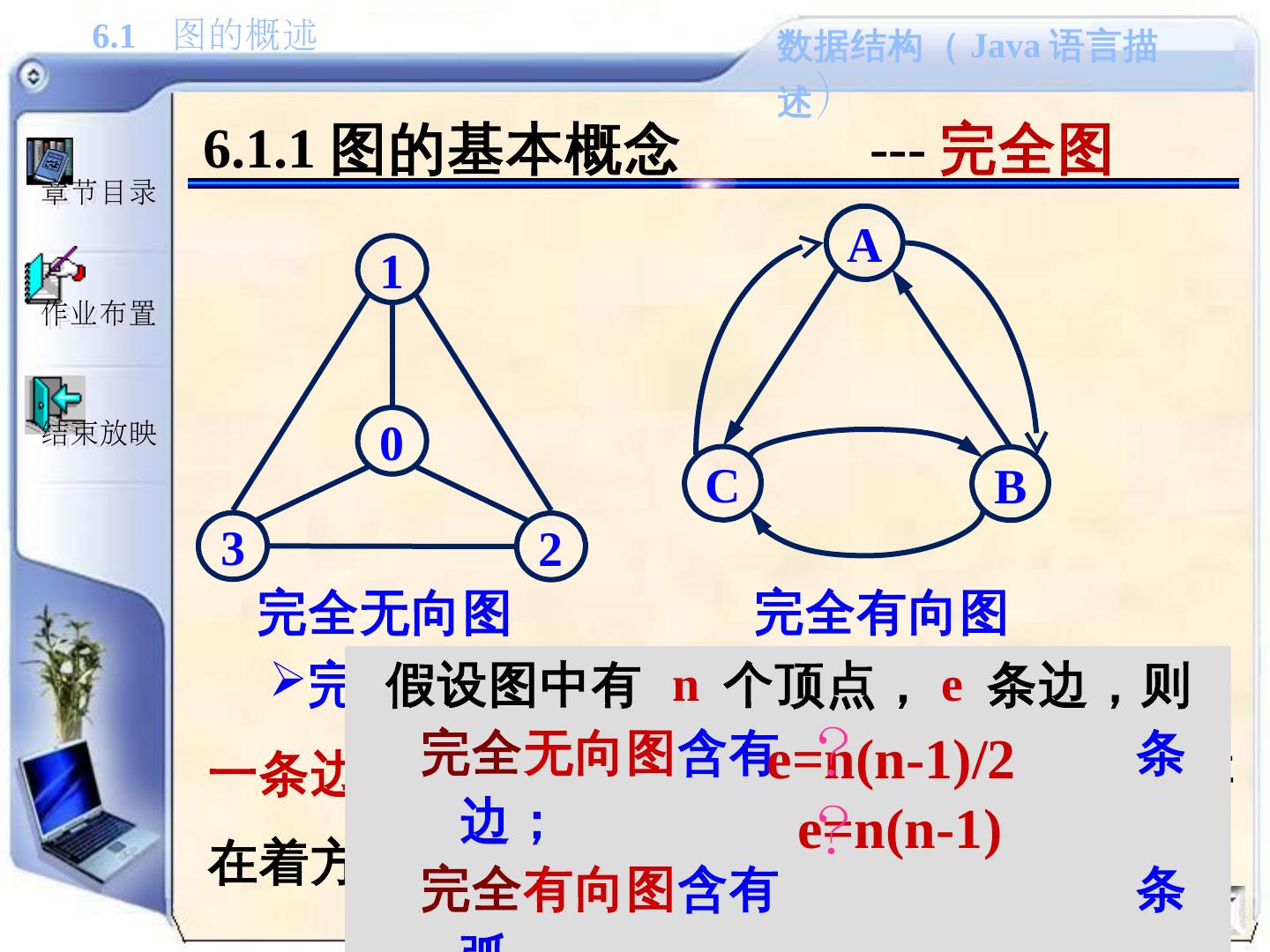
11 .6.1.1 图的基本概念 --- 完全图 完全无向图 中的每两个顶点之间都存在着 一条边 ; 完全有向图 中的每两个顶点之间都存在着方向 相反的两条边 0 1 3 2 完全无向图 A C B 完全有向图 假设图中有 n 个顶点, e 条边,则 完全 无向图 含有 条边; 完全 有向图 含有 条弧 e=n(n-1)/2 ? e=n(n-1) ?
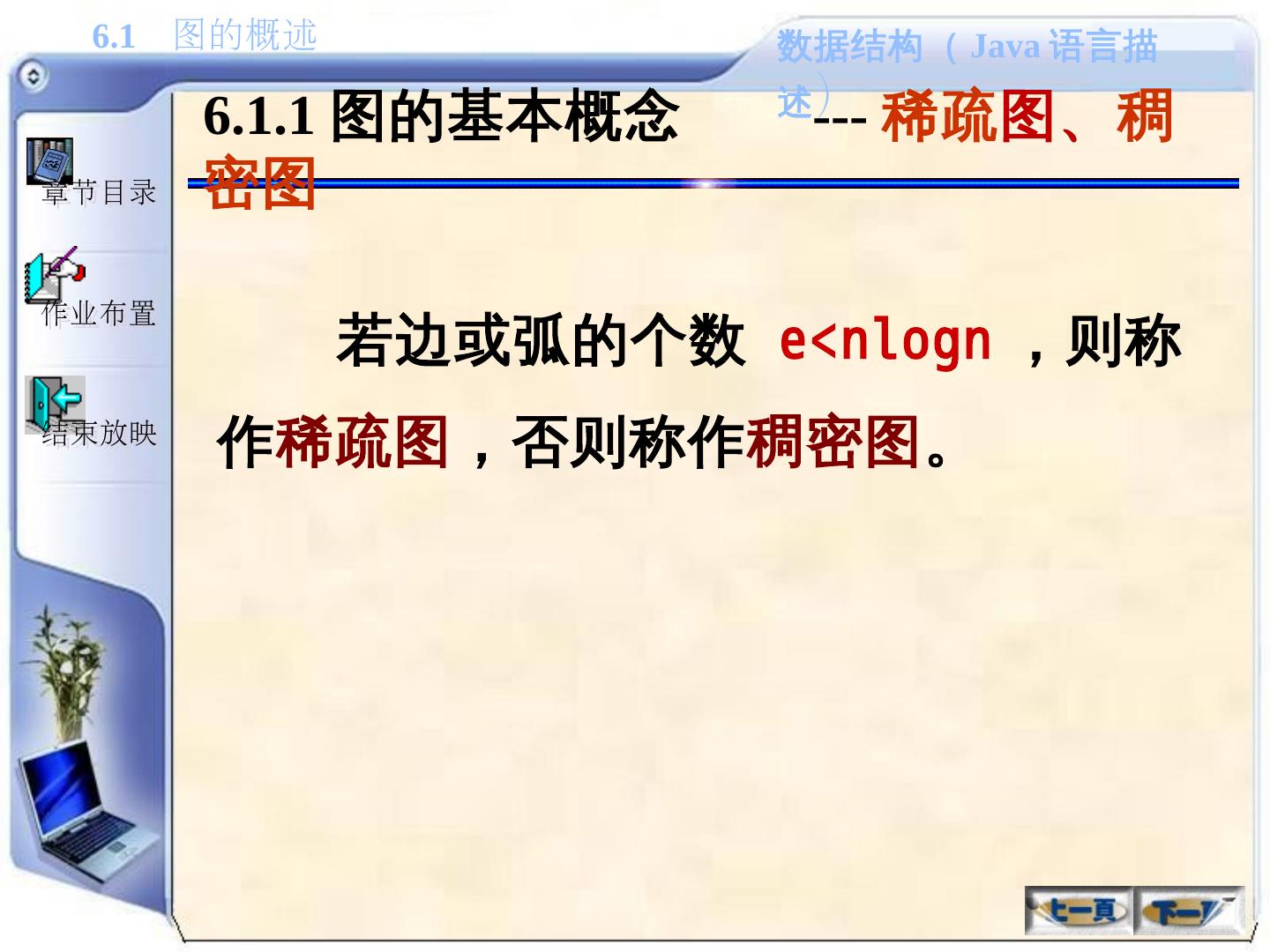
12 .6.1.1 图的基本概念 --- 稀疏 图、 稠密图 若边或弧的个数 e<nlogn ,则称作 稀疏图 ,否则称作 稠密图 。
13 .6.1.1 图的基本概念 --- 子图 子图( Subgraph ) 设有两个图 G = ( V , E ) 和 G ’ = ( V ’ , E ’ ) ,若 V ’ 是 V 的子集,即 V ’ ⊆ V ,并且 E ’ 是 E 的子集,即 E ’ ⊆ E ,则称 G ’ 为 G 的子图,记为 G ’ ⊆ G 。 生成子图( Spanning Subgraph) 若 G ’ 为 G 的子图,并且 V ’ = V ,则称 G ’ 为 G 的生成子图,即包含原图中所有顶点的子图。
14 .6.1.1 图的基本概念 --- 子图 0 1 3 4 2 无向图 G 1 0 0 1 0 1 3 4 2 无向图 G 1 的生成子图 0 1 3 4 2 无向图 G 1 的生成子图
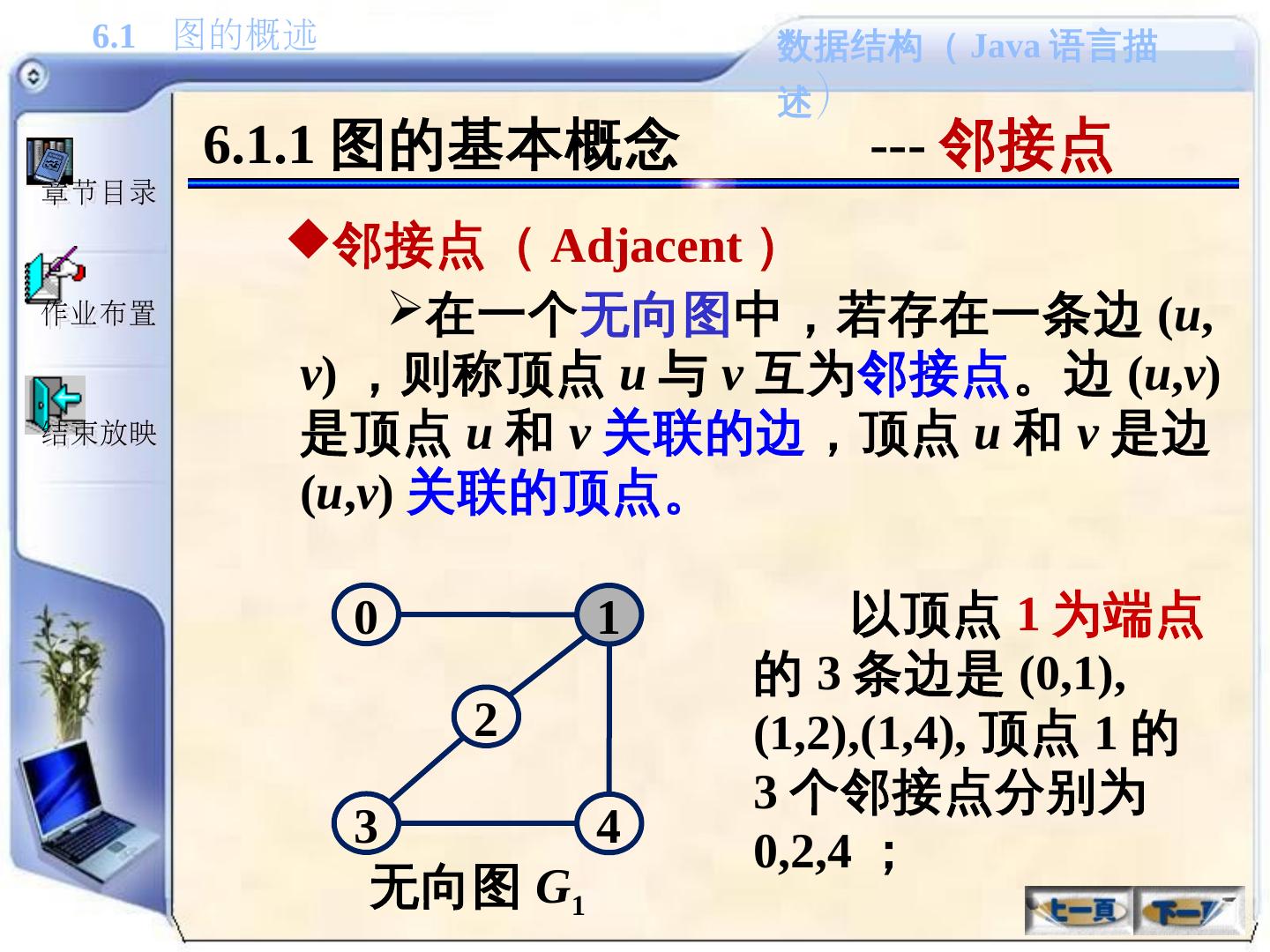
15 .6.1.1 图的基本概念 --- 邻接点 邻接点( Adjacent ) 在一个 无向图 中,若存在一条边 ( u , v ) ,则称顶点 u 与 v 互为 邻接点 。边 ( u , v ) 是顶点 u 和 v 关联的边 ,顶点 u 和 v 是边 ( u , v ) 关联的顶点。 以顶点 1 为端点 的 3 条边是 (0,1),(1,2),(1,4), 顶点 1 的 3 个邻接点分别为 0,2,4 ; 0 1 3 4 2 无向图 G 1
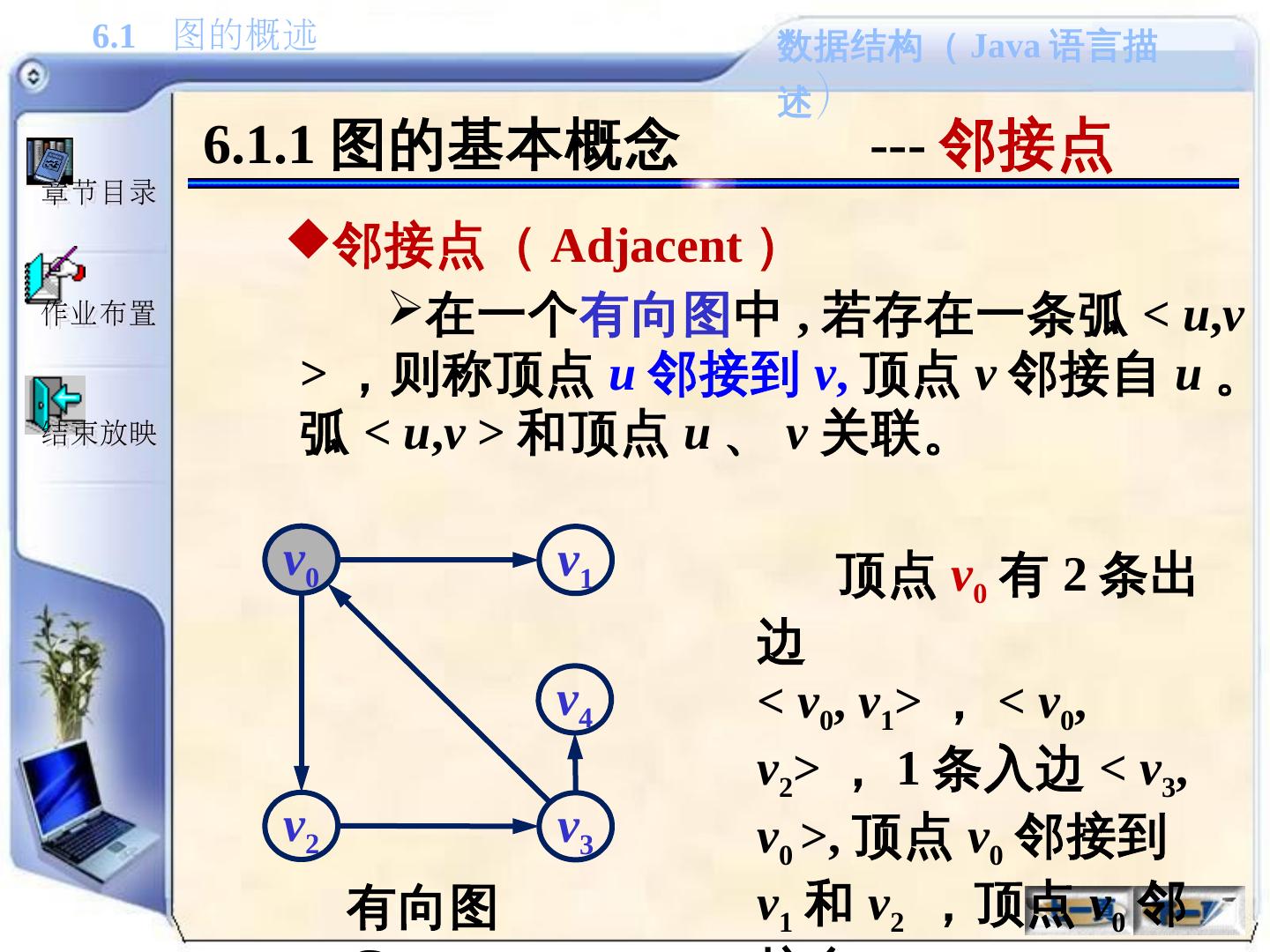
16 .6.1.1 图的基本概念 --- 邻接点 邻接点( Adjacent ) 在一个 有向图 中 , 若存在一条弧 < u , v > ,则称顶点 u 邻接到 v , 顶点 v 邻接自 u 。弧 < u , v > 和顶点 u 、 v 关联。 顶点 v 0 有 2 条出边 < v 0 , v 1 > , < v 0 , v 2 > , 1 条入边 < v 3 , v 0 >, 顶点 v 0 邻接到 v 1 和 v 2 ,顶点 v 0 邻接自 v 3 . v 0 v 1 v 2 v 3 v 4 有向图 G 2
17 .6.1.1 图的基本概念 --- 顶点的度 顶点的度( Degree ) 顶点的度是图中与该顶点相关联边的数目,记为 D ( v ) 。 若一个 图 有 n 个顶点和 e 条边,则该图所有顶点的度之和与边数满足如下关系
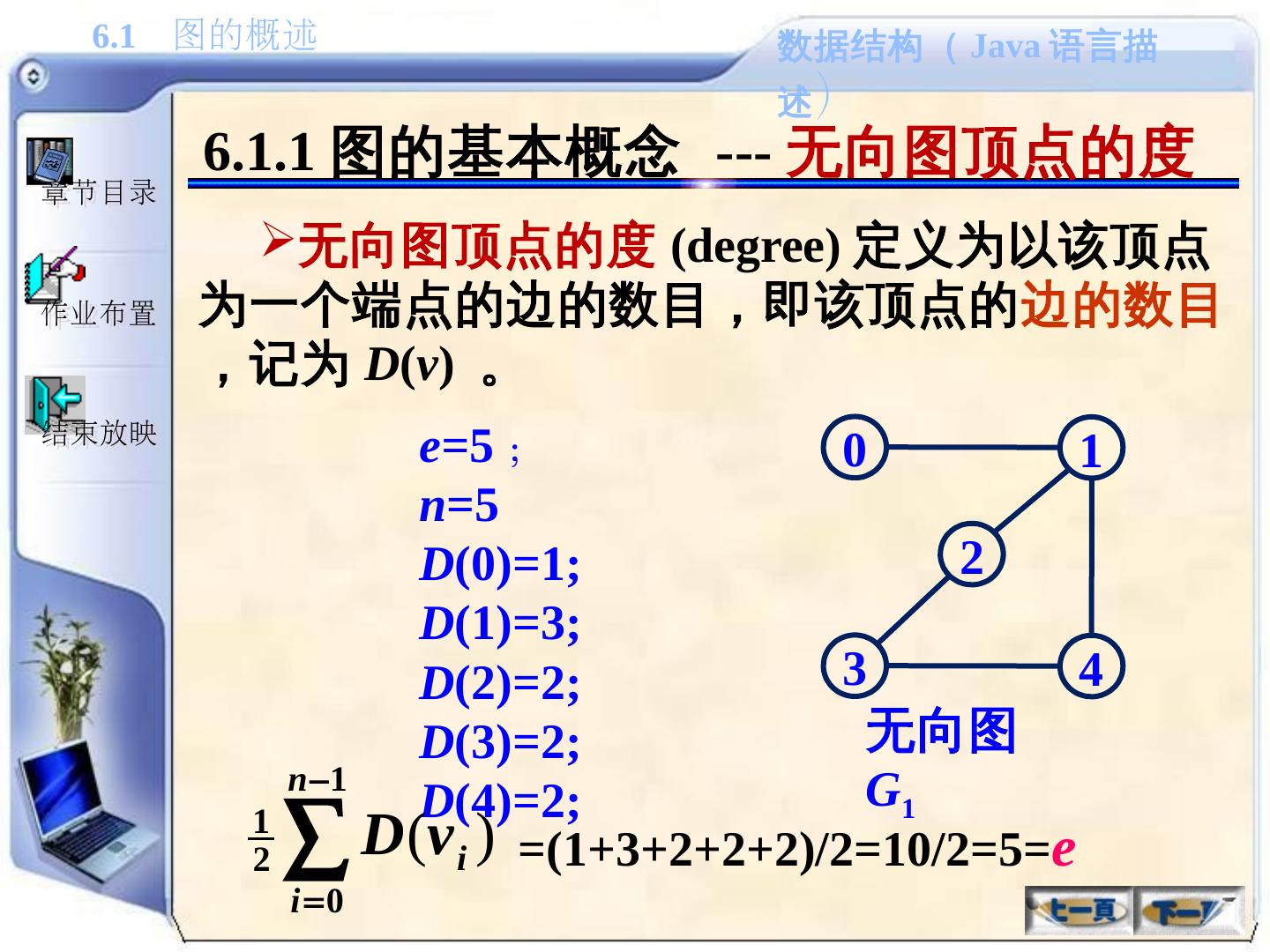
18 .6.1.1 图的基本概念 --- 无向图顶点的度 无向图顶点的度 (degree) 定义为以该顶点为一个端点的边的数目,即该顶点的 边的数目 ,记为 D ( v ) 。 e= 5 ; n =5 D (0)=1; D (1)=3; D (2)=2; D (3)=2; D (4)=2; 0 1 3 4 2 无向图 G 1 =(1+3+2+2+2)/2=10/2=5= e
19 .6.1.1 图的基本概念 --- 有向图顶点的度 有向图 顶点的度 顶点 v 的 入边数目 是该顶点的 入度 (In Degree) ,记为 ID ( v ) ; 顶点 v 的 出边数目 是该顶点的 出度 (Out Degree) ,记为 OD ( v ) ; 顶点 v 的度等于它的入度和出度之和,即 D ( v )= ID ( v )+ OD ( v )
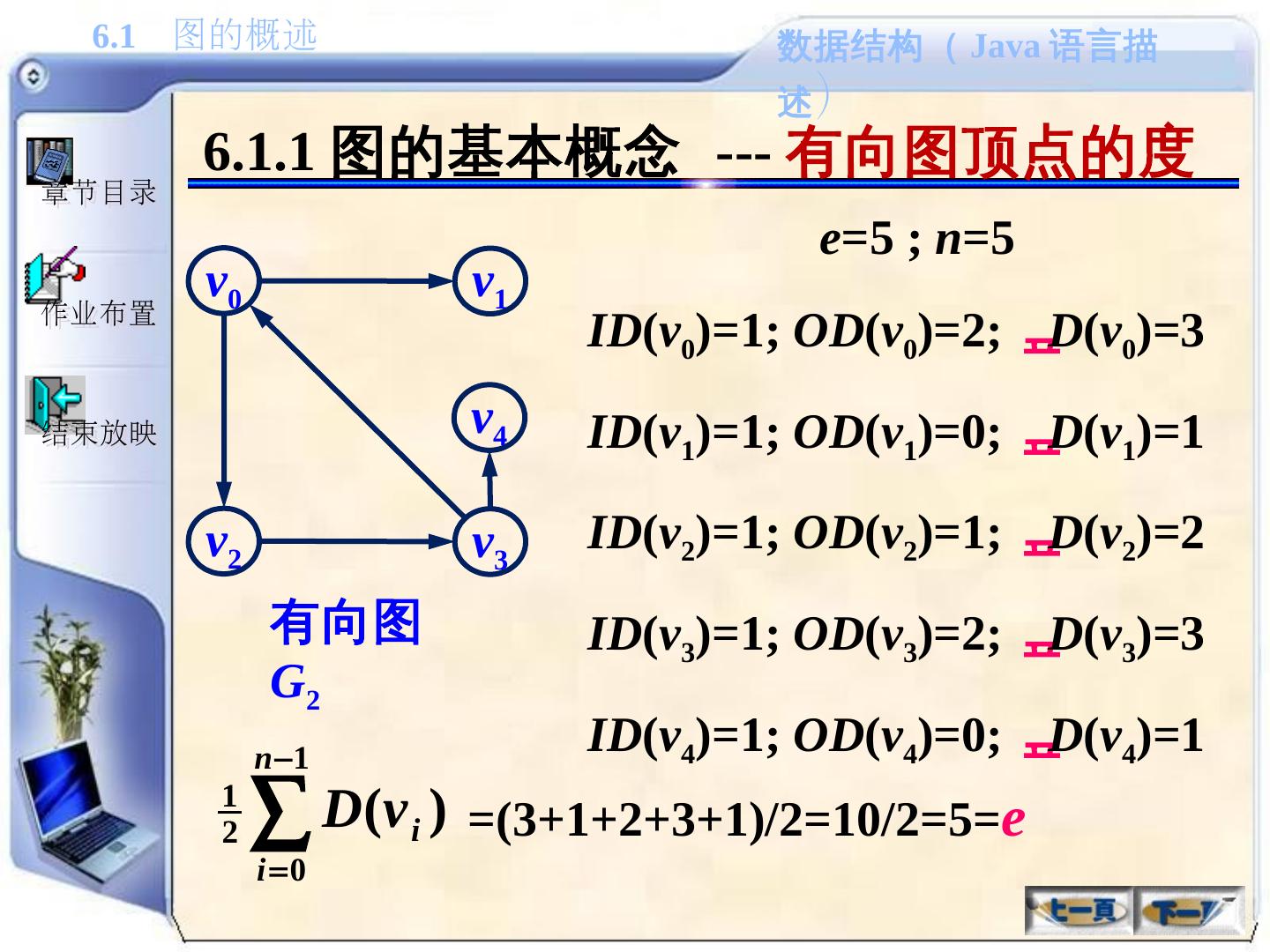
20 .6.1.1 图的基本概念 --- 有向图顶点的度 v 0 v 1 v 2 v 3 v 4 有向图 G 2 e= 5 ; n =5 ID ( v 0 )=1; OD ( v 0 )=2; D ( v 0 )=3 ID ( v 1 )=1; OD ( v 1 )=0; D ( v 1 )=1 ID ( v 2 )=1; OD ( v 2 )=1; D ( v 2 )=2 ID ( v 3 )=1; OD ( v 3 )=2; D ( v 3 )=3 ID ( v 4 )=1; OD ( v 4 )=0; D ( v 4 )=1 =(3+1+2+3+1)/2=10/2=5= e
21 .6.1.1 图的基本概念 --- 路径、回路 路径 (Path) 在一个图中,路径是从顶点 u 到顶点 v 所经过的顶点序列,即 ( u =v i0 , v i1 , …, v im = v ) 。 路径长度 是指该路径上边的数目。 回路: 第一个顶点和最后一个顶点相同的路径称为回路或环。 A B E C F
22 .6.1.1 图的基本概念 --- 路径、回路 初等路径 序列中顶点不重复出现的路径称为初等路径 初等回路 除了 第一 个顶点和 最后 一个顶点之外,其余顶点不重复出现的回路 A B E C F
23 .6.1.1 图的基本概念 --- 路径、回路 v 0 v 1 v 2 v 3 有向图 G 5 路径 ( v 0 , v 2 , v 3 , v 0 ) 是初等回路 其路径长度为 3 从顶点 v 0 到顶点 v 1 的一条路径 ( v 0 , v 2 , v 3 , v 1 ) 是初等路径 , 其路径长度为 3 从顶点 v 0 到顶点 v 1 的另一条路径 ( v 0 , v 2 , v 3 , v 0 , v 1 ) 不是初等路径 其路径长度为 4
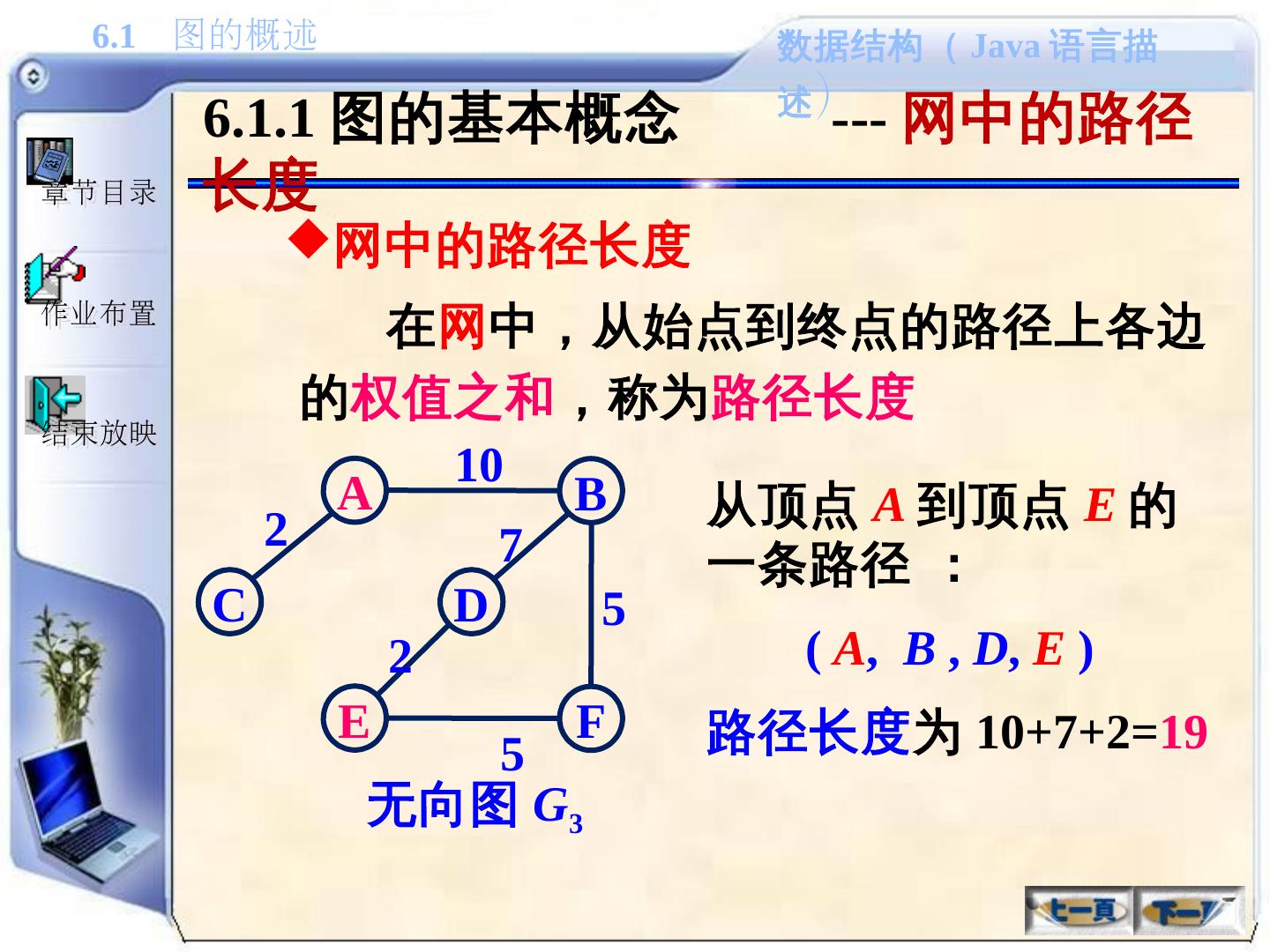
24 .6.1.1 图的基本概念 --- 网中的路径长度 网中的路径长度 在 网 中,从始点到终点的路径上各边的 权值之和 ,称为 路径长度 A B E F D C 2 10 2 7 5 5 无向图 G 3 从顶点 A 到顶点 E 的一条路径 : ( A , B , D , E ) 路径长度 为 10+7+2= 19
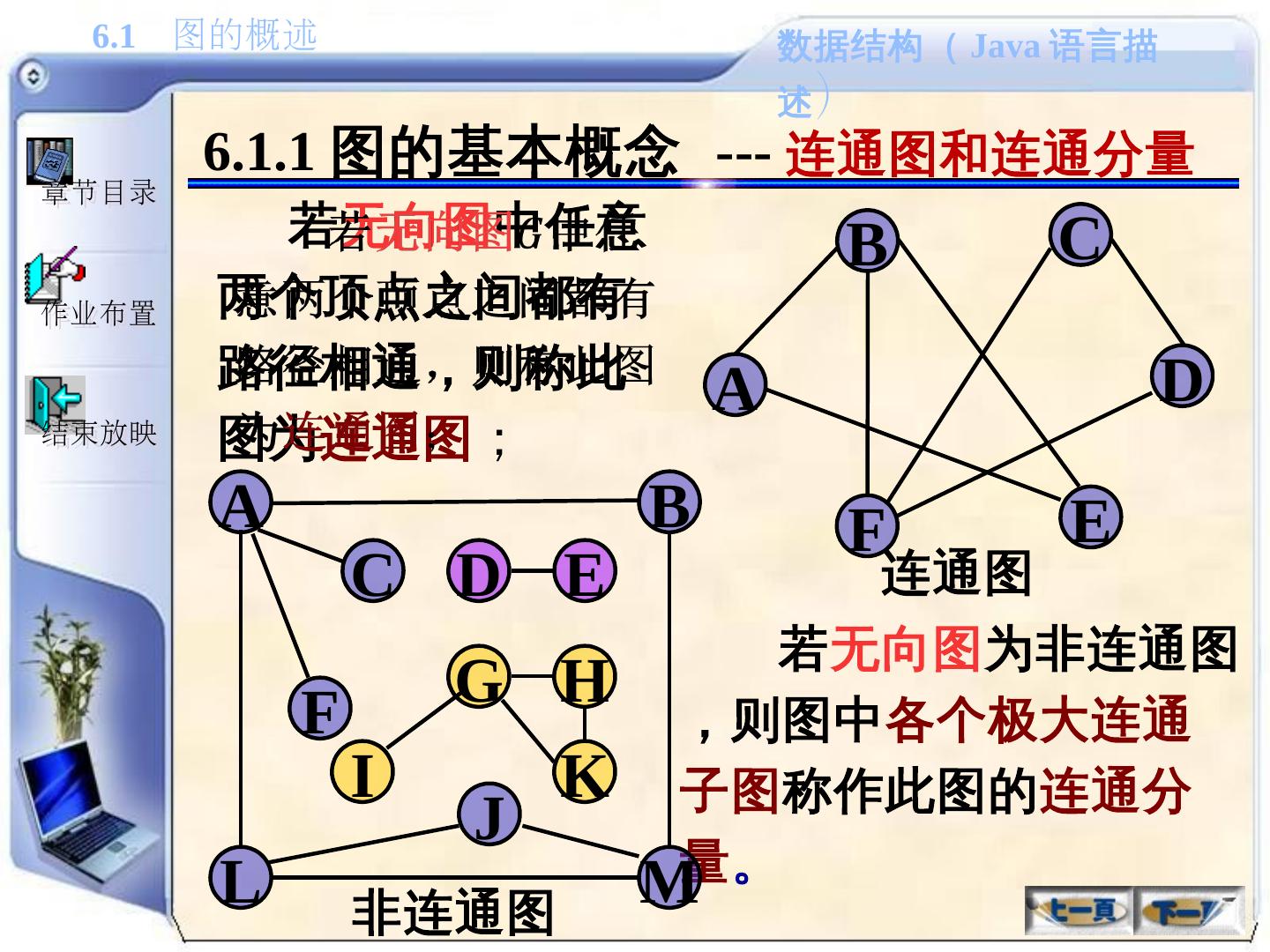
25 .6.1.1 图的基本概念 --- 连通图和连通分量 若 无向图 中任意两个顶点之间都有路径相通,则称此图为 连通图 ; 若 无向图 为非连通图,则图中 各个极大连通子图 称作此图的 连通分量 。 B A C D F E A B L C M H E F K G I D J 连通图 非连通图
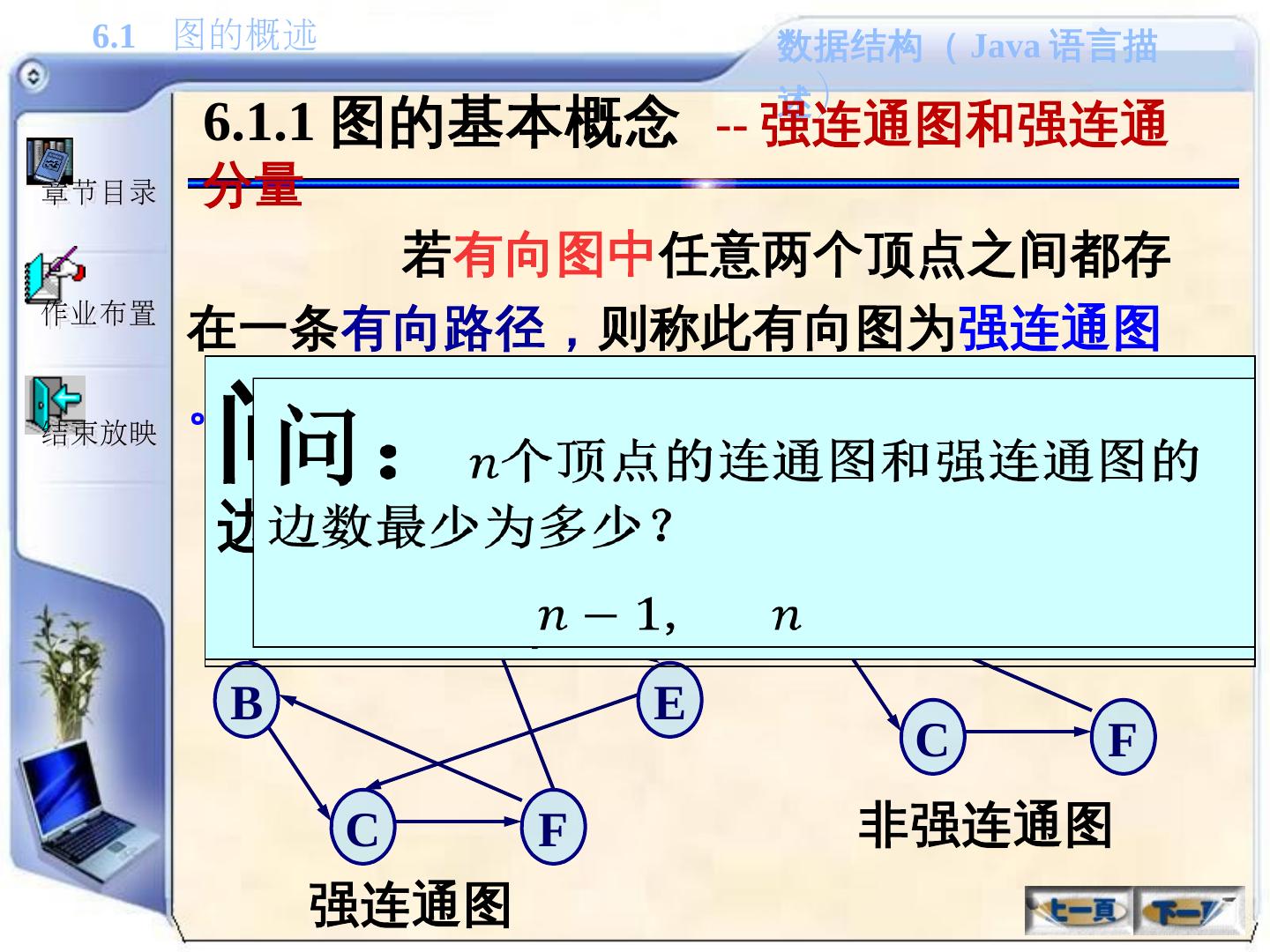
26 .6.1.1 图的基本概念 -- 强连通图和强连通分量 若 有向图中 任意两个顶点之间都存在一条 有向路径, 则称此有向图为 强连通图。 A B E C F 否则,其各个极大强连通子图称作它的 强连通分量 。 A B C F 强连通图 非强连通图 问: 个顶点的连通图和强连通图的边数最少为多少? ,
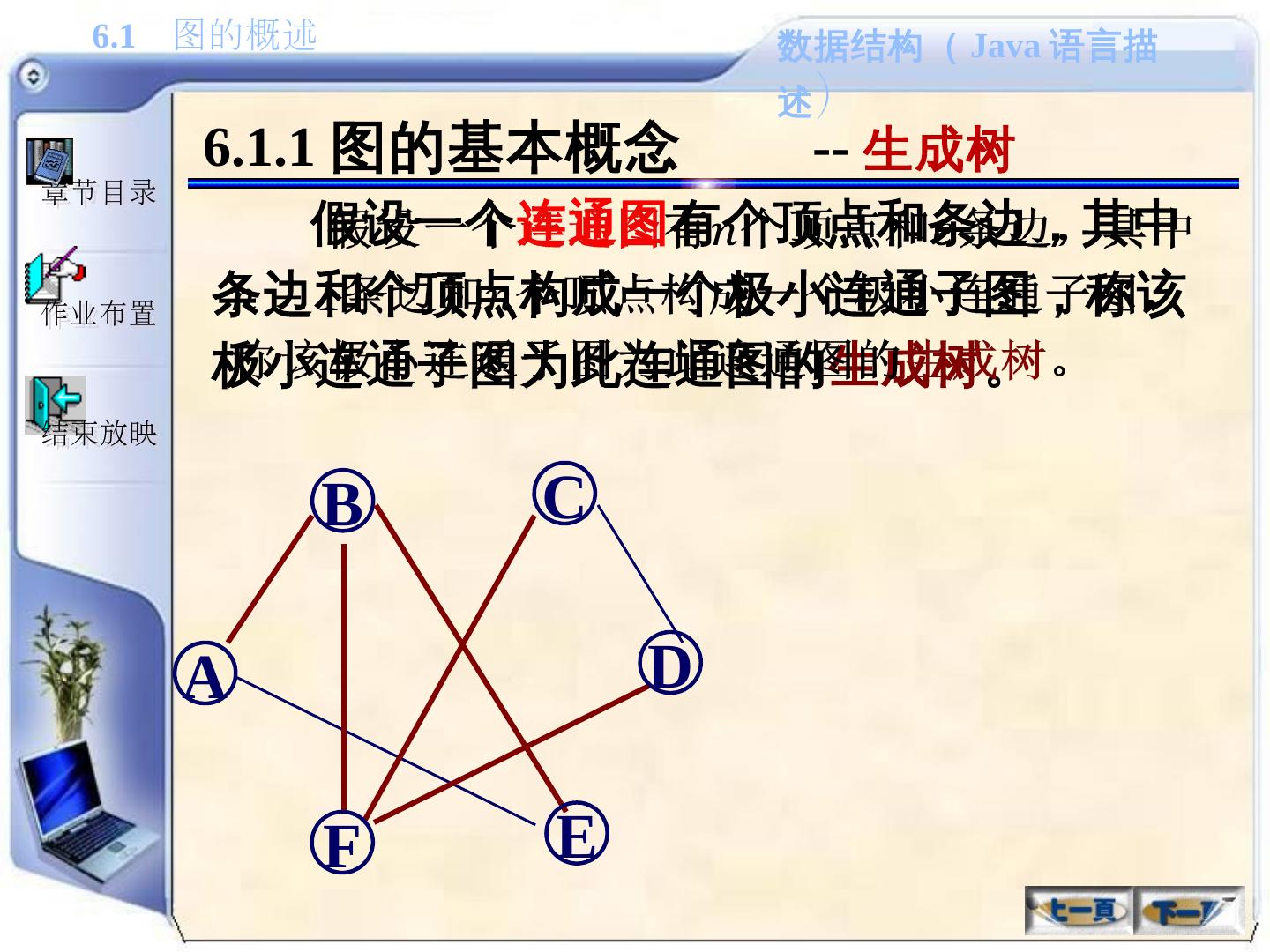
27 .6.1.1 图的基本概念 -- 生成树 假设 一个 连通图 有 个 顶点 和 条 边, 其中 条 边 和 个 顶点构成一个极小连通子图,称该极小连通子图为此连通图的 生成树 。 B A C D F E
28 .3 个 连通分量 6.1.1 图的基本概念 --- 生成森林 A C D E F H K B G I M L J 非边通图 A C D E F H K B G I M L J 对 非连通图 ,则称由各个连通分量的生成树的集合为此非连通图的 生成森林 。
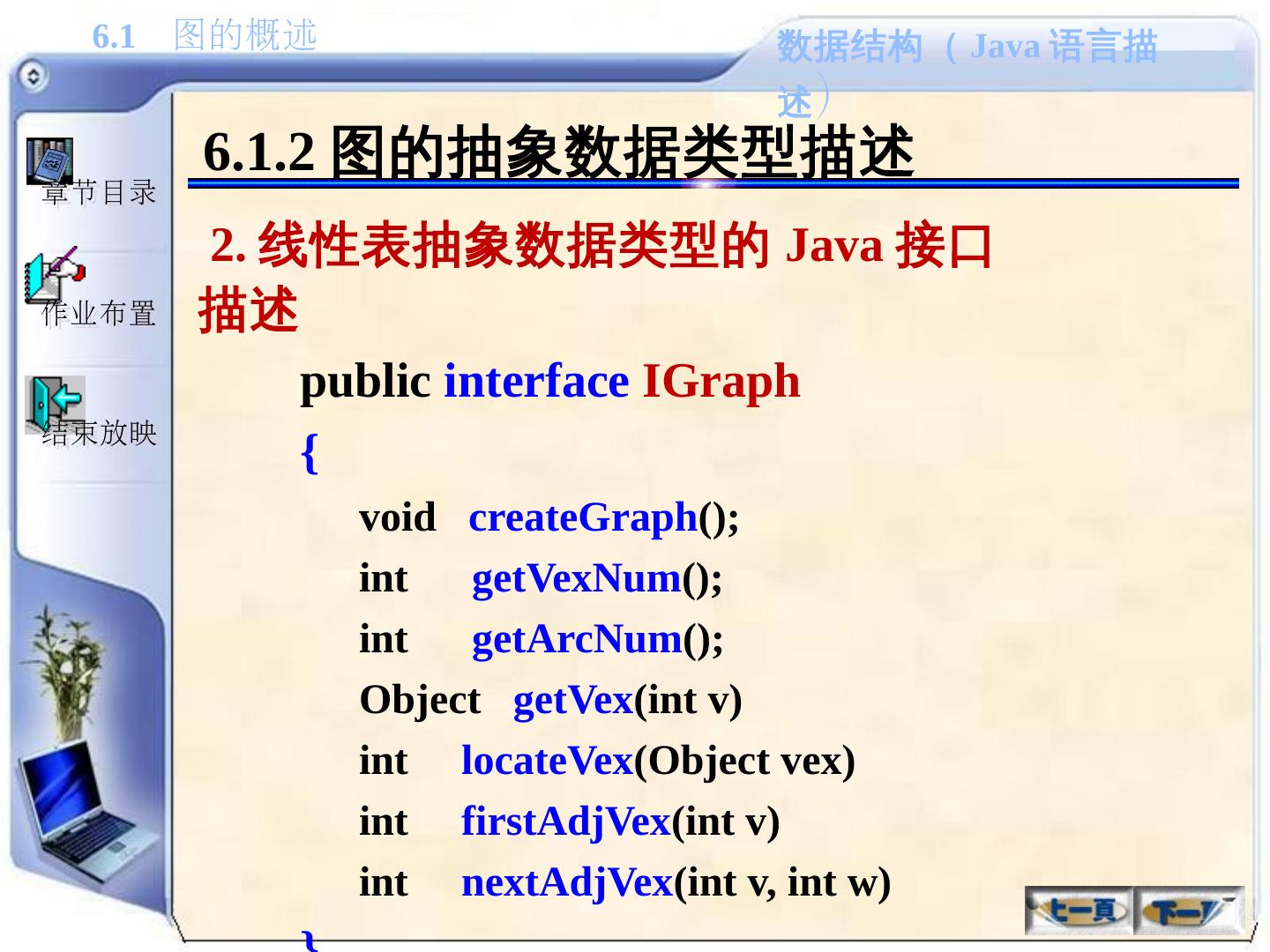
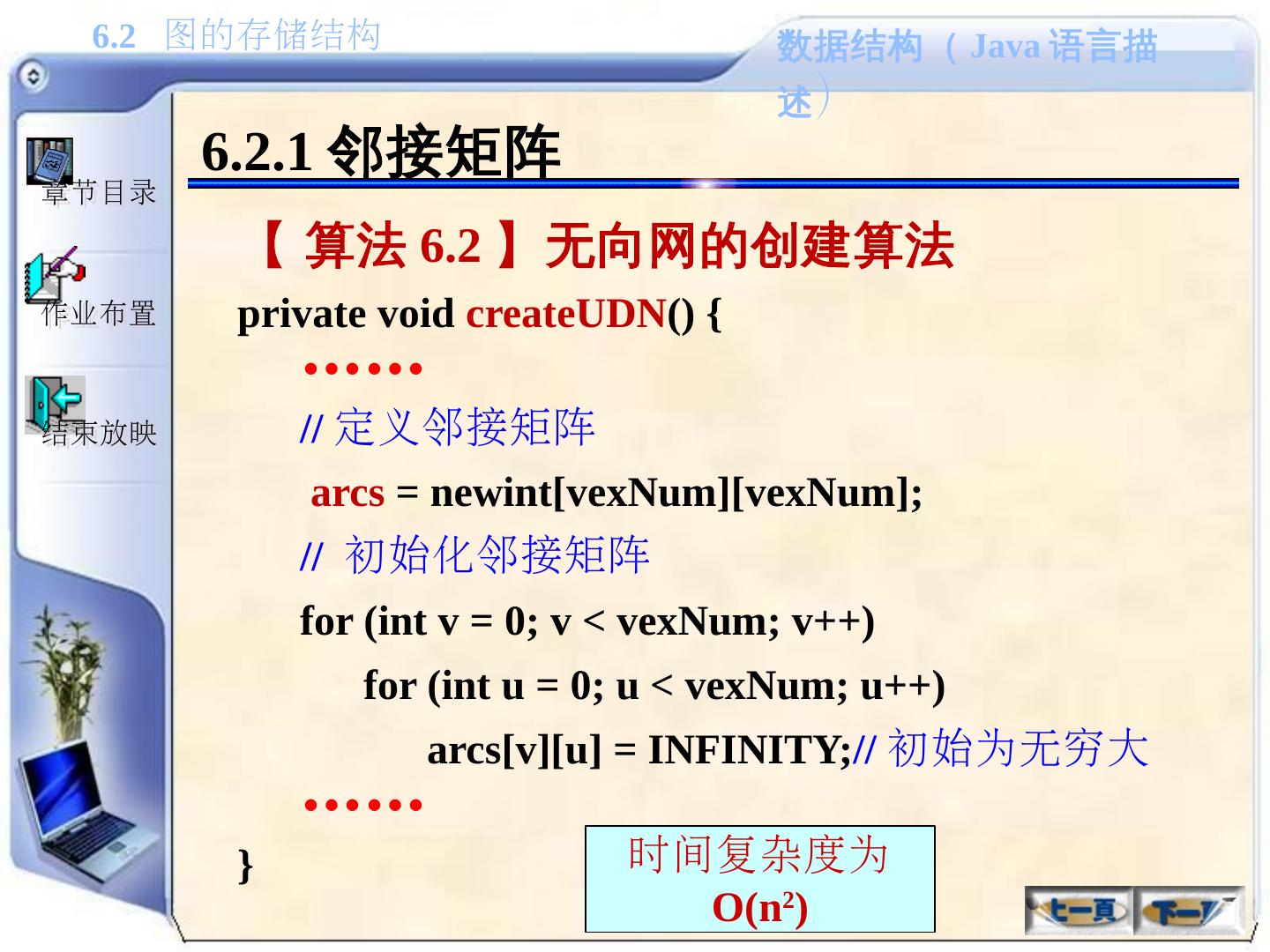
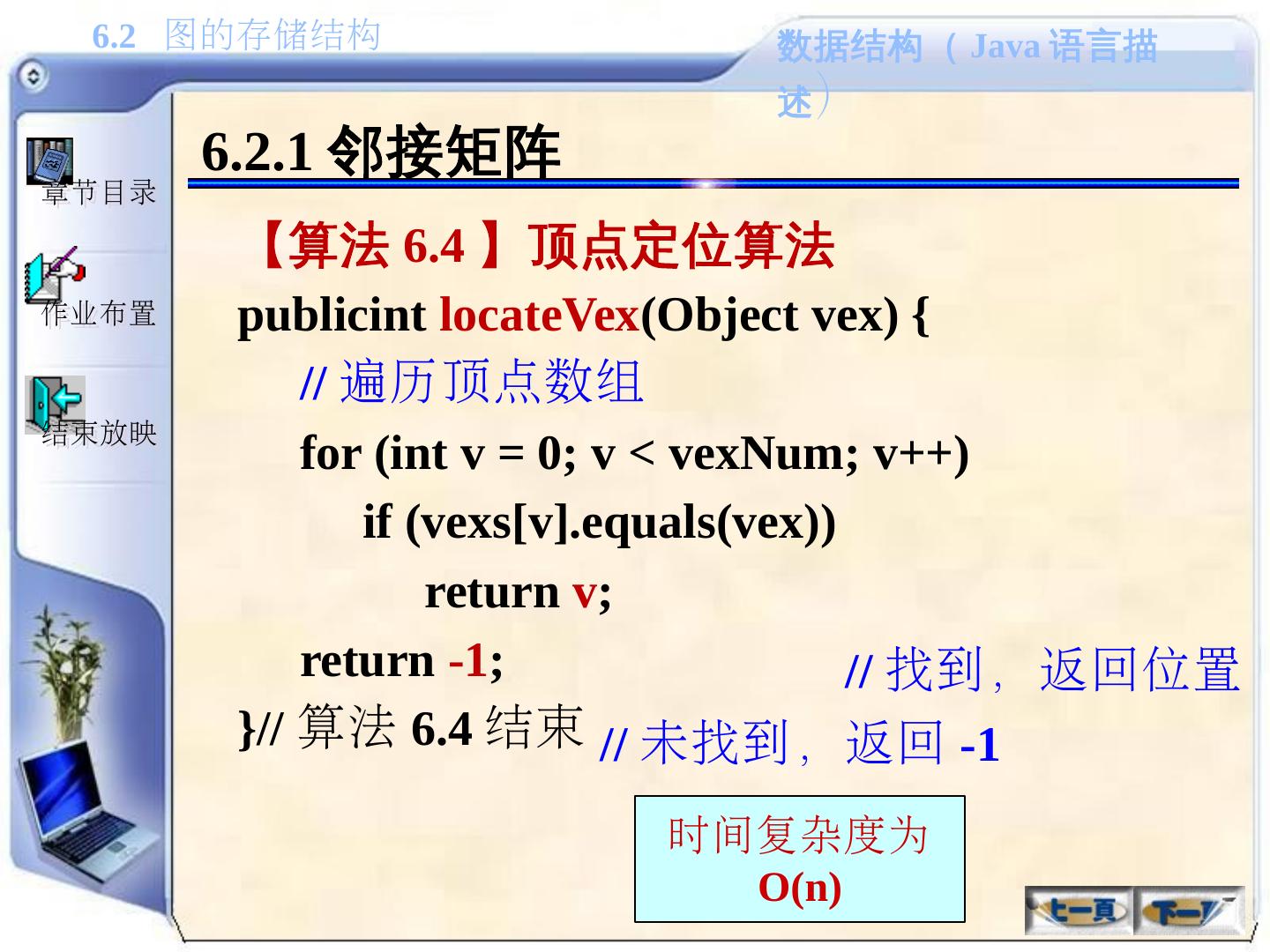
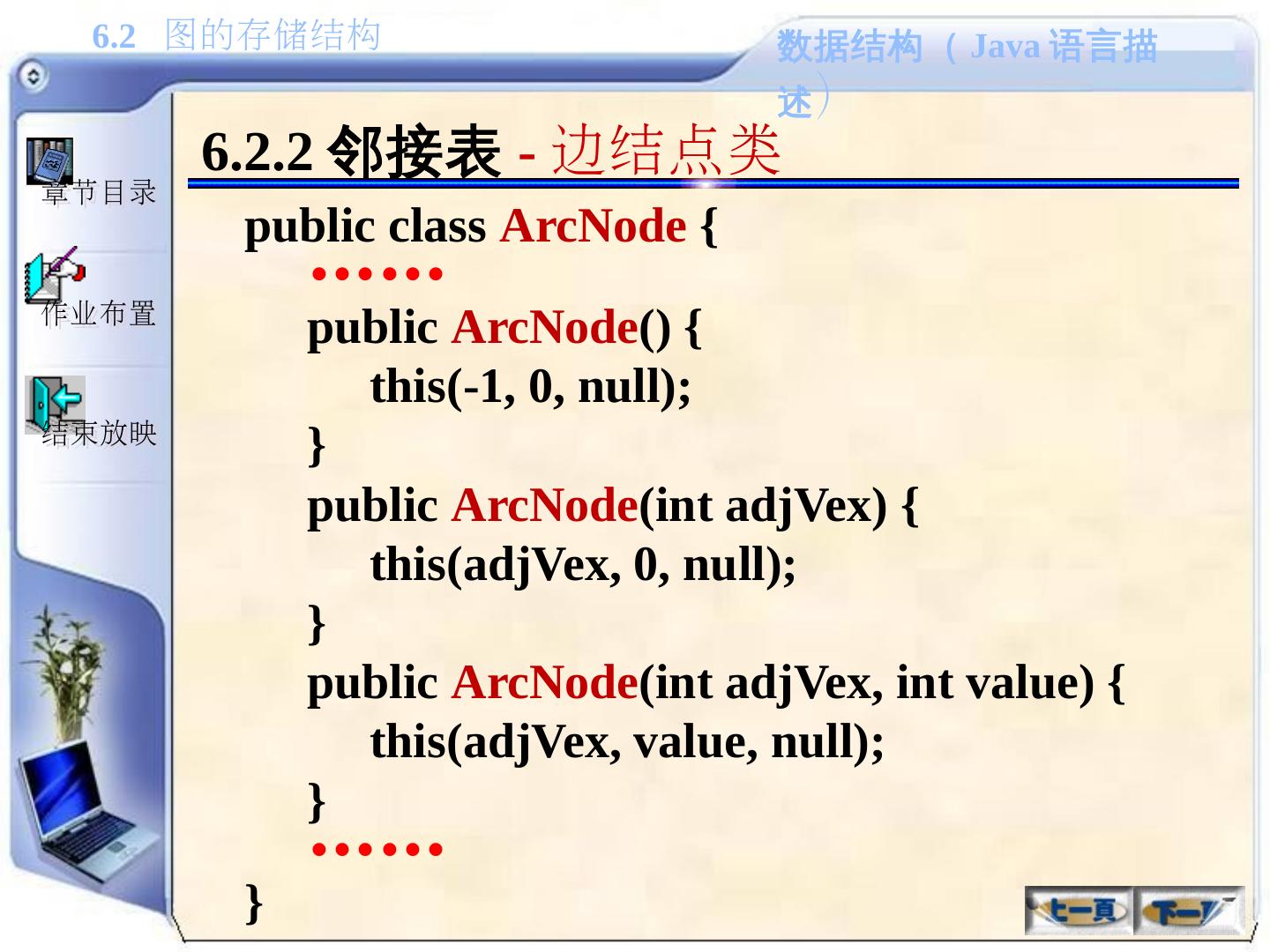
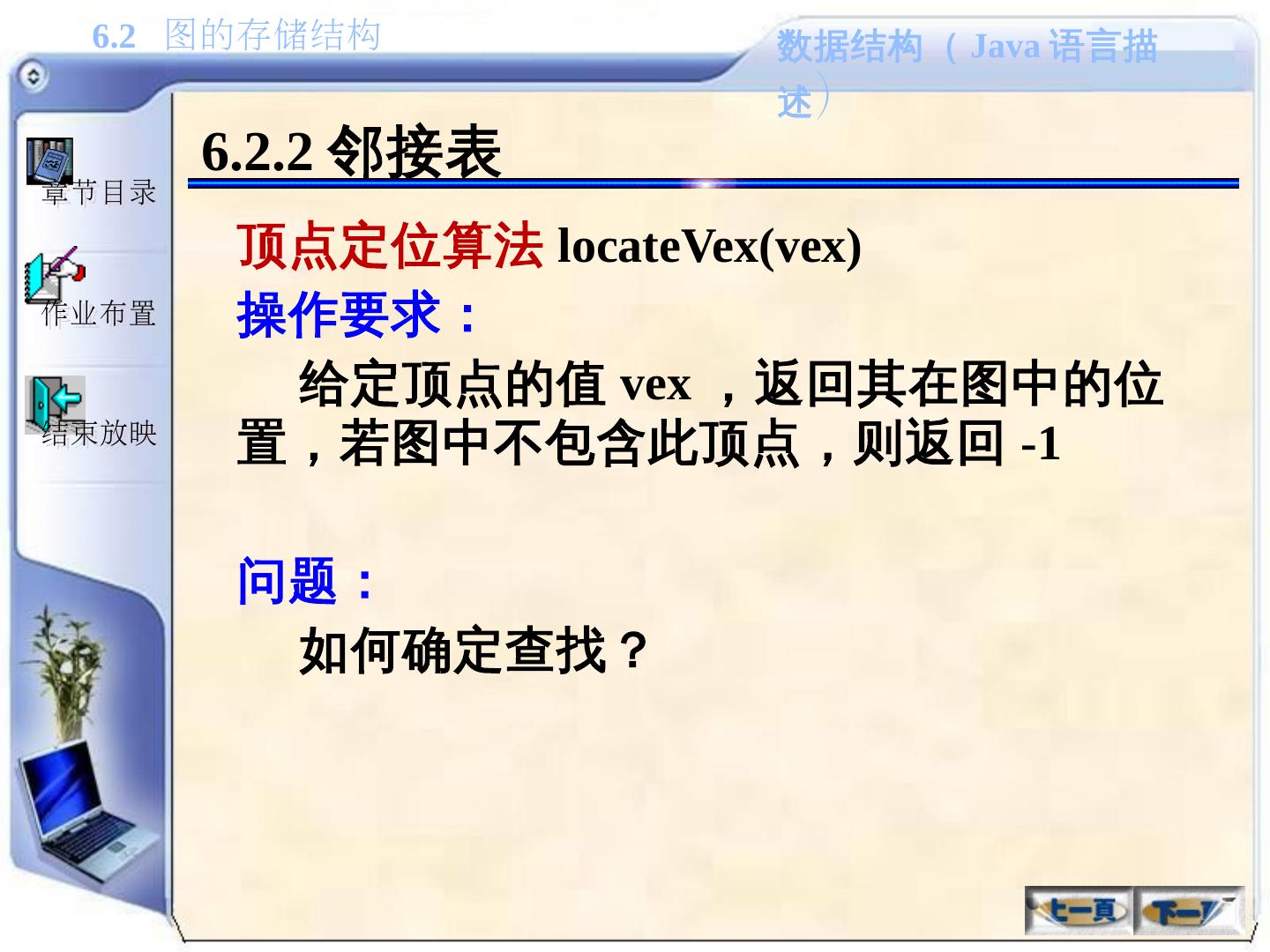
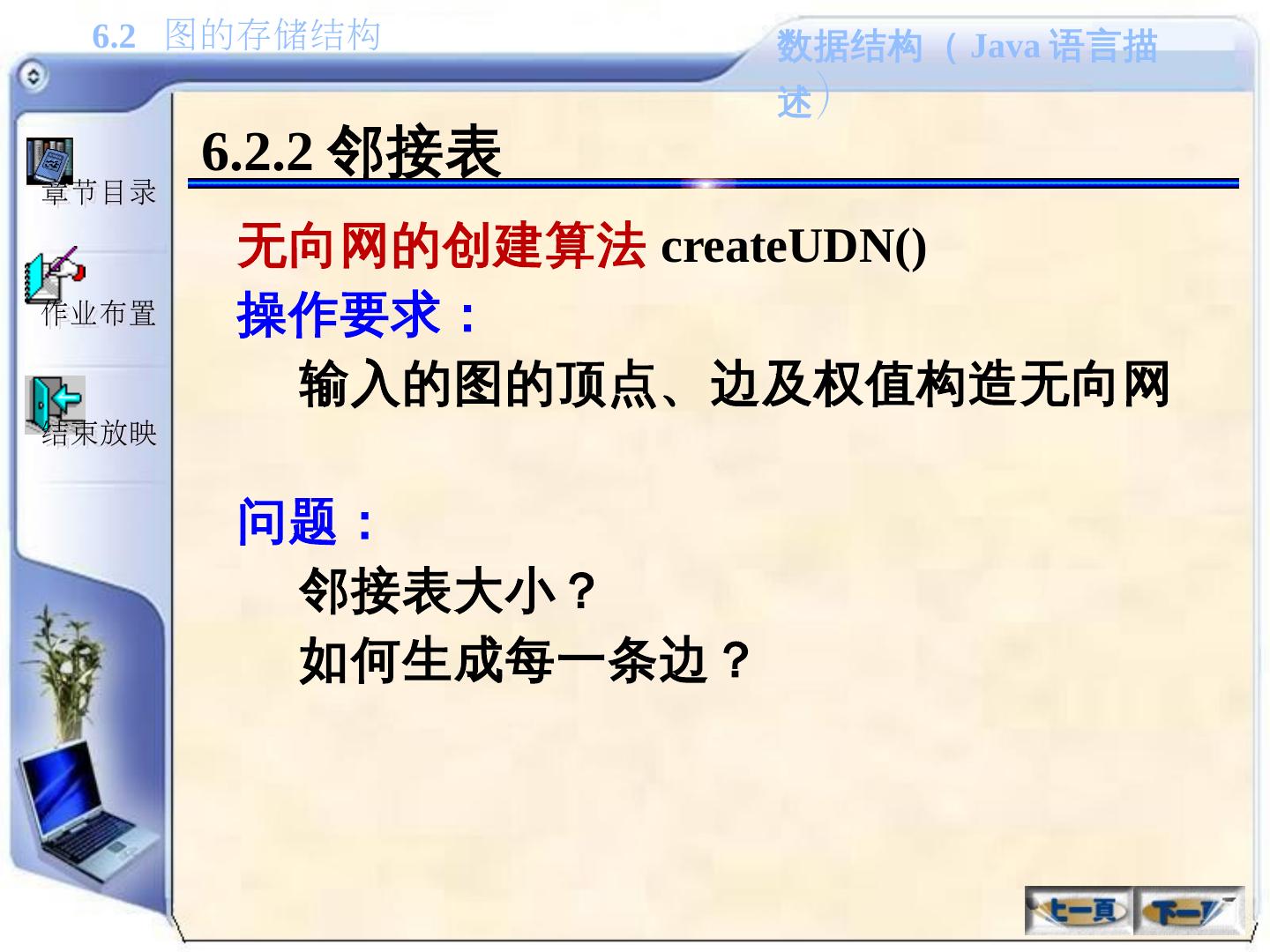
29 .6.1.2 图的抽象数据类型描述 1. 基本操作( 1 ) 1 )创建一个图 createGraph() 2 )返回图中的顶点数 getVexNum() 3 )返回图中的边数 getArcNum() 4 )给定顶点的位置 v ,返回其对应的顶点值,其中: 0 ≤ v<vexNum ( vexNum 为顶点数) getVex(v) 5 )给定顶点的值 vex ,返回其在图中的位置,如果图中不包含此顶点,则返回 -1 locateVex(vex)