呼之欲出。 恩格尔系数变化表

1 .核心素养导向的 数学教学变革 人民教育出版社 章建跃 zhangjy@pep.com.cn 

2 . 一、如何理解数学学科核心素养 • “ 教育的根本任务在于立德树人”，这就是 整个教育改革的核心任务。 • 如何落实“立德树人”的根本任务？抓手在 哪里？ • 教育部的顶层设计是“以学生发展核心素 养为统领”，各学科教学都要为学生核心 素养的发展作出独特的贡献，从而实现 “立德树人”根本任务。 

3 .• 数学教育中的“立德树人”，以数学学科核心素 养为统领。 • 数学学科核心素养是通过数学学习而逐步形成 的具有数学特征的关键能力、必备品格与价值 观念。 • 表现： 会用数学眼光观察世界；会用数学思维思 考世界；会用数学语言表达世界。 • 高中课标提炼了六个数学学科核心素养要素： 数学抽象、逻辑推理、数学建模、数学运算、 直观想象、数据分析。 

4 .理解数学学科核心素养的几个角度 • 数学教育中“立德树人”的内涵； • 从与学生发展核心素养关系的角度； • 从数学学科特点出发； • 数学课程目标的发展角度。 —— 数学学科核心素养“是什么”？深化数学 教育改革中提出核心素养导向有什么历史 的必然性？能否“举例子”？ 

5 .数学教育“立德树人”的基本内涵 • 帮助学生掌握现代生活和进一步学习所必需 的数学知识、技能、思想和方法； • 提升学生的数学素养，引导学生会用数学眼 光观察世界，会用数学思维思考世界，会用 数学语言表达世界； • 促进学生思维能力、实践能力和创新意识的 发展； • 在学生形成正确人生观、价值观、世界观等 方面发挥独特作用。 

6 .数学学科核心素养与学生发展核心素养 • 中国学生发展核心素养：文化基础（人文 底蕴、科学精神）、自主发展（学会学习 、健康生活）、社会参与（责任担当、实 践创新） • 数学教育对发展学生核心素养的独特贡献 ，主要体现在科学精神（理性思维、批判 质疑、勇于探究）、学会学习（乐学善学 、勤于反思、信息意识）和实践创新（劳 动意识、问题解决、技术应用）上。 

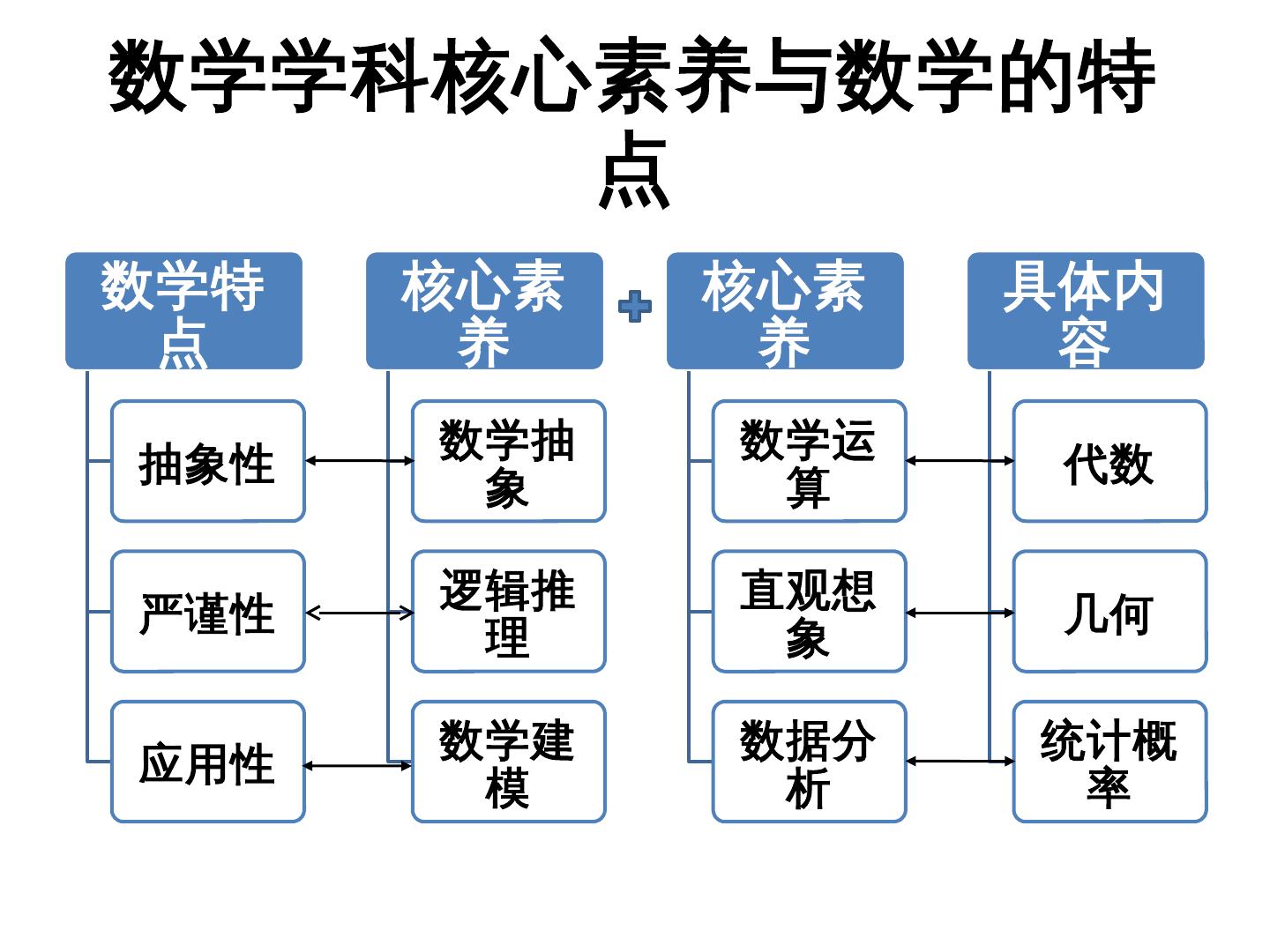
7 .数学学科核心素养与数学的特 点 数学特 核心素 核心素 具体内 点 养 养 容 数学抽 数学运 抽象性 代数 象 算 逻辑推 直观想 严谨性 几何 理 象 数学建 数据分 统计概 应用性 模 析 率 

8 . 数学课程目标的发展 • 是“三维目标”的进一步融合； • 是义教的八个“核心概念”（ 数感、符号意 识、空间观念、几何直观、数据分析观念 、运算能力、推理能力、模型思想）的进 一步整合； • 以“四基”“四能”为载体； • 双基、三大能力是数学育人目标的内核— —与时俱进丰富内涵，万变不离其宗！ 

9 .• 新一轮数学课改的核心任务是提升学生的 数学学科核心素养，为学生发展核心素养 作出独特贡献。 • 要有具体措施，要把数学学科核心素养落 实在数学教育的各个环节。 

10 . 二、新教材的体系 • 普通高中教科书 · 数学（ A 版）结构体系 

11 .三、关于落实核心素养的思考 1 ．理性思维是数学素养的灵魂 • 发展学生的理性思维（特别是逻辑思维） ，使学生学会有逻辑地、创造性地思考， 学会使用数学语言表达与交流，成为善于 认识和解决问题的人才，是数学课程的主 要任务。 

12 . 例 1 如何研究“相交线” • 研究对象是什么？ • 两条直线相交所形成的几何图形 • 研究内容是什么？ • 两条直线相交形成四个角，这些角之间的 相互关系 • 如何发现这些角的相互关系？ 

13 . 探究过程 • 四个角的关系 • ∠1+∠ 2+∠ 3+∠ 4=360° • 三个角的关系 • 变化中不存在不变性——没有固定的关系 • 两个角的关系 （ 1 ）两两配对有 6 对角，即∠ 1 和∠ 2 ， ∠ 1 和∠ 3 ，∠ 1 和∠ 4 ，∠ 2 和∠ 3 ，∠ 2 和∠ 4 ，∠ 3 和∠ 4 。 

14 .（ 2 ）∠ 1 和∠ 2 的关系如何研究？ • 从角的定义出发：两个角的顶点的关系、边 的关系，得到∠ 1 与∠ 2 的位置特点。 • 顶点重合；一边重合，称这两个角“相邻”；另 一边互为反向延长线，所以两个角“互补”。 • 用几何语言准确表达即为邻补角的定义：∠ 1 与∠ 2 有一条公共边 OA ，它们的另一边互为 反向延长线，即∠ 1 与∠ 2 互补，具有这种关 系的两个角，互为邻补角． 

15 .（ 3 ）其余 5 对角的关系的研究 • 让学生类比∠ 1 与∠ 2 的位置关系的研究 过程，对其余 5 对角的边的位置关系进行 自主探究，并作出分类，得出对顶角的定 义，再得出：两条直线相交所形成的 4 个 角中，两两之间的位置关系，根据两个角 的边之间特殊的位置关系，分成两类，一 类是邻补角，一类是对顶角。 

16 . 接下去研究什么？ • 已经研究了两条直线相交形成的 6 对角的 位置关系，发现可以分为两类。那么，邻 补角、对顶角分别有怎样的数量关系呢？ 这就是接下来要研究的问题。 • 定性到定量——研究几何问题的基本之道 。 

17 .如何让学生感受证明“对顶角相等”的必 要性 • 从一个给定的图形中得到“对顶角相等”，但任意 两个对顶角都相等吗？ • 观察剪刀剪纸的过程，这个过程中什么在变化 ？对顶角的相等关系总能保持吗？为什么？ • 在一个平面内的两条相交线，不仅 AB ， CD 的 位置关系可以改变，交点 O 的位置也可以改变。 在这些变化过程中，对顶角仍然相等吗？你如 何使人相信：如果两个角具有对顶角的位置关 系，那么它们就一定相等？你能把道理完整地 写出来吗？ 

18 . 思考题 • 你认为教材为什么把平行线的研究内容安 排在“三线八角”之后？ • 在“三线八角”的基础上，如何引导学生发 现平行线的判断与性质？ 

19 .进一步地：如何研究位置关系的性质？ • 两条直线平行，从“同位角相等”、“内错角 相等”以及“同旁内角互补”可以想到，这时 的“性质”是与“第三条直线”构成某种关系 ——平行、相交，相交时又形成一些角， 然后看由两条直线平行这一位置关系（条 件）所决定的这些角之间有什么确定的关 系。 

20 .• 从方法论的高度看，研究两个几何元素的某 种位置关系的性质，就是探索在这种位置关 系下的两个几何元素与其他（同类）几何元 素所形成的图形中出现的确定关系（不变性 和不变量）。 • 具体方法是让“其他几何元素”动起来，看“变 化中的不变性、不变量”——这是教学设计 的源头。 

21 . 例 2 直线与平面平行的性质 • 位置关系（大前提）：直线 l ∥ 平面 α ； • 探究性质的思路：直线 l 、平面 α 与其他直 线、平面所形成的确定关系，可以得到命题 ： （ 1 ）如果 a∥l （小前提） ，那么 a ∥α ； （ 2 ）如果 a ∥α ，那么 a ∥l ； （ 3 ）如果 a ⊥l ，那么 a⊥α ； （ 4 ）如果 a⊥α ，那么 a⊥ l ； 

22 .（ 5 ）如果 β∥l ，那么 β∥α ； （ 6 ）如果 β∥α ，那么 β∥l ； （ 7 ）如果 β⊥l ，那么 β⊥α ； （ 8 ）如果 β ⊥ α ，那么 β ⊥l 。 

23 .（ 9 ）与“公理”相联系，直线 l 与平面 α 内 任意一点 A 确定一个平面 β ， α ∩ β=m ，那么 m∥l ； （ 10 ） l∥α ，所以 l∩α =Φ 。如果 m 在 α 内，则或者 m∥l ，或者 m 与 l 是异面直 线。 （ 11 ）直线 m 与直线 l 异面，则过直线 m 有且只有一个平面与直线 l 平行。 （ 12 ） l∥α ， β∩γ=l ， α∩ β=l1 ， α∩γ=l 2 ， 那么 l1∥l2 。 

24 . 例 3 两个平面垂直的性质与判定 • 研究对象是什么？ • 研究内容是什么？ • 如何引导学生发现性质？ • 一般地，什么叫“几何图形的性质”？几何 性质分为哪些类型？ • 教材的变化 

25 .2 ．数学育人要发挥数学的内在力量，数 学育人要用数学的方式 • 数学是思维的科学，具有“追求最大限度的 一般性模式特别是一般性算法的倾向”； • 有一种研究的“基本套路”； • 有一套具有普适性的思考结构和交流的符 号形式，这种结构和符号形式是强大的， 富有逻辑，简明而且精确，是人们可以借 助于理解和处理周围环境的一种思维方式 。 

26 . 教材如何体现“数学的方式” • 以发展学生数学素养为追求，根据学生的 认知规律，螺旋上升地安排教学内容，特 别是要让重要的（往往也是难以一次完成 的）数学概念、思想方法得到反复理解的 机会。——心理性 • 以“事实——概念——性质（关系）——结 构（联系）——应用”为明线； • 以“事实——方法——方法论——数学学科 本质观”为暗线。 

27 .从数学思维、思想或核心素养角度看 • “ 事实——概念”主要是“抽象”（在周而复始的运 动过程中，涉及哪些量，它们之间的关系如何， 可以用怎样的数学方式表示）； • “ 概念——性质”主要是“推理”，包括通过归纳推 理发现性质，通过（逻辑）演绎推理证明性质； • “ 性质——结构”主要也是“推理”，是建立相关知 识之间的联系而形成结构功能良好、迁移能力强 大的数学认知结构的过程； • “ 概念、性质、结构——应用”主要是“建模”，是 用数学知识解决数学内外的问题。 

28 .• 在整个教学内容的展开过程中，都要发挥“一 般观念”的作用，加强“如何思考”、“如何发 现”的启发和引导，特别是在概念的抽象要做 什么、“几何性质”“代数性质”“函数性质”指什 么等问题上要及时引导，以使学生明确思考 方向。 • “ 不在知其然，而在知其所以然；不在知其所 以然，而在何由以知其所以然”； • “ 启发学者，示以思维之道耳”。 • 当前的教学，主要问题是数学没有讲好，老 师不知道如何“示以思维之道”。我们应当加 强这方面的研究。 

29 .例 4 有理数的知识结构图