linear discriminant analysis

1 .Linear Discriminant Analysis Linear Discriminant Analysis Jia Li Department of Statistics The Pennsylvania State University Email: jiali@stat.psu.edu http://www.stat.psu.edu/∼jiali Jia Li http://www.stat.psu.edu/∼jiali 

2 .Linear Discriminant Analysis Notation K The prior probability of class k is πk , k=1 πk = 1. πk is usually estimated simply by empirical frequencies of the training set # samples in class k π ˆk = Total # of samples The class-conditional density of X in class G = k is fk (x). Compute the posterior probability fk (x)πk Pr (G = k | X = x) = K l=1 fl (x)πl By MAP (the Bayes rule for 0-1 loss) ˆ (x) = arg max Pr (G = k | X = x) G k = arg max fk (x)πk k Jia Li http://www.stat.psu.edu/∼jiali 

3 .Linear Discriminant Analysis Class Density Estimation Linear and quadratic discriminant analysis: Gaussian densities. Mixtures of Gaussians. General nonparametric density estimates. Naive Bayes: assume each of the class densities are products of marginal densities, that is, all the variables are independent. Jia Li http://www.stat.psu.edu/∼jiali 

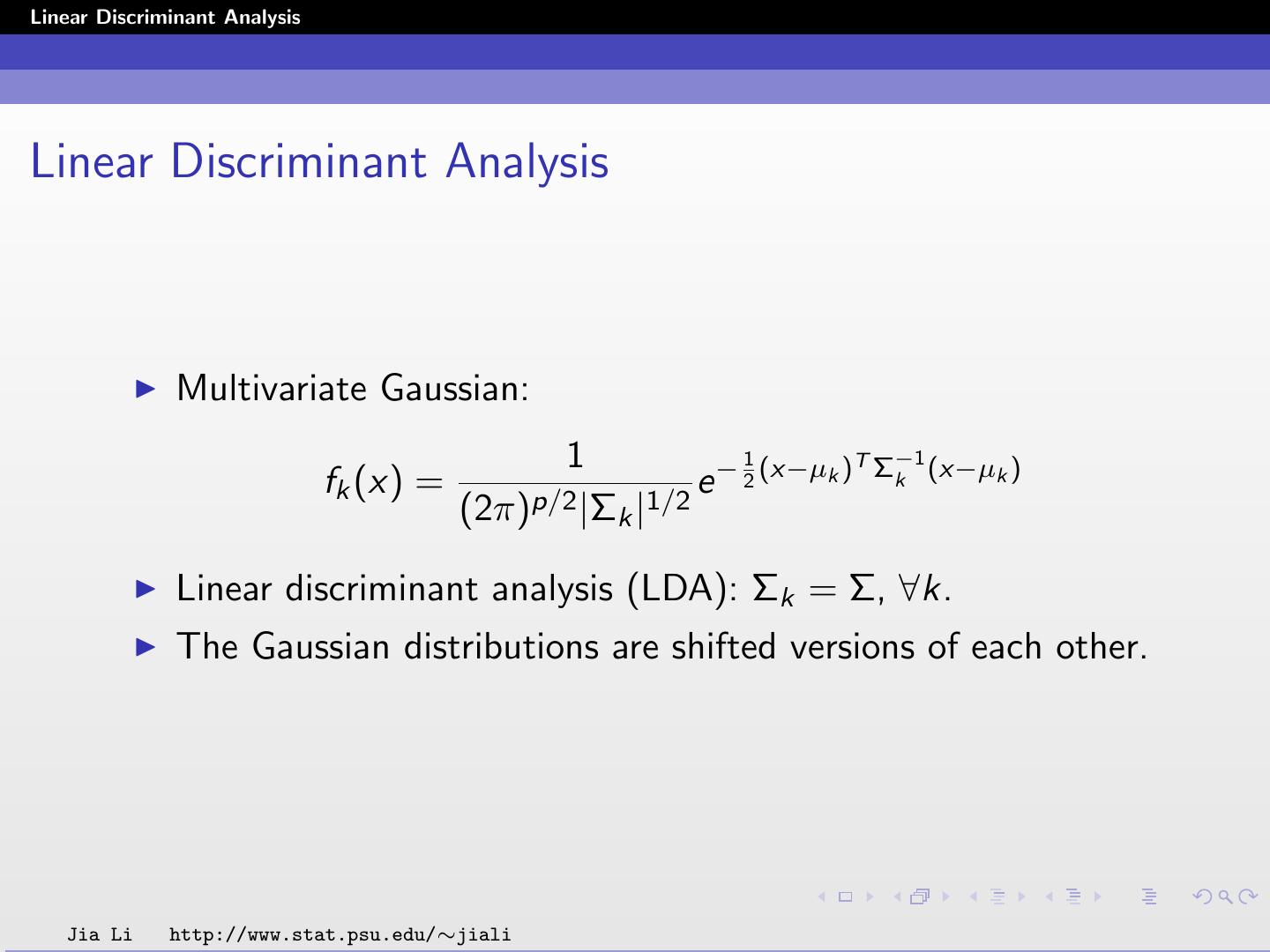
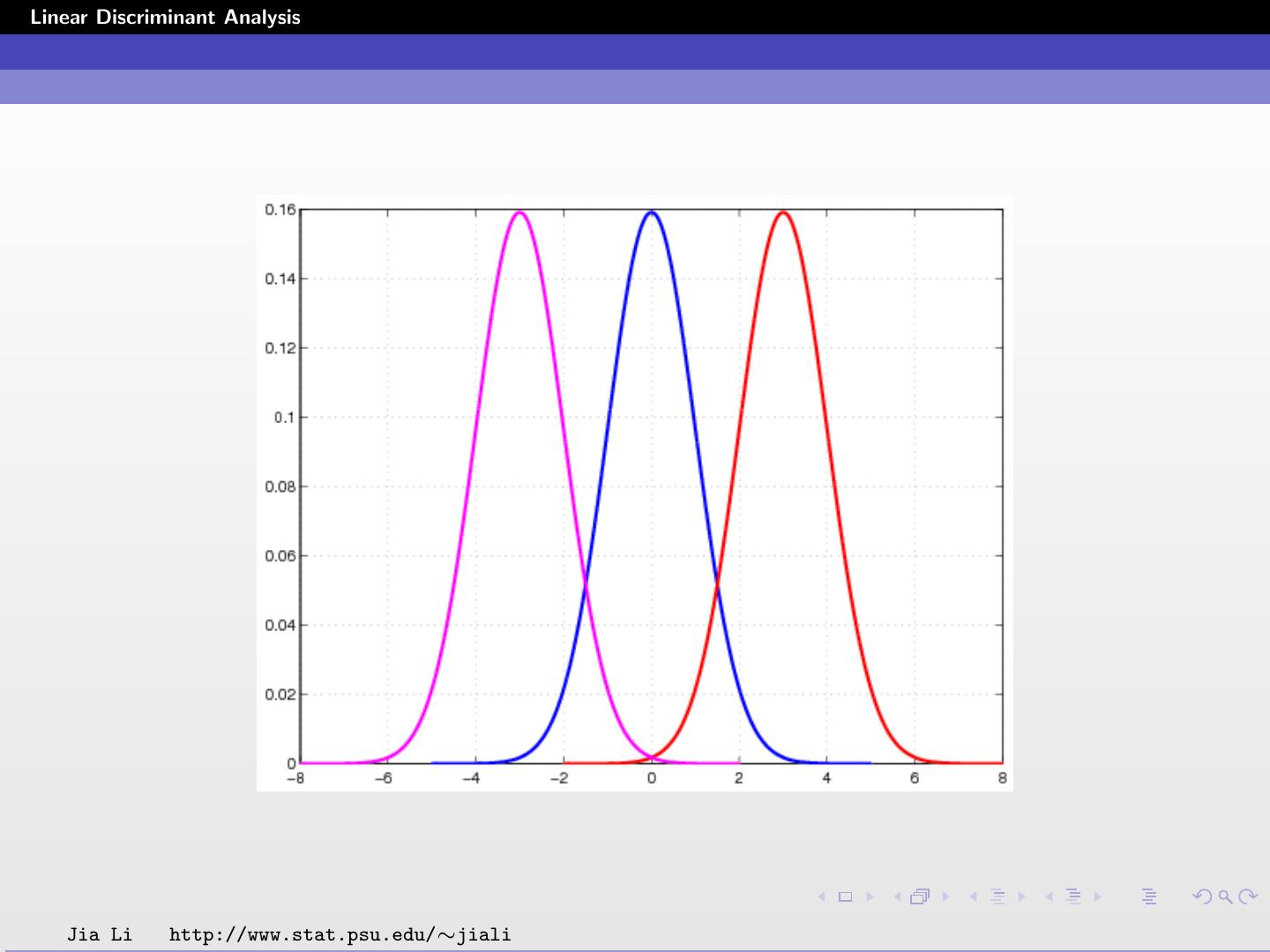
4 .Linear Discriminant Analysis Linear Discriminant Analysis Multivariate Gaussian: 1 1 T Σ−1 (x−µ ) fk (x) = e − 2 (x−µk ) k k (2π)p/2 |Σ k |1/2 Linear discriminant analysis (LDA): Σk = Σ, ∀k. The Gaussian distributions are shifted versions of each other. Jia Li http://www.stat.psu.edu/∼jiali 

5 .Linear Discriminant Analysis Jia Li http://www.stat.psu.edu/∼jiali 

6 .Linear Discriminant Analysis Jia Li http://www.stat.psu.edu/∼jiali 

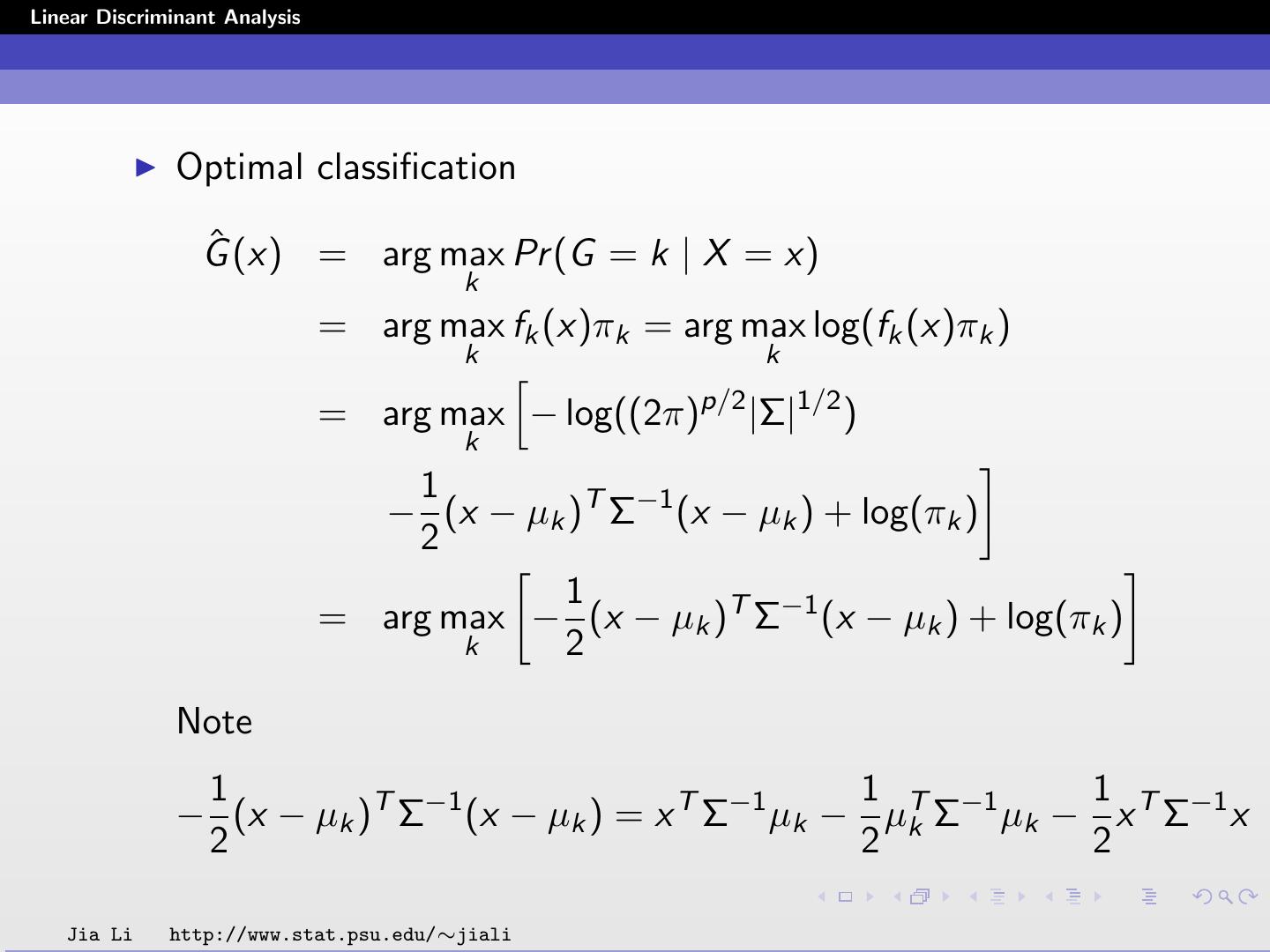
7 .Linear Discriminant Analysis Optimal classification ˆ (x) = arg max Pr (G = k | X = x) G k = arg max fk (x)πk = arg max log(fk (x)πk ) k k = arg max − log((2π)p/2 |Σ|1/2 ) k 1 − (x − µk )T Σ−1 (x − µk ) + log(πk ) 2 1 = arg max − (x − µk )T Σ−1 (x − µk ) + log(πk ) k 2 Note 1 1 1 − (x − µk )T Σ−1 (x − µk ) = x T Σ−1 µk − µT Σ−1 µk − x T Σ−1 x 2 2 k 2 Jia Li http://www.stat.psu.edu/∼jiali 

8 .Linear Discriminant Analysis To sum up ˆ (x) = arg max x T Σ−1 µk − 1 µT Σ−1 µk + log(πk ) G k 2 k Define the linear discriminant function 1 δk (x) = x T Σ−1 µk − µT Σ−1 µk + log(πk ) . 2 k Then ˆ (x) = arg max δk (x) . G k The decision boundary between class k and l is: {x : δk (x) = δl (x)} . Or equivalently the following holds πk 1 log − (µk + µl )T Σ−1 (µk − µl ) + x T Σ−1 (µk − µl ) = 0. πl 2 Jia Li http://www.stat.psu.edu/∼jiali 

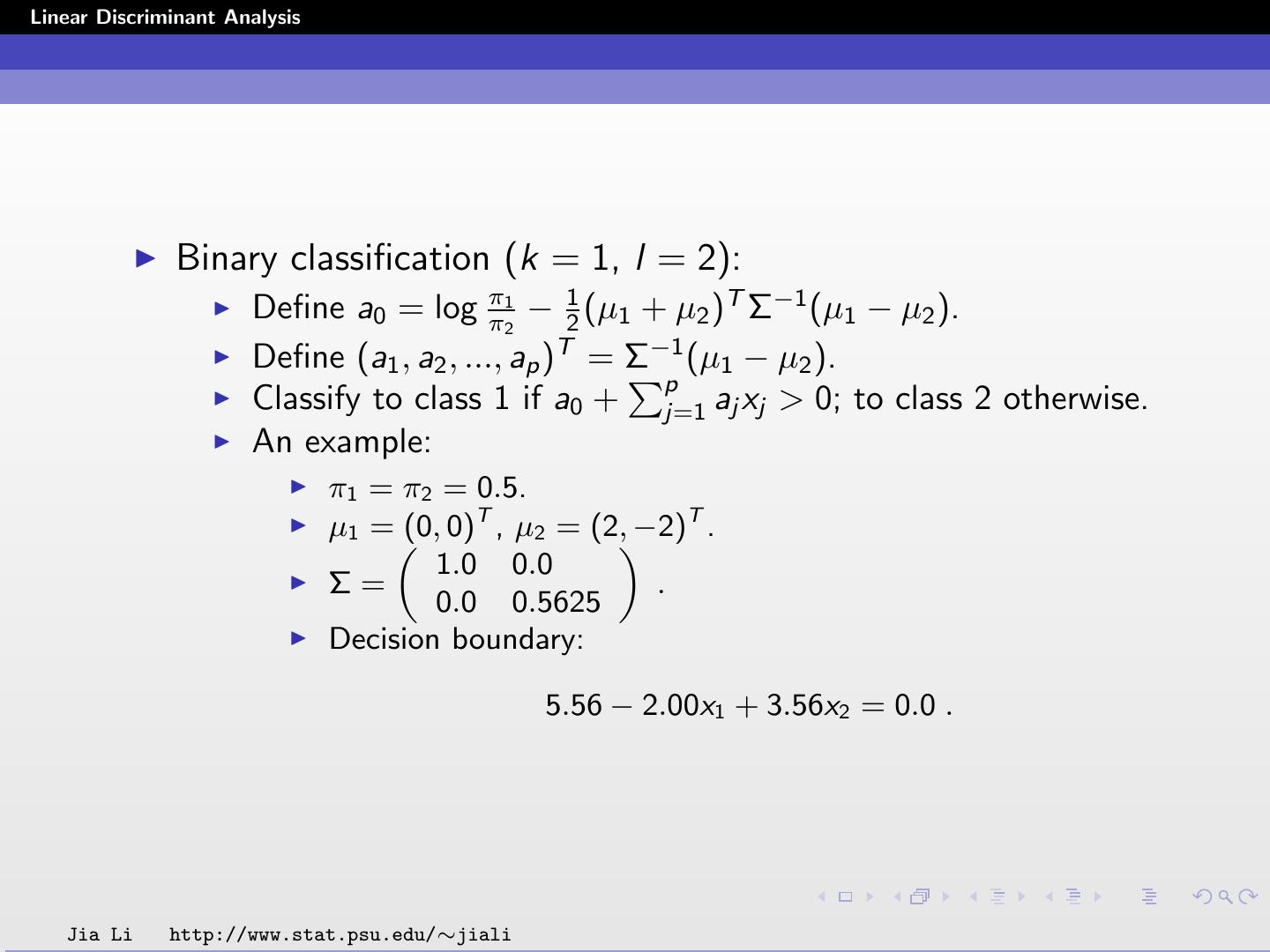
9 .Linear Discriminant Analysis Binary classification (k = 1, l = 2): Define a0 = log ππ12 − 12 (µ1 + µ2 )T Σ−1 (µ1 − µ2 ). Define (a1 , a2 , ..., ap )T = Σ−1 (µ1 − µ2 ). p Classify to class 1 if a0 + j=1 aj xj > 0; to class 2 otherwise. An example: π1 = π2 = 0.5. µ1 =„(0, 0)T , µ2 = (2,«−2)T . 1.0 0.0 Σ= . 0.0 0.5625 Decision boundary: 5.56 − 2.00x1 + 3.56x2 = 0.0 . Jia Li http://www.stat.psu.edu/∼jiali 

10 .Linear Discriminant Analysis Jia Li http://www.stat.psu.edu/∼jiali 

11 .Linear Discriminant Analysis Estimate Gaussian Distributions In practice, we need to estimate the Gaussian distribution. π ˆk = Nk /N, where Nk is the number of class-k samples. µ ˆk = (i) gi =k x /Nk . ˆ= K (i) − µ Σ k=1 gi =k (x ˆk )(x (i) − µ ˆk )T /(N − K ). Note that x (i) denotes the ith sample vector. Jia Li http://www.stat.psu.edu/∼jiali 

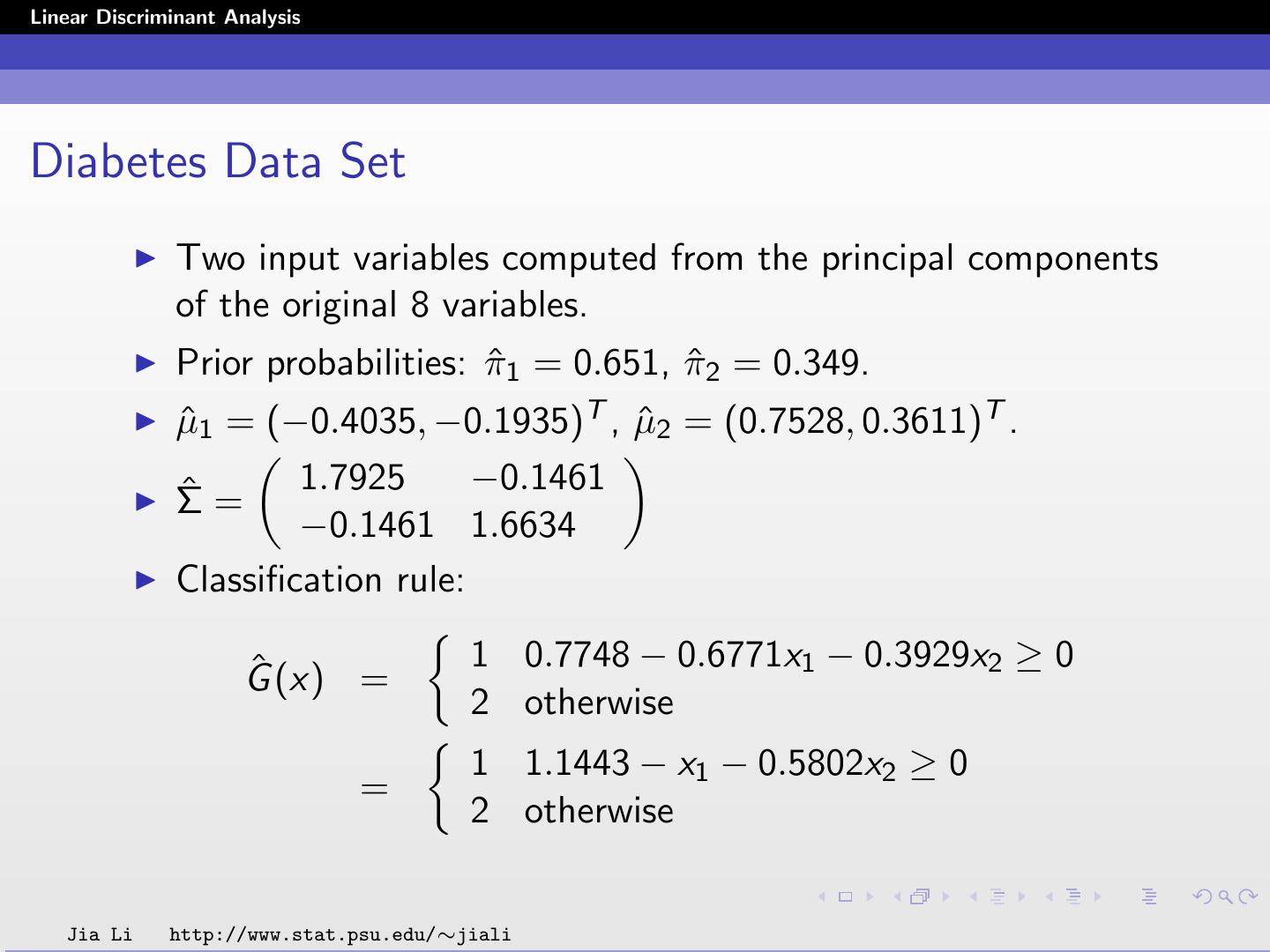
12 .Linear Discriminant Analysis Diabetes Data Set Two input variables computed from the principal components of the original 8 variables. Prior probabilities: π ˆ1 = 0.651, π ˆ2 = 0.349. ˆ1 = (−0.4035, −0.1935)T , µ µ ˆ2 = (0.7528, 0.3611)T . ˆ = 1.7925 −0.1461 Σ −0.1461 1.6634 Classification rule: ˆ (x) = 1 0.7748 − 0.6771x1 − 0.3929x2 ≥ 0 G 2 otherwise 1 1.1443 − x1 − 0.5802x2 ≥ 0 = 2 otherwise Jia Li http://www.stat.psu.edu/∼jiali 

13 .Linear Discriminant Analysis The scatter plot follows. Without diabetes: stars (class 1), with diabetes: circles (class 2). Solid line: classification boundary obtained by LDA. Dash dot line: boundary obtained by linear regression of indicator matrix. Jia Li http://www.stat.psu.edu/∼jiali 

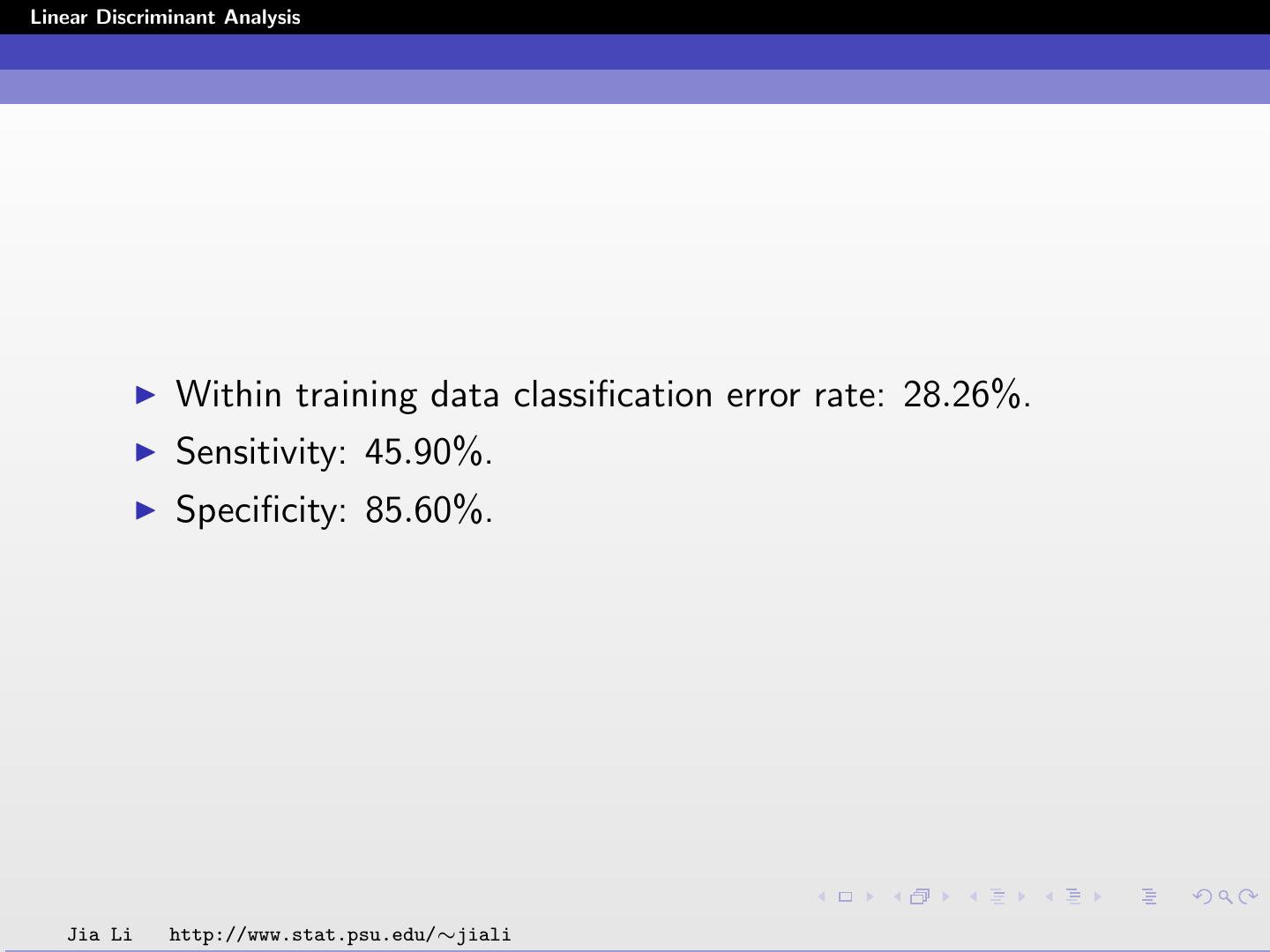
14 .Linear Discriminant Analysis Within training data classification error rate: 28.26%. Sensitivity: 45.90%. Specificity: 85.60%. Jia Li http://www.stat.psu.edu/∼jiali 

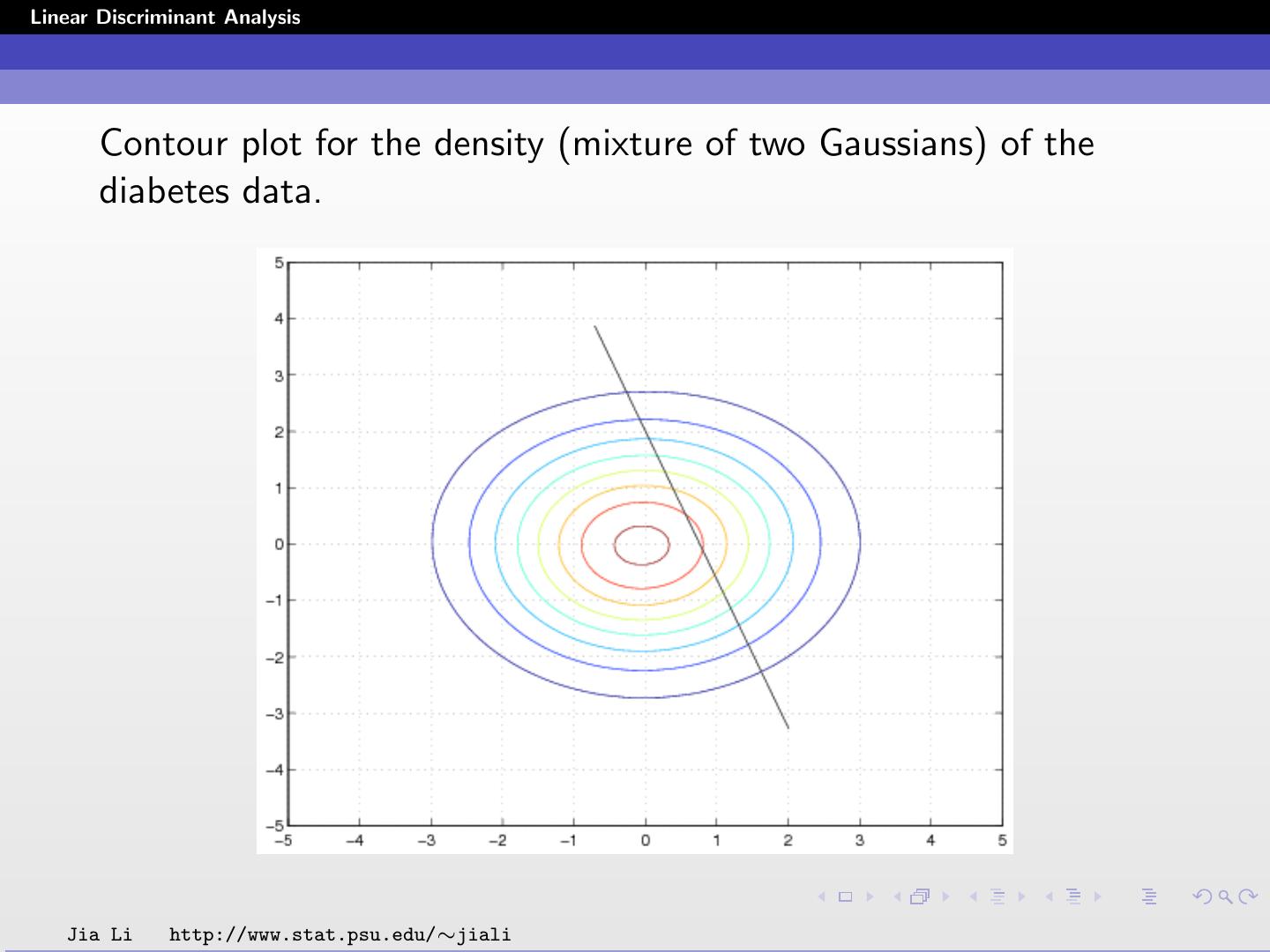
15 .Linear Discriminant Analysis Contour plot for the density (mixture of two Gaussians) of the diabetes data. Jia Li http://www.stat.psu.edu/∼jiali 

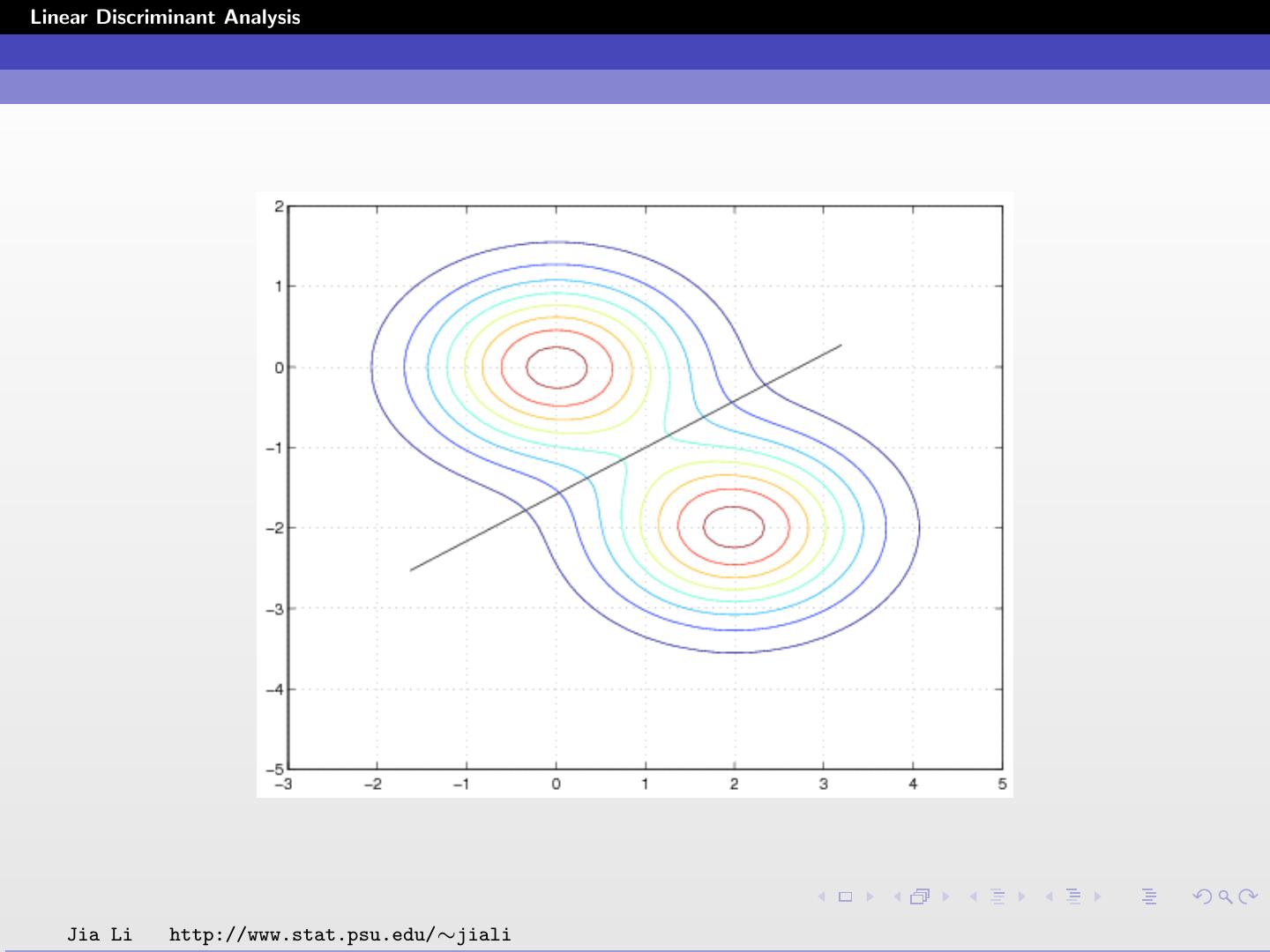
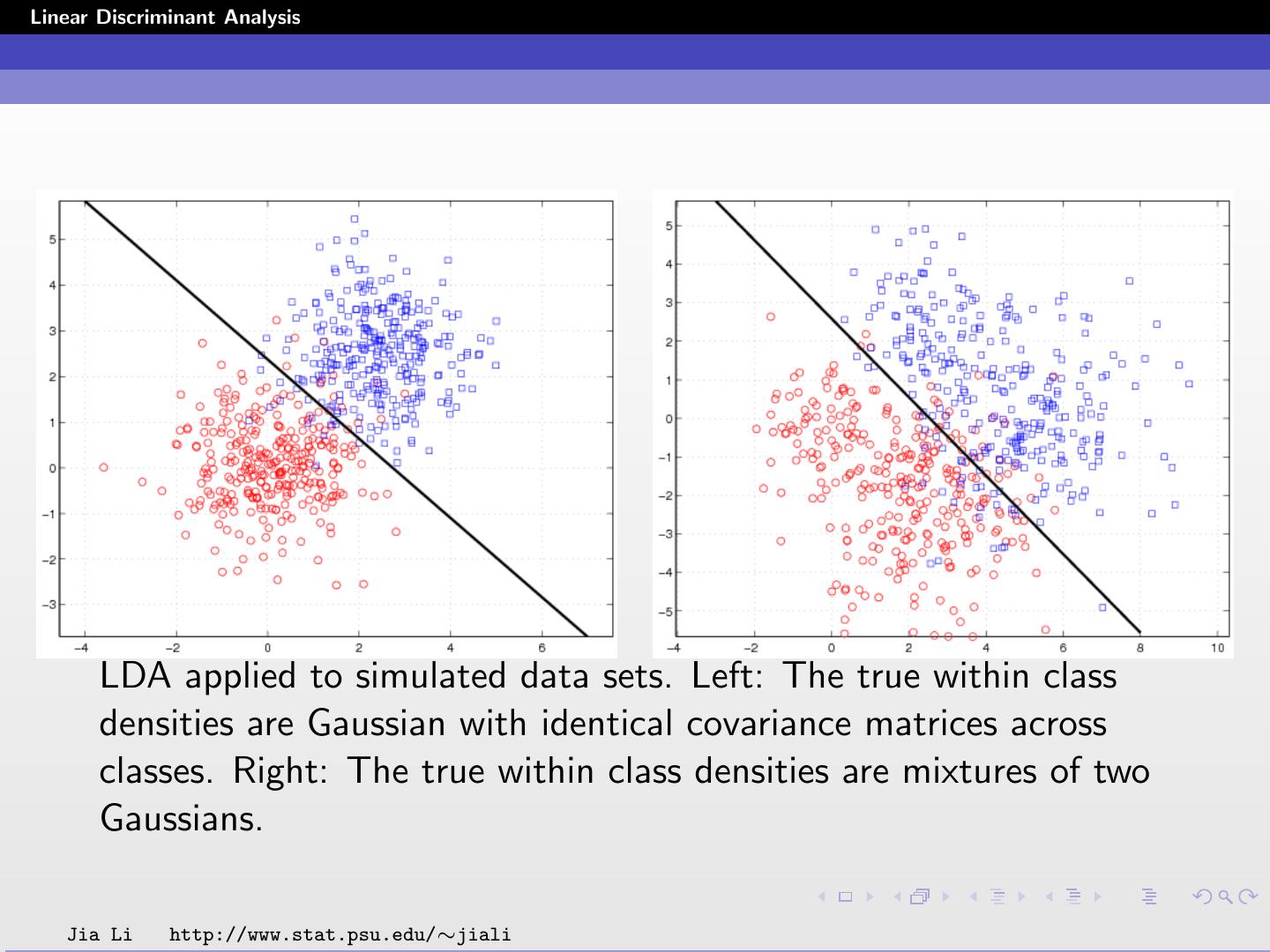
16 .Linear Discriminant Analysis Simulated Examples LDA is not necessarily bad when the assumptions about the density functions are violated. In certain cases, LDA may yield poor results. Jia Li http://www.stat.psu.edu/∼jiali 

17 .Linear Discriminant Analysis LDA applied to simulated data sets. Left: The true within class densities are Gaussian with identical covariance matrices across classes. Right: The true within class densities are mixtures of two Gaussians. Jia Li http://www.stat.psu.edu/∼jiali 

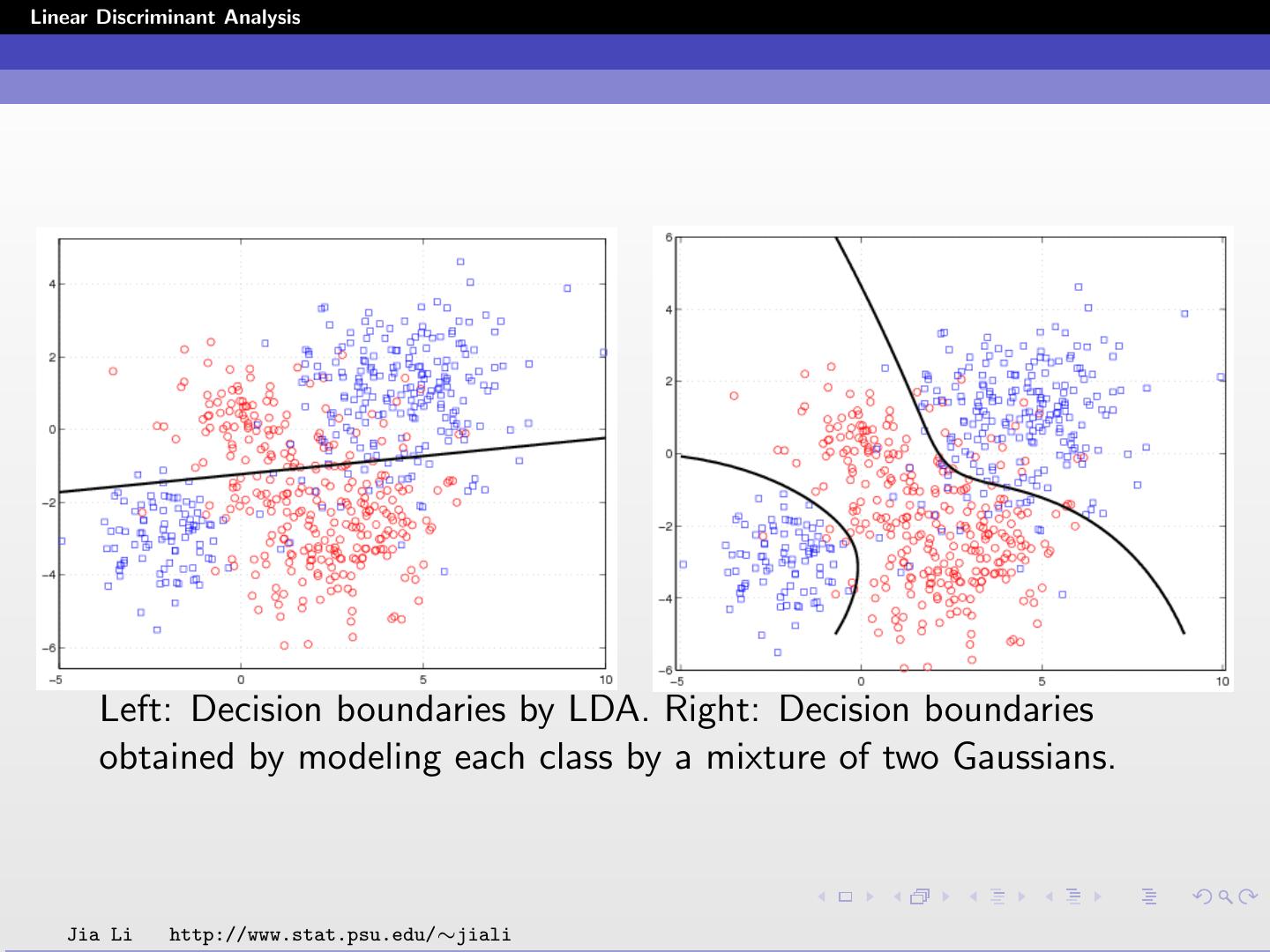
18 .Linear Discriminant Analysis Left: Decision boundaries by LDA. Right: Decision boundaries obtained by modeling each class by a mixture of two Gaussians. Jia Li http://www.stat.psu.edu/∼jiali 

19 .Linear Discriminant Analysis Quadratic Discriminant Analysis (QDA) Estimate the covariance matrix Σk separately for each class k, k = 1, 2, ..., K . Quadratic discriminant function: 1 1 δk (x) = − log |Σk | − (x − µk )T Σ−1 k (x − µk ) + log πk . 2 2 Classification rule: ˆ (x) = arg max δk (x) . G k Decision boundaries are quadratic equations in x. QDA fits the data better than LDA, but has more parameters to estimate. Jia Li http://www.stat.psu.edu/∼jiali 

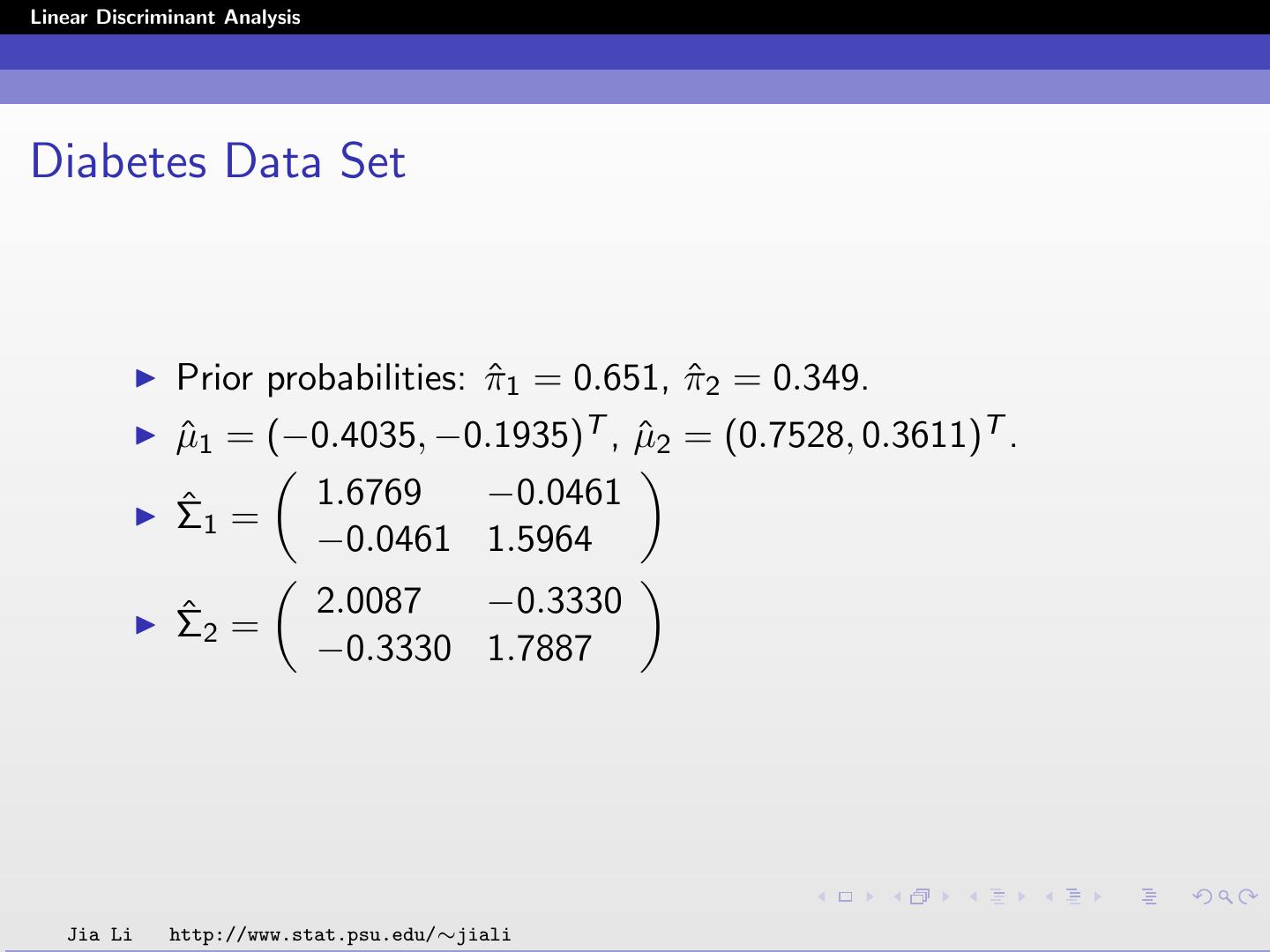
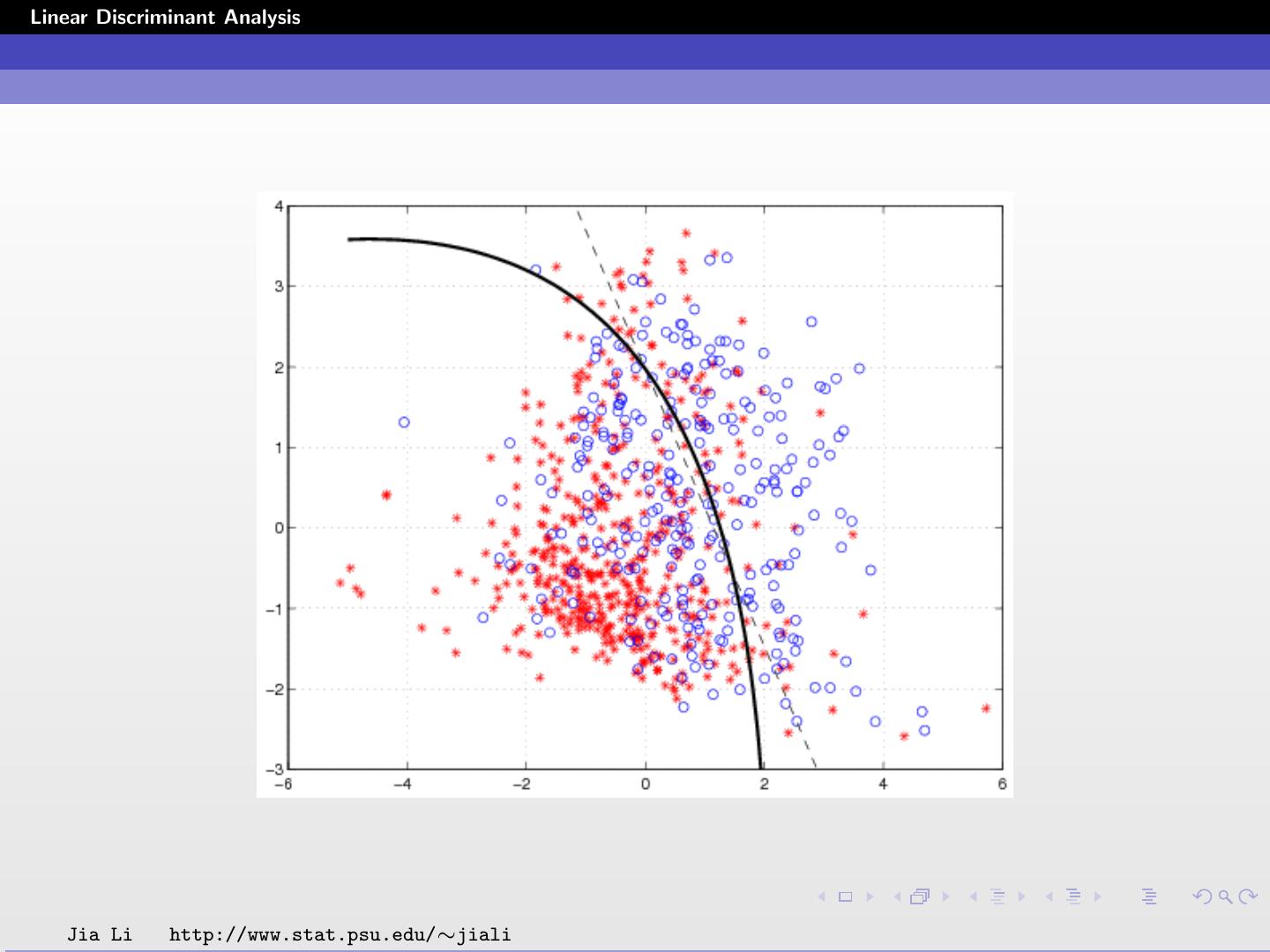
20 .Linear Discriminant Analysis Diabetes Data Set Prior probabilities: π ˆ1 = 0.651, π ˆ2 = 0.349. ˆ1 = (−0.4035, −0.1935)T , µ µ ˆ2 = (0.7528, 0.3611)T . ˆ 1 = 1.6769 −0.0461 Σ −0.0461 1.5964 ˆ2 = 2.0087 −0.3330 Σ −0.3330 1.7887 Jia Li http://www.stat.psu.edu/∼jiali 

21 .Linear Discriminant Analysis Jia Li http://www.stat.psu.edu/∼jiali 

22 .Linear Discriminant Analysis Within training data classification error rate: 29.04%. Sensitivity: 45.90%. Specificity: 84.40%. Sensitivity is the same as that obtained by LDA, but specificity is slightly lower. Jia Li http://www.stat.psu.edu/∼jiali 

23 .Linear Discriminant Analysis LDA on Expanded Basis Expand input space to include X1 X2 , X12 , and X22 . Input is five dimensional: X = (X1 , X2 , X1 X2 , X12 , X22 ).     −0.4035 0.7528   −0.1935     0.3611   µ ˆ1 =   0.0321   µ ˆ2 =   −0.0599    1.8363   2.5680  1.6306 1.9124   1.7925 −0.1461 −0.6254 0.3548 0.5215  −0.1461 1.6634 0.6073 −0.7421 1.2193  ˆ =   Σ  −0.6254 0.6073 3.5751 −1.1118 −0.5044    0.3548 −0.7421 −1.1118 12.3355 −0.0957  0.5215 1.2193 −0.5044 −0.0957 4.4650 Jia Li http://www.stat.psu.edu/∼jiali 

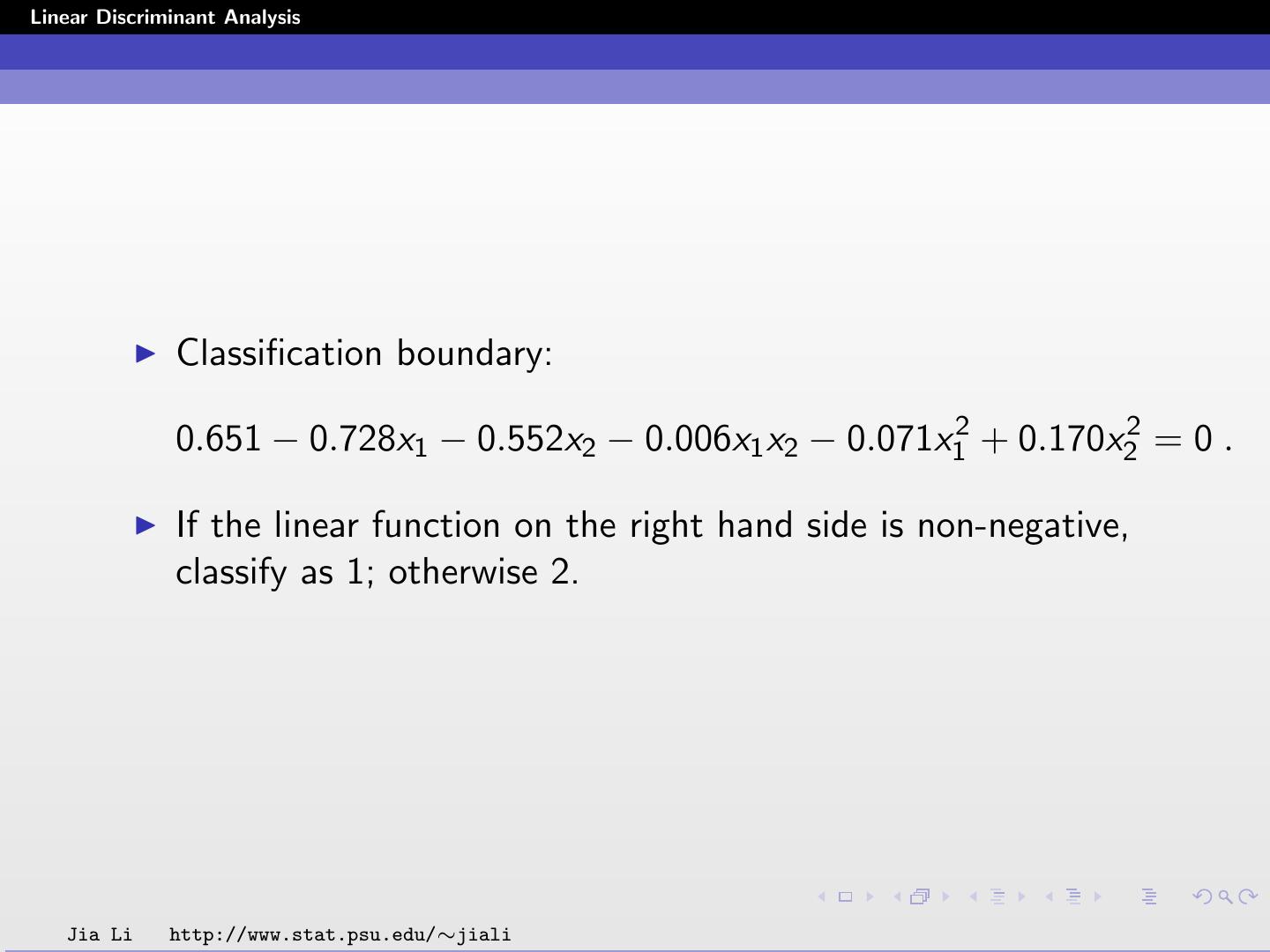
24 .Linear Discriminant Analysis Classification boundary: 0.651 − 0.728x1 − 0.552x2 − 0.006x1 x2 − 0.071x12 + 0.170x22 = 0 . If the linear function on the right hand side is non-negative, classify as 1; otherwise 2. Jia Li http://www.stat.psu.edu/∼jiali 

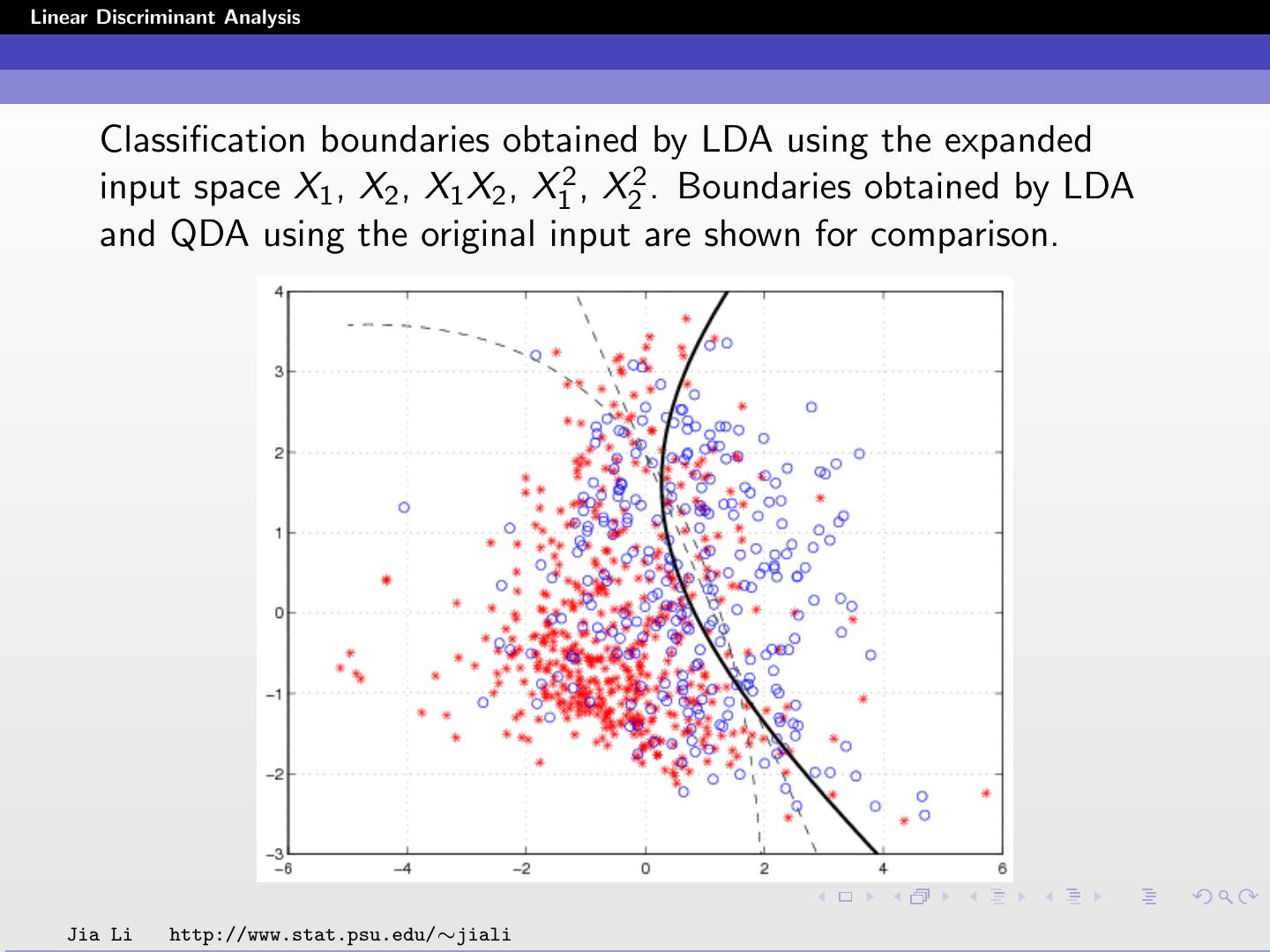
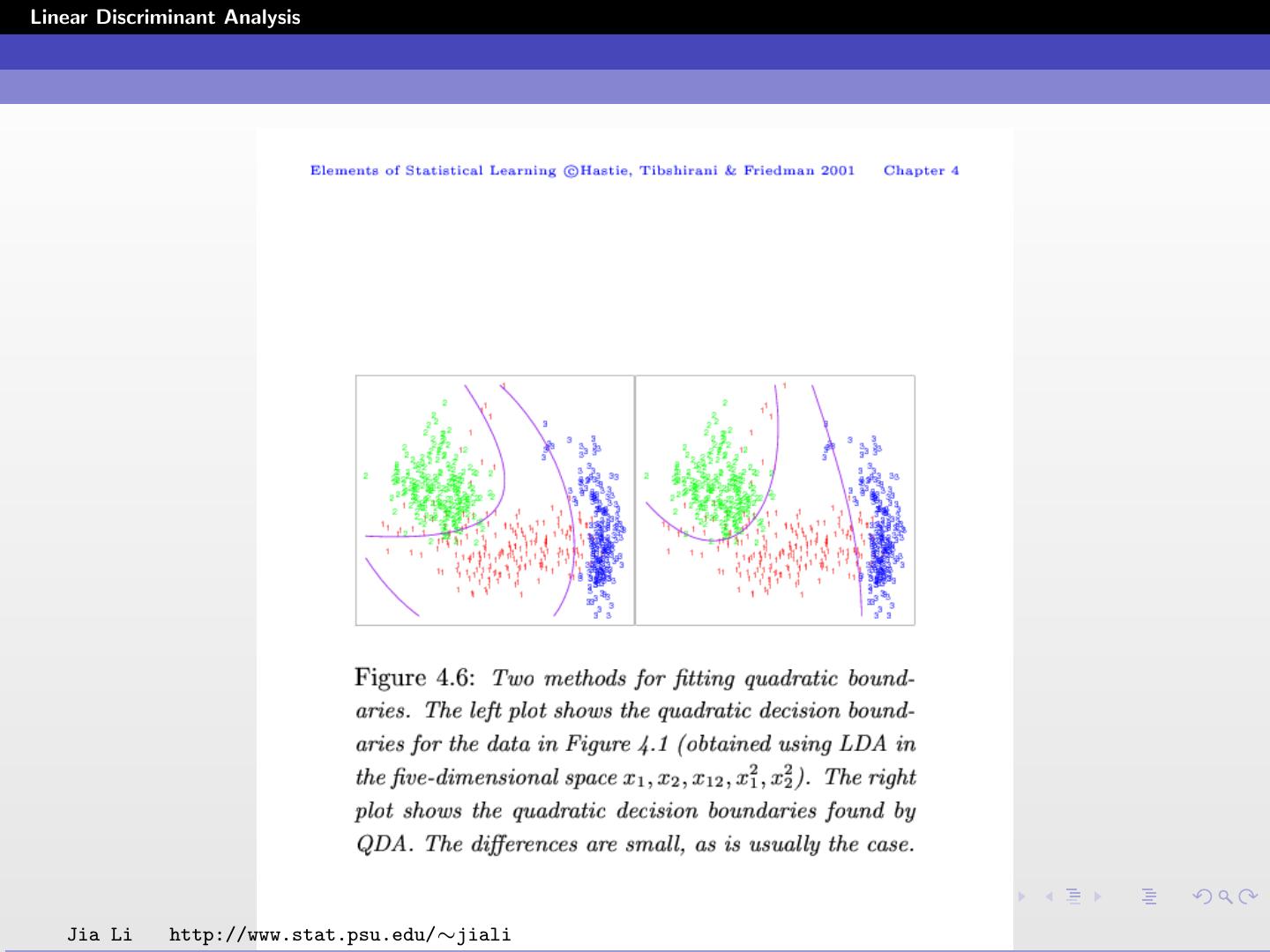
25 .Linear Discriminant Analysis Classification boundaries obtained by LDA using the expanded input space X1 , X2 , X1 X2 , X12 , X22 . Boundaries obtained by LDA and QDA using the original input are shown for comparison. Jia Li http://www.stat.psu.edu/∼jiali 

26 .Linear Discriminant Analysis Within training data classification error rate: 26.82%. Sensitivity: 44.78%. Specificity: 88.40%. The within training data classification error rate is lower than those by LDA and QDA with the original input. Jia Li http://www.stat.psu.edu/∼jiali 

27 .Linear Discriminant Analysis Jia Li http://www.stat.psu.edu/∼jiali