k-center and dendrogram clustering

1 .K-Center and Dendrogram Clustering K-Center and Dendrogram Clustering Jia Li Department of Statistics The Pennsylvania State University Email: jiali@stat.psu.edu http://www.stat.psu.edu/∼jiali Jia Li http://www.stat.psu.edu/∼jiali 

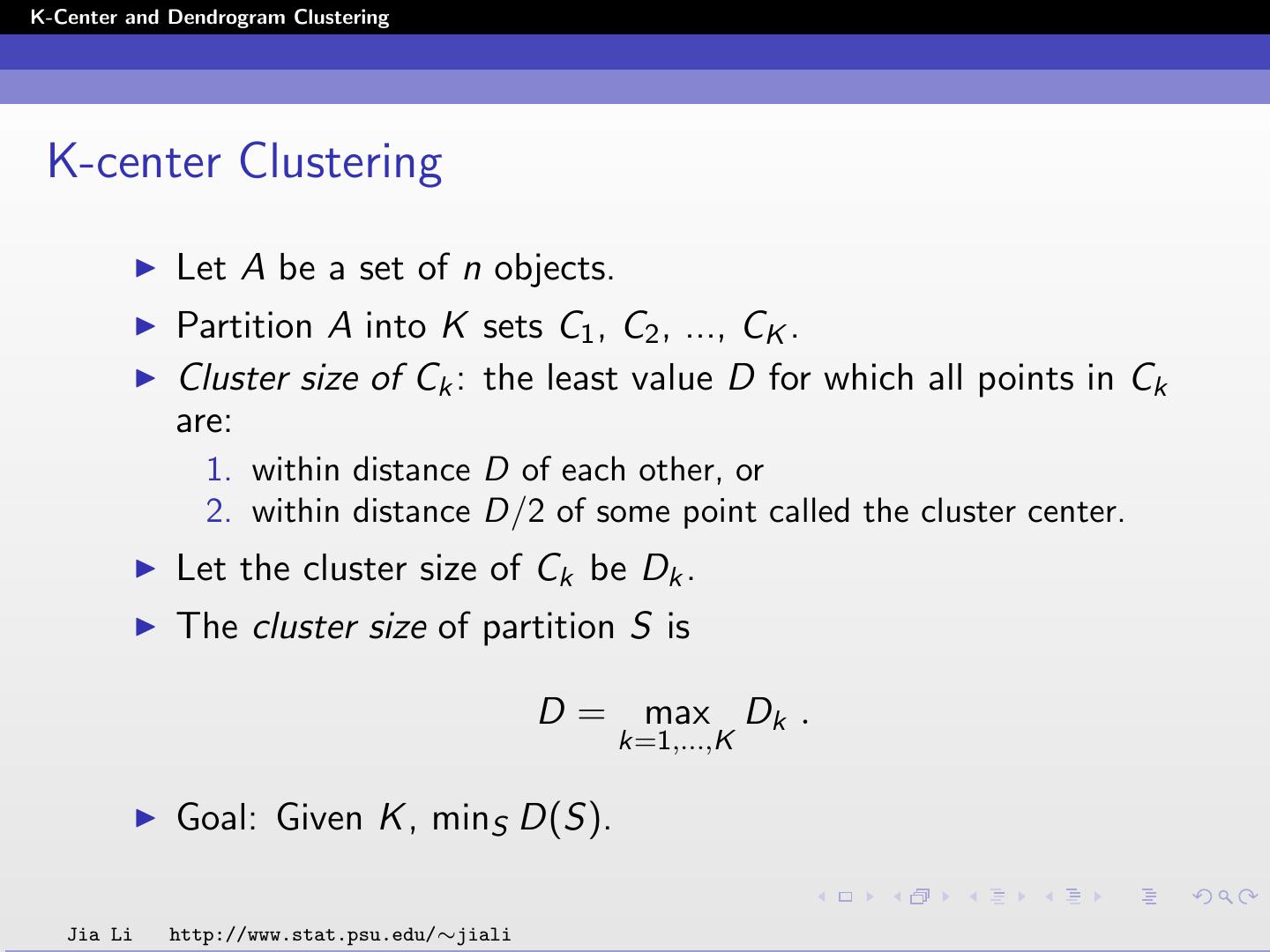
2 .K-Center and Dendrogram Clustering K-center Clustering Let A be a set of n objects. Partition A into K sets C1 , C2 , ..., CK . Cluster size of Ck : the least value D for which all points in Ck are: 1. within distance D of each other, or 2. within distance D/2 of some point called the cluster center. Let the cluster size of Ck be Dk . The cluster size of partition S is D = max Dk . k=1,...,K Goal: Given K , minS D(S). Jia Li http://www.stat.psu.edu/∼jiali 

3 .K-Center and Dendrogram Clustering Comparison with k-means Assume the distance between vectors is the squared Euclidean distance. K-means: K min (xi − µk )T (xi − µk ) S k=1 i:xi ∈Ck where µk is the centroid for cluster Ck . In particular, 1 µk = xi . Nk i:xi ∈Ck K-center: min max max (xi − µk )T (xi − µk ) . S k=1,...,K i:xi ∈Ck where µk is called the “centroid”, but may not be the mean vector. Jia Li http://www.stat.psu.edu/∼jiali 

4 .K-Center and Dendrogram Clustering Another formulation of k-center: min max max L(xi , xj ) . S k=1,...,K i,j:xi ,xj ∈Ck L(xi , xj ) denotes any distance between a pair of objects. Jia Li http://www.stat.psu.edu/∼jiali 

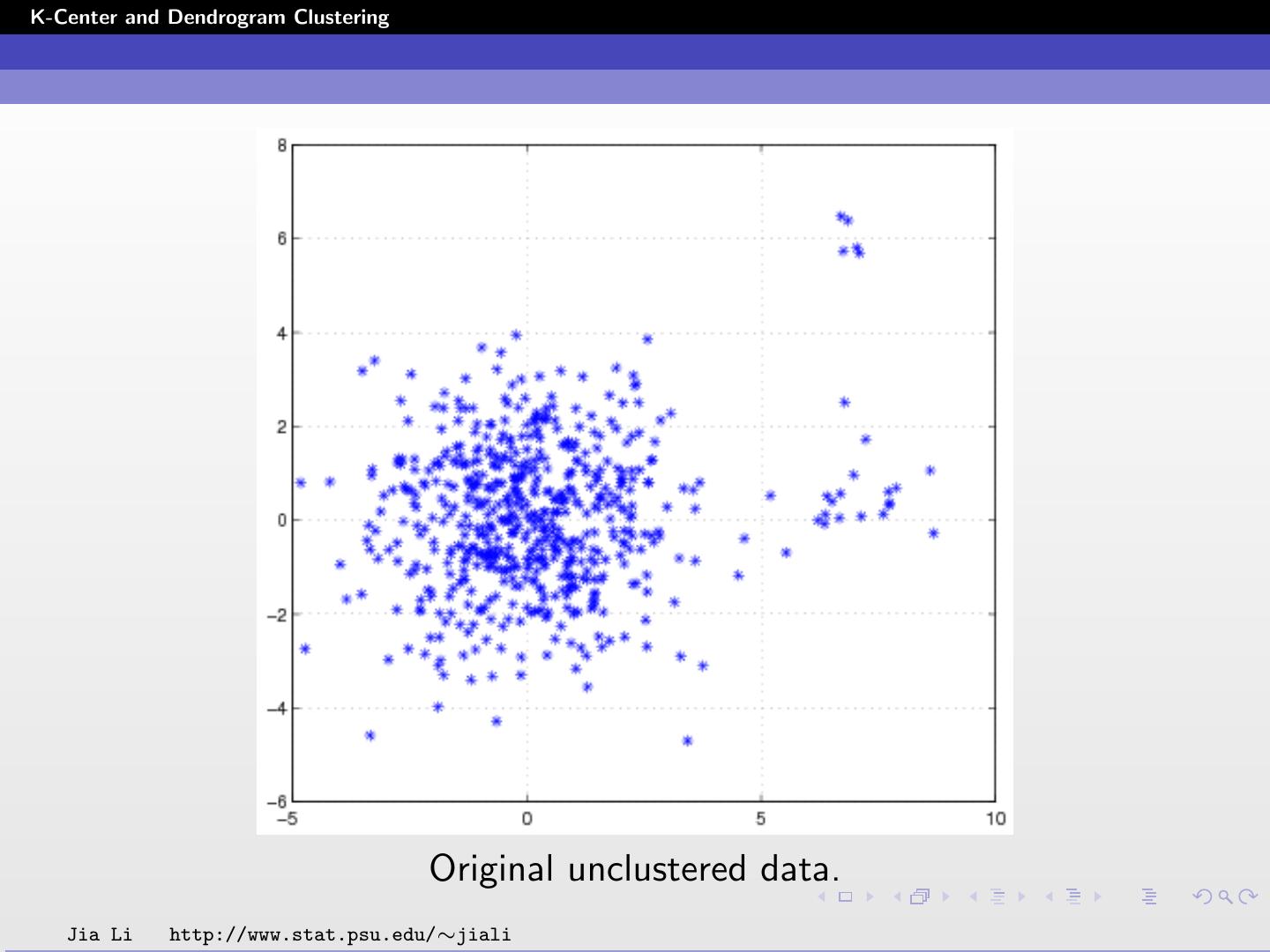
5 .K-Center and Dendrogram Clustering Original unclustered data. Jia Li http://www.stat.psu.edu/∼jiali 

6 .K-Center and Dendrogram Clustering Clustering by k-means. K-means Clustering by k-center. K-center focuses on average distance. focuses on worst scenario. Jia Li http://www.stat.psu.edu/∼jiali 

7 .K-Center and Dendrogram Clustering Greedy Algorithm Choose a subset H from S consisting K points that are farthest apart from each other. Each point hk ∈ H represents one cluster Ck . Point xi is partitioned into cluster Ck if L(xi , hk ) = min L(xi , hk ) . k =1,...,K Only need pairwise distance L(xi , xj ) for any xi , xj ∈ S. Hence, xi can be a non-vector representation of the objects. Jia Li http://www.stat.psu.edu/∼jiali 

8 .K-Center and Dendrogram Clustering The greedy algorithm achieves an approximation factor of 2 as long as the distance measure L satisfies the triangle inequality. That is, if D ∗ = min max max L(xi , xj ) S k=1,...,K i,j:xi ,xj ∈Ck then the greedy algorithm guarantees that D ≤ 2D ∗ . The relation holds if the cluster size is defined in the sense of centralized clustering. Jia Li http://www.stat.psu.edu/∼jiali 

9 .K-Center and Dendrogram Clustering Pseudo Code H denotes the set of cluster representative objects {h1 , ..., hk } ⊂ S. Let cluster (xi ) be the identity of the cluster xi ∈ S belongs to. Let dist(xi ) be the distance between xi and its closest cluster representative object: dist(xi ) = min L(xi , hj ) . hj ∈H Jia Li http://www.stat.psu.edu/∼jiali 

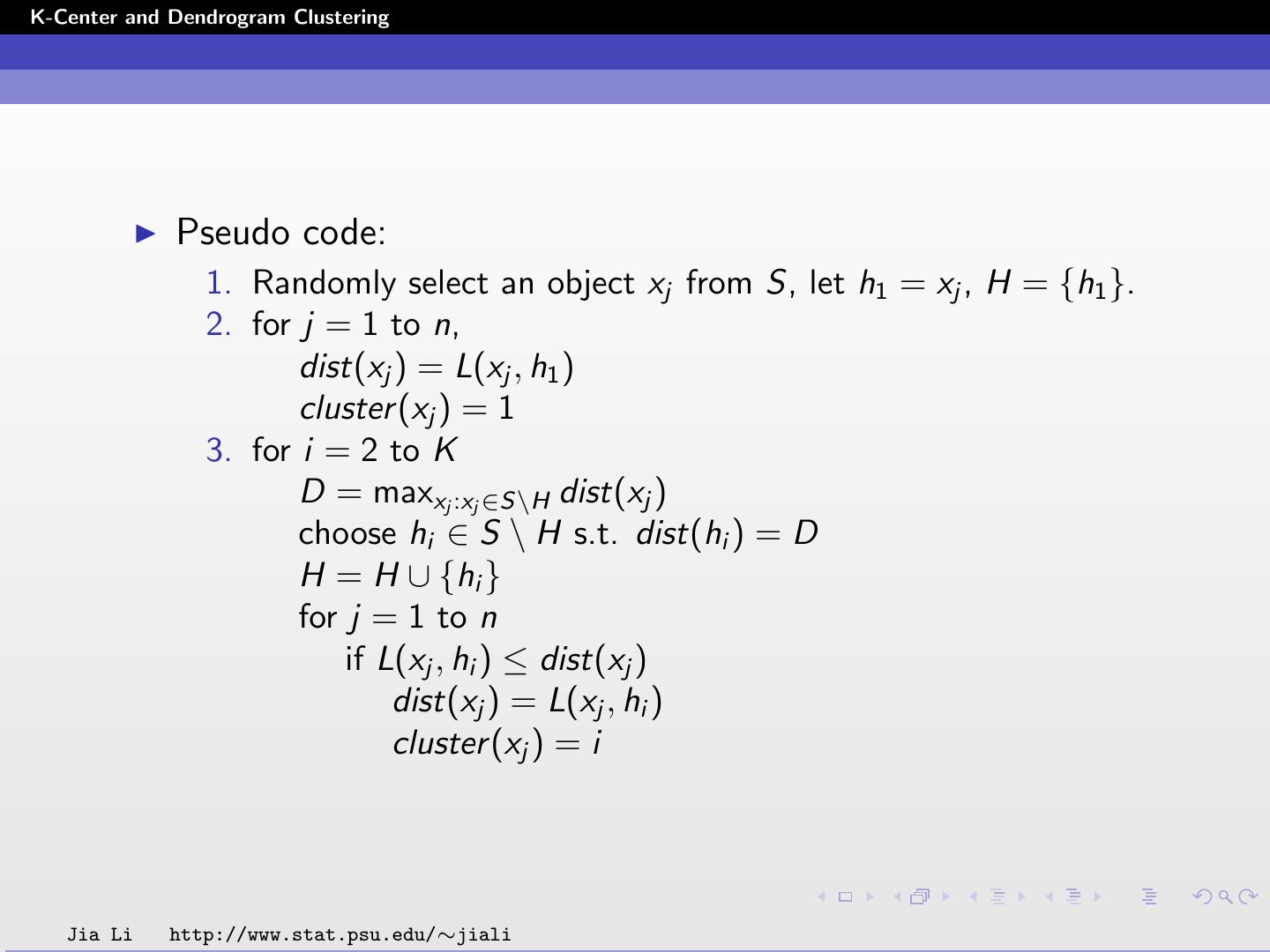
10 .K-Center and Dendrogram Clustering Pseudo code: 1. Randomly select an object xj from S, let h1 = xj , H = {h1 }. 2. for j = 1 to n, dist(xj ) = L(xj , h1 ) cluster (xj ) = 1 3. for i = 2 to K D = maxxj :xj ∈S\H dist(xj ) choose hi ∈ S \ H s.t. dist(hi ) = D H = H ∪ {hi } for j = 1 to n if L(xj , hi ) ≤ dist(xj ) dist(xj ) = L(xj , hi ) cluster (xj ) = i Jia Li http://www.stat.psu.edu/∼jiali 

11 .K-Center and Dendrogram Clustering Algorithm Property The running time of the algorithm is O(Kn). Let the partition obtained by the greedy algorithm be S˜ and the optimal partition be S ∗ . Let the cluster size of S˜ be D˜ and that of S ∗ be D ∗ . The cluster size is defined in the pairwise distance sense. It can be proved that D ˜ ≤ 2D ∗ . We have the approximation factor of 2 result if cluster size of a partition S is defined in the sense of centralized clustering. Jia Li http://www.stat.psu.edu/∼jiali 

12 .K-Center and Dendrogram Clustering Key Ideas for Proof Let Dj be the cluster size of the partition generated by {h1 , ..., hj }. D1 ≥ D2 ≥ D3 · · · . For ∀i < j, L(hi , hj ) ≥ Dj−1 . For ∀j, ∃i < j, s.t., L(hi , hj ) = Dj−1 . Consider optimal partition S ∗ with k clusters and the minimum size D ∗ . Suppose the greedy algorithm generates centroids {h1 , ..., hk , hk+1 }. By the pigeonhole principle, at least two centroids fall into one cluster of the partition S ∗ . Let the two centroids be 1 ≤ i < j ≤ k + 1. Then L(hi , hj ) ≤ 2D ∗ , by the triangle inequality, and the fact they lie in the same cluster. Also L(hi , hj ) ≥ Dj−1 ≥ Dk . Thus Dk ≤ 2D ∗ . Jia Li http://www.stat.psu.edu/∼jiali 

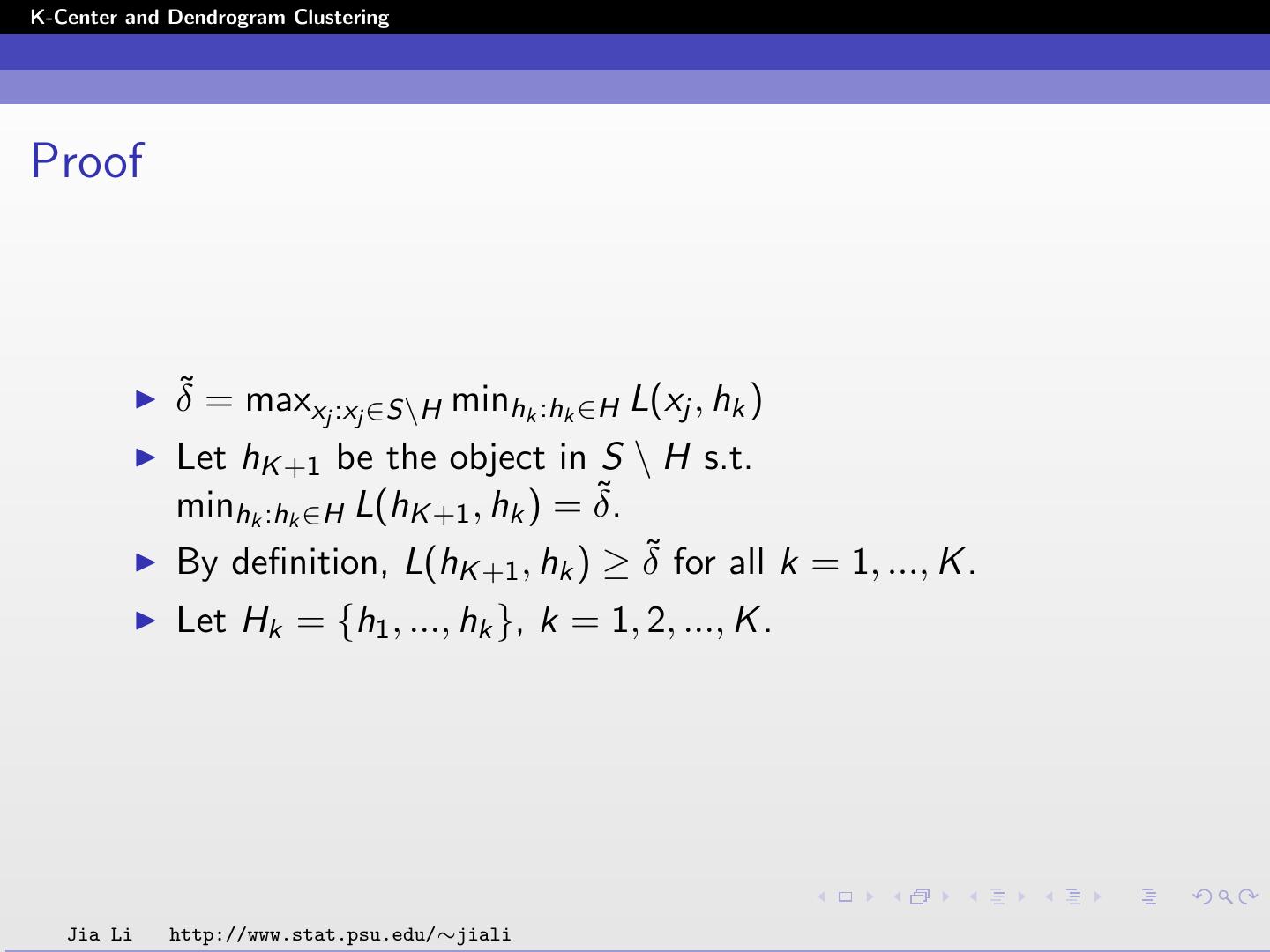
13 .K-Center and Dendrogram Clustering Proof δ˜ = maxxj :xj ∈S\H minhk :hk ∈H L(xj , hk ) Let hK +1 be the object in S \ H s.t. ˜ minhk :hk ∈H L(hK +1 , hk ) = δ. By definition, L(hK +1 , hk ) ≥ δ˜ for all k = 1, ..., K . Let Hk = {h1 , ..., hk }, k = 1, 2, ..., K . Jia Li http://www.stat.psu.edu/∼jiali 

14 .K-Center and Dendrogram Clustering Consider the distance between any hi and hj , i < j ≤ K without loss of generality. According to the greedy algorithm: min L(hj , hk ) ≥ min L(xl , hk ) hk :hk ∈Hj−1 hk :hk ∈Hj−1 for any xl ∈ S \ Hj . Since hK +1 ∈ S \ H and S \ H ⊂ S \ Hj , L(hj , hi ) ≥ min L(hj , hk ) hk :hk ∈Hj−1 ≥ min L(hK +1 , hk ) hk :hk ∈Hj−1 ≥ min L(hK +1 , hk ) hk :hk ∈H = δ˜ Jia Li http://www.stat.psu.edu/∼jiali 

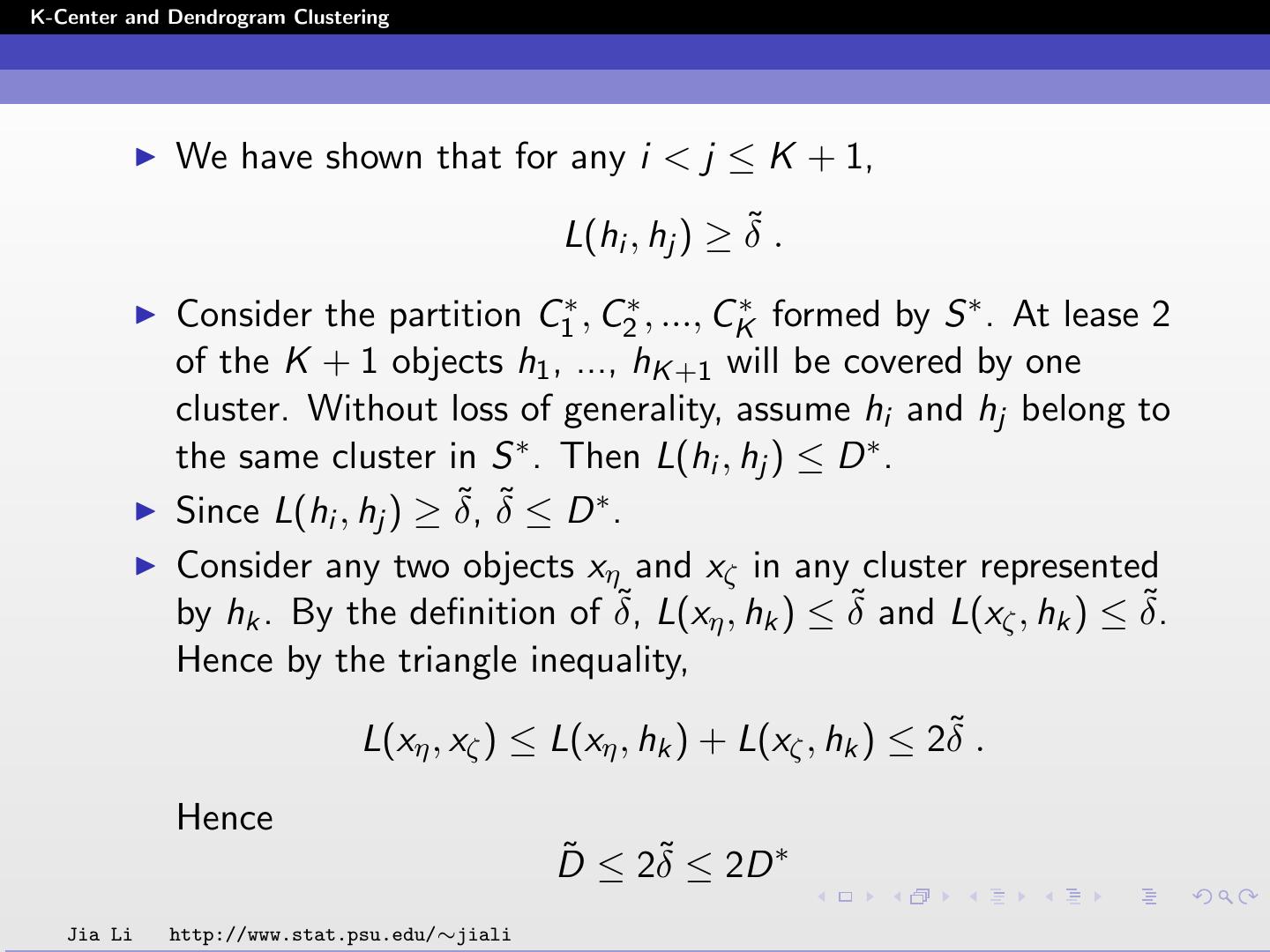
15 .K-Center and Dendrogram Clustering We have shown that for any i < j ≤ K + 1, L(hi , hj ) ≥ δ˜ . Consider the partition C1∗ , C2∗ , ..., CK∗ formed by S ∗ . At lease 2 of the K + 1 objects h1 , ..., hK +1 will be covered by one cluster. Without loss of generality, assume hi and hj belong to the same cluster in S ∗ . Then L(hi , hj ) ≤ D ∗ . ˜ δ˜ ≤ D ∗ . Since L(hi , hj ) ≥ δ, Consider any two objects xη and xζ in any cluster represented by hk . By the definition of δ,˜ L(xη , hk ) ≤ δ˜ and L(xζ , hk ) ≤ δ. ˜ Hence by the triangle inequality, L(xη , xζ ) ≤ L(xη , hk ) + L(xζ , hk ) ≤ 2δ˜ . Hence ˜ ≤ 2δ˜ ≤ 2D ∗ D Jia Li http://www.stat.psu.edu/∼jiali 

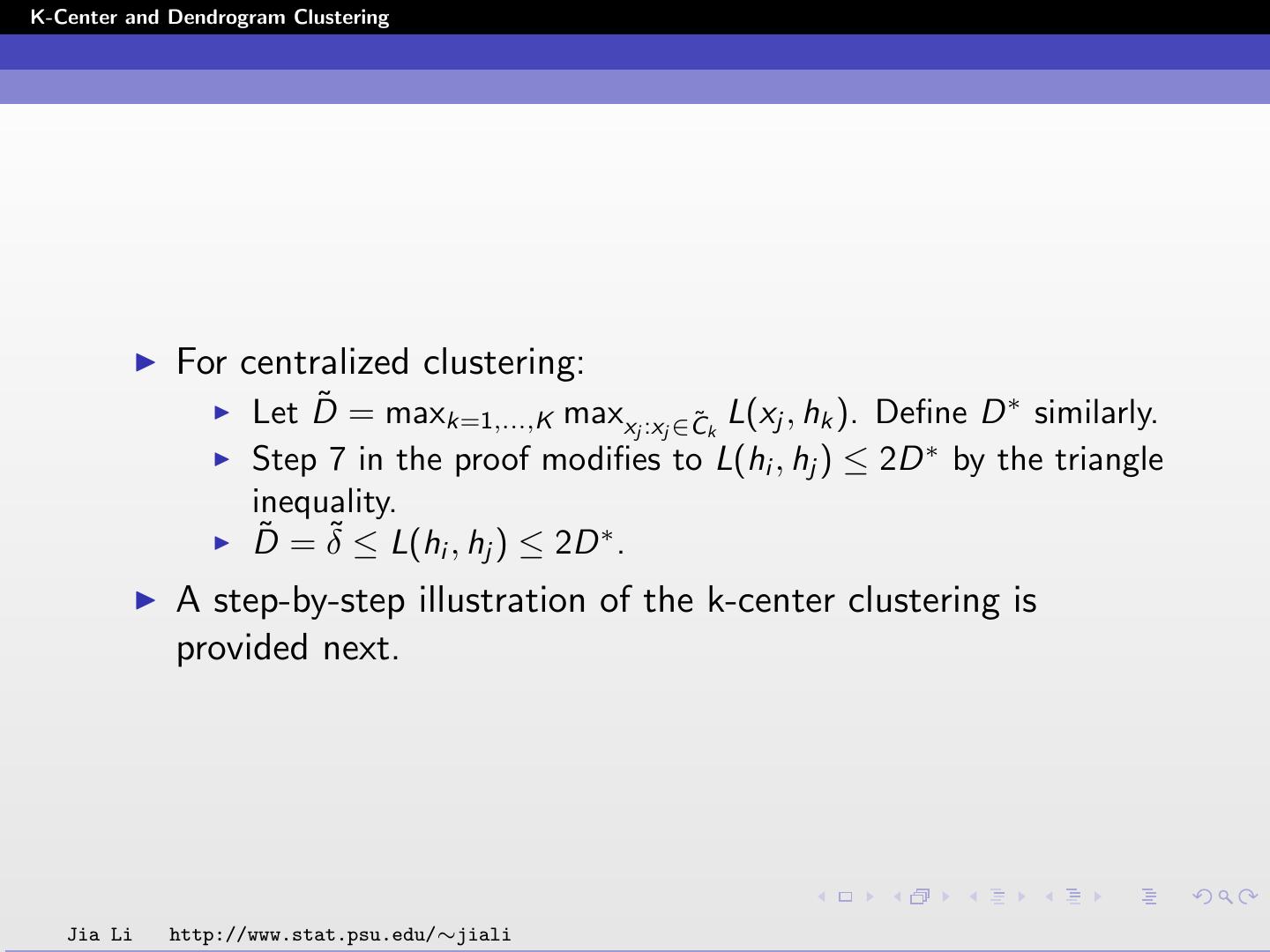
16 .K-Center and Dendrogram Clustering For centralized clustering: ˜ = maxk=1,...,K max Let D ∗ ˜k L(xj , hk ). Define D similarly. xj :xj ∈C ∗ Step 7 in the proof modifies to L(hi , hj ) ≤ 2D by the triangle inequality. D˜ = δ˜ ≤ L(hi , hj ) ≤ 2D ∗ . A step-by-step illustration of the k-center clustering is provided next. Jia Li http://www.stat.psu.edu/∼jiali 

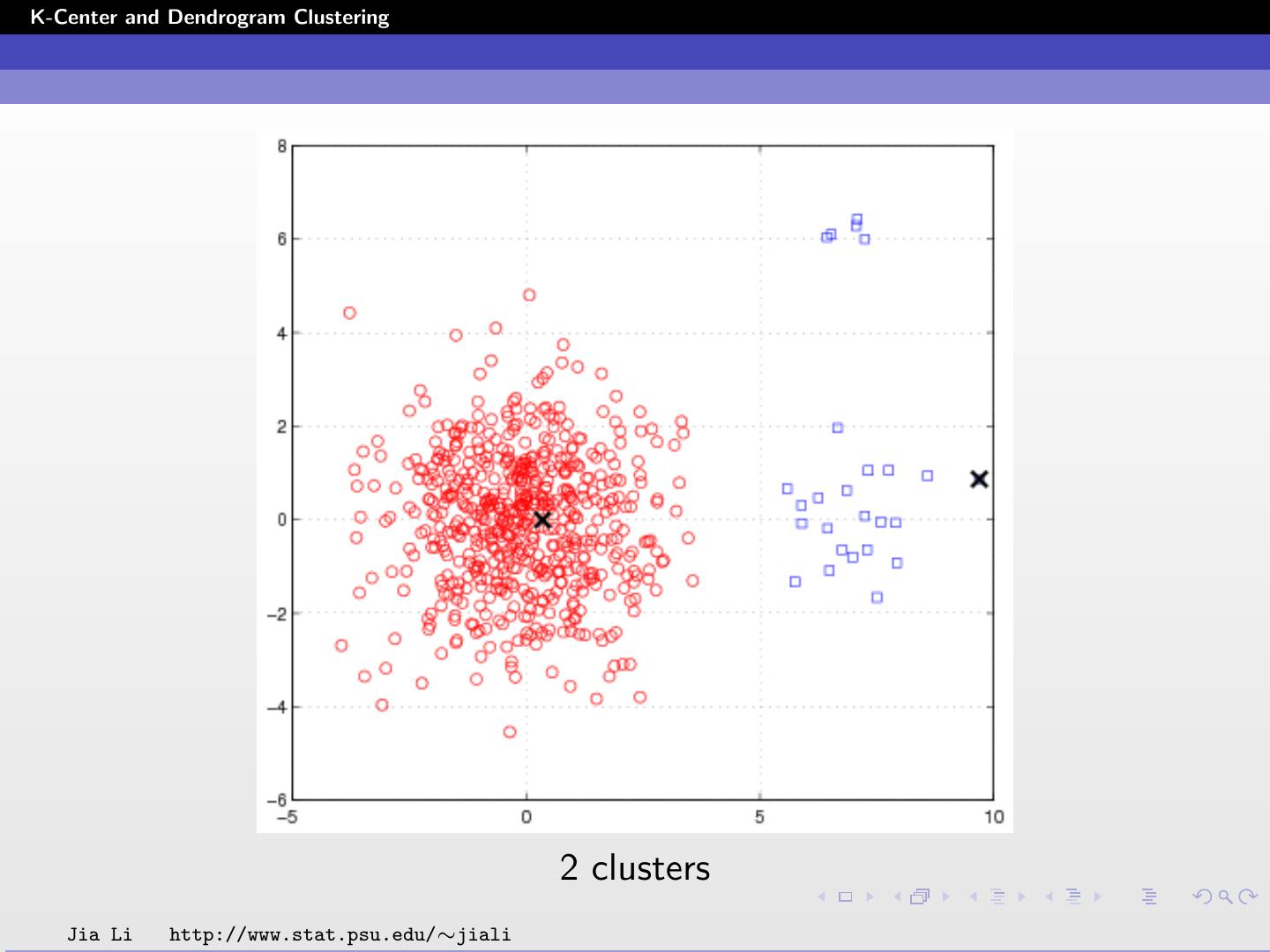
17 .K-Center and Dendrogram Clustering 2 clusters Jia Li http://www.stat.psu.edu/∼jiali 

18 .K-Center and Dendrogram Clustering 3 clusters Jia Li http://www.stat.psu.edu/∼jiali 

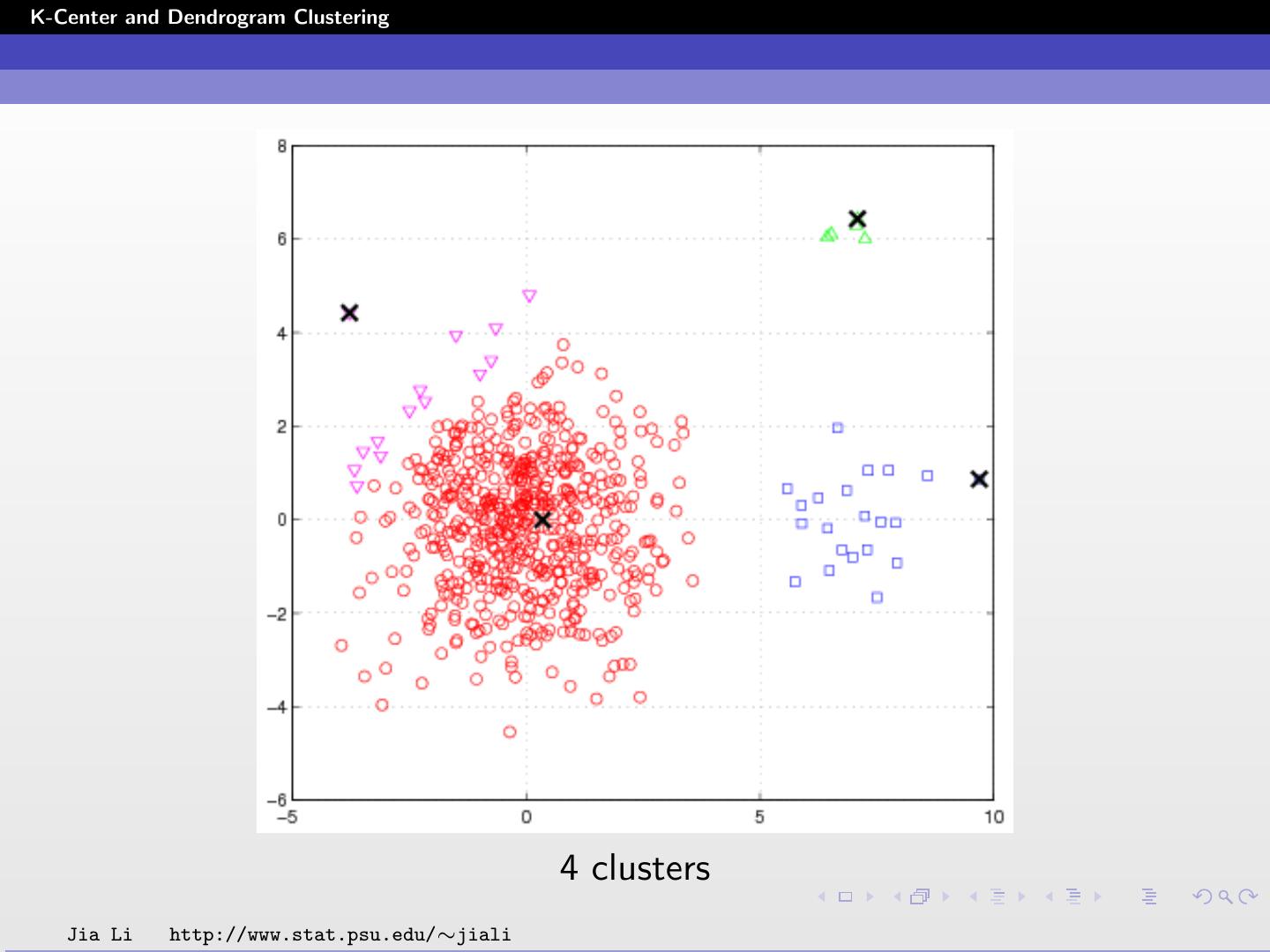
19 .K-Center and Dendrogram Clustering 4 clusters Jia Li http://www.stat.psu.edu/∼jiali 

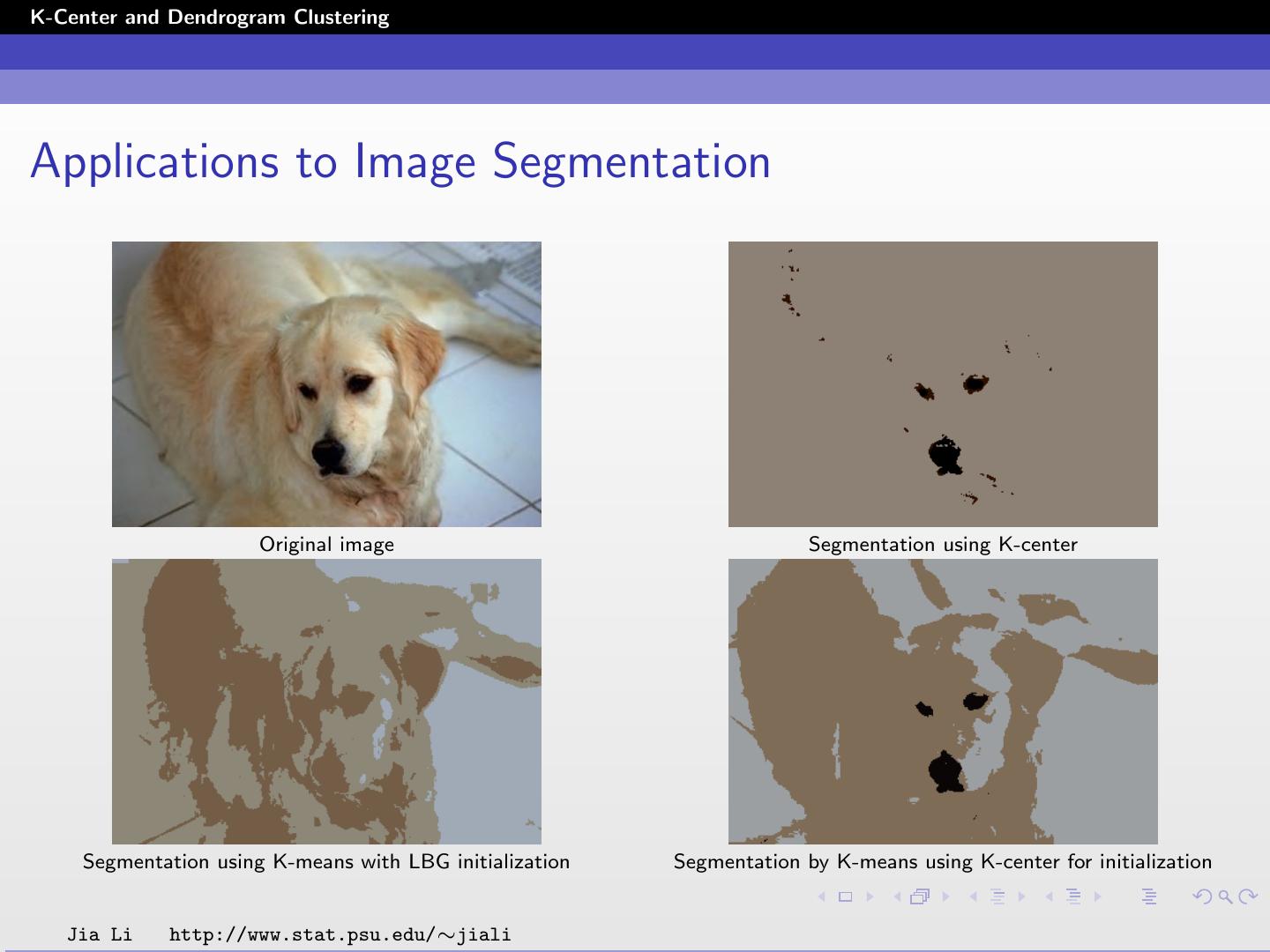
20 .K-Center and Dendrogram Clustering Applications to Image Segmentation Original image Segmentation using K-center Segmentation using K-means with LBG initialization Segmentation by K-means using K-center for initialization Jia Li http://www.stat.psu.edu/∼jiali 

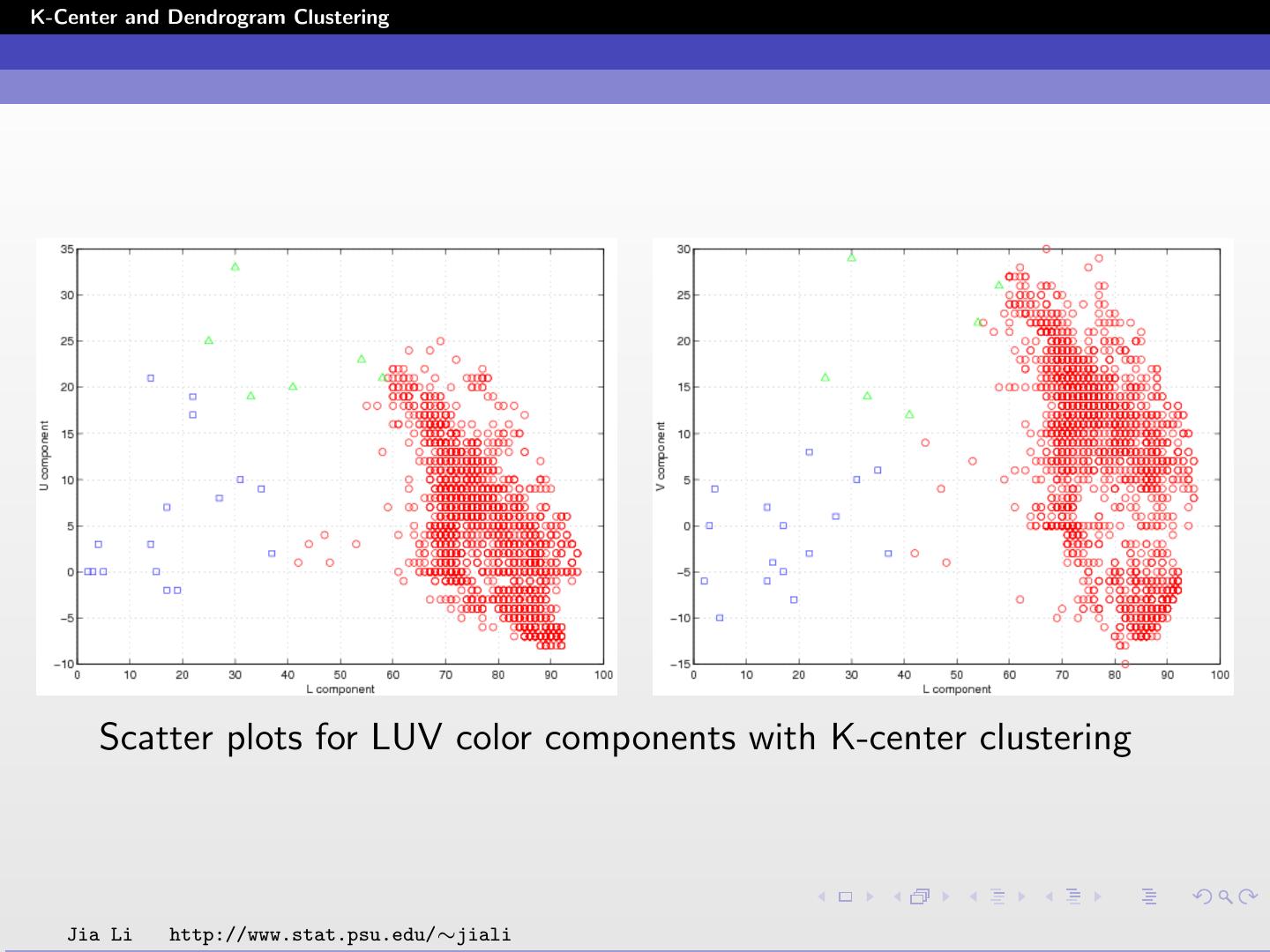
21 .K-Center and Dendrogram Clustering Scatter plots for LUV color components with K-center clustering Jia Li http://www.stat.psu.edu/∼jiali 

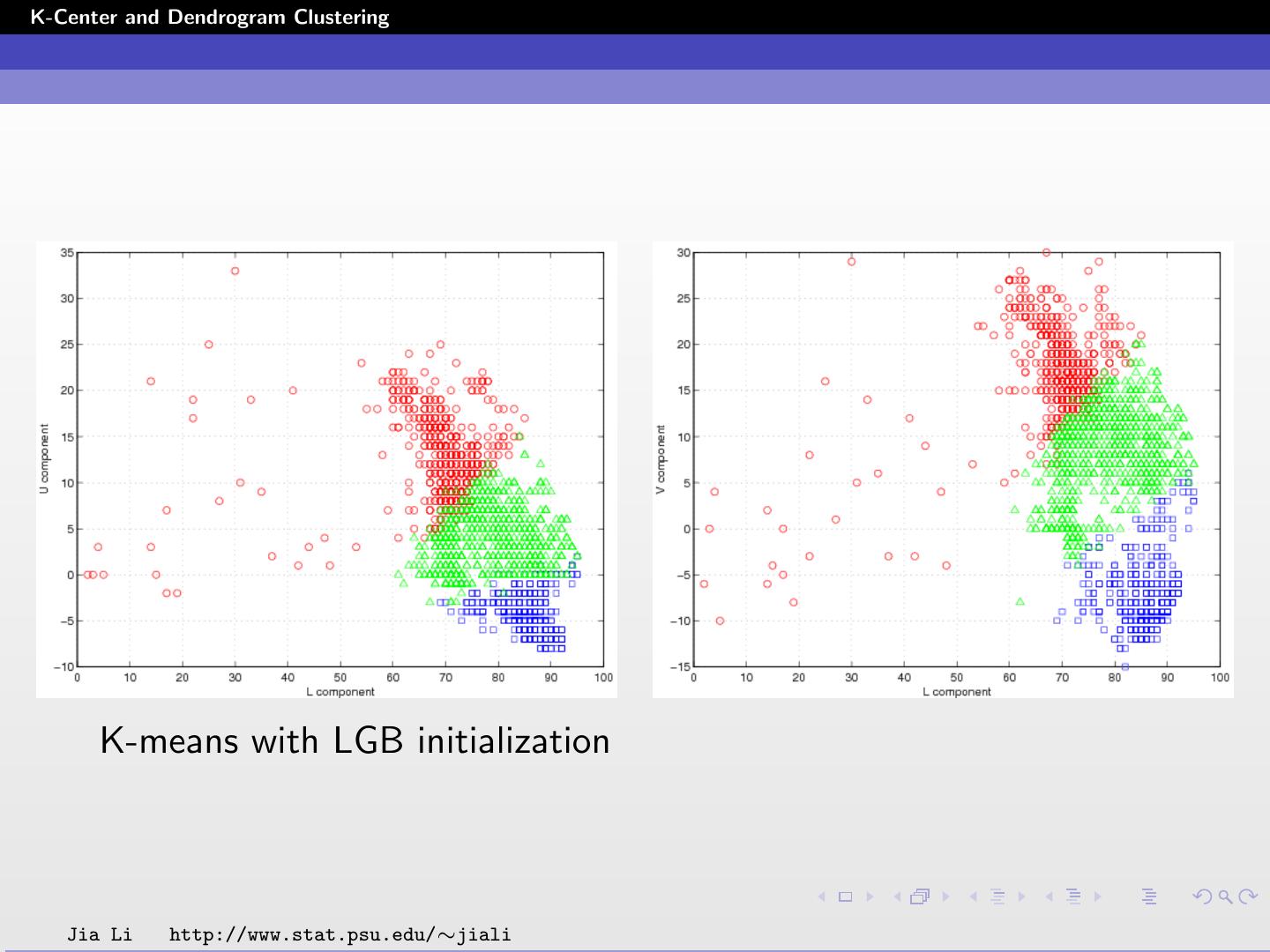
22 .K-Center and Dendrogram Clustering K-means with LGB initialization Jia Li http://www.stat.psu.edu/∼jiali 

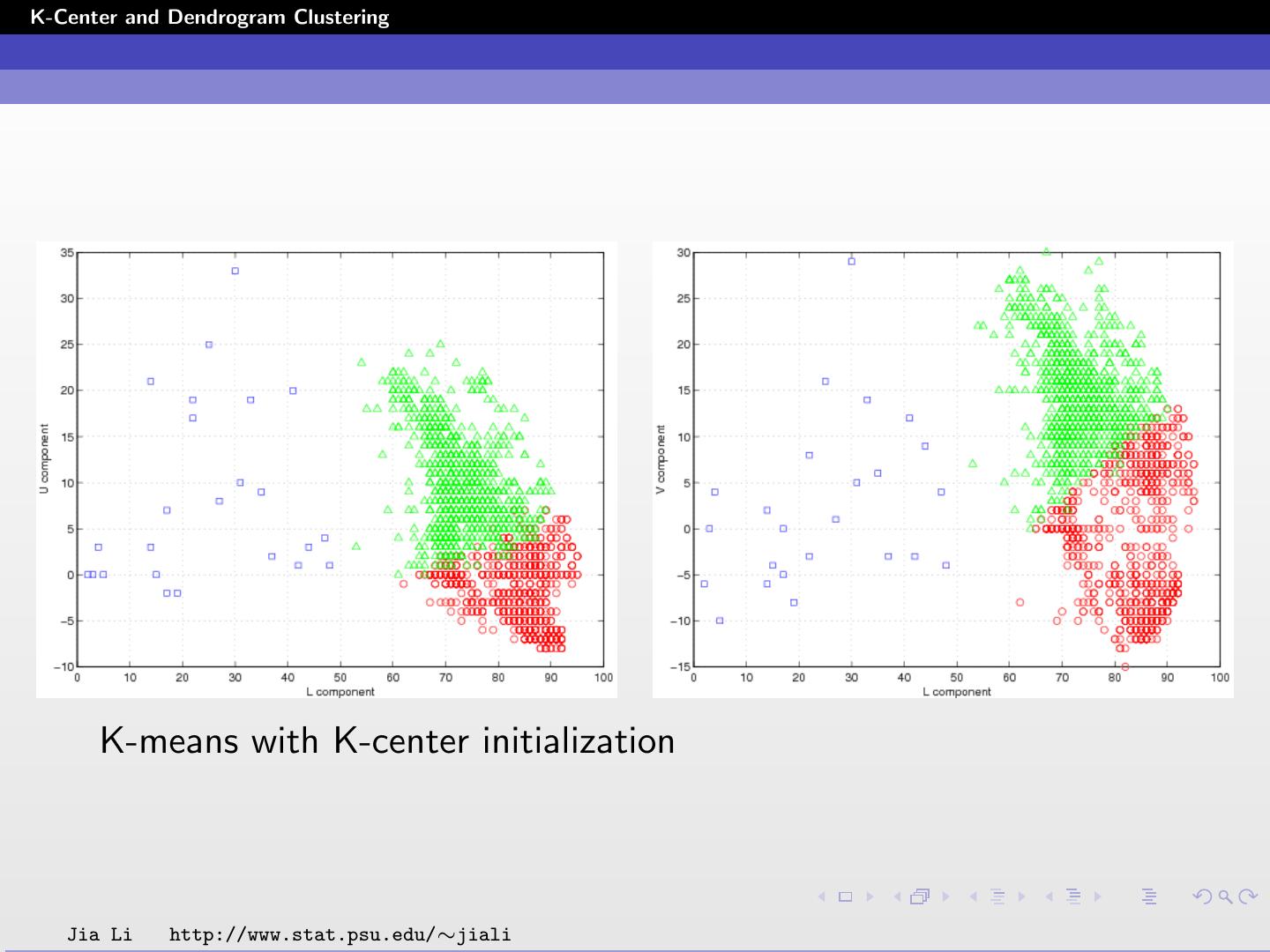
23 .K-Center and Dendrogram Clustering K-means with K-center initialization Jia Li http://www.stat.psu.edu/∼jiali 

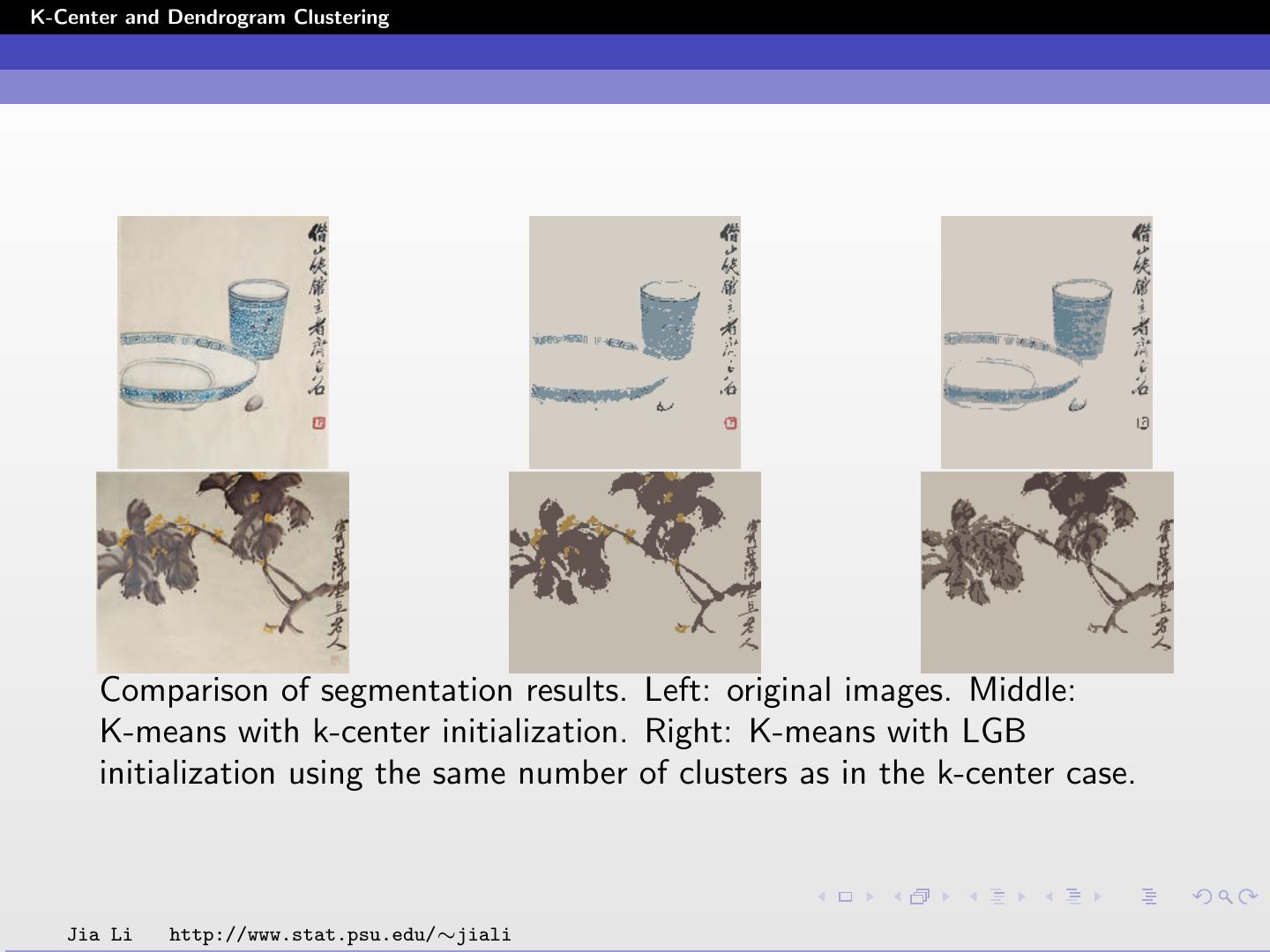
24 .K-Center and Dendrogram Clustering Comparison of segmentation results. Left: original images. Middle: K-means with k-center initialization. Right: K-means with LGB initialization using the same number of clusters as in the k-center case. Jia Li http://www.stat.psu.edu/∼jiali 

25 .K-Center and Dendrogram Clustering Comparison of segmentation results. Left: original images. Middle: K-means with k-center initialization. Right: K-means with LGB initialization using the same number of clusters as in the k-center case. Jia Li http://www.stat.psu.edu/∼jiali 

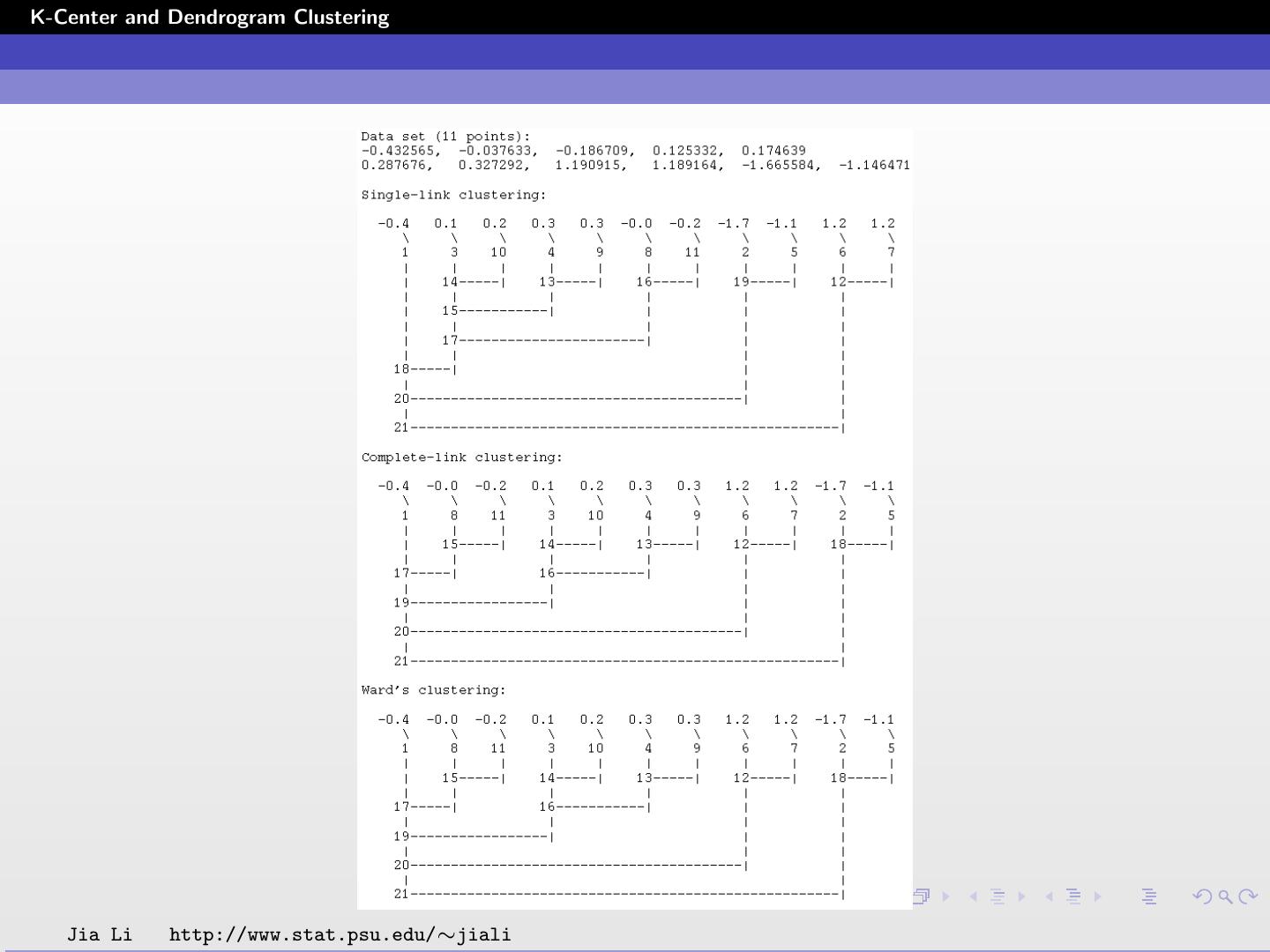
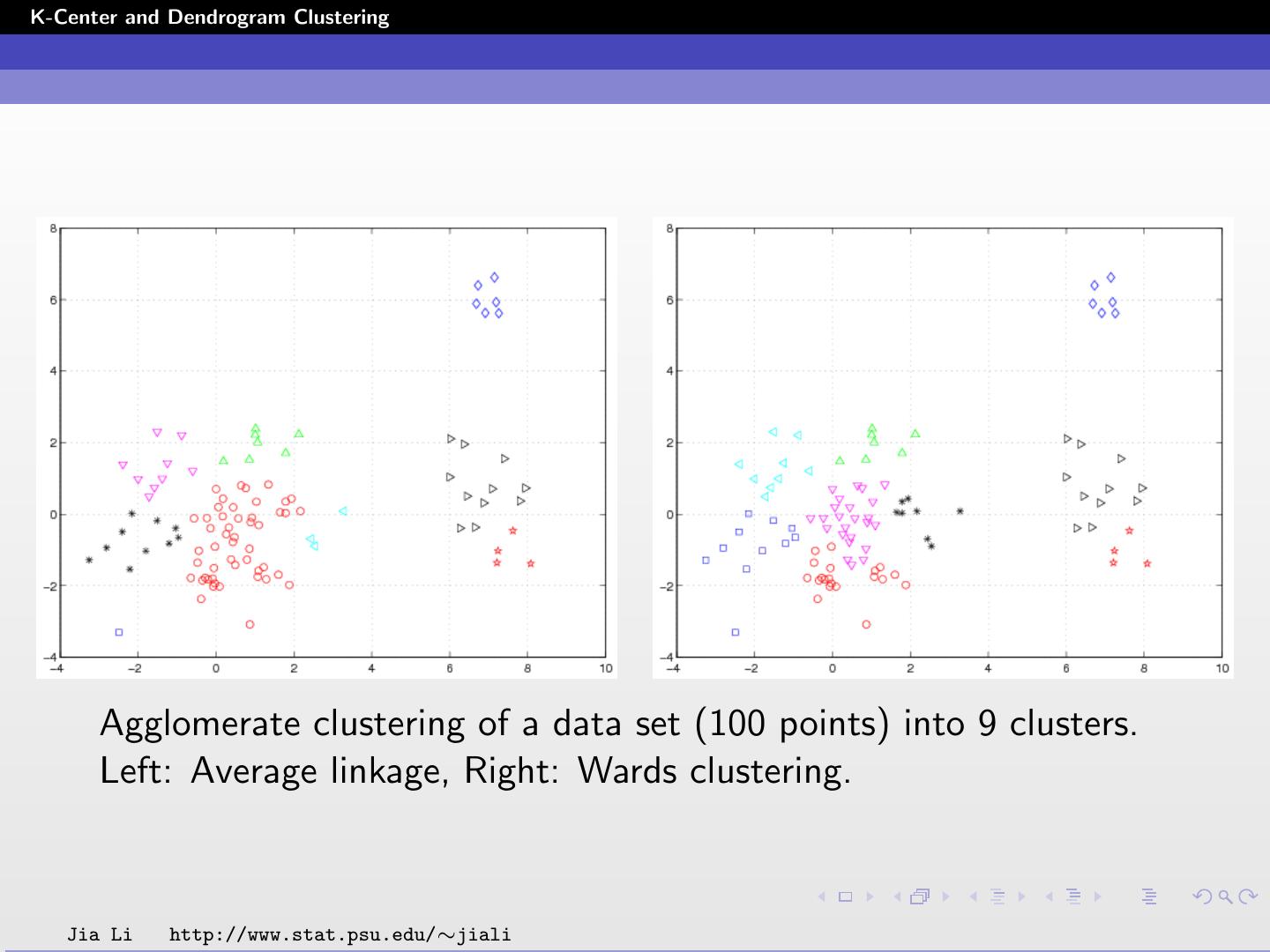
26 .K-Center and Dendrogram Clustering Agglomerative Clustering Generate clusters in a hierarchical way. Let the data set be A = {x1 , ..., xn }. Start with n clusters, each containing one data point. Merge the two clusters with minimum pairwise distance. Update between-cluster distance. Iterate the merging procedure. The clustering procedure can be visualized by a tree structure called dendrogram. Jia Li http://www.stat.psu.edu/∼jiali 

27 .K-Center and Dendrogram Clustering Definition for between-cluster distance? For clusters containing only one data point, the between-cluster distance is the between-object distance. For clusters containing multiple data points, the between-cluster distance is an agglomerative version of the between-object distances. Examples: minimum or maximum between-objects distances for objects in the two clusters. The agglomerative between-cluster distance can often be computed recursively. Jia Li http://www.stat.psu.edu/∼jiali 

28 .K-Center and Dendrogram Clustering Example Distances Suppose cluster r and s are two clusters merged into a new cluster t. Let k be any other cluster. Denote between-cluster distance by D(·, ·). How to get D(t, k) from D(r , k) and D(s, k)? Single-link clustering: D(t, k) = min(D(r , k), D(s, k)) D(t, k) is the minimum distance between two objects in cluster t and k respectively. Complete-link clustering: D(t, k) = max(D(r , k), D(s, k)) D(t, k) is the maximum distance between two objects in cluster t and k respectively. Jia Li http://www.stat.psu.edu/∼jiali 

29 .K-Center and Dendrogram Clustering How to get D(t, k) from D(r , k) and D(s, k)? Average linkage clustering: Unweighted case: nr ns D(t, k) = D(r , k) + D(s, k) nr + ns nr + ns Weighted case: 1 1 D(t, k) = D(r , k) + D(s, k) 2 2 D(t, k) is the average distance between two objects in cluster t and k respectively. For the unweighted case, the number of elements in each cluster is taken into consideration, while in the weighted case each cluster is weighted equally. So objects in smaller cluster are weighted more heavily than those in larger clusters. Jia Li http://www.stat.psu.edu/∼jiali