Hidden Markov Model

1 .Hidden Markov Model Hidden Markov Model Jia Li Department of Statistics The Pennsylvania State University Email: jiali@stat.psu.edu http://www.stat.psu.edu/∼jiali Jia Li http://www.stat.psu.edu/∼jiali 

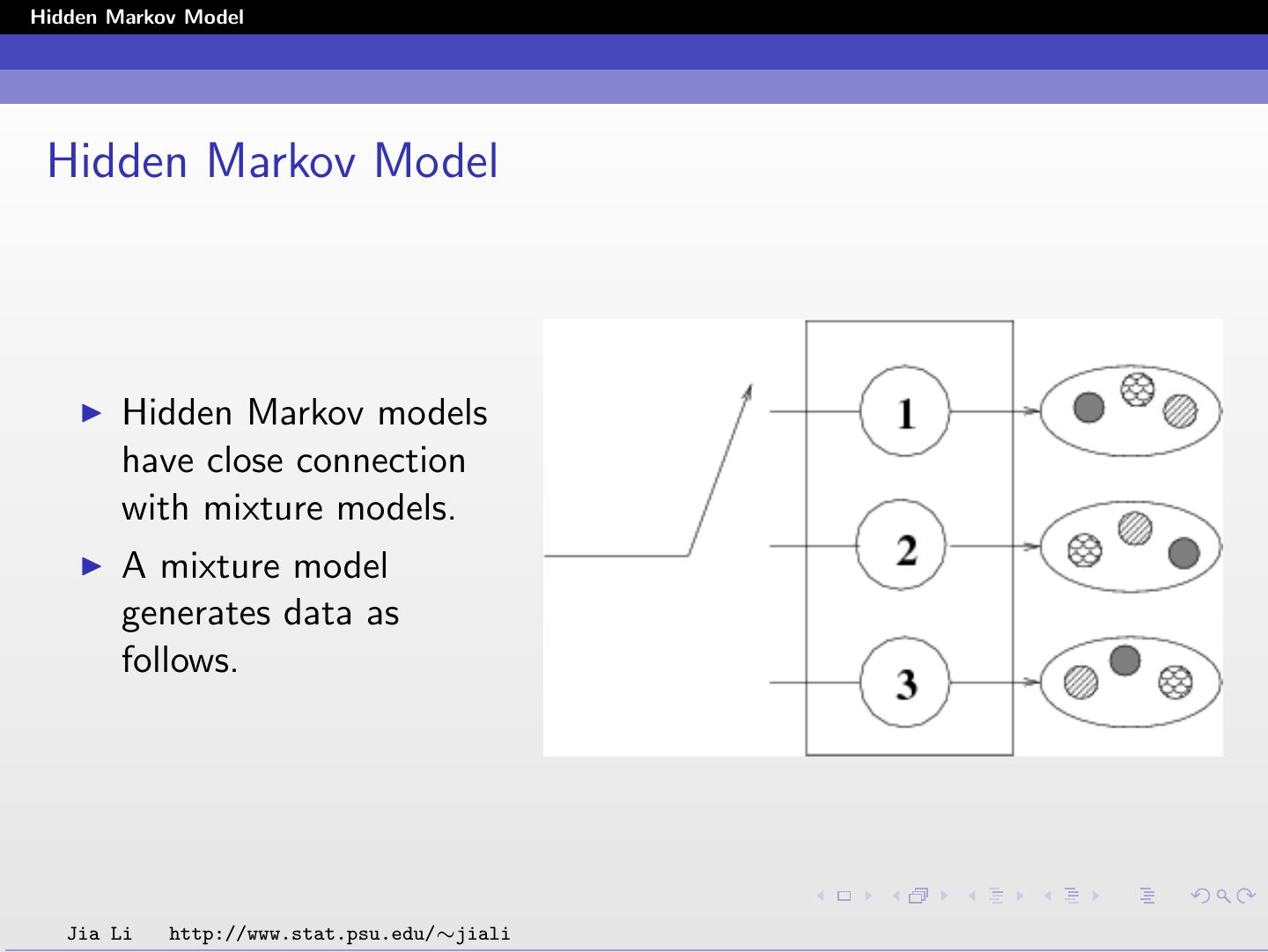
2 .Hidden Markov Model Hidden Markov Model Hidden Markov models have close connection with mixture models. A mixture model generates data as follows. Jia Li http://www.stat.psu.edu/∼jiali 

3 .Hidden Markov Model For sequence or spatial data, the assumption of independent samples is too constrained. The statistical dependence among samples may bear critical information. Examples: Speech signal Genomic sequences Jia Li http://www.stat.psu.edu/∼jiali 

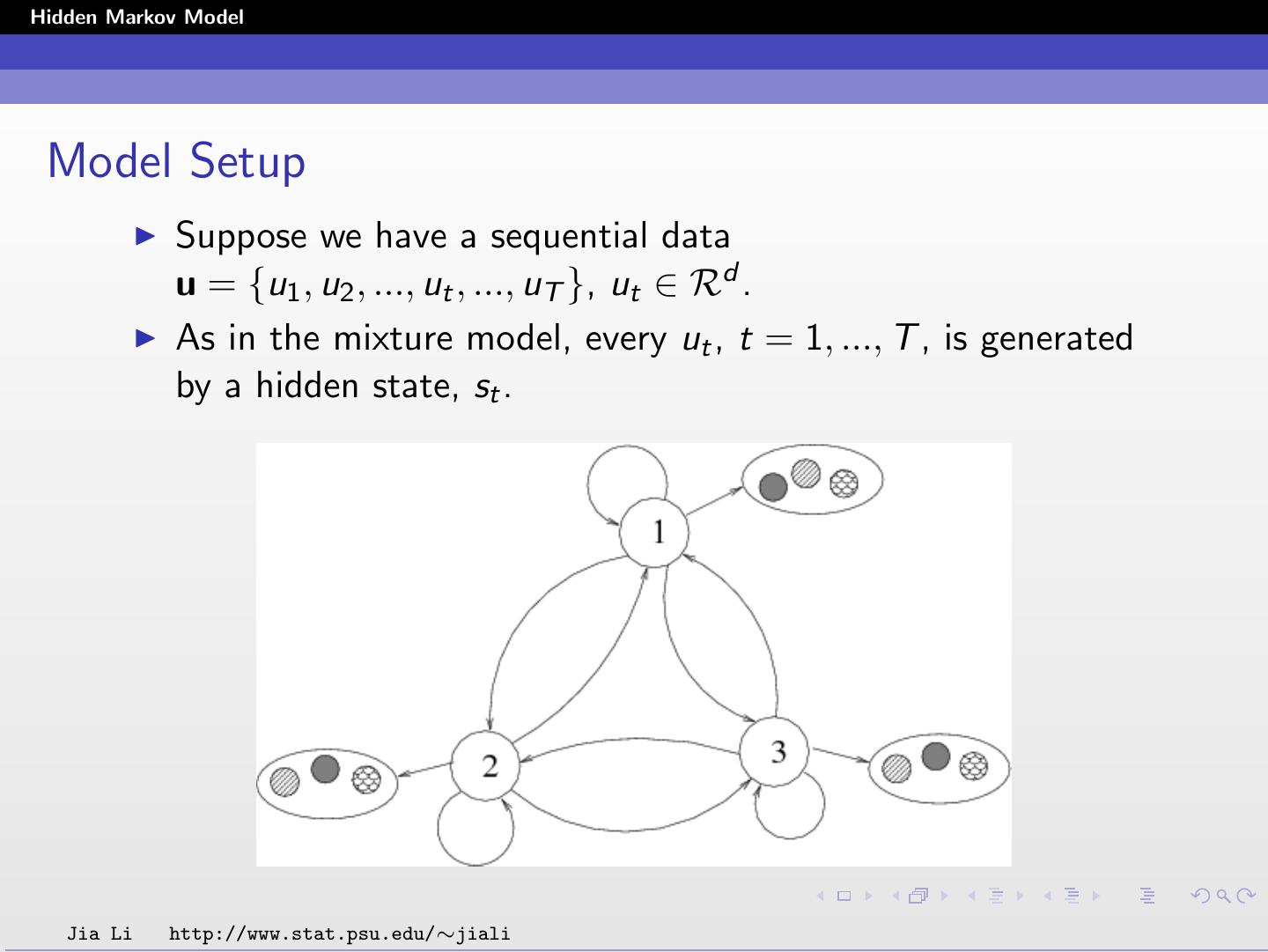
4 .Hidden Markov Model Model Setup Suppose we have a sequential data u = {u1 , u2 , ..., ut , ..., uT }, ut ∈ Rd . As in the mixture model, every ut , t = 1, ..., T , is generated by a hidden state, st . Jia Li http://www.stat.psu.edu/∼jiali 

5 .Hidden Markov Model The underlying states follow a Markov chain. Given present, the future is independent of the past: P(st+1 | st , st−1 , ..., s0 ) = P(st+1 | st ) . Transition probabilities: ak,l = P(st+1 = l | st = k) , k, l = 1, 2, ..., M, where M is the total number of states. Initial probabilities of states: πk . M M ak,l = 1 for any k , πk = 1 . l=1 k=1 Jia Li http://www.stat.psu.edu/∼jiali 

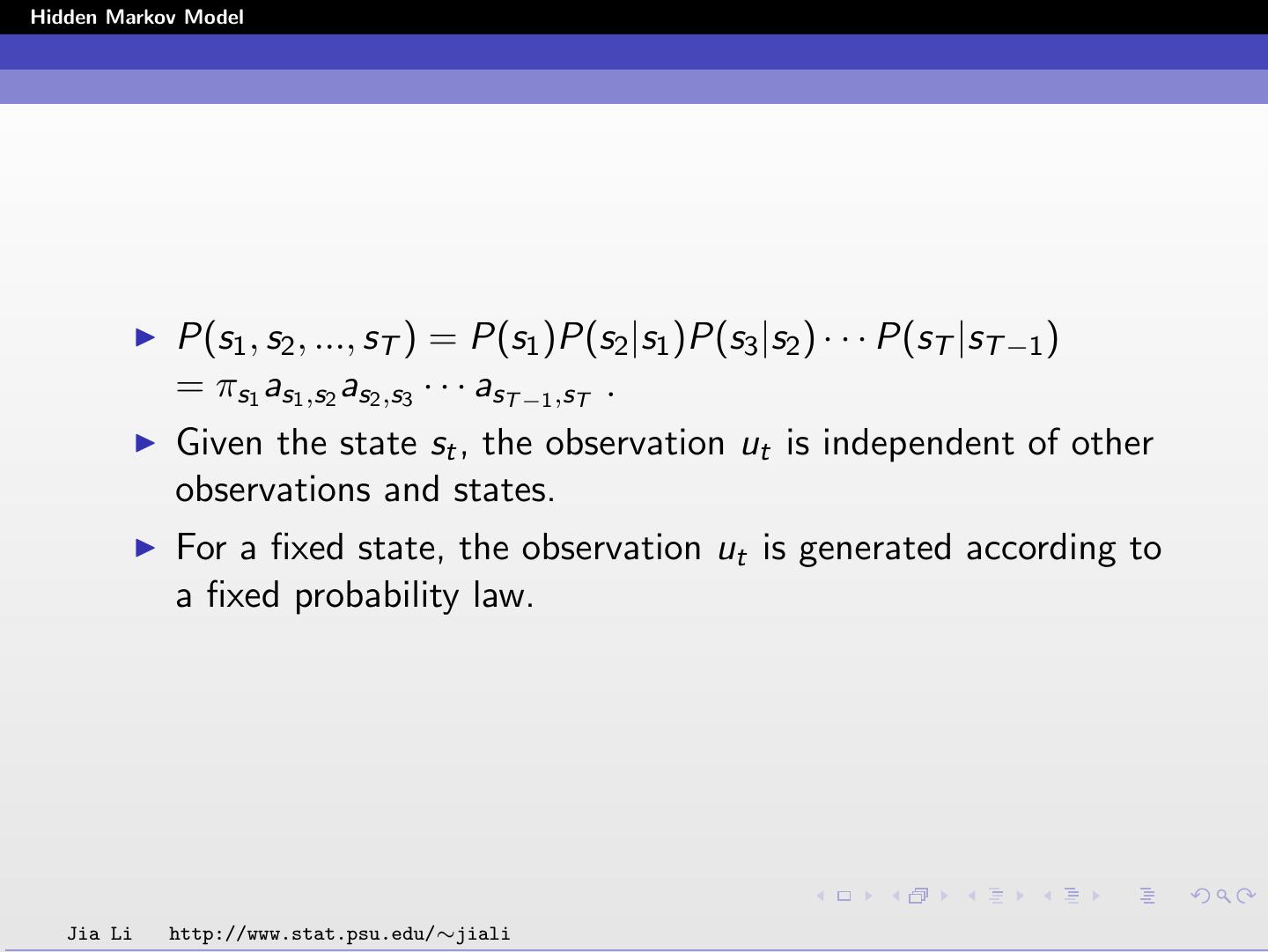
6 .Hidden Markov Model P(s1 , s2 , ..., sT ) = P(s1 )P(s2 |s1 )P(s3 |s2 ) · · · P(sT |sT −1 ) = πs1 as1 ,s2 as2 ,s3 · · · asT −1 ,sT . Given the state st , the observation ut is independent of other observations and states. For a fixed state, the observation ut is generated according to a fixed probability law. Jia Li http://www.stat.psu.edu/∼jiali 

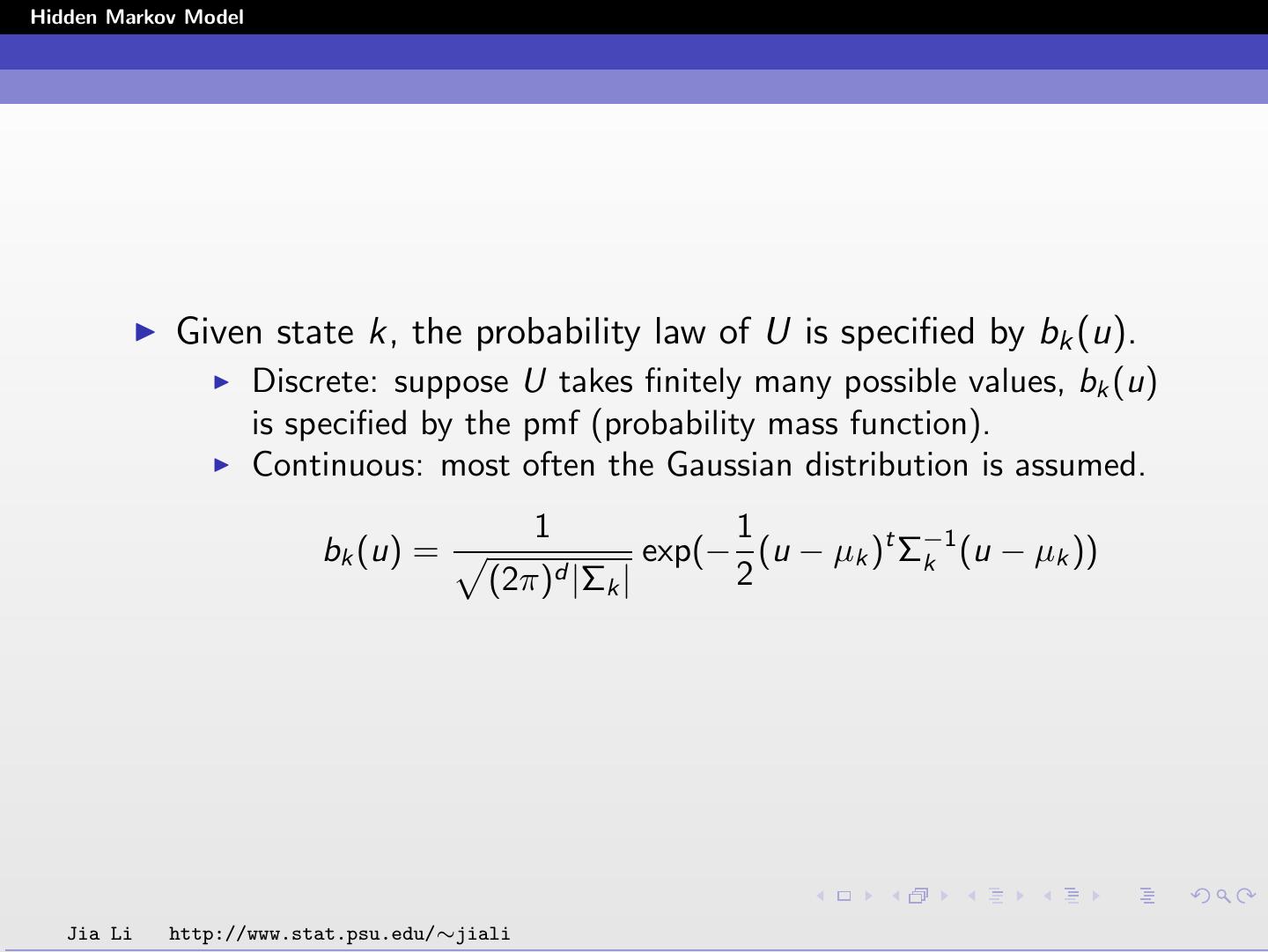
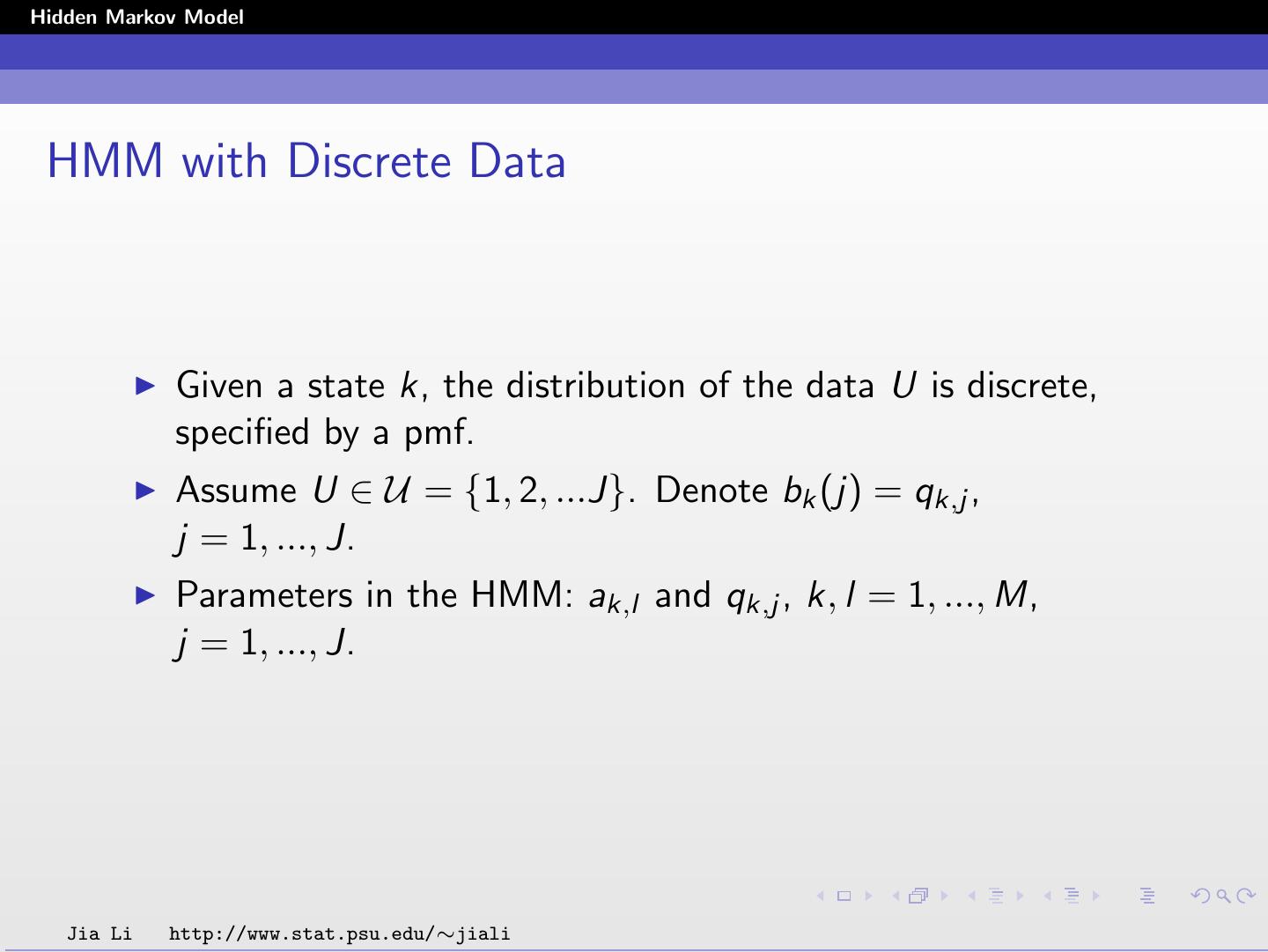
7 .Hidden Markov Model Given state k, the probability law of U is specified by bk (u). Discrete: suppose U takes finitely many possible values, bk (u) is specified by the pmf (probability mass function). Continuous: most often the Gaussian distribution is assumed. 1 1 bk (u) = exp(− (u − µk )t Σ−1 k (u − µk )) (2π)d |Σ k| 2 Jia Li http://www.stat.psu.edu/∼jiali 

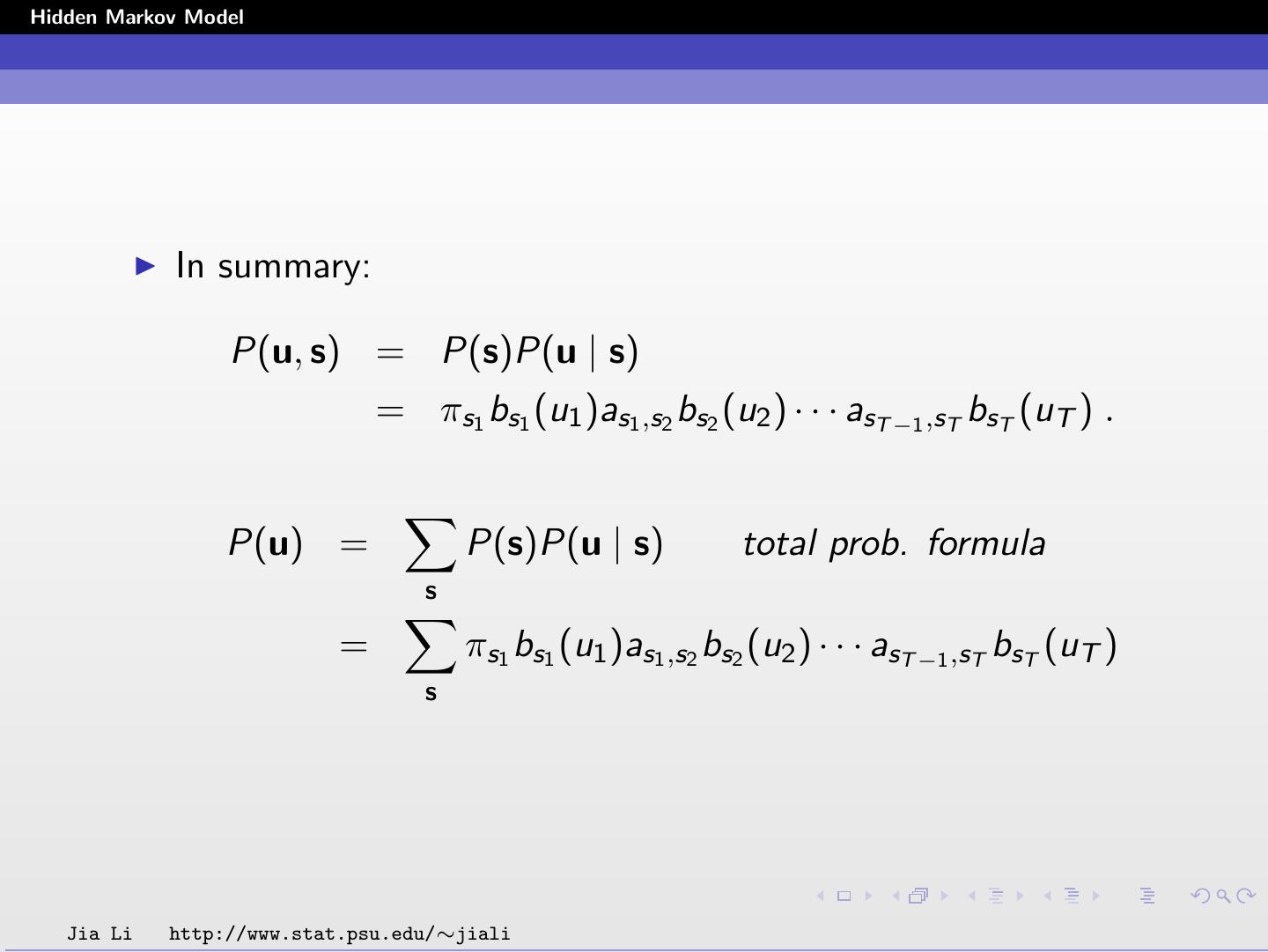
8 .Hidden Markov Model In summary: P(u, s) = P(s)P(u | s) = πs1 bs1 (u1 )as1 ,s2 bs2 (u2 ) · · · asT −1 ,sT bsT (uT ) . P(u) = P(s)P(u | s) total prob. formula s = πs1 bs1 (u1 )as1 ,s2 bs2 (u2 ) · · · asT −1 ,sT bsT (uT ) s Jia Li http://www.stat.psu.edu/∼jiali 

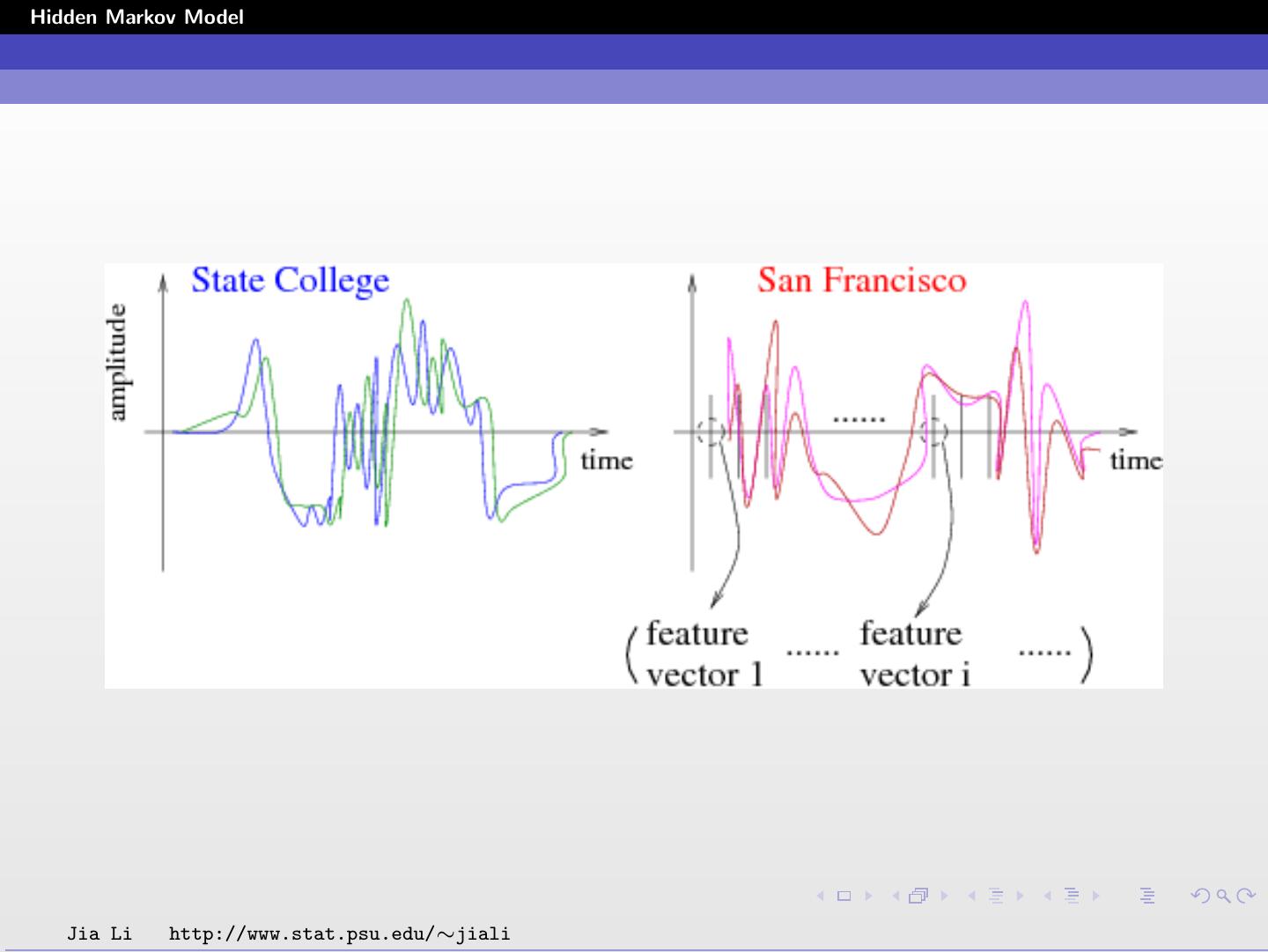
9 .Hidden Markov Model Example Suppose we have a video sequence and would like to automatically decide whether a speaker is in a frame. Two underlying states: with a speaker (state 1) vs. without a speaker (state 2). From frame 1 to T , let st , t = 1, ..., T denotes whether there is a speaker in the frame. It does not seem appropriate to assume that st ’s are independent. We may assume the state sequence follows a Markov chain. If one frame contains a speaker, it is highly likely that the next frame also contains a speaker because of the strong frame-to-frame dependence. On the other hand, a frame without a speaker is much more likely to be followed by another frame without a speaker. Jia Li http://www.stat.psu.edu/∼jiali 

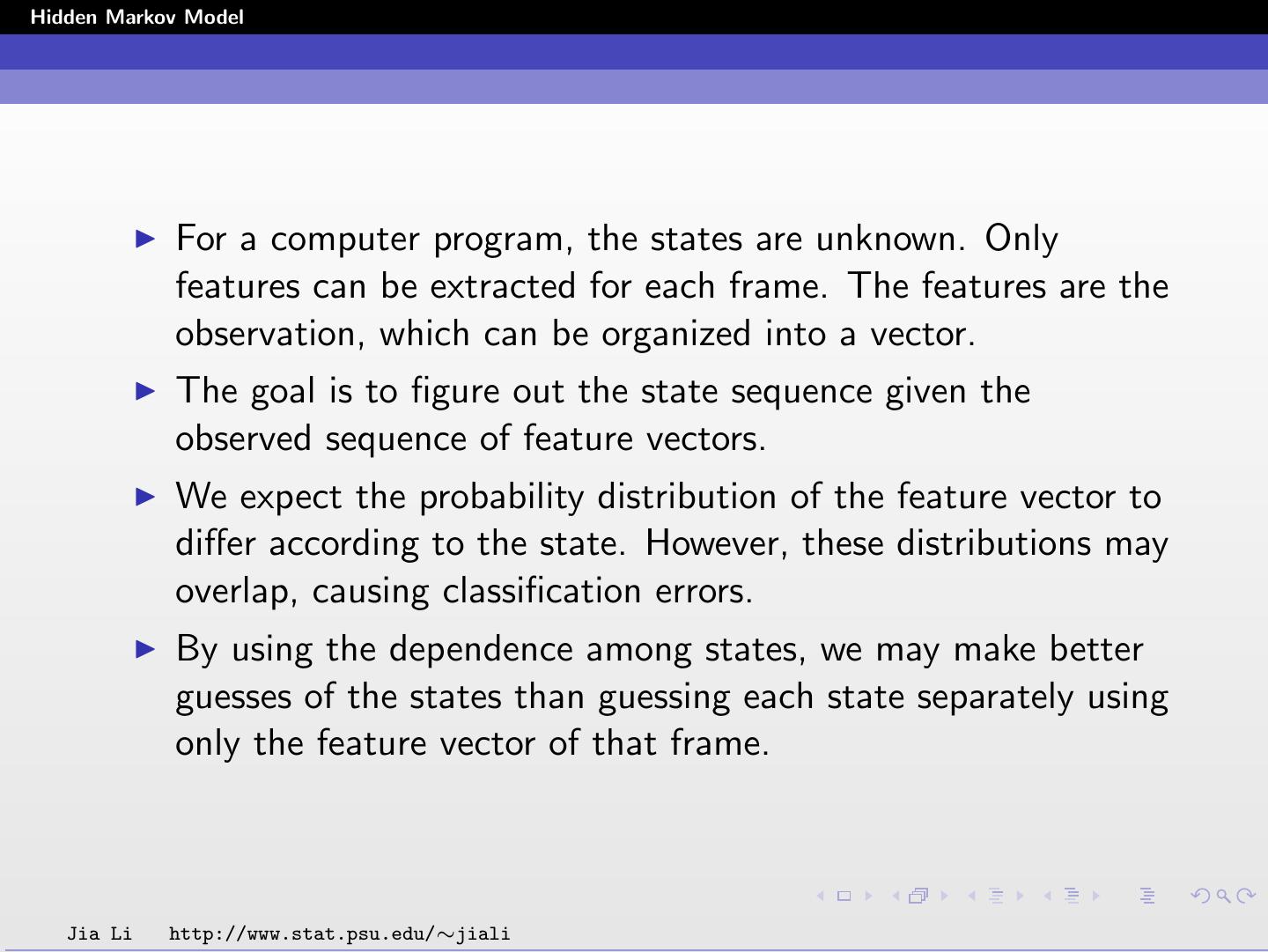
10 .Hidden Markov Model For a computer program, the states are unknown. Only features can be extracted for each frame. The features are the observation, which can be organized into a vector. The goal is to figure out the state sequence given the observed sequence of feature vectors. We expect the probability distribution of the feature vector to differ according to the state. However, these distributions may overlap, causing classification errors. By using the dependence among states, we may make better guesses of the states than guessing each state separately using only the feature vector of that frame. Jia Li http://www.stat.psu.edu/∼jiali 

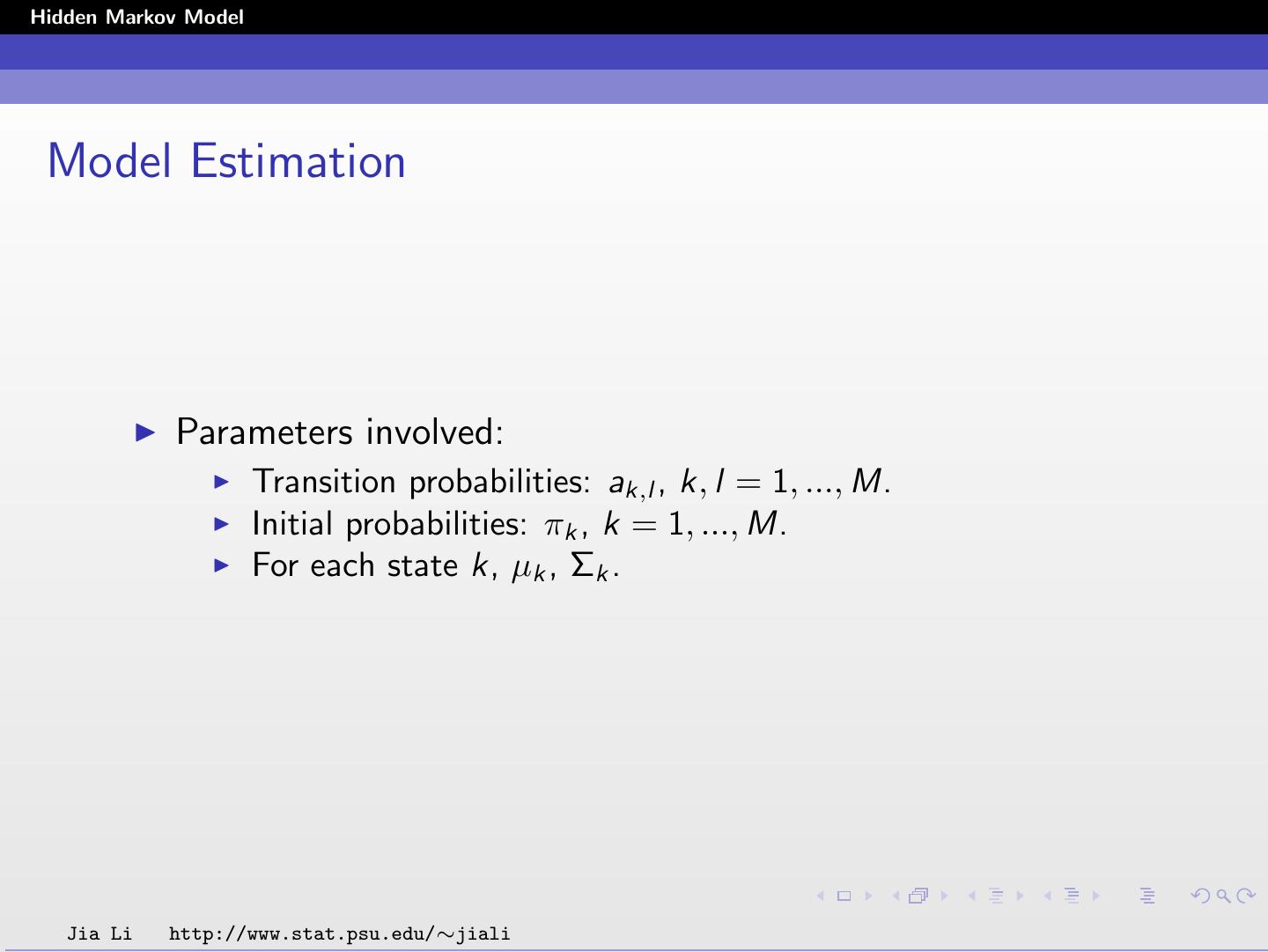
11 .Hidden Markov Model Model Estimation Parameters involved: Transition probabilities: ak,l , k, l = 1, ..., M. Initial probabilities: πk , k = 1, ..., M. For each state k, µk , Σk . Jia Li http://www.stat.psu.edu/∼jiali 

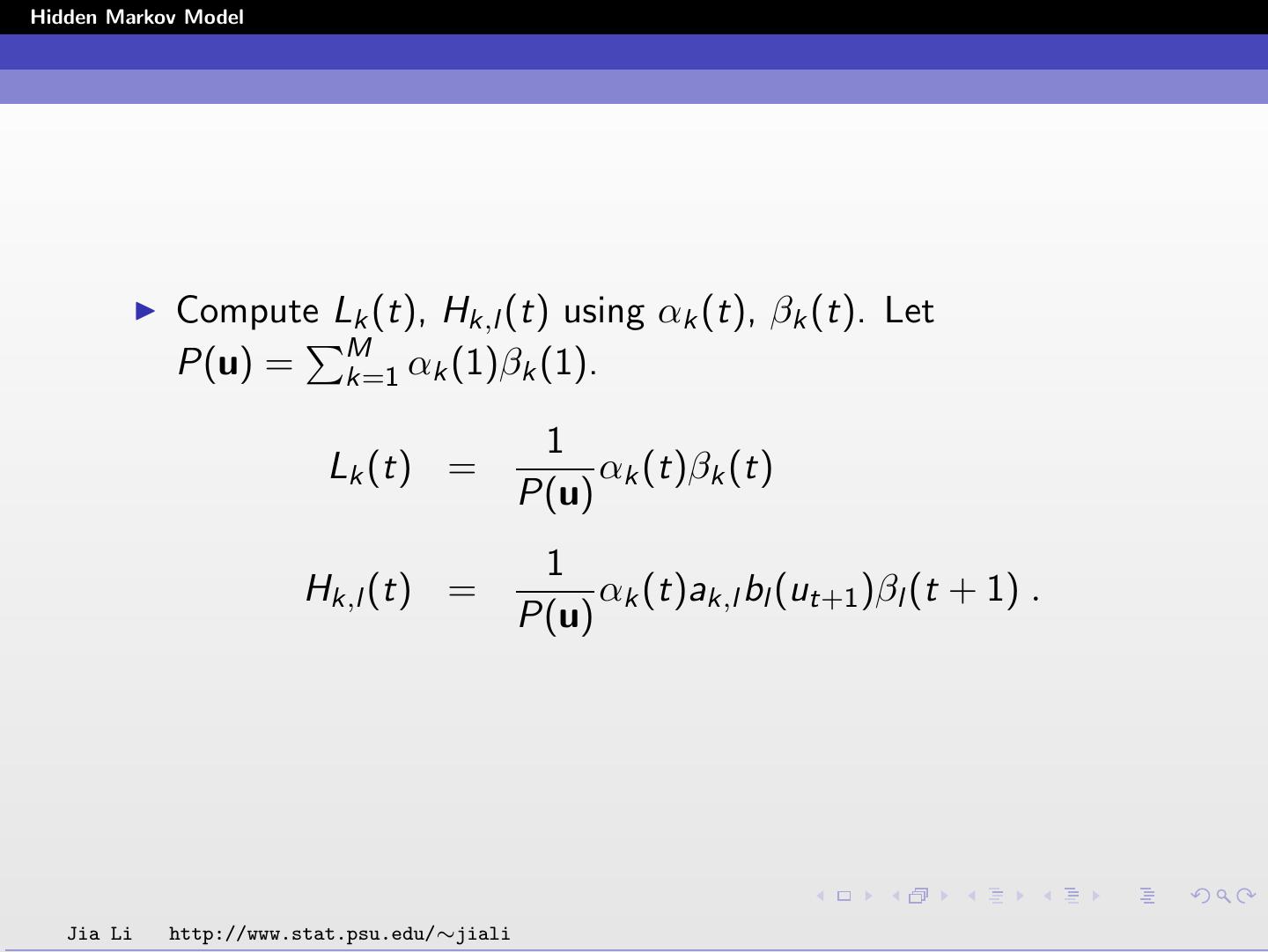
12 .Hidden Markov Model Definitions Under a given set of parameters, let Lk (t) be the conditional probability of being in state k at position t given the entire observed sequence u = {u1 , u2 , ..., uT }. Lk (t) = P(st = k|u) = P(s | u)I (st = k) . s Under a given set of parameters, let Hk,l (t) be the conditional probability of being in state k at position t and being in state l at position t + 1, i.e., seeing a transition from k to l at t, given the entire observed sequence u. Hk,l (t) = P(st = k, st+1 = l|u) = P(s | u)I (st = k)I (st+1 = l) s M M Note that Lk (t) = l=1 Hk,l (t), k=1 Lk (t) = 1. Jia Li http://www.stat.psu.edu/∼jiali 

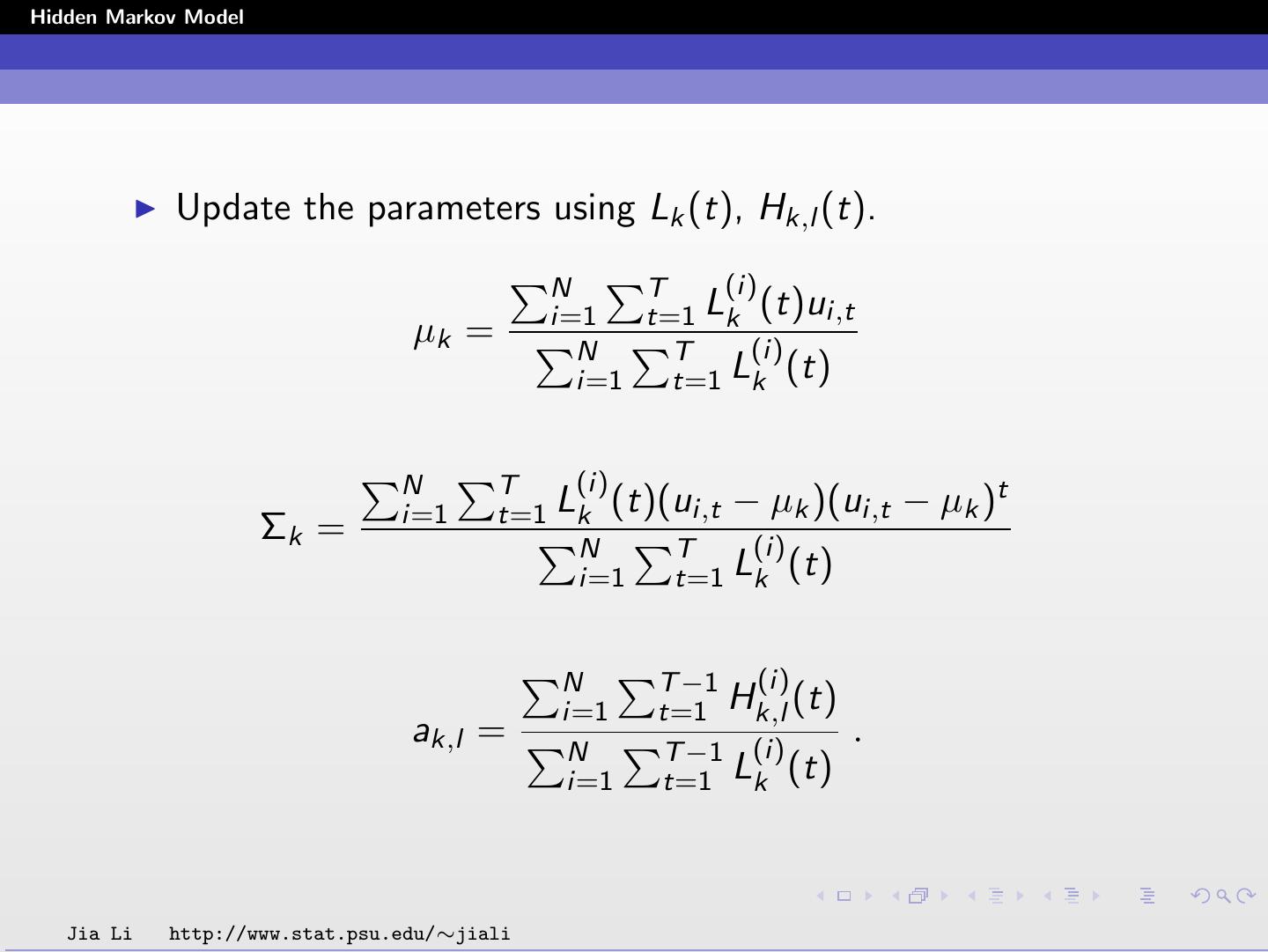
13 .Hidden Markov Model Maximum likelihood estimation by EM: E step: Under the current set of parameters, compute Lk (t) and Hk,l (t), for k, l = 1, ..., M, t = 1, ..., T . M step: Update parameters. T t=1 Lk (t)ut µk = T t=1 Lk (t) T t=1 Lk (t)(ut − µk )(ut − µk )t Σk = T t=1 Lk (t) T −1 t=1 Hk,l (t) ak,l = T −1 . t=1 Lk (t) Jia Li http://www.stat.psu.edu/∼jiali 

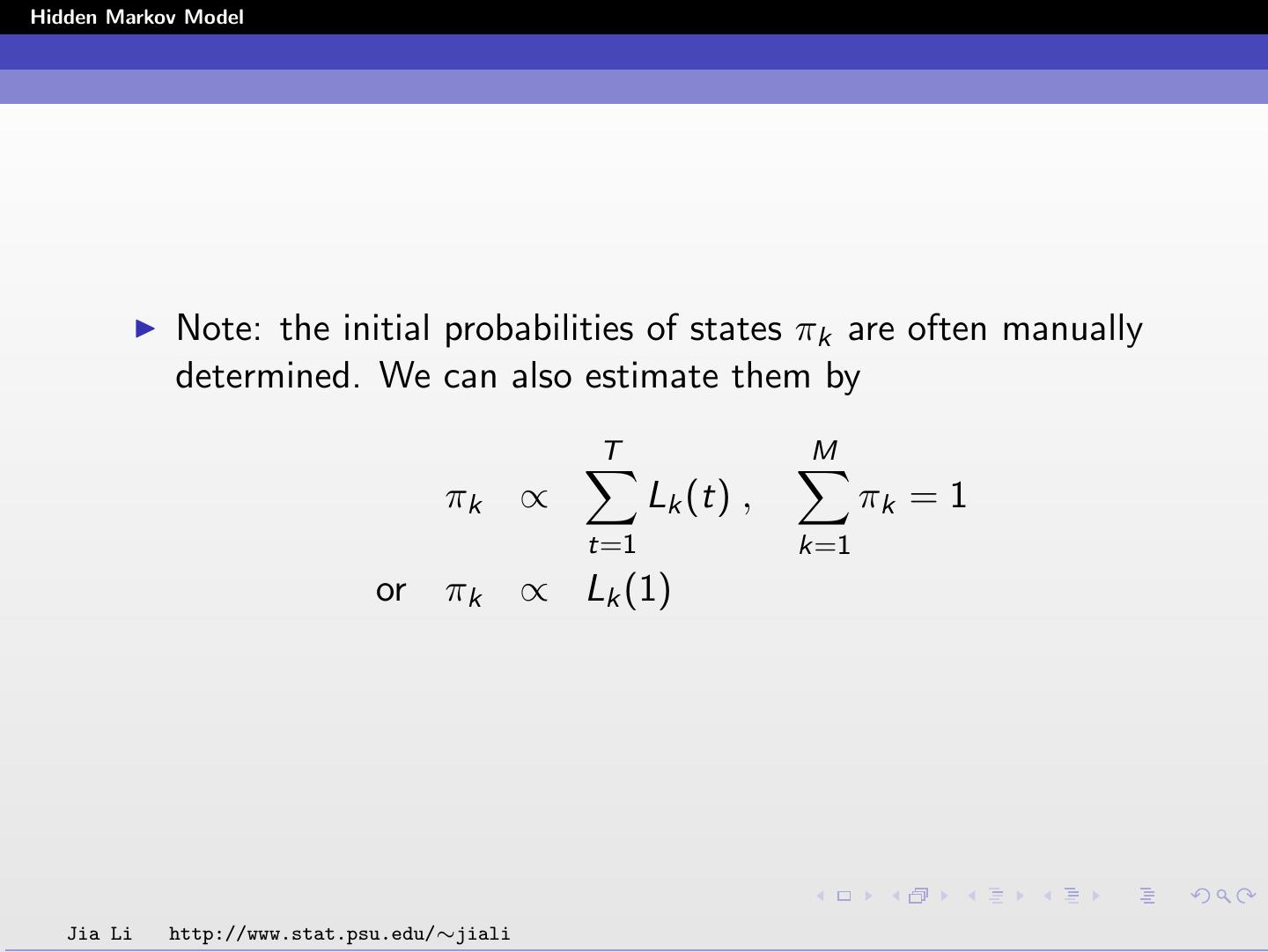
14 .Hidden Markov Model Note: the initial probabilities of states πk are often manually determined. We can also estimate them by T M πk ∝ Lk (t) , πk = 1 t=1 k=1 or πk ∝ Lk (1) Jia Li http://www.stat.psu.edu/∼jiali 

15 .Hidden Markov Model Comparison with the Mixture Model Lk (t) is playing the same role as the posterior probability of a component (state) given the observation, i.e., pt,k . Lk (t) = P(st = k|u1 , u2 , ..., ut , ..., uT ) pt,k = P(st = k|ut ) If we view a mixture model as a special hidden Markov model with the underlying state process being i.i.d (a reduced Markov chain), pt,k is exactly Lk (t). Jia Li http://www.stat.psu.edu/∼jiali 

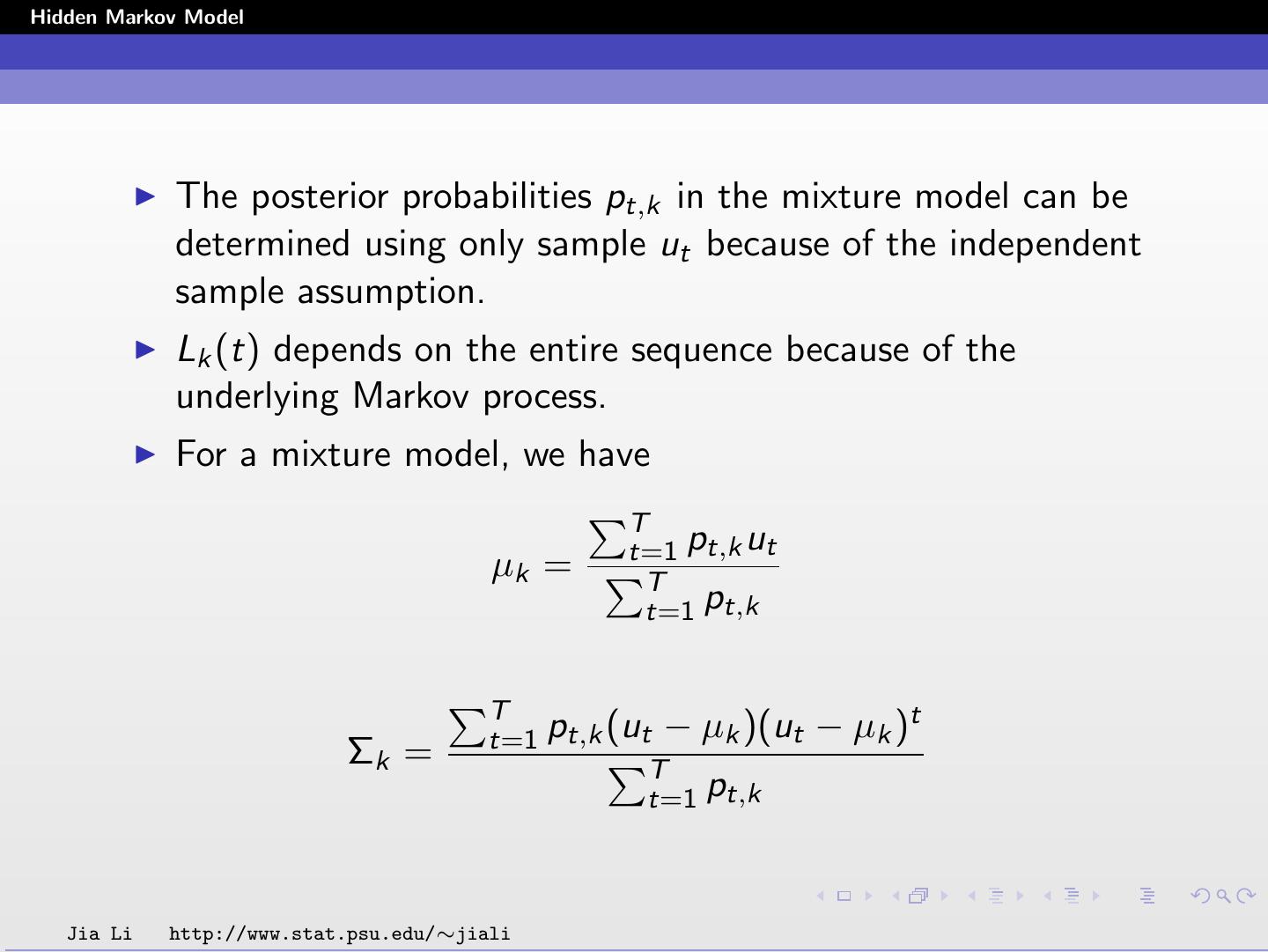
16 .Hidden Markov Model The posterior probabilities pt,k in the mixture model can be determined using only sample ut because of the independent sample assumption. Lk (t) depends on the entire sequence because of the underlying Markov process. For a mixture model, we have T t=1 pt,k ut µk = T t=1 pt,k T t=1 pt,k (ut − µk )(ut − µk )t Σk = T t=1 pt,k Jia Li http://www.stat.psu.edu/∼jiali 

17 .Hidden Markov Model Derivation from EM The incomplete data are u = {ut : t = 1, ..., T }. The complete data are x = {st , ut : t = 1, ..., T }. Note Q(θ |θ) = E (log(f (x|θ ))|u, θ). Let M = {1, 2, ..., M}. Jia Li http://www.stat.psu.edu/∼jiali 

18 .Hidden Markov Model The function f (x | θ ) is f (x | θ ) = P(s | θ )P(u | s, θ ) = P(s | ak,l : k, l ∈ M)P(u | s, µk , Σk : k ∈ M) T T = πs 1 ast−1 ,st × P(ut | µst , Σst ) . t=2 t=1 We then have T log f (x | θ ) = log(πs1 ) + log ast−1 ,st + t=2 T log P(ut | µst , Σst ) (1) t=1 Jia Li http://www.stat.psu.edu/∼jiali 

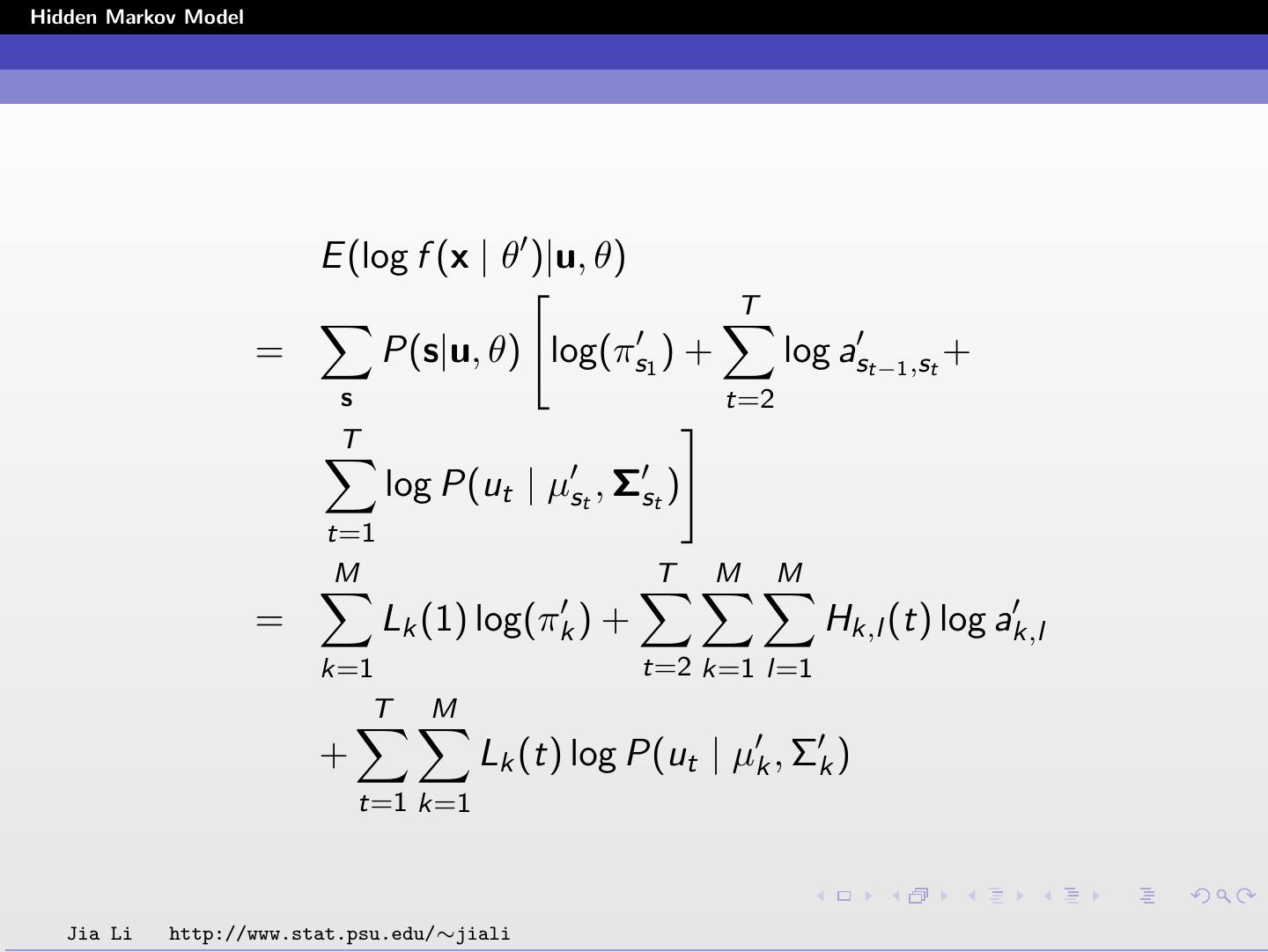
19 .Hidden Markov Model E (log f (x | θ )|u, θ) T = P(s|u, θ) log(πs1 ) + log ast−1 ,st + s t=2 T log P(ut | µst , Σst ) t=1 M T M M = Lk (1) log(πk ) + Hk,l (t) log ak,l k=1 t=2 k=1 l=1 T M + Lk (t) log P(ut | µk , Σk ) t=1 k=1 Jia Li http://www.stat.psu.edu/∼jiali 

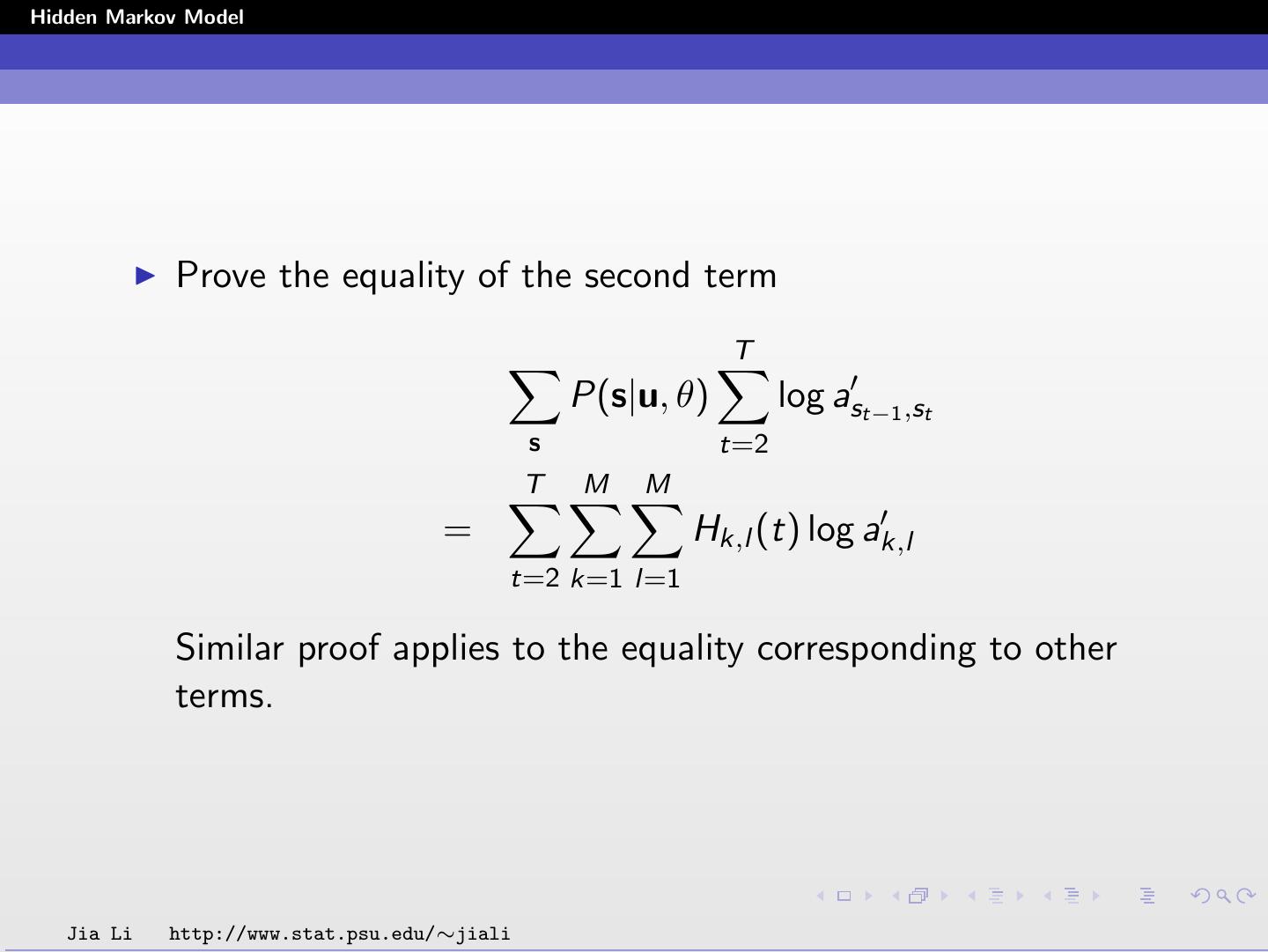
20 .Hidden Markov Model Prove the equality of the second term T P(s|u, θ) log ast−1 ,st s t=2 T M M = Hk,l (t) log ak,l t=2 k=1 l=1 Similar proof applies to the equality corresponding to other terms. Jia Li http://www.stat.psu.edu/∼jiali 

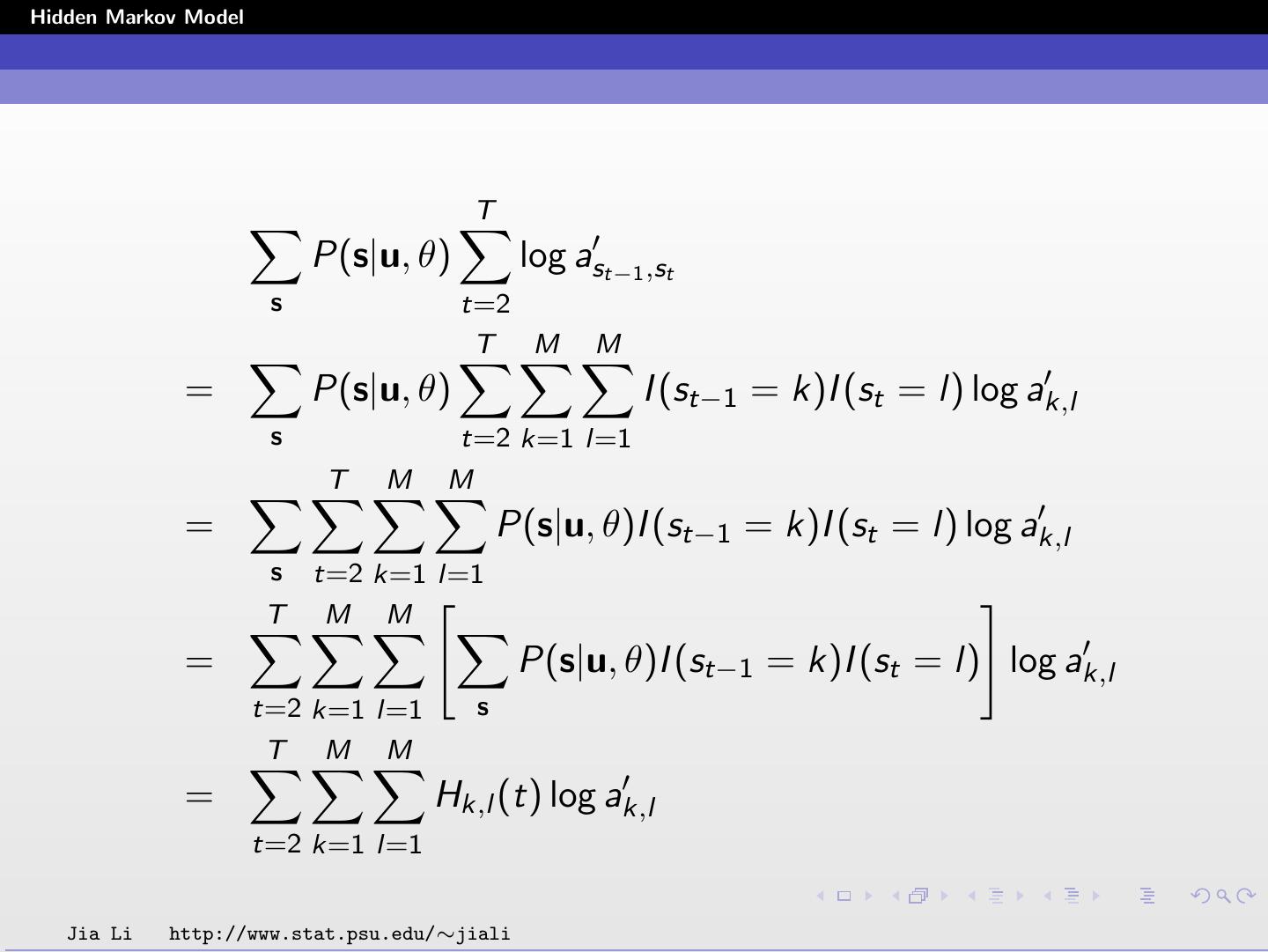
21 .Hidden Markov Model T P(s|u, θ) log ast−1 ,st s t=2 T M M = P(s|u, θ) I (st−1 = k)I (st = l) log ak,l s t=2 k=1 l=1 T M M = P(s|u, θ)I (st−1 = k)I (st = l) log ak,l s t=2 k=1 l=1 T M M = P(s|u, θ)I (st−1 = k)I (st = l) log ak,l t=2 k=1 l=1 s T M M = Hk,l (t) log ak,l t=2 k=1 l=1 Jia Li http://www.stat.psu.edu/∼jiali 

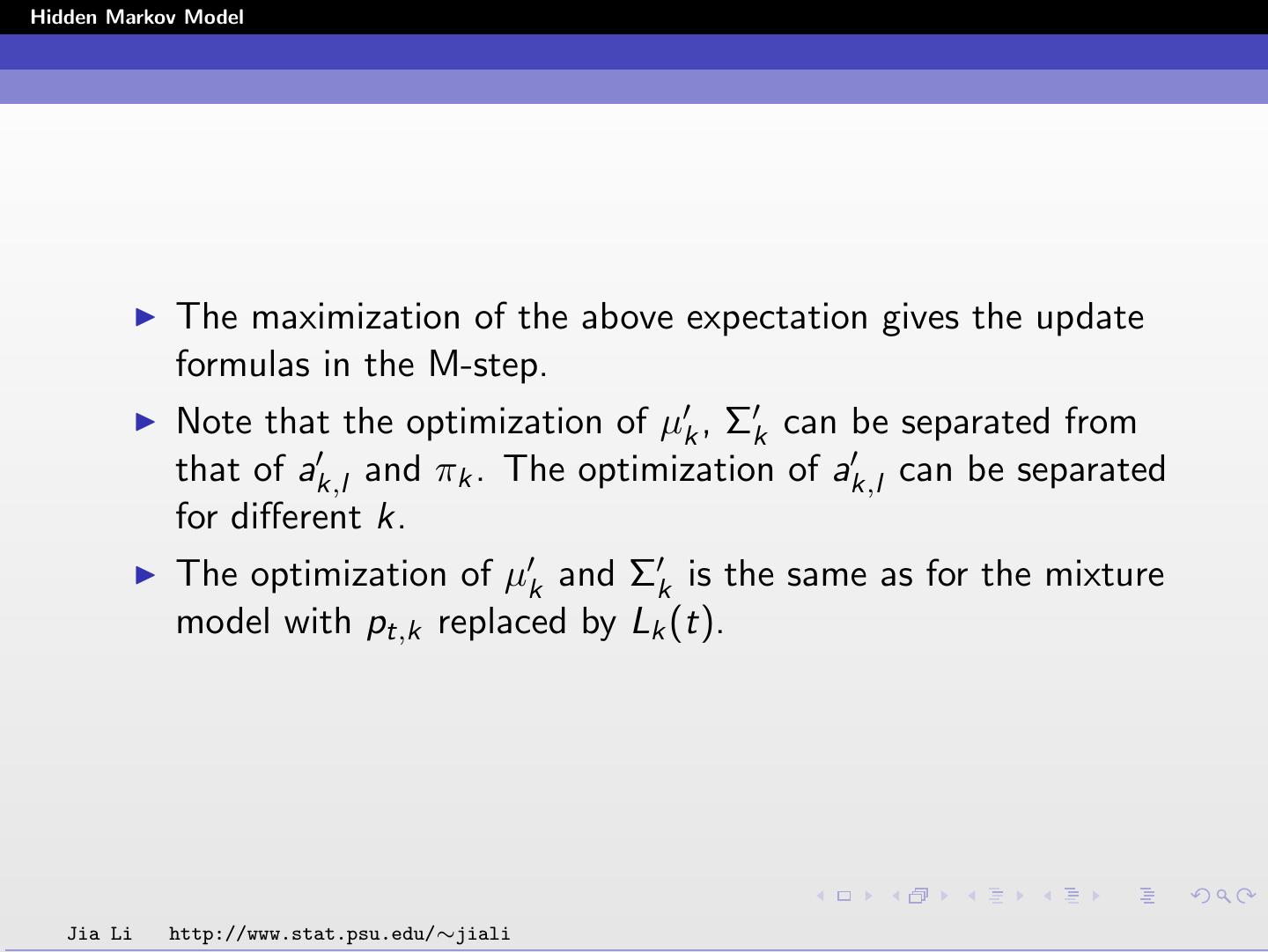
22 .Hidden Markov Model The maximization of the above expectation gives the update formulas in the M-step. Note that the optimization of µk , Σk can be separated from that of ak,l and πk . The optimization of ak,l can be separated for different k. The optimization of µk and Σk is the same as for the mixture model with pt,k replaced by Lk (t). Jia Li http://www.stat.psu.edu/∼jiali 

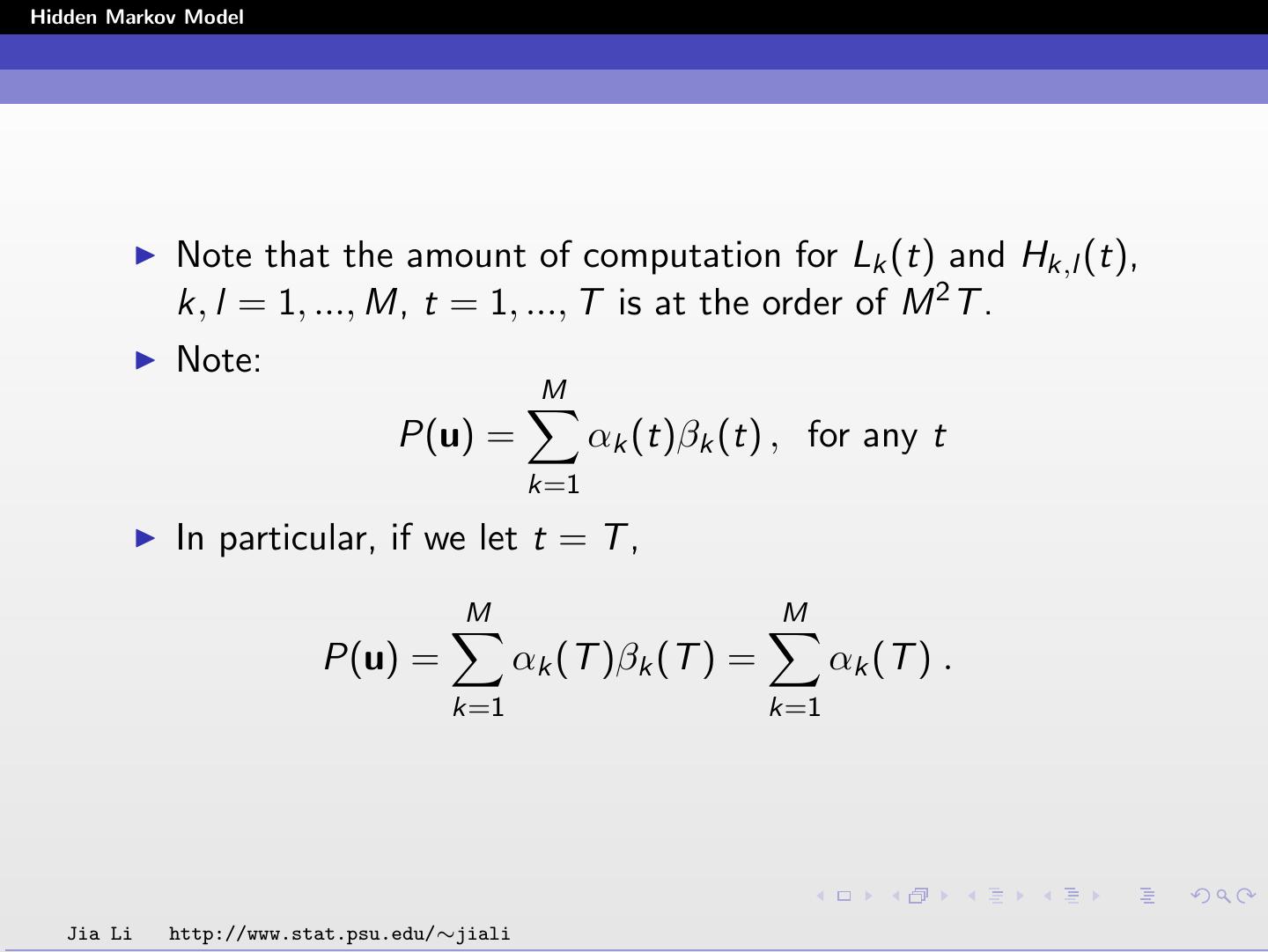
23 .Hidden Markov Model Forward-Backward Algorithm The forward-backward algorithm is used to compute Lk (t) and Hk,l (t) efficiently. The amount of computation needed is at the order of M 2 T . Memory required is at the order of MT . Define the forward probability αk (t) as the joint probability of observing the first t vectors uτ , τ = 1, ..., t, and being in state k at time t. αk (t) = P(u1 , u2 , ..., ut , st = k) Jia Li http://www.stat.psu.edu/∼jiali 

24 .Hidden Markov Model This probability can be evaluated by the following recursive formula: αk (1) = πk bk (u1 ) 1 ≤ k ≤ M M αk (t) = bk (ut ) αl (t − 1)al,k , l=1 1 < t ≤ T, 1 ≤ k ≤ M . Jia Li http://www.stat.psu.edu/∼jiali 

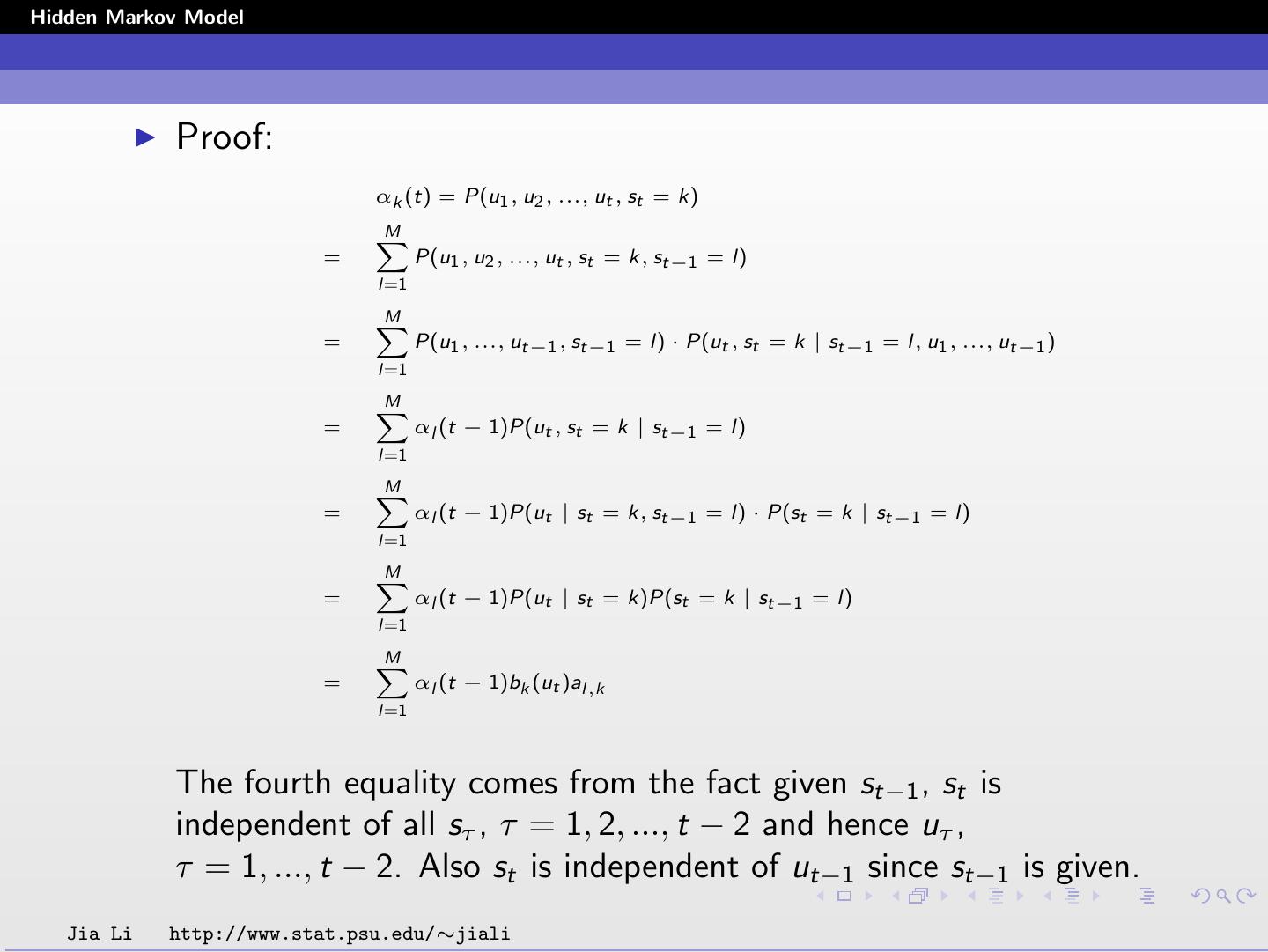
25 .Hidden Markov Model Proof: αk (t) = P(u1 , u2 , ..., ut , st = k) M X = P(u1 , u2 , ..., ut , st = k, st−1 = l) l=1 M X = P(u1 , ..., ut−1 , st−1 = l) · P(ut , st = k | st−1 = l, u1 , ..., ut−1 ) l=1 M X = αl (t − 1)P(ut , st = k | st−1 = l) l=1 M X = αl (t − 1)P(ut | st = k, st−1 = l) · P(st = k | st−1 = l) l=1 M X = αl (t − 1)P(ut | st = k)P(st = k | st−1 = l) l=1 M X = αl (t − 1)bk (ut )al,k l=1 The fourth equality comes from the fact given st−1 , st is independent of all sτ , τ = 1, 2, ..., t − 2 and hence uτ , τ = 1, ..., t − 2. Also st is independent of ut−1 since st−1 is given. Jia Li http://www.stat.psu.edu/∼jiali 

26 .Hidden Markov Model Define the backward probability βk (t) as the conditional probability of observing the vectors after time t, uτ , τ = t + 1, ..., T , given the state at time t is k. βk (t) = P(ut+1 , ..., uT | st = k) , 1 ≤ t ≤ T − 1 Set βk (T ) = 1 , for all k . As with the forward probability, the backward probability can be evaluated using the following recursion βk (T ) = 1 M βk (t) = ak,l bl (ut+1 )βl (t + 1) 1≤t<T . l=1 Jia Li http://www.stat.psu.edu/∼jiali 

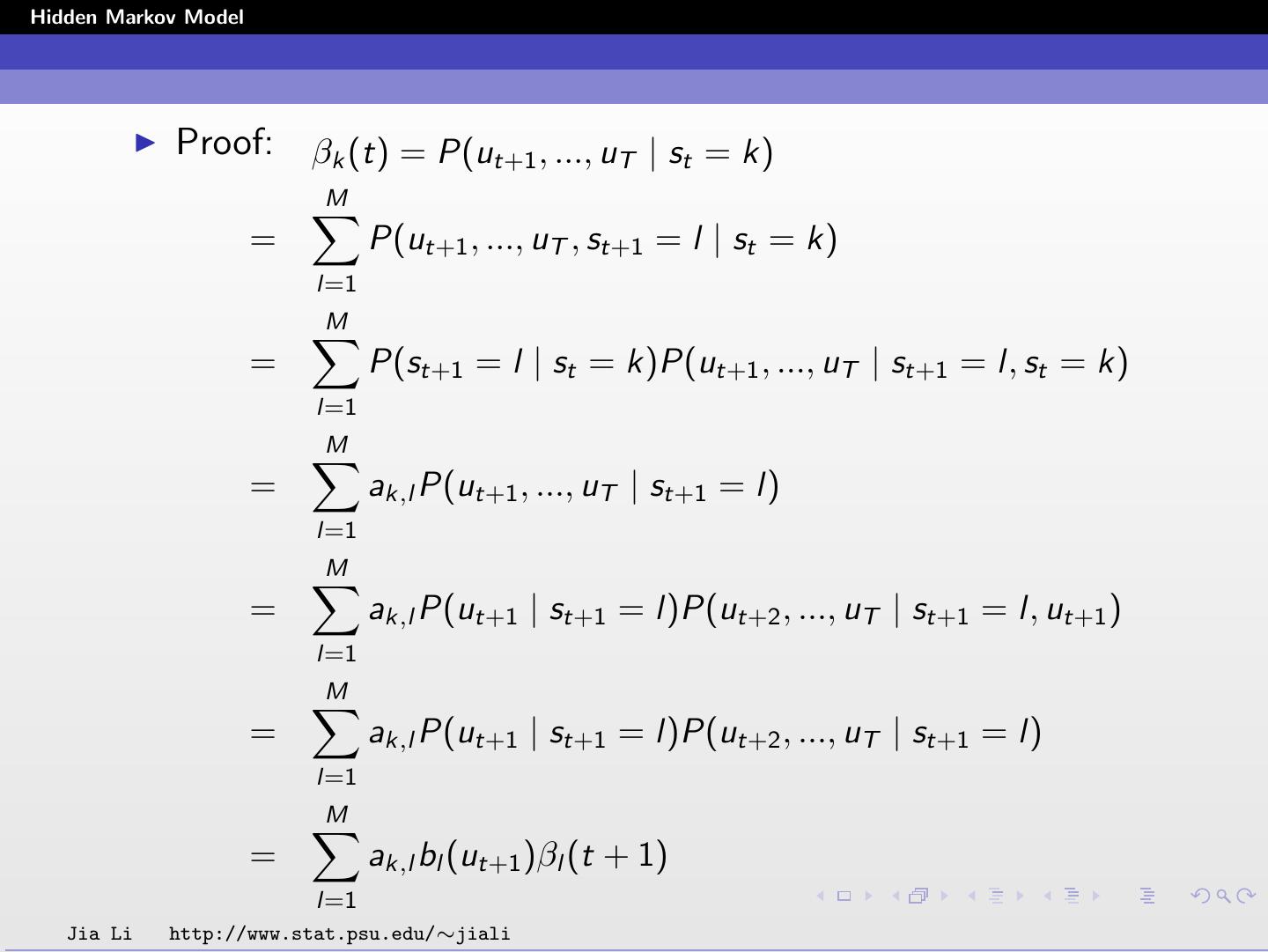
27 .Hidden Markov Model Proof: βk (t) = P(ut+1 , ..., uT | st = k) M = P(ut+1 , ..., uT , st+1 = l | st = k) l=1 M = P(st+1 = l | st = k)P(ut+1 , ..., uT | st+1 = l, st = k) l=1 M = ak,l P(ut+1 , ..., uT | st+1 = l) l=1 M = ak,l P(ut+1 | st+1 = l)P(ut+2 , ..., uT | st+1 = l, ut+1 ) l=1 M = ak,l P(ut+1 | st+1 = l)P(ut+2 , ..., uT | st+1 = l) l=1 M = ak,l bl (ut+1 )βl (t + 1) l=1 Jia Li http://www.stat.psu.edu/∼jiali 

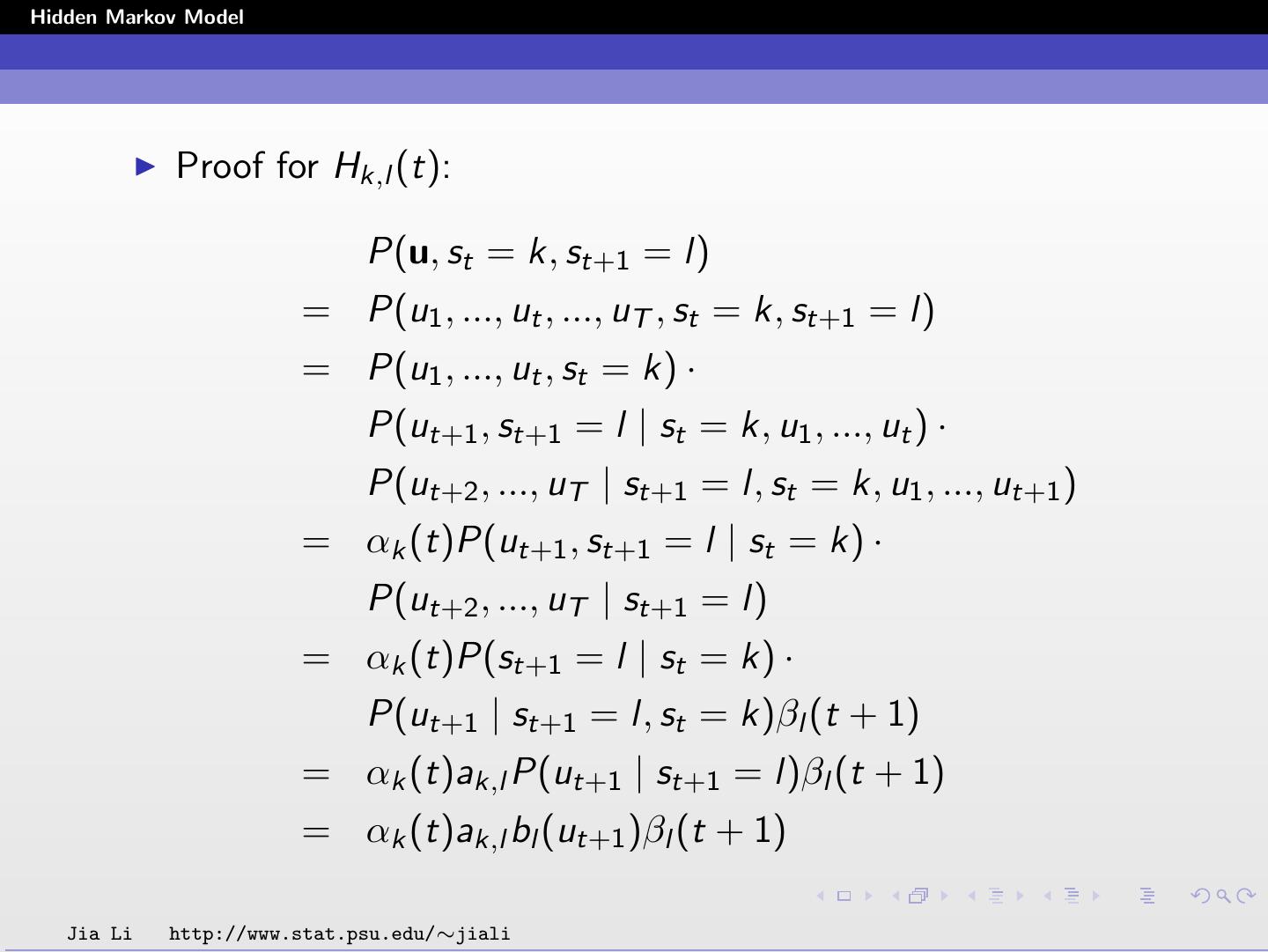
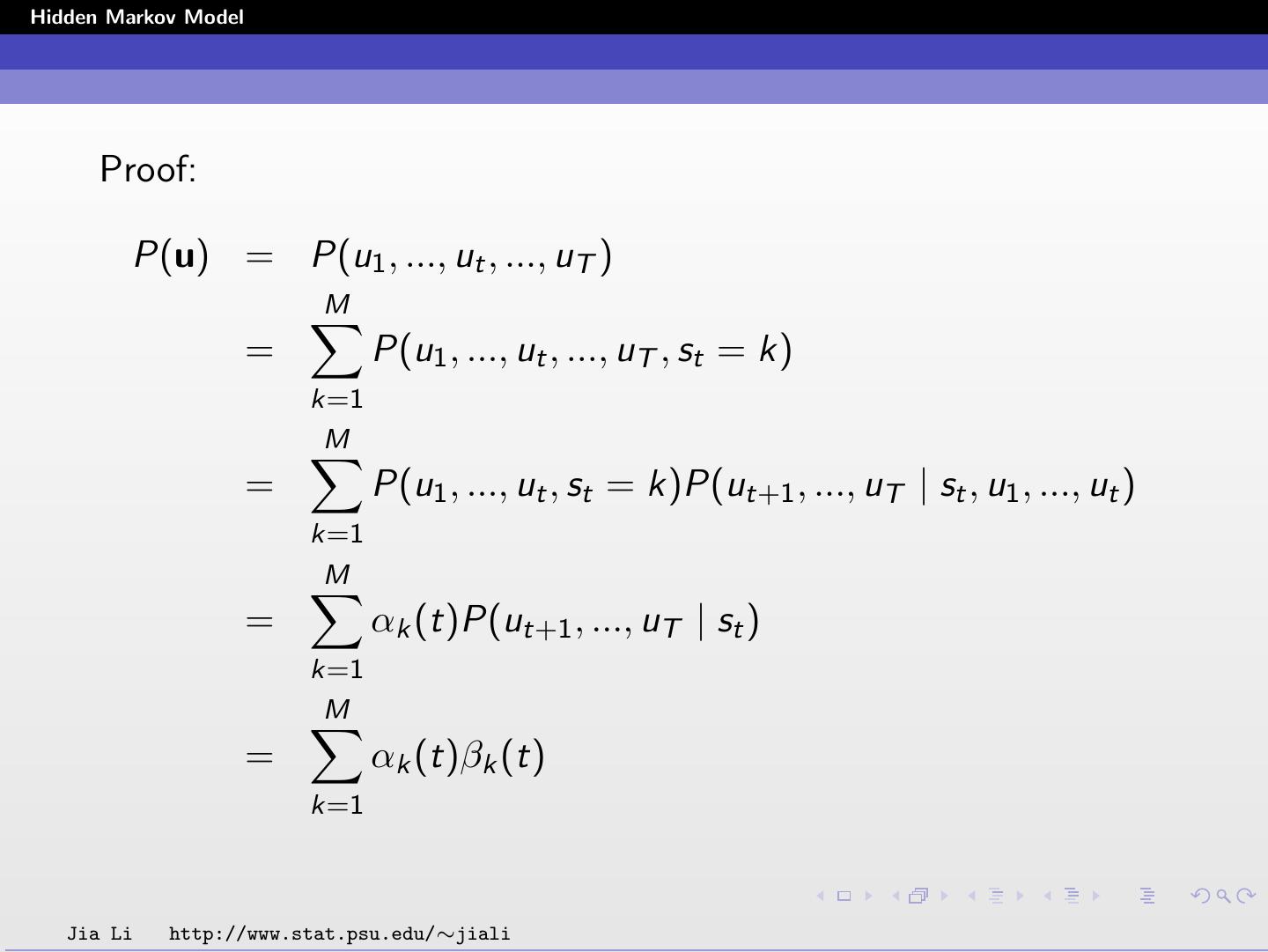
28 .Hidden Markov Model The probabilities Lk (t) and Hk,l (t) are solved by P(u, st = k) Lk (t) = P(st = k | u) = P(u) 1 = αk (t)βk (t) P(u) Hk,l (t) = P(st = k, st+1 = l | u) P(u, st = k, st+1 = l) = P(u) 1 = αk (t)ak,l bl (ut+1 )βl (t + 1) . P(u) Jia Li http://www.stat.psu.edu/∼jiali 

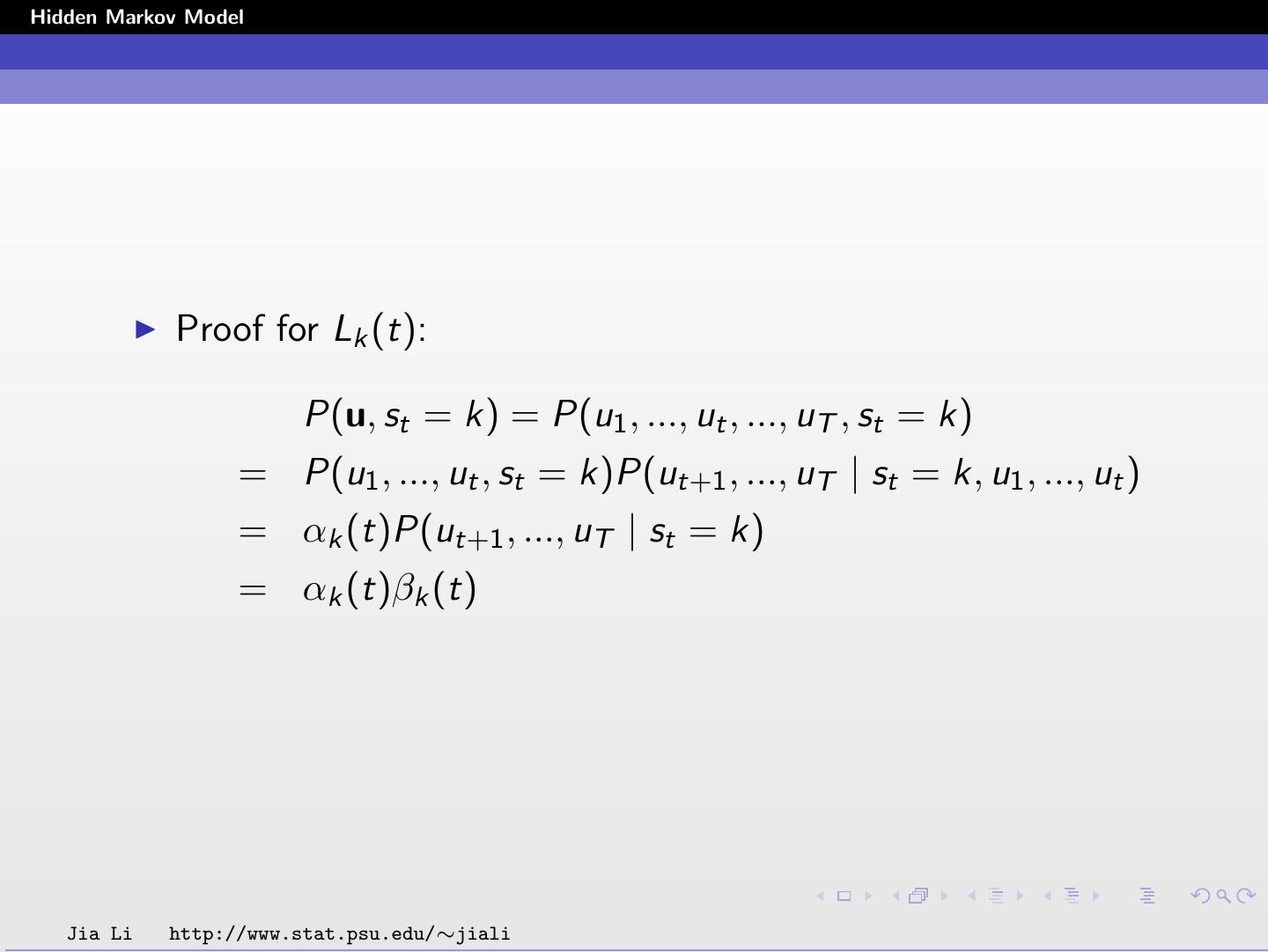
29 .Hidden Markov Model Proof for Lk (t): P(u, st = k) = P(u1 , ..., ut , ..., uT , st = k) = P(u1 , ..., ut , st = k)P(ut+1 , ..., uT | st = k, u1 , ..., ut ) = αk (t)P(ut+1 , ..., uT | st = k) = αk (t)βk (t) Jia Li http://www.stat.psu.edu/∼jiali