classification/decision trees2

1 .Classification/Decision Trees (II) Classification/Decision Trees (II) Jia Li Department of Statistics The Pennsylvania State University Email: jiali@stat.psu.edu http://www.stat.psu.edu/∼jiali Jia Li http://www.stat.psu.edu/∼jiali 

2 .Classification/Decision Trees (II) Right Sized Trees Let the expected misclassification rate of a tree T be R ∗ (T ). Recall the resubstitution estimate for R ∗ (T ) is R(T ) = r (t)p(t) = R(t) . ˜ t∈T ˜ t∈T R(T ) is biased downward. R(t) ≥ R(tL ) + R(tR ) . Jia Li http://www.stat.psu.edu/∼jiali 

3 .Classification/Decision Trees (II) Digit recognition example No. Terminal Nodes R(T ) R ts (T ) 71 .00 .42 63 .00 .40 The estimate R(T ) becomes increasingly less 58 .03 .39 accurate as the trees 40 .10 .32 grow larger. 34 .12 .32 19 .29 .31 The estimate R ts decreases first when the 10 .29 .30 tree becomes larger, hits 9 .32 .34 minimum at the tree with 7 .41 .47 10 terminal nodes, and 6 .46 .54 begins to increase when 5 .53 .61 the tree further grows. 2 .75 .82 1 .86 .91 Jia Li http://www.stat.psu.edu/∼jiali 

4 .Classification/Decision Trees (II) Preliminaries for Pruning Grow a very large tree Tmax . 1. Until all terminal nodes are pure (contain only one class) or contain only identical measurement vectors. 2. When the number of data in each terminal node is no greater than a certain threshold, say 5, or even 1. 3. As long as the tree is sufficiently large, the size of the initial tree is not critical. Jia Li http://www.stat.psu.edu/∼jiali 

5 .Classification/Decision Trees (II) 1. Descendant: a node t is a descendant of node t if there is a connected path down the tree leading from t to t . 2. Ancestor: t is an ancestor of t if t is its descendant. 3. A branch Tt of T with root node t ∈ T consists of the node t and all descendants of t in T . 4. Pruning a branch Tt from a tree T consists of deleting from T all descendants of t, that is, cutting off all of Tt except its root node. The tree pruned this way will be denoted by T − Tt . 5. If T is gotten from T by successively pruning off branches, then T is called a pruned subtree of T and denoted by T ≺ T . Jia Li http://www.stat.psu.edu/∼jiali 

6 .Classification/Decision Trees (II) Subtrees Even for a moderate sized Tmax , there is an enormously large number of subtrees and an even larger number ways to prune the initial tree to them. A “selective” pruning procedure is needed. The pruning is optimal in a certain sense. The search for different ways of pruning should be of manageable computational load. Jia Li http://www.stat.psu.edu/∼jiali 

7 .Classification/Decision Trees (II) Minimal Cost-Complexity Pruning Definition for the cost-complexity measure: For any subtree T Tmax , define its complexity as |T ˜ |, the number of terminal nodes in T . Let α ≥ 0 be a real number called the complexity parameter and define the cost-complexity measure Rα (T ) as ˜| . Rα (T ) = R(T ) + α|T Jia Li http://www.stat.psu.edu/∼jiali 

8 .Classification/Decision Trees (II) For each value of α, find the subtree T (α) that minimizes Rα (T ), i.e., Rα (T (α)) = min Rα (T ) . T Tmax If α is small, the penalty for having a large number of terminal nodes is small and T (α) tends to be large. For α sufficiently large, the minimizing subtree T (α) will consist of the root node only. Jia Li http://www.stat.psu.edu/∼jiali 

9 .Classification/Decision Trees (II) Since there are at most a finite number of subtrees of Tmax , Rα (T (α)) yields different values for only finitely many α’s. T (α) continues to be the minimizing tree when α increases until a jump point is reached. Two questions: Is there a unique subtree T Tmax which minimizes Rα (T )? In the minimizing sequence of trees T1 , T2 , ..., is each subtree obtained by pruning upward from the previous subtree, i.e., does the nesting T1 T2 · · · {t1 } hold? Jia Li http://www.stat.psu.edu/∼jiali 

10 .Classification/Decision Trees (II) Definition: The smallest minimizing subtree T (α) for complexity parameter α is defined by the conditions: 1. Rα (T (α)) = minT Tmax Rα (T ) 2. If Rα (T ) = Rα (T (α)), then T (α) T. If subtree T (α) exists, it must be unique. It can be proved that for every value of α, there exists a smallest minimizing subtree. Jia Li http://www.stat.psu.edu/∼jiali 

11 .Classification/Decision Trees (II) The starting point for the pruning is not Tmax , but rather T1 = T (0), which is the smallest subtree of Tmax satisfying R(T1 ) = R(Tmax ) . Let tL and tR be any two terminal nodes in Tmax descended from the same parent node t. If R(t) = R(tL ) + R(tR ), prune off tL and tR . Continue the process until no more pruning is possible. The resulting tree is T1 . Jia Li http://www.stat.psu.edu/∼jiali 

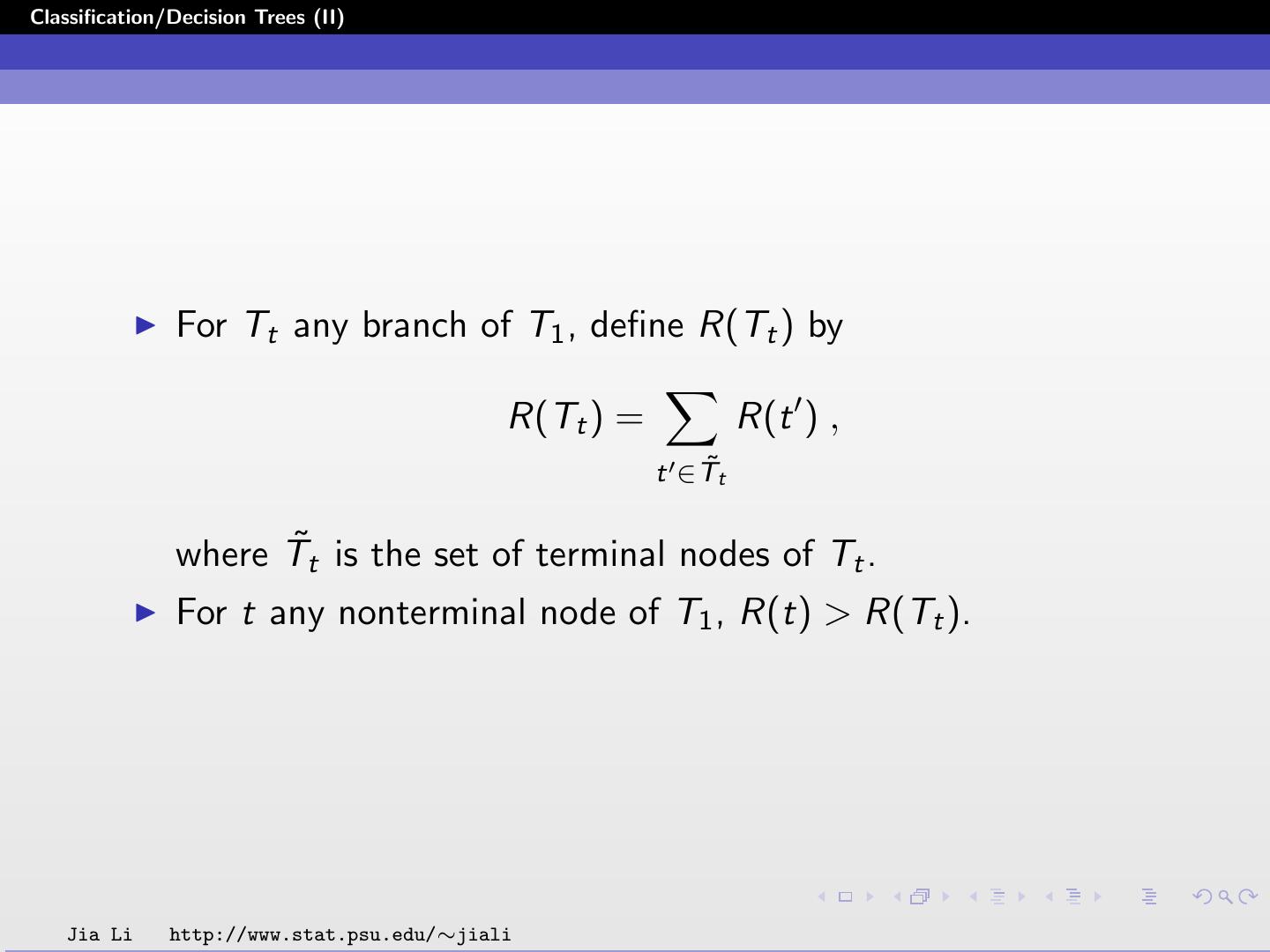
12 .Classification/Decision Trees (II) For Tt any branch of T1 , define R(Tt ) by R(Tt ) = R(t ) , t ∈T˜t where T˜t is the set of terminal nodes of Tt . For t any nonterminal node of T1 , R(t) > R(Tt ). Jia Li http://www.stat.psu.edu/∼jiali 

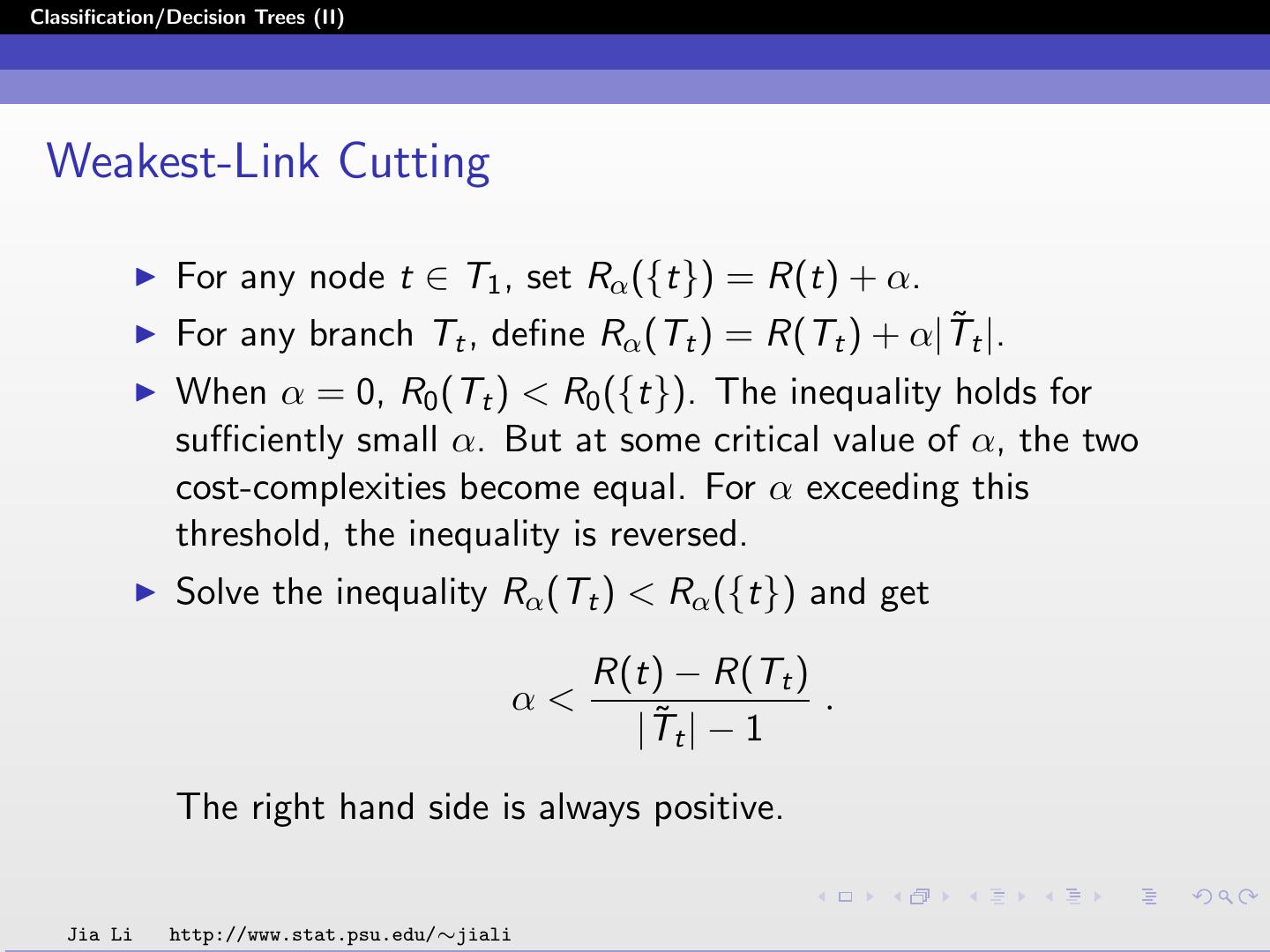
13 .Classification/Decision Trees (II) Weakest-Link Cutting For any node t ∈ T1 , set Rα ({t}) = R(t) + α. ˜t |. For any branch Tt , define Rα (Tt ) = R(Tt ) + α|T When α = 0, R0 (Tt ) < R0 ({t}). The inequality holds for sufficiently small α. But at some critical value of α, the two cost-complexities become equal. For α exceeding this threshold, the inequality is reversed. Solve the inequality Rα (Tt ) < Rα ({t}) and get R(t) − R(Tt ) α< . ˜t | − 1 |T The right hand side is always positive. Jia Li http://www.stat.psu.edu/∼jiali 

14 .Classification/Decision Trees (II) Define a function g1 (t), t ∈ T1 by R(t)−R(Tt ) ˜1 ˜ t |−1 , |T t∈ /T g1 (t) = +∞, t∈T˜1 Define the weakest link ¯t1 in T1 as the node such that g1 (¯t1 ) = min g1 (t) . t∈T1 and put α2 = g1 (¯t1 ). Jia Li http://www.stat.psu.edu/∼jiali 

15 .Classification/Decision Trees (II) When α increases, ¯t1 is the first node that becomes more preferable than the branch T¯t1 descended from it. α2 is the first value after α1 = 0 that yields a strict subtree of T1 with a smaller cost-complexity at this complexity parameter. That is, for all α1 ≤ α < α2 , the tree with smallest cost-complexity is T1 . Let T2 = T1 − T¯t1 . Jia Li http://www.stat.psu.edu/∼jiali 

16 .Classification/Decision Trees (II) Repeat the previous steps. Use T2 instead of T1 , find the weakest link in T2 and prune off at the weakest link node. R(t)−R(T2t ) ˜2 ˜ 2t |−1 , |T t ∈ T2 , t ∈ /T g2 (t) = +∞, t∈T ˜2 g2 (¯t2 ) = min g2 (t) t∈T2 α3 = g2 (¯t2 ) T3 = T2 − T¯t2 If at any stage, there are multiple weakest links, for instance, if gk (¯tk ) = gk (¯tk ), then define Tk+1 = Tk − T¯tk − T¯tk . Two branches are either nested or share no node. Jia Li http://www.stat.psu.edu/∼jiali 

17 .Classification/Decision Trees (II) A decreasing sequence of nested subtrees are obtained: T1 T2 T3 ··· {t1 } . Theorem: The {αk } are an increasing sequence, that is, αk < αk+1 , k ≥ 1, where α1 = 0. For k ≥ 1, αk ≤ α < αk+1 , T (α) = T (αk ) = Tk . Jia Li http://www.stat.psu.edu/∼jiali 

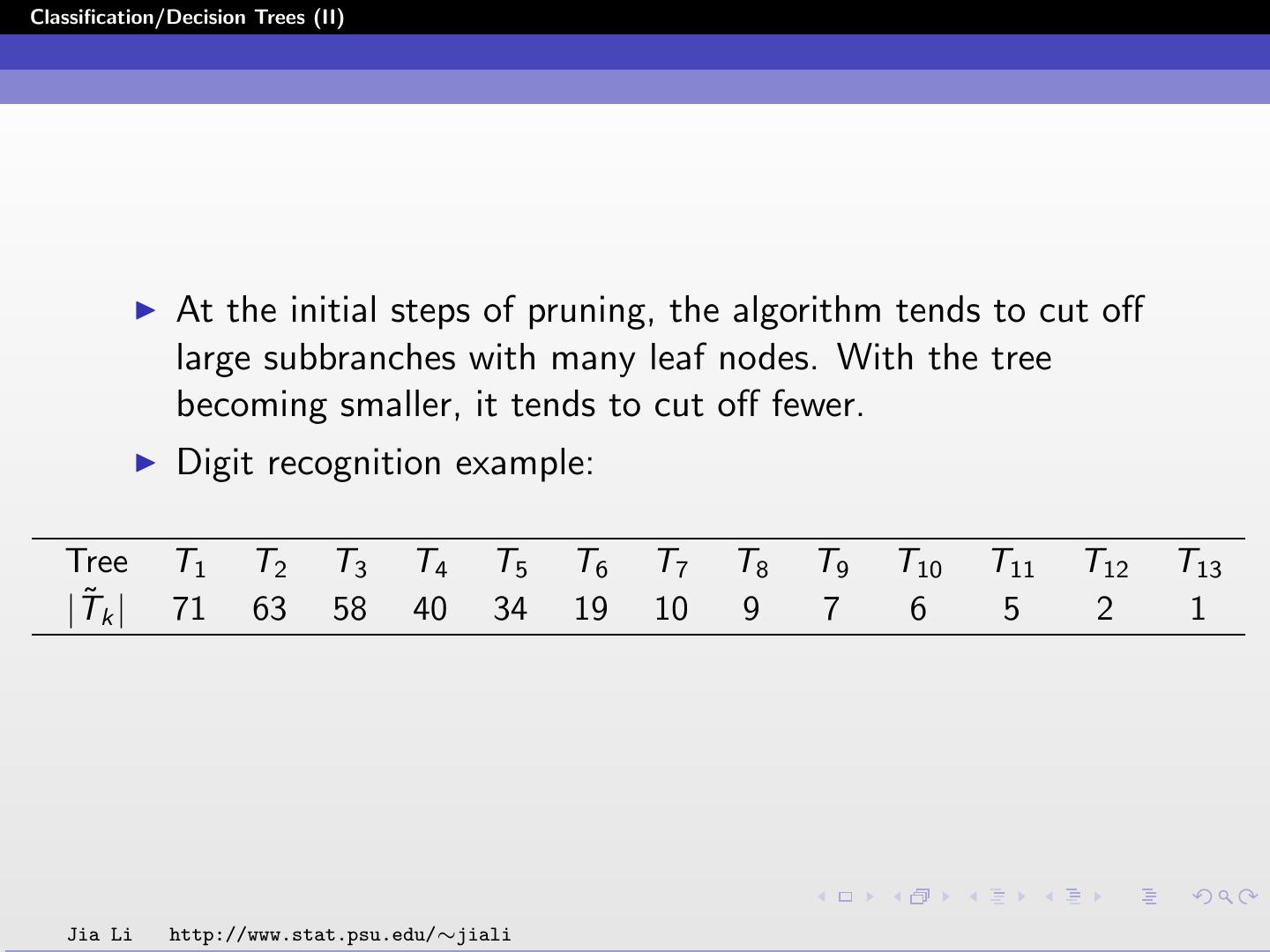
18 .Classification/Decision Trees (II) At the initial steps of pruning, the algorithm tends to cut off large subbranches with many leaf nodes. With the tree becoming smaller, it tends to cut off fewer. Digit recognition example: Tree T1 T2 T3 T4 T5 T6 T7 T8 T9 T10 T11 T12 T13 ˜k | |T 71 63 58 40 34 19 10 9 7 6 5 2 1 Jia Li http://www.stat.psu.edu/∼jiali 

19 .Classification/Decision Trees (II) Best Pruned Subtree Two approaches to choose the best pruned subtree: Use a test sample set. Cross-validation Use a test set to compute the classification error rate of each minimum cost-complexity subtree. Choose the subtree with the minimum test error rate. Cross validation: tree structures are not stable. When the training data set changes slightly, there may be large structural change in the tree. It is difficult to correspond a subtree trained from the entire data set to a subtree trained from a majority part of it. Focus on choosing the right complexity parameter α. Jia Li http://www.stat.psu.edu/∼jiali 

20 .Classification/Decision Trees (II) Pruning by Cross-Validation Consider V -fold cross-validation. The original learning sample L is divided by random selection into V subsets, Lv , v = 1, ..., V . Let the training sample set in each fold be L(v ) = L − Lv . The tree grown on the original set is Tmax . V accessory trees (v ) Tmax are grown on L(v ) . Jia Li http://www.stat.psu.edu/∼jiali 

21 .Classification/Decision Trees (II) For each value of the complexity parameter α, let T (α), T (v ) (α), v = 1, ..., V , be the corresponding minimal (v ) cost-complexity subtrees of Tmax , Tmax . For each maximum tree, we obtain a sequence of jump points of α: α1 < α2 < α3 · · · < αk < · · · . To find the corresponding minimal cost-complexity subtree at α, find αk from the list such that αk ≤ α < αk+1 . Then the subtree corresponding to αk is the subtree for α. Jia Li http://www.stat.psu.edu/∼jiali 

22 .Classification/Decision Trees (II) The cross-validation error rate of T (α) is computed by V (v ) 1 Nmiss R CV (T (α)) = (v ) , V N v =1 where N (v ) is the number of samples in the test set Lv in fold (v ) v ; and Nmiss is the number of misclassified samples in Lv (v ) using T (v ) (α), a pruned tree of Tmax trained from L(v ) . Although α is continuous, there are only finite minimum cost-complexity trees grown on L. Jia Li http://www.stat.psu.edu/∼jiali 

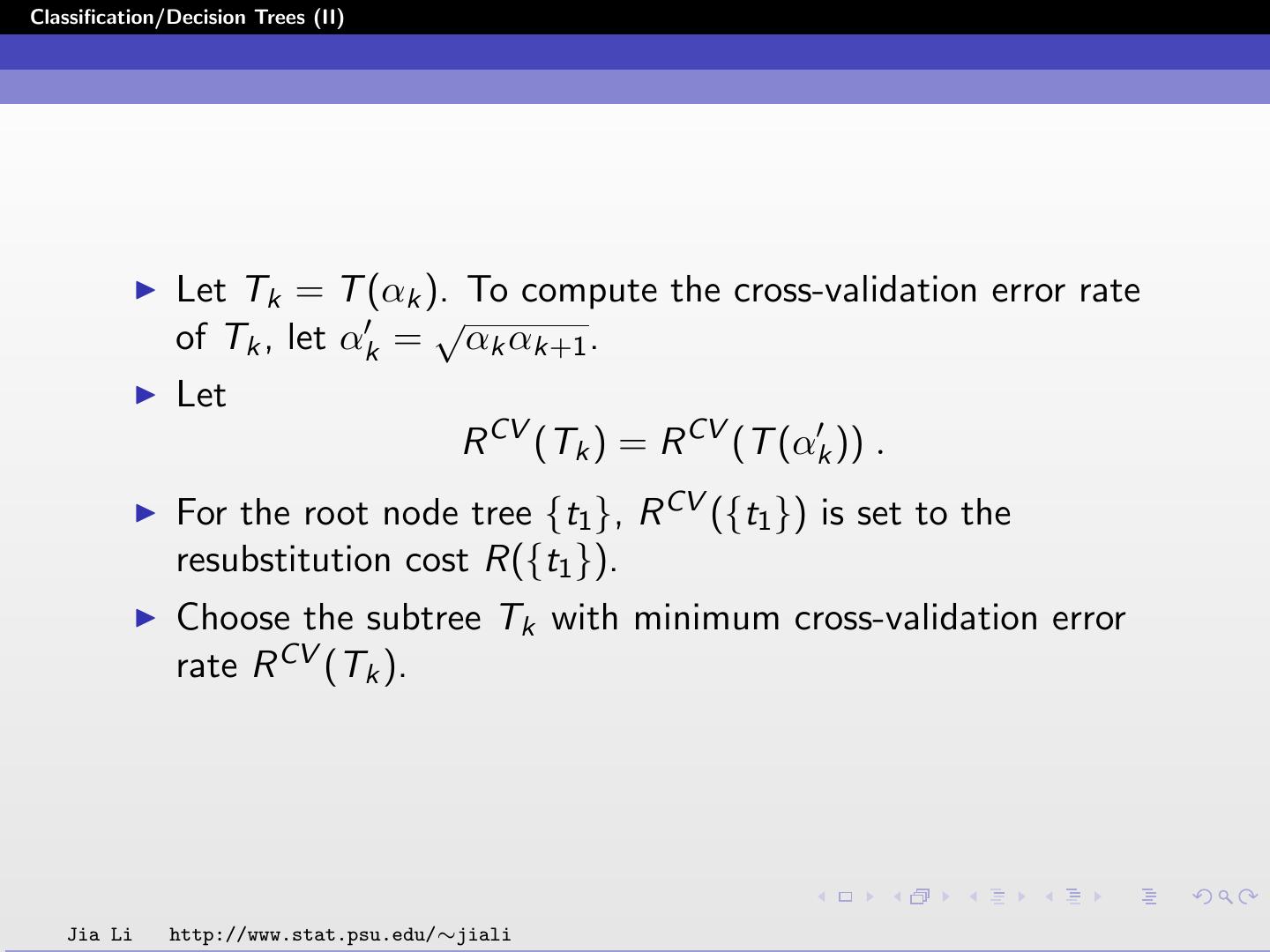
23 .Classification/Decision Trees (II) Let Tk = T (αk ). To compute the cross-validation error rate √ of Tk , let αk = αk αk+1 . Let R CV (Tk ) = R CV (T (αk )) . For the root node tree {t1 }, R CV ({t1 }) is set to the resubstitution cost R({t1 }). Choose the subtree Tk with minimum cross-validation error rate R CV (Tk ). Jia Li http://www.stat.psu.edu/∼jiali 

24 .Classification/Decision Trees (II) Computation Involved 1. Grow V + 1 maximum trees. 2. For each of the V + 1 trees, find the sequence of subtrees with minimum cost-complexity. 3. Suppose the maximum tree grown on the original data set Tmax has K subtrees. 4. For each of the (K − 1) αk , compute the misclassification rate of each of the V test sample set, average the error rates and set the mean to the cross-validation error rate. 5. Find the subtree of Tmax with minimum R CV (Tk ). Jia Li http://www.stat.psu.edu/∼jiali