classification/decision trees（I）

1 .Classification/Decision Trees (I) Classification/Decision Trees (I) Jia Li Department of Statistics The Pennsylvania State University Email: jiali@stat.psu.edu http://www.stat.psu.edu/∼jiali Jia Li http://www.stat.psu.edu/∼jiali 

2 .Classification/Decision Trees (I) Tree Structured Classifier Reference: Classification and Regression Trees by L. Breiman, J. H. Friedman, R. A. Olshen, and C. J. Stone, Chapman & Hall, 1984. A Medical Example (CART): Predict high risk patients who will not survive at least 30 days on the basis of the initial 24-hour data. 19 variables are measured during the first 24 hours. These include blood pressure, age, etc. Jia Li http://www.stat.psu.edu/∼jiali 

3 .Classification/Decision Trees (I) A tree structure classification rule for the medical example Jia Li http://www.stat.psu.edu/∼jiali 

4 .Classification/Decision Trees (I) Denote the feature space by X . The input vector X ∈ X contains p features X1 , X2 , ..., Xp , some of which may be categorical. Tree structured classifiers are constructed by repeated splits of subsets of X into two descendant subsets, beginning with X itself. Definitions: node, terminal node (leaf node), parent node, child node. The union of the regions occupied by two child nodes is the region occupied by their parent node. Every leaf node is assigned with a class. A query is associated with class of the leaf node it lands in. Jia Li http://www.stat.psu.edu/∼jiali 

5 .Classification/Decision Trees (I) Notation A node is denoted by t. Its left child node is denoted by tL and right by tR . The collection of all the nodes is denoted by T ; and the ˜. collection of all the leaf nodes by T A split is denoted by s. The set of splits is denoted by S. Jia Li http://www.stat.psu.edu/∼jiali 

6 .Classification/Decision Trees (I) Jia Li http://www.stat.psu.edu/∼jiali 

7 .Classification/Decision Trees (I) The Three Elements The construction of a tree involves the following three elements: 1. The selection of the splits. 2. The decisions when to declare a node terminal or to continue splitting it. 3. The assignment of each terminal node to a class. Jia Li http://www.stat.psu.edu/∼jiali 

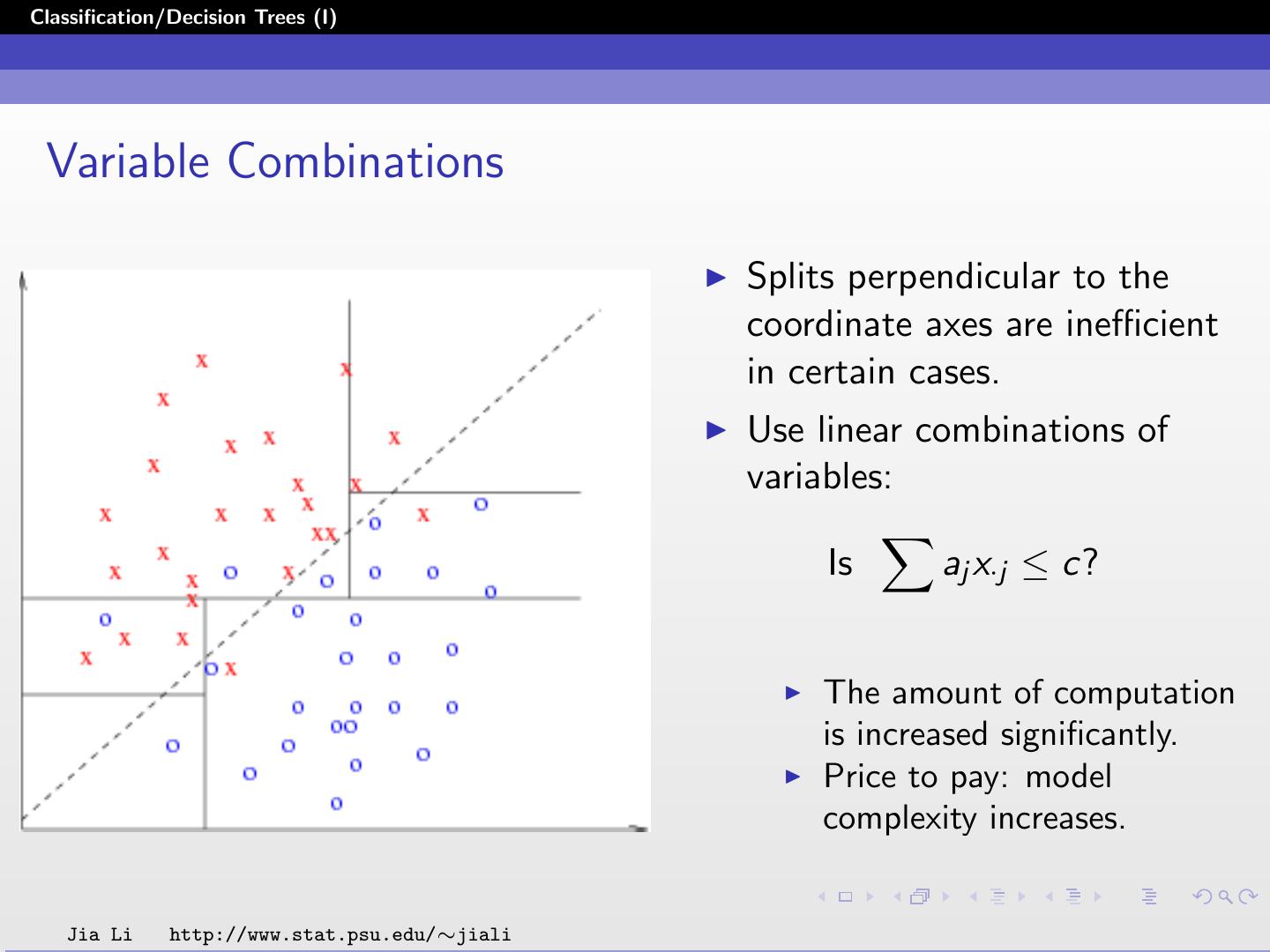
8 .Classification/Decision Trees (I) In particular, we need to decide the following: 1. A set Q of binary questions of the form {Is X ∈ A?}, A ⊆ X . 2. A goodness of split criterion Φ(s, t) that can be evaluated for any split s of any node t. 3. A stop-splitting rule. 4. A rule for assigning every terminal node to a class. Jia Li http://www.stat.psu.edu/∼jiali 

9 .Classification/Decision Trees (I) Standard Set of Questions The input vector X = (X1 , X2 , ..., Xp ) contains features of both categorical and ordered types. Each split depends on the value of only a unique variable. For each ordered variable Xj , Q includes all questions of the form {Is Xj ≤ c?} for all real-valued c. Since the training data set is finite, there are only finitely many distinct splits that can be generated by the question {Is Xj ≤ c?}. Jia Li http://www.stat.psu.edu/∼jiali 

10 .Classification/Decision Trees (I) If Xj is categorical, taking values, say in{1, 2, ..., M}, then Q contains all questions of the form {Is Xj ∈ A?} . A ranges over all subsets of {1, 2, ..., M}. The splits for all p variables constitute the standard set of questions. Jia Li http://www.stat.psu.edu/∼jiali 

11 .Classification/Decision Trees (I) Goodness of Split The goodness of split is measured by an impurity function defined for each node. Intuitively, we want each leaf node to be “pure”, that is, one class dominates. Jia Li http://www.stat.psu.edu/∼jiali 

12 .Classification/Decision Trees (I) The Impurity Function Definition: An impurity function is a function φ defined on the set of all K -tuples of numbers (p1 , ..., pK ) satisfying pj ≥ 0, j = 1, ..., K , j pj = 1 with the properties: 1. φ is a maximum only at the point ( K1 , K1 , ..., K1 ). 2. φ achieves its minimum only at the points (1, 0, ..., 0), (0, 1, 0, ..., 0), ..., (0, 0, ..., 0, 1). 3. φ is a symmetric function of p1 , ..., pK , i.e., if you permute pj , φ remains constant. Jia Li http://www.stat.psu.edu/∼jiali 

13 .Classification/Decision Trees (I) Definition: Given an impurity function φ, define the impurity measure i(t) of a node t as i(t) = φ(p(1 | t), p(2 | t), ..., p(K | t)) , where p(j | t) is the estimated probability of class j within node t. Goodness of a split s for node t, denoted by Φ(s, t), is defined by Φ(s, t) = ∆i(s, t) = i(t) − pR i(tR ) − pL i(tL ) , where pR and pL are the proportions of the samples in node t that go to the right node tR and the left node tL respectively. Jia Li http://www.stat.psu.edu/∼jiali 

14 .Classification/Decision Trees (I) Define I (t) = i(t)p(t), that is, the impurity function of node t weighted by the estimated proportion of data that go to node t. The impurity of tree T , I (T ) is defined by I (T ) = I (t) = i(t)p(t) . ˜ t∈T ˜ t∈T Note for any node t the following equations hold: p(tL ) + p(tR ) = p(t) pL = p(tL )/p(t), pR = p(tR )/p(t) pL + pR = 1 Jia Li http://www.stat.psu.edu/∼jiali 

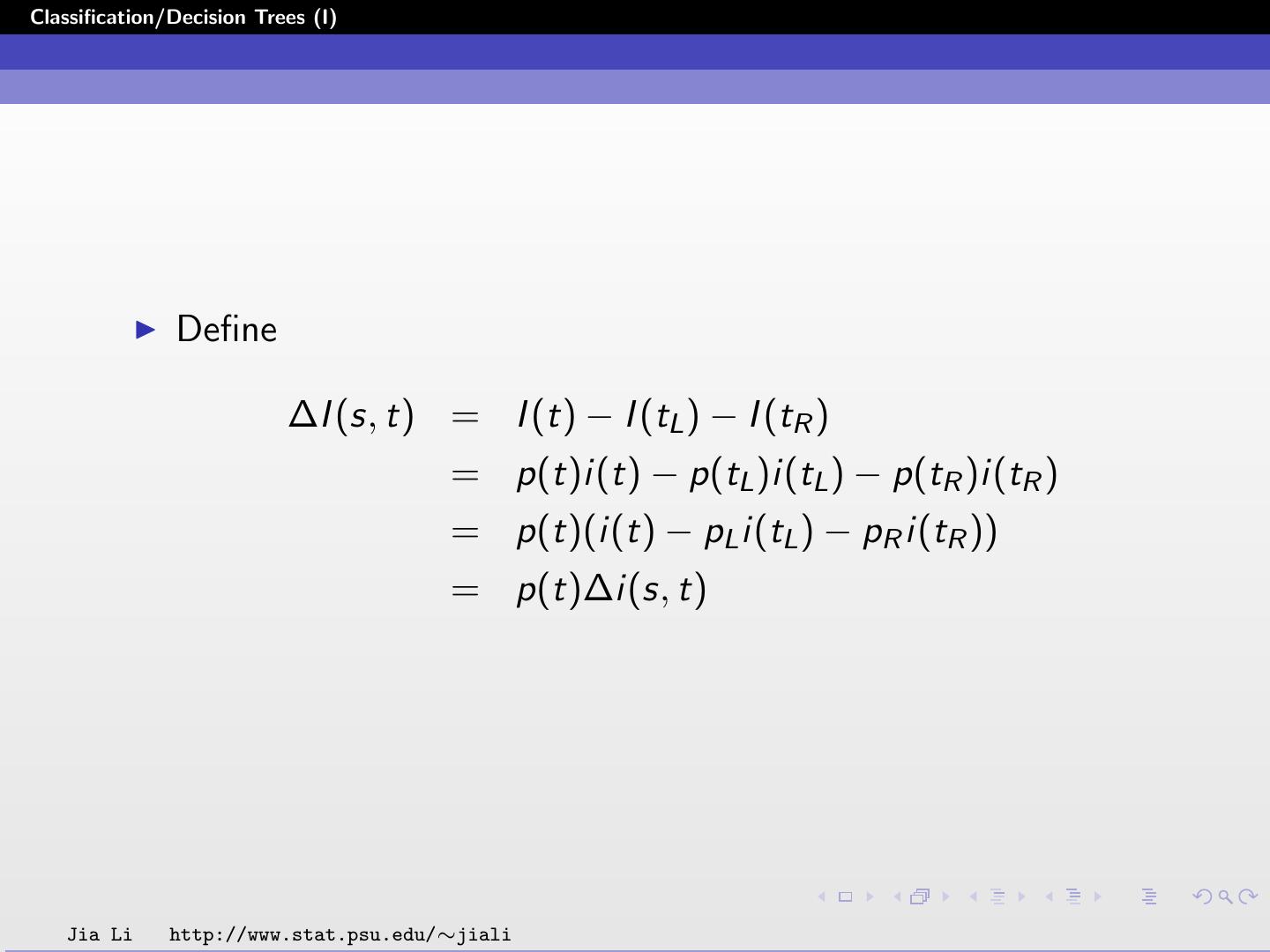
15 .Classification/Decision Trees (I) Define ∆I (s, t) = I (t) − I (tL ) − I (tR ) = p(t)i(t) − p(tL )i(tL ) − p(tR )i(tR ) = p(t)(i(t) − pL i(tL ) − pR i(tR )) = p(t)∆i(s, t) Jia Li http://www.stat.psu.edu/∼jiali 

16 .Classification/Decision Trees (I) Possible impurity function: K 1. Entropy: j=1 pj log p1j . If pj = 0, use the limit limpj →0 pj log pj = 0. 2. Misclassification rate: 1 − maxj pj . K K 3. Gini index: j=1 pj (1 − pj ) = 1 − j=1 pj2 . Gini index seems to work best in practice for many problems. The twoing rule: At a node t, choose the split s that maximizes  2 pL pR  |p(j | tL ) − p(j | tR )| . 4 j Jia Li http://www.stat.psu.edu/∼jiali 

17 .Classification/Decision Trees (I) Estimate the posterior probabilities of classes in each node The total number of samples is N and the number of samples in class j, 1 ≤ j ≤ K , is Nj . The number of samples going to node t is N(t); the number of samples with class j going to node t is Nj (t). K j=1 Nj (t) = N(t). Nj (tL ) + Nj (tR ) = Nj (t). For a full tree (balanced), the sum of N(t) over all the t’s at the same level is N. Jia Li http://www.stat.psu.edu/∼jiali 

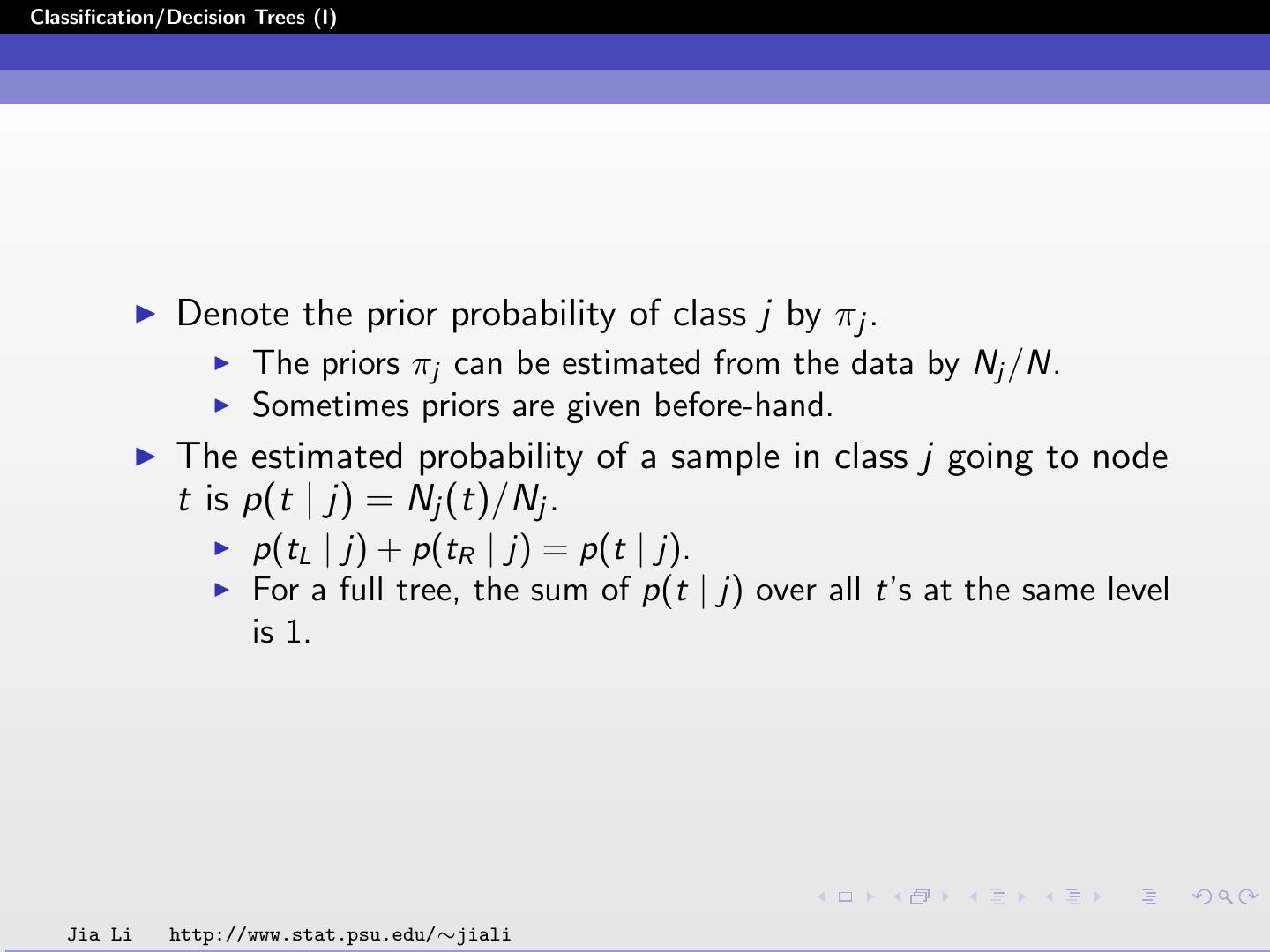
18 .Classification/Decision Trees (I) Denote the prior probability of class j by πj . The priors πj can be estimated from the data by Nj /N. Sometimes priors are given before-hand. The estimated probability of a sample in class j going to node t is p(t | j) = Nj (t)/Nj . p(tL | j) + p(tR | j) = p(t | j). For a full tree, the sum of p(t | j) over all t’s at the same level is 1. Jia Li http://www.stat.psu.edu/∼jiali 

19 .Classification/Decision Trees (I) The joint probability of a sample being in class j and going to node t is thus: p(j, t) = πj p(t | j) = πj Nj (t)/Nj . The probability of any sample going to node t is: K K p(t) = p(j, t) = πj Nj (t)/Nj . j=1 j=1 Note p(tL ) + p(tR ) = p(t). The probability of a sample being in class j given that it goes to node t is: p(j | t) = p(j, t)/p(t) . K For any t, j=1 p(j | t) = 1. Jia Li http://www.stat.psu.edu/∼jiali 

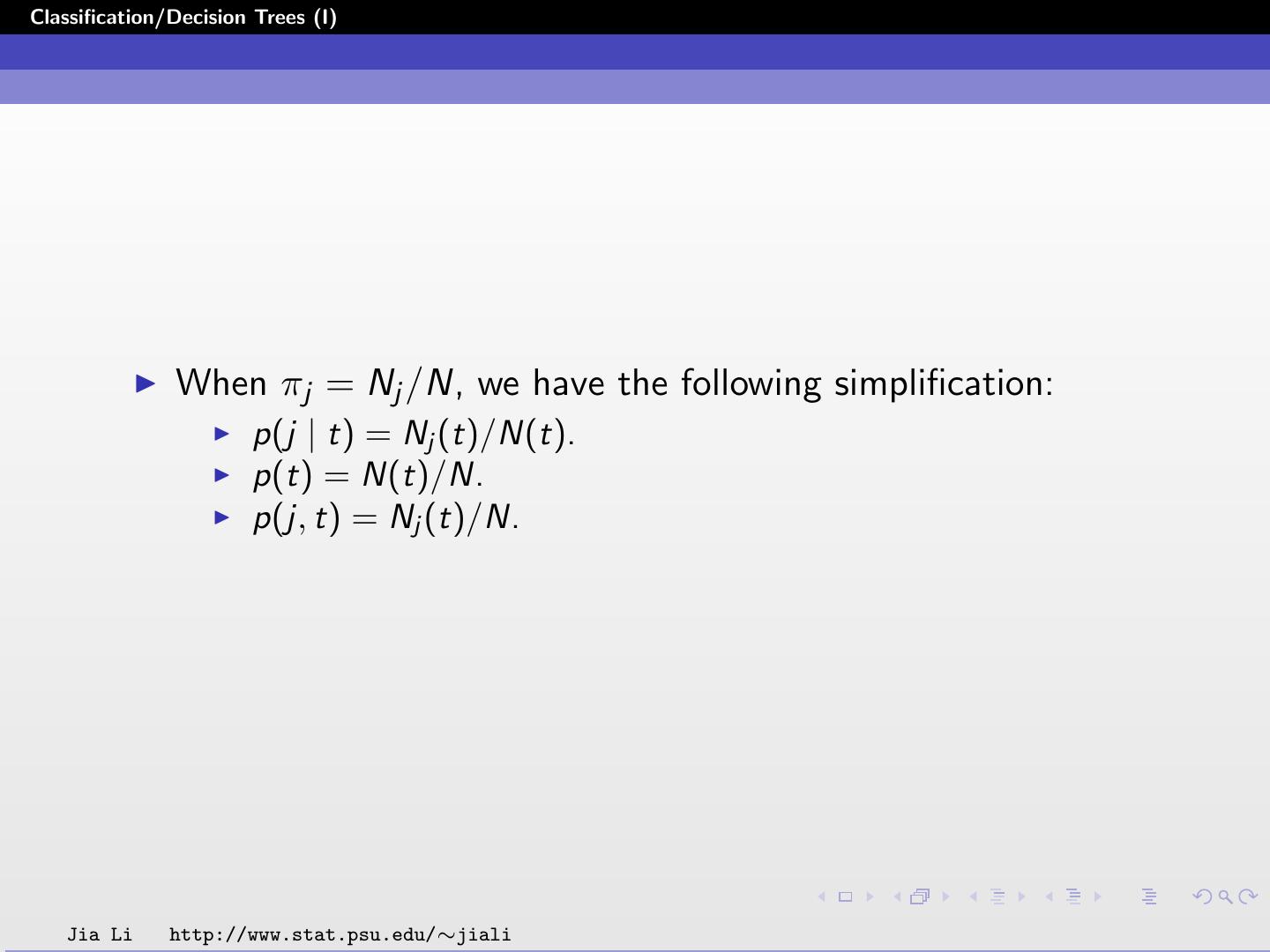
20 .Classification/Decision Trees (I) When πj = Nj /N, we have the following simplification: p(j | t) = Nj (t)/N(t). p(t) = N(t)/N. p(j, t) = Nj (t)/N. Jia Li http://www.stat.psu.edu/∼jiali 

21 .Classification/Decision Trees (I) Stopping Criteria A simple criteria: stop splitting a node t when max ∆I (s, t) < β , s∈S where β is a chosen threshold. The above stopping criteria is unsatisfactory. A node with a small decrease of impurity after one step of splitting may have a large decrease after multiple levels of splits. Jia Li http://www.stat.psu.edu/∼jiali 

22 .Classification/Decision Trees (I) Class Assignment Rule A class assignment rule assigns a class j = {1, ..., K } to every ˜ . The class assigned to node t ∈ T terminal node t ∈ T ˜ is denoted by κ(t). For 0-1 loss, the class assignment rule is: κ(t) = arg max p(j | t) . j Jia Li http://www.stat.psu.edu/∼jiali 

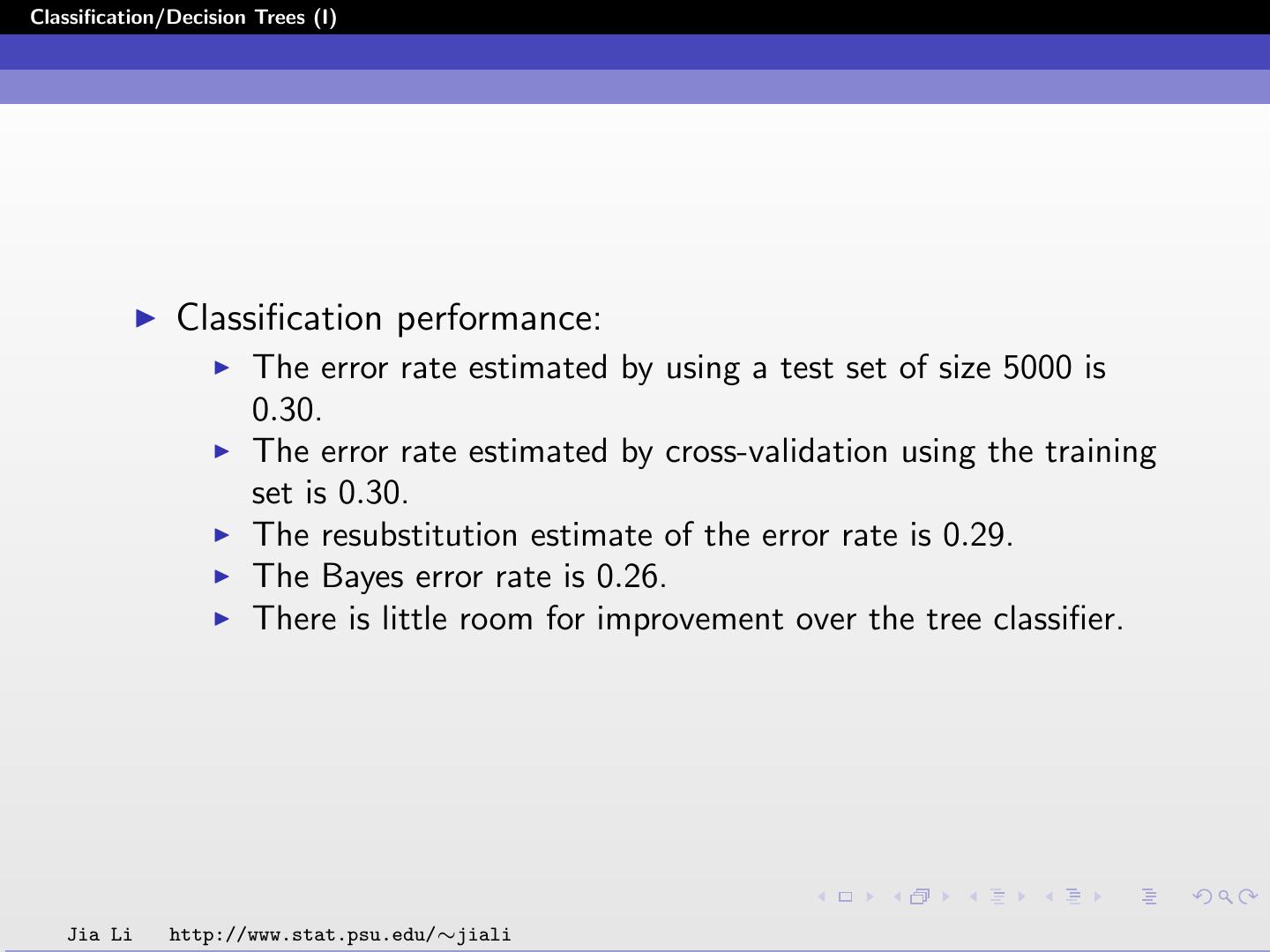
23 .Classification/Decision Trees (I) The resubstitution estimate r (t) of the probability of misclassification, given that a case falls into node t is r (t) = 1 − max p(j | t) = 1 − p(κ(t) | t) . j Denote R(t) = r (t)p(t). The resubstitution estimate for the overall misclassification rate R(T ) of the tree classifier T is: R(T ) = R(t) . ˜ t∈T Jia Li http://www.stat.psu.edu/∼jiali 

24 .Classification/Decision Trees (I) Proposition: For any split of a node t into tL and tR , R(t) ≥ R(tL ) + R(tR ) . Proof: Denote j ∗ = κ(t). p(j ∗ | t) = p(j ∗ , tL | t) + p(j ∗ , tR | t) = p(j ∗ | tL )p(tL | t) + p(j ∗ | tR )p(tR | t) = pL p(j ∗ | tL ) + pR p(j ∗ | tR ) ≤ pL max p(j | tL ) + pR max p(j | tR ) j j Jia Li http://www.stat.psu.edu/∼jiali 

25 .Classification/Decision Trees (I) Hence, r (t) = 1 − p(j ∗ | t) ≥ 1 − pL max p(j | tL ) + pR max p(j | tR ) j j = pL (1 − max p(j | tL )) + pR (1 − max p(j | tR )) j j = pL r (tL ) + pR r (tR ) Finally, R(t) = p(t)r (t) ≥ p(t)pL r (tL ) + p(t)pR r (tR ) = p(tL )r (tL ) + p(tR )r (tR ) = R(tL ) + R(tR ) Jia Li http://www.stat.psu.edu/∼jiali 

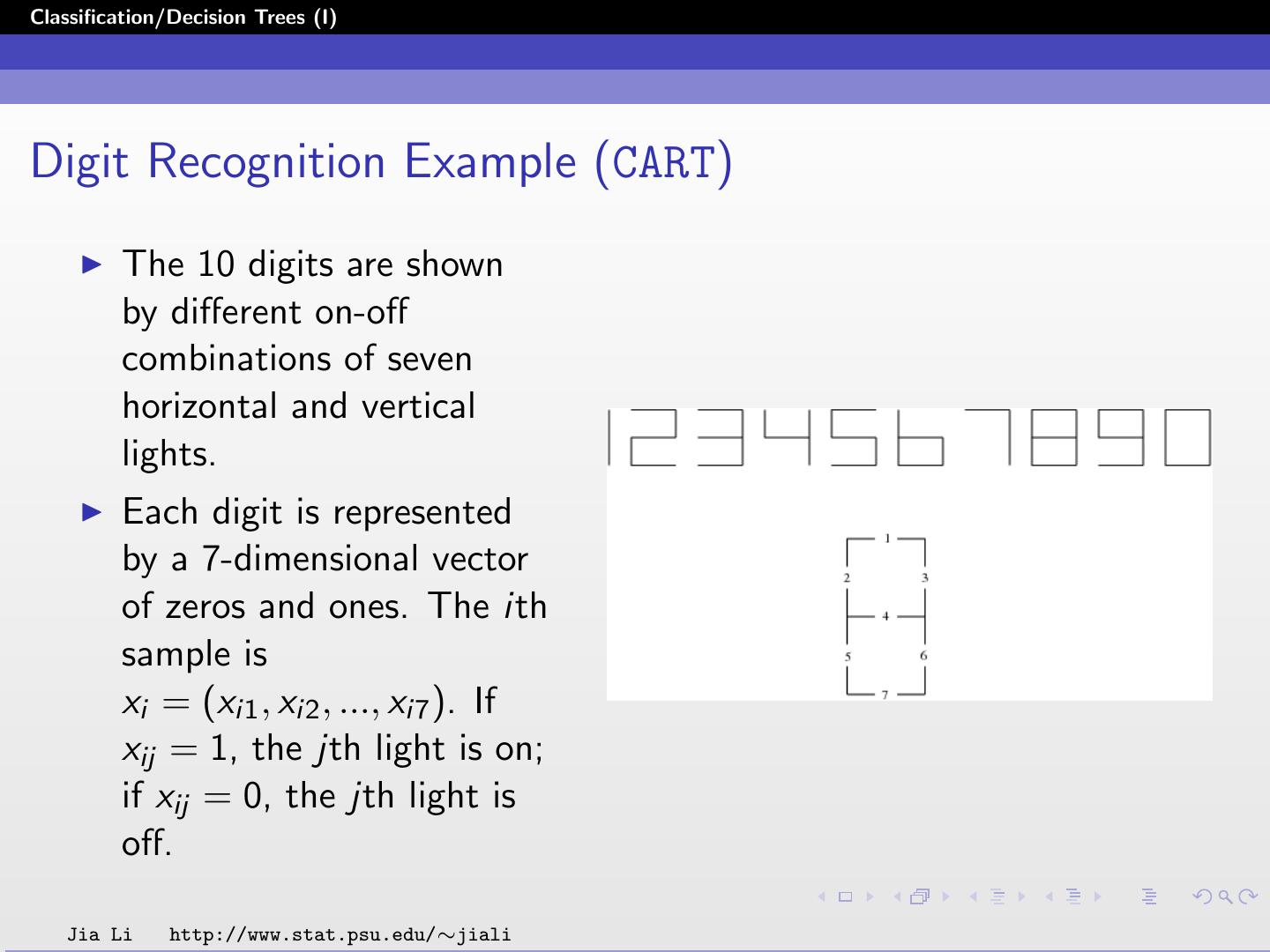
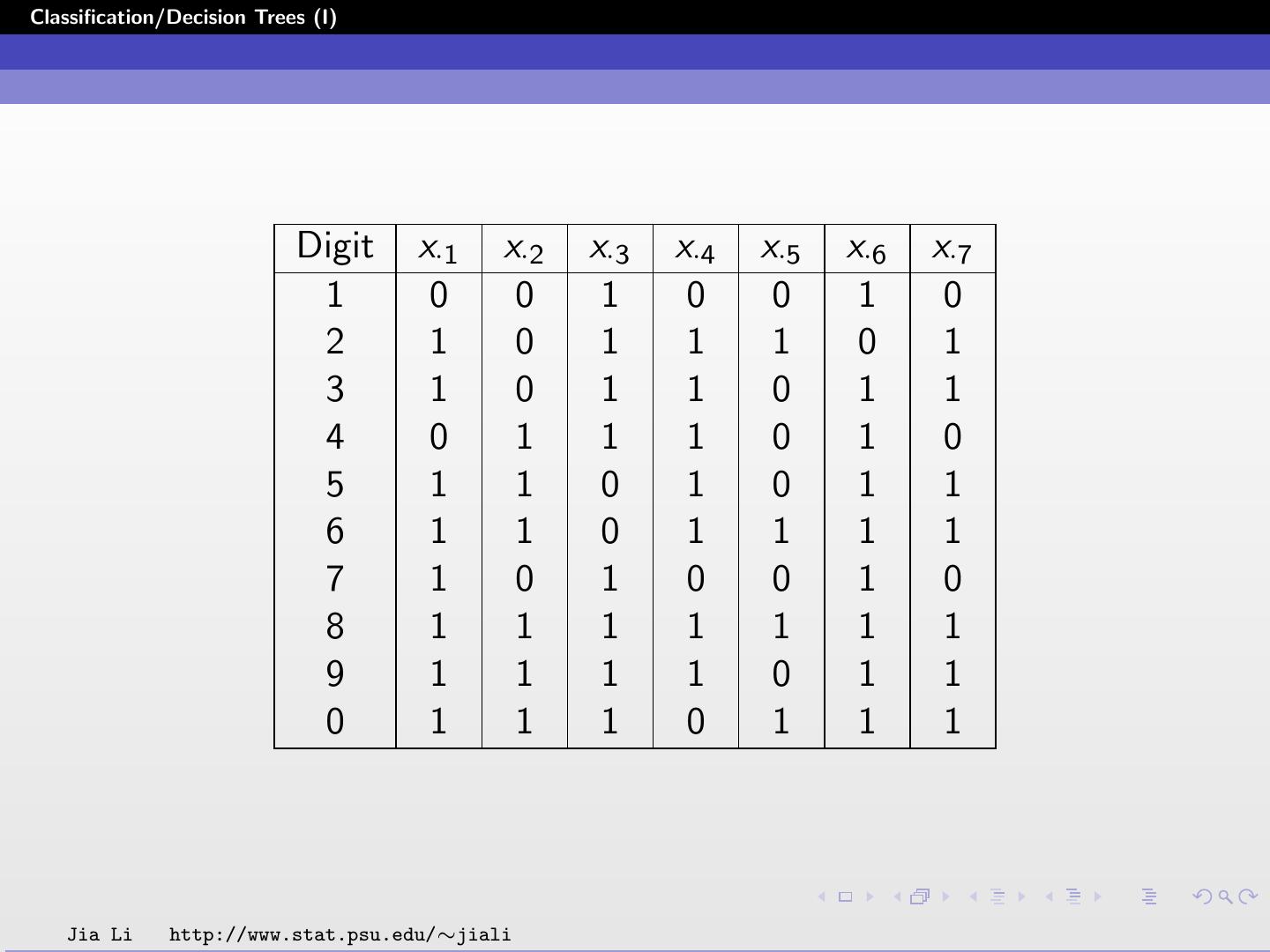
26 .Classification/Decision Trees (I) Digit Recognition Example (CART) The 10 digits are shown by different on-off combinations of seven horizontal and vertical lights. Each digit is represented by a 7-dimensional vector of zeros and ones. The ith sample is xi = (xi1 , xi2 , ..., xi7 ). If xij = 1, the jth light is on; if xij = 0, the jth light is off. Jia Li http://www.stat.psu.edu/∼jiali 

27 .Classification/Decision Trees (I) Digit x·1 x·2 x·3 x·4 x·5 x·6 x·7 1 0 0 1 0 0 1 0 2 1 0 1 1 1 0 1 3 1 0 1 1 0 1 1 4 0 1 1 1 0 1 0 5 1 1 0 1 0 1 1 6 1 1 0 1 1 1 1 7 1 0 1 0 0 1 0 8 1 1 1 1 1 1 1 9 1 1 1 1 0 1 1 0 1 1 1 0 1 1 1 Jia Li http://www.stat.psu.edu/∼jiali 

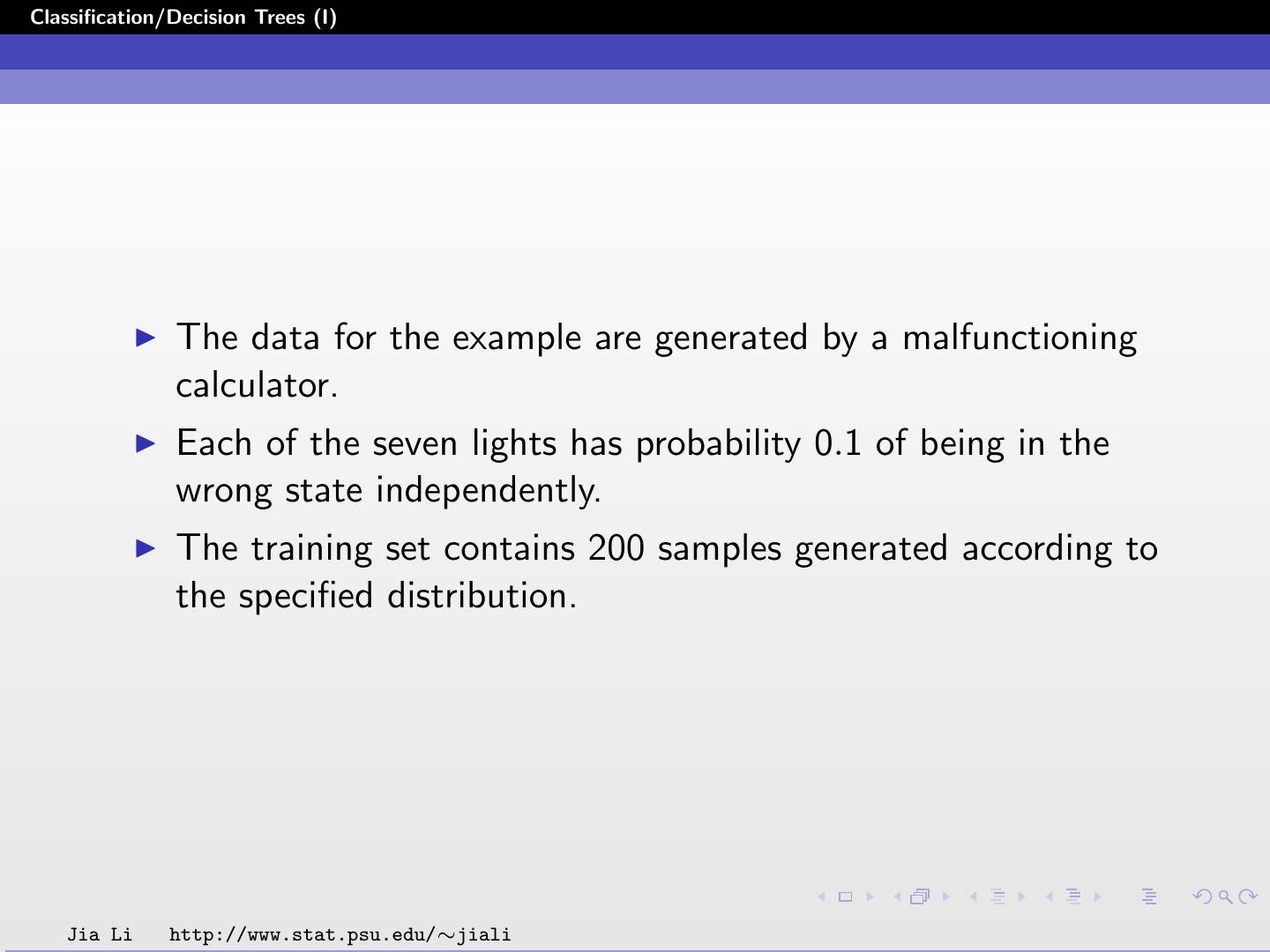
28 .Classification/Decision Trees (I) The data for the example are generated by a malfunctioning calculator. Each of the seven lights has probability 0.1 of being in the wrong state independently. The training set contains 200 samples generated according to the specified distribution. Jia Li http://www.stat.psu.edu/∼jiali 

29 .Classification/Decision Trees (I) A tree structured classifier is applied. The set of questions Q contains: Is x·j = 0?, j = 1, 2, ..., 7. The twoing rule is used in splitting. The pruning cross-validation method is used to choose the right sized tree. Jia Li http://www.stat.psu.edu/∼jiali