bagging and boosting: brief introduction

1 .Bagging and Boosting: Brief Introduction Bagging and Boosting: Brief Introduction Jia Li Department of Statistics The Pennsylvania State University Email: jiali@stat.psu.edu http://www.stat.psu.edu/∼jiali Jia Li http://www.stat.psu.edu/∼jiali 

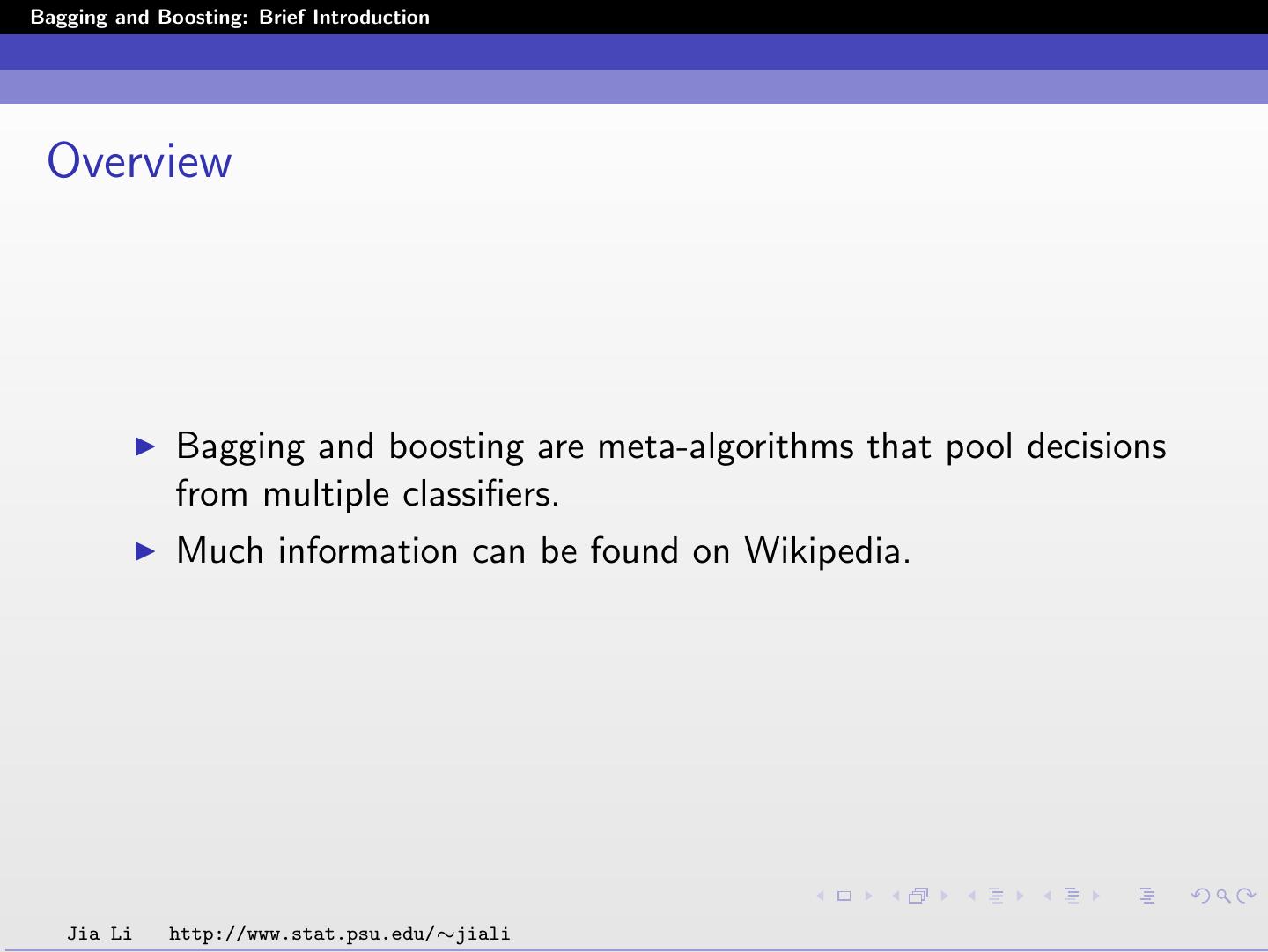
2 .Bagging and Boosting: Brief Introduction Overview Bagging and boosting are meta-algorithms that pool decisions from multiple classifiers. Much information can be found on Wikipedia. Jia Li http://www.stat.psu.edu/∼jiali 

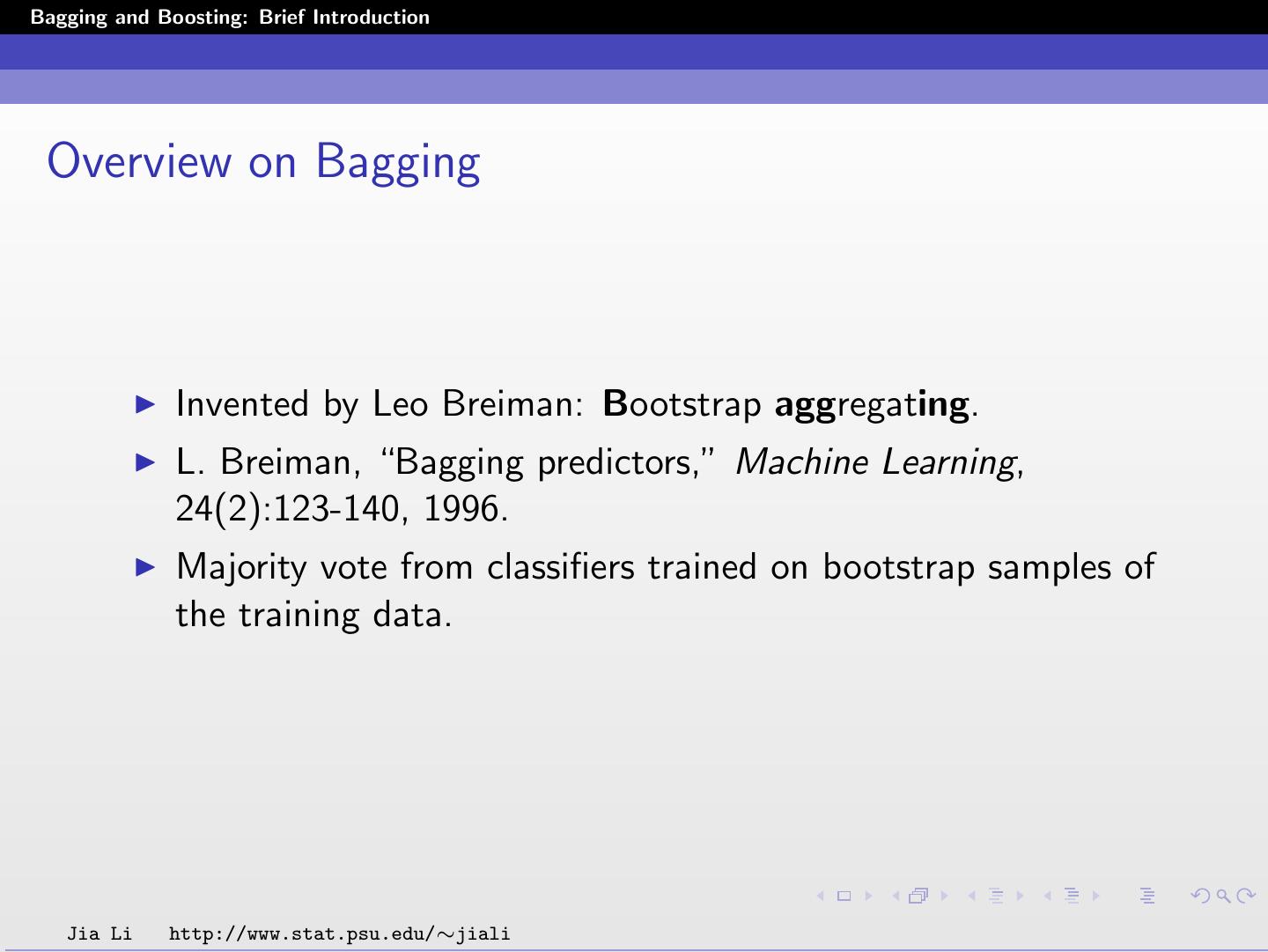
3 .Bagging and Boosting: Brief Introduction Overview on Bagging Invented by Leo Breiman: Bootstrap aggregating. L. Breiman, “Bagging predictors,” Machine Learning, 24(2):123-140, 1996. Majority vote from classifiers trained on bootstrap samples of the training data. Jia Li http://www.stat.psu.edu/∼jiali 

4 .Bagging and Boosting: Brief Introduction Bagging Generate B bootstrap samples of the training data: random sampling with replacement. Train a classifier or a regression function using each bootstrap sample. For classification: majority vote on the classification results. For regression: average on the predicted values. Reduces variation. Improves performance for unstable classifiers which vary significantly with small changes in the data set, e.g., CART. Found to improve CART a lot, but not the nearest neighbor classifier. Jia Li http://www.stat.psu.edu/∼jiali 

5 .Bagging and Boosting: Brief Introduction Overview on Boosting Iteratively learning weak classifiers Final result is the weighted sum of the results of weak classifiers. Many different kinds of boosting algorithms: Adaboost (Adaptive boosting) by Y. Freund and R. Schapire is the first. Examples of other boosting algorithms: LPBoost: Linear Programming Boosting is a margin-maximizing classification algorithm with boosting. BrownBoost: increase robustness against noisy datasets. Discard points that are repeatedly misclassified. LogitBoost: J. Friedman, T. Hastie and R. Tibshirani, “Additive logistic regression: a statistical view of boosting,” Annals of Statistics, 28(2), 337-407, 2000. Jia Li http://www.stat.psu.edu/∼jiali 

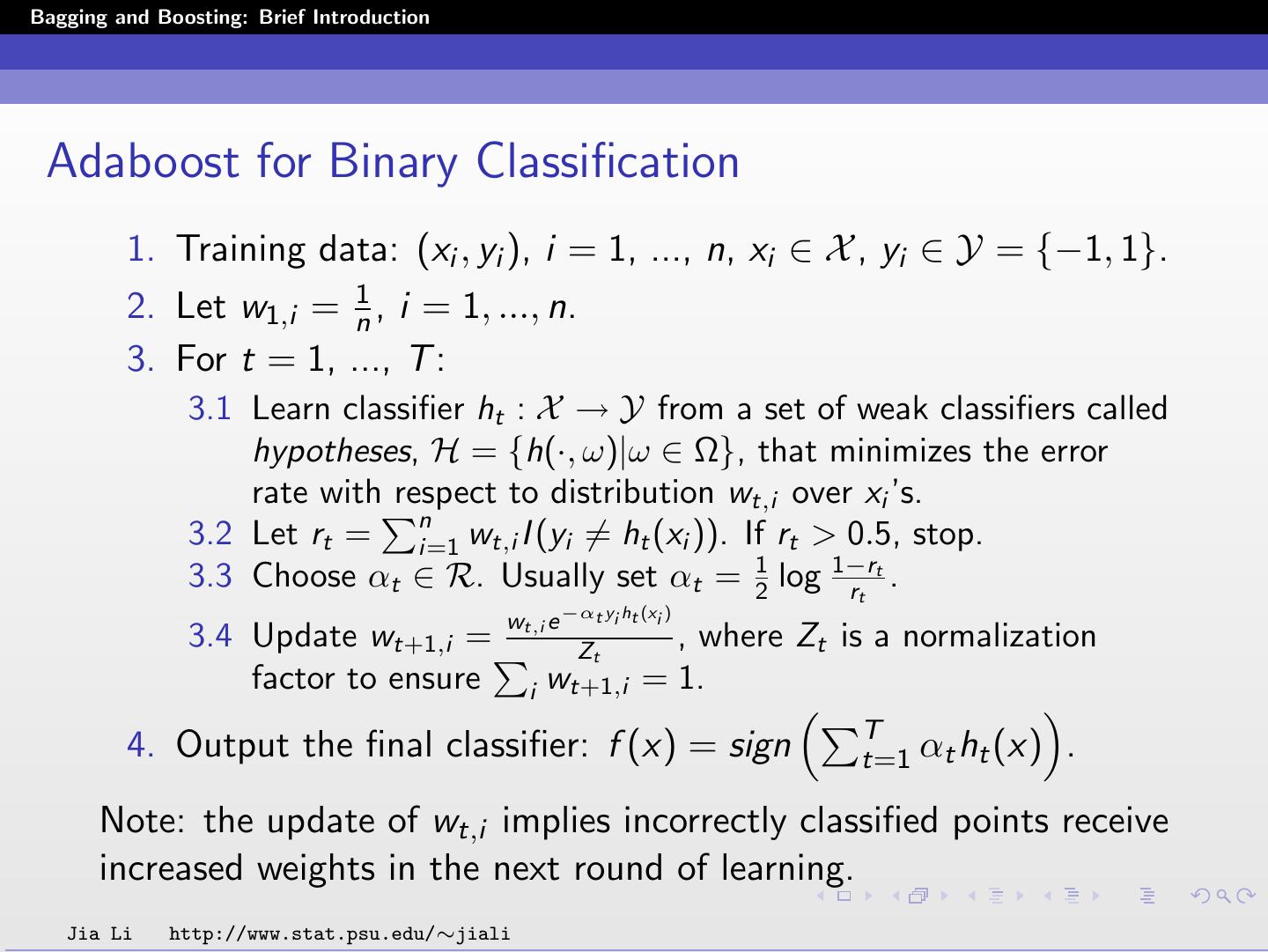
6 .Bagging and Boosting: Brief Introduction Adaboost for Binary Classification 1. Training data: (xi , yi ), i = 1, ..., n, xi ∈ X , yi ∈ Y = {−1, 1}. 2. Let w1,i = n1 , i = 1, ..., n. 3. For t = 1, ..., T : 3.1 Learn classifier ht : X → Y from a set of weak classifiers called hypotheses, H = {h(·, ω)|ω ∈ Ω}, that minimizes the error rate with respect to distribution wt,i over xi ’s. n 3.2 Let rt = i=1 wt,i I (yi = ht (xi )). If rt > 0.5, stop. 3.3 Choose αt ∈ R. Usually set αt = 12 log 1−r rt . t wt,i e −αt yi ht (xi ) 3.4 Update wt+1,i = Zt , where Zt is a normalization factor to ensure i w t+1,i = 1. T 4. Output the final classifier: f (x) = sign t=1 αt ht (x) . Note: the update of wt,i implies incorrectly classified points receive increased weights in the next round of learning. Jia Li http://www.stat.psu.edu/∼jiali