- 快召唤伙伴们来围观吧
- 微博 QQ QQ空间 贴吧
- 文档嵌入链接
- 复制
- 微信扫一扫分享
- 已成功复制到剪贴板
World Models
展开查看详情
1 . World Models David Ha 1 Jurgen ¨ Schmidhuber 2 3 Abstract We explore building generative neural network models of popular reinforcement learning arXiv:1803.10122v4 [cs.LG] 9 May 2018 environments. Our world model can be trained quickly in an unsupervised manner to learn a compressed spatial and temporal representation of the environment. By using features extracted from the world model as inputs to an agent, we can train a very compact and simple policy that can solve the required task. We can even train our agent entirely inside of its own hallucinated dream generated by its world model, and transfer this policy back into the actual environment. An interactive version of this paper is available at Figure 1. A World Model, from Scott McCloud’s Understanding Comics. (McCloud, 1993; E, 2012) https://worldmodels.github.io current motor actions (Keller et al., 2012; Leinweber et al., 2017). We are able to instinctively act on this predictive 1. Introduction model and perform fast reflexive behaviours when we face danger (Mobbs et al., 2015), without the need to consciously Humans develop a mental model of the world based on plan out a course of action. what they are able to perceive with their limited senses. The decisions and actions we make are based on this internal Take baseball for example. A batter has milliseconds to de- model. Jay Wright Forrester, the father of system dynamics, cide how they should swing the bat – shorter than the time described a mental model as: it takes for visual signals to reach our brain. The reason we are able to hit a 100 mph fastball is due to our ability to The image of the world around us, which we carry in our instinctively predict when and where the ball will go. For head, is just a model. Nobody in his head imagines all professional players, this all happens subconsciously. Their the world, government or country. He has only selected muscles reflexively swing the bat at the right time and loca- concepts, and relationships between them, and uses those tion in line with their internal models’ predictions (Gerrit to represent the real system. (Forrester, 1971) et al., 2013). They can quickly act on their predictions of To handle the vast amount of information that flows through the future without the need to consciously roll out possible our daily lives, our brain learns an abstract representation future scenarios to form a plan (Hirshon, 2013). of both spatial and temporal aspects of this information. We are able to observe a scene and remember an abstract description thereof (Cheang & Tsao, 2017; Quiroga et al., 2005). Evidence also suggests that what we perceive at any given moment is governed by our brain’s prediction of the future based on our internal model (Nortmann et al., 2015; Gerrit et al., 2013). One way of understanding the predictive model inside of our brains is that it might not be about just predicting the future in general, but predicting future sensory data given our 1 Figure 2. What we see is based on our brain’s prediction of the Google Brain 2 NNAISENSE 3 Swiss AI Lab, IDSIA (USI & SUPSI) future (Kitaoka, 2002; Watanabe et al., 2018).
2 . World Models In many reinforcement learning (RL) problems (Kaelbling can learn a highly compact policy to perform its task. et al., 1996; Sutton & Barto, 1998; Wiering & van Otterlo, Although there is a large body of research relating to model- 2012), an artificial agent also benefits from having a good based reinforcement learning, this article is not meant to be representation of past and present states, and a good pre- a review (Arulkumaran et al., 2017; Schmidhuber, 2015b) of dictive model of the future (Werbos, 1987; Silver, 2017), the current state of the field. Instead, the goal of this article is preferably a powerful predictive model implemented on a to distill several key concepts from a series of papers 1990– general purpose computer such as a recurrent neural network 2015 on combinations of RNN-based world models and (RNN) (Schmidhuber, 1990a;b; 1991a). controllers (Schmidhuber, 1990a;b; 1991a; 1990c; 2015a). We will also discuss other related works in the literature that share similar ideas of learning a world model and training an agent using this model. In this article, we present a simplified framework that we can use to experimentally demonstrate some of the key concepts from these papers, and also suggest further insights to effec- tively apply these ideas to various RL environments. We use similar terminology and notation as On Learning to Think: Algorithmic Information Theory for Novel Combinations of RL Controllers and RNN World Models (Schmidhuber, 2015a) when describing our methodology and experiments. Figure 3. In this work, we build probabilistic generative models of OpenAI Gym environments. The RNN-based world models are trained using collected observations recorded from the actual game 2. Agent Model environment. After training the world models, we can use them We present a simple model inspired by our own cognitive mimic the complete environment and train agents using them. system. In this model, our agent has a visual sensory compo- Large RNNs are highly expressive models that can learn nent that compresses what it sees into a small representative rich spatial and temporal representations of data. However, code. It also has a memory component that makes predic- many model-free RL methods in the literature often only tions about future codes based on historical information. use small neural networks with few parameters. The RL Finally, our agent has a decision-making component that de- algorithm is often bottlenecked by the credit assignment cides what actions to take based only on the representations problem, which makes it hard for traditional RL algorithms created by its vision and memory components. to learn millions of weights of a large model, hence in practice, smaller networks are used as they iterate faster to a good policy during training. Ideally, we would like to be able to efficiently train large RNN-based agents. The backpropagation algorithm (Lin- nainmaa, 1970; Kelley, 1960; Werbos, 1982) can be used to train large neural networks efficiently. In this work we look at training a large neural network1 to tackle RL tasks, by dividing the agent into a large world model and a small con- troller model. We first train a large neural network to learn a model of the agent’s world in an unsupervised manner, and then train the smaller controller model to learn to perform a task using this world model. A small controller lets the training algorithm focus on the credit assignment problem Figure 4. Our agent consists of three components that work closely on a small search space, while not sacrificing capacity and together: Vision (V), Memory (M), and Controller (C) expressiveness via the larger world model. By training the agent through the lens of its world model, we show that it 2.1. VAE (V) Model 1 Typical model-free RL models have in the order of 103 to The environment provides our agent with a high dimensional 106 model parameters. We look at training models in the order of input observation at each time step. This input is usually 107 parameters, which is still rather small compared to state-of- the-art deep learning models with 108 to even 109 parameters. In a 2D image frame that is part of a video sequence. The principle, the procedure described in this article can take advantage role of the V model is to learn an abstract, compressed of these larger networks if we wanted to use them. representation of each observed input frame.
3 . World Models Original Observed Frame Reconstructed Frame Encoder z Decoder Figure 5. Flow diagram of a Variational Autoencoder (VAE). Here, we use a simple Variational Autoencoder (Kingma & Welling, 2013; Rezende et al., 2014) as our V model to Figure 7. SketchRNN (Ha & Eck, 2017) is an example of a MDN- compress each image frame into a small latent vector z. RNN used to predict the next pen strokes of a sketch drawing. We use a similar model to predict the next latent vector zt . 2.2. MDN-RNN (M) Model While it is the role of the V model to compress what the 2.3. Controller (C) Model agent sees at each time frame, we also want to compress The Controller (C) model is responsible for determining the what happens over time. For this purpose, the role of the course of actions to take in order to maximize the expected M model is to predict the future. The M model serves as a cumulative reward of the agent during a rollout of the en- predictive model of the future z vectors that V is expected to vironment. In our experiments, we deliberately make C as produce. Since many complex environments are stochastic simple and small as possible, and trained separately from V in nature, we train our RNN to output a probability density and M, so that most of our agent’s complexity resides in the function p(z) instead of a deterministic prediction of z. world model (V and M). C is a simple single layer linear model that maps zt and ht directly to action at at each time step: at = Wc [zt ht ] + bc (1) In this linear model, Wc and bc are the weight matrix and bias vector that maps the concatenated input vector [zt ht ] to the output action vector at . 2.4. Putting V, M, and C Together The following flow diagram illustrates how V, M, and C Figure 6. RNN with a Mixture Density Network output layer. The MDN outputs the parameters of a mixture of Gaussian distribution interacts with the environment: used to sample a prediction of the next latent vector z. In our approach, we approximate p(z) as a mixture of Gaus- sian distribution, and train the RNN to output the probability distribution of the next latent vector zt+1 given the current and past information made available to it. More specifically, the RNN will model P (zt+1 | at , zt , ht ), where at is the action taken at time t and ht is the hidden state of the RNN at time t. During sampling, we can adjust a temperature parameter τ to control model uncertainty, as done in (Ha & Eck, 2017) – we will find adjusting τ to be useful for training our controller later on. Figure 8. Flow diagram of our Agent model. The raw observation This approach is known as a Mixture Density Net- is first processed by V at each time step t to produce zt . The input work (Bishop, 1994) combined with a RNN (MDN-RNN) into C is this latent vector zt concatenated with M’s hidden state (Graves, 2013; Ha, 2017a), and has been applied in the ht at each time step. C will then output an action vector at for motor control, and will affect the environment. M will then take past for sequence generation problems such as generating the current zt and action at as an input to update its own hidden handwriting (Graves, 2013) and sketches (Ha & Eck, 2017). state to produce ht+1 to be used at time t + 1.
4 . World Models Below is the pseudocode for how our agent model is used 3.1. World Model for Feature Extraction in the OpenAI Gym (Brockman et al., 2016) environment: A predictive world model can help us extract useful repre- def rollout(controller): sentations of space and time. By using these features as ’’’ env, rnn, vae are ’’’ inputs of a controller, we can train a compact and minimal ’’’ global variables ’’’ controller to perform a continuous control task, such as obs = env.reset() learning to drive from pixel inputs for a top-down car racing h = rnn.initial_state() environment called CarRacing-v0 (Klimov, 2016). done = False cumulative_reward = 0 while not done: z = vae.encode(obs) a = controller.action([z, h]) obs, reward, done = env.step(a) cumulative_reward += reward h = rnn.forward([a, z, h]) return cumulative_reward Running this function on a given controller C will return the cumulative reward during a rollout. This minimal design for C also offers important practical benefits. Advances in deep learning provided us with the tools to train large, sophisticated models efficiently, pro- vided we can define a well-behaved, differentiable loss func- tion. Our V and M models are designed to be trained effi- Figure 9. Our agent learning to navigate in CarRacing-v0. ciently with the backpropagation algorithm using modern In this environment, the tracks are randomly generated for GPU accelerators, so we would like most of the model’s each trial, and our agent is rewarded for visiting as many complexity, and model parameters to reside in V and M. tiles as possible in the least amount of time. The agent The number of parameters of C, a linear model, is mini- controls three continuous actions: steering left/right, accel- mal in comparison. This choice allows us to explore more eration, and brake. unconventional ways to train C – for example, even us- ing evolution strategies (ES) (Rechenberg, 1973; Schwefel, To train our V model, we first collect a dataset of 10,000 1977) to tackle more challenging RL tasks where the credit random rollouts of the environment. We have first an agent assignment problem is difficult. acting randomly to explore the environment multiple times, and record the random actions at taken and the resulting To optimize the parameters of C, we chose the Covariance- observations from the environment. We use this dataset to Matrix Adaptation Evolution Strategy (CMA-ES) (Hansen, train V to learn a latent space of each frame observed. We 2016; Hansen & Ostermeier, 2001) as our optimization train our VAE to encode each frame into low dimensional algorithm since it is known to work well for solution spaces latent vector z by minimizing the difference between a given of up to a few thousand parameters. We evolve parameters frame and the reconstructed version of the frame produced of C on a single machine with multiple CPU cores running by the decoder from z. multiple rollouts of the environment in parallel. We can now use our trained V model to pre-process each For more specific information about the models, training pro- frame at time t into zt to train our M model. Using this cedures, and environments used in our experiments, please pre-processed data, along with the recorded random actions refer to the Appendix section. at taken, our MDN-RNN can now be trained to model P (zt+1 | at , zt , ht ) as a mixture of Gaussians.3 3. Car Racing Experiment and obtain a mediocre score, CarRacing-v0 defines solving as getting average reward of 900 over 100 consecutive trials, which In this section, we describe how we can train the Agent means the agent can only afford very few driving mistakes. model described earlier to solve a car racing task. To our 3 In principle, we can train both models together in an end-to- knowledge, our agent is the first known solution to achieve end manner, although we found that training each separately is the score required to solve this task.2 more practical, and also achieves satisfactory results. Training each model only required less than an hour of computation time on 2 We find this task interesting because although it is not difficult a single GPU. We can also train individual VAE and MDN-RNN to train an agent to wobble around randomly generated tracks models without having to exhaustively tune hyperparameters.
5 . World Models In this experiment, the world model (V and M) has no knowl- 3.3. Experiment Results edge about the actual reward signals from the environment. Its task is simply to compress and predict the sequence of V Model Only image frames observed. Only the Controller (C) Model has access to the reward information from the environment. Training an agent to drive is not a difficult task if we have a Since there are a mere 867 parameters inside the linear con- good representation of the observation. Previous works (Hn- troller model, evolutionary algorithms such as CMA-ES are ermann, 2017; Bling, 2015; Lau, 2016) have shown that well suited for this optimization task. with a good set of hand-engineered information about the observation, such as LIDAR information, angles, positions We can use the VAE to reconstruct each frame using zt at and velocities, one can easily train a small feed-forward each time step to visualize the quality of the information the network to take this hand-engineered input and output a agent actually sees during a rollout. The figure below is a satisfactory navigation policy. For this reason, we first want VAE model trained on screenshots from CarRacing-v0. to test our agent by handicapping C to only have access to V but not M, so we define our controller as at = Wc zt + bc . Figure 10. Despite losing details during this lossy compression process, latent vector z captures the essence of each image frame. In the online version of this article, one can load randomly chosen screenshots to be encoded into a small latent vector z, which is used to reconstruct the original screenshot. One can also experiment with adjusting the values of the z vector Figure 11. Limiting our controller to see only zt , but not ht results using the slider bars to see how it affects the reconstruction, in wobbly and unstable driving behaviours. or randomize z to observe the space of possible screenshots. Although the agent is still able to navigate the race track 3.2. Procedure in this setting, we notice it wobbles around and misses the tracks on sharper corners. This handicapped agent achieved To summarize the Car Racing experiment, below are the an average score of 632 ± 251 over 100 random trials, steps taken: in line with the performance of other agents on OpenAI Gym’s leaderboard (Klimov, 2016) and traditional Deep RL 1. Collect 10,000 rollouts from a random policy. methods such as A3C (Khan & Elibol, 2016; Jang et al., 2017). Adding a hidden layer to C’s policy network helps 2. Train VAE (V) to encode frames into z ∈ R32 . to improve the results to 788 ± 141, but not quite enough to 3. Train MDN-RNN (M) to model P (zt+1 | at , zt , ht ). solve this environment. 4. Define Controller (C) as at = Wc [zt ht ] + bc . Full World Model (V and M) 5. Use CMA-ES to solve for a Wc and bc that maximizes The representation zt provided by our V model only cap- the expected cumulative reward. tures a representation at a moment in time and does not have much predictive power. In contrast, M is trained to do one thing, and to do it really well, which is to predict zt+1 . Since M ODEL PARAMETER C OUNT M’s prediction of zt+1 is produced from the RNN’s hidden VAE 4,348,547 state ht at time t, this vector is a good candidate for the set MDN-RNN 422,368 of learned features we can give to our agent. Combining zt C ONTROLLER 867 with ht gives our controller C a good representation of both the current observation, and what to expect in the future.
6 . World Models 3.4. Car Racing Dreams Since our world model is able to model the future, we are also able to have it come up with hypothetical car racing sce- narios on its own. We can ask it to produce the probability distribution of zt+1 given the current states, sample a zt+1 and use this sample as the real observation. We can put our trained C back into this hallucinated environment generated by M. The following image from an interactive demo in the online version of this article shows how our world model can be used to hallucinate the car racing environment: Figure 12. Driving is more stable if we give our controller access to both zt and ht . We see that allowing the agent to access the both zt and ht greatly improves its driving capability. The driving is more stable, and the agent is able to seemingly attack the sharp corners effectively. Furthermore, we see that in making these fast reflexive driving decisions during a car race, the agent does not need to plan ahead and roll out hypothetical scenarios of the future. Since ht contain information about the probability distribution of the future, the agent can just query the RNN instinctively to guide its action decisions. Like a seasoned Formula One driver or the baseball player discussed earlier, the agent can instinctively predict when and where to navigate in the heat of the moment. M ETHOD AVG . S CORE DQN (P RIEUR , 2017) 343 ± 18 Figure 13. Our agent driving inside of its own dream world. Here, A3C ( CONTINUOUS ) (JANG ET AL ., 2017) 591 ± 45 we deploy our trained policy into a fake environment generated A3C ( DISCRETE ) (K HAN & E LIBOL , 2016) 652 ± 10 by the MDN-RNN, and rendered using the VAE’s decoder. In the CEOBILLIONAIRE (G YM L EADERBOARD ) 838 ± 11 demo, one can override the agent’s actions as well as adjust τ to V MODEL 632 ± 251 control the uncertainty of the environment generated by M. V MODEL WITH HIDDEN LAYER 788 ± 141 F ULL W ORLD M ODEL 906 ± 21 4. VizDoom Experiment Table 1. CarRacing-v0 scores achieved using various methods. 4.1. Learning Inside of a Dream Our agent is able to achieve a score of 906 ± 21 over 100 We have just seen that a policy learned inside of the real random trials, effectively solving the task and obtaining new environment appears to somewhat function inside of the state of the art results. Previous attempts (Khan & Elibol, dream environment. This begs the question – can we train 2016; Jang et al., 2017) using Deep RL methods obtained our agent to learn inside of its own dream, and transfer this average scores of 591–652 range, and the best reported policy back to the actual environment? solution on the leaderboard obtained an average score of 838 ± 11 over 100 random trials. Traditional Deep RL If our world model is sufficiently accurate for its purpose, methods often require pre-processing of each frame, such and complete enough for the problem at hand, we should as employing edge-detection (Jang et al., 2017), in addition be able to substitute the actual environment with this world to stacking a few recent frames (Khan & Elibol, 2016; Jang model. After all, our agent does not directly observe the re- et al., 2017) into the input. In contrast, our world model ality, but only sees what the world model lets it see. In takes in a stream of raw RGB pixel images and directly this experiment, we train an agent inside the hallucina- learns a spatial-temporal representation. To our knowledge, tion generated by its world model trained to mimic a Viz- our method is the first reported solution to solve this task. Doom (Kempka et al., 2016) environment.
7 . World Models To summarize the Take Cover experiment, below are the steps taken: 1. Collect 10,000 rollouts from a random policy. 2. Train VAE (V) to encode each frame into a latent vector z ∈ R64 , and use V to convert the images collected from (1) into the latent space representation. 3. Train MDN-RNN (M) to model P (zt+1 , dt+1 | at , zt , ht ). 4. Define Controller (C) as at = Wc [zt ht ]. 5. Use CMA-ES to solve for a Wc that maximizes the expected survival time inside the virtual environment. Figure 14. Our final agent solving VizDoom: Take Cover. 6. Use learned policy from (5) on actual environment. The agent must learn to avoid fireballs shot by monsters from the other side of the room with the sole intent of killing the agent. There are no explicit rewards in this environment, M ODEL PARAMETER C OUNT so to mimic natural selection, the cumulative reward can be defined to be the number of time steps the agent manages to VAE 4,446,915 MDN-RNN 1,678,785 stay alive during a rollout. Each rollout of the environment C ONTROLLER 1,088 runs for a maximum of 2100 time steps (∼ 60 seconds), and the task is considered solved if the average survival time over 100 consecutive rollouts is greater than 750 time steps (∼ 20 seconds) (Paquette, 2016). 4.3. Training Inside of the Dream After some training, our controller learns to navigate around 4.2. Procedure the dream environment and escape from deadly fireballs The setup of our VizDoom experiment is largely the same launched by monsters generated by M. Our agent achieved as the Car Racing task, except for a few key differences. In a score of ∼ 900 time steps in the virtual environment. the Car Racing task, M is only trained to model the next zt . Since we want to build a world model we can train our agent in, our M model here will also predict whether the agent dies in the next frame (as a binary event donet , or dt for short), in addition to the next frame zt . Since the M model can predict the done state in addi- tion to the next observation, we now have all of the in- gredients needed to make a full RL environment. We first build an OpenAI Gym environment interface by wrapping a gym.Env interface over our M if it were a real Gym en- vironment, and then train our agent inside of this virtual environment instead of using the actual environment. In this simulation, we do not need the V model to encode any real pixel frames during the hallucination process, so our agent will therefore only train entirely in a latent space environment. This has many advantages as we will see. This virtual environment has an identical interface to the real environment, so after the agent learns a satisfactory policy in the virtual environment, we can easily deploy this policy back into the actual environment to see how well the Figure 15. Our agent discovers a policy to avoid hallucinated fire- policy transfers over. balls. In the online version of this article, the reader can interact with the environment inside this demo.
8 . World Models Here, our RNN-based world model is trained to mimic a complete game environment designed by human program- mers. By learning only from raw image data collected from random episodes, it learns how to simulate the essential aspects of the game – such as the game logic, enemy be- haviour, physics, and also the 3D graphics rendering. For instance, if the agent selects the left action, the M model learns to move the agent to the left and adjust its internal representation of the game states accordingly. It also learns to block the agent from moving beyond the walls on both sides of the level if the agent attempts to move too far in Figure 17. An interactive VAE of Doom in the online article. either direction. Occasionally, the M model needs to keep track of multiple fireballs being shot from several different monsters and coherently move them along in their intended We see that even though the V model is not able to capture all directions. It must also detect whether the agent has been of the details of each frame correctly, for instance, getting killed by one of these fireballs. the number of monsters correct, the agent is still able to use the learned policy to navigate in the real environment. Unlike the actual game environment, however, we note As the virtual environment cannot even keep track of the that it is possible to add extra uncertainty into the virtual exact number of monsters in the first place, an agent that is environment, thus making the game more challenging in able to survive the noisier and uncertain virtual nightmare the dream environment. We can do this by increasing the environment will thrive in the original, cleaner environment. temperature τ parameter during the sampling process of zt+1 . By increasing the uncertainty, our dream environment 4.5. Cheating the World Model becomes more difficult compared to the actual environment. The fireballs may move more randomly in a less predictable In our childhood, we may have encountered ways to exploit path compared to the actual game. Sometimes the agent video games in ways that were not intended by the original may even die due to sheer misfortune, without explanation. game designer (Wikipedia, 2017). Players discover ways to collect unlimited lives or health, and by taking advantage We find agents that perform well in higher temperature of these exploits, they can easily complete an otherwise settings generally perform better in the normal setting. In difficult game. However, in the process of doing so, they fact, increasing τ helps prevent our controller from taking may have forfeited the opportunity to learn the skill required advantage of the imperfections of our world model – we to master the game as intended by the game designer. will discuss this in more depth later on. For instance, in our initial experiments, we noticed that our 4.4. Transfer Policy to Actual Environment agent discovered an adversarial policy to move around in such a way so that the monsters in this virtual environment governed by the M model never shoots a single fireball dur- ing some rollouts. Even when there are signs of a fireball forming, the agent will move in a way to extinguish the fire- balls magically as if it has superpowers in the environment. Because our world model is only an approximate probabilis- tic model of the environment, it will occasionally generate trajectories that do not follow the laws governing the actual environment. As we saw previously, even the number of monsters on the other side of the room in the actual environ- ment is not exactly reproduced by the world model. Like Figure 16. Deploying our policy learned inside of the dream RNN a child who learns that objects in the air usually fall to the environment back into the actual VizDoom environment. ground, the child might also imagine unrealistic superheroes who fly across the sky. For this reason, our world model We took the agent trained inside of the virtual environment will be exploitable by the controller, even if in the actual and tested its performance on the original VizDoom scenario. environment such exploits do not exist. The score over 100 random consecutive trials is ∼ 1100 time steps, far beyond the required score of 750 time steps, and And since we are using the M model to generate a virtual also much higher than the score obtained inside the more dream environment for our agent, we are also giving the difficult virtual environment. controller access to all of the hidden states of M. This is
9 . World Models essentially granting our agent access to all of the internal to ignore a flawed M, or exploit certain useful parts of M states and memory of the game engine, rather than only the for arbitrary computational purposes including hierarchical game observations that the player gets to see. Therefore our planning etc. This is not what we do here though – our agent can efficiently explore ways to directly manipulate the present approach is still closer to some of the older systems hidden states of the game engine in its quest to maximize its (Schmidhuber, 1990a;b; 1991a), where a RNN M is used to expected cumulative reward. The weakness of this approach predict and plan ahead step by step. Unlike this early work, of learning a policy inside a learned dynamics model is that however, we use evolution for C (like in Learning to Think) our agent can easily find an adversarial policy that can fool rather than traditional RL combined with RNNs, which has our dynamics model – it’ll find a policy that looks good the advantage of both simplicity and generality. under our dynamics model, but will fail in the actual envi- To make it more difficult for our C model to exploit defi- ronment, usually because it visits states where the model is ciencies of the M model, we chose to use the MDN-RNN wrong because they are away from the training distribution. as the dynamics model, which models the distribution of possible outcomes in the actual environment, rather than merely predicting a deterministic future. Even if the actual environment is deterministic, the MDN-RNN would in ef- fect approximate it as a stochastic environment. This has the advantage of allowing us to train our C model inside a more stochastic version of any environment – we can simply adjust the temperature parameter τ to control the amount of randomness in the M model, hence controlling the tradeoff between realism and exploitability. Using a mixture of Gaussian model may seem like overkill given that the latent space encoded with the VAE model is just a single diagonal Gaussian distribution. However, the discrete modes in a mixture density model is useful for environments with random discrete events, such as whether a monster decides to shoot a fireball or stay put. While a single diagonal Gaussian might be sufficient to encode individual frames, a RNN with a mixture density output layer makes it easier to model the logic behind a more complicated environment with discrete random states. For instance, if we set the temperature parameter to a very Figure 18. Agent discovers an adversarial policy to automatically low value of τ = 0.1, effectively training our C model extinguish fireballs after they are fired during some rollouts. with a M model that is almost identical to a deterministic This weakness could be the reason that many previous works LSTM, the monsters inside this dream environment fail to that learn dynamics models of RL environments but do not shoot fireballs, no matter what the agent does, due to mode actually use those models to fully replace the actual envi- collapse. The M model is not able to jump to another mode ronments (Oh et al., 2015; Chiappa et al., 2017). Like in the in the mixture of Gaussian model where fireballs are formed M model proposed in (Schmidhuber, 1990a;b; 1991a), the and shot. Whatever policy learned inside of this dream will dynamics model is a deterministic model, making the model achieve a perfect score of 2100 most of the time, but will easily exploitable by the agent if it is not perfect. Using obviously fail when unleashed into the harsh reality of the Bayesian models, as in PILCO (Deisenroth & Rasmussen, actual world, underperforming even a random policy. 2011), helps to address this issue with the uncertainty es- Note again, however, that the simpler and more robust ap- timates to some extent, however, they do not fully solve proach in Learning to Think does not insist on using M the problem. Recent work (Nagabandi et al., 2017) com- for step by step planning. Instead, C can learn to use M’s bines the model-based approach with traditional model-free subroutines (parts of M’s weight matrix) for arbitrary com- RL training by first initializing the policy network with the putational purposes but can also learn to ignore M when M learned policy, but must subsequently rely on model-free is useless and when ignoring M yields better performance. methods to fine-tune this policy in the actual environment. Nevertheless, at least in our present C–M variant, M’s pre- In Learning to Think (Schmidhuber, 2015a), it is accept- dictions are essential for teaching C, more like in some of able that the RNN M is not always a reliable predictor. A the early C–M systems (Schmidhuber, 1990a;b; 1991a), but (potentially evolution-based) RNN C can in principle learn combined with evolution or black box optimization.
10 . World Models By making the temperature τ an adjustable parameter of We have shown that one iteration of this training loop was the M model, we can see the effect of training the C model enough to solve simple tasks. For more difficult tasks, we on hallucinated virtual environments with different levels need our controller in Step 2 to actively explore parts of the of uncertainty, and see how well they transfer over to the environment that is beneficial to improve its world model. actual environment. We experimented with varying the An exciting research direction is to look at ways to incorpo- temperature of the virtual environment and observing the rate artificial curiosity and intrinsic motivation (Schmidhu- resulting average score over 100 random rollouts of the ber, 2010; 2006; 1991b; Pathak et al., 2017; Oudeyer et al., actual environment after training the agent inside of the 2007) and information seeking (Schmidhuber et al., 1994; virtual environment with a given temperature: Gottlieb et al., 2013) abilities in an agent to encourage novel exploration (Lehman & Stanley, 2011). In particular, we T EMPERATURE τ V IRTUAL S CORE ACTUAL S CORE can augment the reward function based on improvement 0.10 2086 ± 140 193 ± 58 in compression quality (Schmidhuber, 2010; 2006; 1991b; 0.50 2060 ± 277 196 ± 50 2015a). 1.00 1145 ± 690 868 ± 511 1.15 918 ± 546 1092 ± 556 In the present approach, since M is a MDN-RNN that mod- 1.30 732 ± 269 753 ± 139 els a probability distribution for the next frame, if it does R ANDOM P OLICY N/A 210 ± 108 a poor job, then it means the agent has encountered parts G YM L EADER N/A 820 ± 58 of the world that it is not familiar with. Therefore we can adapt and reuse M’s training loss function to encourage Table 2. Take Cover scores at various temperature settings. curiosity. By flipping the sign of M’s loss function in the We see that while increasing the temperature of the M model actual environment, the agent will be encouraged to explore makes it more difficult for the C model to find adversarial parts of the world that it is not familiar with. The new data policies, increasing it too much will make the virtual envi- it collects may improve the world model. ronment too difficult for the agent to learn anything, hence The iterative training procedure requires the M model to in practice it is a hyperparameter we can tune. The tempera- not only predict the next observation x and done, but also ture also affects the types of strategies the agent discovers. predict the action and reward for the next time step. This For example, although the best score obtained is 1092 ± may be required for more difficult tasks. For instance, if our 556 with τ = 1.15, increasing τ a notch to 1.30 results in a agent needs to learn complex motor skills to walk around its lower score but at the same time a less risky strategy with a environment, the world model will learn to imitate its own lower variance of returns. For comparison, the best score on C model that has already learned to walk. After difficult the OpenAI Gym leaderboard (Paquette, 2016) is 820 ± 58. motor skills, such as walking, is absorbed into a large world model with lots of capacity, the smaller C model can rely on 5. Iterative Training Procedure the motor skills already absorbed by the world model and focus on learning more higher level skills to navigate itself In our experiments, the tasks are relatively simple, so a rea- using the motor skills it had already learned. sonable world model can be trained using a dataset collected from a random policy. But what if our environments become more sophisticated? In any difficult environment, only parts of the world are made available to the agent only after it learns how to strategically navigate through its world. For more complicated tasks, an iterative training procedure is required. We need our agent to be able to explore its world, and constantly collect new observations so that its world Figure 19. How information becomes memory. model can be improved and refined over time. An iterative An interesting connection to the neuroscience literature is training procedure (Schmidhuber, 2015a) is as follows: the work on hippocampal replay that examines how the brain replays recent experiences when an animal rests or sleeps. 1. Initialize M, C with random model parameters. Replaying recent experiences plays an important role in memory consolidation (Foster, 2017) – where hippocampus- 2. Rollout to actual environment N times. Save all actions dependent memories become independent of the hippocam- at and observations xt during rollouts to storage. pus over a period of time. As (Foster, 2017) puts it, replay is 3. Train M to model P (xt+1 , rt+1 , at+1 , dt+1 |xt , at , ht ) less like dreaming and more like thought. We invite readers and train C to optimize expected rewards inside of M. to read Replay Comes of Age (Foster, 2017) for a detailed overview of replay from a neuroscience perspective with 4. Go back to (2) if task has not been completed. connections to theoretical reinforcement learning.
11 . World Models Iterative training could allow the C–M model to develop a Here we are interested in modelling dynamics observed natural hierarchical way to learn. Recent works about self- from high dimensional visual data where our input is a play in RL (Sukhbaatar et al., 2017; Bansal et al., 2017; Al- sequence of raw pixel frames. Shedivat et al., 2017) and PowerPlay (Schmidhuber, 2013; In robotic control applications, the ability to learn the dy- Srivastava et al., 2012) also explores methods that lead to namics of a system from observing only camera-based video a natural curriculum learning (Schmidhuber, 2002), and inputs is a challenging but important problem. Early work we feel this is one of the more exciting research areas of on RL for active vision trained an FNN to take the cur- reinforcement learning. rent image frame of a video sequence to predict the next frame (Schmidhuber & Huber, 1991), and use this predic- 6. Related Work tive model to train a fovea-shifting control network trying to find targets in a visual scene. To get around the diffi- There is extensive literature on learning a dynamics model, culty of training a dynamical model to learn directly from and using this model to train a policy. Many concepts first high-dimensional pixel images, researchers explored using explored in the 1980s for feed-forward neural networks neural networks to first learn a compressed representation of (FNNs) (Werbos, 1987; Munro, 1987; Robinson & Fallside, the video frames. Recent work along these lines (Wahlstrm 1989; Werbos, 1989; Nguyen & Widrow, 1989) and in the et al., 2014; 2015) was able to train controllers using the bot- 1990s for RNNs (Schmidhuber, 1990a;b; 1991a; 1990c) laid tleneck hidden layer of an autoencoder as low-dimensional some of the groundwork for Learning to Think (Schmidhu- feature vectors to control a pendulum from pixel inputs. ber, 2015a). The more recent PILCO (Deisenroth & Ras- Learning a model of the dynamics from a compressed la- mussen, 2011; Duvenaud, 2016; McAllister & Rasmussen, tent space enable RL algorithms to be much more data- 2016) is a probabilistic model-based search policy method efficient (Finn et al., 2015; Watter et al., 2015; Finn, 2017). designed to solve difficult control problems. Using data We invite readers to watch Finn’s lecture on Model-Based collected from the environment, PILCO uses a Gaussian RL (Finn, 2017) to learn more. process (GP) model to learn the system dynamics, and then uses this model to sample many trajectories in order to train Video game environments are also popular in model-based a controller to perform a desired task, such as swinging up RL research as a testbed for new ideas. (Matthew Guzdial, a pendulum, or riding a unicycle. 2017) used a feed-forward convolutional neural network (CNN) to learn a forward simulation model of a video game. Learning to predict how different actions affect future states in the environment is useful for game-play agents, since if our agent can predict what happens in the future given its current state and action, it can simply select the best action that suits its goal. This has been demonstrated not only in early work (Nguyen & Widrow, 1989; Schmidhu- ber & Huber, 1991) (when compute was a million times more expensive than today) but also in recent studies (Doso- vitskiy & Koltun, 2016) on several competitive VizDoom environments. The works mentioned above use FNNs to predict the next video frame. We may want to use models that can capture longer term time dependencies. RNNs are powerful models suitable for sequence modelling (Graves, 2013). In a lecture Figure 20. A controller with internal RNN model of the world called Hallucination with RNNs (Graves, 2015), Graves (Schmidhuber, 1990a). demonstrated the ability of RNNs to learn a probabilistic model of Atari game environments. He trained RNNs to While Gaussian processes work well with a small set of learn the structure of such a game and then showed that they low dimension data, their computational complexity makes can hallucinate similar game levels on its own. them difficult to scale up to model a large history of high dimensional observations. Other recent works (Gal et al., Using RNNs to develop internal models to reason about 2016; Depeweg et al., 2016) use Bayesian neural networks the future has been explored as early as 1990 in a pa- instead of GPs to learn a dynamics model. These methods per called Making the World Differentiable (Schmidhuber, have demonstrated promising results on challenging control 1990a), and then further explored in (Schmidhuber, 1990b; tasks (Hein et al., 2017), where the states are known and well 1991a; 1990c). A more recent paper called Learning to defined, and the observation is relatively low dimensional. Think (Schmidhuber, 2015a) presented a unifying frame-
12 . World Models work for building a RNN-based general problem solver that We have demonstrated the possibility of training an agent can learn a world model of its environment and also learn to to perform tasks entirely inside of its simulated latent space reason about the future using this model. Subsequent works dream world. This approach offers many practical benefits. have used RNN-based models to generate many frames into For instance, running computationally intensive game en- the future (Chiappa et al., 2017; Oh et al., 2015; Denton gines require using heavy compute resources for rendering & Birodkar, 2017), and also as an internal model to reason the game states into image frames, or calculating physics about the future (Silver et al., 2016; Weber et al., 2017; not immediately relevant to the game. We may not want Watters et al., 2017). to waste cycles training an agent in the actual environment, but instead train the agent as many times as we want in- In this work, we used evolution strategies to train our con- side its simulated environment. Training agents in the real troller, as it offers many benefits. For instance, we only need world is even more expensive, so world models that are to provide the optimizer with the final cumulative reward, trained incrementally to simulate reality may prove to be rather than the entire history. ES is also easy to parallelize – useful for transferring policies back to the real world. Our we can launch many instances of rollout with different approach may complement sim2real approaches outlined in solutions to many workers and quickly compute a set of (Bousmalis et al., 2017; Higgins et al., 2017). cumulative rewards in parallel. Recent works (Fernando et al., 2017; Salimans et al., 2017; Ha, 2017b; Stanley & Furthermore, we can take advantage of deep learning frame- Clune, 2017) have confirmed that ES is a viable alternative works to accelerate our world model simulations using to traditional Deep RL methods on many strong baselines. GPUs in a distributed environment. The benefit of imple- menting the world model as a fully differentiable recurrent Before the popularity of Deep RL methods (Mnih et al., computation graph also means that we may be able to train 2013), evolution-based algorithms have been shown to be our agents in the dream directly using the backpropagation effective at solving RL tasks (Stanley & Miikkulainen, 2002; algorithm to fine-tune its policy to maximize an objective Gomez et al., 2008; Gomez & Schmidhuber, 2005; Gauci function (Schmidhuber, 1990a;b; 1991a). & Stanley, 2010; Sehnke et al., 2010; Miikkulainen, 2013). Evolution-based algorithms have even been able to solve The choice of using a VAE for the V model and training it difficult RL tasks from high dimensional pixel inputs (Kout- as a standalone model also has its limitations, since it may nik et al., 2013; Hausknecht et al., 2013; Parker & Bryant, encode parts of the observations that are not relevant to a 2012). More recent works (Alvernaz & Togelius, 2017) task. After all, unsupervised learning cannot, by definition, combine VAE and ES, which is similar to our approach. know what will be useful for the task at hand. For instance, it reproduced unimportant detailed brick tile patterns on the 7. Discussion side walls in the Doom environment, but failed to reproduce task-relevant tiles on the road in the Car Racing environment. By training together with a M model that predicts rewards, the VAE may learn to focus on task-relevant areas of the image, but the tradeoff here is that we may not be able to reuse the VAE effectively for new tasks without retraining. Learning task-relevant features has connections to neuro- science as well. Primary sensory neurons are released from inhibition when rewards are received, which suggests that they generally learn task-relevant features, rather than just any features, at least in adulthood (Pi et al., 2013). Another concern is the limited capacity of our world model. While modern storage devices can store large amounts of historical data generated using the iterative training proce- dure, our LSTM (Hochreiter & Schmidhuber, 1997; Gers et al., 2000)-based world model may not be able to store all of the recorded information inside its weight connections. While the human brain can hold decades and even centuries of memories to some resolution (Bartol et al., 2015), our neural networks trained with backpropagation have more limited capacity and suffer from issues such as catastrophic forgetting (Ratcliff, 1990; French, 1994; Kirkpatrick et al., Figure 21. Ancient drawing (1990) of a RNN-based controller in- 2016). Future work may explore replacing the small MDN- teracting with an environment (Schmidhuber, 1990a).
13 . World Models RNN network with higher capacity models (Shazeer et al., A. Appendix 2017; Ha et al., 2016; Suarez, 2017; van den Oord et al., 2016; Vaswani et al., 2017), or incorporating an external In this section we will describe in more details the models memory module (Gemici et al., 2017), if we want our agent and training methods used in this work. to learn to explore more complicated worlds. A.1. Variational Autoencoder Like early RNN-based C–M systems (Schmidhuber, 1990a;b; 1991a; 1990c), ours simulates possible futures time step by time step, without profiting from human-like hierarchical planning or abstract reasoning, which often ig- nores irrelevant spatial-temporal details. However, the more general Learning To Think (Schmidhuber, 2015a) approach is not limited to this rather naive approach. Instead it allows a recurrent C to learn to address subroutines of the recurrent M, and reuse them for problem solving in arbitrary com- putable ways, e.g., through hierarchical planning or other kinds of exploiting parts of M’s program-like weight matrix. A recent One Big Net (Schmidhuber, 2018) extension of the C–M approach collapses C and M into a single network, and uses PowerPlay-like (Schmidhuber, 2013; Srivastava et al., 2012) behavioural replay (where the behaviour of a teacher net is compressed into a student net (Schmidhuber, 1992)) to avoid forgetting old prediction and control skills when learning new ones. Experiments with those more general approaches are left for future work. Figure 22. Description of tensor shapes at each layer of ConvVAE. We trained a Convolutional Variational Autoencoder Acknowledgements (ConvVAE) model as the V Model of our agent. Unlike We would like to thank Blake Richards, Kai Arulkumaran, vanilla autoencoders, enforcing a Gaussian prior over the Ankur Handa, Kory Mathewson, Kyle McDonald, Denny latent vector z also limits the amount of information capac- Britz, Elwin Ha and Natasha Jaques for their thoughtful ity for compressing each frame, but this Gaussian prior also feedback on this article, and for offering their valuable per- makes the world model more robust to unrealistic z vectors spectives and insights from their areas of expertise. generated by the M Model. The interactive online version of this article was built using As the environment may give us observations as high di- distill.pub’s web technology. We would like to thank mensional pixel images, we first resize each image to 64x64 Chris Olah and the rest of the Distill editorial team for pixels before and use this resized image as the V Model’s their valuable feedback and generous editorial support, in observation. Each pixel is stored as three floating point val- addition to supporting the use of their Distill technology. ues between 0 and 1 to represent each of the RGB channels. The ConvVAE takes in this 64x64x3 input tensor and passes The interative demos on worldmodels.github.io this data through 4 convolutional layers to encode it into were all built using p5.js. Deploying all of these machine low dimension vectors µ and σ, each of size Nz . The latent learning models in a web browser was made possible with vector z is sampled from the Gaussian prior N (µ, σI). In deeplearn.js, a hardware-accelerated machine learn- the Car Racing task, Nz is 32 while for the Doom task Nz is ing framework for the browser, developed by the People+AI 64. The latent vector z is passed through 4 of deconvolution Research Initiative (PAIR) team at Google. A special thanks layers used to decode and reconstruct the image. goes to Nikhil Thorat and Daniel Smilkov for their help during the development process. Each convolution and deconvolution layer uses a stride of 2. The layers are indicated in the diagram in Italics as We would to extend our thanks to Alex Graves, Douglas Eck, Activation-type Output Channels x Filter Size. All convolu- Mike Schuster, Rajat Monga, Vincent Vanhoucke, Jeff Dean tional and deconvolutional layers use relu activations except and the Google Brain team for helpful feedback and for for the output layer as we need the output to be between encouraging us to explore this area of research. Experiments 0 and 1. We trained the model for 1 epoch over the data were performed on Ubuntu virtual machines provided by collected from a random policy, using L2 distance between Google Cloud Platform. Any errors here are our own and the input image and the reconstruction to quantify the recon- do not reflect opinions of our proofreaders and colleagues. struction loss we optimize for, in addition to KL loss.
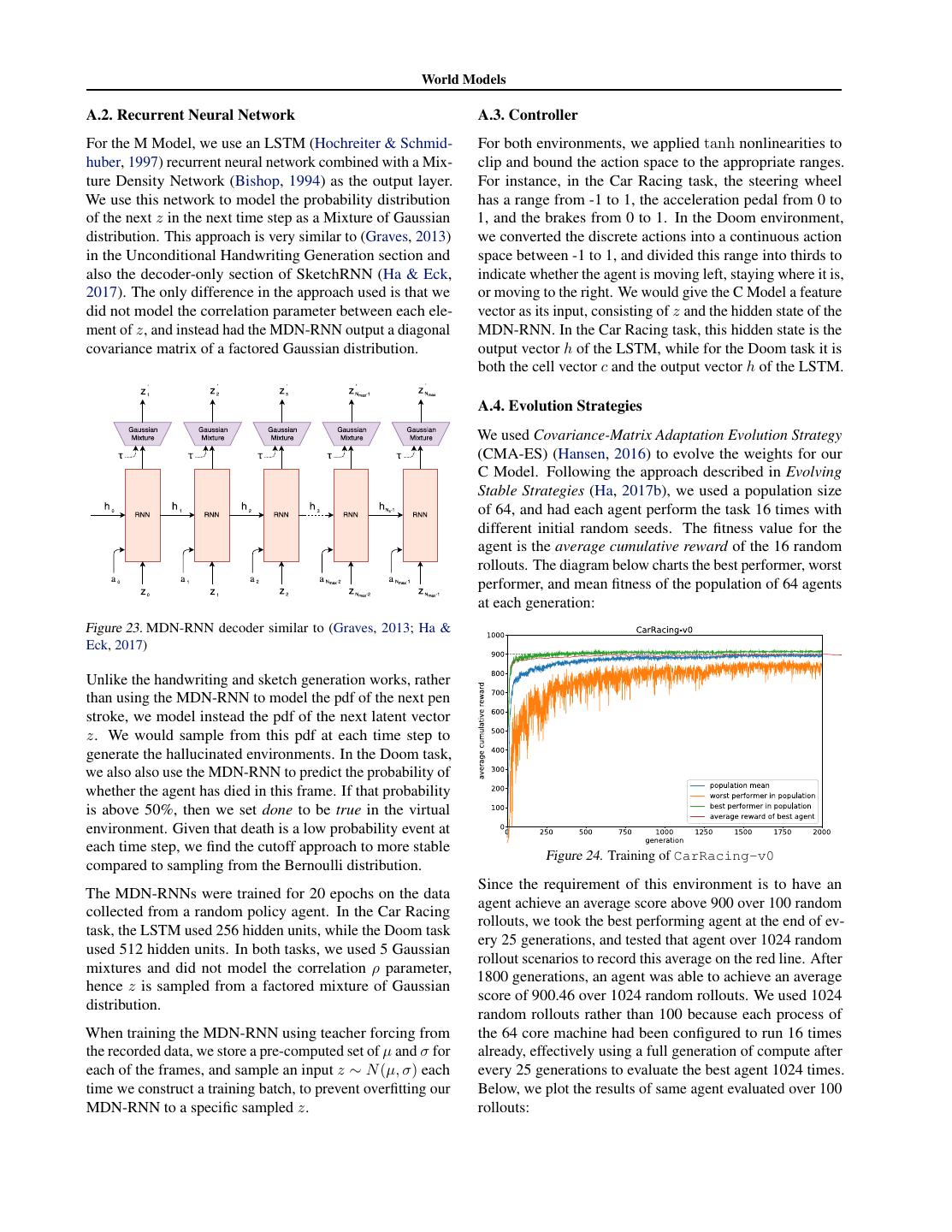
14 . World Models A.2. Recurrent Neural Network A.3. Controller For the M Model, we use an LSTM (Hochreiter & Schmid- For both environments, we applied tanh nonlinearities to huber, 1997) recurrent neural network combined with a Mix- clip and bound the action space to the appropriate ranges. ture Density Network (Bishop, 1994) as the output layer. For instance, in the Car Racing task, the steering wheel We use this network to model the probability distribution has a range from -1 to 1, the acceleration pedal from 0 to of the next z in the next time step as a Mixture of Gaussian 1, and the brakes from 0 to 1. In the Doom environment, distribution. This approach is very similar to (Graves, 2013) we converted the discrete actions into a continuous action in the Unconditional Handwriting Generation section and space between -1 to 1, and divided this range into thirds to also the decoder-only section of SketchRNN (Ha & Eck, indicate whether the agent is moving left, staying where it is, 2017). The only difference in the approach used is that we or moving to the right. We would give the C Model a feature did not model the correlation parameter between each ele- vector as its input, consisting of z and the hidden state of the ment of z, and instead had the MDN-RNN output a diagonal MDN-RNN. In the Car Racing task, this hidden state is the covariance matrix of a factored Gaussian distribution. output vector h of the LSTM, while for the Doom task it is both the cell vector c and the output vector h of the LSTM. A.4. Evolution Strategies We used Covariance-Matrix Adaptation Evolution Strategy (CMA-ES) (Hansen, 2016) to evolve the weights for our C Model. Following the approach described in Evolving Stable Strategies (Ha, 2017b), we used a population size of 64, and had each agent perform the task 16 times with different initial random seeds. The fitness value for the agent is the average cumulative reward of the 16 random rollouts. The diagram below charts the best performer, worst performer, and mean fitness of the population of 64 agents at each generation: Figure 23. MDN-RNN decoder similar to (Graves, 2013; Ha & Eck, 2017) Unlike the handwriting and sketch generation works, rather than using the MDN-RNN to model the pdf of the next pen stroke, we model instead the pdf of the next latent vector z. We would sample from this pdf at each time step to generate the hallucinated environments. In the Doom task, we also also use the MDN-RNN to predict the probability of whether the agent has died in this frame. If that probability is above 50%, then we set done to be true in the virtual environment. Given that death is a low probability event at each time step, we find the cutoff approach to more stable Figure 24. Training of CarRacing-v0 compared to sampling from the Bernoulli distribution. Since the requirement of this environment is to have an The MDN-RNNs were trained for 20 epochs on the data agent achieve an average score above 900 over 100 random collected from a random policy agent. In the Car Racing rollouts, we took the best performing agent at the end of ev- task, the LSTM used 256 hidden units, while the Doom task ery 25 generations, and tested that agent over 1024 random used 512 hidden units. In both tasks, we used 5 Gaussian rollout scenarios to record this average on the red line. After mixtures and did not model the correlation ρ parameter, 1800 generations, an agent was able to achieve an average hence z is sampled from a factored mixture of Gaussian score of 900.46 over 1024 random rollouts. We used 1024 distribution. random rollouts rather than 100 because each process of When training the MDN-RNN using teacher forcing from the 64 core machine had been configured to run 16 times the recorded data, we store a pre-computed set of µ and σ for already, effectively using a full generation of compute after each of the frames, and sample an input z ∼ N (µ, σ) each every 25 generations to evaluate the best agent 1024 times. time we construct a training batch, to prevent overfitting our Below, we plot the results of same agent evaluated over 100 MDN-RNN to a specific sampled z. rollouts:
15 . World Models A.5. DoomRNN We conducted a similar experiment on the hallucinated Doom environment we called DoomRNN. Please note that we have not actually attempted to train our agent on the actual VizDoom environment, and had only used VizDoom for the purpose of collecting training data using a random policy. DoomRNN is more computationally efficient com- pared to VizDoom as it only operates in latent space without the need to render a screenshot at each time step, and does not require running the actual Doom game engine. Figure 25. Histogram of cumulative rewards. Score is 906 ± 21. We also experimented with an agent that has access to only the z vector from the VAE, and not letting it see the RNN’s hidden states. We tried 2 variations, where in the first varia- tion, the C Model mapped z directly to the action space a. In second variation, we attempted to add a hidden layer with 40 tanh activations between z and a, increasing the number of model parameters of the C Model to 1443, making it more comparable with the original setup. Figure 28. Training of DoomRNN. In the virtual DoomRNN environment we constructed, we increased the temperature slightly and used τ = 1.15 to make the agent learn in a more challenging environment. The best agent managed to obtain an average score of 959 over 1024 random rollouts (the highest score of the red line in the diagram). This same agent achieved an average score of 1092 ± 556 over 100 random rollouts when de- ployed to the actual DoomTakeCover-v0 (Paquette, 2016) environment. Figure 26. When agent sees only zt , score is 632 ± 251. Figure 29. Histogram of time steps survived in the actual VizDoom environment over 100 consecutive trials. Score is 1092 ± 556. Figure 27. When agent sees only zt , with a hidden layer, score is 788 ± 141.
16 . World Models References Chiappa, S., Racaniere, S., Wierstra, D., and Mohamed, S. Recurrent environment simulators. ArXiv preprint, Al-Shedivat, M., Bansal, T., Burda, Y., Sutskever, I., Mor- April 2017. URL https://arxiv.org/abs/ datch, I., and Abbeel, P. Continuous adaptation via 1704.02254. meta-learning in nonstationary and competitive environ- ments. ArXiv preprint, October 2017. URL https: Deisenroth, M. and Rasmussen, C. Pilco: A model- //arxiv.org/abs/1710.03641. based and data-efficient approach to policy search. 2011. URL http://mlg.eng.cam.ac.uk/pub/ Alvernaz, S. and Togelius, J. Autoencoder-augmented neu- pdf/DeiRas11.pdf. roevolution for visual doom playing. ArXiv preprint, July 2017. URL https://arxiv.org/abs/1707. Denton, E. and Birodkar, V. Unsupervised learning of dis- 03902. entangled representations from video. ArXiv preprint, May 2017. URL https://arxiv.org/abs/1705. Arulkumaran, K., Deisenroth, M. P., Brundage, M., and 10915. Bharath, A. A. Deep reinforcement learning: A brief survey. IEEE Signal Processing Magazine, 34(6):26–38, Depeweg, S., Hernandez-Lobato, J, Doshi-Velez, F., and Nov 2017. ISSN 1053-5888. doi: 10.1109/MSP.2017. Udluft, S. Learning and policy search in stochastic dy- 2743240. URL https://arxiv.org/abs/1708. namical systems with bayesian neural networks. ArXiv 05866. preprint, May 2016. URL https://arxiv.org/ abs/1605.07127. Bansal, T., Pachocki, J., Sidor, S., Sutskever, I., and Mor- Dosovitskiy, A. and Koltun, V. Learning to act by predicting datch, I. Emergent complexity via multi-agent compe- the future. ArXiv preprint, November 2016. URL https: tition. ArXiv preprint, October 2017. URL https: //arxiv.org/abs/1611.01779. //arxiv.org/abs/1710.03748. Duvenaud, David. Lecture slides on pilco. CSC Bartol, Thomas M, Jr, Bromer, Cailey, Kinney, Justin, 2541 Course at University of Toronto, 2016. URL Chirillo, Michael A, Bourne, Jennifer N, Harris, Kris- https://www.cs.toronto.edu/˜duvenaud/ ten M, and Sejnowski, Terrence J. Nanoconnectomic courses/csc2541/slides/pilco.pdf. upper bound on the variability of synaptic plasticity. eLife Sciences Publications, Ltd, 2015. doi: 10.7554/ E, M. More thoughts from understanding comics by scott eLife.10778. URL https://doi.org/10.7554/ mccloud, 2012. URL https://goo.gl/5Tndi4. eLife.10778. Fernando, C., Banarse, D., Blundell, C., Zwols, Y., Ha, D., Bishop, Christopher M. Mixture density networks. Tech- Rusu, A., Pritzel, A., and Wierstra, D. Pathnet: Evolution nical Report, 1994. URL http://publications. channels gradient descent in super neural networks. ArXiv aston.ac.uk/373/. preprint, January 2017. URL https://arxiv.org/ abs/1701.08734. Bling, Seth. Mar i/o kart, 2015. URL https://youtu. be/S9Y_I9vY8Qw. Finn, C., Tan, X., Duan, Y., Darrell, T., Levine, S., and Abbeel, P. Deep spatial autoencoders for visuomotor Bousmalis, K., Irpan, A., Wohlhart, P., Bai, Y., Kelcey, learning. ArXiv preprint, September 2015. URL https: M., Kalakrishnan, M., Downs, L., Ibarz, J., Pastor, P., //arxiv.org/abs/1509.06113. Konolige, K., Levine, S., and Vanhoucke, V. Using sim- Finn, Chelsea. Model-based rl lecture at deep rl boot- ulation and domain adaptation to improve efficiency of camp 2017, 2017. URL https://youtu.be/ deep robotic grasping. ArXiv e-prints, September 2017. iC2a7M9voYU?t=44m35s. URL https://arxiv.org/abs/1709.07857. Forrester, Jay Wright. Counterintuitive behavior of so- Brockman, G., Cheung, V., Pettersson, L., Schneider, J., cial systems, 1971. URL https://en.wikipedia. Schulman, J., Tang, J., and Zaremba, W. Openai gym. org/wiki/Mental_model. [Online; accessed 01- ArXiv preprint, June 2016. URL https://arxiv. Nov-2017]. org/abs/1606.01540. Foster, David J. Replay comes of age. Annual Cheang, L. and Tsao, D. The code for facial identity Review of Neuroscience, 40(1):581–602, 2017. in the primate brain. Cell, 2017. doi: 10.1016/j.cell. doi: 10.1146/annurev-neuro-072116-031538. 2017.05.011. URL http://www.cell.com/cell/ URL https://doi.org/10.1146/ fulltext/S0092-8674%2817%2930538-X. annurev-neuro-072116-031538.
17 . World Models French, Robert M. Catastrophic interference in connec- Graves, Alex. Hallucination with recurrent neural net- tionist networks: Can it be predicted, can it be pre- works, 2015. URL https://www.youtube.com/ vented? In Cowan, J. D., Tesauro, G., and Alspector, watch?v=-yX1SYeDHbg&t=49m33s. J. (eds.), Advances in Neural Information Processing Sys- tems 6, pp. 1176–1177. Morgan-Kaufmann, 1994. URL Ha, D. Recurrent neural network tutorial https://goo.gl/jwpLsk. for artists. blog.otoro.net, 2017a. URL http://blog.otoro.net/2017/01/01/ Gal, Y., McAllister, R., and Rasmussen, C. Improving recurrent-neural-network-artist/. pilco with bayesian neural network dynamics models. April 2016. URL http://mlg.eng.cam.ac.uk/ Ha, D. Evolving stable strategies. blog.otoro.net, yarin/PDFs/DeepPILCO.pdf. 2017b. URL http://blog.otoro.net/2017/ 11/12/evolving-stable-strategies/. Gauci, Jason and Stanley, Kenneth O. Autonomous evolu- tion of topographic regularities in artificial neural net- Ha, D. and Eck, D. A neural representation of works. Neural Computation, 22(7):1860–1898, July sketch drawings. ArXiv preprint, April 2017. 2010. ISSN 0899-7667. doi: 10.1162/neco.2010. URL https://magenta.tensorflow.org/ 06-09-1042. URL http://eplex.cs.ucf.edu/ sketch-rnn-demo. papers/gauci_nc10.pdf. Ha, D., Dai, A., and Le, Q. Hypernetworks. ArXiv preprint, Gemici, M., Hung, C., Santoro, A., Wayne, G., Mohamed, September 2016. URL https://arxiv.org/abs/ S., Rezende, D., Amos, D., and Lillicrap, T. Generative 1609.09106. temporal models with memory. ArXiv preprint, Febru- Hansen, N. The cma evolution strategy: A tutorial. ArXiv ary 2017. URL https://arxiv.org/abs/1702. preprint, 2016. URL https://arxiv.org/abs/ 04649. 1604.00772. Gerrit, M., Fischer, J., and Whitney, D. Motion-dependent representation of space in area mt+. Neuron, 2013. doi: Hansen, Nikolaus and Ostermeier, Andreas. Completely 10.1016/j.neuron.2013.03.010. URL http://dx.doi. derandomized self-adaptation in evolution strategies. org/10.1016/j.neuron.2013.03.010. Evolutionary Computation, 9(2):159–195, June 2001. ISSN 1063-6560. doi: 10.1162/106365601750190398. Gers, F., Schmidhuber, J., and Cummins, F. Learning to URL http://www.cmap.polytechnique.fr/ forget: Continual prediction with lstm. Neural Computa- ˜nikolaus.hansen/cmaartic.pdf. tion, 12(10):2451–2471, October 2000. ISSN 0899-7667. doi: 10.1162/089976600300015015. URL ftp://ftp. Hausknecht, M., Lehman, J., Miikkulainen, R., and Stone, P. idsia.ch/pub/juergen/FgGates-NC.pdf. A neuroevolution approach to general atari game playing. IEEE Transactions on Computational Intelligence and Gomez, F. and Schmidhuber, J. Co-evolving recurrent AI in Games, 2013. URL http://www.cs.utexas. neurons learn deep memory pomdps. Proceedings of edu/˜ai-lab/?atari. the 7th Annual Conference on Genetic and Evolution- ary Computation, pp. 491–498, 2005. doi: 10.1145/ Hein, D., Depeweg, S., Tokic, M., Udluft, S., Hentschel, A., 1068009.1068092. URL ftp://ftp.idsia.ch/ Runkler, T., and Sterzing, V. A benchmark environment pub/juergen/gecco05gomez.pdf. motivated by industrial control problems. ArXiv preprint, September 2017. URL https://arxiv.org/abs/ Gomez, F., Schmidhuber, J., and Miikkulainen, R. Accel- 1709.09480. erated neural evolution through cooperatively coevolved synapses. Journal of Machine Learning Research, 9: Higgins, I., Pal, A., Rusu, A., Matthey, L., Burgess, C., 937–965, June 2008. ISSN 1532-4435. URL http:// Pritzel, A., Botvinick, M., Blundell, C., and Lerchner, people.idsia.ch/˜juergen/gomez08a.pdf. A. Darla: Improving zero-shot transfer in reinforcement learning. ArXiv e-prints, July 2017. URL https:// Gottlieb, J., Oudeyer, P., Lopes, M., and Baranes, A. arxiv.org/abs/1707.08475. Information-seeking, curiosity, and attention: compu- tational and neural mechanisms. Cell, September 2013. Hirshon, B. Tracking fastballs, 2013. URL http: doi: 10.1016/j.tics.2013.09.001. URL http://www. //sciencenetlinks.com/science-news/ pyoudeyer.com/TICSCuriosity2013.pdf. science-updates/tracking-fastballs/. Graves, Alex. Generating sequences with recurrent neu- Hochreiter, Sepp and Schmidhuber, Juergen. Long short- ral networks. ArXiv preprint, 2013. URL https: term memory. Neural Computation, 1997. URL ftp: //arxiv.org/abs/1308.0850. //ftp.idsia.ch/pub/juergen/lstm.pdf.
18 . World Models Hnermann, Jan. Self-driving cars in the browser, 2017. reinforcement learning. Proceedings of the 15th An- URL http://janhuenermann.com/projects/ nual Conference on Genetic and Evolutionary Compu- learning-to-drive. tation, pp. 1061–1068, 2013. doi: 10.1145/2463372. 2463509. URL http://people.idsia.ch/ Jang, S., Min, J., and Lee, C. Reinforcement ˜juergen/compressednetworksearch.html. car racing with a3c. 2017. URL https: //www.scribd.com/document/358019044/ Lau, Ben. Using keras and deep determinis- Reinforcement-Car-Racing-with-A3C. tic policy gradient to play torcs, 2016. URL https://yanpanlau.github.io/2016/ Kaelbling, L. P., Littman, M. L., and Moore, A. W. Rein- 10/11/Torcs-Keras.html. forcement learning: a survey. Journal of AI research, 4: 237–285, 1996. Lehman, Joel and Stanley, Kenneth. Abandoning objec- Keller, GeorgB., Bonhoeffer, Tobias, and Hbener, tives: Evolution through the search for novelty alone. Mark. Sensorimotor mismatch signals in primary Evolutionary Computation, 19(2):189–223, 2011. ISSN visual cortex of the behaving mouse. Neuron, 1063-6560. URL http://eplex.cs.ucf.edu/ 74(5):809 – 815, 2012. ISSN 0896-6273. doi: noveltysearch/userspage/. https://doi.org/10.1016/j.neuron.2012.03.040. URL Leinweber, Marcus, Ward, Daniel R., Sobczak, Jan M., http://www.sciencedirect.com/science/ Attinger, Alexander, and Keller, Georg B. A senso- article/pii/S0896627312003844. rimotor circuit in mouse cortex for visual flow predic- Kelley, H. J. Gradient theory of optimal flight paths. ARS tions. Neuron, 95(6):1420 – 1432.e5, 2017. ISSN 0896- Journal, 30(10):947–954, 1960. 6273. doi: https://doi.org/10.1016/j.neuron.2017.08. 036. URL http://www.sciencedirect.com/ Kempka, Michael, Wydmuch, Marek, Runc, Grzegorz, science/article/pii/S0896627317307791. Toczek, Jakub, and Jaskowski, Wojciech. Vizdoom: A doom-based ai research platform for visual reinforcement Linnainmaa, S. The representation of the cumulative round- learning. In IEEE Conference on Computational Intelli- ing error of an algorithm as a taylor expansion of the local gence and Games, pp. 341–348, Santorini, Greece, Sep rounding errors. Master’s thesis, Univ. Helsinki, 1970. 2016. IEEE. URL http://arxiv.org/abs/1605. 02097. The best paper award. Matthew Guzdial, Boyang Li, Mark O. Riedl. Game engine learning from video. In Proceedings of the Khan, M. and Elibol, O. Car racing using re- Twenty-Sixth International Joint Conference on Artifi- inforcement learning. 2016. URL https: cial Intelligence, IJCAI-17, pp. 3707–3713, 2017. doi: //web.stanford.edu/class/cs221/2017/ 10.24963/ijcai.2017/518. URL https://doi.org/ restricted/p-final/elibol/final.pdf. 10.24963/ijcai.2017/518. Kingma, D. and Welling, M. Auto-encoding variational McAllister, R. and Rasmussen, C. Data-efficient reinforce- bayes. ArXiv preprint, 2013. URL https://arxiv. ment learning in continuous-state pomdps. ArXiv preprint, org/abs/1312.6114. February 2016. URL https://arxiv.org/abs/ 1602.02523. Kirkpatrick, J., Pascanu, R., Rabinowitz, N., Veness, J., Des- jardins, G., Rusu, A.and Milan, K., Quan, J., Ramalho, McCloud, Scott. Understanding Comics: The In- T., Grabska-Barwinska, A., Hassabis, D., Clopath, C., visible Art. Tundra Publishing, 1993. URL Kumaran, D., and Hadsell, R. Overcoming catastrophic https://en.wikipedia.org/wiki/ forgetting in neural networks. ArXiv preprint, Decem- Understanding_Comics. ber 2016. URL https://arxiv.org/abs/1612. 00796. Miikkulainen, R. Evolving neural networks. IJCNN, August 2013. URL http://nn.cs.utexas.edu/ Kitaoka, Akiyoshi. Akiyoshi’s illusion pages, 2002. URL downloads/slides/miikkulainen.ijcnn13. http://www.ritsumei.ac.jp/˜akitaoka/ pdf. index-e.html. Klimov, Oleg. Carracing-v0, 2016. URL https://gym. Mnih, V., Kavukcuoglu, K., Silver, D., Graves, A., openai.com/envs/CarRacing-v0/. Antonoglou, I., Wierstra, D., and Riedmiller, M. Playing atari with deep reinforcement learning. ArXiv preprint, Koutnik, J., Cuccu, G., Schmidhuber, J., and Gomez, F. December 2013. URL https://arxiv.org/abs/ Evolving large-scale neural networks for vision-based 1312.5602.
19 . World Models Mobbs, Dean, Hagan, Cindy C., Dalgleish, Tim, Silston, Prieur, Luc. Deep-q learning for box2d racecar rl problem., Brian, and Prvost, Charlotte. The ecology of human 2017. URL https://goo.gl/VpDqSw. fear: survival optimization and the nervous system., 2015. URL https://www.frontiersin.org/ Quiroga, R., Reddy, L., Kreiman, G., Koch, C., and Fried, I. article/10.3389/fnins.2015.00055. Invariant visual representation by single neurons in the hu- man brain. Nature, 2005. doi: 10.1038/nature03687. URL Munro, P. W. A dual back-propagation scheme for scalar http://www.nature.com/nature/journal/ reinforcement learning. Proceedings of the Ninth Annual v435/n7045/abs/nature03687.html. Conference of the Cognitive Science Society, Seattle, WA, pp. 165–176, 1987. Ratcliff, Rodney Mark. Connectionist models of recognition memory: constraints imposed by learning and forgetting Nagabandi, A., Kahn, G., Fearing, R., and Levine, S. Neural functions. Psychological review, 97 2:285–308, 1990. network dynamics for model-based deep reinforcement learning with model-free fine-tuning. ArXiv preprint, Au- Rechenberg, I. Evolutionsstrategie: optimierung technis- gust 2017. URL https://arxiv.org/abs/1708. cher systeme nach prinzipien der biologischen evolu- 02596. tion. Frommann-Holzboog, 1973. URL https://en. Nguyen, N. and Widrow, B. The truck backer-upper: An ex- wikipedia.org/wiki/Ingo_Rechenberg. ample of self learning in neural networks. In Proceedings Rezende, D., Mohamed, S., and Wierstra, D. Stochastic of the International Joint Conference on Neural Networks, backpropagation and approximate inference in deep gen- pp. 357–363. IEEE Press, 1989. erative models. ArXiv preprint, 2014. URL https: Nortmann, Nora, Rekauzke, Sascha, Onat, Selim, Knig, //arxiv.org/abs/1401.4082. Peter, and Jancke, Dirk. Primary visual cortex repre- Robinson, T. and Fallside, F. Dynamic reinforcement driven sents the difference between past and present. Cerebral error propagation networks with application to game play- Cortex, 25(6):1427–1440, 2015. doi: 10.1093/cercor/ ing. In CogSci 89, 1989. bht318. URL http://dx.doi.org/10.1093/ cercor/bht318. Salimans, T., Ho, J., Chen, X., Sidor, S., and Sutskever, Oh, J., Guo, X., Lee, H., Lewis, R., and Singh, S. Action- I. Evolution strategies as a scalable alternative to re- conditional video prediction using deep networks in atari inforcement learning. ArXiv preprint, 2017. URL games. ArXiv preprint, July 2015. URL https:// https://arxiv.org/abs/1703.03864. arxiv.org/abs/1507.08750. Schmidhuber, J. Making the world differentiable: Oudeyer, P., Kaplan, F., and Hafner, V. Intrinsic motivation On using self-supervised fully recurrent neural systems for autonomous mental development. Trans. networks for dynamic reinforcement learning and Evol. Comp, apr 2007. doi: 10.1109/TEVC.2006.890271. planning in non-stationary environments. 1990a. URL http://www.pyoudeyer.com/ims.pdf. URL http://people.idsia.ch/˜juergen/ FKI-126-90_(revised)bw_ocr.pdf. Paquette, Philip. Doomtakecover-v0, 2016. URL https://gym.openai.com/envs/ Schmidhuber, J. An on-line algorithm for dynamic re- DoomTakeCover-v0/. inforcement learning and planning in reactive environ- Parker, M. and Bryant, B. Neuro-visual control in ments. 1990 IJCNN International Joint Conference the quake ii environment. IEEE Transactions on on Neural Networks, pp. 253–258 vol.2, June 1990b. Computational Intelligence and AI in Games, 2012. doi: 10.1109/IJCNN.1990.137723. URL ftp://ftp. URL https://www.cse.unr.edu/˜bdbryant/ idsia.ch/pub/juergen/ijcnn90.ps.gz. papers/parker-2012-tciaig.pdf. Schmidhuber, J. A possibility for implementing curiosity Pathak, D., Agrawal, P., A., Efros, and Darrell, T. Curiosity- and boredom in model-building neural controllers. Pro- driven exploration by self-supervised prediction. ArXiv ceedings of the First International Conference on Simula- preprint, May 2017. URL https://pathak22. tion of Adaptive Behavior on From Animals to Animats, github.io/noreward-rl/. pp. 222–227, 1990c. URL ftp://ftp.idsia.ch/ pub/juergen/curiositysab.pdf. Pi, H., Hangya, B., Kvitsiani, D., Sanders, J., Huang, Z., and Kepecs, A. Cortical interneurons that specialize Schmidhuber, J. Reinforcement learning in markovian and in disinhibitory control. Nature, November 2013. doi: non-markovian environments. Advances in Neural Infor- 10.1038/nature12676. URL http://dx.doi.org/ mation Processing Systems 3, pp. 500–506, 1991a. URL 10.1038/nature12676. https://goo.gl/ij1uYQ.
20 . World Models Schmidhuber, J. Curious model-building control systems. In Sehnke, F., Osendorfer, C., Ruckstieb, T., Graves, A., Proc. International Joint Conference on Neural Networks, Peters, J., and Schmidhuber, J. Parameter-exploring Singapore, pp. 1458–1463, 1991b. policy gradients. Neural Networks, 23(4):551– 559, 2010. doi: 10.1016/j.neunet.2009.12.004. Schmidhuber, J. Learning complex, extended sequences URL http://citeseerx.ist.psu. using the principle of history compression. Neural Com- edu/viewdoc/download;jsessionid= putation, 4(2):234–242, 1992. (Based on TR FKI-148-91, A64D1AE8313A364B814998E9E245B40A? TUM, 1991). doi=10.1.1.180.7104&rep=rep1&type=pdf. Schmidhuber, J. Optimal ordered problem solver. ArXiv Shazeer, N., Mirhoseini, A., Maziarz, K., Davis, A., Le, preprint, July 2002. URL https://arxiv.org/ Q., Hinton, G., and Dean, J. Outrageously large neural abs/cs/0207097. networks: The sparsely-gated mixture-of-experts layer. Schmidhuber, J. Developmental robotics, optimal artificial ArXiv preprint, January 2017. URL https://arxiv. curiosity, creativity, music, and the fine arts. Connection org/abs/1701.06538. Science, 18(2):173–187, 2006. Silver, D., van Hasselt, H., Hessel, M., Schaul, T., Guez, A., Schmidhuber, J. Formal theory of creativity, fun, and intrin- Harley, T., Dulac-Arnold, G., Reichert, D., Rabinowitz, sic motivation (1990-2010). IEEE Trans. Autonomous N., Barreto, A., and Degris, T. The predictron: End- Mental Development, 2010. URL http://people. to-end learning and planning. ArXiv preprint, Decem- idsia.ch/˜juergen/creativity.html. ber 2016. URL https://arxiv.org/abs/1612. 08810. Schmidhuber, J. Powerplay: Training an increasingly gen- eral problem solver by continually searching for the sim- Silver, David. David silver’s lecture on inte- plest still unsolvable problem. Frontiers in Psychology, grating learning and planning, 2017. URL 4:313, 2013. ISSN 1664-1078. doi: 10.3389/fpsyg.2013. http://www0.cs.ucl.ac.uk/staff/d. 00313. URL https://www.frontiersin.org/ silver/web/Teaching_files/dyna.pdf. article/10.3389/fpsyg.2013.00313. Srivastava, R., Steunebrink, B., and Schmidhuber, J. First ex- Schmidhuber, J. On learning to think: Algorithmic infor- periments with powerplay. ArXiv preprint, October 2012. mation theory for novel combinations of reinforcement URL https://arxiv.org/abs/1210.8385. learning controllers and recurrent neural world models. ArXiv preprint, 2015a. URL https://arxiv.org/ Stanley, Kenneth and Clune, Jeff. Welcoming the era abs/1511.09249. of deep neuroevolution, 2017. URL https://eng. uber.com/deep-neuroevolution/. Schmidhuber, J. Deep learning in neural networks: An overview. Neural Networks, 61:85–117, 2015b. doi: Stanley, Kenneth O. and Miikkulainen, Risto. Evolving 10.1016/j.neunet.2014.09.003. Published online 2014; neural networks through augmenting topologies. Evolu- based on TR arXiv:1404.7828 [cs.NE]. tionary Computation, 10(2):99–127, 2002. URL http: Schmidhuber, J. One big net for everything. Preprint //nn.cs.utexas.edu/?stanley:ec02. arXiv:1802.08864 [cs.AI], February 2018. URL https: Suarez, Joseph. Language modeling with recurrent highway //arxiv.org/abs/1802.08864. hypernetworks. In Guyon, I., Luxburg, U. V., Bengio, S., Schmidhuber, J. and Huber, R. Learning to generate ar- Wallach, H., Fergus, R., Vishwanathan, S., and Garnett, tificial fovea trajectories for target detection. Interna- R. (eds.), Advances in Neural Information Processing tional Journal of Neural Systems, 2(1-2):125–134, 1991. Systems 30, pp. 3269–3278. Curran Associates, Inc., 2017. doi: 10.1142/S012906579100011X. URL ftp://ftp. URL https://goo.gl/4nqHXw. idsia.ch/pub/juergen/attention.pdf. Sukhbaatar, S., Lin, Z., Kostrikov, I., Synnaeve, G., Szlam, Schmidhuber, J., Storck, J., and Hochreiter, S. Reinforce- A., and Fergus, R. Intrinsic motivation and automatic ment driven information acquisition in nondeterministic curricula via asymmetric self-play. ArXiv preprint, Octo- environments. Technical Report FKI- -94, TUM Depart- ber 2017. URL https://arxiv.org/abs/1703. ment of Informatics, 1994. 05407. Schwefel, H. Numerical Optimization of Computer Models. Sutton, Richard S. and Barto, Andrew G. Intro- John Wiley and Sons, Inc., New York, NY, USA, 1977. duction to Reinforcement Learning. MIT Press, ISBN 0471099880. URL https://en.wikipedia. Cambridge, MA, USA, 1st edition, 1998. ISBN org/wiki/Hans-Paul_Schwefel. 0262193981. URL http://ufal.mff.cuni.
21 . World Models cz/˜straka/courses/npfl114/2016/ Werbos, Paul J. Applications of advances in nonlinear sen- sutton-bookdraft2016sep.pdf. sitivity analysis. In System modeling and optimization, pp. 762–770. Springer, 1982. van den Oord, A., Dieleman, S., Zen, H., Simonyan, K., Vinyals, O., Graves, A., Kalchbrenner, N., Senior, A., Wiering, Marco and van Otterlo, Martijn. Reinforcement and Kavukcuoglu, K. Wavenet: A generative model Learning. Springer, 2012. for raw audio. ArXiv preprint, September 2016. URL https://arxiv.org/abs/1609.03499. Wikipedia, Authors. Video game exploits, 2017. URL https://en.wikipedia.org/wiki/Video_ Vaswani, A., Shazeer, N., Parmar, N., Uszkoreit, J., Jones, game_exploits. [Online; accessed 01-Nov-2017]. L., Gomez, A, Kaiser, L., and Polosukhin, I. Attention is all you need. ArXiv preprint, June 2017. URL https: //arxiv.org/abs/1706.03762. Wahlstrm, N., Schn, T., and Deisenroth, M. Learning deep dynamical models from image pixels. ArXiv preprint, October 2014. URL https://arxiv.org/abs/ 1410.7550. Wahlstrm, N., Schn, T., and Deisenroth, M. From pixels to torques: Policy learning with deep dynamical models. ArXiv preprint, June 2015. URL https://arxiv. org/abs/1502.02251. Watanabe, Eiji, Kitaoka, Akiyoshi, Sakamoto, Kiwako, Yasugi, Masaki, and Tanaka, Kenta. Illusory mo- tion reproduced by deep neural networks trained for prediction. Frontiers in Psychology, 9:345, 2018. ISSN 1664-1078. doi: 10.3389/fpsyg.2018. 00345. URL https://www.frontiersin.org/ article/10.3389/fpsyg.2018.00345. Watter, M., Springenberg, J., Boedecker, J., and Riedmiller, M. Embed to control: A locally linear latent dynam- ics model for control from raw images. ArXiv preprint, June 2015. URL https://arxiv.org/abs/1506. 07365. Watters, N., Tacchetti, A., Weber, T., Pascanu, R., Battaglia, P., and Zoran, D. Visual interaction networks. ArXiv preprint, June 2017. URL https://arxiv.org/ abs/1706.01433. Weber, T., Racanire, S., Reichert, D., Buesing, L., Guez, A., Rezende, D., Badia, A., Vinyals, O., Heess, N., Li, Y., Pascanu, R., Battaglia, P., Silver, D., and Wierstra, D. Imagination-augmented agents for deep reinforcement learning. ArXiv preprint, July 2017. URL https:// arxiv.org/abs/1707.06203. Werbos, P. J. Learning how the world works: Specifications for predictive networks in robots and brains. In Proceed- ings of IEEE International Conference on Systems, Man and Cybernetics, N.Y., 1987. Werbos, P. J. Neural networks for control and system identi- fication. In Proceedings of IEEE/CDC Tampa, Florida, 1989.