- 快召唤伙伴们来围观吧
- 微博 QQ QQ空间 贴吧
- 文档嵌入链接
- 复制
- 微信扫一扫分享
- 已成功复制到剪贴板
Universal Language Model Fine-tuning for Text Classification
展开查看详情
1 . Universal Language Model Fine-tuning for Text Classification Jeremy Howard∗ Sebastian Ruder∗ fast.ai Insight Centre, NUI Galway University of San Francisco Aylien Ltd., Dublin j@fast.ai sebastian@ruder.io Abstract While Deep Learning models have achieved state-of-the-art on many NLP tasks, these models Inductive transfer learning has greatly im- are trained from scratch, requiring large datasets, arXiv:1801.06146v5 [cs.CL] 23 May 2018 pacted computer vision, but existing ap- and days to converge. Research in NLP focused proaches in NLP still require task-specific mostly on transductive transfer (Blitzer et al., modifications and training from scratch. 2007). For inductive transfer, fine-tuning pre- We propose Universal Language Model trained word embeddings (Mikolov et al., 2013), Fine-tuning (ULMFiT), an effective trans- a simple transfer technique that only targets a fer learning method that can be applied to model’s first layer, has had a large impact in prac- any task in NLP, and introduce techniques tice and is used in most state-of-the-art models. that are key for fine-tuning a language Recent approaches that concatenate embeddings model. Our method significantly outper- derived from other tasks with the input at different forms the state-of-the-art on six text clas- layers (Peters et al., 2017; McCann et al., 2017; sification tasks, reducing the error by 18- Peters et al., 2018) still train the main task model 24% on the majority of datasets. Further- from scratch and treat pretrained embeddings as more, with only 100 labeled examples, it fixed parameters, limiting their usefulness. matches the performance of training from In light of the benefits of pretraining (Erhan scratch on 100× more data. We open- et al., 2010), we should be able to do better than source our pretrained models and code1 . randomly initializing the remaining parameters of our models. However, inductive transfer via fine- 1 Introduction tuning has been unsuccessful for NLP (Mou et al., 2016). Dai and Le (2015) first proposed fine- Inductive transfer learning has had a large impact tuning a language model (LM) but require millions on computer vision (CV). Applied CV models (in- of in-domain documents to achieve good perfor- cluding object detection, classification, and seg- mance, which severely limits its applicability. mentation) are rarely trained from scratch, but in- We show that not the idea of LM fine-tuning but stead are fine-tuned from models that have been our lack of knowledge of how to train them ef- pretrained on ImageNet, MS-COCO, and other fectively has been hindering wider adoption. LMs datasets (Sharif Razavian et al., 2014; Long et al., overfit to small datasets and suffered catastrophic 2015a; He et al., 2016; Huang et al., 2017). forgetting when fine-tuned with a classifier. Com- Text classification is a category of Natural Lan- pared to CV, NLP models are typically more shal- guage Processing (NLP) tasks with real-world ap- low and thus require different fine-tuning methods. plications such as spam, fraud, and bot detection We propose a new method, Universal Language (Jindal and Liu, 2007; Ngai et al., 2011; Chu et al., Model Fine-tuning (ULMFiT) that addresses these 2012), emergency response (Caragea et al., 2011), issues and enables robust inductive transfer learn- and commercial document classification, such as ing for any NLP task, akin to fine-tuning ImageNet for legal discovery (Roitblat et al., 2010). models: The same 3-layer LSTM architecture— 1 http://nlp.fast.ai/ulmfit. with the same hyperparameters and no addi- Equal contribution. Jeremy focused on the algorithm de- velopment and implementation, Sebastian focused on the ex- tions other than tuned dropout hyperparameters— periments and writing. outperforms highly engineered models and trans-
2 .fer learning approaches on six widely studied text et al. (2017), and McCann et al. (2017) who use classification tasks. On IMDb, with 100 labeled language modeling, paraphrasing, entailment, and examples, ULMFiT matches the performance of Machine Translation (MT) respectively for pre- training from scratch with 10× and—given 50k training. Specifically, Peters et al. (2018) require unlabeled examples—with 100× more data. engineered custom architectures, while we show state-of-the-art performance with the same basic Contributions Our contributions are the follow- architecture across a range of tasks. In CV, hyper- ing: 1) We propose Universal Language Model columns have been nearly entirely superseded by Fine-tuning (ULMFiT), a method that can be used end-to-end fine-tuning (Long et al., 2015a). to achieve CV-like transfer learning for any task for NLP. 2) We propose discriminative fine-tuning, Multi-task learning A related direction is slanted triangular learning rates, and gradual multi-task learning (MTL) (Caruana, 1993). This unfreezing, novel techniques to retain previous is the approach taken by Rei (2017) and Liu et al. knowledge and avoid catastrophic forgetting dur- (2018) who add a language modeling objective ing fine-tuning. 3) We significantly outperform the to the model that is trained jointly with the main state-of-the-art on six representative text classifi- task model. MTL requires the tasks to be trained cation datasets, with an error reduction of 18-24% from scratch every time, which makes it inefficient on the majority of datasets. 4) We show that our and often requires careful weighting of the task- method enables extremely sample-efficient trans- specific objective functions (Chen et al., 2017). fer learning and perform an extensive ablation analysis. 5) We make the pretrained models and Fine-tuning Fine-tuning has been used success- our code available to enable wider adoption. fully to transfer between similar tasks, e.g. in QA (Min et al., 2017), for distantly supervised senti- 2 Related work ment analysis (Severyn and Moschitti, 2015), or MT domains (Sennrich et al., 2015) but has been Transfer learning in CV Features in deep neu- shown to fail between unrelated ones (Mou et al., ral networks in CV have been observed to tran- 2016). Dai and Le (2015) also fine-tune a lan- sition from general to task-specific from the first guage model, but overfit with 10k labeled exam- to the last layer (Yosinski et al., 2014). For this ples and require millions of in-domain documents reason, most work in CV focuses on transferring for good performance. In contrast, ULMFiT lever- the first layers of the model (Long et al., 2015b). ages general-domain pretraining and novel fine- Sharif Razavian et al. (2014) achieve state-of-the- tuning techniques to prevent overfitting even with art results using features of an ImageNet model as only 100 labeled examples and achieves state-of- input to a simple classifier. In recent years, this the-art results also on small datasets. approach has been superseded by fine-tuning ei- ther the last (Donahue et al., 2014) or several of 3 Universal Language Model Fine-tuning the last layers of a pretrained model and leaving the remaining layers frozen (Long et al., 2015a). We are interested in the most general inductive transfer learning setting for NLP (Pan and Yang, Hypercolumns In NLP, only recently have 2010): Given a static source task TS and any tar- methods been proposed that go beyond transfer- get task TT with TS = TT , we would like to im- ring word embeddings. The prevailing approach prove performance on TT . Language modeling is to pretrain embeddings that capture additional can be seen as the ideal source task and a counter- context via other tasks. Embeddings at different part of ImageNet for NLP: It captures many facets levels are then used as features, concatenated ei- of language relevant for downstream tasks, such as ther with the word embeddings or with the in- long-term dependencies (Linzen et al., 2016), hi- puts at intermediate layers. This method is known erarchical relations (Gulordava et al., 2018), and as hypercolumns (Hariharan et al., 2015) in CV2 sentiment (Radford et al., 2017). In contrast to and is used by Peters et al. (2017), Peters et al. tasks like MT (McCann et al., 2017) and entail- (2018), Wieting and Gimpel (2017), Conneau ment (Conneau et al., 2017), it provides data in 2 A hypercolumn at a pixel in CV is the vector of activa- near-unlimited quantities for most domains and tions of all CNN units above that pixel. In analogy, a hyper- column for a word or sentence in NLP is the concatenation of languages. Additionally, a pretrained LM can be embeddings at different layers in a pretrained model. easily adapted to the idiosyncrasies of a target
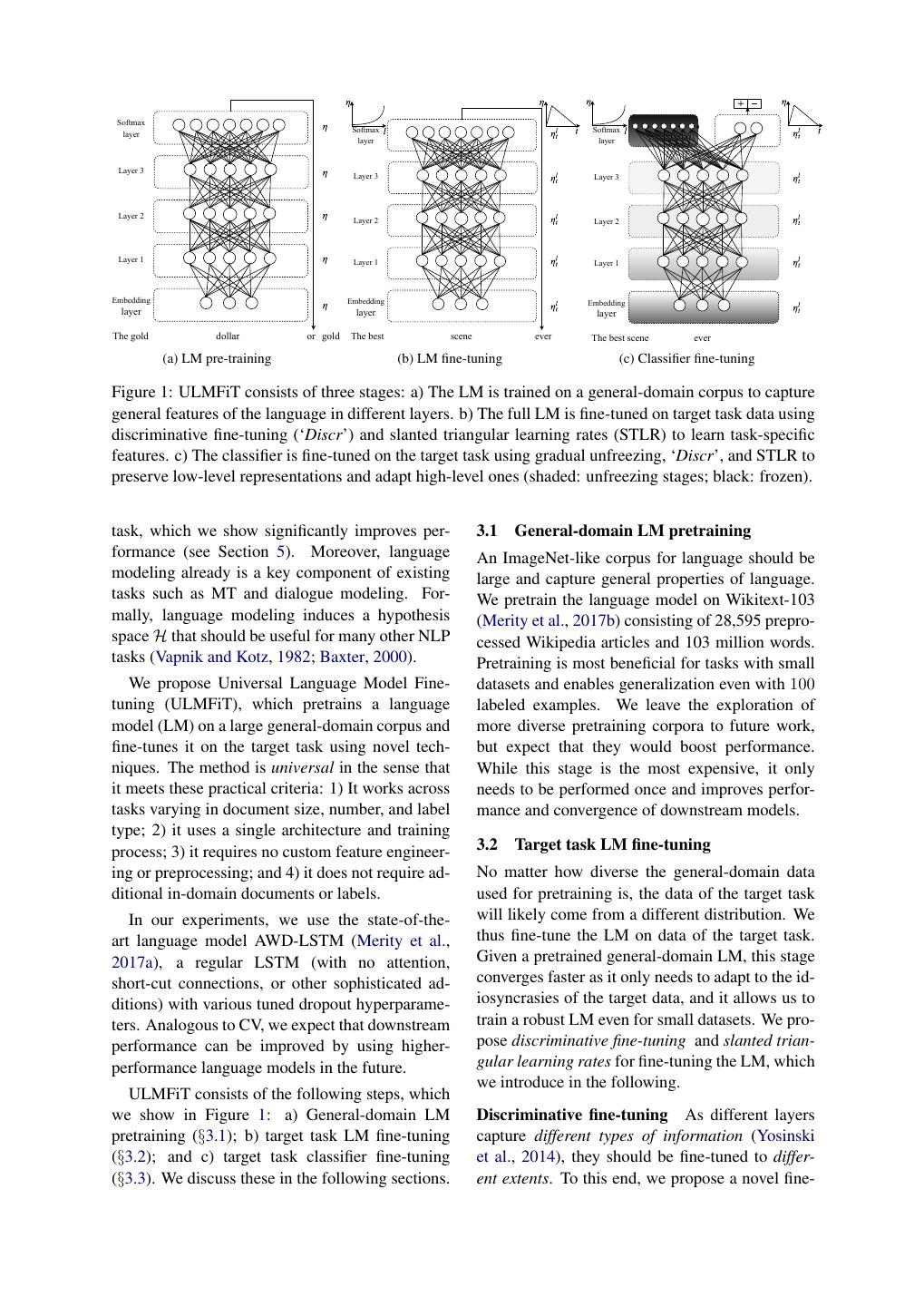
3 . Softmax Softmax Softmax layer layer layer Layer 3 Layer 3 Layer 3 Layer 2 Layer 2 Layer 2 Layer 1 Layer 1 Layer 1 Embedding Embedding Embedding layer layer layer The gold dollar or gold The best scene ever The best scene ever (a) LM pre-training (b) LM fine-tuning (c) Classifier fine-tuning Figure 1: ULMFiT consists of three stages: a) The LM is trained on a general-domain corpus to capture general features of the language in different layers. b) The full LM is fine-tuned on target task data using discriminative fine-tuning (‘Discr’) and slanted triangular learning rates (STLR) to learn task-specific features. c) The classifier is fine-tuned on the target task using gradual unfreezing, ‘Discr’, and STLR to preserve low-level representations and adapt high-level ones (shaded: unfreezing stages; black: frozen). 1/1 1/1 1/1 task, which we show significantly improves per- 3.1 General-domain LM pretraining formance (see Section 5). Moreover, language An ImageNet-like corpus for language should be modeling already is a key component of existing large and capture general properties of language. tasks such as MT and dialogue modeling. For- We pretrain the language model on Wikitext-103 mally, language modeling induces a hypothesis (Merity et al., 2017b) consisting of 28,595 prepro- space H that should be useful for many other NLP cessed Wikipedia articles and 103 million words. tasks (Vapnik and Kotz, 1982; Baxter, 2000). Pretraining is most beneficial for tasks with small We propose Universal Language Model Fine- datasets and enables generalization even with 100 tuning (ULMFiT), which pretrains a language labeled examples. We leave the exploration of model (LM) on a large general-domain corpus and more diverse pretraining corpora to future work, fine-tunes it on the target task using novel tech- but expect that they would boost performance. niques. The method is universal in the sense that While this stage is the most expensive, it only it meets these practical criteria: 1) It works across needs to be performed once and improves perfor- tasks varying in document size, number, and label mance and convergence of downstream models. type; 2) it uses a single architecture and training process; 3) it requires no custom feature engineer- 3.2 Target task LM fine-tuning ing or preprocessing; and 4) it does not require ad- No matter how diverse the general-domain data ditional in-domain documents or labels. used for pretraining is, the data of the target task In our experiments, we use the state-of-the- will likely come from a different distribution. We art language model AWD-LSTM (Merity et al., thus fine-tune the LM on data of the target task. 2017a), a regular LSTM (with no attention, Given a pretrained general-domain LM, this stage short-cut connections, or other sophisticated ad- converges faster as it only needs to adapt to the id- ditions) with various tuned dropout hyperparame- iosyncrasies of the target data, and it allows us to ters. Analogous to CV, we expect that downstream train a robust LM even for small datasets. We pro- performance can be improved by using higher- pose discriminative fine-tuning and slanted trian- performance language models in the future. gular learning rates for fine-tuning the LM, which we introduce in the following. ULMFiT consists of the following steps, which we show in Figure 1: a) General-domain LM Discriminative fine-tuning As different layers pretraining (§3.1); b) target task LM fine-tuning capture different types of information (Yosinski (§3.2); and c) target task classifier fine-tuning et al., 2014), they should be fine-tuned to differ- (§3.3). We discuss these in the following sections. ent extents. To this end, we propose a novel fine-
4 .tuning method, discriminative fine-tuning3 . the LR, cut is the iteration when we switch from Instead of using the same learning rate for all increasing to decreasing the LR, p is the fraction of layers of the model, discriminative fine-tuning al- the number of iterations we have increased or will lows us to tune each layer with different learning decrease the LR respectively, ratio specifies how rates. For context, the regular stochastic gradient much smaller the lowest LR is from the maximum descent (SGD) update of a model’s parameters θ at LR ηmax , and ηt is the learning rate at iteration t. time step t looks like the following (Ruder, 2016): We generally use cut f rac = 0.1, ratio = 32 and ηmax = 0.01. θt = θt−1 − η · ∇θ J(θ) (1) STLR modifies triangular learning rates (Smith, 2017) with a short increase and a long decay pe- where η is the learning rate and ∇θ J(θ) is the gra- riod, which we found key for good performance.5 dient with regard to the model’s objective func- In Section 5, we compare against aggressive co- tion. For discriminative fine-tuning, we split the sine annealing, a similar schedule that has recently parameters θ into {θ1 , . . . , θL } where θl contains been used to achieve state-of-the-art performance the parameters of the model at the l-th layer and in CV (Loshchilov and Hutter, 2017).6 L is the number of layers of the model. Similarly, we obtain {η 1 , . . . , η L } where η l is the learning rate of the l-th layer. The SGD update with discriminative fine- tuning is then the following: θtl = θt−1 l − η l · ∇θl J(θ) (2) We empirically found it to work well to first choose the learning rate η L of the last layer by fine-tuning only the last layer and using η l−1 = η l /2.6 as the learning rate for lower layers. Slanted triangular learning rates For adapting its parameters to task-specific features, we would like the model to quickly converge to a suitable Figure 2: The slanted triangular learning rate region of the parameter space in the beginning schedule used for ULMFiT as a function of the of training and then refine its parameters. Using number of training iterations. the same learning rate (LR) or an annealed learn- ing rate throughout training is not the best way 3.3 Target task classifier fine-tuning to achieve this behaviour. Instead, we propose slanted triangular learning rates (STLR), which Finally, for fine-tuning the classifier, we augment first linearly increases the learning rate and then the pretrained language model with two additional linearly decays it according to the following up- linear blocks. Following standard practice for date schedule, which can be seen in Figure 2: CV classifiers, each block uses batch normaliza- tion (Ioffe and Szegedy, 2015) and dropout, with cut = T · cut f rac ReLU activations for the intermediate layer and a softmax activation that outputs a probability dis- t/cut, if t < cut p= tribution over target classes at the last layer. Note 1 − cut·(1/cut f rac−1) , otherwise (3) t−cut that the parameters in these task-specific classi- 1 + p · (ratio − 1) fier layers are the only ones that are learned from ηt = ηmax · scratch. The first linear layer takes as the input the ratio pooled last hidden layer states. where T is the number of training iterations4 , cut f rac is the fraction of iterations we increase Concat pooling The signal in text classification 3 tasks is often contained in a few words, which may An unrelated method of the same name exists for deep 5 Boltzmann machines (Salakhutdinov and Hinton, 2009). We also credit personal communication with the author. 4 6 In other words, the number of epochs times the number While Loshchilov and Hutter (2017) use multiple anneal- of updates per epoch. ing cycles, we generally found one cycle to work best.
5 .occur anywhere in the document. As input docu- Dataset Type # classes # examples ments can consist of hundreds of words, informa- TREC-6 Question 6 5.5k tion may get lost if we only consider the last hid- IMDb Sentiment 2 25k den state of the model. For this reason, we con- Yelp-bi Sentiment 2 560k catenate the hidden state at the last time step hT Yelp-full Sentiment 5 650k of the document with both the max-pooled and the AG Topic 4 120k mean-pooled representation of the hidden states DBpedia Topic 14 560k over as many time steps as fit in GPU memory H = {h1 , . . . , hT }: Table 1: Text classification datasets and tasks with hc = [hT , maxpool(H), meanpool(H)] (4) number of classes and training examples. where [] is concatenation. are back-propagated to the batches whose hidden Fine-tuning the target classifier is the most crit- states contributed to the final prediction. In prac- ical part of the transfer learning method. Overly tice, we use variable length backpropagation se- aggressive fine-tuning will cause catastrophic for- quences (Merity et al., 2017a). getting, eliminating the benefit of the information captured through language modeling; too cautious Bidirectional language model Similar to exist- fine-tuning will lead to slow convergence (and re- ing work (Peters et al., 2017, 2018), we are not sultant overfitting). Besides discriminative fine- limited to fine-tuning a unidirectional language tuning and triangular learning rates, we propose model. For all our experiments, we pretrain both a gradual unfreezing for fine-tuning the classifier. forward and a backward LM. We fine-tune a clas- sifier for each LM independently using BPT3C Gradual unfreezing Rather than fine-tuning all and average the classifier predictions. layers at once, which risks catastrophic forgetting, we propose to gradually unfreeze the model start- 4 Experiments ing from the last layer as this contains the least While our approach is equally applicable to se- general knowledge (Yosinski et al., 2014): We quence labeling tasks, we focus on text classifica- first unfreeze the last layer and fine-tune all un- tion tasks in this work due to their important real- frozen layers for one epoch. We then unfreeze the world applications. next lower frozen layer and repeat, until we fine- tune all layers until convergence at the last itera- 4.1 Experimental setup tion. This is similar to ‘chain-thaw’ (Felbo et al., Datasets and tasks We evaluate our method on 2017), except that we add a layer at a time to the six widely-studied datasets, with varying numbers set of ‘thawed’ layers, rather than only training a of documents and varying document length, used single layer at a time. by state-of-the-art text classification and transfer While discriminative fine-tuning, slanted trian- learning approaches (Johnson and Zhang, 2017; gular learning rates, and gradual unfreezing all McCann et al., 2017) as instances of three com- are beneficial on their own, we show in Section mon text classification tasks: sentiment analy- 5 that they complement each other and enable our sis, question classification, and topic classifica- method to perform well across diverse datasets. tion. We show the statistics for each dataset and BPTT for Text Classification (BPT3C) Lan- task in Table 1. guage models are trained with backpropagation Sentiment Analysis For sentiment analysis, we through time (BPTT) to enable gradient propa- evaluate our approach on the binary movie review gation for large input sequences. In order to IMDb dataset (Maas et al., 2011) and on the binary make fine-tuning a classifier for large documents and five-class version of the Yelp review dataset feasible, we propose BPTT for Text Classifica- compiled by Zhang et al. (2015). tion (BPT3C): We divide the document into fixed- length batches of size b. At the beginning of each Question Classification We use the six-class batch, the model is initialized with the final state version of the small TREC dataset (Voorhees and of the previous batch; we keep track of the hid- Tice, 1999) dataset of open-domain, fact-based den states for mean and max-pooling; gradients questions divided into broad semantic categories.
6 . Model Test Model Test CoVe (McCann et al., 2017) 8.2 CoVe (McCann et al., 2017) 4.2 TREC-6 IMDb oh-LSTM (Johnson and Zhang, 2016) 5.9 TBCNN (Mou et al., 2015) 4.0 Virtual (Miyato et al., 2016) 5.9 LSTM-CNN (Zhou et al., 2016) 3.9 ULMFiT (ours) 4.6 ULMFiT (ours) 3.6 Table 2: Test error rates (%) on two text classification datasets used by McCann et al. (2017). AG DBpedia Yelp-bi Yelp-full Char-level CNN (Zhang et al., 2015) 9.51 1.55 4.88 37.95 CNN (Johnson and Zhang, 2016) 6.57 0.84 2.90 32.39 DPCNN (Johnson and Zhang, 2017) 6.87 0.88 2.64 30.58 ULMFiT (ours) 5.01 0.80 2.16 29.98 Table 3: Test error rates (%) on text classification datasets used by Johnson and Zhang (2017). Topic classification For topic classification, we used in (Merity et al., 2017a). evaluate on the large-scale AG news and DBpedia ontology datasets created by Zhang et al. (2015). Baselines and comparison models For each task, we compare against the current state-of-the- Pre-processing We use the same pre-processing art. For the IMDb and TREC-6 datasets, we com- as in earlier work (Johnson and Zhang, 2017; Mc- pare against CoVe (McCann et al., 2017), a state- Cann et al., 2017). In addition, to allow the lan- of-the-art transfer learning method for NLP. For guage model to capture aspects that might be rel- the AG, Yelp, and DBpedia datasets, we com- evant for classification, we add special tokens for pare against the state-of-the-art text categorization upper-case words, elongation, and repetition. method by Johnson and Zhang (2017). Hyperparameters We are interested in a model 4.2 Results that performs robustly across a diverse set of tasks. To this end, if not mentioned otherwise, we use the For consistency, we report all results as error rates same set of hyperparameters across tasks, which (lower is better). We show the test error rates we tune on the IMDb validation set. We use on the IMDb and TREC-6 datasets used by Mc- the AWD-LSTM language model (Merity et al., Cann et al. (2017) in Table 2. Our method outper- 2017a) with an embedding size of 400, 3 layers, forms both CoVe, a state-of-the-art transfer learn- 1150 hidden activations per layer, and a BPTT ing method based on hypercolumns, as well as the batch size of 70. We apply dropout of 0.4 to state-of-the-art on both datasets. On IMDb, we layers, 0.3 to RNN layers, 0.4 to input embed- reduce the error dramatically by 43.9% and 22% ding layers, 0.05 to embedding layers, and weight with regard to CoVe and the state-of-the-art re- dropout of 0.5 to the RNN hidden-to-hidden ma- spectively. This is promising as the existing state- trix. The classifier has a hidden layer of size 50. of-the-art requires complex architectures (Peters We use Adam with β1 = 0.7 instead of the de- et al., 2018), multiple forms of attention (McCann fault β1 = 0.9 and β2 = 0.99, similar to (Dozat et al., 2017) and sophisticated embedding schemes and Manning, 2017). We use a batch size of 64, (Johnson and Zhang, 2016), while our method em- a base learning rate of 0.004 and 0.01 for fine- ploys a regular LSTM with dropout. We note tuning the LM and the classifier respectively, and that the language model fine-tuning approach of tune the number of epochs on the validation set of Dai and Le (2015) only achieves an error of 7.64 each task7 . We otherwise use the same practices vs. 4.6 for our method on IMDb, demonstrating the benefit of transferring knowledge from a large 7 On small datasets such as TREC-6, we fine-tune the LM ImageNet-like corpus using our fine-tuning tech- only for 15 epochs without overfitting, while we can fine-tune longer on larger datasets. We found 50 epochs to be a good niques. IMDb in particular is reflective of real- default for fine-tuning the classifier. world datasets: Its documents are generally a few
7 .Figure 3: Validation error rates for supervised and semi-supervised ULMFiT vs. training from scratch with different numbers of training examples on IMDb, TREC-6, and AG (from left to right). paragraphs long—similar to emails (e.g for legal Pretraining IMDb TREC-6 AG discovery) and online comments (e.g for commu- Without pretraining 5.63 10.67 5.52 nity management); and sentiment analysis is simi- With pretraining 5.00 5.69 5.38 lar to many commercial applications, e.g. product response tracking and support email routing. Table 4: Validation error rates for ULMFiT with On TREC-6, our improvement—similar as the and without pretraining. improvements of state-of-the-art approaches—is not statistically significant, due to the small size of the 500-examples test set. Nevertheless, the com- a task with a small number of labels. We evalu- petitive performance on TREC-6 demonstrates ate ULMFiT on different numbers of labeled ex- that our model performs well across different amples in two settings: only labeled examples are dataset sizes and can deal with examples that range used for LM fine-tuning (‘supervised’); and all from single sentences—in the case of TREC-6— task data is available and can be used to fine-tune to several paragraphs for IMDb. Note that despite the LM (‘semi-supervised’). We compare ULM- pretraining on more than two orders of magnitude FiT to training from scratch—which is necessary less data than the 7 million sentence pairs used by for hypercolumn-based approaches. We split off McCann et al. (2017), we consistently outperform balanced fractions of the training data, keep the their approach on both datasets. validation set fixed, and use the same hyperparam- We show the test error rates on the larger AG, eters as before. We show the results in Figure 3. DBpedia, Yelp-bi, and Yelp-full datasets in Table On IMDb and AG, supervised ULMFiT with 3. Our method again outperforms the state-of- only 100 labeled examples matches the perfor- the-art significantly. On AG, we observe a simi- mance of training from scratch with 10× and 20× larly dramatic error reduction by 23.7% compared more data respectively, clearly demonstrating the to the state-of-the-art. On DBpedia, Yelp-bi, and benefit of general-domain LM pretraining. If we Yelp-full, we reduce the error by 4.8%, 18.2%, allow ULMFiT to also utilize unlabeled exam- 2.0% respectively. ples (50k for IMDb, 100k for AG), at 100 labeled examples, we match the performance of training 5 Analysis from scratch with 50× and 100× more data on AG In order to assess the impact of each contribution, and IMDb respectively. On TREC-6, ULMFiT we perform a series of analyses and ablations. We significantly improves upon training from scratch; run experiments on three corpora, IMDb, TREC- as examples are shorter and fewer, supervised and 6, and AG that are representative of different tasks, semi-supervised ULMFiT achieve similar results. genres, and sizes. For all experiments, we split off 10% of the training set and report error rates on Impact of pretraining We compare using no this validation set with unidirectional LMs. We pretraining with pretraining on WikiText-103 fine-tune the classifier for 50 epochs and train all (Merity et al., 2017b) in Table 4. Pretraining is methods but ULMFiT with early stopping. most useful for small and medium-sized datasets, which are most common in commercial applica- Low-shot learning One of the main benefits of tions. However, even for large datasets, pretrain- transfer learning is being able to train a model for ing improves performance.
8 . LM IMDb TREC-6 AG Classifier fine-tuning IMDb TREC-6 AG Vanilla LM 5.98 7.41 5.76 From scratch 9.93 13.36 6.81 AWD-LSTM LM 5.00 5.69 5.38 Full 6.87 6.86 5.81 Full + discr 5.57 6.21 5.62 Table 5: Validation error rates for ULMFiT with a Last 6.49 16.09 8.38 vanilla LM and the AWD-LSTM LM. Chain-thaw 5.39 6.71 5.90 Freez 6.37 6.86 5.81 LM fine-tuning IMDb TREC-6 AG Freez + discr 5.39 5.86 6.04 Freez + stlr 5.04 6.02 5.35 No LM fine-tuning 6.99 6.38 6.09 Freez + cos 5.70 6.38 5.29 Full 5.86 6.54 5.61 Freez + discr + stlr 5.00 5.69 5.38 Full + discr 5.55 6.36 5.47 Full + discr + stlr 5.00 5.69 5.38 Table 7: Validation error rates for ULMFiT with different methods to fine-tune the classifier. Table 6: Validation error rates for ULMFiT with different variations of LM fine-tuning. of 0.001 and 0.0001 for the last and all other layers respectively for ‘Chain-thaw’ as in (Felbo et al., Impact of LM quality In order to gauge the im- 2017), and a learning rate of 0.001 otherwise. We portance of choosing an appropriate LM, we com- show the results in Table 7. pare a vanilla LM with the same hyperparame- Fine-tuning the classifier significantly improves ters without any dropout8 with the AWD-LSTM over training from scratch, particularly on the LM with tuned dropout parameters in Table 5. small TREC-6. ‘Last’, the standard fine-tuning Using our fine-tuning techniques, even a regular method in CV, severely underfits and is never LM reaches surprisingly good performance on the able to lower the training error to 0. ‘Chain- larger datasets. On the smaller TREC-6, a vanilla thaw’ achieves competitive performance on the LM without dropout runs the risk of overfitting, smaller datasets, but is outperformed significantly which decreases performance. on the large AG. ‘Freez’ provides similar per- Impact of LM fine-tuning We compare no fine- formance as ‘Full’. ‘Discr’ consistently boosts tuning against fine-tuning the full model (Erhan the performance of ‘Full’ and ‘Freez’, except et al., 2010) (‘Full’), the most commonly used for the large AG. Cosine annealing is competi- fine-tuning method, with and without discrimi- tive with slanted triangular learning rates on large native fine-tuning (‘Discr’) and slanted triangular data, but under-performs on smaller datasets. Fi- learning rates (‘Stlr’) in Table 6. Fine-tuning the nally, full ULMFiT classifier fine-tuning (bottom LM is most beneficial for larger datasets. ‘Discr’ row) achieves the best performance on IMDB and and ‘Stlr’ improve performance across all three TREC-6 and competitive performance on AG. Im- datasets and are necessary on the smaller TREC-6, portantly, ULMFiT is the only method that shows where regular fine-tuning is not beneficial. excellent performance across the board—and is therefore the only universal method. Impact of classifier fine-tuning We compare training from scratch, fine-tuning the full model Classifier fine-tuning behavior While our re- (‘Full’), only fine-tuning the last layer (‘Last’) sults demonstrate that how we fine-tune the clas- (Donahue et al., 2014), ‘Chain-thaw’ (Felbo et al., sifier makes a significant difference, fine-tuning 2017), and gradual unfreezing (‘Freez’). We fur- for inductive transfer is currently under-explored thermore assess the importance of discriminative in NLP as it mostly has been thought to be un- fine-tuning (‘Discr’) and slanted triangular learn- helpful (Mou et al., 2016). To better understand ing rates (‘Stlr’). We compare the latter to an the fine-tuning behavior of our model, we compare alternative, aggressive cosine annealing schedule the validation error of the classifier fine-tuned with (‘Cos’) (Loshchilov and Hutter, 2017). We use a ULMFiT and ‘Full’ during training in Figure 4. learning rate η L = 0.01 for ‘Discr’, learning rates On all datasets, fine-tuning the full model leads 8 To avoid overfitting, we only train the vanilla LM classi- to the lowest error comparatively early in train- fier for 5 epochs and keep dropout of 0.4 in the classifier. ing, e.g. already after the first epoch on IMDb.
9 . Given that transfer learning and particularly fine-tuning for NLP is under-explored, many fu- ture directions are possible. One possible direc- tion is to improve language model pretraining and fine-tuning and make them more scalable: for ImageNet, predicting far fewer classes only in- curs a small performance drop (Huh et al., 2016), while recent work shows that an alignment be- tween source and target task label sets is impor- tant (Mahajan et al., 2018)—focusing on predict- ing a subset of words such as the most frequent ones might retain most of the performance while speeding up training. Language modeling can also be augmented with additional tasks in a multi-task learning fashion (Caruana, 1993) or enriched with additional supervision, e.g. syntax-sensitive de- pendencies (Linzen et al., 2016) to create a model that is more general or better suited for certain downstream tasks, ideally in a weakly-supervised Figure 4: Validation error rate curves for fine- manner to retain its universal properties. tuning the classifier with ULMFiT and ‘Full’ on Another direction is to apply the method to IMDb, TREC-6, and AG (top to bottom). novel tasks and models. While an extension to sequence labeling is straightforward, other tasks with more complex interactions such as entailment The error then increases as the model starts to or question answering may require novel ways to overfit and knowledge captured through pretrain- pretrain and fine-tune. Finally, while we have ing is lost. In contrast, ULMFiT is more sta- provided a series of analyses and ablations, more ble and suffers from no such catastrophic forget- studies are required to better understand what ting; performance remains similar or improves un- knowledge a pretrained language model captures, til late epochs, which shows the positive effect of how this changes during fine-tuning, and what in- the learning rate schedule. formation different tasks require. Impact of bidirectionality At the cost of train- 7 Conclusion ing a second model, ensembling the predictions of a forward and backwards LM-classifier brings a We have proposed ULMFiT, an effective and ex- performance boost of around 0.5–0.7. On IMDb tremely sample-efficient transfer learning method we lower the test error from 5.30 of a single model that can be applied to any NLP task. We have also to 4.58 for the bidirectional model. proposed several novel fine-tuning techniques that in conjunction prevent catastrophic forgetting and 6 Discussion and future directions enable robust learning across a diverse range of tasks. Our method significantly outperformed ex- While we have shown that ULMFiT can achieve isting transfer learning techniques and the state- state-of-the-art performance on widely used text of-the-art on six representative text classification classification tasks, we believe that language tasks. We hope that our results will catalyze new model fine-tuning will be particularly useful in the developments in transfer learning for NLP. following settings compared to existing transfer learning approaches (Conneau et al., 2017; Mc- Acknowledgments Cann et al., 2017; Peters et al., 2018): a) NLP for non-English languages, where training data for su- We thank the anonymous reviewers for their valu- pervised pretraining tasks is scarce; b) new NLP able feedback. Sebastian is supported by Irish tasks where no state-of-the-art architecture exists; Research Council Grant Number EBPPG/2014/30 and c) tasks with limited amounts of labeled data and Science Foundation Ireland Grant Number (and some amounts of unlabeled data). SFI/12/RC/2289.
10 .References Bjarke Felbo, Alan Mislove, Anders Søgaard, Iyad Rahwan, and Sune Lehmann. 2017. Using millions Jonathan Baxter. 2000. A Model of Inductive Bias of emoji occurrences to learn any-domain represen- Learning. Journal of Artificial Intelligence Research tations for detecting sentiment, emotion and sar- 12:149–198. casm. In Proceedings of the 2017 Conference on Empirical Methods in Natural Language Process- John Blitzer, Mark Dredze, and Fernando Pereira. ing. 2007. Biographies, bollywood, boom-boxes and blenders: Domain adaptation for sentiment Kristina Gulordava, Piotr Bojanowski, Edouard Grave, classification. Annual Meeting-Association Tal Linzen, and Marco Baroni. 2018. Colorless for Computational Linguistics 45(1):440. green recurrent networks dream hierarchically. In https://doi.org/10.1109/IRPS.2011.5784441. Proceedings of NAACL-HLT 2018. Cornelia Caragea, Nathan McNeese, Anuj Jaiswal, Bharath Hariharan, Pablo Arbel´aez, Ross Girshick, and Greg Traylor, Hyun-Woo Kim, Prasenjit Mitra, Jitendra Malik. 2015. Hypercolumns for object seg- Dinghao Wu, Andrea H Tapia, Lee Giles, Bernard J mentation and fine-grained localization. In Proceed- Jansen, et al. 2011. Classifying text messages for the ings of the IEEE Conference on Computer Vision haiti earthquake. In Proceedings of the 8th interna- and Pattern Recognition. pages 447–456. tional conference on information systems for crisis response and management (ISCRAM2011). Citeseer. Kaiming He, Xiangyu Zhang, Shaoqing Ren, and Jian Sun. 2016. Deep Residual Learning for Image Rich Caruana. 1993. Multitask learning: A Recognition. In Proceedings of the IEEE Confer- knowledge-based source of inductive bias. In Pro- ence on Computer Vision and Pattern Recognition. ceedings of the Tenth International Conference on Machine Learning. Gao Huang, Zhuang Liu, Kilian Q. Weinberger, and Laurens van der Maaten. 2017. Densely Connected Zhao Chen, Vijay Badrinarayanan, Chen-Yu Lee, and Convolutional Networks. In Proceedings of CVPR Andrew Rabinovich. 2017. GradNorm: Gradient 2017. Normalization for Adaptive Loss Balancing in Deep Multitask Networks pages 1–10. Minyoung Huh, Pulkit Agrawal, and Alexei A Efros. Zi Chu, Steven Gianvecchio, Haining Wang, and Sushil 2016. What makes ImageNet good for transfer Jajodia. 2012. Detecting automation of twitter ac- learning? arXiv preprint arXiv:1608.08614 . counts: Are you a human, bot, or cyborg? IEEE Transactions on Dependable and Secure Computing Sergey Ioffe and Christian Szegedy. 2015. Batch nor- 9(6):811–824. malization: Accelerating deep network training by reducing internal covariate shift. In International Alexis Conneau, Douwe Kiela, Holger Schwenk, Lo¨ıc Conference on Machine Learning. pages 448–456. Barrault, and Antoine Bordes. 2017. Supervised Learning of Universal Sentence Representations Nitin Jindal and Bing Liu. 2007. Review spam de- from Natural Language Inference Data. In Proceed- tection. In Proceedings of the 16th international ings of the 2017 Conference on Empirical Methods conference on World Wide Web. ACM, pages 1189– in Natural Language Processing. 1190. Andrew M. Dai and Quoc V. Le. 2015. Semi- Rie Johnson and Tong Zhang. 2016. Supervised and supervised Sequence Learning. Advances in Neu- semi-supervised text categorization using lstm for ral Information Processing Systems (NIPS ’15) region embeddings. In International Conference on http://arxiv.org/abs/1511.01432. Machine Learning. pages 526–534. Jeff Donahue, Yangqing Jia, Oriol Vinyals, Judy Hoff- Rie Johnson and Tong Zhang. 2017. Deep pyramid man, Ning Zhang, Eric Tzeng, and Trevor Darrell. convolutional neural networks for text categoriza- 2014. Decaf: A deep convolutional activation fea- tion. In Proceedings of the 55th Annual Meeting of ture for generic visual recognition. In International the Association for Computational Linguistics (Vol- conference on machine learning. pages 647–655. ume 1: Long Papers). volume 1, pages 562–570. Timothy Dozat and Christopher D. Manning. 2017. Tal Linzen, Emmanuel Dupoux, and Yoav Gold- Deep Biaffine Attention for Neural Dependency berg. 2016. Assessing the ability of lstms to Parsing. In Proceedings of ICLR 2017. learn syntax-sensitive dependencies. arXiv preprint arXiv:1611.01368 . Dumitru Erhan, Yoshua Bengio, Aaron Courville, Pierre-Antoine Manzagol, Pascal Vincent, and Samy Liyuan Liu, Jingbo Shang, Frank Xu, Xiang Ren, Huan Bengio. 2010. Why does unsupervised pre-training Gui, Jian Peng, and Jiawei Han. 2018. Empower help deep learning? Journal of Machine Learning sequence labeling with task-aware neural language Research 11(Feb):625–660. model. In Proceedings of AAAI 2018.
11 .Jonathan Long, Evan Shelhamer, and Trevor Darrell. Neural Networks in NLP Applications? Proceed- 2015a. Fully convolutional networks for semantic ings of 2016 Conference on Empirical Methods in segmentation. In Proceedings of the IEEE Confer- Natural Language Processing . ence on Computer Vision and Pattern Recognition. pages 3431–3440. Lili Mou, Hao Peng, Ge Li, Yan Xu, Lu Zhang, and Zhi Jin. 2015. Discriminative neural sentence mod- Mingsheng Long, Yue Cao, Jianmin Wang, and eling by tree-based convolution. In Proceedings of Michael I. Jordan. 2015b. Learning Transferable the 2015 Conference on Empirical Methods in Nat- Features with Deep Adaptation Networks. In Pro- ural Language Processing. ceedings of the 32nd International Conference on Machine learning (ICML ’15). volume 37. EWT Ngai, Yong Hu, YH Wong, Yijun Chen, and Xin Sun. 2011. The application of data mining tech- Ilya Loshchilov and Frank Hutter. 2017. SGDR: niques in financial fraud detection: A classifica- Stochastic Gradient Descent with Warm Restarts. In tion framework and an academic review of literature. Proceedings of the Internal Conference on Learning Decision Support Systems 50(3):559–569. Representations 2017. Sinno Jialin Pan and Qiang Yang. 2010. A survey on Andrew L Maas, Raymond E Daly, Peter T Pham, Dan transfer learning. IEEE Transactions on Knowledge Huang, Andrew Y Ng, and Christopher Potts. 2011. and Data Engineering 22(10):1345–1359. Learning word vectors for sentiment analysis. In Matthew E Peters, Waleed Ammar, Chandra Bhagavat- Proceedings of the 49th Annual Meeting of the Asso- ula, and Russell Power. 2017. Semi-supervised se- ciation for Computational Linguistics: Human Lan- quence tagging with bidirectional language models. guage Technologies-Volume 1. Association for Com- In Proceedings of ACL 2017. putational Linguistics, pages 142–150. Matthew E Peters, Mark Neumann, Mohit Iyyer, Matt Dhruv Mahajan, Ross Girshick, Vignesh Ramanathan, Gardner, Christopher Clark, Kenton Lee, and Luke Kaiming He, Manohar Paluri, Yixuan Li, Ashwin Zettlemoyer. 2018. Deep contextualized word rep- Bharambe, and Laurens van der Maaten. 2018. Ex- resentations. In Proceedings of NAACL 2018. ploring the Limits of Weakly Supervised Pretraining . Alec Radford, Rafal Jozefowicz, and Ilya Sutskever. 2017. Learning to generate reviews and discovering Bryan McCann, James Bradbury, Caiming Xiong, and sentiment. arXiv preprint arXiv:1704.01444 . Richard Socher. 2017. Learned in Translation: Con- textualized Word Vectors. In Advances in Neural Marek Rei. 2017. Semi-supervised multitask learning Information Processing Systems. for sequence labeling. In Proceedings of ACL 2017. Stephen Merity, Nitish Shirish Keskar, and Richard Herbert L Roitblat, Anne Kershaw, and Patrick Oot. Socher. 2017a. Regularizing and Optimiz- 2010. Document categorization in legal electronic ing LSTM Language Models. arXiv preprint discovery: computer classification vs. manual re- arXiv:1708.02182 . view. Journal of the Association for Information Science and Technology 61(1):70–80. Stephen Merity, Caiming Xiong, James Bradbury, and Richard Socher. 2017b. Pointer Sentinel Mixture Sebastian Ruder. 2016. An overview of gradient Models. In Proceedings of the International Con- descent optimization algorithms. arXiv preprint ference on Learning Representations 2017. arXiv:1609.04747 . Ruslan Salakhutdinov and Geoffrey Hinton. 2009. Tomas Mikolov, Kai Chen, Greg Corrado, and Jeffrey Deep boltzmann machines. In Artificial Intelligence Dean. 2013. Distributed Representations of Words and Statistics. pages 448–455. and Phrases and their Compositionality. In Ad- vances in Neural Information Processing Systems. Rico Sennrich, Barry Haddow, and Alexandra Birch. 2015. Improving neural machine translation Sewon Min, Minjoon Seo, and Hannaneh Hajishirzi. models with monolingual data. arXiv preprint 2017. Question Answering through Transfer Learn- arXiv:1511.06709 . ing from Large Fine-grained Supervision Data. In Proceedings of the 55th Annual Meeting of the As- Aliaksei Severyn and Alessandro Moschitti. 2015. sociation for Computational Linguistics (Short Pa- UNITN: Training Deep Convolutional Neural Net- pers). work for Twitter Sentiment Classification. Proceed- ings of the 9th International Workshop on Semantic Takeru Miyato, Andrew M Dai, and Ian Good- Evaluation (SemEval 2015) pages 464–469. fellow. 2016. Adversarial training methods for semi-supervised text classification. arXiv preprint Ali Sharif Razavian, Hossein Azizpour, Josephine Sul- arXiv:1605.07725 . livan, and Stefan Carlsson. 2014. Cnn features off- the-shelf: an astounding baseline for recognition. In Lili Mou, Zhao Meng, Rui Yan, Ge Li, Yan Xu, Proceedings of the IEEE conference on computer vi- Lu Zhang, and Zhi Jin. 2016. How Transferable are sion and pattern recognition. pages 806–813.
12 .Leslie N Smith. 2017. Cyclical learning rates for train- ing neural networks. In Applications of Computer Vision (WACV), 2017 IEEE Winter Conference on. IEEE, pages 464–472. Vladimir Naumovich Vapnik and Samuel Kotz. 1982. Estimation of dependences based on empirical data, volume 40. Springer-Verlag New York. Ellen M Voorhees and Dawn M Tice. 1999. The trec-8 question answering track evaluation. In TREC. vol- ume 1999, page 82. John Wieting and Kevin Gimpel. 2017. Revisiting Re- current Networks for Paraphrastic Sentence Embed- dings. In Proceedings of the 55th Annual Meeting of the Association for Computational Linguistics (ACL 2017). Jason Yosinski, Jeff Clune, Yoshua Bengio, and Hod Lipson. 2014. How transferable are features in deep neural networks? In Advances in neural information processing systems. pages 3320–3328. Xiang Zhang, Junbo Zhao, and Yann LeCun. 2015. Character-level convolutional networks for text clas- sification. In Advances in neural information pro- cessing systems. pages 649–657. Peng Zhou, Zhenyu Qi, Suncong Zheng, Jiaming Xu, Hongyun Bao, and Bo Xu. 2016. Text classification improved by integrating bidirectional lstm with two- dimensional max pooling. In Proceedings of COL- ING 2016.