聚类

1 .魏秀参 周旺

2 .第九章 ：聚类

3 .大纲 聚类任务 性能度量 距离计算 原型聚类 密度聚类 层次聚类

4 .大纲 聚类任务 性能度量 距离计算 原型聚类 密度聚类 层次聚类

5 .聚类任务 在 “无监督学习” 任务 中研究最多、应用最广 . 聚类目标：将数据集中的样本划分为若干个通常不相交的子集（“簇”， cluster ） . 聚类既可以作为一个单独过程（用于找寻数据内在的分布结构）， 也可作为分类等其他学习任务的前驱过程 .

6 .聚类任务 形式化描述 假定样本集 包含 个无标记样本 , 每个样本 是一个 维的特征向量 ， 聚类算法将样本集 划分成 个不相交的簇 。其中 ，且 。。 相应地，用 表示样本 的“簇标记”（即 cluster label ） , 即 。于是，聚类的结果可用包含 个元素的簇标记向量 表示。

7 .聚类任务 形式化描述 假定样本集 包含 个无标记样本 , 每个样本 是一个 维的特征向量 ， 聚类算法将样本集 划分成 个不相交的簇 。其中 ，且 。。 相应地，用 表示样本 的“簇标记”（即 cluster label ） , 即 。于是，聚类的结果可用包含 个元素的簇标记向量 表示。

8 .性能度量 聚类性能度量 ， 亦称为聚类“有效性指标”（ validity index ） 直观来讲： 我们希望“物以类聚”，即同一簇的样本尽可能彼此相似，不同簇的样本尽可能不同。换言之， 聚类结果的“簇内相似度”（ intra-cluster similarity ）高 ， 且“簇间相似度”（ inter-cluster similarity ）低，这样的聚类效果较好 .

9 .性能度量 聚类性能度量： 外部指标 (external index) 将聚类结果与某个“参考模型” (reference model) 进行比较。 内部指标 (internal index) 直接考察聚类结果而不用任何参考模型。

10 .性能度量 对数据集 ，假定通过聚类得到的簇划分为 ，参考模型给出的簇划分为 . 相应地，令 与 分 别 表示与 和 对应的簇标记向量 . 我们将样本两两配对考虑，定义

11 .性能度量 - 外部指标 Jaccard 系数（ Jaccard Coefficient, JC ） FM 指数（ Fowlkes and Mallows Index, FMI ） Rand 指数（ Rand Index, RI ） [0,1] 区间内 , 越大越好 .

12 .性能度量 – 内部指标 考虑聚类结果的簇划分 ，定义 簇 内样本间的平均距离 簇 内样本间的最远距离 簇 与簇 最近样本间的距离 簇 与簇 中心点间的距离

13 .性能度量 – 内部指标 DB 指数（ Davies- Bouldin Index, DBI ） Dunn 指数（ Dunn Index, DI ） 越小越好 . 越大越好 .

14 .性能度量 – 内部指标 DB 指数（ Davies- Bouldin Index, DBI ） Dunn 指数（ Dunn Index, DI ） 越小越好 . 越大越好 .

15 .距离计算 距离度量的性质： 非负性： 同一性： 当且仅当 对称性： 直递性：

16 .距离计算 距离度量的性质： 非负性： 同一性： 当且仅当 对称性： 直递性： 常用距离： 闵可夫斯基距离（ Minkowski distance ） : p=2: 欧氏距离（ Euclidean distance ） . p=1 ：曼哈顿距离（ Manhattan distance ） .

17 .距离计算 属性介绍 连续属性 (continuous attribute) 在定义域上有无穷多个可能的取值 离散属性 (categorical attribute) 在 定义域 上是有限个可能 的 取值

18 .距离计算 属性介绍 连续属性 (continuous attribute) 在定义域上有无穷多个可能的取值 离散属性 (categorical attribute) 在 定义域 上是有限个可能 的 取值 有序属性 (ordinal attribute) 例如定义域为 {1,2,3} 的离散属性，“ 1 ”与“ 2 ”比较接近、与“ 3 ”比较远，称为“有序属性”。 无序属性 (non-ordinal attribute) 例如定义域为 { 飞机，火车，轮船 } 这样的离散属性，不能直接在属性值上进行计算，称为“无序属性”。

19 .距离度量 Value Difference Metric, VDM （处理无序属性）： 令 表示属性 上取值为 的样本数， 表示在第 个样本簇中在属性 上取值为 的样本数， 为样本数，则属性 上两个离散值 与 之间的 VDM 距离为

20 .距离度量 MinkovDM p （处理混合属性）： 加权距离 （样本中不同属性的重要性不同时） ：

21 .距离度量 MinkovDM p （处理混合属性）： 加权距离 （样本中不同属性的重要性不同时） ：

22 .原型聚类 原型聚类 也称为“基于原型的聚类” (prototype-based clustering) ，此类算法假设聚类结构能通过一组原型刻画。 算法过程： 通常情况下，算法先对原型进行初始化，再对原型进行迭代更新求解。 接下来，介绍几种著名的原型聚类算法 k 均值算法、学习向量量化算法、高斯混合聚类算法。

23 .原型聚类 – k 均值算法 给定数据集 ， k 均值 算法针对聚类所得簇划分 最小化平方误差 其中， 是簇 的均值向量。 值在一定程度上刻画了簇内样本围绕簇均值向量的紧密程度， 值越小，则簇内样本相似度越高。

24 .原型聚类 – k 均值算法 给定数据集 ， k 均值 算法针对聚类所得簇划分 最小化平方误差 其中， 是簇 的均值向量。 值在一定程度上刻画了簇内样本围绕簇均值向量的紧密程度， 值越小，则簇内样本相似度越高。 算法流程（迭代优化）： 初始化每个簇的均值向量 repeat 1. （更新）簇划分； 2. 计算每个簇的均值向量 until 当前均值向量均未更新

25 .原型聚类 – k 均值算法 算法伪代码：

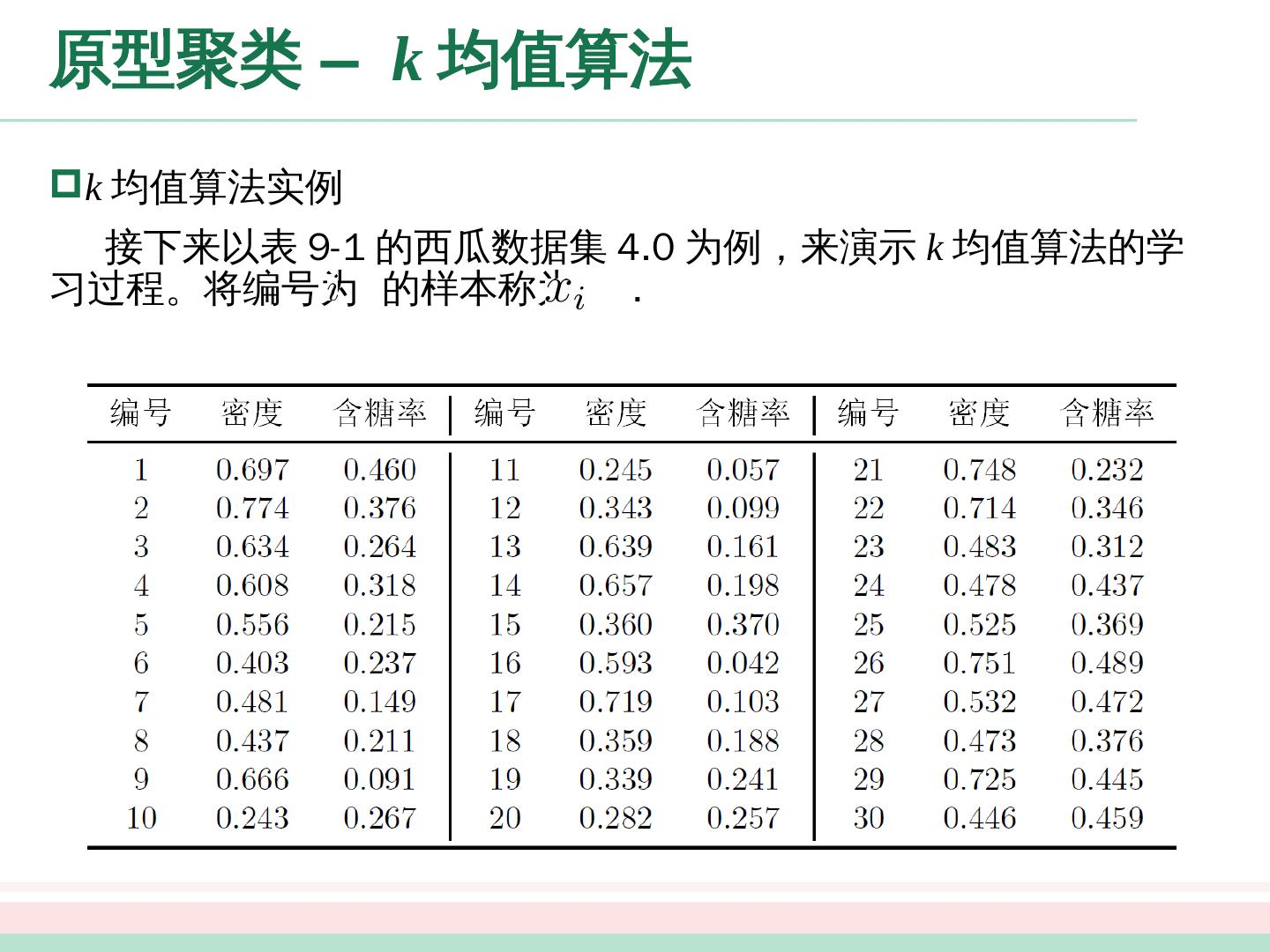
26 .原型聚类 – k 均值算法 k 均值 算法实例 接下来以表 9-1 的西瓜数据集 4.0 为例，来演示 k 均值算法的学习过程。将编号为 的样本称为 .

27 .原型聚类 – k 均值算法 k 均值 算法实例 假定聚类簇数 k = 3 ，算法开始时，随机选择 3 个样本 作为初始均值向量，即 。 考察样本 ，它与当前均值向量 的距离分别为 0.369 ， 0.506 ， 0.166 ，因此 将被划入簇 中。类似的，对数据集中的所有样本考察一遍后，可得当前簇划分为 于是，可以从分别求得新的均值向量 不断 重复上述过程，如下图所示。

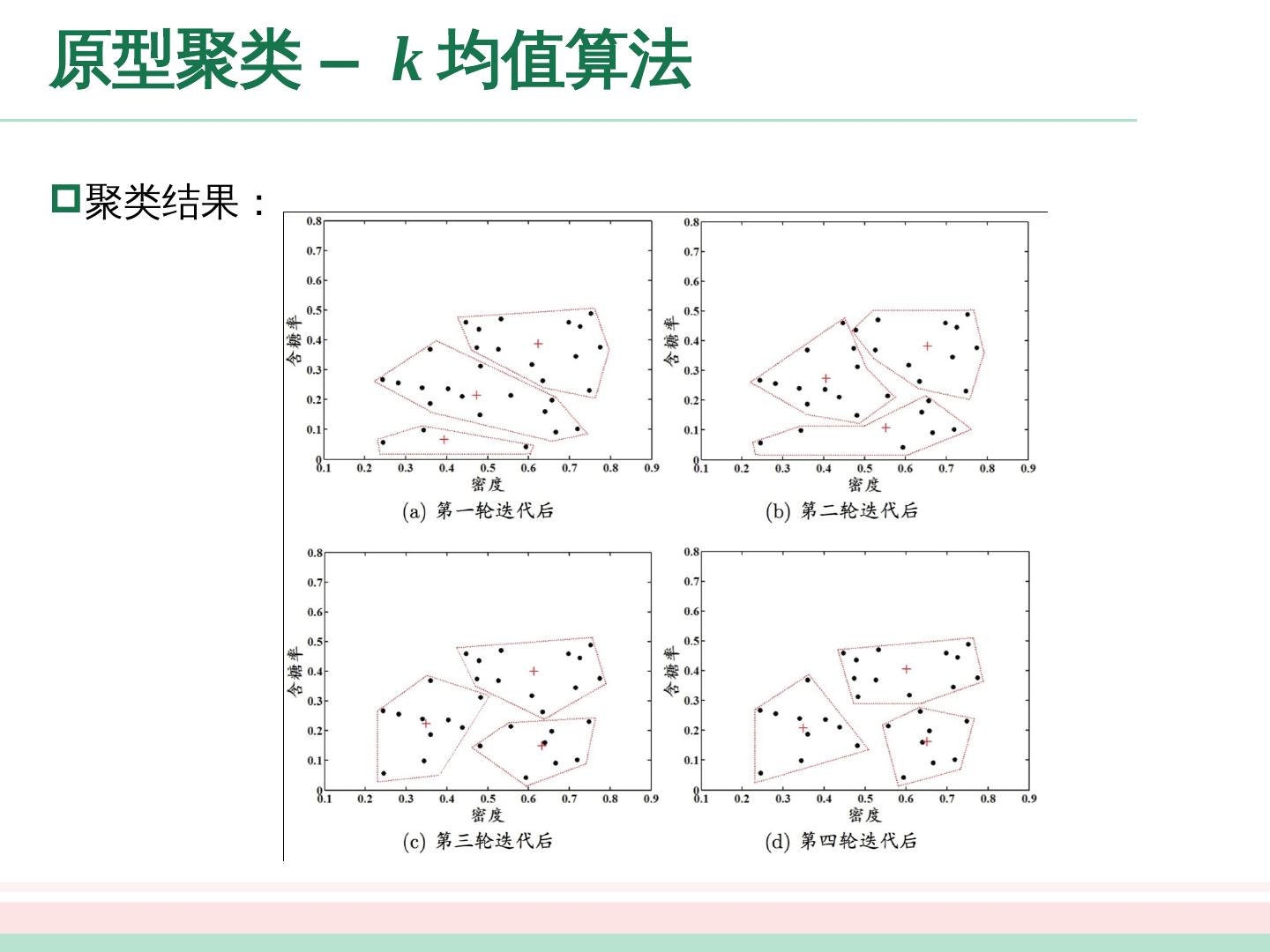
28 .原型聚类 – k 均值算法 聚类结果：

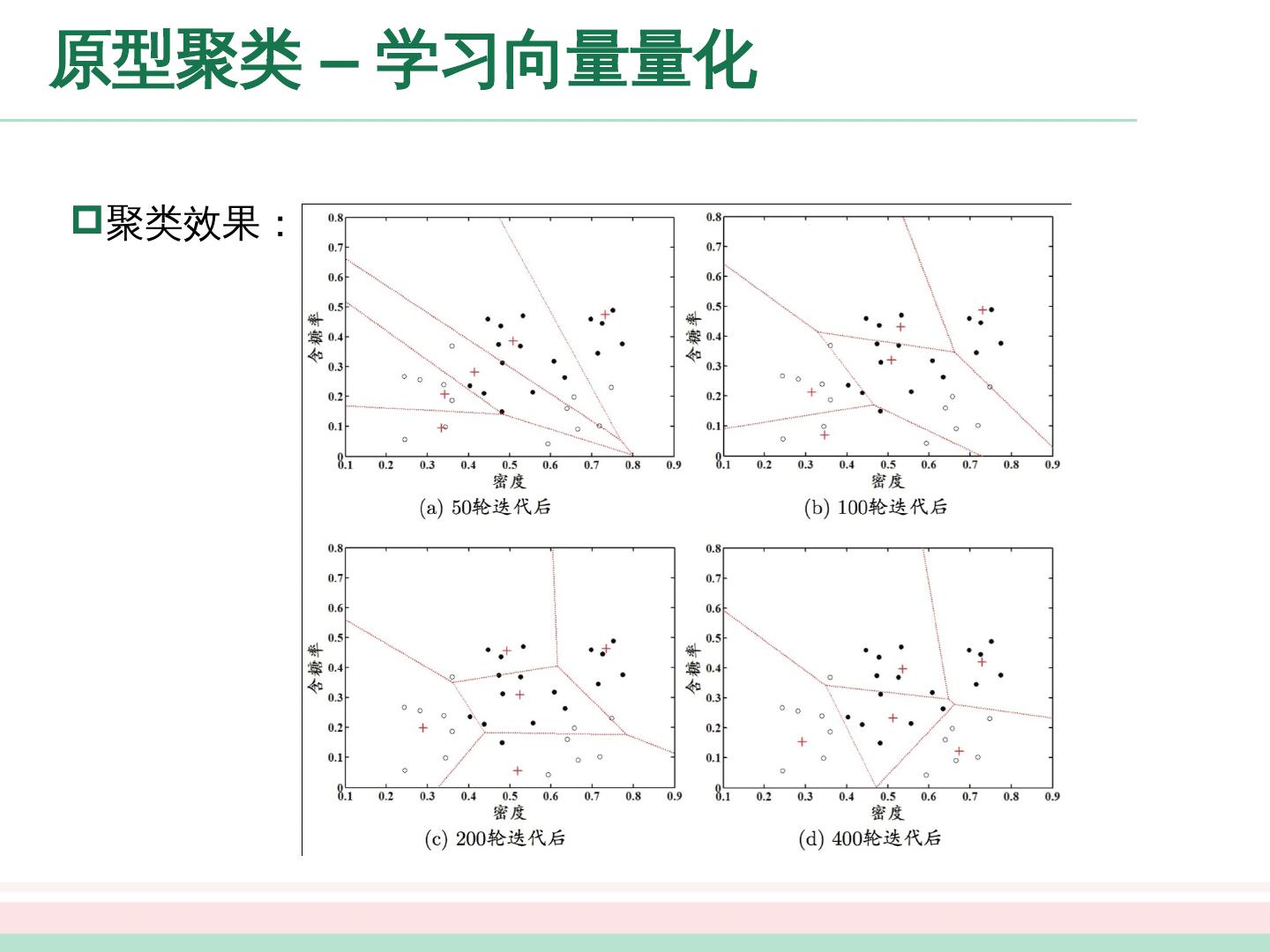
29 .原型聚类 – 学习向量量化 学习向量量化（ Learning Vector Quantization, LVQ ） 与一般聚类算法不同的是， LVQ 假设数据样本带有类别标记，学习过程中利用 样本的这些监督信息来辅助 聚类 . 给定样本集 ， LVQ 的目标是学得一组 维原型向量 ，每个原型向量代表一个聚类簇。