- 快召唤伙伴们来围观吧
- 微博 QQ QQ空间 贴吧
- 文档嵌入链接
- 复制
- 微信扫一扫分享
- 已成功复制到剪贴板
Support Vector Machines
展开查看详情
1 .张腾
2 .第六章 : 支持向量机
3 .大纲 间隔与支持向量 对偶问题 核函数 软间隔与正则化 支持向量回归 核方法
4 .引子 线性模型 :在 样本空间 中 寻找 一个超平面 , 将不同 类别的样本分开 . 0
5 .引子 -Q: 将训练样本分开的超平面可能有很多 , 哪一个好呢 ? 0
6 .引子 -Q: 将训练样本分开的超平面可能有很多 , 哪一个好呢 ? -A: 应选择 ” 正中间 ”, 容忍性好 , 鲁棒性高 , 泛化能力最强 . 0
7 .间隔与支持向量 超平面方程 : 间隔 0 支持向量
8 .支持向量机基本型 最大间隔 : 寻找 参数 和 , 使得 最大 .
9 .支持向量机基本型 最大间隔 : 寻找 参数 和 , 使得 最大 .
10 .对偶问题 拉格朗日乘子法 第一 步:引入拉格朗日乘子 得到拉格朗日函数 第二 步:令 对 和 的 偏导为零可 得 第三步:回代
11 .解的稀疏性 最终模型: KKT 条件: 支持向量 机解的 稀疏性 : 训练完成后 , 大部分的训练样本都不需保留 , 最终 模型仅与支持向量有关 .
12 .求解方法 - SMO 基本思路:不断 执行如下两个步骤直至 收敛 . 第一 步: 选取一对需更新的 变量 和 . 第二 步:固定 和 以外 的参数 , 求解对偶问题更新 和 . 仅 考虑 和 时 , 对偶问题的约束变为 偏移项 :通过支持向量来确定 . 用一个变量表示另一个变量 , 回代入对偶问题可 得一 个单变量的二次规划 , 该问题具有 闭式 解 .
13 .求解方法 - SMO 基本思路:不断 执行如下两个步骤直至 收敛 . 第一 步: 选取一对需更新的 变量 和 . 第二 步:固定 和 以外 的参数 , 求解对偶问题更新 和 . 仅 考虑 和 时 , 对偶问题的约束变为 偏移项 :通过支持向量来确定 . 用一个变量表示另一个变量 , 回代入对偶问题可 得一 个单变量的二次规划 , 该问题具有 闭式 解 .
14 .线性不可分 -Q: 若不存在一 个能正确划分两类样本的 超平面 , 怎么办 ? -A: 将 样本从原始空间映射到一个 更高维 的特征空间 , 使得样本在这个特征空间内线性可分 .
15 .核支持向量机 设样本 映射后的向量为 , 划分超平面为 . 原始问题 对偶 问题 预测 只以 内积 的形式出现
16 .核函数 基本想法:不显式地设计核映射 , 而是设计 核函数 . Mercer 定理 ( 充分非必要 ) : 只要一个对称函数所对应的核矩阵 半正定 , 则 它就能作为 核函数来使用 . 常用核函数:
17 .核函数 基本想法:不显式地设计核映射 , 而是设计 核函数 . Mercer 定理 ( 充分非必要 ) : 只要一个对称函数所对应的核矩阵 半正定 , 则 它就能作为 核函数来使用 . 常用核函数:
18 .软间隔 -Q: 现实中 , 很难 确定合适的核函数使得训练样本在特征空间中线性可 分 ; 同时一个线性可分的结果也很难断定是否是有过拟合造成的 . -A: 引入 ” 软间隔 ” 的概念 , 允许 支持向量机在一些样本 上 不 满足约束 . 0 不满足约束的样本
19 .0/1 损失函数 基本想法:最大化 间隔的同时 , 让不 满足约束的样本应 尽可能少 . 其中 是 ”0/1 损失函数 ” 存在的问题: 0/1 损失函数非凸、非连续 , 不易优化!
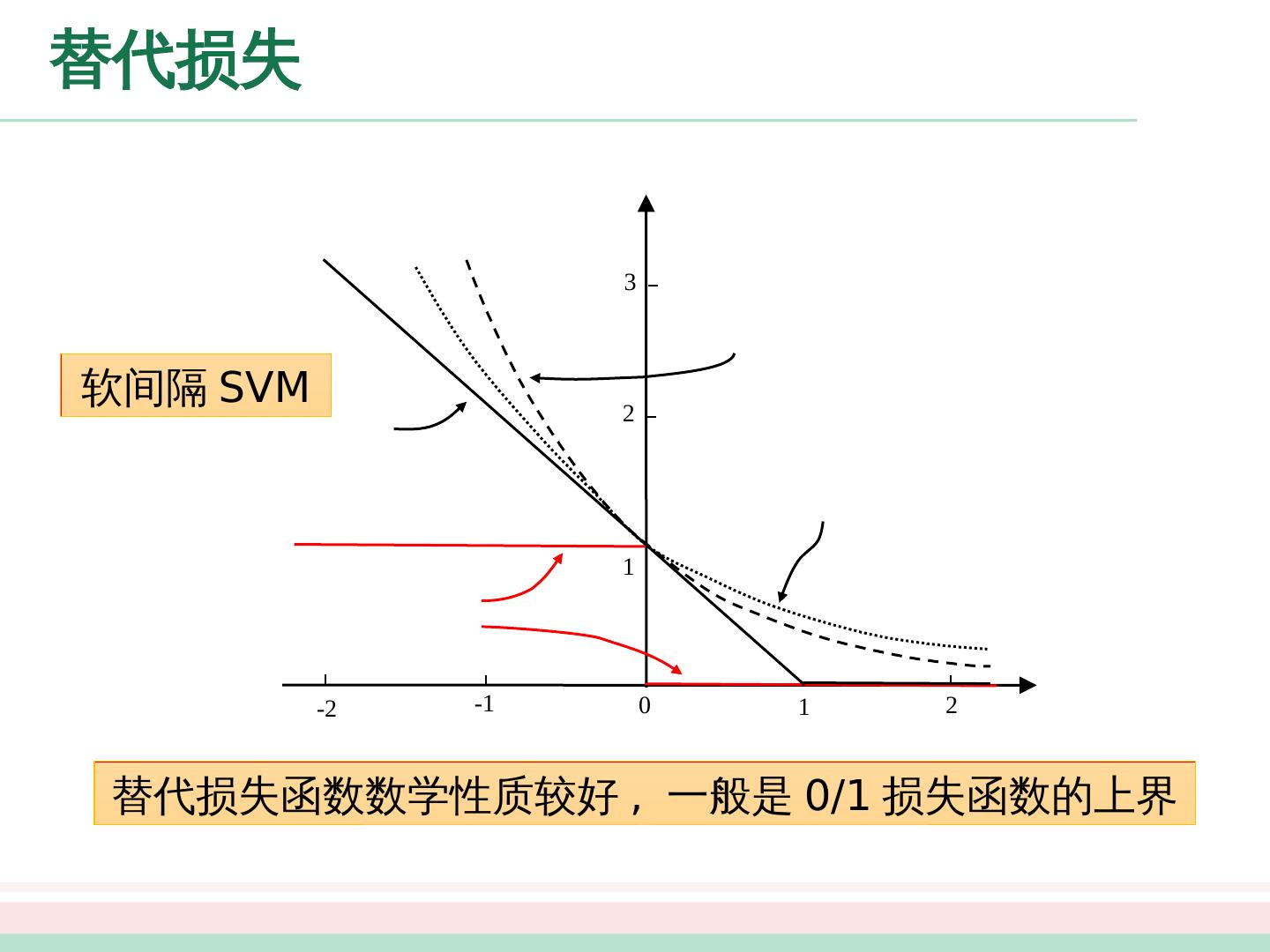
20 .替代损失 0 1 2 -1 -2 1 2 3 替代 损失函数数学性质较好 , 一般是 0/1 损失函数的上界 软 间隔 SVM
21 .软 间隔 支持向量机 原始问题 对偶 问题 根据 KKT 条件可推得最终 模型仅与支持向量 有关 , 也即 h inge 损失函数依然保持了支持 向量机解的 稀疏 性 .
22 .正则化 支持向量机学习模型的更一般形式 通过替换上面两个部分 , 可以得到 许多 其他学习模型 对数几率 回归 (Logistic Regression) 最小绝对收缩选择算子 (LASSO) …… 结构风险 , 描述 模型的某些性质 经验风险 , 描述 模型与训练数据的契合程度
23 .正则化 支持向量机学习模型的更一般形式 通过替换上面两个部分 , 可以得到 许多 其他学习模型 对数几率 回归 (Logistic Regression) 最小绝对收缩选择算子 (LASSO) …… 结构风险 , 描述 模型的某些性质 经验风险 , 描述 模型与训练数据的契合程度
24 .支持向量 回归 特点 : 允许模型输出和实际输出间存在 的偏差 . 0 间隔带
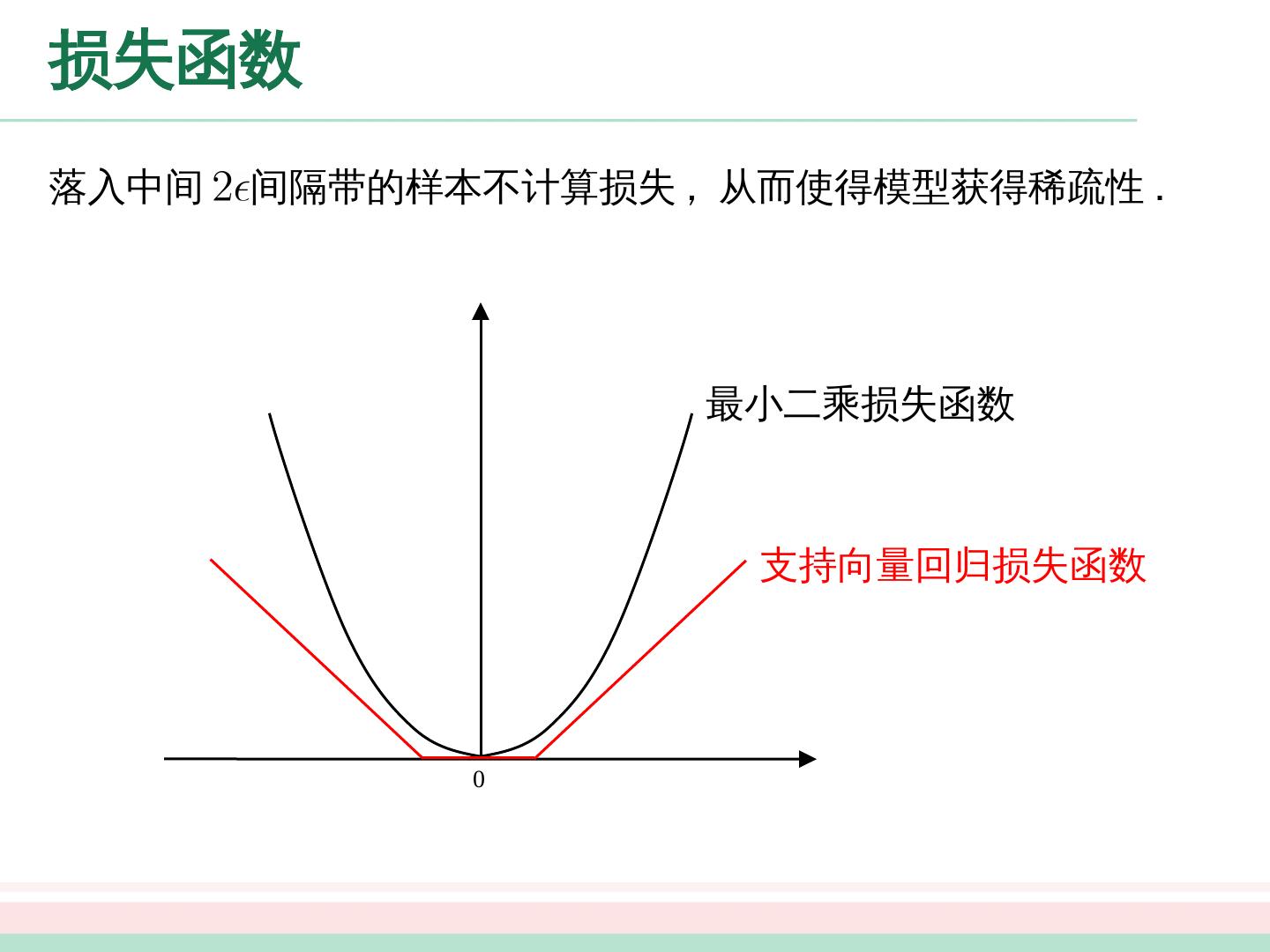
25 .损失函数 落入中间 间隔带的样本不计算损失 , 从而使得模型获得稀疏性 . 0 最小二 乘损失函数 支持向量回归损失函数
26 .形式化 原始问题 对偶 问题 预测
27 .形式化 原始问题 对偶 问题 预测
28 .表示定理 结论 : 无论是支持向量机还是支持向量回归 , 学得的模型总可以表示成 核函数的线性组合 . 更一般的结论 ( 表示定理 ): 对于任意 单调增函数 和任意 非负损失函数 , 优化问题 的解总可以写为 . 支持向量机 支持向量回归
29 .核线性判别分析 通过表示定理可以得到很多线性模型的 ” 核化 ” 版本 核 SVM 核 LDA 核 PCA …… 核 LDA: 先将样本映射到高维特征空间 , 然后在此特征空间中做线性判别分析