- 快召唤伙伴们来围观吧
- 微博 QQ QQ空间 贴吧
- 文档嵌入链接
- 复制
- 微信扫一扫分享
- 已成功复制到剪贴板
半监督学习
展开查看详情
1 .陈加略
2 .第十三章 :半监督学习
3 .背景 ( 半监督学习 ) 隔壁老王 品瓜师 吃
4 .背景(半监督学习) 品瓜师 吃 模型 有标记样本 无标记样本 直推学习 (纯)半监督学习 待测数据
5 .背景(主动学习) 品瓜师 吃
6 .背景(主动学习) 品瓜师 吃 主动学习 待测数据 模型 有标记样本 无标记样本 标注者
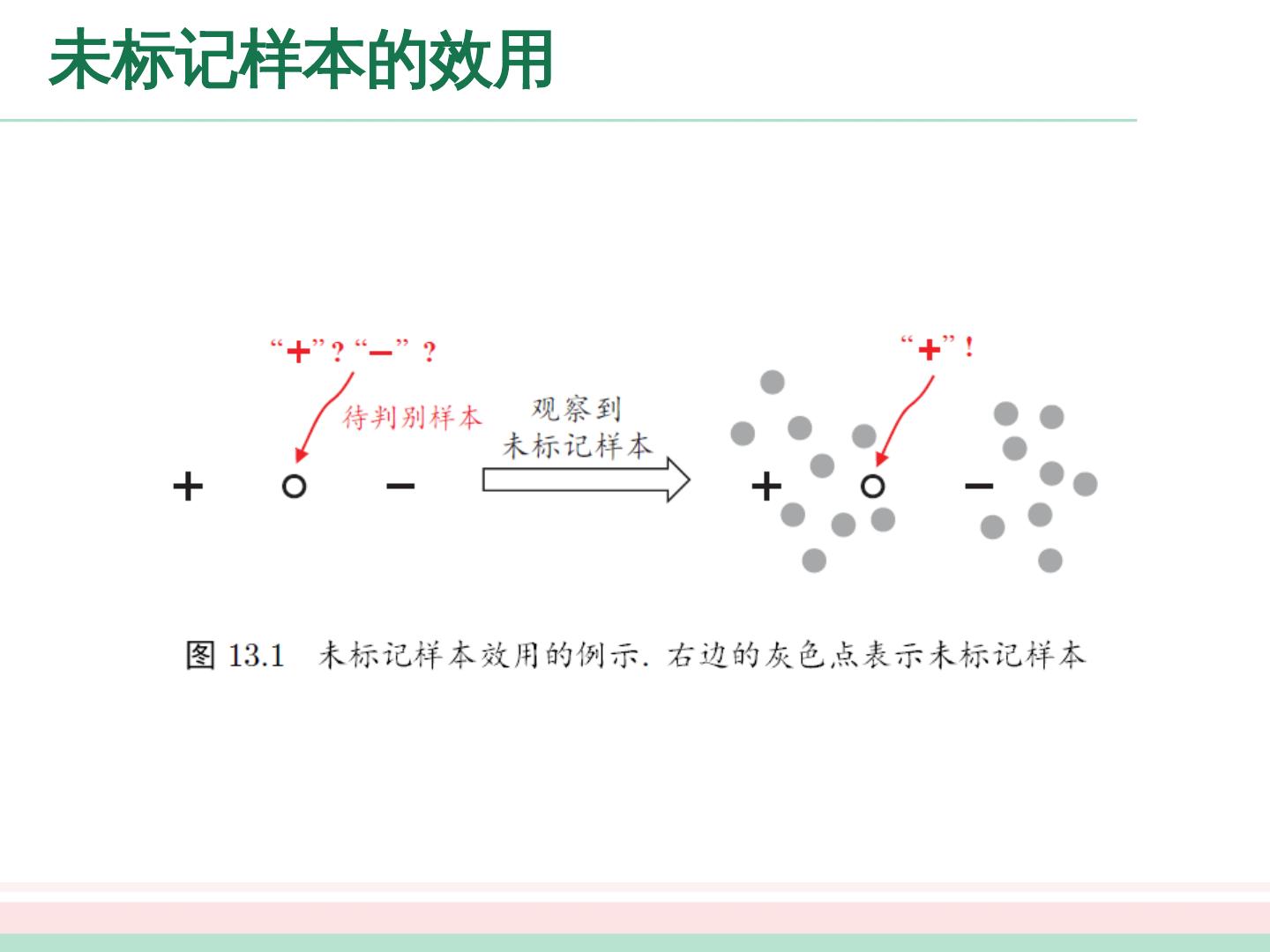
7 .未标记样本的效用
8 .未标记样本的假设 要利用未标记样本,必然要做一些将未标记样本所揭示的数据分布信息与类别标记相联系的假设,其中有两种常见的假设。 聚类假设( clustering assumption ): 假设数据存在簇结构,同一簇的样本属于同一类别。 流形假设( manifold assumption ): 假设数据分布在一个流形结构上,邻近的样本具有相似的输出值。 流形假设可看做聚类假设的推广
9 .大纲 未标记样本 生成式方法 半监督 SVM 图半监督学习 基于分歧的方法 半监督聚类
10 .生成式方法 假设样本由这个假设意味着混合成分 高斯混合模型生成 , 且每个类别对应一个高斯混合 成分: 其中 ,
11 .生成式方法 由最大化后验概率可知:
12 .生成式方法 假设样本独立同分布,且由同一个高斯混合模型生成,则对数似然函数是:
13 .生成式方法 高斯混合的参数估计可以采用 EM 算法求解,迭代更新式如下: E 步:根据当前模型参数计算未标记样本属于各高斯混合成分的概率。
14 .生成式方法 M 步:基于 更新模型参数
15 .生成式方法 将上述过程中的高斯混合模型换成 混合专家 模型 , 朴素贝叶斯 模型 等即可推导出其他的生成式半监督学习 算法。 此类方法简单、易于实现 , 在 有标记数据极少 的情形下往往比其他 方法性能更好。 然而 , 此类方法有一个关键 : 模型假设必须准确 , 即假设的生成 式模型 必须与真实数据分布吻合 ; 否则利用未标记数据反而会显著降低泛化 性能。
16 .生成式方法 将上述过程中的高斯混合模型换成 混合专家 模型 , 朴素贝叶斯 模型 等即可推导出其他的生成式半监督学习 算法。 此类方法简单、易于实现 , 在 有标记数据极少 的情形下往往比其他 方法性能更好。 然而 , 此类方法有一个关键 : 模型假设必须准确 , 即假设的生成 式模型 必须与真实数据分布吻合 ; 否则利用未标记数据反而会显著降低泛化 性能。
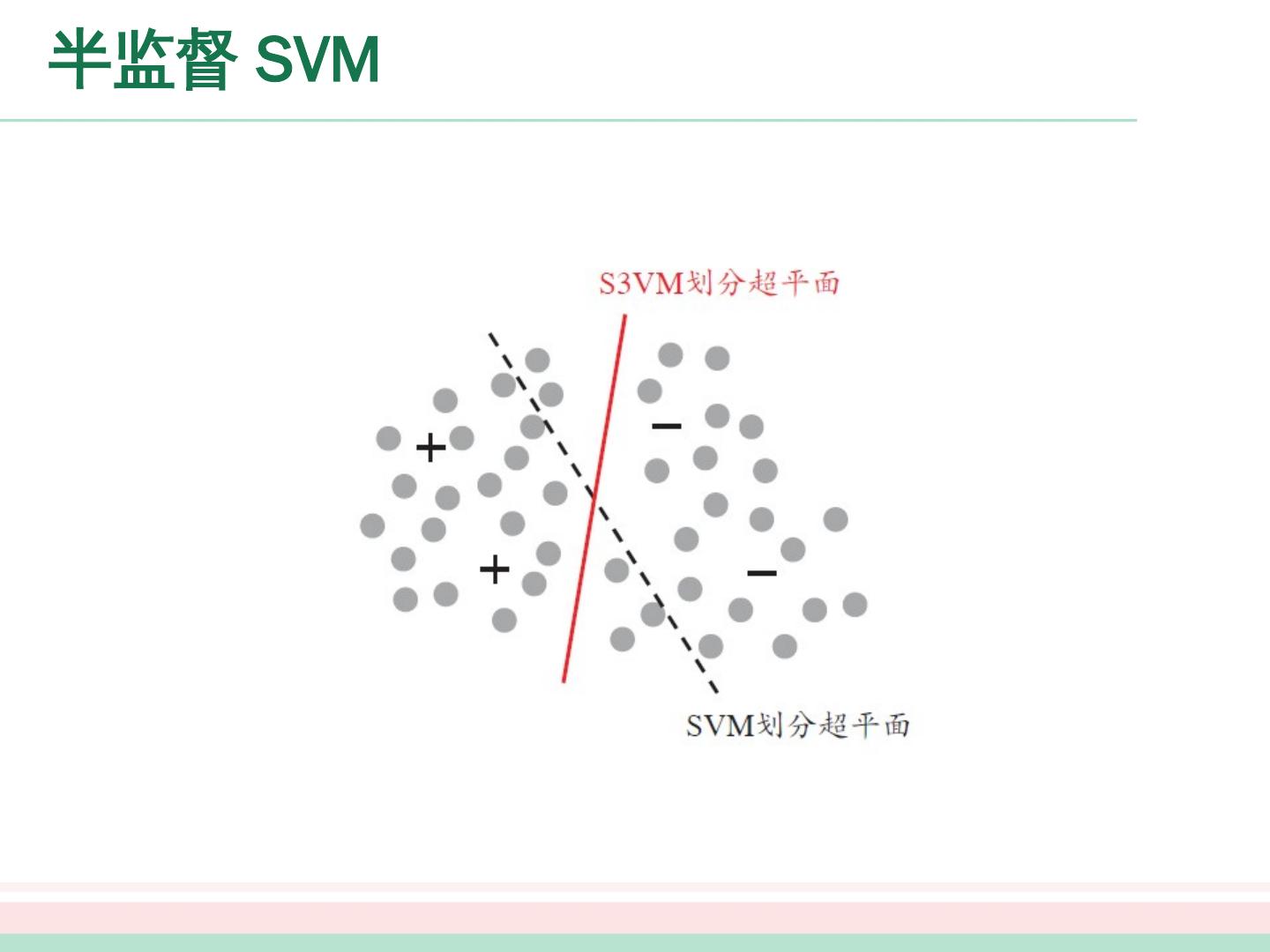
17 .半监督 SVM
18 .半监督 SVM 半 监督支持向量机中最著名的是 TSVM(Transductive Support Vector Machine)
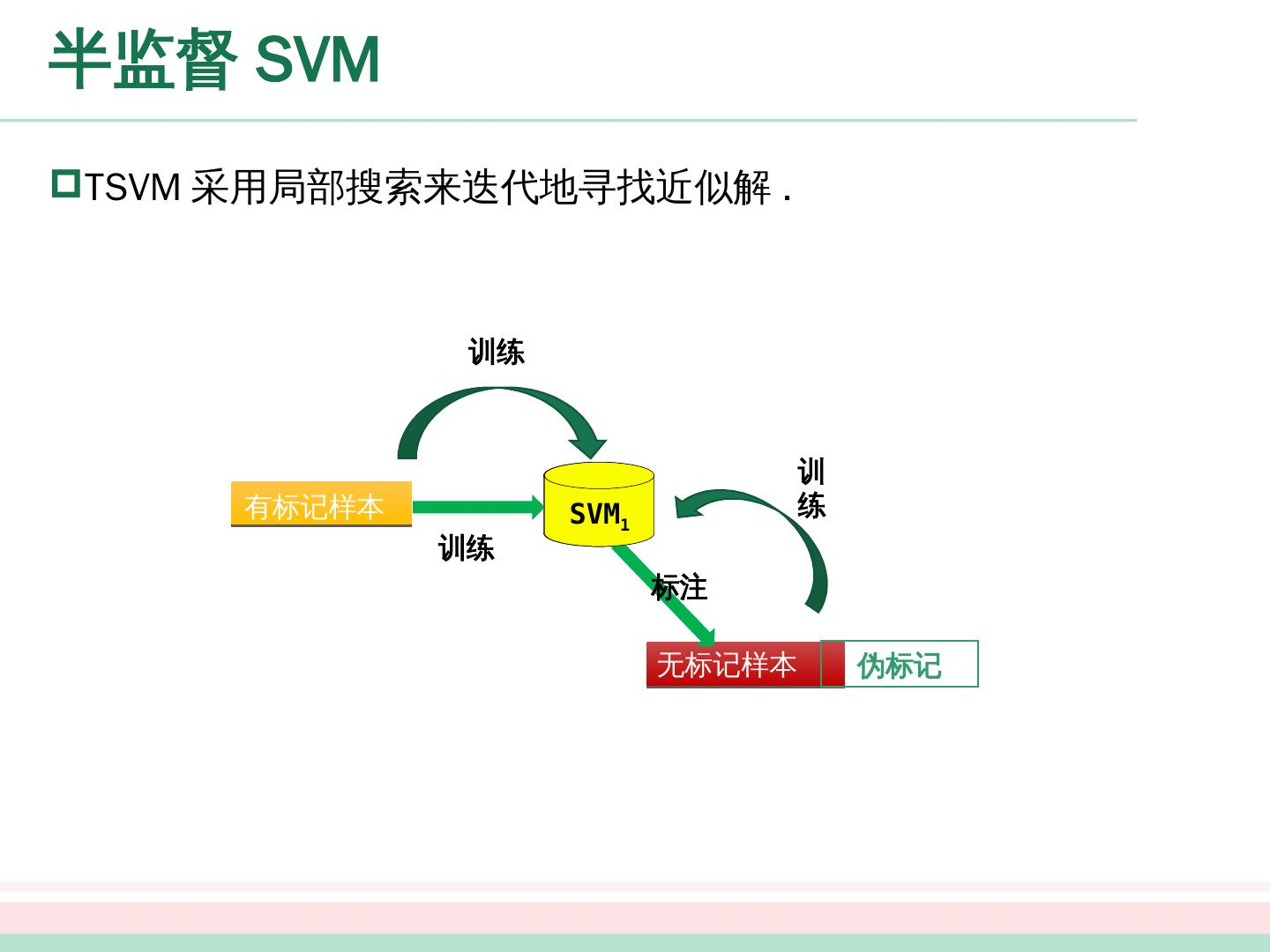
19 .半监督 SVM TSVM 采用局部搜索来迭代地 寻找近似解 . 无标记样本 有标记样本 SVM 0 伪标记 SVM 1 训练 训练 训练 标注
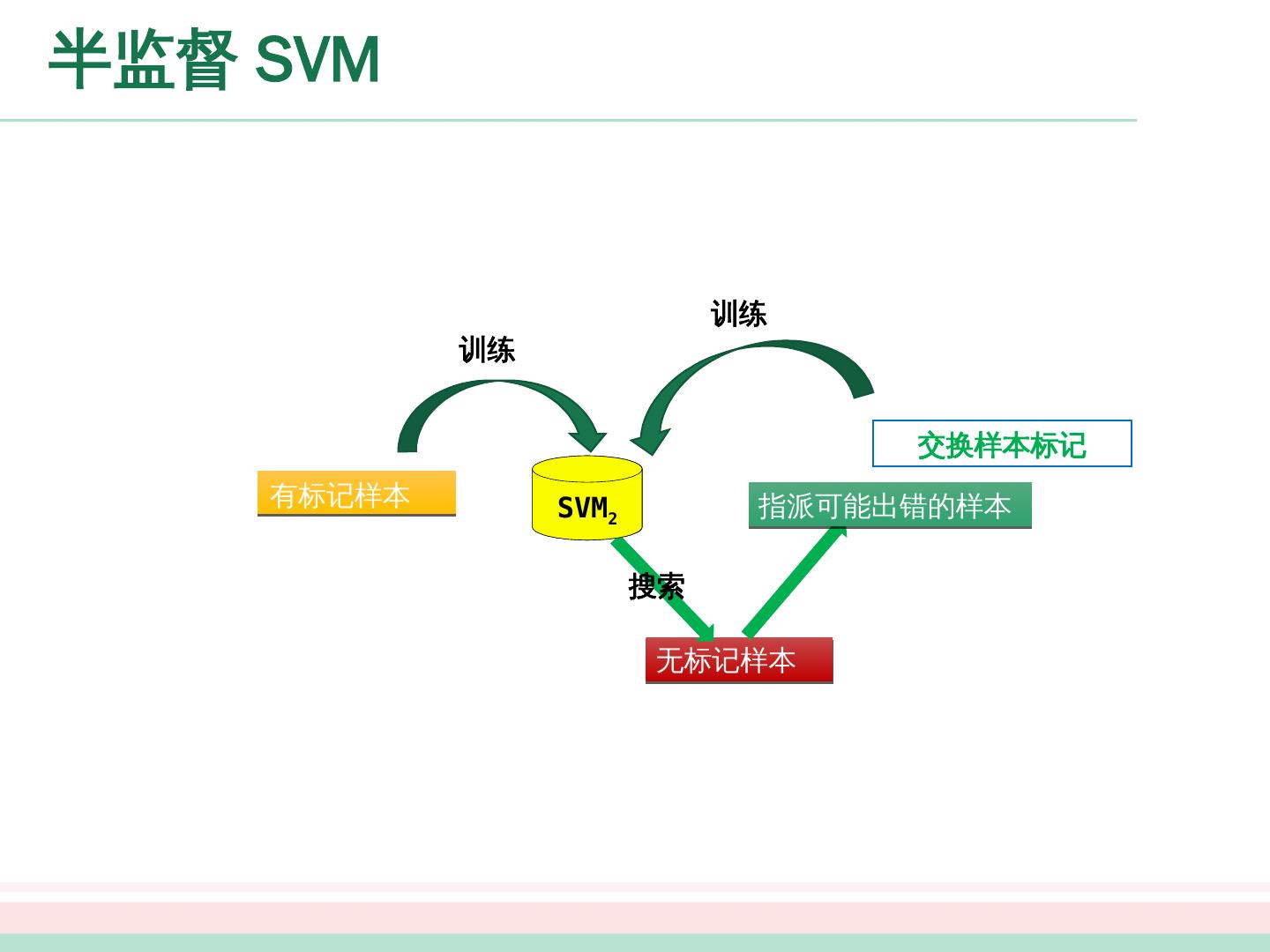
20 .半监督 SVM SVM 1 无标记样本 搜索 指派可能出错的样本 交换样本标记 有标记样本 训练 训练 SVM 2
21 .半监督 SVM 未标记样本的伪标记不准确
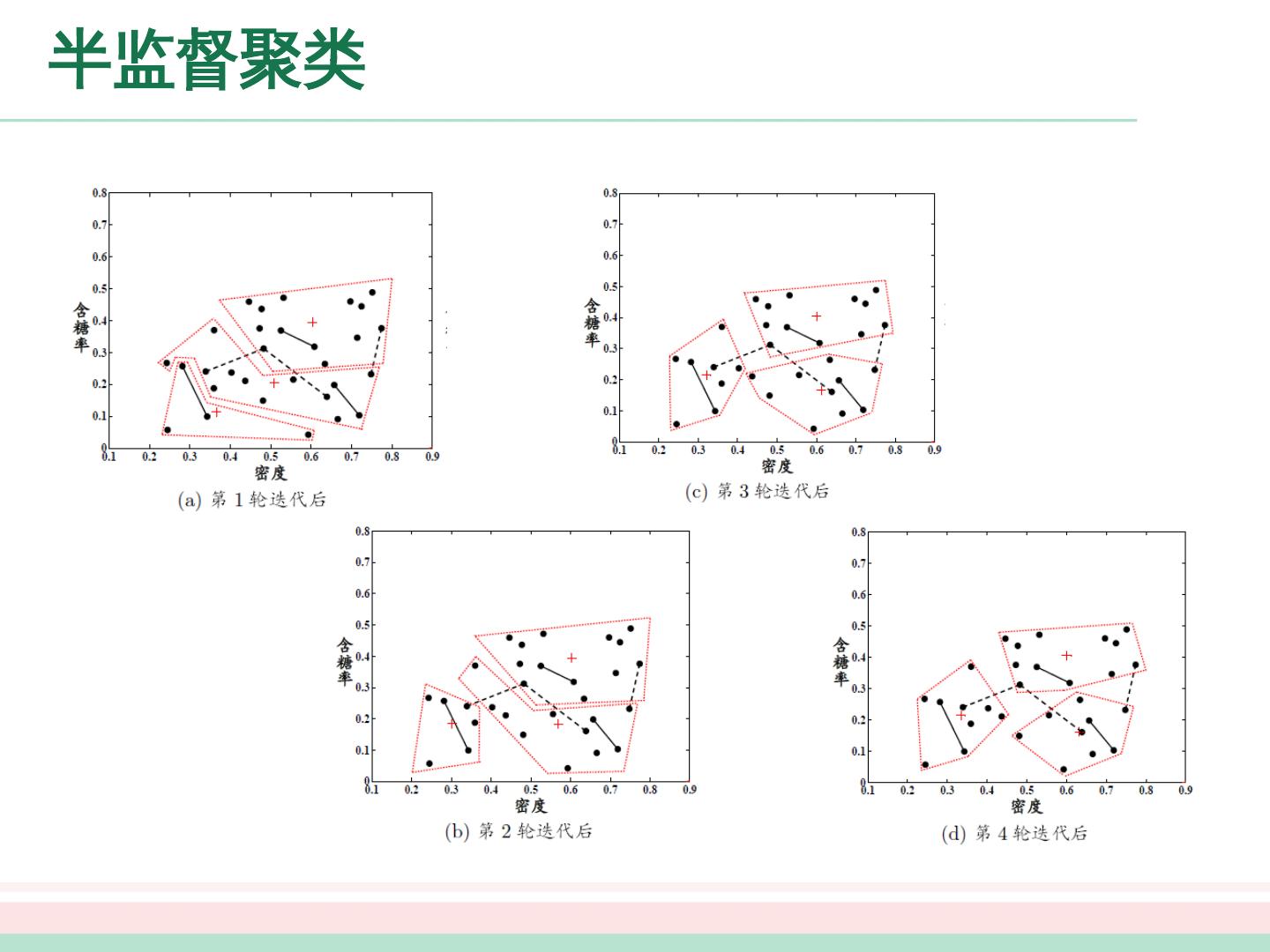
22 .半监督 SVM 未标记样本进行标记指派及调整的过程中 , 有可能出现 类别不平衡 问题 , 即某类的样本远多于另 一类。 为了减轻 类别 不平衡性所造成的不利影响 , 可 对算法 稍加改进 : 将 优化目标 中的 项 拆分 为 与 两 项 , 并在初始化 时令:
23 .半监督 SVM 显然 , 搜寻标记指派可能出错的每一对未标记样本进行调整 , 仍是 一个 涉及 巨大计算开销 的大规模优化 问题 。 因此 , 半监督 SVM 研究的一个 重点 是如何 设计出高效的优化求解 策略 。 例如基于图核 (graph kernel) 函数梯度 下降的 Laplacian SVM[Chapelle and Zien, 2005] 、基于标记均值 估计的 meanS3VM[Li et al., 2009] 等 .
24 .半监督 SVM 显然 , 搜寻标记指派可能出错的每一对未标记样本进行调整 , 仍是 一个 涉及 巨大计算开销 的大规模优化 问题 。 因此 , 半监督 SVM 研究的一个 重点 是如何 设计出高效的优化求解 策略 。 例如基于图核 (graph kernel) 函数梯度 下降的 Laplacian SVM[Chapelle and Zien, 2005] 、基于标记均值 估计的 meanS3VM[Li et al., 2009] 等 .
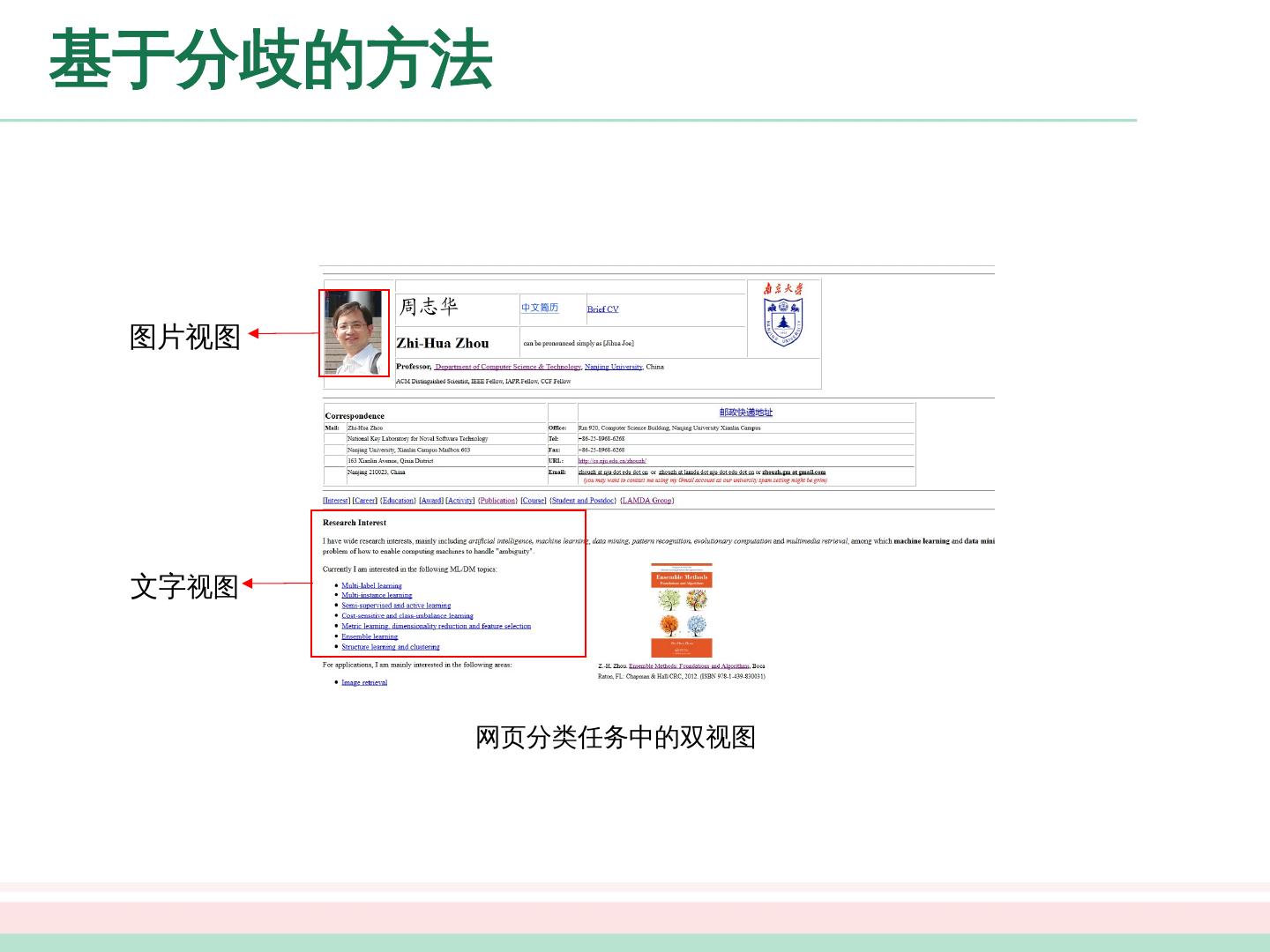
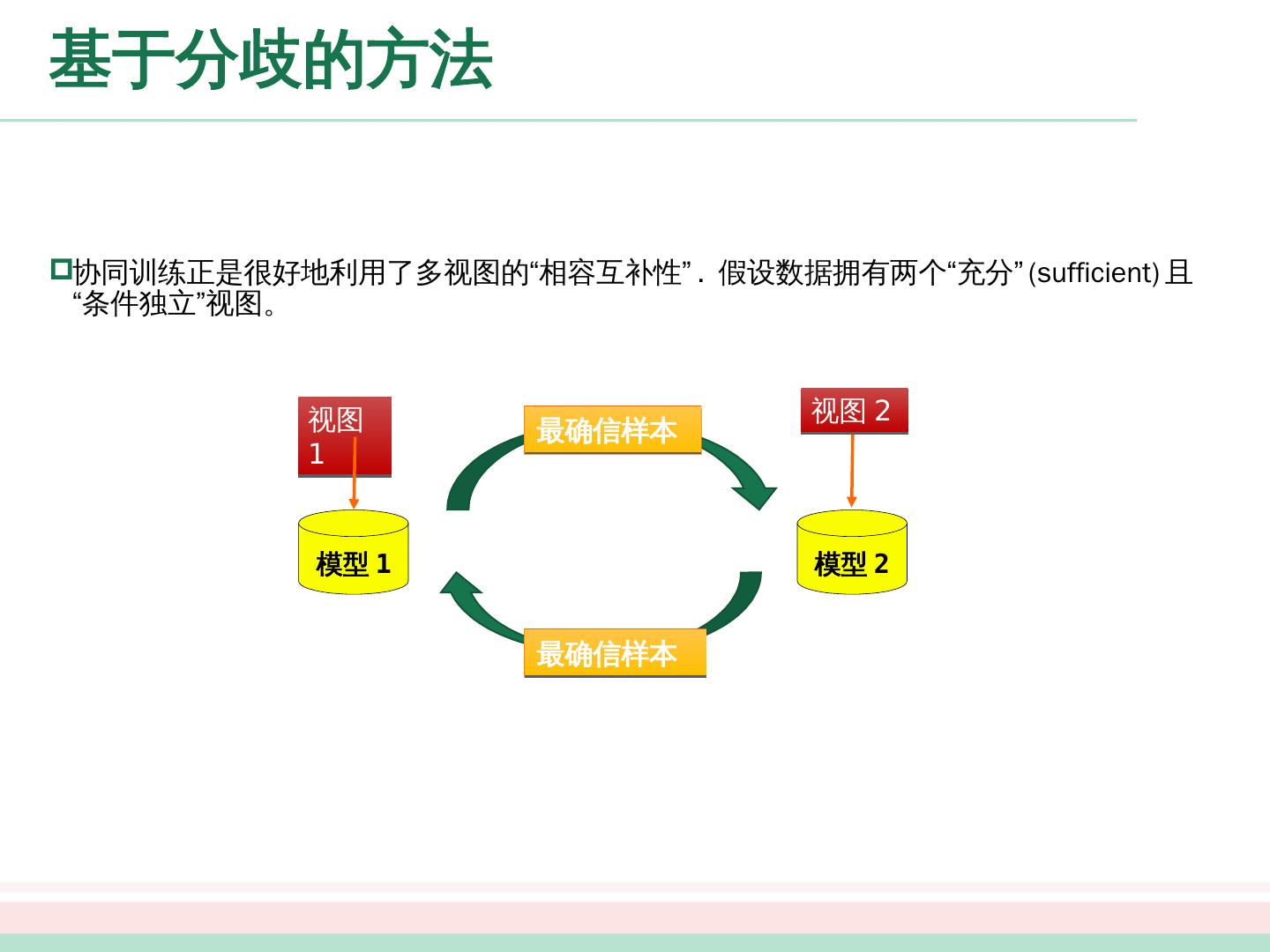
25 .图半监督学习 给定一个数据集 , 我们可将其映射为一个图 , 数据集中每个样本对应于图 中一 个结点 , 若两个样本之间的 相似度很高 ( 或相关性很强 ), 则对应的结点之间 存在 一条边 , 边的 “强度” (strength) 正比于样本之间的 相似度 ( 或相关性 ) 。 我们可 将有标记样本所对应的结点想象为染过色 , 而未标记样本所对应的结点则 尚未 染色 . 于是 , 半监督学习就对应于“颜色”在图上扩散或传播的 过程。 由于 一个 图对应了一个矩阵 , 这就使得我们能基于矩阵运算来进行半监督学习算法 的推导 与 分析 。
26 .图半监督学习 我们先基于 构建 一个 图 ,其中结点集 边集 E 可表示为一个亲和矩阵 (affinity matrix ), 常 基于高斯函数定义为 :
27 .图半监督学习 假定从 图 将学得一个实值函数 。 直观上讲 相似的样本应具有相似的标记 , 即 得到最优 结果于是 可定义关于 f 的“能量函数” (energy function)[Zhu et al., 2003]:
28 .图半监督学习 采用分块矩阵表示方式 : 由 可 得 :
29 .图半监督学习