- 快召唤伙伴们来围观吧
- 微博 QQ QQ空间 贴吧
- 文档嵌入链接
- 复制
- 微信扫一扫分享
- 已成功复制到剪贴板
神经网络学习
展开查看详情
1 . Learning I Linda Shapiro EE/CSE 576 1
2 . Learning • AI/Vision systems are complex and may have many parameters. • It is impractical and often impossible to encode all the knowledge a system needs. • Different types of data may require very different parameters. • Instead of trying to hard code all the knowledge, it makes sense to learn it. 2
3 . Learning from Observations • Supervised Learning – learn a function from a set of training examples which are preclassified feature vectors. feature vector class (shape,color) Given a previously unseen (square, red) I feature vector, what is the (square, blue) I rule that tells us if it is in (circle, red) II class I or class II? (circle blue) II (triangle, red) I (triangle, green) I (circle, green) ? (ellipse, blue) II (triangle, blue) ? (ellipse, red) II 3
4 . Real Observations %Training set of Calenouria and Dorenouria @DATA 0,1,1,0,0,0,0,0,0,1,1,2,3,0,1,2,0,0,0,0,0,0,0,0,1,0,0,1, 0,2,0,0,0,0,1,1,1,0,1,8,0,7,0,0,0,1,0,0,0,0,0,0,0,0,0,0,0,0,1,0,0, 3,3,4,0,2,1,0,1,1,1,0,0,0,0,1,0,0,1,1,cal 0,1,0,0,0,1,0,0,0,4,1,2 ,2,0,1,0,0,0,0,0,1,0,0,3,0,2,0,0,1,1,0,0,1,0,0,0,1,0,1,6,1,8,2,0,0, 0,0,1,0,0,0,0,0,0,0,0,0,0,1,1,0,0,1,2,0,5,0,0,0,0,0,0,0,1,3,0,0,0,0, 0,cal 0,0,1,0,1,0,0,1,0,1,0,0,1,0,3,0,1,0,0,2,0,0,0,0,1,3,0,0,0,0,0,0,1,0, 2,0,2,0,1,8,0,5,0,1,0,1,0,1,1,0,0,0,0,0,0,0,0,0,2,2,0,0,3,0,0,2,1,1, 5,0,0,0,2,1,3,2,0,1,0,0,cal 0,0,0,0,0,0,0,0,2,0,0,1,2,0,1,1,0,0,0,1 ,0,0,0,0,0,0,0,0,0,1,0,0,0,1,0,0,3,0,0,4,1,8,0,0,0,1,0,0,0,0,0,1,0,1 ,0,1,0,0,0,0,0,0,4,2,0,2,1,1,2,1,1,0,0,0,0,2,0,0,2,2,cal ... 4
5 . Learning from Observations • Unsupervised Learning – No classes are given. The idea is to find patterns in the data. This generally involves clustering. • Reinforcement Learning – learn from feedback after a decision is made. 5
6 . Topics to Cover • Inductive Learning – decision trees – ensembles – neural nets – kernel machines • Unsupervised Learning – K-Means Clustering – Expectation Maximization (EM) algorithm 6
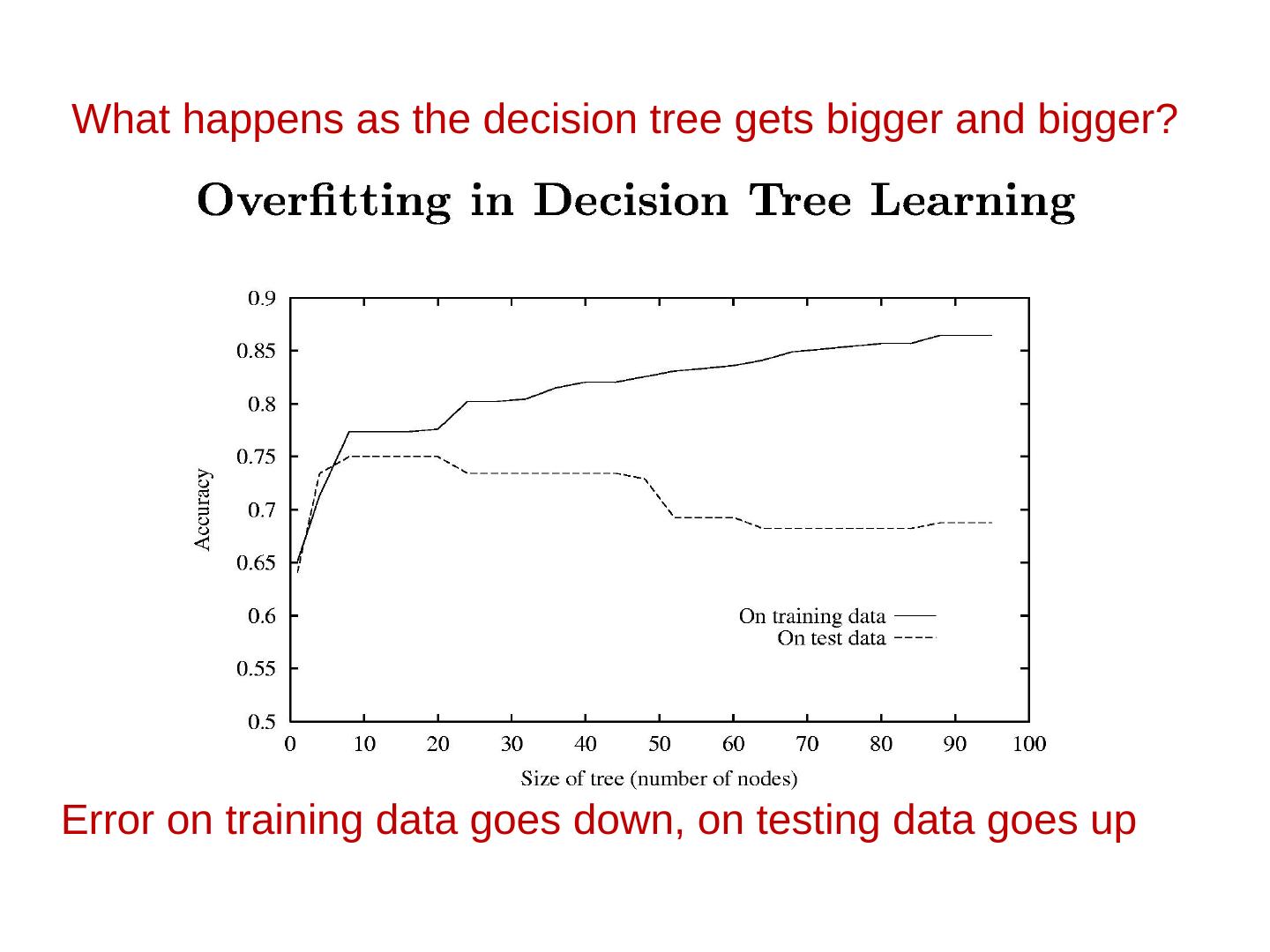
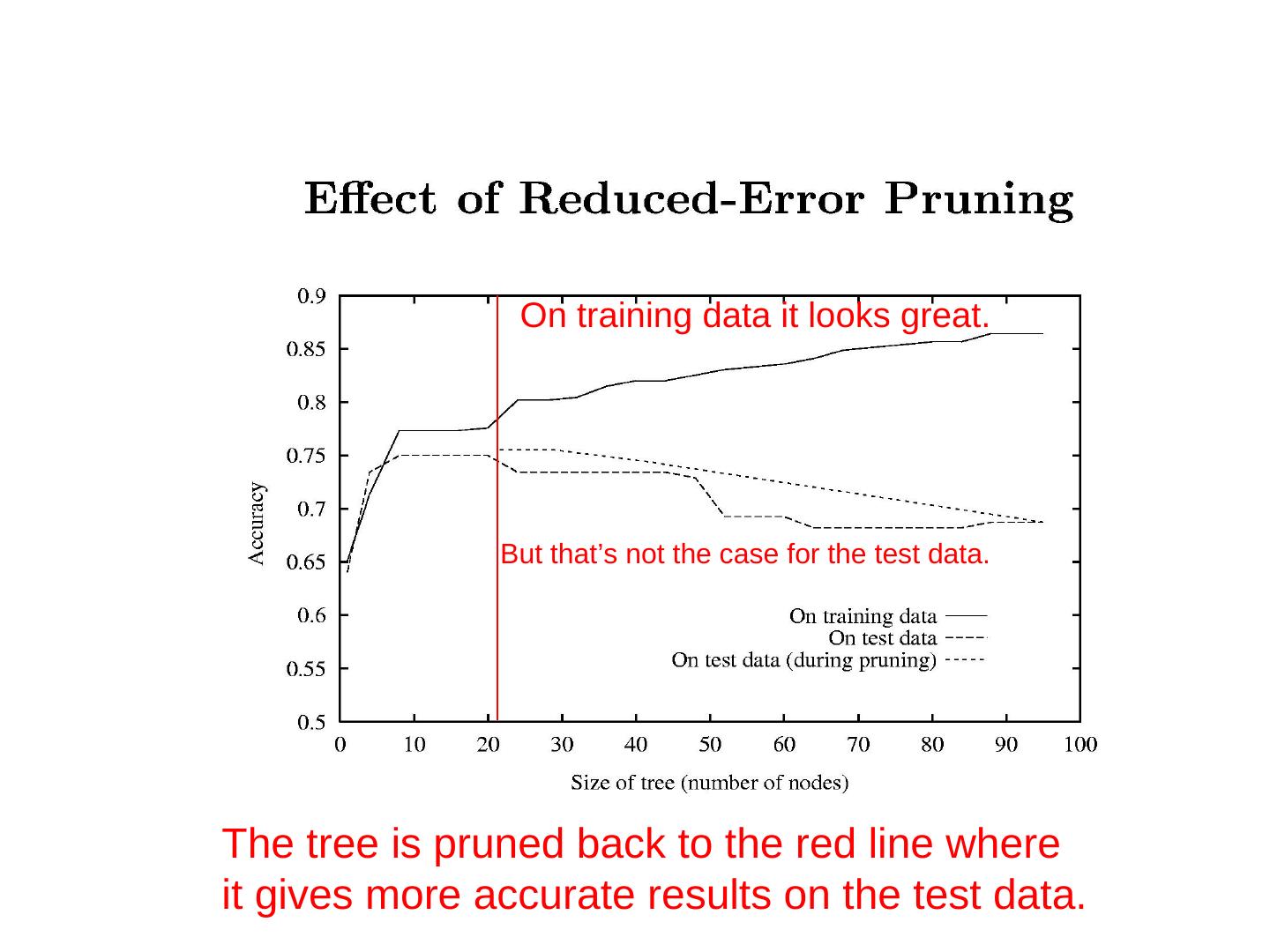
7 . Decision Trees • Theory is well-understood. • Often used in pattern recognition problems. • Has the nice property that you can easily understand the decision rule it has learned. 7
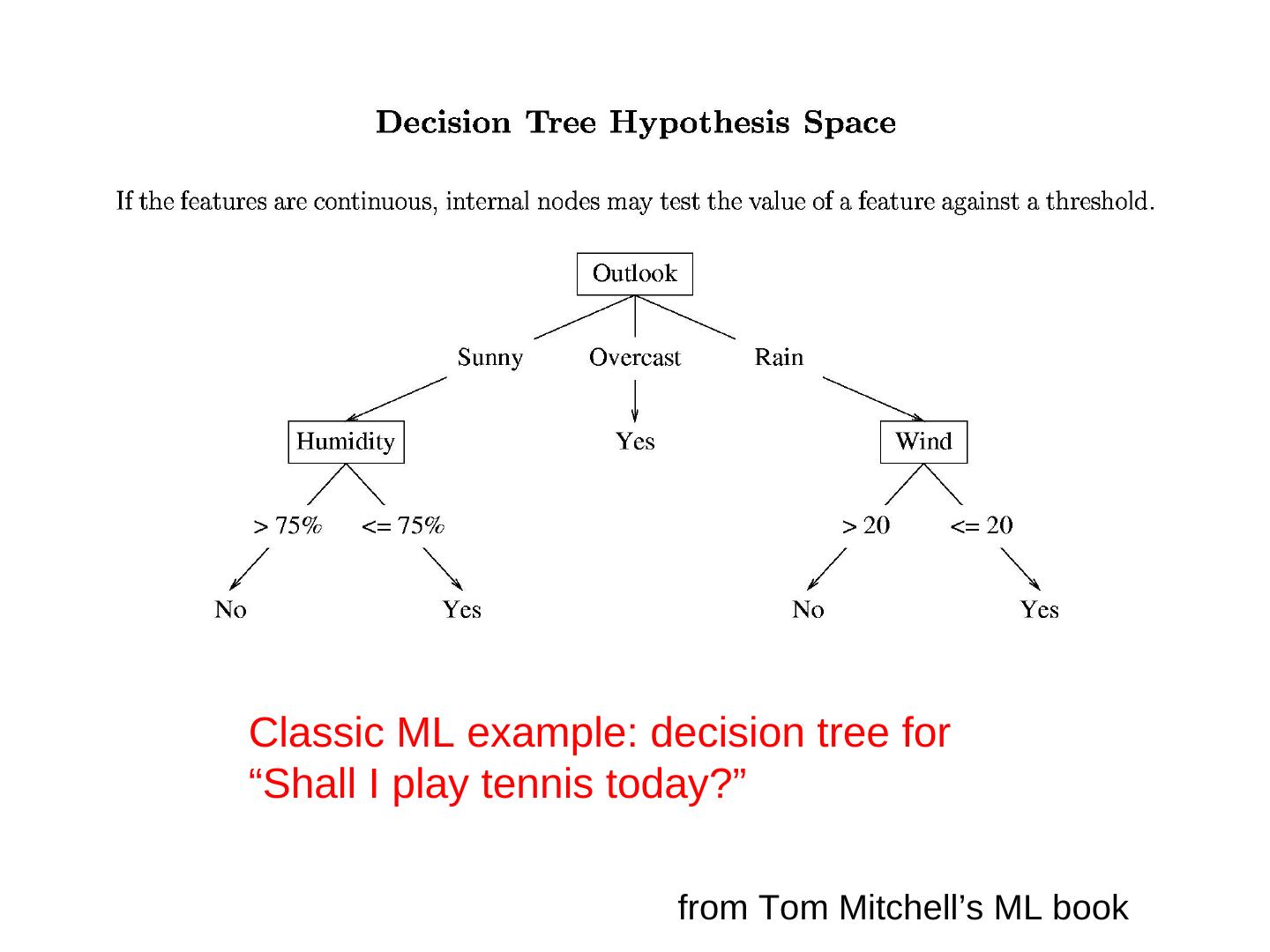
8 .Classic ML example: decision tree for “Shall I play tennis today?” 8 from Tom Mitchell’s ML book
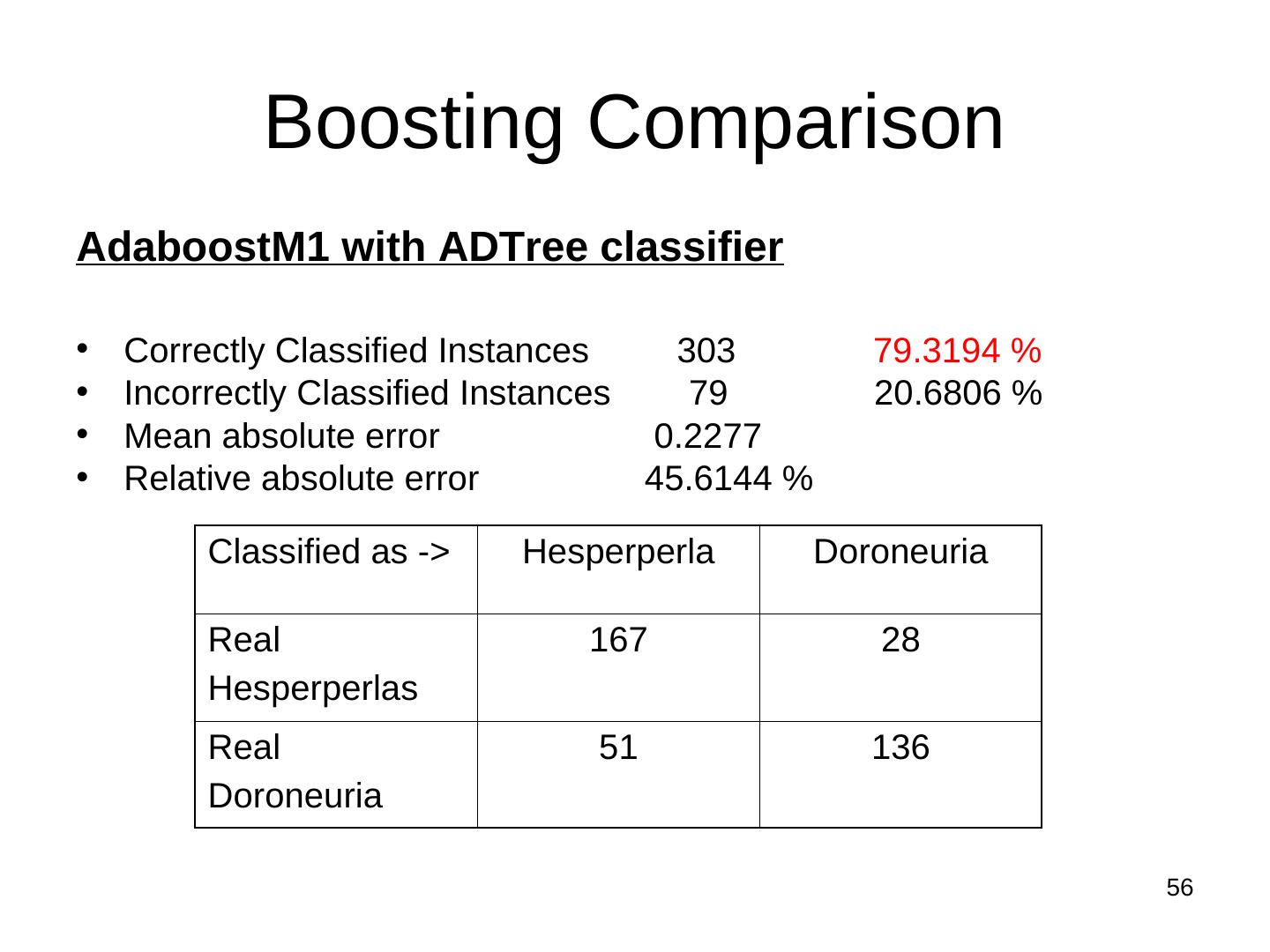
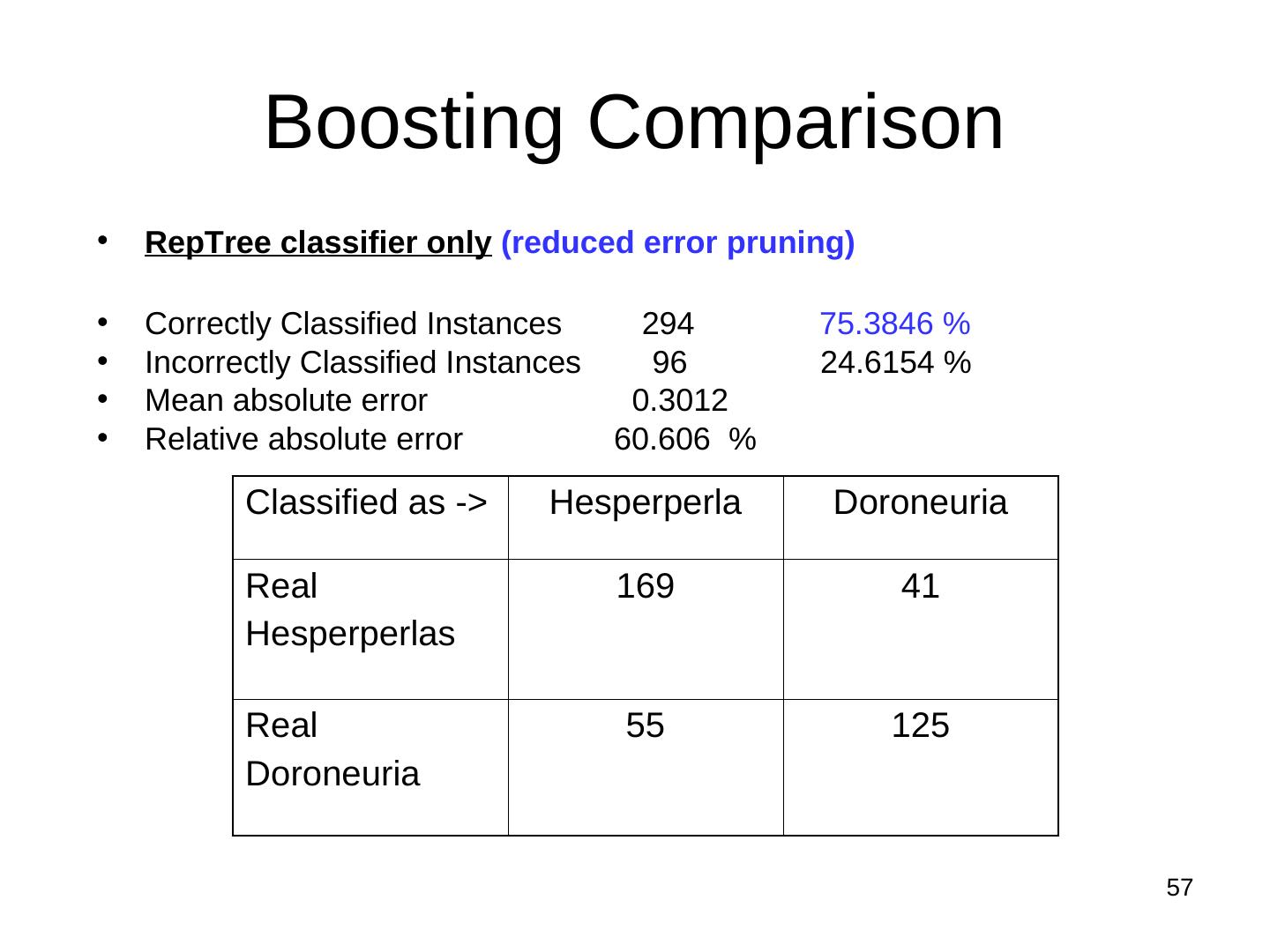
9 . A Real Decision Tree (WEKA) part23 < 0.5 Dorenouria | part29 < 3.5 | | part34 < 0.5 | | | part8 < 2.5 | | | | part2 < 0.5 | | | | | part63 < 3.5 | | | | | | part20 < 1.5 : dor (53/12) [25/8] Calenouria | | | | | | part20 >= 1.5 | | | | | | | part37 < 2.5 : cal (6/0) [5/2] | | | | | | | part37 >= 2.5 : dor (3/1) [2/0] | | | | | part63 >= 3.5 : dor (14/0) [3/0] | | | | part2 >= 0.5 : cal (21/8) [10/4] | | | part8 >= 2.5 : dor (14/0) [14/0] | | part34 >= 0.5 : cal (38/12) [18/4] | part29 >= 3.5 : dor (32/0) [10/2] part23 >= 0.5 | part29 < 7.5 : cal (66/8) [35/12] | part29 >= 7.5 | | part24 < 5.5 : dor (9/0) [4/0] | | part24 >= 5.5 : cal (4/0) [4/0] 9
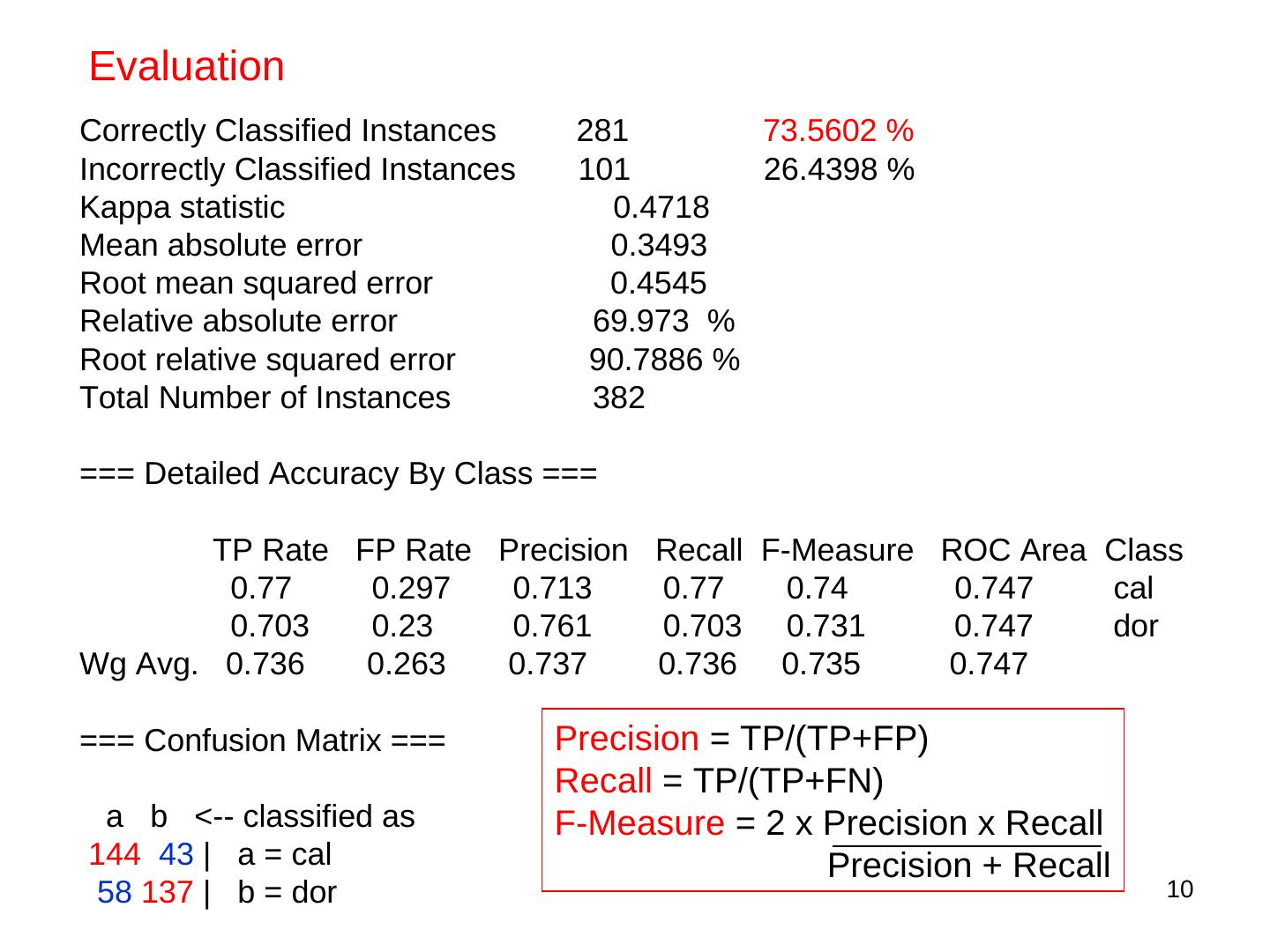
10 .Evaluation Correctly Classified Instances 281 73.5602 % Incorrectly Classified Instances 101 26.4398 % Kappa statistic 0.4718 Mean absolute error 0.3493 Root mean squared error 0.4545 Relative absolute error 69.973 % Root relative squared error 90.7886 % Total Number of Instances 382 === Detailed Accuracy By Class === TP Rate FP Rate Precision Recall F-Measure ROC Area Class 0.77 0.297 0.713 0.77 0.74 0.747 cal 0.703 0.23 0.761 0.703 0.731 0.747 dor Wg Avg. 0.736 0.263 0.737 0.736 0.735 0.747 === Confusion Matrix === Precision = TP/(TP+FP) Recall = TP/(TP+FN) a b <-- classified as F-Measure = 2 x Precision x Recall 144 43 | a = cal Precision + Recall 58 137 | b = dor 10
11 . Properties of Decision Trees • They divide the decision space into axis parallel rectangles and label each rectangle as one of the k classes. • They can represent Boolean functions. • They are variable size and deterministic. • They can represent discrete or continuous parameters. • They can be learned from training data. 11
12 .Learning Algorithm for Decision Trees Growtree(S) /* Binary version */ if (y==0 for all (x,y) in S) return newleaf(0) else if (y==1 for all (x,y) in S) return newleaf(1) else choose best attribute xj S0 = (x,y) with xj = 0 S1 = (x,y) with xj = 1 return new node(xj, Growtree(S0), Growtree(S1)) end How do we choose the best attribute? What should that attribute do for us? 12
13 . Shall I play tennis today? Which attribute should be selected? “training data” 13 witten&eibe
14 . Criterion for attribute selection • Which is the best attribute? – The one that will result in the smallest tree – Heuristic: choose the attribute that produces the “purest” nodes • Need a good measure of purity! – Maximal when? – Minimal when? 14
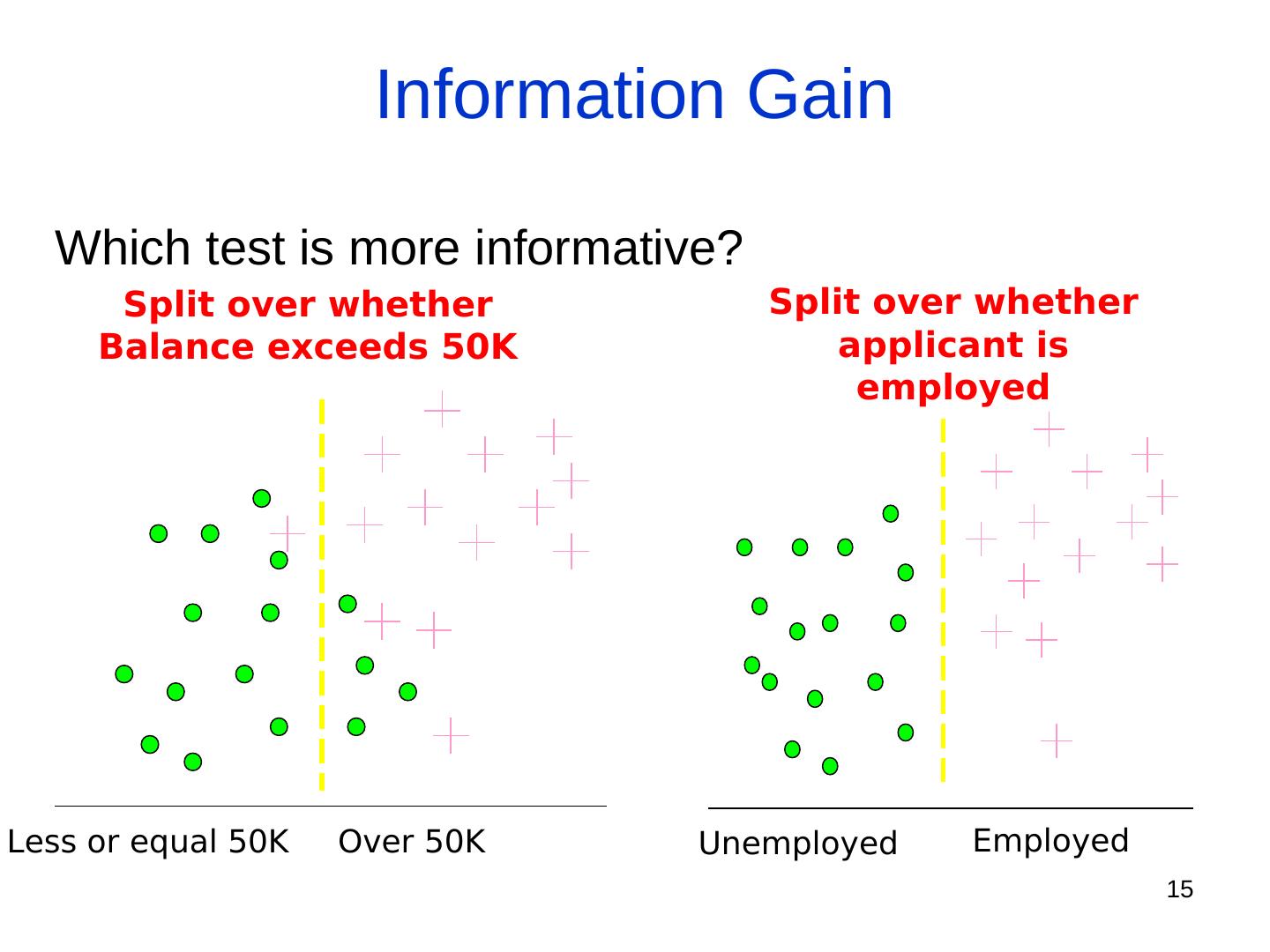
15 . Information Gain Which test is more informative? Split over whether Split over whether Balance exceeds 50K applicant is employed Less or equal 50K Over 50K Unemployed Employed 15
16 . Information Gain Impurity/Entropy (informal) – Measures the level of impurity in a group of examples 16
17 . Impurity Very impure group Less impure Minimum impurity 17
18 . Entropy: a common way to measure impurity • Entropy = i pi log 2 pi pi is the probability of class i Compute it as the proportion of class i in the set. 16/30 are green circles; 14/30 are pink crosses log2(16/30) = -.9; log2(14/30) = -1.1 Entropy = -(16/30)(-.9) –(14/30)(-1.1) = .99 • Entropy comes from information theory. The higher the entropy the more the information content. What does that mean for learning from examples? 18
19 . 2-Class Cases: Minimum • What is the entropy of a group in which impurity all examples belong to the same class? – entropy = - 1 log21 = 0 not a good training set for learning • What is the entropy of a group with Maximum 50% in either class? impurity – entropy = -0.5 log20.5 – 0.5 log20.5 =1 good training set for learning 19
20 . Information Gain • We want to determine which attribute in a given set of training feature vectors is most useful for discriminating between the classes to be learned. • Information gain tells us how important a given attribute of the feature vectors is. • We will use it to decide the ordering of attributes in the nodes of a decision tree. 20
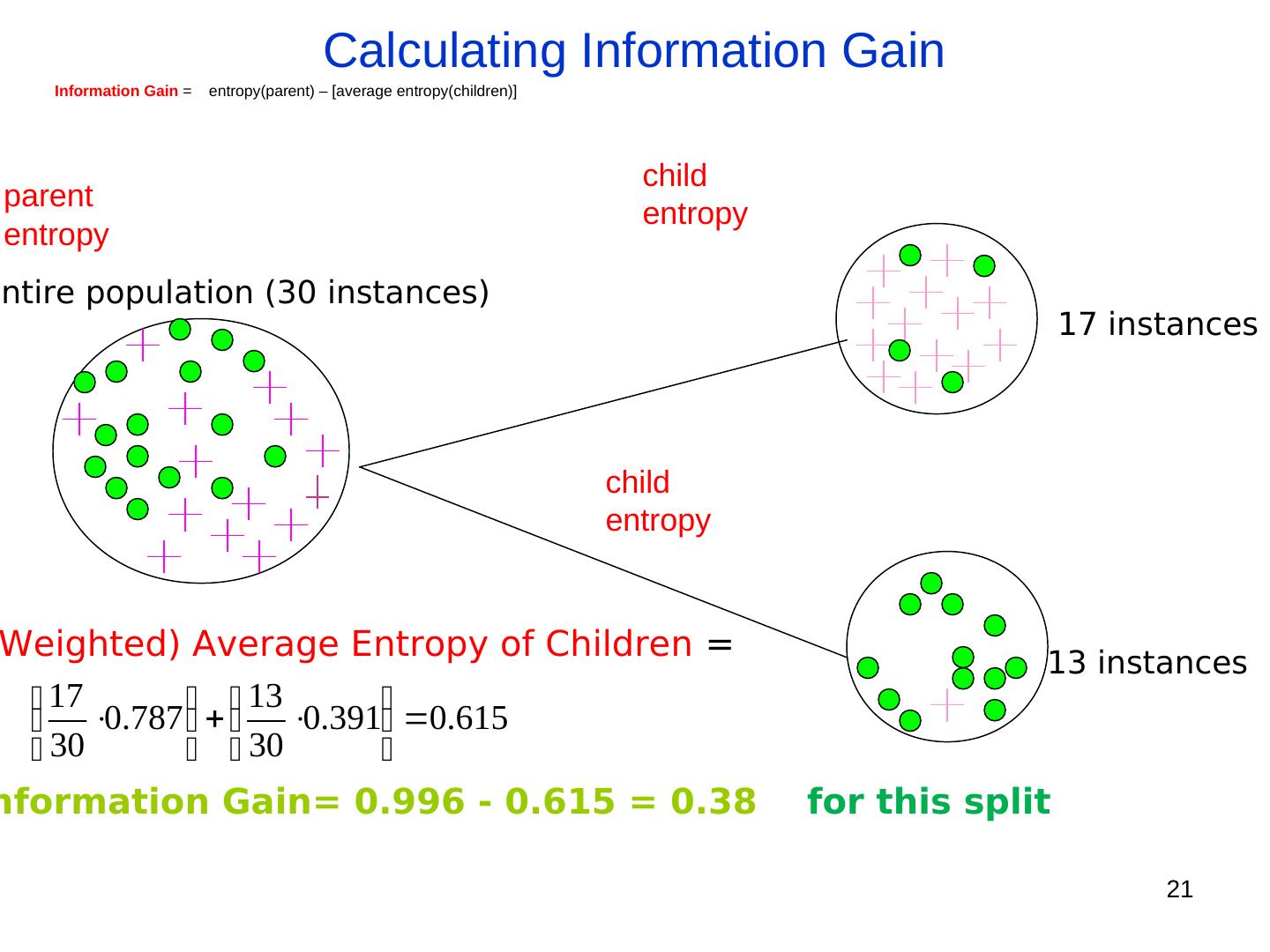
21 . Calculating Information Gain Information Gain = entropy(parent) – [average entropy(children)] child parent entropy entropy Entire population (30 instances) 17 instances child entropy Weighted) Average Entropy of Children = 13 instances 17 13 0.787 0.391 0.615 30 30 nformation Gain= 0.996 - 0.615 = 0.38 for this split 21
22 . Entropy-Based Automatic Decision Tree Construction Training Set S Node 1 x1=(f11,f12,…f1m) What feature x2=(f21,f22, f2m) should be used? . What values? . xn=(fn1,f22, f2m) Quinlan suggested information gain in his ID3 system and later the gain ratio, both based on entropy. 22
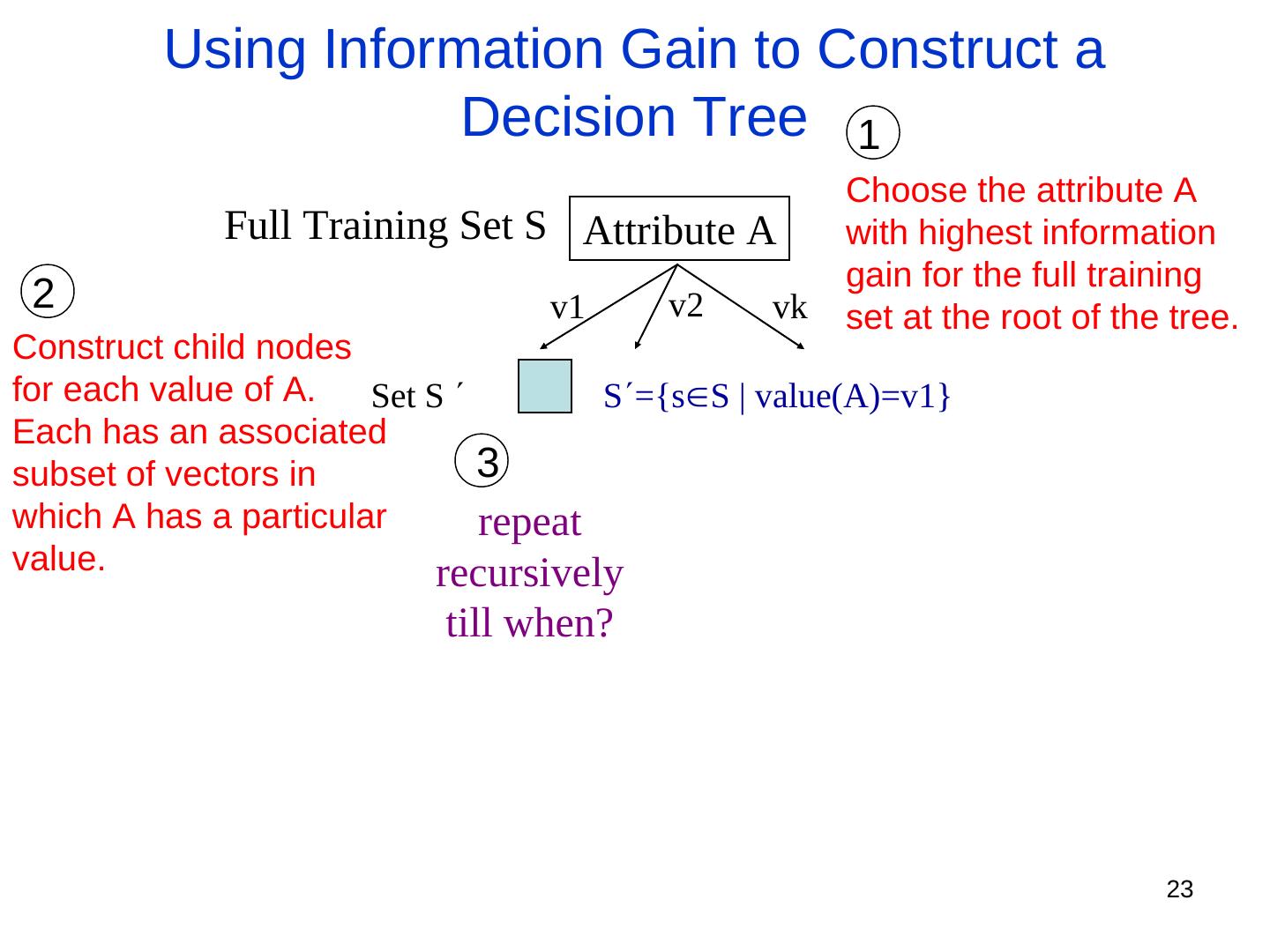
23 . Using Information Gain to Construct a Decision Tree 1 Choose the attribute A Full Training Set S Attribute A with highest information gain for the full training 2 v1 v2 vk set at the root of the tree. Construct child nodes for each value of A. Set S S={ssS | value(A)=v1} Each has an associated subset of vectors in 3 which A has a particular repeat value. recursively till when? 23
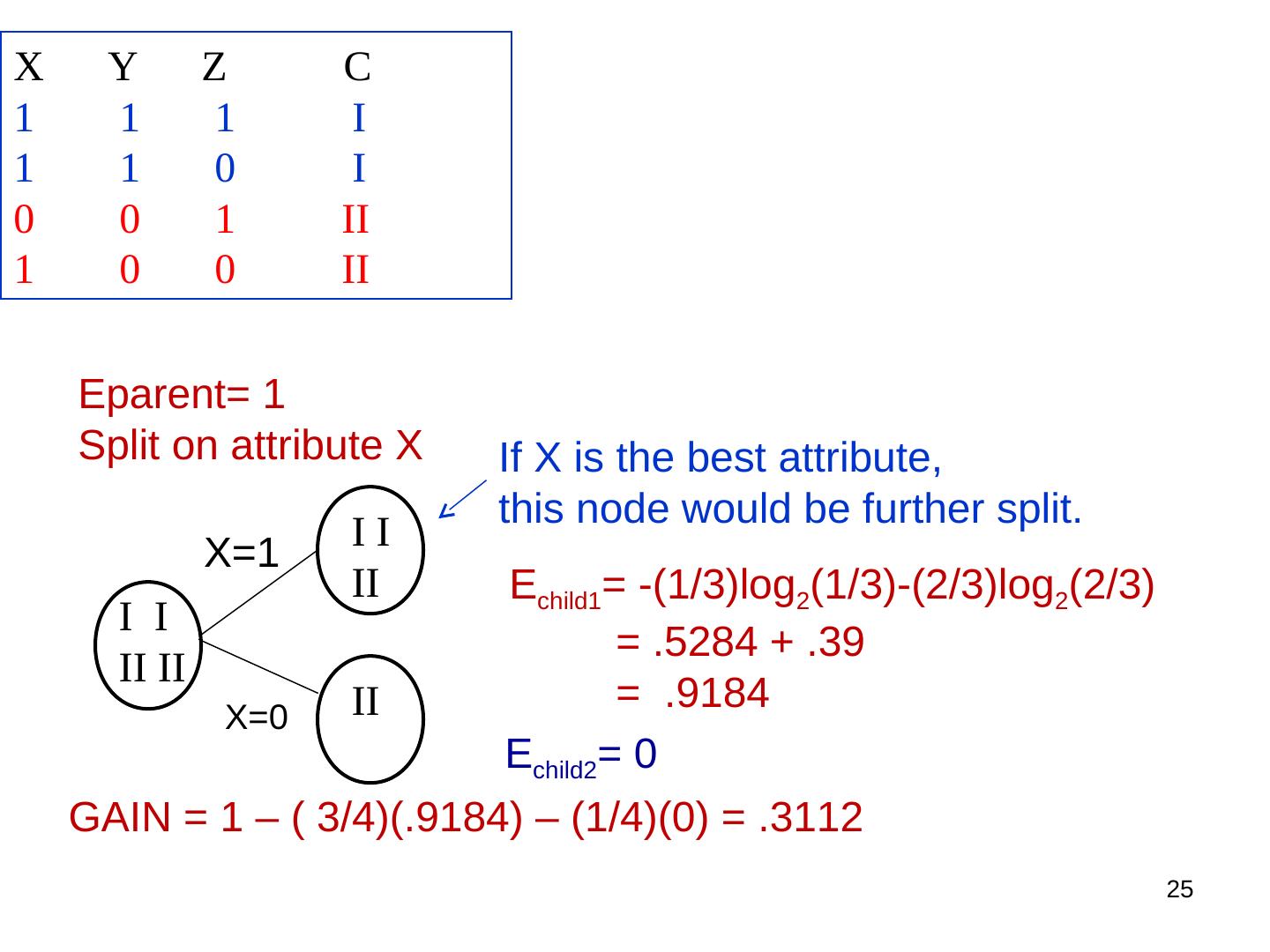
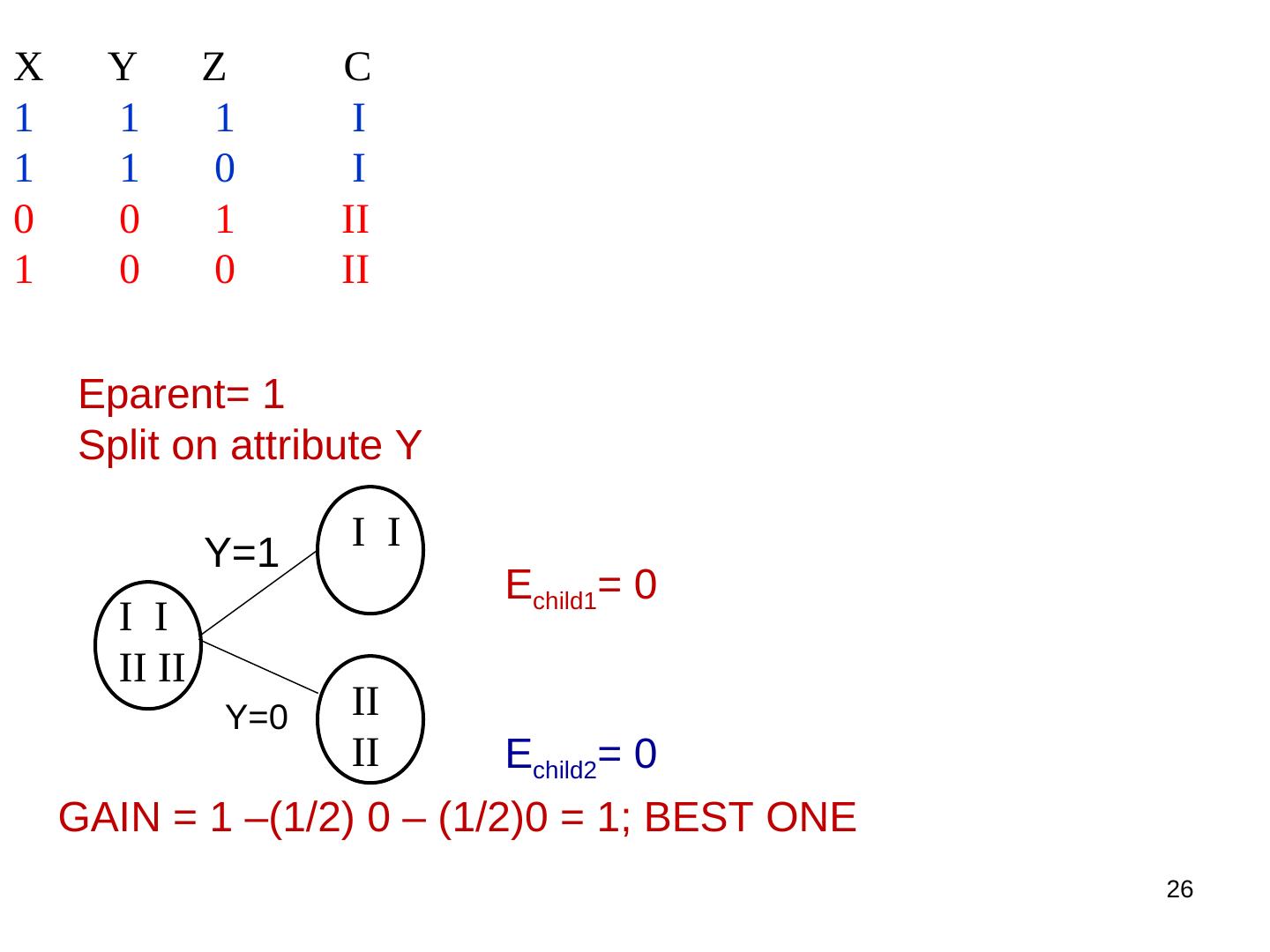
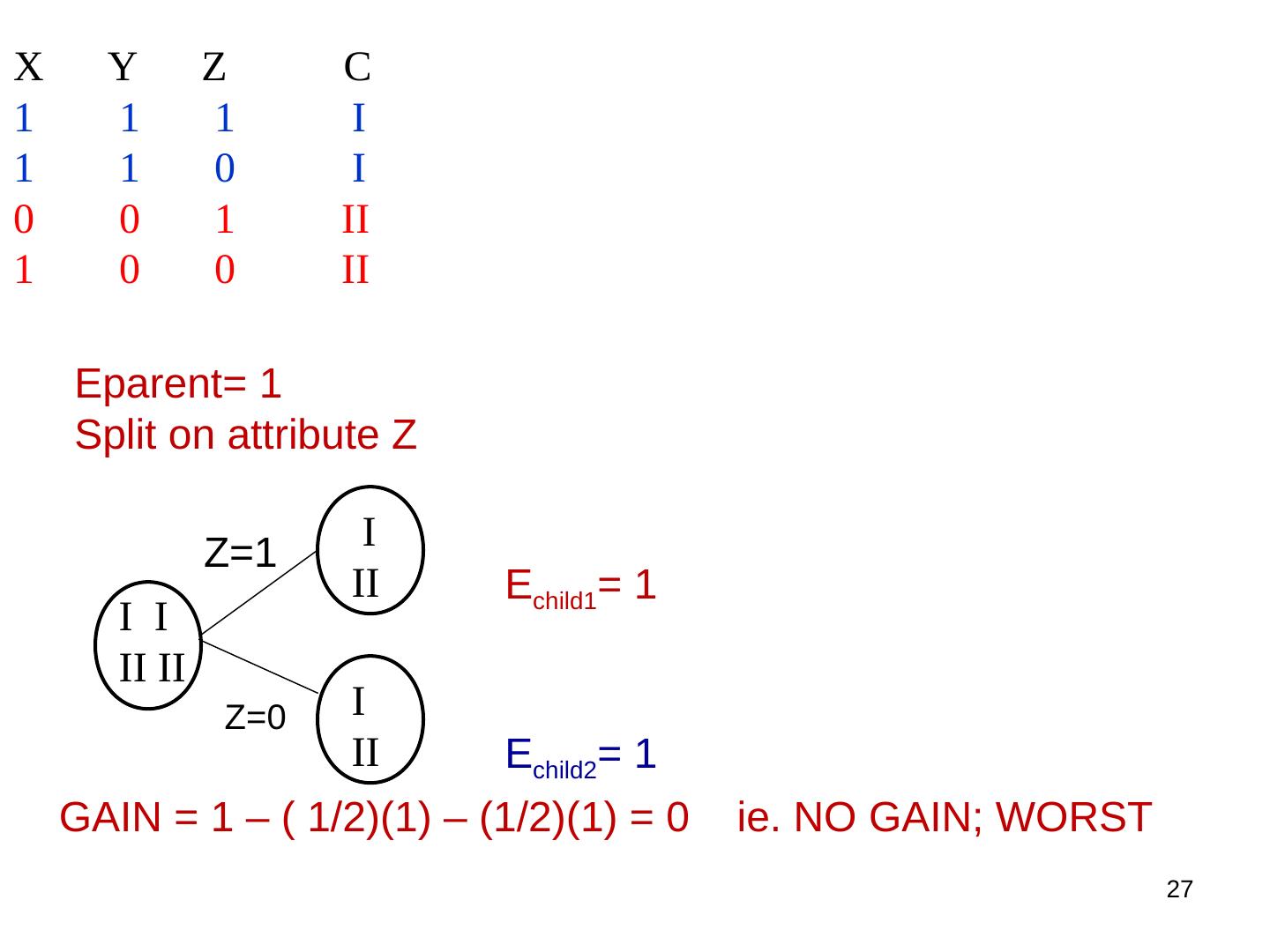
24 . Simple Example Training Set: 3 features and 2 classes X Y Z C 1 1 1 I 1 1 0 I 0 0 1 II 1 0 0 II How would you distinguish class I from class II? 24
25 .X Y Z C 1 1 1 I 1 1 0 I 0 0 1 II 1 0 0 II Eparent= 1 Split on attribute X If X is the best attribute, this node would be further split. II X=1 II Echild1= -(1/3)log2(1/3)-(2/3)log2(2/3) I I = .5284 + .39 II II II = .9184 X=0 Echild2= 0 GAIN = 1 – ( 3/4)(.9184) – (1/4)(0) = .3112 25
26 .X Y Z C 1 1 1 I 1 1 0 I 0 0 1 II 1 0 0 II Eparent= 1 Split on attribute Y I I Y=1 Echild1= 0 I I II II Y=0 II II Echild2= 0 GAIN = 1 –(1/2) 0 – (1/2)0 = 1; BEST ONE 26
27 .X Y Z C 1 1 1 I 1 1 0 I 0 0 1 II 1 0 0 II Eparent= 1 Split on attribute Z I Z=1 II Echild1= 1 I I II II Z=0 I II Echild2= 1 GAIN = 1 – ( 1/2)(1) – (1/2)(1) = 0 ie. NO GAIN; WORST 27
28 . Portion of a fake training set for character recognition Decision tree for this training set. What would be different about a real training set?
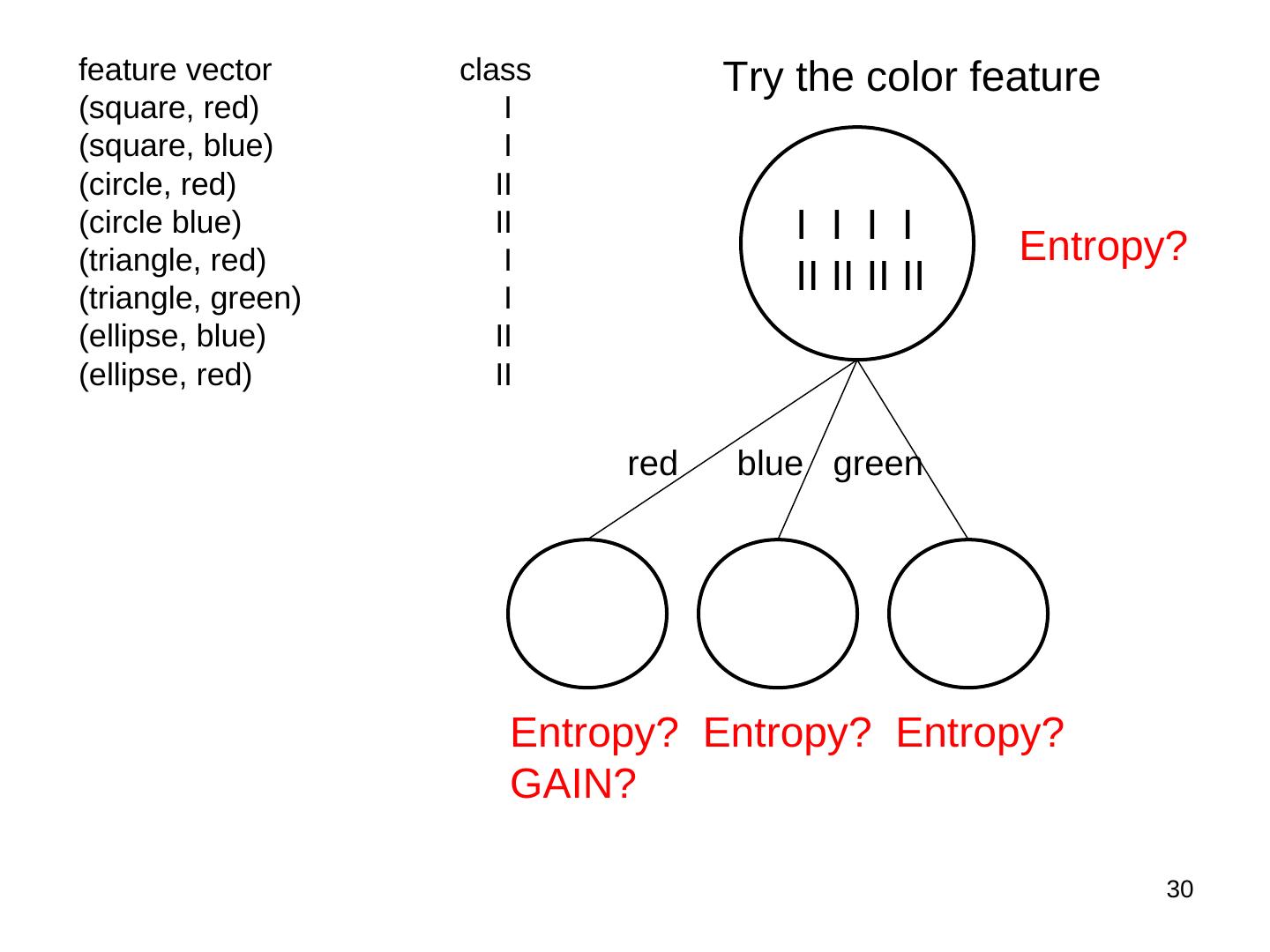
29 .feature vector class Try the shape feature (square, red) I (square, blue) I (circle, red) II (circle blue) II I I I I (triangle, red) I Entropy? (triangle, green) I II II II II (ellipse, blue) II (ellipse, red) II square ellipse circle triangle I I II II I I II II Entropy? Entropy? Entropy? Entropy? GAIN? 29