- 快召唤伙伴们来围观吧
- 微博 QQ QQ空间 贴吧
- 文档嵌入链接
- 复制
- 微信扫一扫分享
- 已成功复制到剪贴板
线性模型
展开查看详情
1 .李绍园 刘冲
2 .第三章 : 线性模型
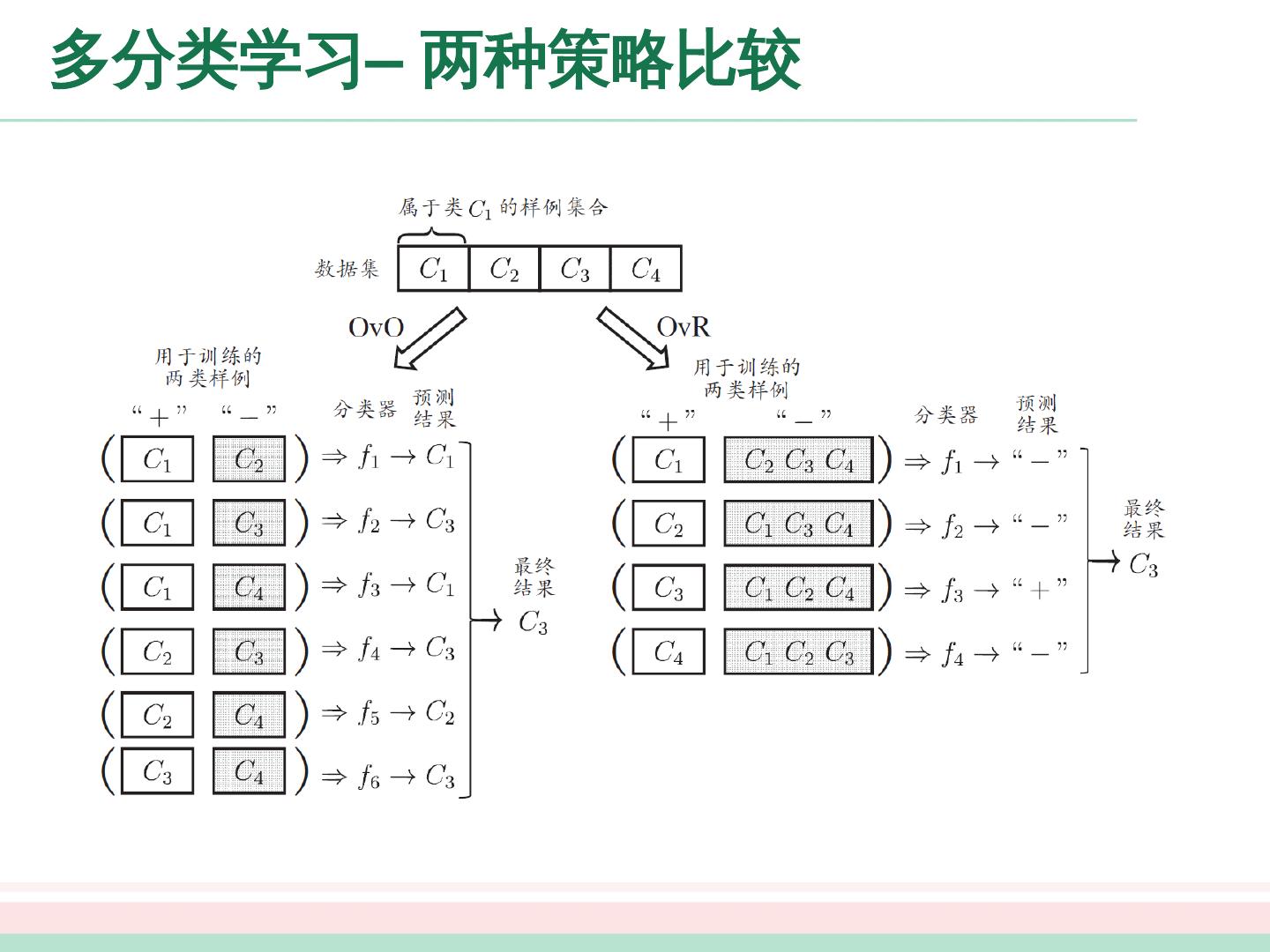
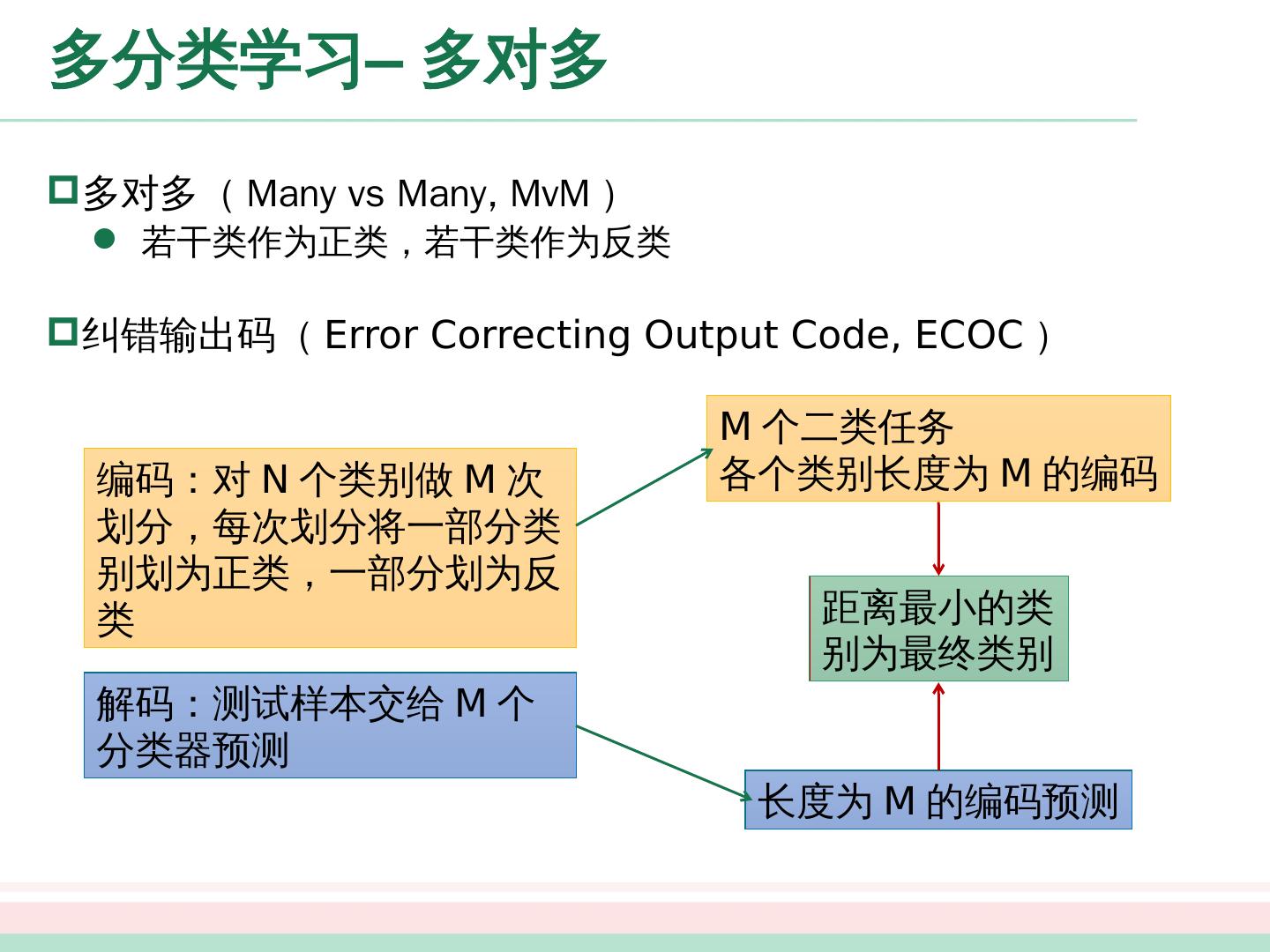
3 .目录 线性回归 最小二乘法 二 分类 任务 对数几率回归 线性判别分析 多分类任务 一对一 一对其余 多对多 类别不平衡问题
4 .基本形式 线性模型一般形式 是由属性描述的示例,其中 是 在第 个属性上的取值 向量形式 其中
5 .线性模型优点 形式简单、易于建模 可解释性 非线性模型的 基础 引入层级结构或高维 映射 一个例子 综合考虑色泽、根蒂和敲声来判断西瓜好不好 其中根蒂的系数最大,表明根蒂最要紧;而敲声的系数比色泽大,说明敲声比色泽更重要
6 .线性回归 给定数据集 其中 , 线性回归( linear regression )目的 学得一个线性模型以尽可能准确地预测实值输出标记 离散属性处理 有“序”关系 连续 化为连续值 无“序”关系 有 k 个属性值,则转换为 k 维向量
7 .线性回归 单一属性的线性回归目标 参数 / 模型估计:最小二乘法( least square method) 使得
8 .线性回归 - 最小二乘法 最小化均方误差 分别对 和 求导,可得
9 .线性回归 - 最小二乘法 得到闭式( closed-form )解 其中
10 .多元线性回归 给定数据集 多元线性回归目标 使得
11 .多元线性回归 把 和 吸收入向量形式 ,数据集表示为
12 .令上式为零可得 最优解的闭式解 多元线性回归 - 最小二乘法 最小二乘法( least square method ) 令 ,对 求导得到
13 .多元线性回归 - 满秩讨论 是满秩矩阵或正定矩阵,则 其中 是 的逆矩阵,线性回归模型为 不是满秩矩阵 根据归纳偏好选择解 (参见 1.4 节) 引入正则化 (参加 6.4 节, 11.4 节)
14 .对数线性回归 输出标记 的对数为线性模型 逼近的 目标
15 .线性回归 - 广义线性模型 一般形式 称为联系函数( link function ) 单调可微函数 对数线性回归是 时广义线性模型的特例
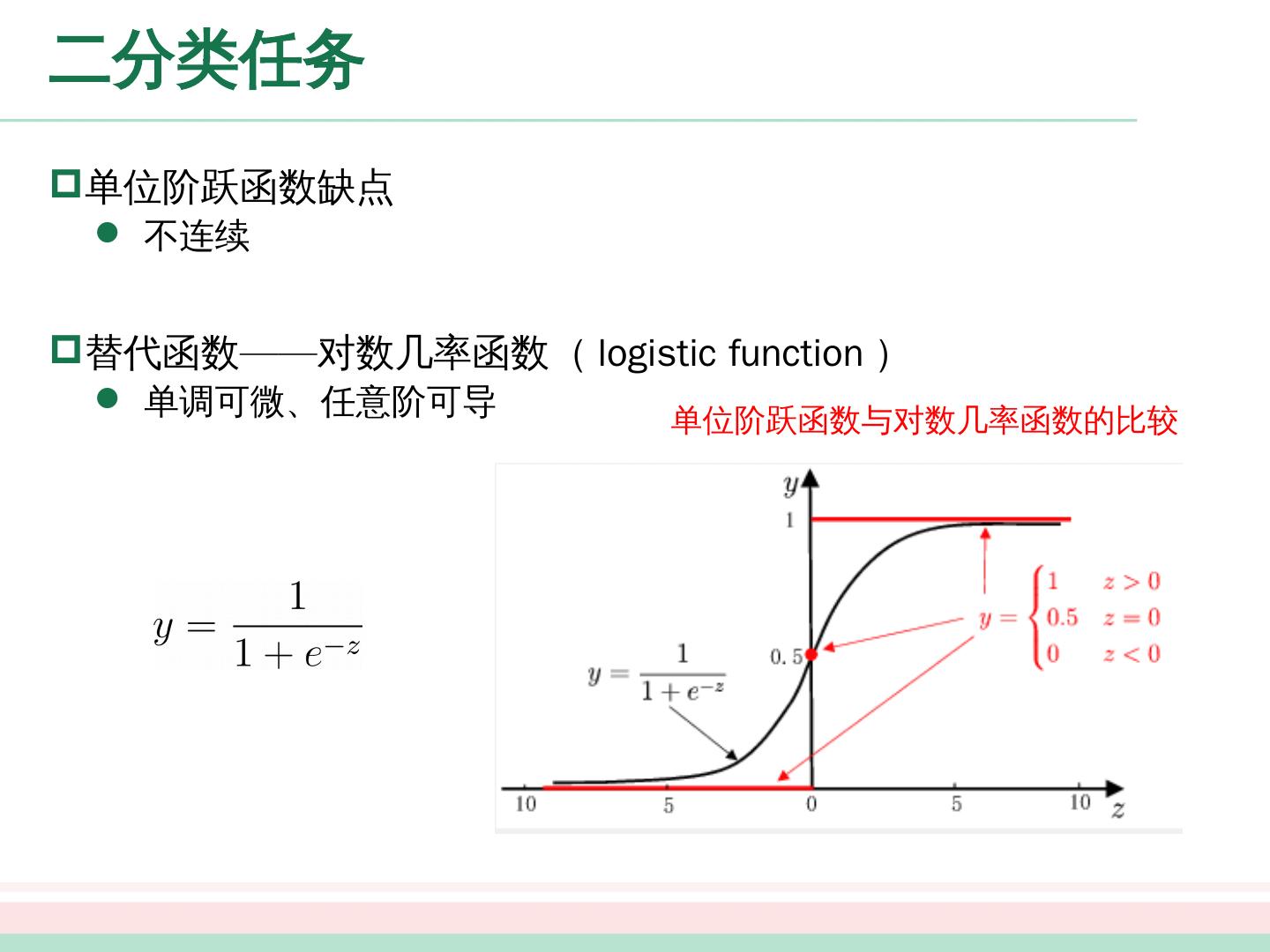
16 .二分类 任务 预测值与输出标记 寻找函数将分类标记与线性回归模型输出联系起来 最理想的函数 —— 单位阶跃函数 预测值大于零就判为正例,小于零就判为反例,预测值为临界值零则可任意判别
17 .二分类 任务 单位阶跃函数缺点 不连续 替代函数 —— 对数几率函数( logistic function ) 单调可微、任意阶可导 单位阶跃函数与对数几率函数的比较
18 .对数几率回归 运用对数几率函数 对数几率( log odds ) 样本作为正例的相对可能性的对数 对数几率回归优点 无需事先假设数据分布 可得到“类别”的近似概率预测 可直接应用现有数值优化算法求取最优解 变为
19 .对数几率回归 - 极大似然法 对数几率 显然有
20 .对数几率回归 - 极大似然法 极大似然法 ( maximum likelihood ) 给定数据集 最大化样本属于其真实标记的概率 最大化对数似 然函数
21 .对数几率回归 - 极大似然法 转化为最小化负对数似然函数求解 令 , ,则 可简写为 再令 则似然项可重写为 故等价形式为要最小化
22 .对数 几率回归 求解得 牛顿法第 t+1 轮迭代解的更新公式 其中关于 的一阶、二阶导数分别为 高 阶可导连续凸函数,梯度下降法 / 牛顿法 [Boyd and Vandenberghe , 2004]
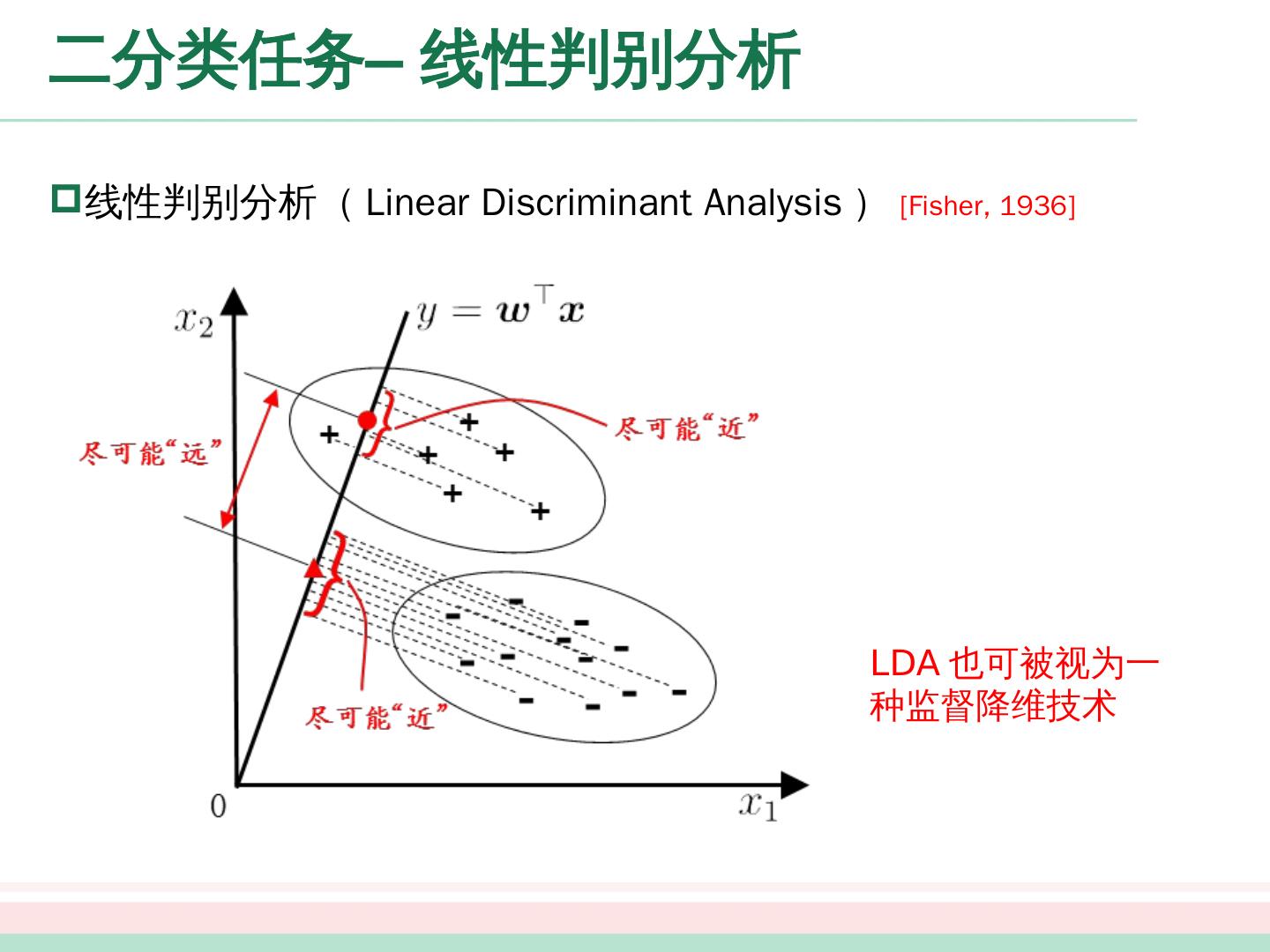
23 .二分类 任务 – 线性判别分析 线性判别分析( Linear Discriminant Analysis ) [Fisher, 1936] LDA 也可被视为一种监督降维技术
24 .二分类 任务 – 线性判别分析 LDA 的思想 欲使同类样例的投影点尽可能接近,可以让同类样例投影点的协方差尽可能小 欲使异类样例的投影点尽可能远离,可以让类中心之间的距离尽可能大 一些变量 第 i 类示例的集合 第 i 类示例的 均值向量 第 i 类示例的协方差 矩阵 两 类样本的中心在直线上的投影: 和 两 类样本的协方差: 和
25 .二分类 任务 – 线性判别分析 最大化目标 类内散度矩阵 类间散度矩阵
26 .二分类 任务 – 线性判别分析 广义瑞利 商( generalized Rayleigh quotient ) 令 ,最大化广义瑞利商等价形式为 运用拉格朗日乘子法
27 .二分类 任务 – 线性判别分析 同向向量 结果 求解 奇异值分解 LDA 的贝叶斯决策论解释 两 类数据同先验、满足高斯分布且协方差相等时, LDA 达到最优分类 同向向量
28 .LDA 推广 – 多分类任务 全局散度矩阵 类内散度矩阵 其中 求解得
29 .LDA 推广 – 多分类任务 优化目标 其中 的闭式解则是 的 N-1 个最大广义特征值所对应的特征向量组成的矩阵 多分类 LDA 将样本投影到 N-1 维空间, N-1 通常远小于数据原有的属性数,因此 LDA 也被视为一种监督降维技术