Edge Detection

1 .Edge Detection EE/CSE 576 Linda Shapiro

2 .Edge Detection EE/CSE 576 Linda Shapiro

3 .Edges are caused by a variety of factors. depth discontinuity surface color discontinuity illumination discontinuity surface normal discontinuity Origin of edges

4 .Characterizing edges An edge is a place of rapid change in the image intensity function image intensity function (along horizontal scanline) first derivative edges correspond to extrema of derivative 4

5 .The gradient of an image: The gradient points in the direction of most rapid change in intensity Image gradient 5

6 .The discrete gradient How can we differentiate a digital image F[ x,y ]? Option 1: reconstruct a continuous image, then take gradient Option 2: take discrete derivative ( “ finite difference ” ) 6

7 .The gradient direction is given by: H ow does this relate to the direction of the edge? The edge strength is given by the gradient magnitude Simple image gradient How would you implement this as a filter? 7 perpendicular or various simplifications 0 -1 1

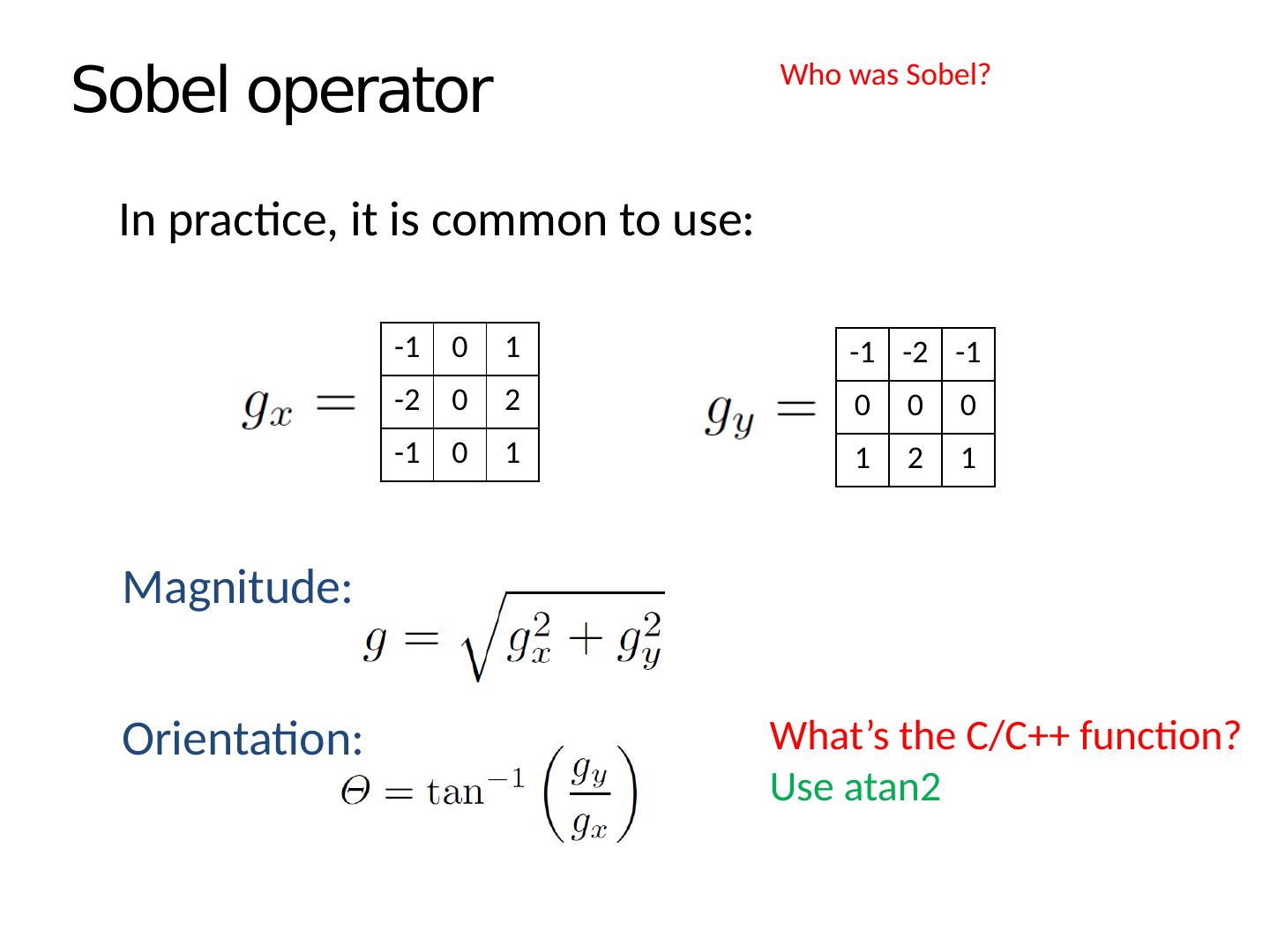
8 .Sobel operator -1 0 1 -2 0 2 -1 0 1 -1 -2 -1 0 0 0 1 2 1 Magnitude: Orientation: In practice, it is common to use: What’s the C/C++ function? Use atan2 Who was Sobel?

9 .Sobel operator Original Orientation Magnitude

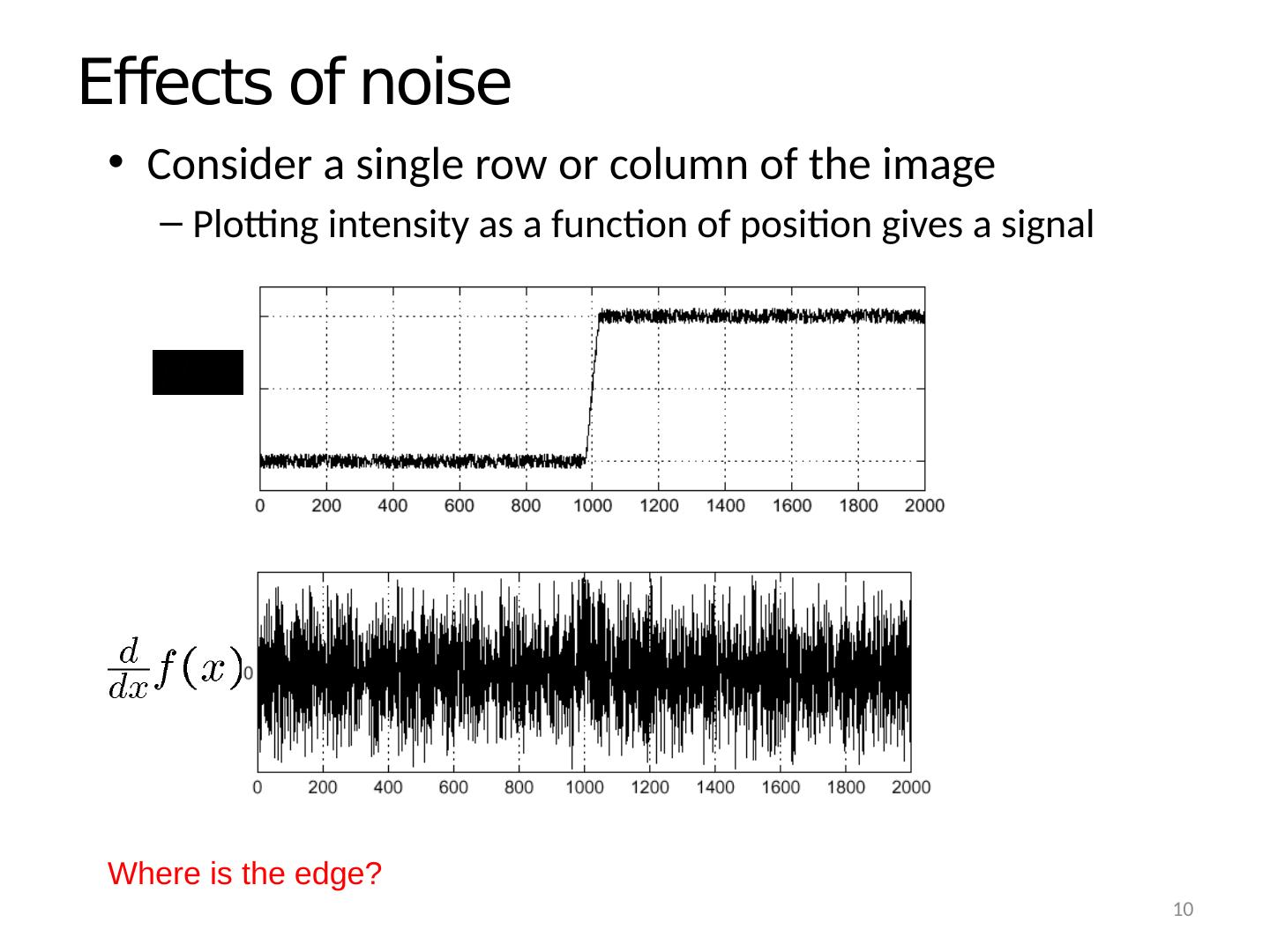
10 .Effects of noise Consider a single row or column of the image Plotting intensity as a function of position gives a signal Where is the edge? 10

11 .Effects of noise Difference filters respond strongly to noise Image noise results in pixels that look very different from their neighbors Generally, the larger the noise the stronger the response What can we do about it? Source: D. Forsyth 11

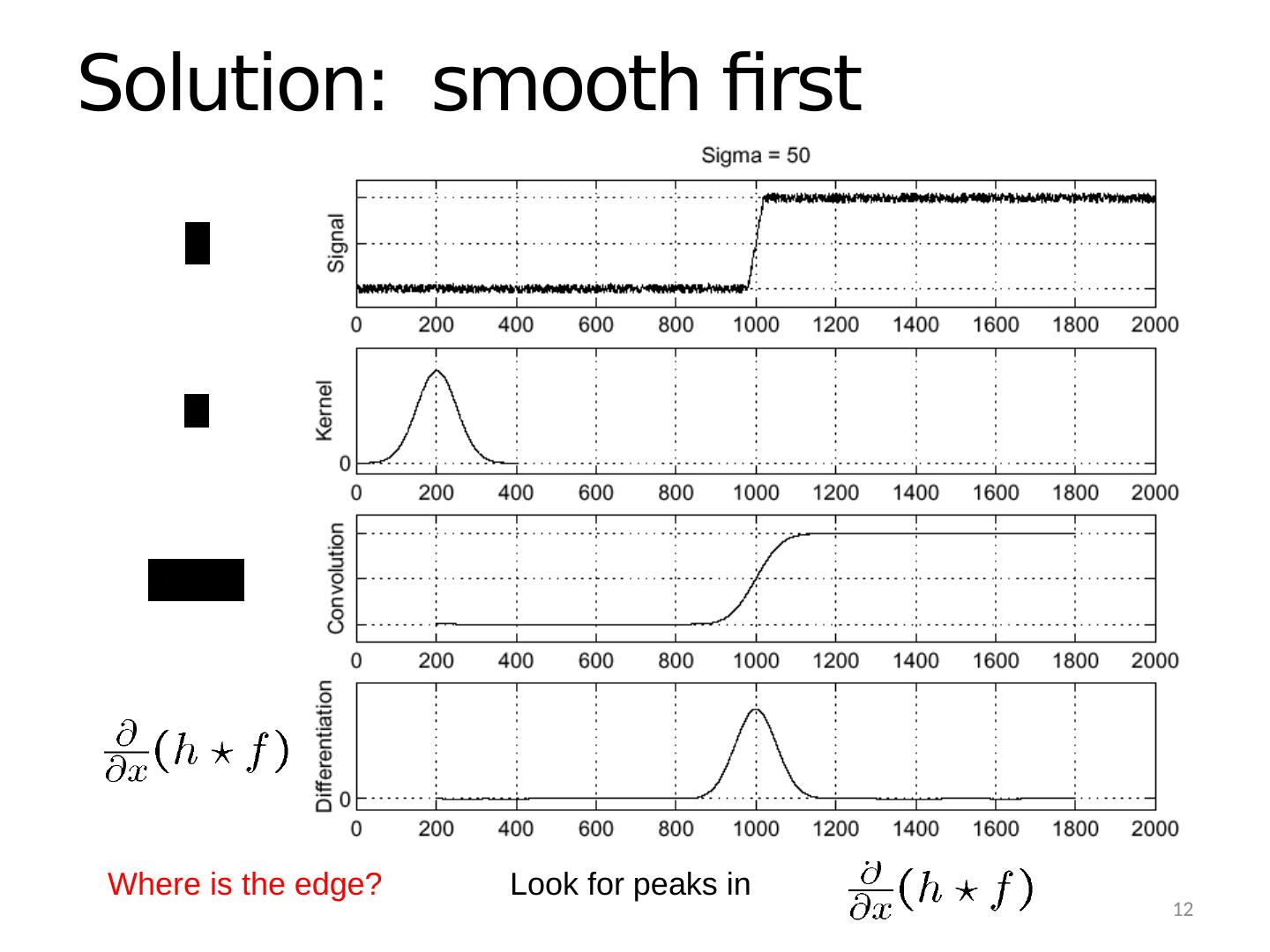
12 .Where is the edge? Solution: smooth first Look for peaks in 12

13 .Differentiation is convolution, and convolution is associative: This saves us one operation: Derivative theorem of convolution f Source: S. Seitz How can we find (local) maxima of a function? 13 We don’t do that.

14 .Remember: Derivative of Gaussian filter x -direction y -direction 14

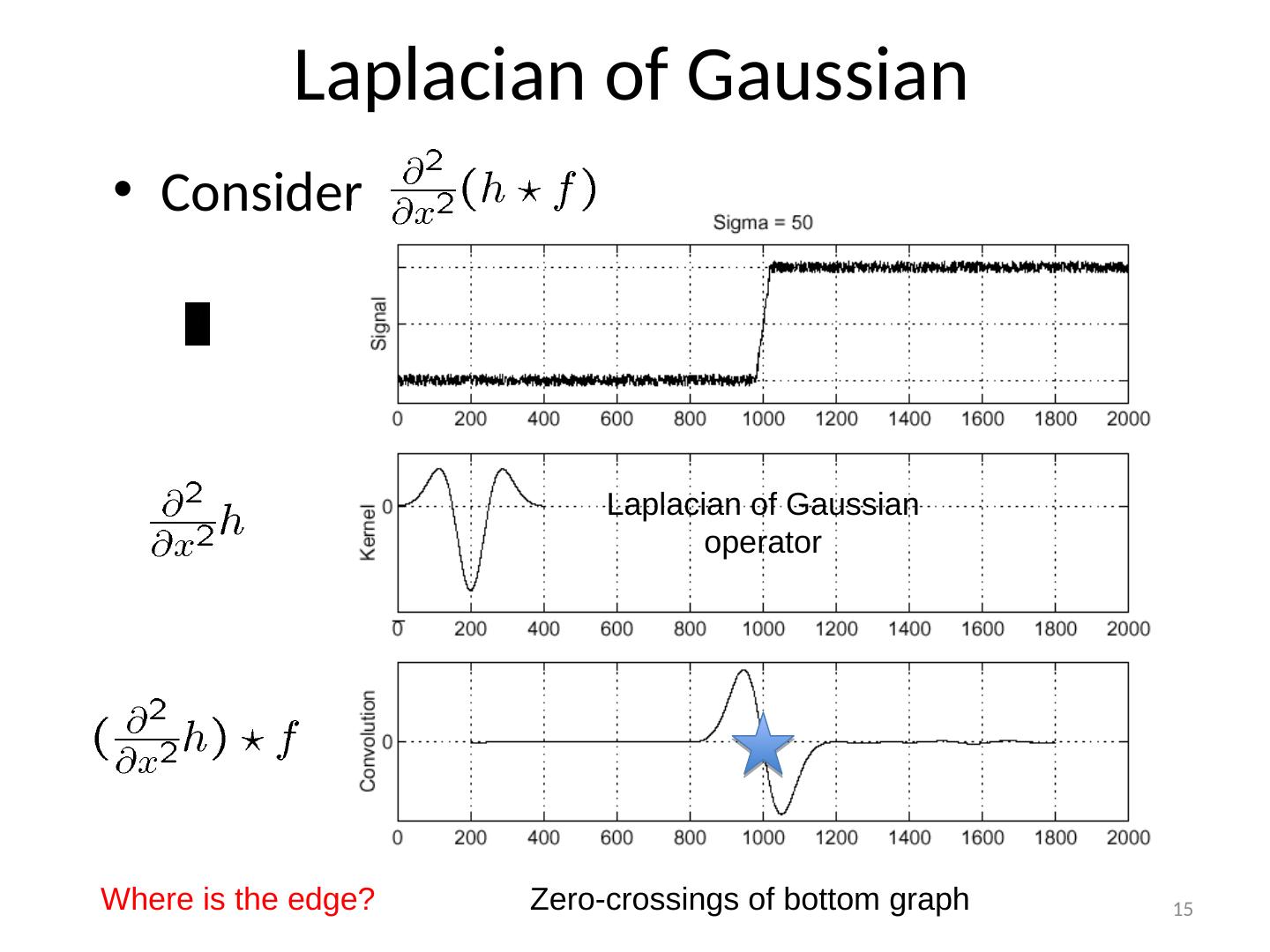
15 .Laplacian of Gaussian Consider Laplacian of Gaussian operator Where is the edge? Zero-crossings of bottom graph 15

16 .2D edge detection filters is the Laplacian operator: Laplacian of Gaussian Gaussian derivative of Gaussian 16

17 .Edge detection by subtraction original 17

18 .Edge detection by subtraction smoothed (5x5 Gaussian) 18

19 .Edge detection by subtraction smoothed – original (scaled by 4, offset +128) 19

20 .Using the LoG Function (Laplacian of Gaussian) The LoG function will be Zero far away from the edge Positive on one side Negative on the other side Zero just at the edge It has simple digital mask implementation(s) So it can be used as an edge operator BUT, THERE’S SOMETHING BETTER 20

21 .Canny edge detector This is probably the most widely used edge detector in computer vision J. Canny, A Computational Approach To Edge Detection , IEEE Trans. Pattern Analysis and Machine Intelligence, 8:679-714, 1986. Source: L. Fei-Fei 21

22 .The Canny edge detector original image (Lena) 22 Note: I hate the Lena images.

23 .The Canny edge detector norm of the gradient 23

24 .The Canny edge detector thresholding 24

25 .Get Orientation at Each Pixel theta = atan2 (- gy , gx ) 25

26 .The Canny edge detector 26

27 .The Canny edge detector thinning (non-maximum suppression) 27

28 .Non-maximum suppression Check if pixel is local maximum along gradient direction Picture from Prem K Kalra 28

29 .Compute Gradients (DoG) X-Derivative of Gaussian Y-Derivative of Gaussian Gradient Magnitude 29