逻辑编程语言

1 .Chapter 16 Logic Programming Languages

2 .Copyright © 2015 Pearson. All rights reserved. 1- 2 Chapter 16 Topics Introduction A Brief Introduction to Predicate Calculus Predicate Calculus and Proving Theorems An Overview of Logic Programming The Origins of Prolog The Basic Elements of Prolog Deficiencies of Prolog Applications of Logic Programming

3 .Copyright © 2015 Pearson. All rights reserved. 1- 3 Introduction Programs in logic languages are expressed in a form of symbolic logic Use a logical inferencing process to produce results Declarative rather that procedural : Only specification of results are stated (not detailed procedures for producing them)

4 .Copyright © 2015 Pearson. All rights reserved. 1- 4 Proposition A logical statement that may or may not be true Consists of objects and relationships of objects to each other

5 .Copyright © 2015 Pearson. All rights reserved. 1- 5 Symbolic Logic Logic which can be used for the basic needs of formal logic: Express propositions Express relationships between propositions Describe how new propositions can be inferred from other propositions Particular form of symbolic logic used for logic programming called predicate calculus

6 .Copyright © 2015 Pearson. All rights reserved. 1- 6 Object Representation Objects in propositions are represented by simple terms: either constants or variables Constant : a symbol that represents an object Variable : a symbol that can represent different objects at different times Different from variables in imperative languages

7 .Copyright © 2015 Pearson. All rights reserved. 1- 7 Compound Terms Atomic propositions consist of compound terms Compound term : one element of a mathematical relation, written like a mathematical function Mathematical function is a mapping Can be written as a table

8 .Copyright © 2015 Pearson. All rights reserved. 1- 8 Parts of a Compound Term Compound term composed of two parts Functor: function symbol that names the relationship Ordered list of parameters (tuple) Examples: student(jon) like(seth, OSX) like(nick, windows) like(jim, linux)

9 .Copyright © 2015 Pearson. All rights reserved. 1- 9 Forms of a Proposition Propositions can be stated in two forms: Fact : proposition is assumed to be true Query : truth of proposition is to be determined Compound proposition: Have two or more atomic propositions Propositions are connected by operators

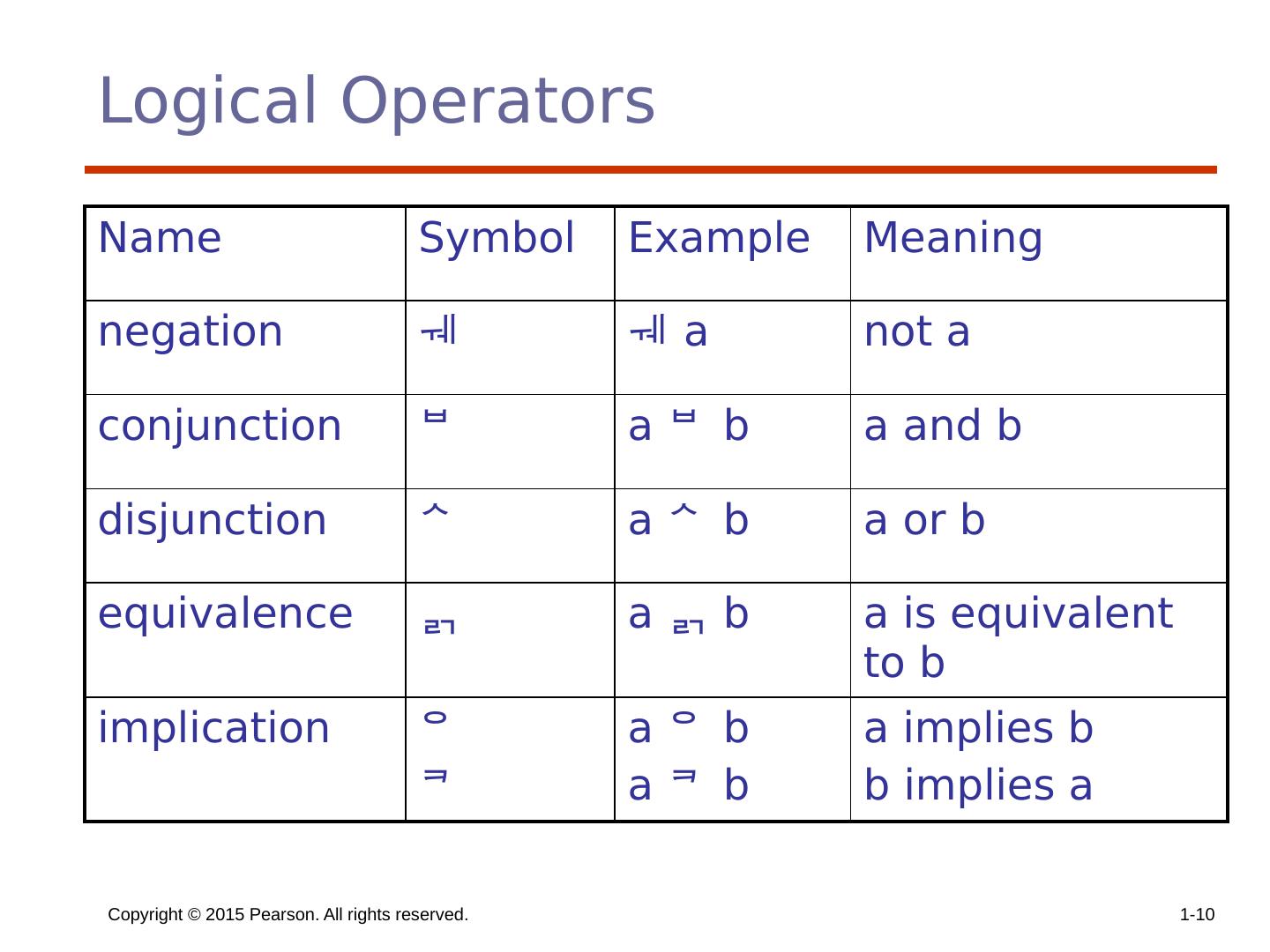
10 .Copyright © 2015 Pearson. All rights reserved. 1- 10 Logical Operators Name Symbol Example Meaning negation   a not a conjunction  a  b a and b disjunction  a  b a or b equivalence  a  b a is equivalent to b implication   a  b a  b a implies b b implies a

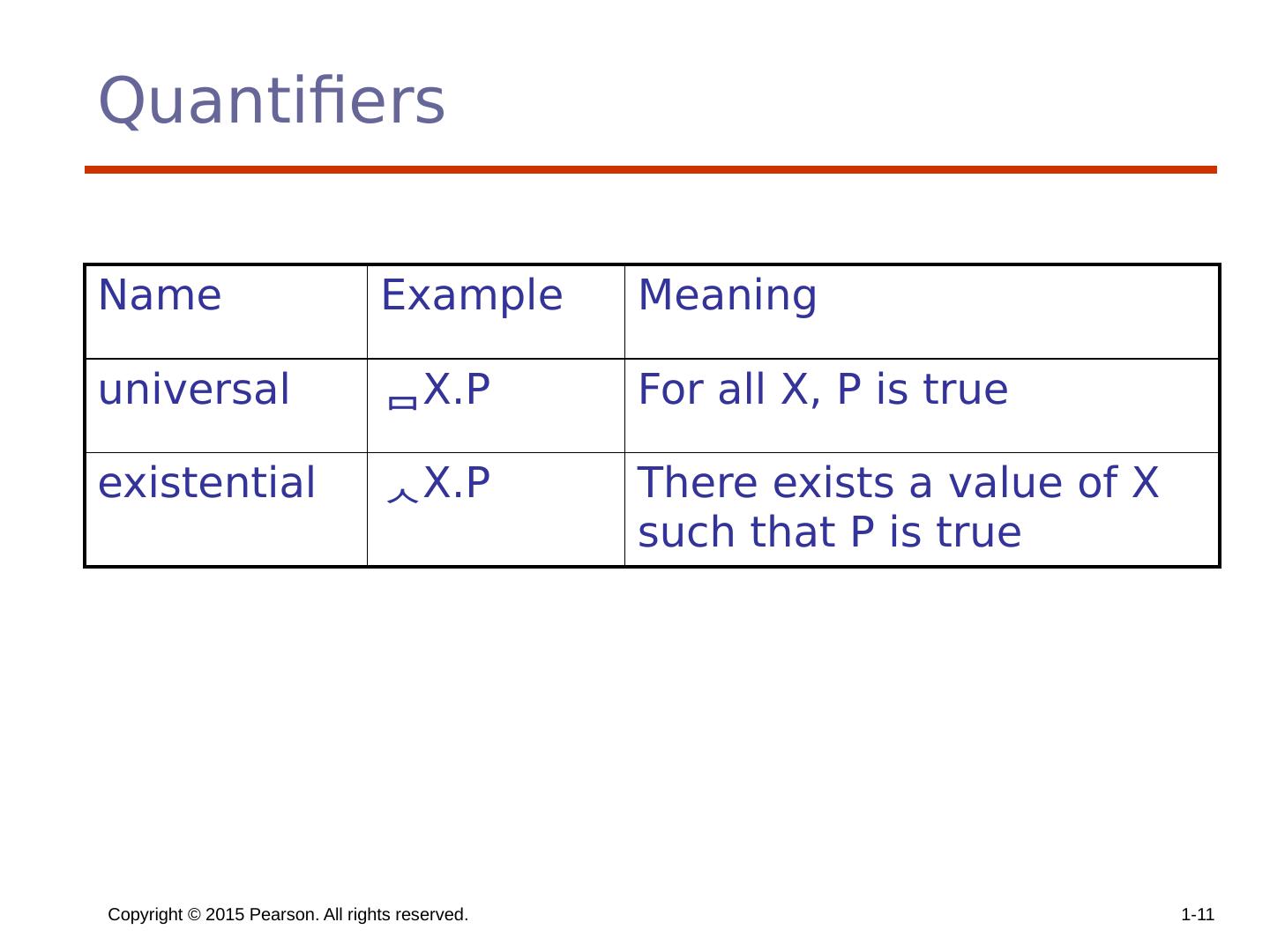
11 .Copyright © 2015 Pearson. All rights reserved. 1- 11 Quantifiers Name Example Meaning universal  X.P For all X, P is true existential  X.P There exists a value of X such that P is true

12 .Copyright © 2015 Pearson. All rights reserved. 1- 12 Clausal Form Too many ways to state the same thing Use a standard form for propositions Clausal form : B 1  B 2  …  B n  A 1  A 2  …  A m means if all the As are true, then at least one B is true Antecedent : right side Consequent : left side

13 .Copyright © 2015 Pearson. All rights reserved. 1- 13 Predicate Calculus and Proving Theorems A use of propositions is to discover new theorems that can be inferred from known axioms and theorems Resolution : an inference principle that allows inferred propositions to be computed from given propositions

14 .Copyright © 2015 Pearson. All rights reserved. 1- 14 Resolution Unification : finding values for variables in propositions that allows matching process to succeed Instantiation : assigning temporary values to variables to allow unification to succeed After instantiating a variable with a value, if matching fails, may need to backtrack and instantiate with a different value

15 .Copyright © 2015 Pearson. All rights reserved. 1- 15 Proof by Contradiction Hypotheses : a set of pertinent propositions Goal : negation of theorem stated as a proposition Theorem is proved by finding an inconsistency

16 .Copyright © 2015 Pearson. All rights reserved. 1- 16 Theorem Proving Basis for logic programming When propositions used for resolution, only restricted form can be used Horn clause - can have only two forms Headed : single atomic proposition on left side Headless : empty left side (used to state facts) Most propositions can be stated as Horn clauses

17 .Copyright © 2015 Pearson. All rights reserved. 1- 17 Overview of Logic Programming Declarative semantics There is a simple way to determine the meaning of each statement Simpler than the semantics of imperative languages Programming is nonprocedural Programs do not state now a result is to be computed, but rather the form of the result

18 .Copyright © 2015 Pearson. All rights reserved. 1- 18 Example: Sorting a List Describe the characteristics of a sorted list, not the process of rearranging a list sort(old_list, new_list)  permute (old_list, new_list)  sorted (new_list) sorted (list)   j such that 1  j < n, list(j)  list (j+1)

19 .Copyright © 2015 Pearson. All rights reserved. 1- 19 The Origins of Prolog University of Aix-Marseille (Calmerauer & Roussel) Natural language processing University of Edinburgh (Kowalski) Automated theorem proving

20 .Copyright © 2015 Pearson. All rights reserved. 1- 20 Terms This book uses the Edinburgh syntax of Prolog Term : a constant, variable, or structure Constant : an atom or an integer Atom : symbolic value of Prolog Atom consists of either: a string of letters, digits, and underscores beginning with a lowercase letter a string of printable ASCII characters delimited by apostrophes

21 .Copyright © 2015 Pearson. All rights reserved. 1- 21 Terms: Variables and Structures Variable : any string of letters, digits, and underscores beginning with an uppercase letter Instantiation : binding of a variable to a value Lasts only as long as it takes to satisfy one complete goal Structure : represents atomic proposition functor ( parameter list )

22 .Copyright © 2015 Pearson. All rights reserved. 1- 22 Fact Statements Used for the hypotheses Headless Horn clauses female(shelley). male(bill). father(bill, jake).

23 .Copyright © 2015 Pearson. All rights reserved. 1- 23 Rule Statements Used for the hypotheses Headed Horn clause Right side: antecedent ( if part) May be single term or conjunction Left side: consequent ( then part) Must be single term Conjunction : multiple terms separated by logical AND operations (implied)

24 .Copyright © 2015 Pearson. All rights reserved. 1- 24 Example Rules ancestor(mary,shelley):- mother(mary,shelley). Can use variables ( universal objects ) to generalize meaning: parent(X,Y):- mother(X,Y). parent(X,Y):- father(X,Y). grandparent(X,Z):- parent(X,Y), parent(Y,Z).

25 .Copyright © 2015 Pearson. All rights reserved. 1- 25 Goal Statements For theorem proving, theorem is in form of proposition that we want system to prove or disprove – goal statement Same format as headless Horn man(fred) Conjunctive propositions and propositions with variables also legal goals father(X, mike)

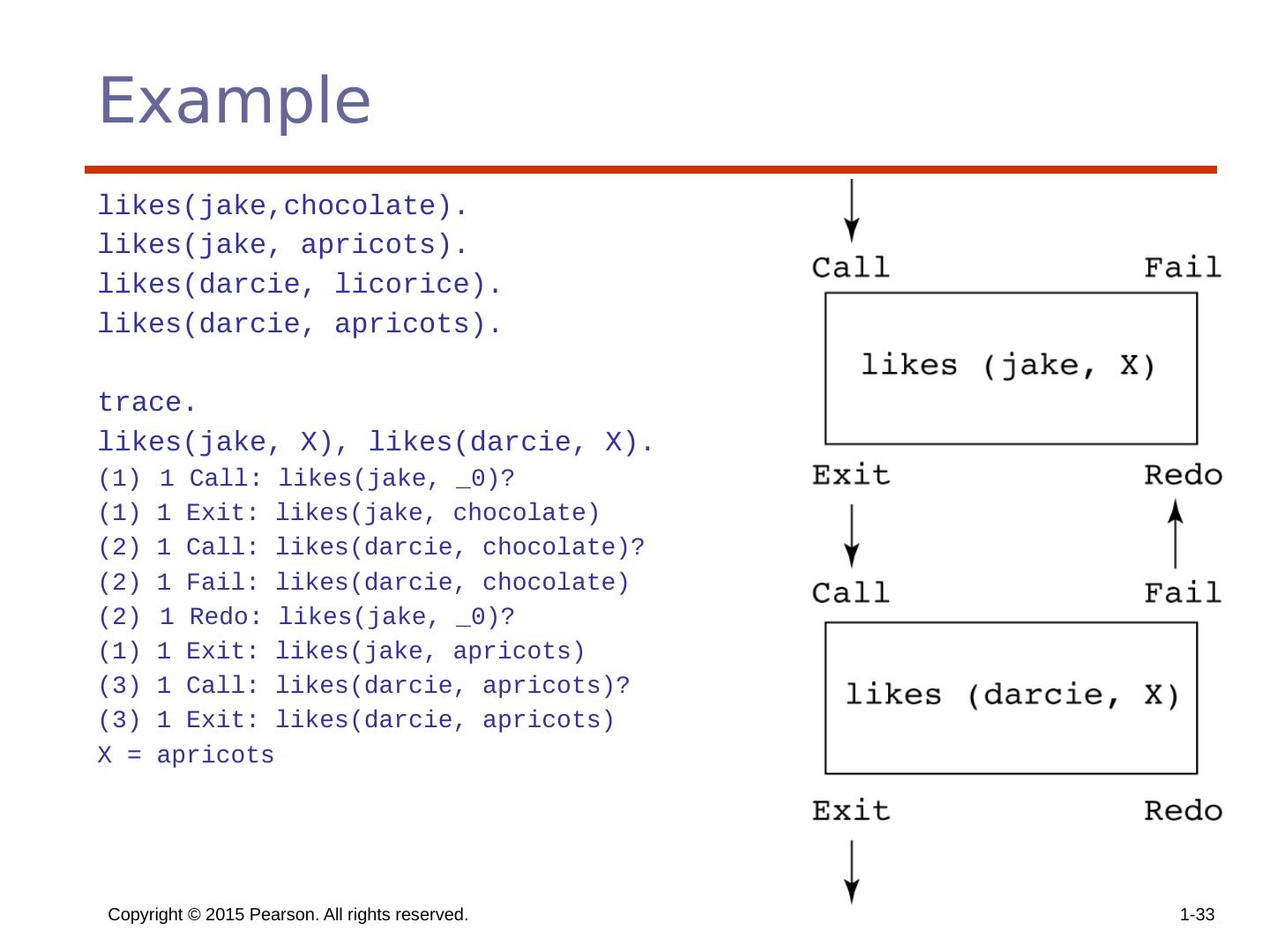
26 .Copyright © 2015 Pearson. All rights reserved. 1- 26 Inferencing Process of Prolog Queries are called goals If a goal is a compound proposition, each of the facts is a subgoal To prove a goal is true, must find a chain of inference rules and/or facts. For goal Q: P 2 :- P 1 P 3 :- P 2 … Q :- P n Process of proving a subgoal called matching, satisfying, or resolution

27 .Copyright © 2015 Pearson. All rights reserved. 1- 27 Approaches Matching is the process of proving a proposition Proving a subgoal is called satisfying the subgoal Bottom-up resolution, forward chaining Begin with facts and rules of database and attempt to find sequence that leads to goal Works well with a large set of possibly correct answers Top-down resolution, backward chaining Begin with goal and attempt to find sequence that leads to set of facts in database Works well with a small set of possibly correct answers Prolog implementations use backward chaining

28 .Copyright © 2015 Pearson. All rights reserved. 1- 28 Subgoal Strategies When goal has more than one subgoal, can use either Depth-first search: find a complete proof for the first subgoal before working on others Breadth-first search: work on all subgoals in parallel Prolog uses depth-first search Can be done with fewer computer resources

29 .Copyright © 2015 Pearson. All rights reserved. 1- 29 Backtracking With a goal with multiple subgoals, if fail to show truth of one of subgoals, reconsider previous subgoal to find an alternative solution: backtracking Begin search where previous search left off Can take lots of time and space because may find all possible proofs to every subgoal