- 快召唤伙伴们来围观吧
- 微博 QQ QQ空间 贴吧
- 文档嵌入链接
- 复制
- 微信扫一扫分享
- 已成功复制到剪贴板
viewing
展开查看详情
1 .Spaces Perspective Viewing CMSC 435/634
2 .Spaces Perspective Coordinate System / Space • Origin + Axes • Reference frame • Convert by matrix • ptable = TableFromPencil ppencil • proom = RoomFromTable TableFromPencil ppencil • proom = RoomFromPencil ppencil
3 .Spaces Perspective Spaces • Object / Model • Logical coordinates for modeling • May have several more levels • World • Common coordinates for everything • View / Camera / Eye • eye/camera at (0,0,0), looking down Z (or -Z) axis • planes: left, right, top, bottom, near/hither, far/yon • Normalized Device Coordinates (NDC) / Clip • Visible portion of scene from (-1,-1,-1) to (1,1,1) • Sometimes one or more components 0 to 1 instead of -1 to 1 • Raster / Pixel / Viewport • 0,0 to x-resolution, y-resolution • Device / Screen • May translate to fit actual screen
4 .Spaces Perspective Nesting Room Desk Desk Podium Board Student Book Notebook Student Notebook Laptop Eraser
5 .Spaces Perspective Matrix Stack • Remember transformation, return to it later • Push a copy, modify the copy, pop • Keep matrix and update matrix and inverse • Push and pop both matrix and inverse together t r a n s f o r m ( WorldFromRoom ) ; push ; t r a n s f o r m ( RoomFromDesk ) ; push ; t r a n s f o r m ( DeskFromStudent ) ; pop ; push ; t r a n s f o r m ( DeskFromBook ) ; ...
6 .Spaces Perspective Model→World / Model→View • Model→World • All shading and rendering in World space • Transform all objects and lights • Ray tracing implicitly does World→Raster • Model→View • Serves just as well for single view
7 .Spaces Perspective World→View • Also called Viewing or Camera transform • LookAt −−→ →− → • from, to , − up −−→ • u v w from • Roll / Pitch / Yaw • Translate to camera center, rotate around camera • Rz Rx Ry T • Can have gimbal lock • Orbit • Rotate around object center, translate out • T Rz R x R y • Also can have gimbal lock
8 .Spaces Perspective View→NDC • Also called Projection transform • Orthographic / Parallel • Translate 2 & Scale to viewvolume r −l 0 0 − rr −l +l 2 t+b 0 t−b 0 − t−b • 2 0 0 n−f − n+f n−f 0 0 0 1 • Perspective • More complicated...
9 .Spaces Perspective NDC→Raster • Also called Viewport transform • [−1, 1], [−1, 1], [−1, 1] → [− 21 , nx − 12 ], [− 12 , ny − 12 ], [− 21 , nz − 12 ]
10 .Spaces Perspective NDC→Raster • Also called Viewport transform • [−1, 1], [−1, 1], [−1, 1] → [− 21 , nx − 12 ], [− 12 , ny − 12 ], [− 21 , nz − 12 ] • Translate to [0, 2], [0, 2], [0, 2]
11 .Spaces Perspective NDC→Raster • Also called Viewport transform • [−1, 1], [−1, 1], [−1, 1] → [− 21 , nx − 12 ], [− 12 , ny − 12 ], [− 21 , nz − 12 ] • Translate to [0, 2], [0, 2], [0, 2] • Scale to [0, nx ], [0, ny ], [0, nz ]
12 .Spaces Perspective NDC→Raster • Also called Viewport transform • [−1, 1], [−1, 1], [−1, 1] → [− 21 , nx − 12 ], [− 12 , ny − 12 ], [− 21 , nz − 12 ] • Translate to [0, 2], [0, 2], [0, 2] • Scale to [0, nx ], [0, ny ], [0, nz ] • Translate to [− 12 , nx − 12 ], [− 12 , ny − 12 ], [− 12 , nz − 21 ]
13 .Spaces Perspective NDC→Raster • Also called Viewport transform • [−1, 1], [−1, 1], [−1, 1] → [− 21 , nx − 12 ], [− 12 , ny − 12 ], [− 21 , nz − 12 ] • Translate to [0, 2], [0, 2], [0, 2] • Scale to [0, nx ], [0, ny ], [0, nz ] • Translate to [− 12 , nx − 12 ], [− 12 , ny − 12 ], [− 12 , nz − 21 ] nx nx −1 2 0 0 2 0 ny ny −1 2 0 2 0 nz nz −1 0 2 2 0 0 0 1
14 .Spaces Perspective Raster→Screen • Usually just a translation • More complicated for tiled displays, domes, etc. • Usually handled by windowing system
15 .Spaces Perspective Perspective View Frustum • Orthographic view volume is a rectangular volume far / yon top left right near / hither bottom
16 .Spaces Perspective Perspective View Frustum • Orthographic view volume is a rectangular volume • Perspective is a truncated pyramid or frustum far / yon top right left near / hither eye bottom
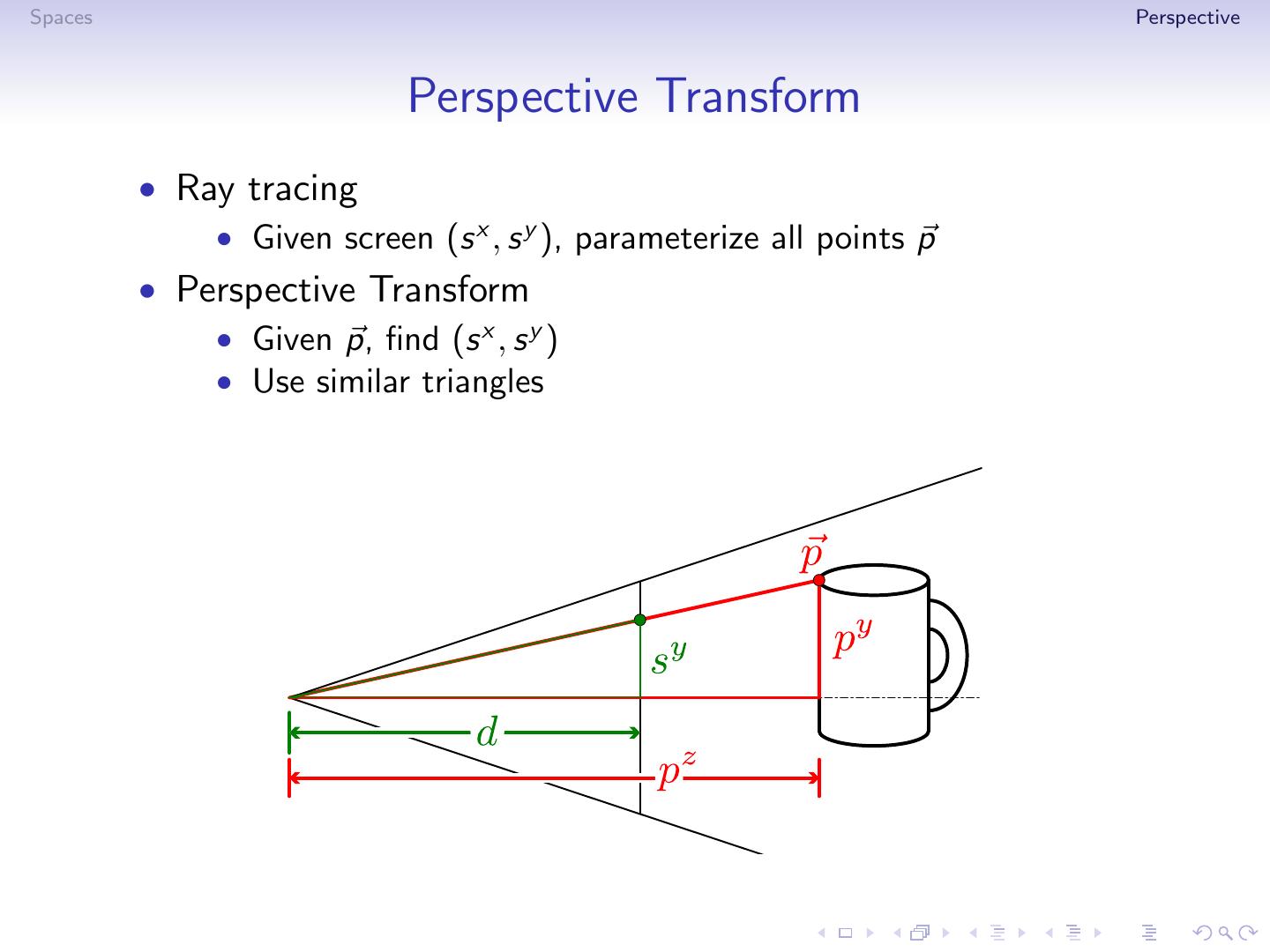
17 .Spaces Perspective Perspective Transform • Ray tracing • Given screen (s x , s y ), parameterize all points p
18 .Spaces Perspective Perspective Transform • Ray tracing • Given screen (s x , s y ), parameterize all points p • Perspective Transform • Given p, find (s x , s y )
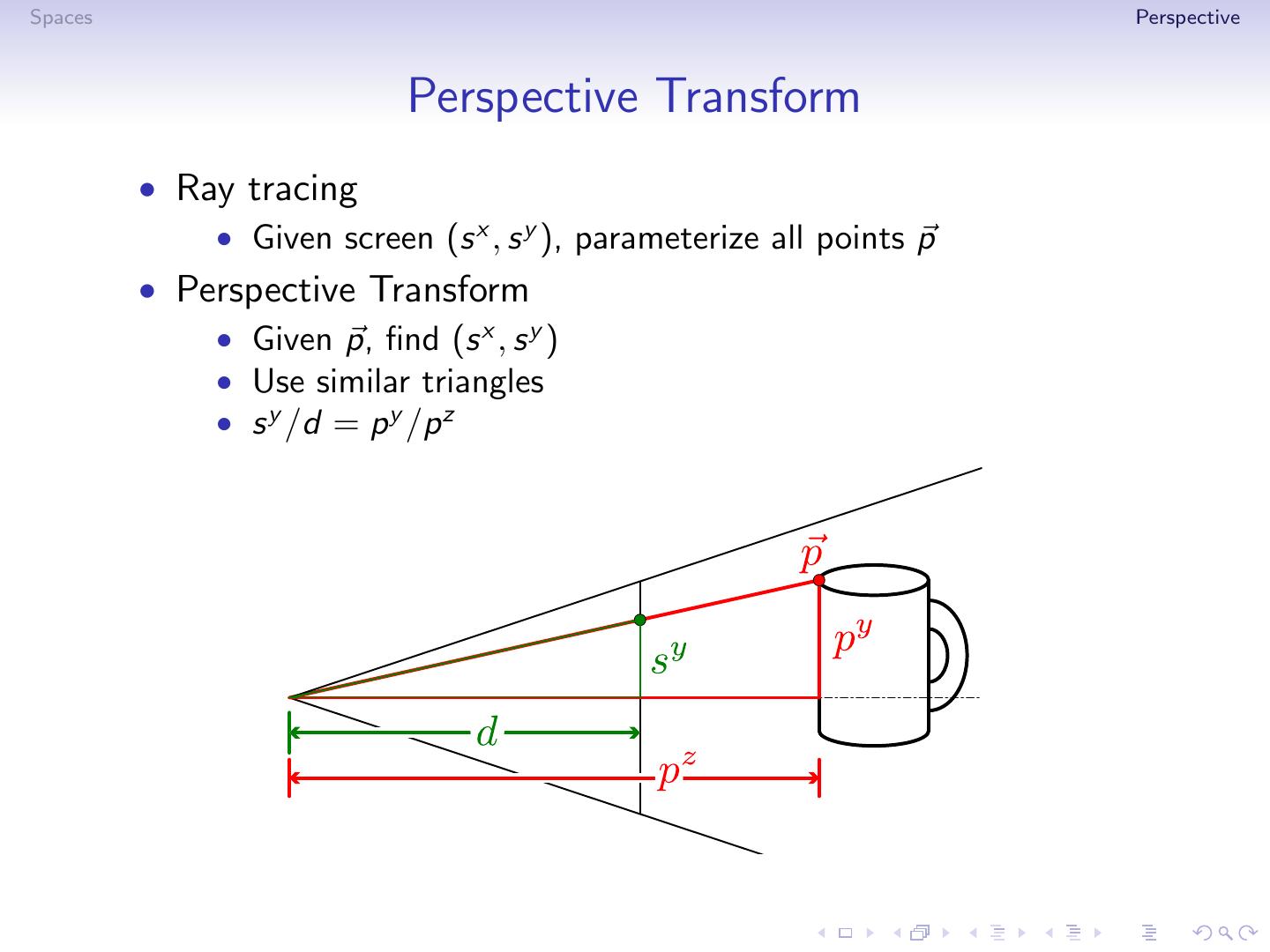
19 .Spaces Perspective Perspective Transform • Ray tracing • Given screen (s x , s y ), parameterize all points p • Perspective Transform • Given p, find (s x , s y ) • Use similar triangles
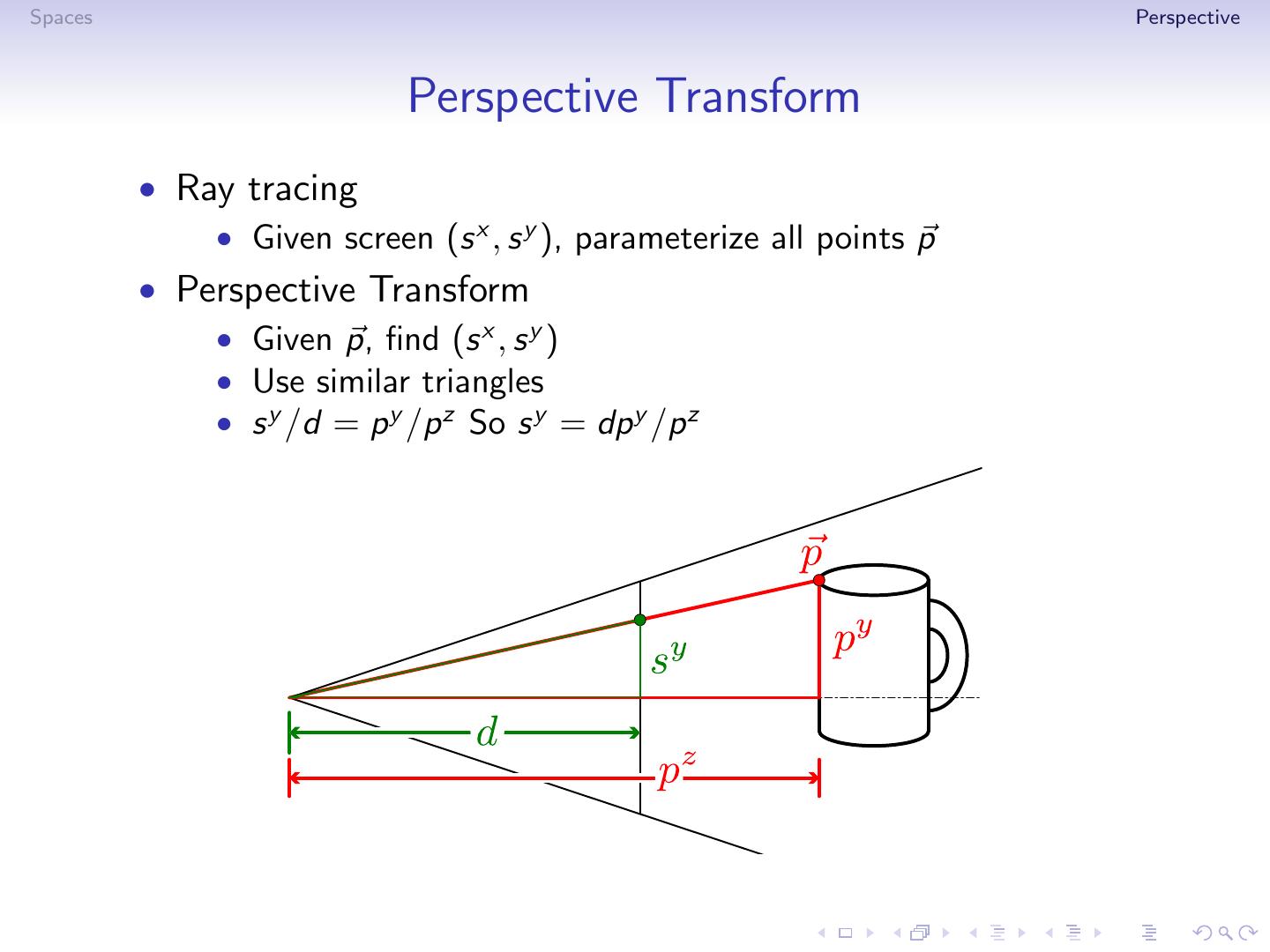
20 .Spaces Perspective Perspective Transform • Ray tracing • Given screen (s x , s y ), parameterize all points p • Perspective Transform • Given p, find (s x , s y ) • Use similar triangles • s y /d = p y /p z
21 .Spaces Perspective Perspective Transform • Ray tracing • Given screen (s x , s y ), parameterize all points p • Perspective Transform • Given p, find (s x , s y ) • Use similar triangles • s y /d = p y /p z So s y = dp y /p z
22 .Spaces Perspective Homogeneous Equations • Same total degree for every term
23 .Spaces Perspective Homogeneous Equations • Same total degree for every term • Introduce a new redundant variable
24 .Spaces Perspective Homogeneous Equations • Same total degree for every term • Introduce a new redundant variable • aX +bY +c = 0
25 .Spaces Perspective Homogeneous Equations • Same total degree for every term • Introduce a new redundant variable • aX +bY +c = 0 • X = x/w , Y = y /w
26 .Spaces Perspective Homogeneous Equations • Same total degree for every term • Introduce a new redundant variable • aX +bY +c = 0 • X = x/w , Y = y /w • a x/w + b y /w + c = 0
27 .Spaces Perspective Homogeneous Equations • Same total degree for every term • Introduce a new redundant variable • aX +bY +c = 0 • X = x/w , Y = y /w • a x/w + b y /w + c = 0 • → ax +by +c w = 0
28 .Spaces Perspective Homogeneous Equations • Same total degree for every term • Introduce a new redundant variable • aX +bY +c = 0 • X = x/w , Y = y /w • a x/w + b y /w + c = 0 • → ax +by +c w = 0 • a X2 + b X Y + c Y2 + d X + e Y + f = 0
29 .Spaces Perspective Homogeneous Equations • Same total degree for every term • Introduce a new redundant variable • aX +bY +c = 0 • X = x/w , Y = y /w • a x/w + b y /w + c = 0 • → ax +by +c w = 0 • a X2 + b X Y + c Y2 + d X + e Y + f = 0 • X = x/w , Y = y /w