优先级队列与堆

1 .CSE 373 : Data Structures & Algorithms Pseudocode ; ADTs; P riority Queues; Heaps Riley Porter Winter 2017 Winter 2017 CSE373: Data Structures & Algorithms 1

2 .Course Logistics Winter 2017 CSE373: Data Structures and Algorithms 2 HW 1 released Monday. Due a week from Tuesday. Java Review Session early next week, room and time TBA and posted on the course website Slides posted and updated from last time with links correctly working in PDF version

3 .Pseudocode Winter 2017 CSE373: Data Structures and Algorithms 3 Describe an algorithm in the steps necessary, write the shape of the code but ignore specific syntax. Algorithm: Count all elements in a list greater than x Pseudocode : int counter // keeps track of number > x while list has more elements { increment counter if current element is > than x move to next element of list }

4 .More Pseudocode Winter 2017 CSE373: Data Structures and Algorithms 4 Algorithm: Given a list of names in the format " firstName lastName ", make a Map of all first names as keys with sets of last names as their values Pseudocode : create the empty result map while list has more names to process { firstName is name split up until space lastName is name split from space to the end if firstName not in the map yet { put firstName in map as a key with an empty set as the value } add lastName to the set for the first name move to the next name in the list }

5 .Pseudocode Practice Winter 2017 CSE373: Data Structures and Algorithms 5 Come up with pseudocode for the following algorithm: Algorithm : Given a list of integers, find th e index of the maximum integer in the list.

6 .Pseudocode Practice Solution Winter 2017 CSE373: Data Structures and Algorithms 6 Algorithm : Given a list of integers, find the index of the maximum integer in the list . if list is not empty: int maxIndex starts at 0 for first index for each index i in the list: if the element at index i is greater than the element at index maxIndex : reset maxIndex to i return maxIndex else: error case: return -1? throw exception?

7 .Terminology Review Abstract Data Type (ADT) Mathematical description of a "thing" with set of operations Algorithm A high level, language-independent description of a step-by-step process Data structure A specific organization of data and family of algorithms for implementing an ADT Implementation of a data structure A specific implementation in a specific language Winter 2017 CSE373: Data Structures and Algorithms 7

8 .Another ADT : Priority Queue A priority queue holds comparable data Given x and y , is x less than, equal to, or greater than y Meaning of the ordering can depend on your data Many data structures require this: dictionaries, sorting Typically elements are comparable types, or have two fields : the priority and the data Winter 2017 8 CSE373: Data Structures & Algorithms

9 .Priority Queue vs Queue Queue : follows First-In-First-Out ordering Example : serving customers at a pharmacy, based on who got there first. Priority Queue : compares priority of elements to determine ordering Example : e mergency room, serves patients with priority based on severity of wounds Winter 2017 9 CSE373: Data Structures & Algorithms

10 .Priorities Each item has a "priority" The lesser item is the one with the greater priority So "priority 1" is more important than "priority 4" Can resolve ties arbitrarily Operations: insert deleteMin is_empty deleteMin returns and deletes the item with greatest priority (lowest priority value) insert is like enqueue , deleteMin is like dequeue But the whole point is to use priorities instead of FIFO Winter 2017 10 CSE373: Data Structures & Algorithms insert deleteMin 6 2 15 23 12 18 45 3 7

11 .Priority Queue Example Given the following, what values are a , b , c and d ? insert element1 with priority 5 insert element2 with priority 3 insert element3 with priority 4 a = deleteMin // a = ? b = deleteMin // b = ? insert element4 with priority 2 insert element5 with priority 6 c = deleteMin // c = ? d = deleteMin // d = ? Winter 2017 11 CSE373: Data Structures & Algorithms

12 .Priority Queue Example Solutions insert element1 with priority 5 insert element2 with priority 3 insert element3 with priority 4 a = deleteMin // a = element2 b = deleteMin // b = element3 insert element4 with priority 2 insert element5 with priority 6 c = deleteMin // c = element4 d = deleteMin / / d = element1 Winter 2017 12 CSE373: Data Structures & Algorithms

13 .Some Applications Run multiple programs in the operating system "critical" before "interactive" before "compute - intensive", or let users set priority level Select print jobs in order of decreasing length "Greedy" algorithms (we’ll revisit this idea) Forward network packets in order of urgency Select most frequent symbols for data compression (Huffman CSE 143) Sorting (first insert all, then repeatedly deleteMin ) Winter 2017 13 CSE373: Data Structures & Algorithms

14 .Possible Implementations Unsorted Array insert by inserting at the end deleteMin by linear search Sorted Circular Array insert by binary search, shift elements over deleteMin by moving “front ” Winter 2017 14 CSE373: Data Structures & Algorithms

15 .More Possible Implementations Unsorted Linked List insert by inserting at the front deleteMin by linear search Sorted Linked List insert by linear search deleteMin remove at front Binary Search Tree insert by search traversal deleteMin by find min traversal Winter 2017 15 CSE373: Data Structures & Algorithms

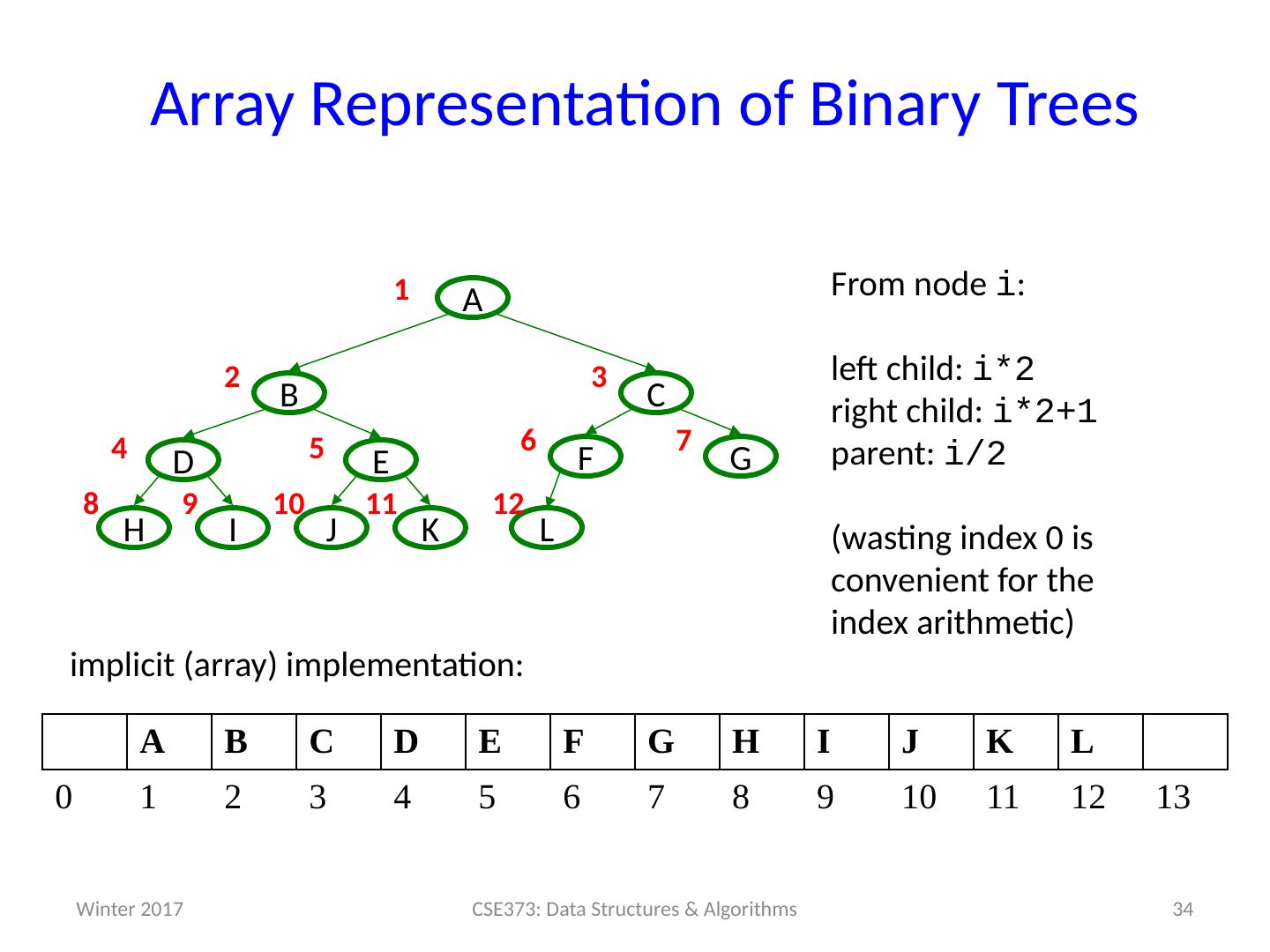
16 .One Implementation: Heap Heaps are implemented with Trees A binary min-heap (or just binary heap or heap ) is a data stru cture with the properties : Structure property: A complet e binary tree Heap property: The priority of every (non-root) node is greater than the priority of its parent Not a binary search tree Winter 2017 16 CSE373: Data Structures & Algorithms

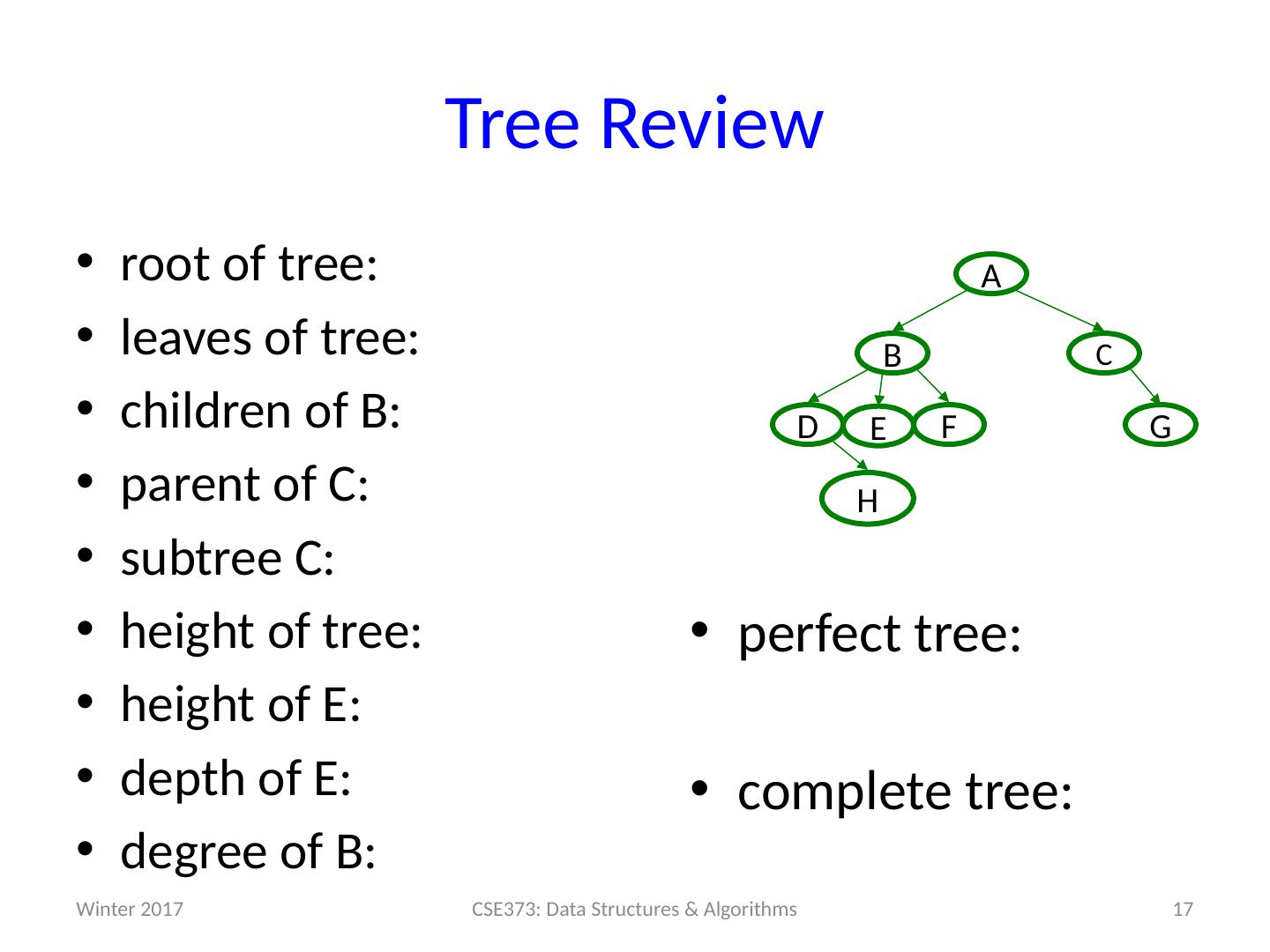
17 .Tree Review root of tree: leaves of tree: children of B: parent of C: subtree C: height of tree: height of E: depth of E: degree of B: Winter 2017 17 CSE373: Data Structures & Algorithms G F D C B A H E perfect tree: complete tree:

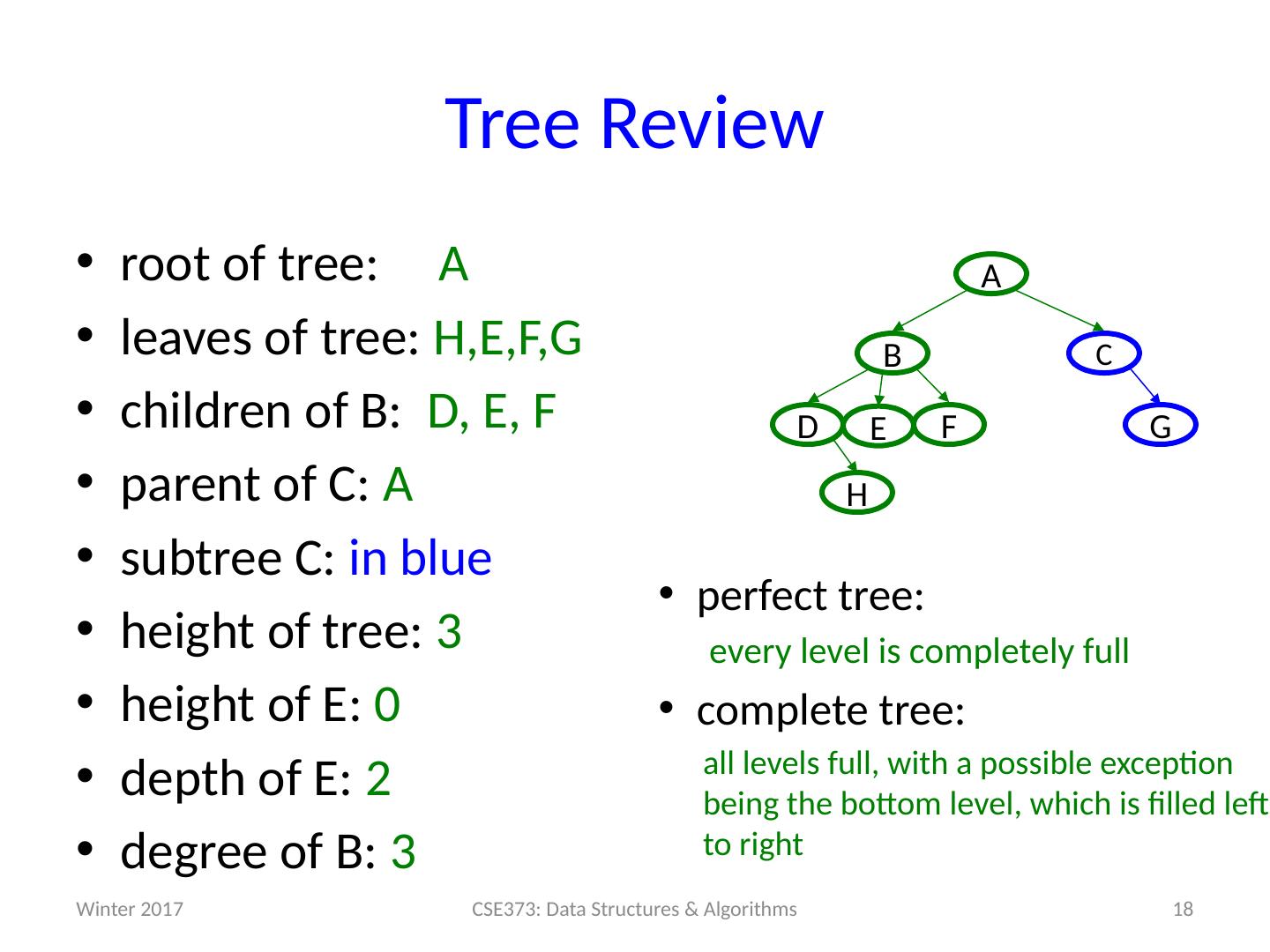
18 .Tree Review root of tree: A leaves of tree: H,E,F,G children of B: D, E, F parent of C: A subtree C: in blue height of tree: 3 height of E: 0 depth of E: 2 degree of B: 3 Winter 2017 18 CSE373: Data Structures & Algorithms G F D C B A H E perfect tree: every level is completely full complete tree: all levels full, with a possible exception being the bottom level, which is filled left to right

19 .Structure Property: Completeness A Binary Heap is a complete binary tree: A binary tree with all levels full, with a possible exception being the bottom level, which is filled left to right Examples: Winter 2017 19 CSE373: Data Structures & Algorithms 99 60 40 80 20 10 50 700 85 30 80 10 40 2 0 400 are these trees complete ?

20 .Structure Property: Completeness A Binary Heap is a complete binary tree: A binary tree with all levels full, with a possible exception being the bottom level, which is filled left to right Examples: Winter 2017 20 CSE373: Data Structures & Algorithms 99 60 40 80 20 10 50 700 85 30 80 10 i ncomplete 40 2 0 400 complete

21 .Structure Property: Completeness A Binary Heap is a complete binary tree: A binary tree with all levels full, with a possible exception being the bottom level, which is filled left to right Examples: Winter 2017 20 CSE373: Data Structures & Algorithms 99 60 40 80 20 10 50 700 85 30 80 10 i ncomplete 40 2 0 400 complete

22 .Structure Property: Completeness A Binary Heap is a complete binary tree: A binary tree with all levels full, with a possible exception being the bottom level, which is filled left to right Examples: Winter 2017 20 CSE373: Data Structures & Algorithms 99 60 40 80 20 10 50 700 85 30 80 10 i ncomplete 40 2 0 400 complete

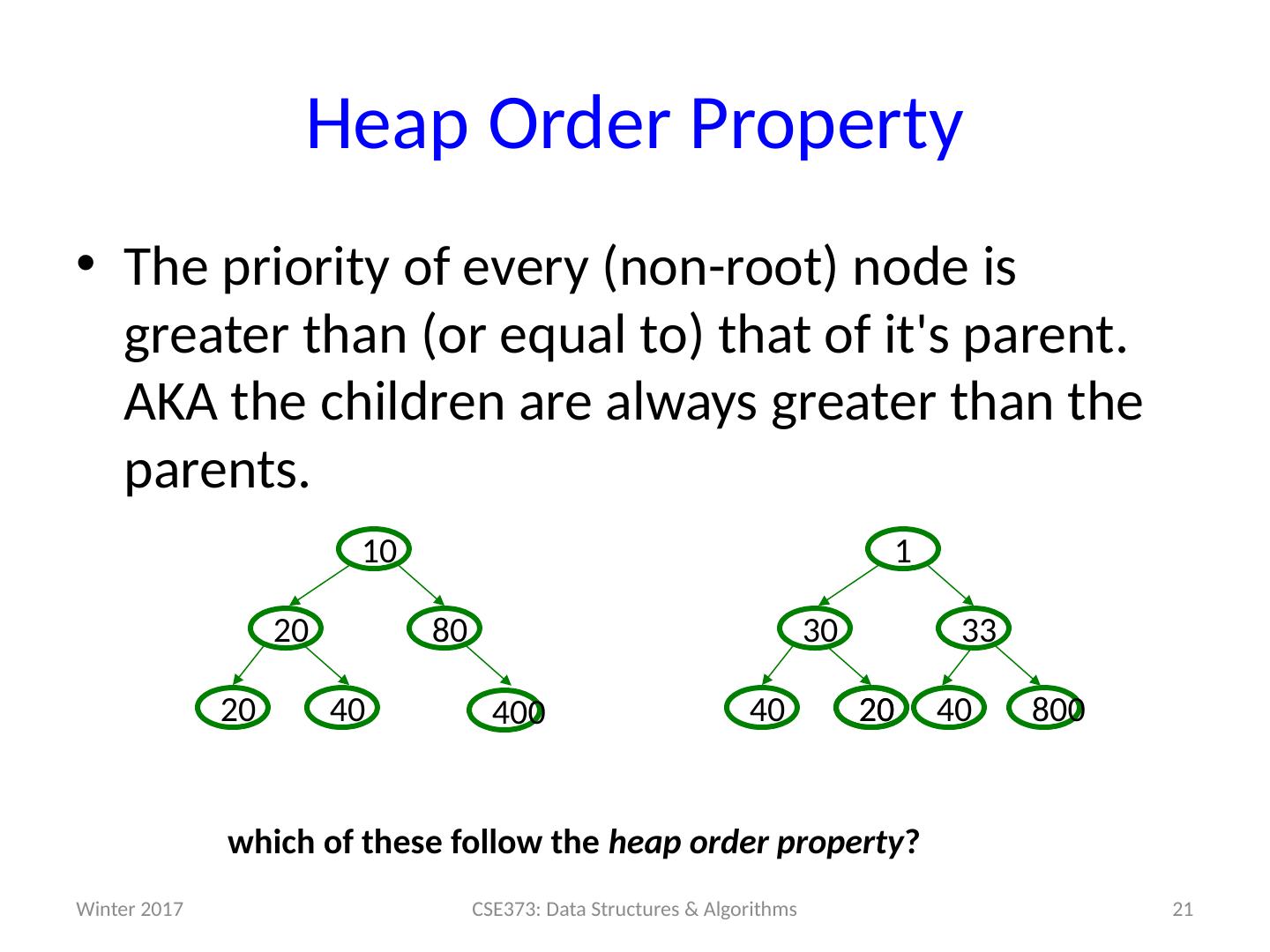
23 .Heaps A binary min-heap (or just binary heap or just heap ) is: Structure property: A complet e binary tree Heap property: The priority of every (non-root) node is greater than (or equal to) the priority of its parent. AKA the children are always greater than the parents . Not a binary search tree Winter 2017 23 CSE373: Data Structures & Algorithms 30 80 10 99 60 40 80 20 10 50 700 85 450 3 1 75 50 8 6 0 10 2 0 15 w hich of these are heaps ?

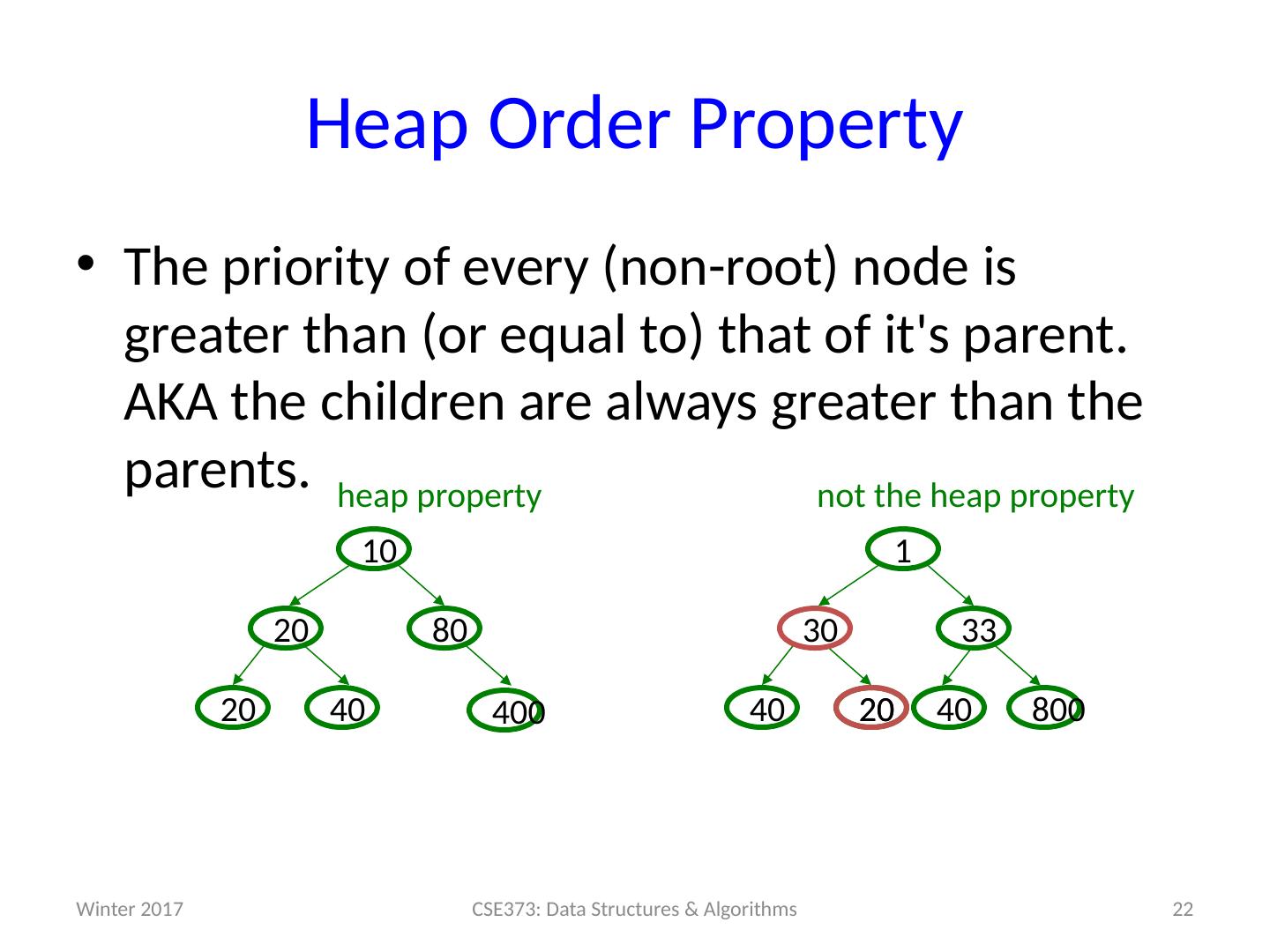
24 .Heaps A binary min-heap (or just binary heap or just heap ) is: Structure property: A complet e binary tree Heap property: The priority of every (non-root) node is greater than (or equal to) the priority of its parent. AKA the children are always greater than the parents. Not a binary search tree Winter 2017 24 CSE373: Data Structures & Algorithms 15 30 80 20 10 99 60 40 80 20 10 50 700 85 not a heap a heap 450 3 1 75 50 8 6 0 n ot a hea p 10 10

25 .Heaps Where is the highest-priority item ? What is the height of a heap with n items ? How do we use heaps to implement the operations in a Priority Queue ADT? Winter 2017 25 CSE373: Data Structures & Algorithms

26 .Heaps Where is the highest-priority item ? At the root (at the top) What is the height of a heap with n items log 2 n (We’ll look at computing this next week) How do we use heaps to implement the operations in a Priority Queue ADT? See following slides Winter 2017 26 CSE373: Data Structures & Algorithms

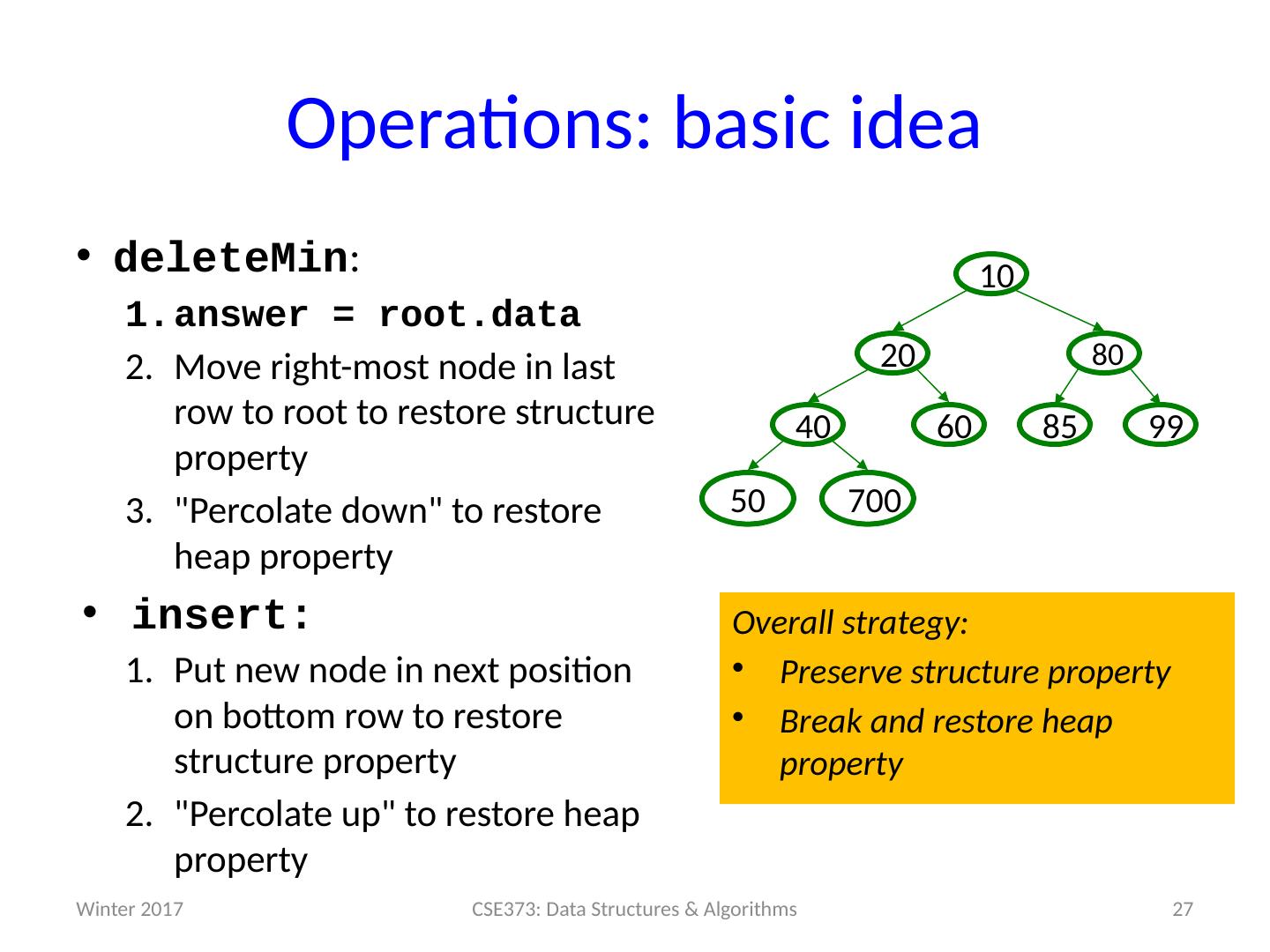
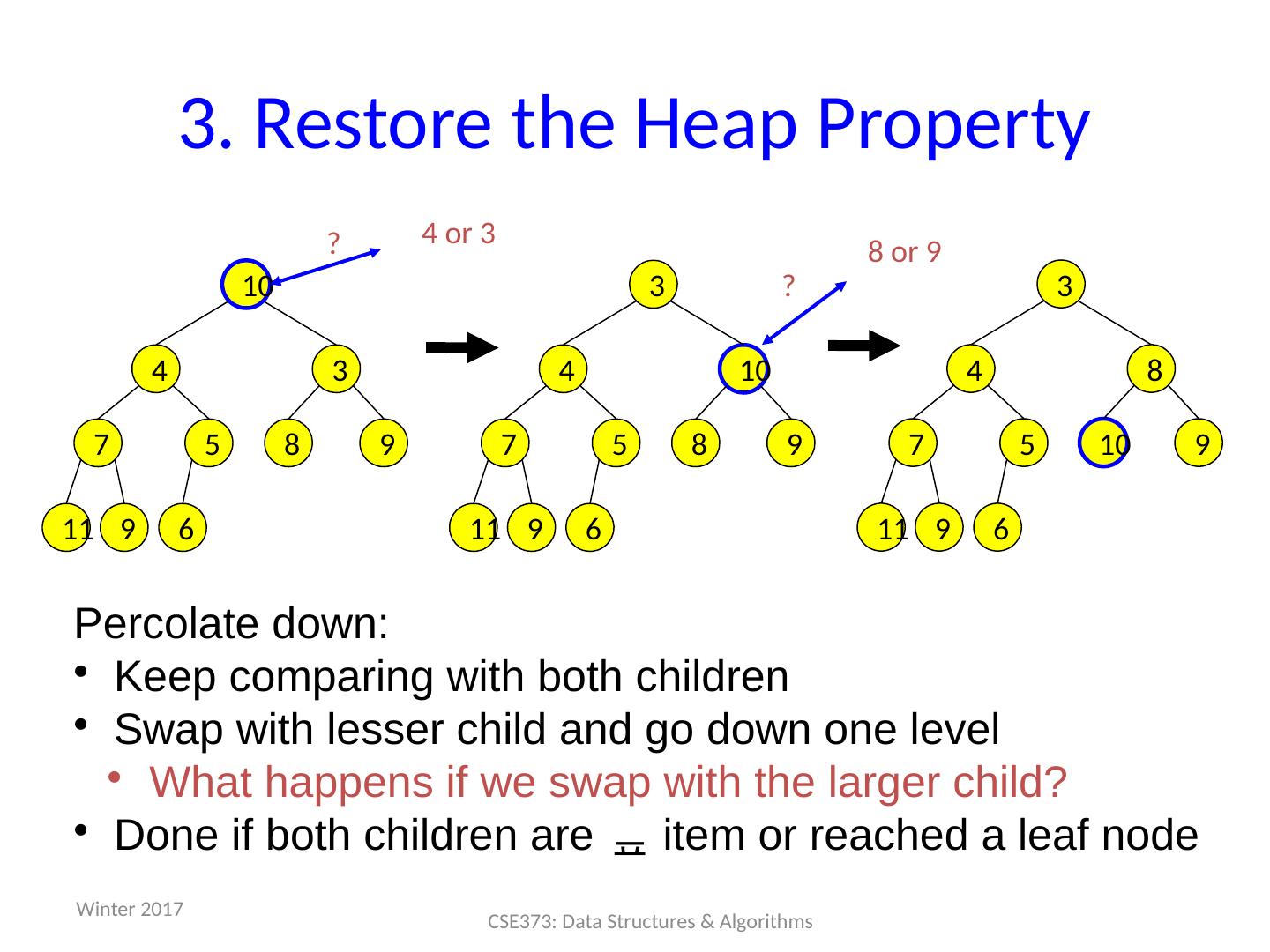
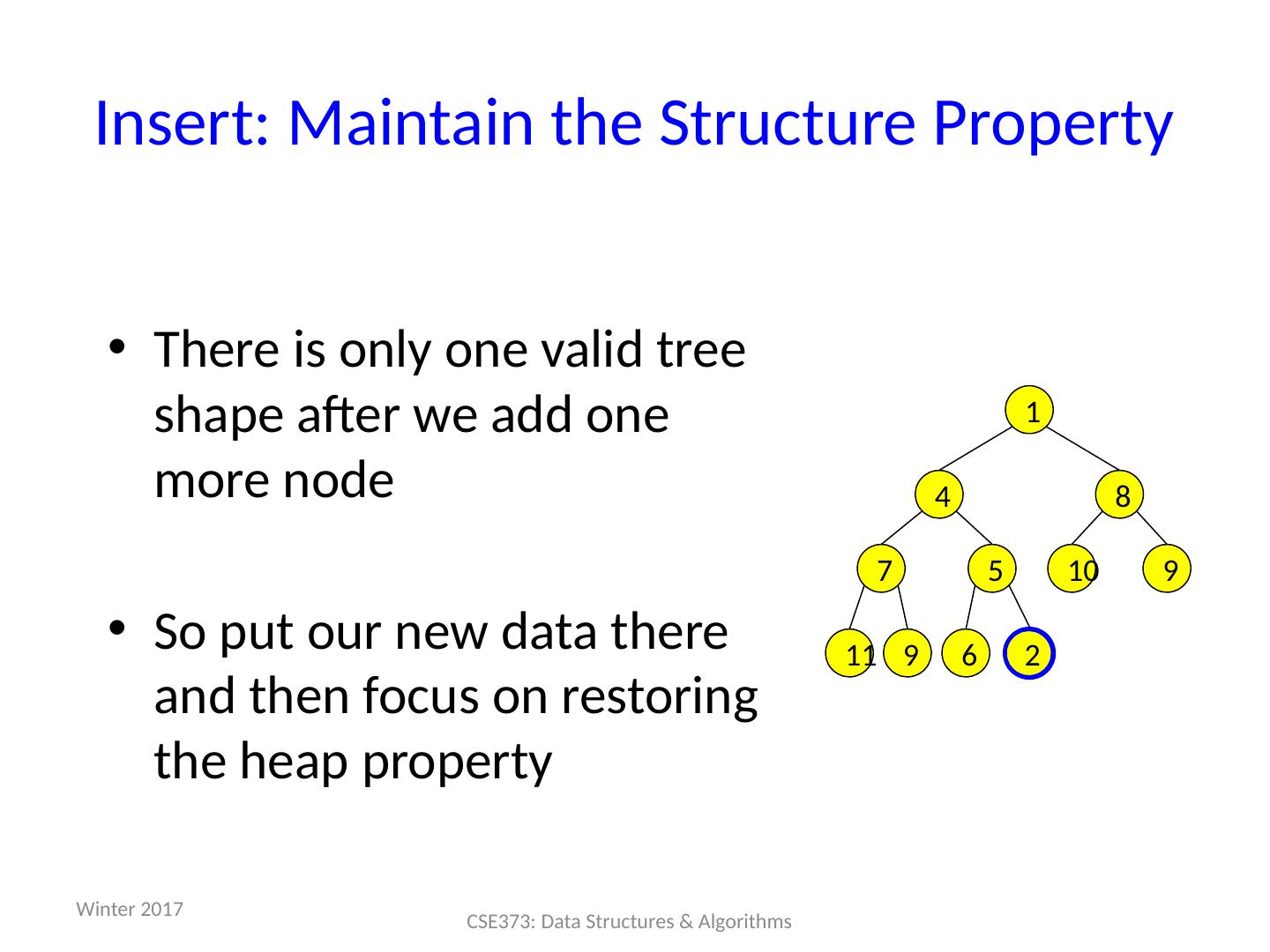
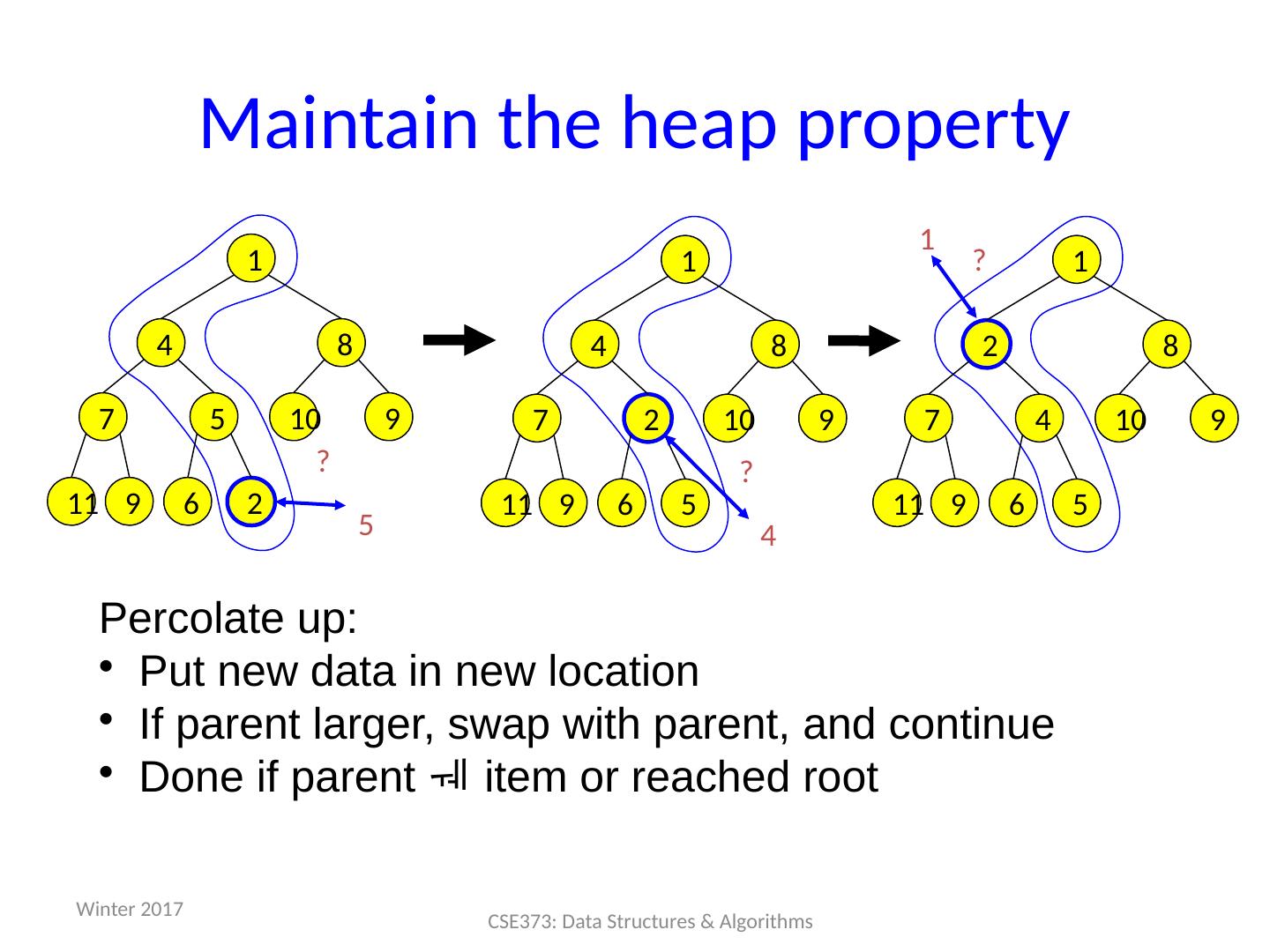
27 .Operations: basic idea deleteMin : answer = root.data Move right-most node in last row to root to restore structure property "Percolate down" to restore heap property insert: Put new node in next position on bottom row to restore structure property "Percolate up" to restore heap property Winter 2017 27 CSE373: Data Structures & Algorithms 99 60 40 80 20 10 50 700 85 Overall strategy: Preserve structure property Break and restore heap property

28 .28 d eleteMin 3 4 9 8 5 7 10 6 9 11 1. Delete (and later return ) value at root node Winter 2017 CSE373: Data Structures & Algorithms 2

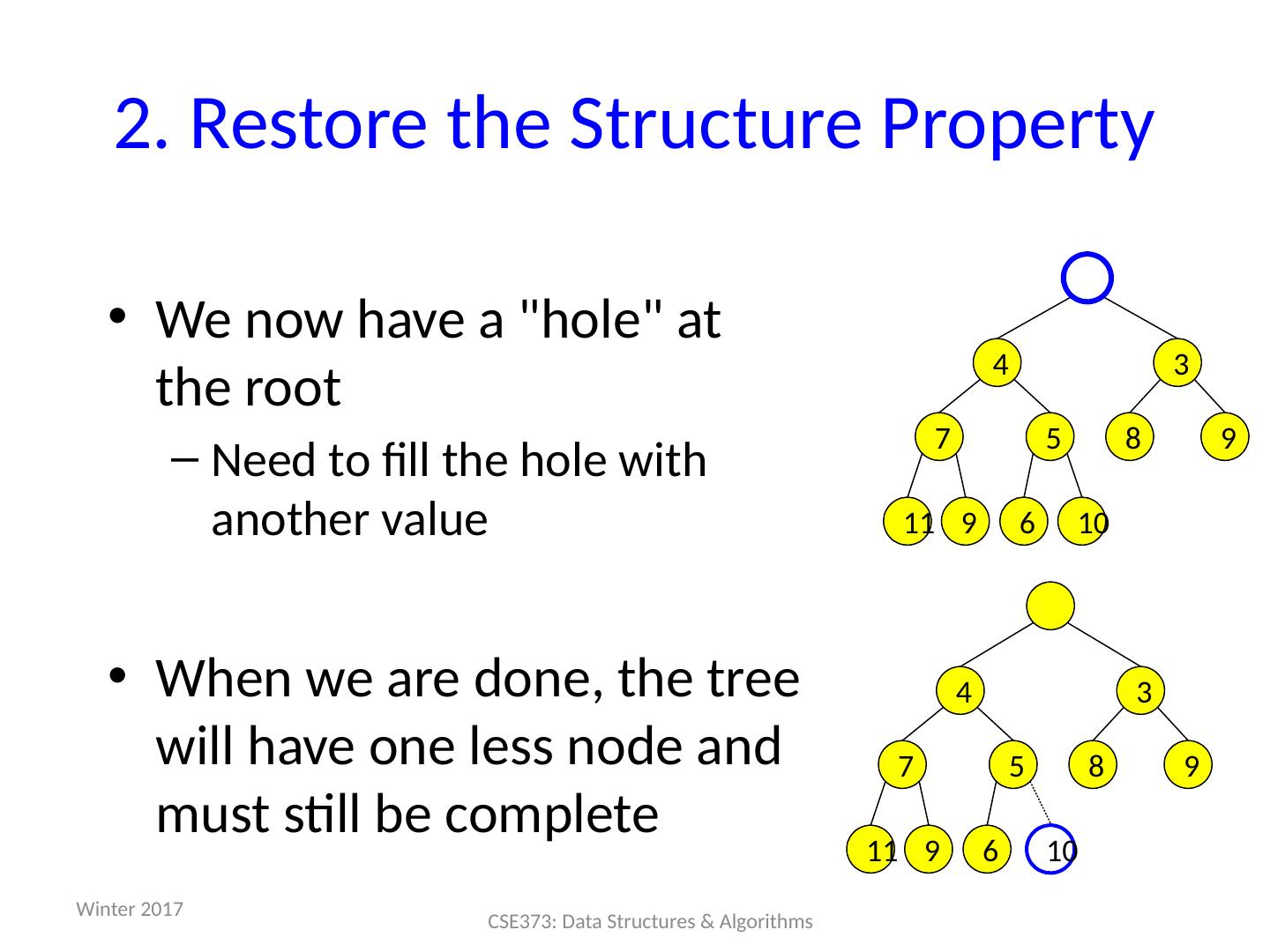
29 .29 2. Restore the Structure Property We now have a "hole" at the root Need to fill the hole with another value When we are done, the tree will have one less node and must still be complete 3 4 9 8 5 7 10 6 9 11 3 4 9 8 5 7 10 6 9 11 Winter 2017 CSE373: Data Structures & Algorithms