数字和C语言

1 .CS 61C: Great Ideas in Computer Architecture Lecture 2 : Numbers & C Language Krste Asanović & Randy Katz http:// inst.eecs.berkeley.edu /~cs61c

2 .Agenda Numbers wrap-up This is not on the exam! Break C Primer Administrivia , Break C Type declarations And in Conclusion, … CS 61c Lecture 2: C Programming Language 2

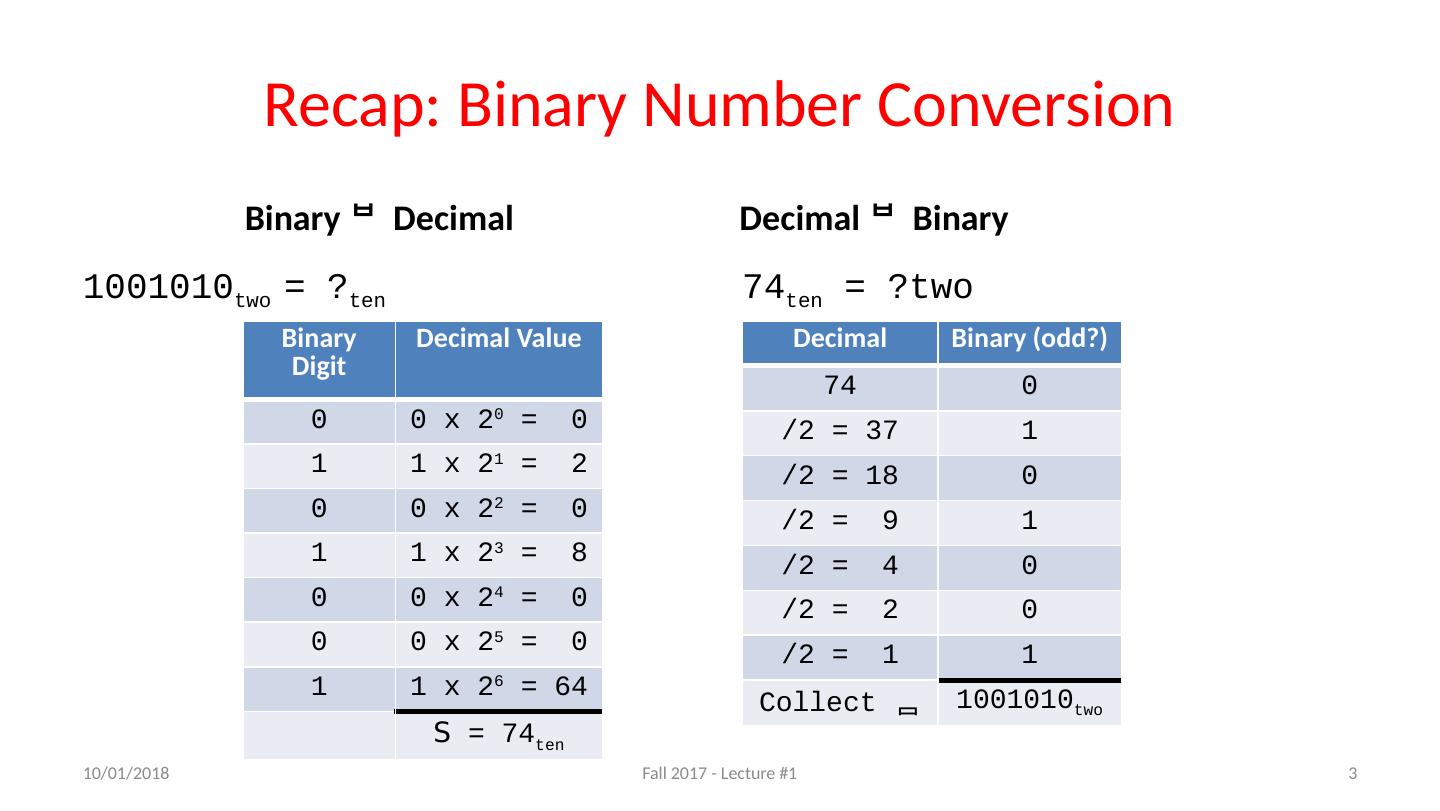
3 .Recap: Binary Number Conversion Binary  Decimal 1001010 two = ? ten Decimal  Binary 74 ten = ?two 8/29/17 3 Fall 2017 - Lecture #1 Binary Digit Decimal Value 0 0 x 2 0 = 0 1 1 x 2 1 = 2 0 0 x 2 2 = 0 1 1 x 2 3 = 8 0 0 x 2 4 = 0 0 0 x 2 5 = 0 1 1 x 2 6 = 64 S = 74 ten Decimal Binary (odd?) 74 0 /2 = 37 1 /2 = 18 0 /2 = 9 1 /2 = 4 0 /2 = 2 0 /2 = 1 1 Collect  1001010 two

4 .Signed Integer Representation How to represent -5? Sign & magnitude (8-bit example): Rules for addition, a + b: If ( a>0 and b>0): add b to a If ( a>0 and b<0): subtract b from a … +0, -0  are they equal? I f so, comparator must handle special case ! (If not equal???) Cumbersome ”Complicated” hardware: reduced speed / increased power Is there a better way? 8/29/17 4 Fall 2017 - Lecture #1 sign 7-bit magnitude (0 … 127)

5 .Going backwards by going forwards How to add -1 to a four-bit number? 8/29/17 5 Fall 2017 - Lecture #1 0111 two = 7 ten ???? two + = -1 ten 0110 two = 6 ten

6 .Going backwards by going forwards Add 10000 two and throw away fifth bit, result unchanged Result wraps around to same value 8/29/17 6 Fall 2017 - Lecture #1 0111 two = 7 ten 10000 two + = 16 ten 1 0111 two = 7 ten + 16 ten 0111 two = 7 ten

7 .Going backwards by going forwards Add ( 10000 two – 1 two = 01111 two ) and throw away fifth bit One less than original value 8/29/17 7 Fall 2017 - Lecture #1 0111 two = 7 ten 0 1111 two + = 16 - 1 ten 1 0110 two = 16 + 6 ten 0110 two = 6 ten

8 .4-bit Example 7 + -3 4 8/29/17 8 7 + -3 + 16 4 + 16 7 + 13 4 + 16 0111 + 1101 1 0100 0100 + 1 0000 Decimal Binary Map negative  positive numbers Example for N=4-bit: -3  2 4 – 3 = 13 “Two’s complement” No special rules for adding positive and negative numbers -8 -7 … -1 0 1 … 7 0 1 … 7 8 9 … 15 + 2 4 = 16 Extra bit is ignored as doesn’t fit in 4 bits.

9 .Two’s Complement (8-bit example) 8/29/17 9 Fall 2017 - Lecture #1 As Signed Decimal As Unsigned Decimal Binary Number -128 128 1000 0000 -127 129 1000 0001 … … … -2 254 1111 1110 -1 255 1111 1111 0 0 0000 0000 1 1 0000 0001 … … ... 127 127 0111 1111 Most-significant bit (MSB) equals sign when interpreted as a signed number +256 +0

10 .Signed versus Unsigned Binary Numbers Both are stored as a collection of bits The same set of bits can be used to represent a signed number or an unsigned number (or a string, or a picture, or a….) It’s up to the operation interpreting the bits 8/29/17 10 Fall 2017 - Lecture #1 1101 two = +13 ten (as an unsigned number) 1101 two = -3 ten (as a signed number) 1101 two = orange ( as a color) 1101 two = cat (as a type of animal) 1101 two = whatever you want it to mean…

11 .Unary Negation (Two’s Complement) 4-bit Example (-8 ten … +7 ten ) Brute Force & Tedious Clever & Elegant 16 ten 10000 two - 3 ten - 0011 two 13 ten 1101 two 16 ten 10000 two - 13 ten - 1101 two 3 ten 0011 two ”largest” 4-bit number + 1 8/29/17 Fall 2017 - Lecture #1 11 15 ten 01111 two - 3 ten - 0011 two 12 ten 1100 two invert + 1 ten + 0001 two 13 ten 1101 two

12 .Your Turn What is the decimal value of the following binary 8-bit 2’s complement number? 1110 0001 two 8/29/17 12 Fall 2017 - Lecture #1 Answer Value RED 33 ten ORANGE -31 ten GREEN 225 ten YELLOW -33 ten

13 .Addition 4-bit Example Unsigned Signed (Two’s Complement) 8/29/17 13 Fall 2017 - Lecture #1 3 ten 0011 two + 4 ten + 0100 two 7 ten 0111 two 3 ten 0011 two + 11 ten + 1011 two 14 ten 1110 two 3 ten 0011 two + 4 ten + 0100 two 7 ten 0111 two 3 ten 0011 two + -5 ten + 1011 two -2 ten 1110 two No special rules for two’s complement signed addition

14 .Overflow 4-bit Example Unsigned addition Signed addition ( Two’s Complement) 8/29/17 14 Fall 2017 - Lecture #1 13 ten 1101 two + 14 ten + 1110 two 27 ten 1 1011 two 7 ten 0111 two + 1 ten + 0001 two 8 ten 0 1000 two -3 ten 1101 two + -2 ten + 1110 two -5 ten 1 1011 two 7 ten 0111 two + 1 ten + 0001 two -8 ten 0 1000 two Carry-out  Overflow Carry-out  Overflow carry-out but no overflow carry-out and overflow no carry-out but overflow no carry-out and no overflow

15 .Addition Overflow Detection 4-bit Example Unsigned addition Carry-out indicates overflow Signed addition ( Two’s Complement) Overflow if Signs of operands are equal AND Sign of result differs from sign of operands No overflow is possible when signs of operands differ 8/29/17 15 Fall 2017 - Lecture #1 Overflow rules depend on the operation ( signed vs unsigned addition)

16 .Adding Numbers of Different Bit Widths What should we assume for upper four bits of first operand? Treat as zeros! “Zero-extension” 8/29/17 16 Fall 2017 - Lecture #1 1101 (4-bit, 13 ten ) 10100101 + (8-bit, 165 ten ) ????0010 (8-bit, ??? ten ) Unsigned addition 0000 1101 (4-bit, 13 ten ) 10100101 + (8-bit, 165 ten ) 1 0110010 (8-bit, 178 ten ) Zero extension

17 .Adding Signed Numbers of Different Bit Widths What should we assume for upper four bits of first operand? Copy sign bit (MSB) of operand into upper bits If sign is 1, copy 1s, if sign is 0 copy 0s “Sign-extension” 8/29/17 17 Fall 2017 - Lecture #1 1 101 (4-bit, -3 ten ) 10100101 + (8-bit, -91 ten ) ????0010 (8-bit, ??? ten ) S igned addition 1111 1 101 (4-bit, -3 ten ) 10100101 + (8-bit, -91 ten ) 10100010 (8-bit, -94 ten ) Sign extension Sign bit

18 .Sign Extension Decimal Binary 4-bit 8-bit 32-bit 3 ten 0011 two 0000 0011 two 0000 0000 0000 0011 two -3 ten 1101 two 1111 1101 two 1111 1111 1111 1101 two 8/29/17 18 Fall 2017 - Lecture #1 When is this relevant? Any time you need a wider version of a narrower operand e.g., adding two integers of different widths

19 .Your Turn Which range of decimals can be expressed with a 6-bit two’s complement number? 8/29/17 19 Fall 2017 - Lecture #1 Answer Range RED -32 … 32 GREEN -64 … 63 ORANGE -31 … 32 YELLOW -32 … 31

20 .Agenda Numbers wrap-up This is not on the exam! Break C Primer Administrivia , Break C Type declarations And in Conclusion, … CS 61c Lecture 2: C Programming Language 20

21 .HotChips 2017: Brains & Dinosaurs Top conference introducing new processor chips CS 61c Lecture 2: C Programming Language 21

22 .CS 61c Lecture 2: C Programming Language 22

23 .Z14, IBM Mainframe, 50+ years on CS 61c Lecture 2: C Programming Language 23

24 .CS 61c Lecture 2: C Programming Language 24

25 .Break! 8/29/17 25 Fall 2017 - Lecture #2

26 .Agenda Numbers wrap-up This is not on the exam! Break C Primer Administrivia , Break C Type declarations And in Conclusion, … CS 61c Lecture 2: C Programming Language 26

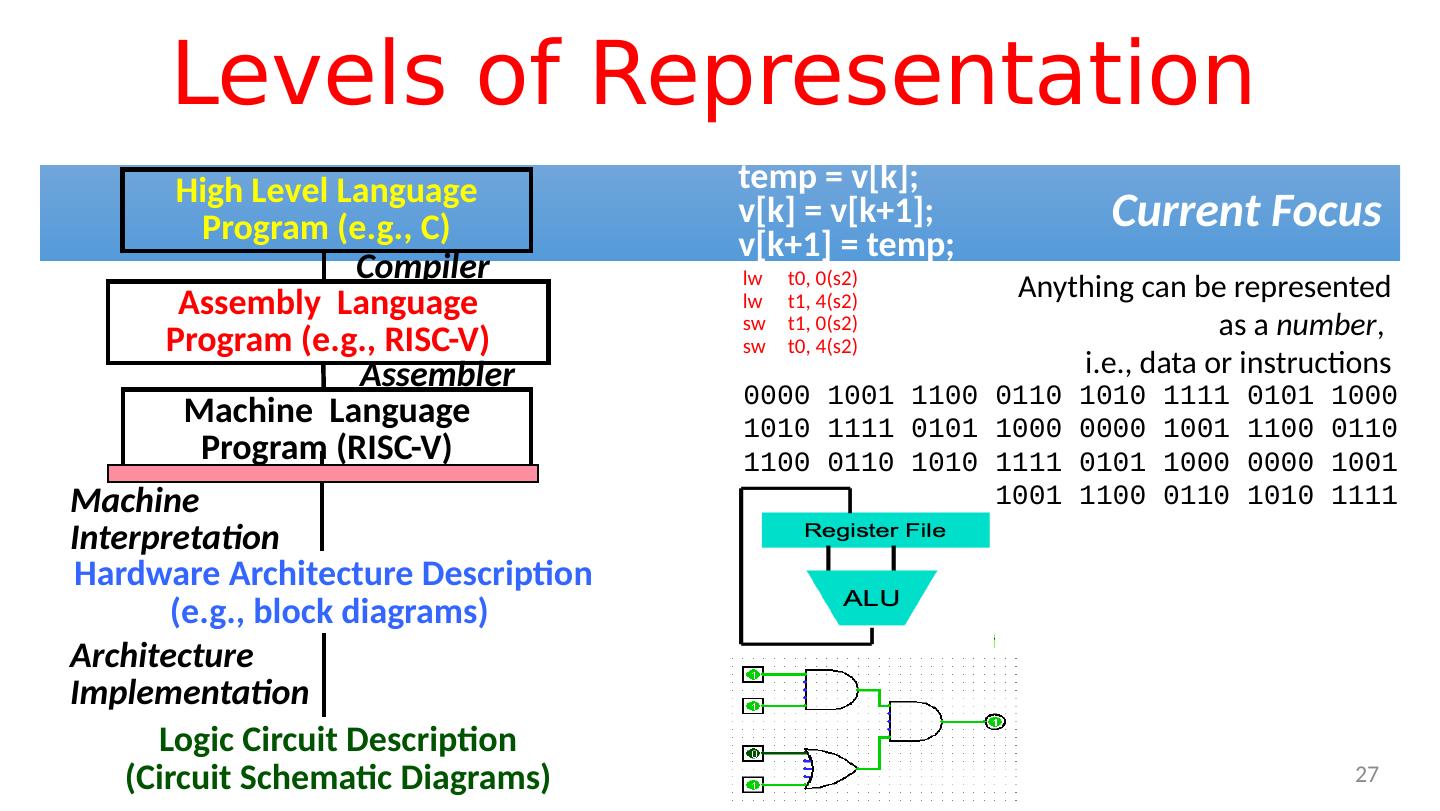
27 .Levels of Representation lw t 0 , 0 (s2 ) lw t 1 , 4 (s2 ) sw t1 , 0 (s2 ) sw t0 , 4 (s2 ) High Level Language Program (e.g., C) Assembly Language Program (e.g., RISC-V) Machine Language Program (RISC-V) Hardware Architecture Description (e.g., block diagrams) Compiler Assembler Machine Interpretation temp = v[k ]; v[k ] = v[k+1]; v[k+1] = temp; 0000 1001 1100 0110 1010 1111 0101 1000 1010 1111 0101 1000 0000 1001 1100 0110 1100 0110 1010 1111 0101 1000 0000 1001 0101 1000 0000 1001 1100 0110 1010 1111 Logic Circuit Description (Circuit Schematic Diagrams) Architecture Implementation Anything can be represented as a number , i.e., data or instructions 27 Current Focus

28 .Introduction to C “The Universal Assembly Language” Languages used in 61C: C Assembly Python used in two labs Prior programming experience helpful, e.g. Java C++ 28 CS 61c Lecture 2: C Programming Language

29 .Survey Who has never written a program in Java or C, C++, Objective-C ? CS 61c Lecture 2: C Programming Language 29