- 快召唤伙伴们来围观吧
- 微博 QQ QQ空间 贴吧
- 文档嵌入链接
- 复制
- 微信扫一扫分享
- 已成功复制到剪贴板
数据结构的图形介绍
展开查看详情
1 .CSE 373: Data Structures & Algorithms Introduction to Graphs Riley Porter Winter 2017 CSE373: Data Structures & Algorithms 1
2 .Announcements Midterms done! Wow! Nicely done everyone. Average was ~68/80, which is ~85% Standard Dev : 7 points Not an easy test, you all rocked it! Congrats! Handed back in section on Thursday Scores on Canvas after lecture HW4 out tonight -> Graphs CSE373: Data Structures & Algorithms 2
3 .Graphs A graph is a formalism for representing relationships among items. One way to write graphs: A graph G = (V,E) A set of vertices , also known as nodes V = {v 1 ,v 2 ,…, v n } A set of edges E = {e 1 ,e 2 ,…, e m } Each edge e i is a pair of vertices ( v j ,v k ) An edge “connects” the vertices Graphs can be directed or undirected 3 CSE373: Data Structures & Algorithms Han Leia Luke V = { Han , Leia , Luke } E = {( Luke , Leia ), ( Han , Leia ), ( Leia , Han )}
4 .Are Graphs An ADT? Can think of graphs as an ADT with operations like isEdge (( v j ,v k )), addVertex ( v new ), … But it is unclear what the “standard operations” are Instead we tend to develop algorithms over graphs and then use data structures that are efficient for those algorithms Many important problems can be solved by: Formulating them in terms of graphs Applying a standard graph algorithm To make the formulation easy and standard, we have a lot of standard terminology about graphs 4 CSE373: Data Structures & Algorithms
5 .Undirected Graphs In undirected graphs , edges have no specific direction Edges are always “two-way” 5 CSE373: Data Structures & Algorithms Thus, ( u,v ) E implies ( v,u ) E Only one of these edges needs to be in the set The other is implicit, so normalize how you check for it Degree of a vertex: number of edges containing that vertex Put another way: the number of adjacent vertices A B C D
6 .Directed Graphs In directed graphs (sometimes called digraphs ), edges have a direction 6 CSE373: Data Structures & Algorithms Thus, ( u,v ) E does not imply ( v,u ) E . Let ( u,v ) E mean u → v C all u the source and v the destination In-degree of a vertex: number of in-bound edges, i.e., edges where the vertex is the destination Out-degree of a vertex: number of out-bound edges i.e., edges where the vertex is the source or 2 edges here A B C D A B C
7 .Self-Edges, Connectedness A self-edge a.k.a. a loop is an edge of the form ( u,u ) Depending on the use/algorithm, a graph may have: No self edges Some self edges All self edges (often therefore implicit, but we will be explicit) A node can have a degree / in-degree / out-degree of zero A graph does not have to be connected Even if every node has non-zero degree 7 CSE373: Data Structures & Algorithms
8 .More Notation For a graph G = (V,E) |V| is the number of vertices |E| is the number of edges (assuming no self loops) Minimum? Maximum for directed ? Maximum for undirected ? If ( u,v ) E Then v is a neighbor of u , i.e., v is adjacent to u Order matters for directed edges u is not adjacent to v unless ( v,u ) E 8 CSE373: Data Structures & Algorithms A B C V = { A , B , C , D } E = {( C , B ), ( A , B ), ( B , A ) ( C , D )} D 0 (| V |*(|V|-1))/ 2 O (|V| 2 ) |V | *( |V|-1) O (|V| 2 )
9 .Weighted Graphs In a weighed graph, each edge has a weight a.k.a. cost Typically numeric (most examples use ints ) Orthogonal to whether graph is directed Some graphs allow negative weights ; many do not 9 CSE373: Data Structures & Algorithms 20 30 35 60 Mukilteo Edmonds Seattle Bremerton Bainbridge Kingston Clinton
10 .Paths and Cycles A path is a list of vertices [v 0 ,v 1 ,…, v n ] such that (v i ,v i+1 ) E for all 0 i < n. Say “a path from v 0 to v n ” A cycle is a path that begins and ends at the same node ( v 0 == v n ) 10 CSE373: Data Structures & Algorithms Seattle San Francisco Dallas Chicago Salt Lake City Cycle : [Seattle , Salt Lake City, Dallas, San Francisco, Seattle] Path : [ Seattle, Chicago, Dallas]
11 .Path Length and Cost Path length : Number of edges in a path Path cost : Sum of weights of edges in a path Example: P= [Seattle, Salt Lake City, Chicago, Dallas, San Francisco, Seattle] 11 CSE373: Data Structures & Algorithms Seattle San Francisco Dallas Chicago Salt Lake City 3.5 2 2 2.5 3 2 2.5 2.5 length( P ) = 5 cost( P ) = 11.5
12 .Simple Paths and Cycles A simple path repeats no vertices, except the first might be the last [ Seattle , Salt Lake City , San Francisco , Dallas ] [ Seattle , Salt Lake City , San Francisco , Dallas , Seattle ] Recall, a cycle is a path that ends where it begins [ Seattle , Salt Lake City , San Francisco , Dallas , Seattle ] [ Seattle , Salt Lake City , Seattle , Dallas , Seattle ] A simple cycle is a cycle and a simple path [ Seattle , Salt Lake City , San Francisco , Dallas , Seattle ] 12 CSE373: Data Structures & Algorithms
13 .Paths and Cycles in Directed Graphs Example: Is there a path from A to D? Does the graph contain any cycles? 13 CSE373: Data Structures & Algorithms A B C D
14 .Paths and Cycles in Directed Graphs Example: Is there a path from A to D? No Does the graph contain any cycles? No 14 CSE373: Data Structures & Algorithms A B C D
15 .Paths and Cycles in Directed Graphs Example: Is there a path from A to D? Does the graph contain any cycles? 15 CSE373: Data Structures & Algorithms A B C D
16 .Paths and Cycles in Directed Graphs Example: Is there a path from A to D ? Yes Does the graph contain any cycles ? No 16 CSE373: Data Structures & Algorithms A B C D
17 .Paths and Cycles in Directed Graphs Example: Is there a path from A to D? Does the graph contain any cycles? 17 CSE373: Data Structures & Algorithms A B C D
18 .Paths and Cycles in Directed Graphs Example: Is there a path from A to D ? Yes Does the graph contain any cycles ? Yes 18 CSE373: Data Structures & Algorithms A B C D
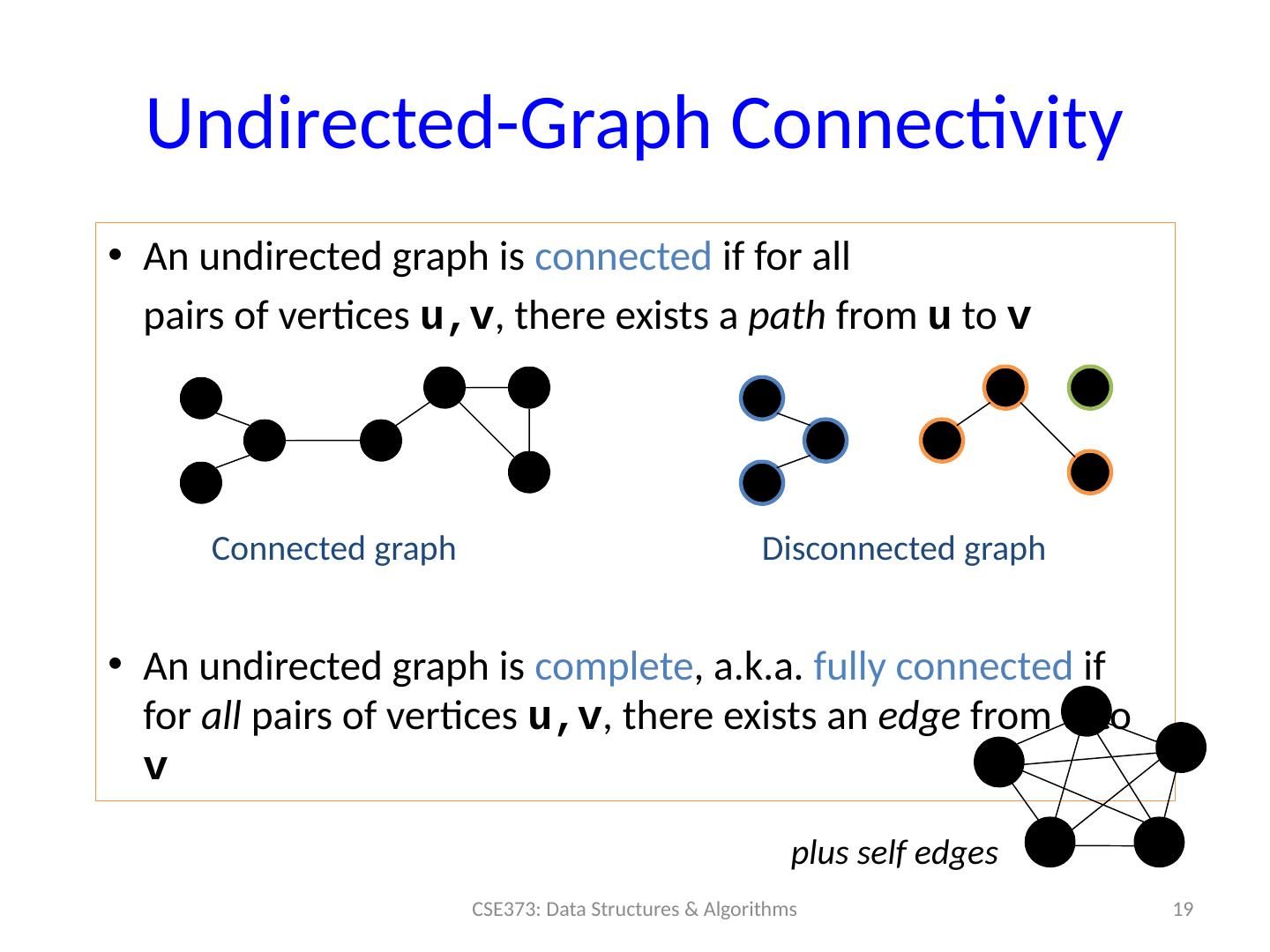
19 .Undirected-Graph Connectivity An undirected graph is connected if for all pairs of vertices u,v , there exists a path from u to v An undirected graph is complete , a.k.a. fully connected if for all pairs of vertices u,v , there exists an edge from u to v 19 CSE373: Data Structures & Algorithms Connected graph Disconnected graph plus self edges
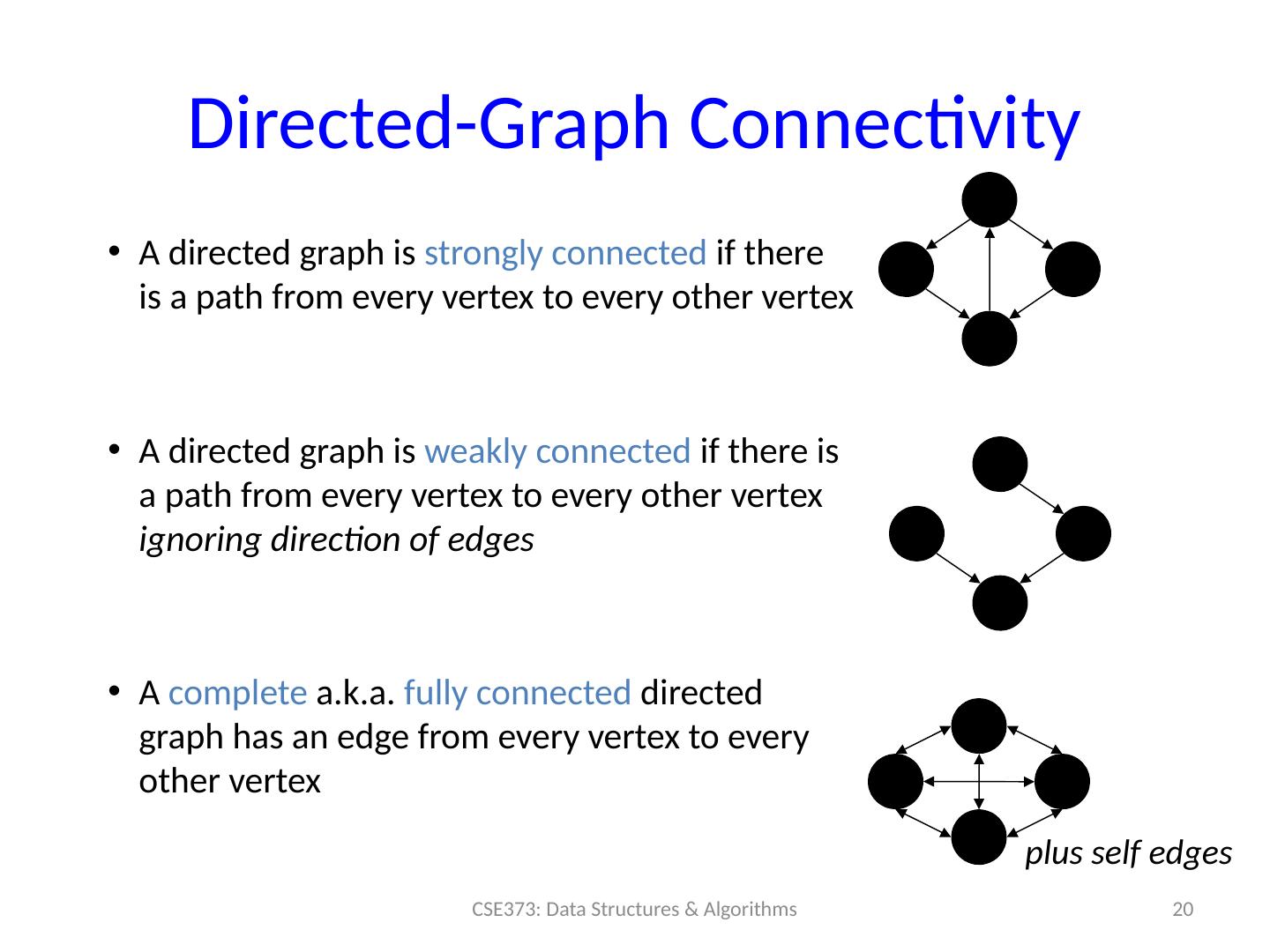
20 .Directed-Graph Connectivity A directed graph is strongly connected if there is a path from every vertex to every other vertex A directed graph is weakly connected if there is a path from every vertex to every other vertex ignoring direction of edges A complete a.k.a. fully connected directed graph has an edge from every vertex to every other vertex 20 CSE373: Data Structures & Algorithms plus self edges
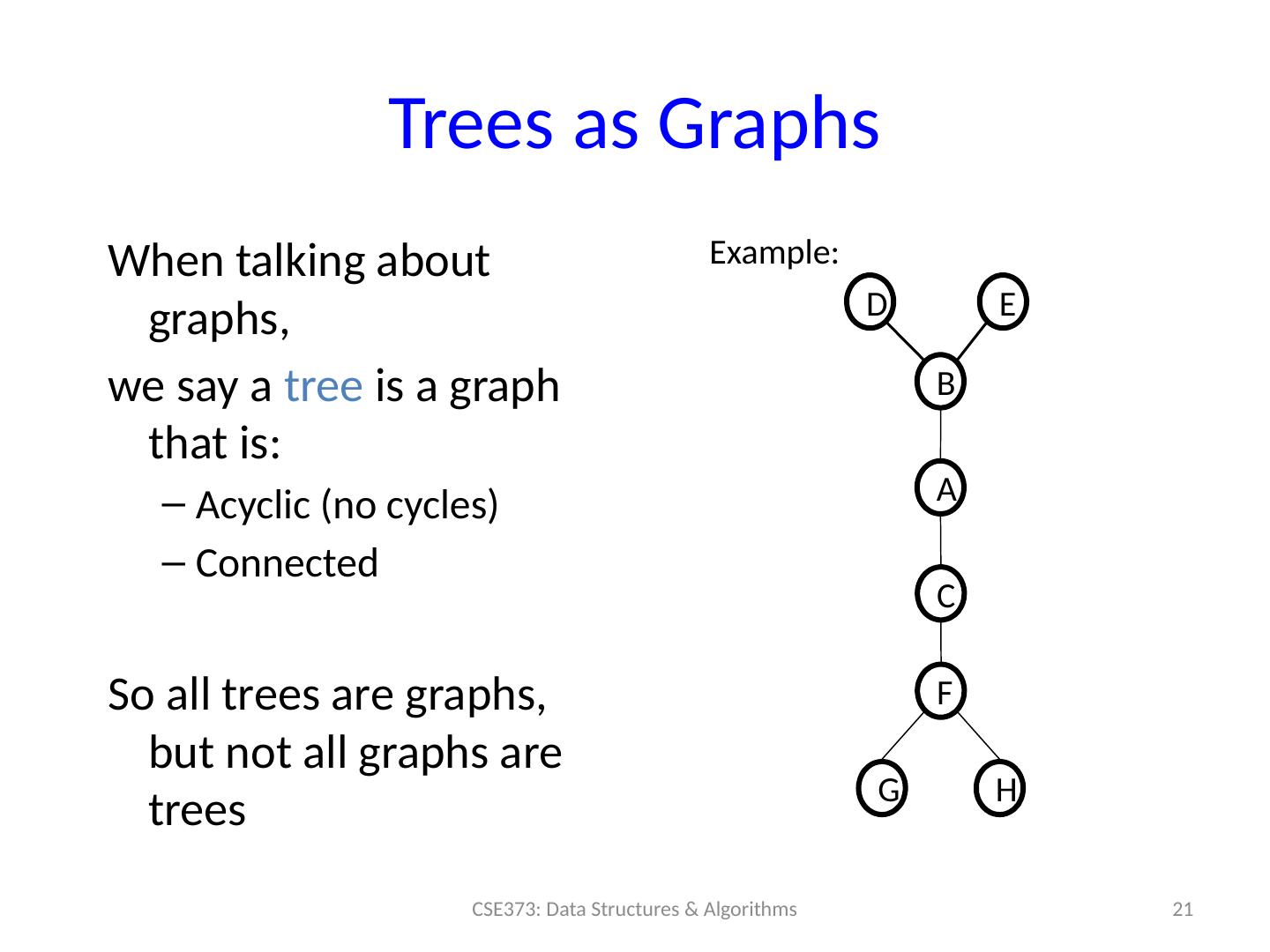
21 .Trees as Graphs When talking about graphs, we say a tree is a graph that is: Acyclic (no cycles) Connected So all trees are graphs, but not all graphs are trees 21 CSE373: Data Structures & Algorithms A B D E C F H G Example:
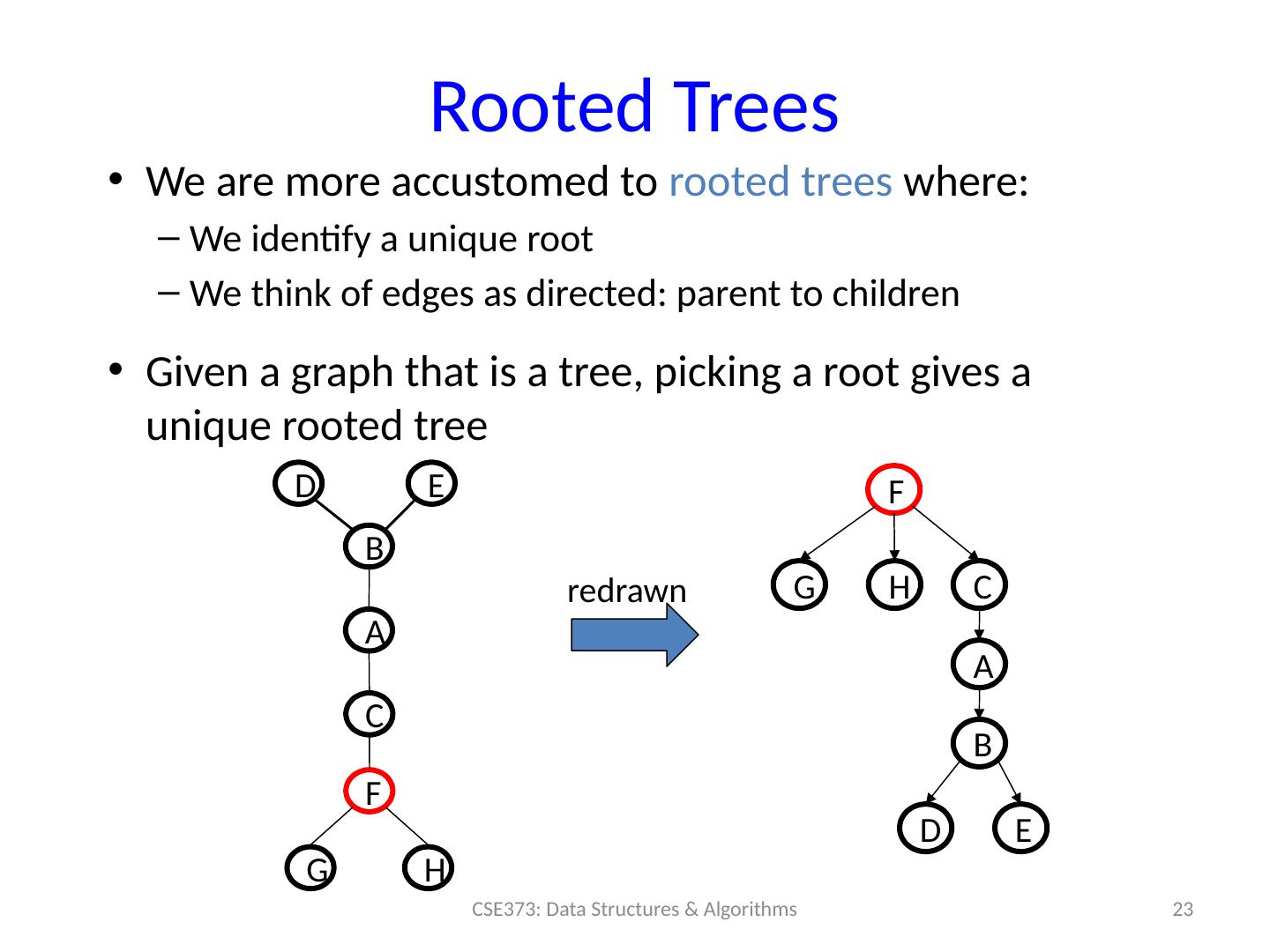
22 .Rooted Trees We are more accustomed to rooted trees where: We identify a unique root We think of edges as directed: parent to children Given a graph that is a tree, picking a root gives a unique rooted tree 22 CSE373: Data Structures & Algorithms A B D E C F H G redrawn A B D E C F H G
23 .Rooted Trees 23 CSE373: Data Structures & Algorithms A B D E C F H G redrawn F G H C A B D E We are more accustomed to rooted trees where: We identify a unique root We think of edges as directed: parent to children Given a graph that is a tree, picking a root gives a unique rooted tree
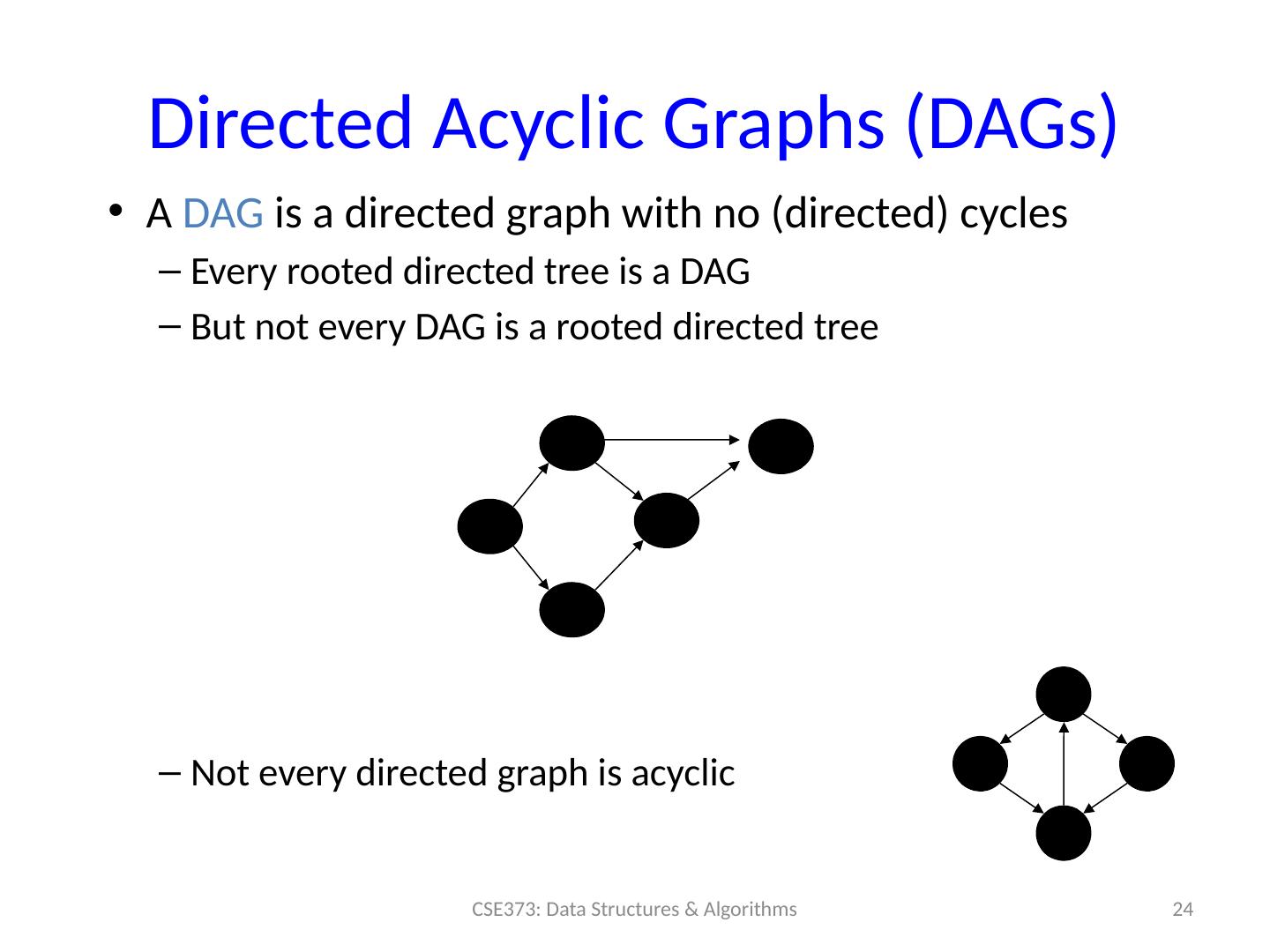
24 .Directed Acyclic Graphs (DAGs) A DAG is a directed graph with no (directed) cycles Every rooted directed tree is a DAG But not every DAG is a rooted directed tree Not every directed graph is acyclic 24 CSE373: Data Structures & Algorithms
25 .Density / Sparsity Recall: In an undirected graph, 0 ≤ |E| < |V| 2 Recall: In a directed graph: 0 ≤ |E| ≤ |V| 2 So for any graph, O (|E|+|V| 2 ) is O (|V| 2 ) Because |E| is often much smaller than its maximum size, we do not always approximate |E| as O (|V| 2 ) This is a correct upper bound , it just is often not tight If it is tight, i.e., |E| is (|V| 2 ) we say the graph is dense If |E| is O (|V|) we say the graph is sparse 25 CSE373: Data Structures & Algorithms
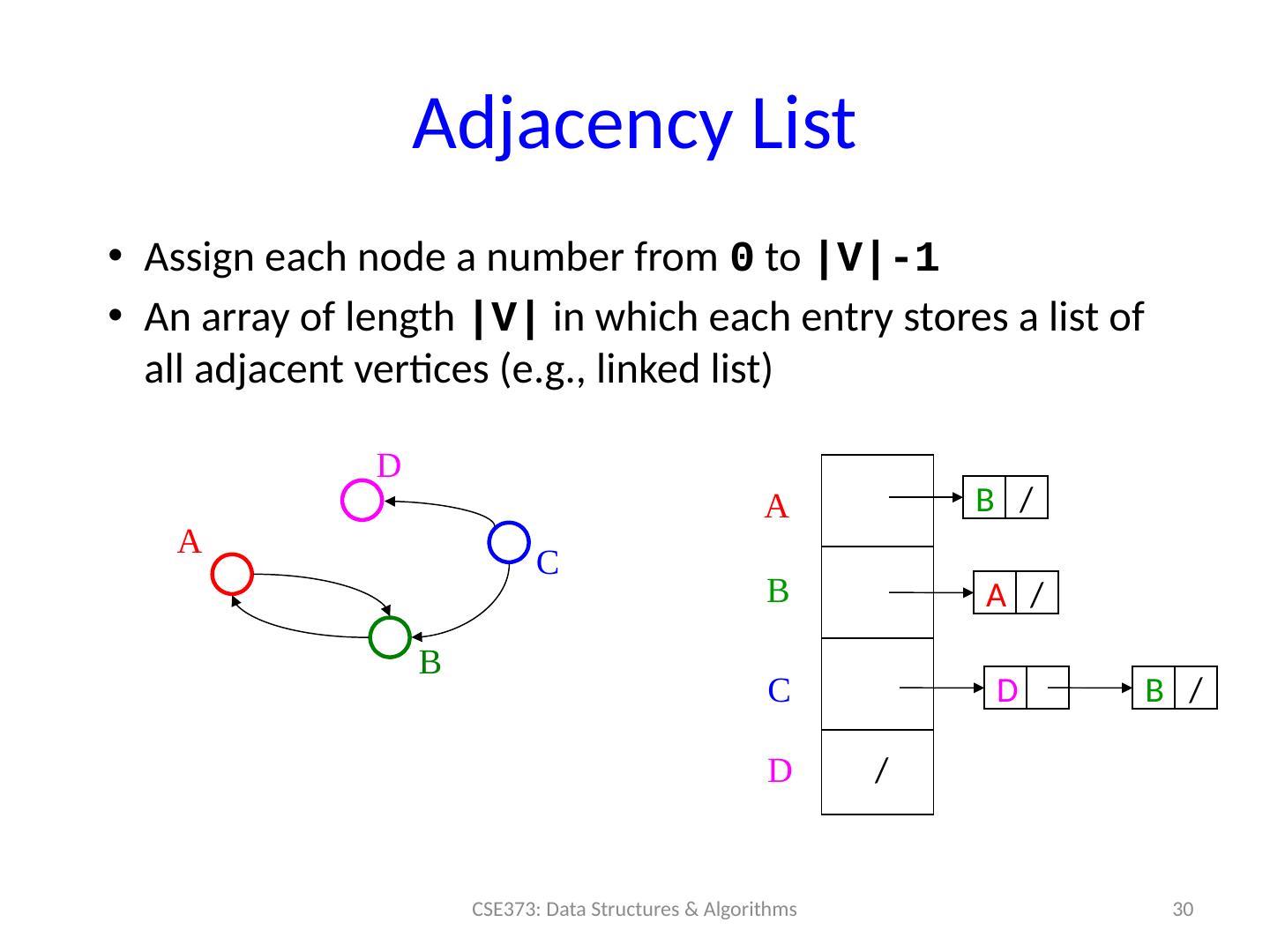
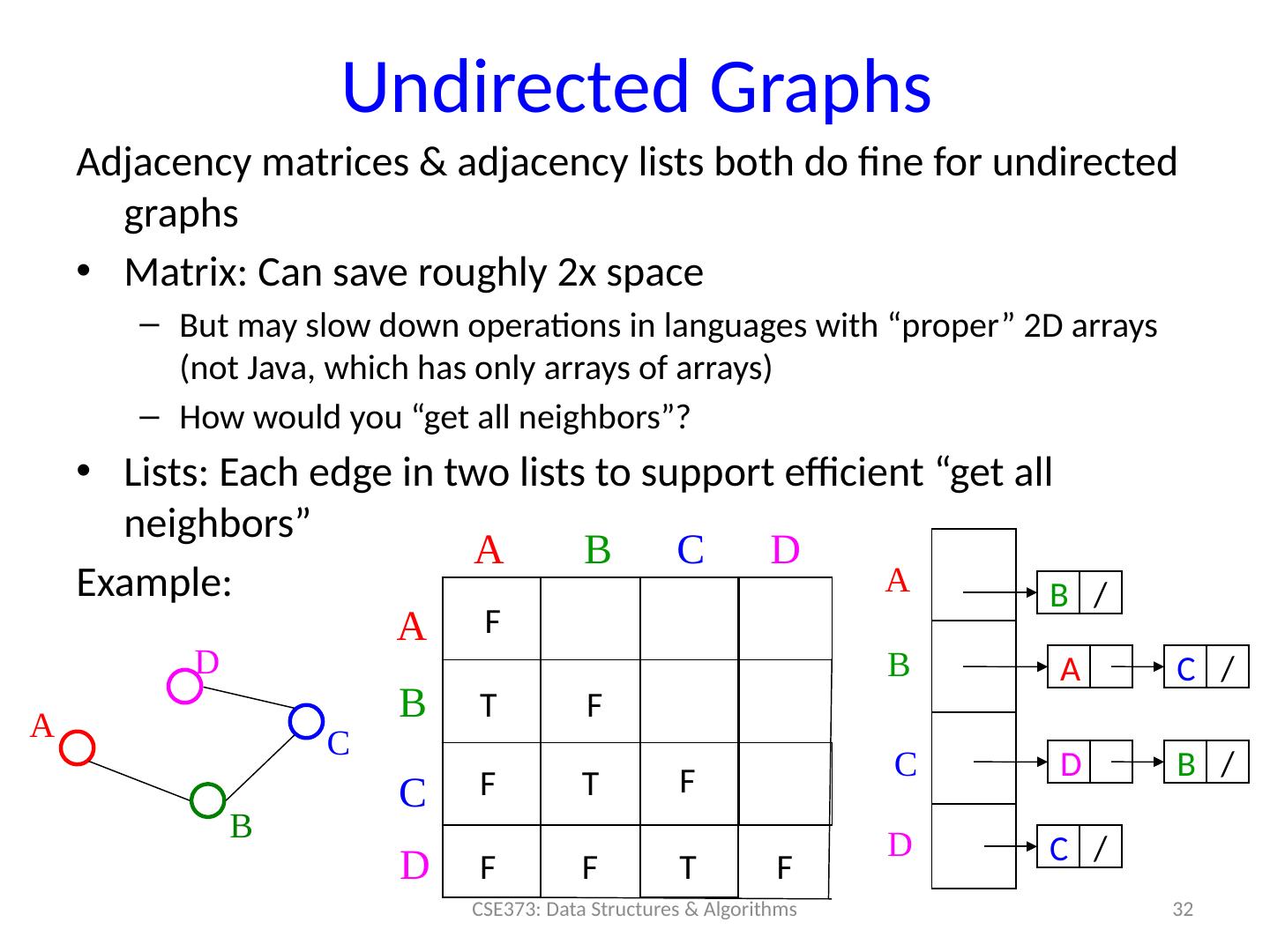
26 .How do we implement this? The “ best” implementation can depend on: P roperties of the graph (e.g., dense vs sparse ) The common queries (e.g., “is ( u,v ) an edge?” vs “what are the neighbors of node u ?”) We’ll discuss the two standard graph representations Adjacency Matrix and Adjacency List Different trade-offs, particularly time versus space 26 CSE373: Data Structures & Algorithms
27 .Adjacency Matrix Assign each vertex/node a number from 0 to |V|-1 A |V| x |V| matrix (i.e., 2-D array) of Booleans (or 1 vs. 0) If M is the matrix, then M[u][v] being true means there is an edge from u to v 27 CSE373: Data Structures & Algorithms A B C A B C D D A B C D T T T T F F F F F F F F F F F F
28 .Adjacency Matrix P roperties Running time to: Get a vertex’s out-edges: Get a vertex’s in-edges: Decide if some edge exists: Insert an edge: Delete an edge: Space requirements: |V| 2 bits Better for sparse or dense graphs? Better for dense graphs CSE373: Data Structures & Algorithms 28 A B C A B C D D T T T T F F F F F F F F F F F F O (|V| ) O (|V| ) O (1) O (1) O (1)
29 .Adjacency Matrix Properties How will the adjacency matrix vary for an undirected graph ? Undirected will be symmetric around the diagonal How can we adapt the representation for weighted graphs ? Instead of a B oolean, store a number in each cell Need some value to represent ‘not an edge’ In some situations, 0 or -1 works A B C A B C D D 7 7 4 2 -1 -1 -1 -1 4 -1 -1 -1 -1 -1 2 -1 CSE373: Data Structures & Algorithms 29 A B C D 2 4 7