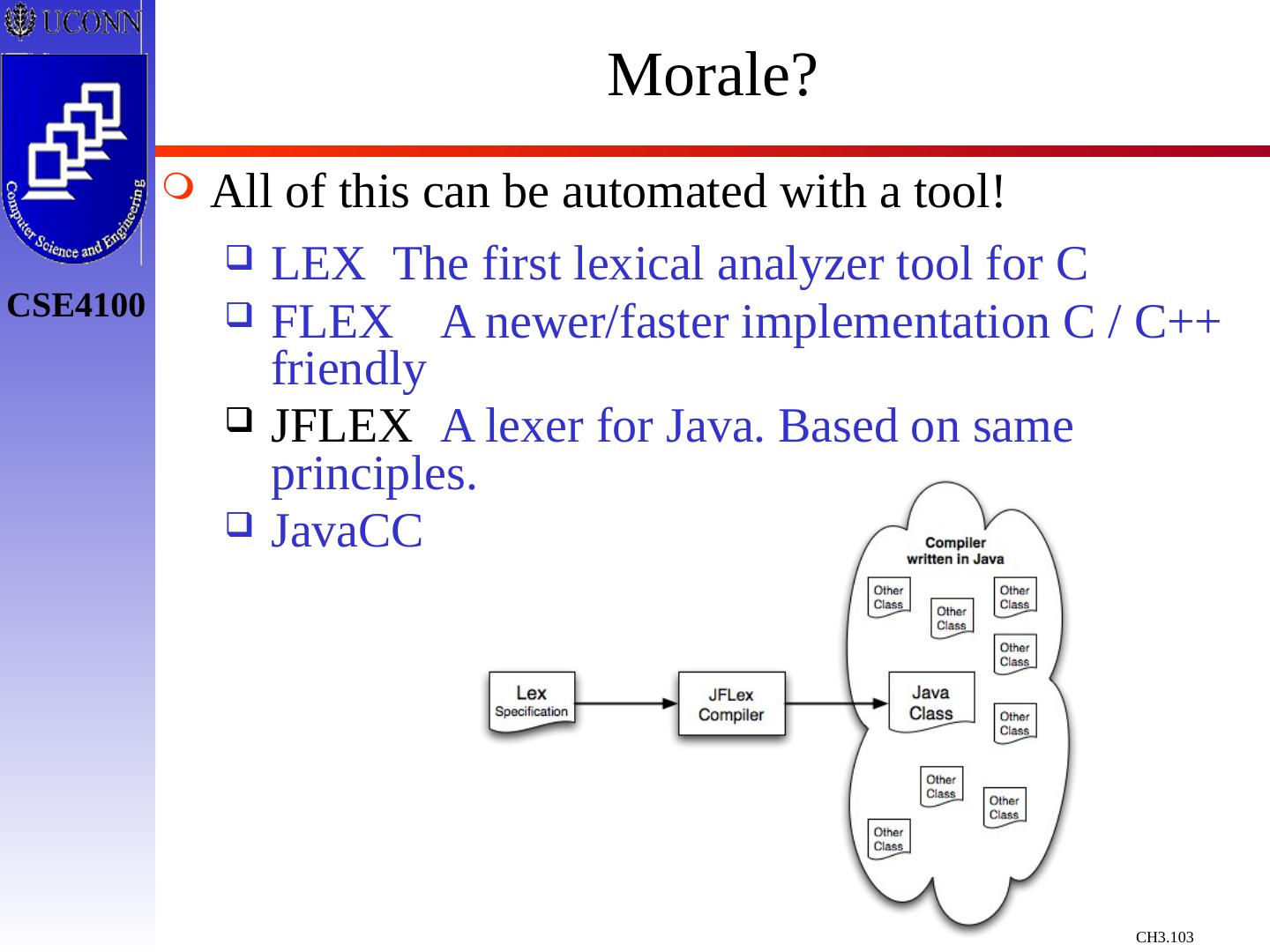
- 快召唤伙伴们来围观吧
- 微博 QQ QQ空间 贴吧
- 文档嵌入链接
- 复制
- 微信扫一扫分享
- 已成功复制到剪贴板
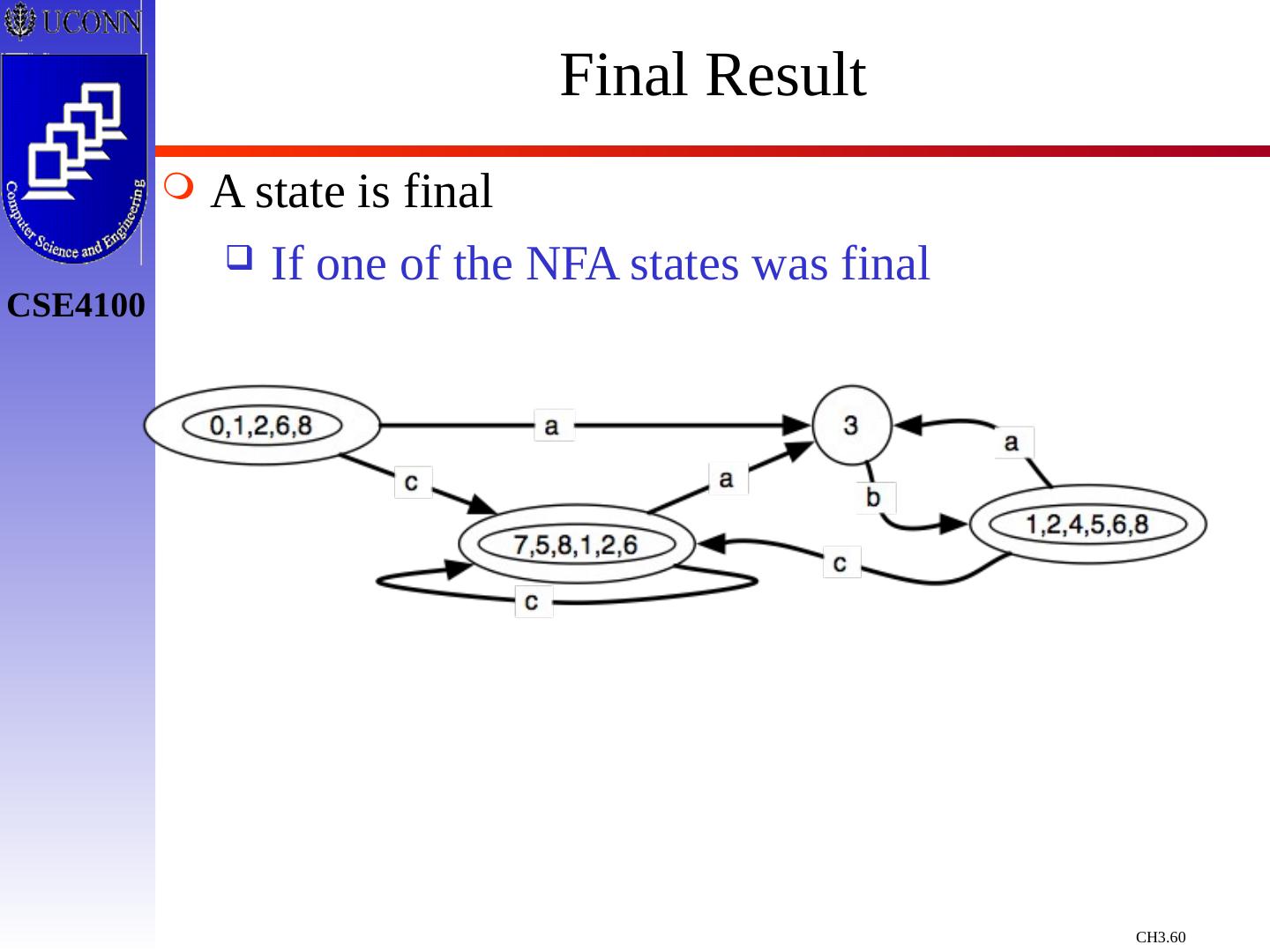
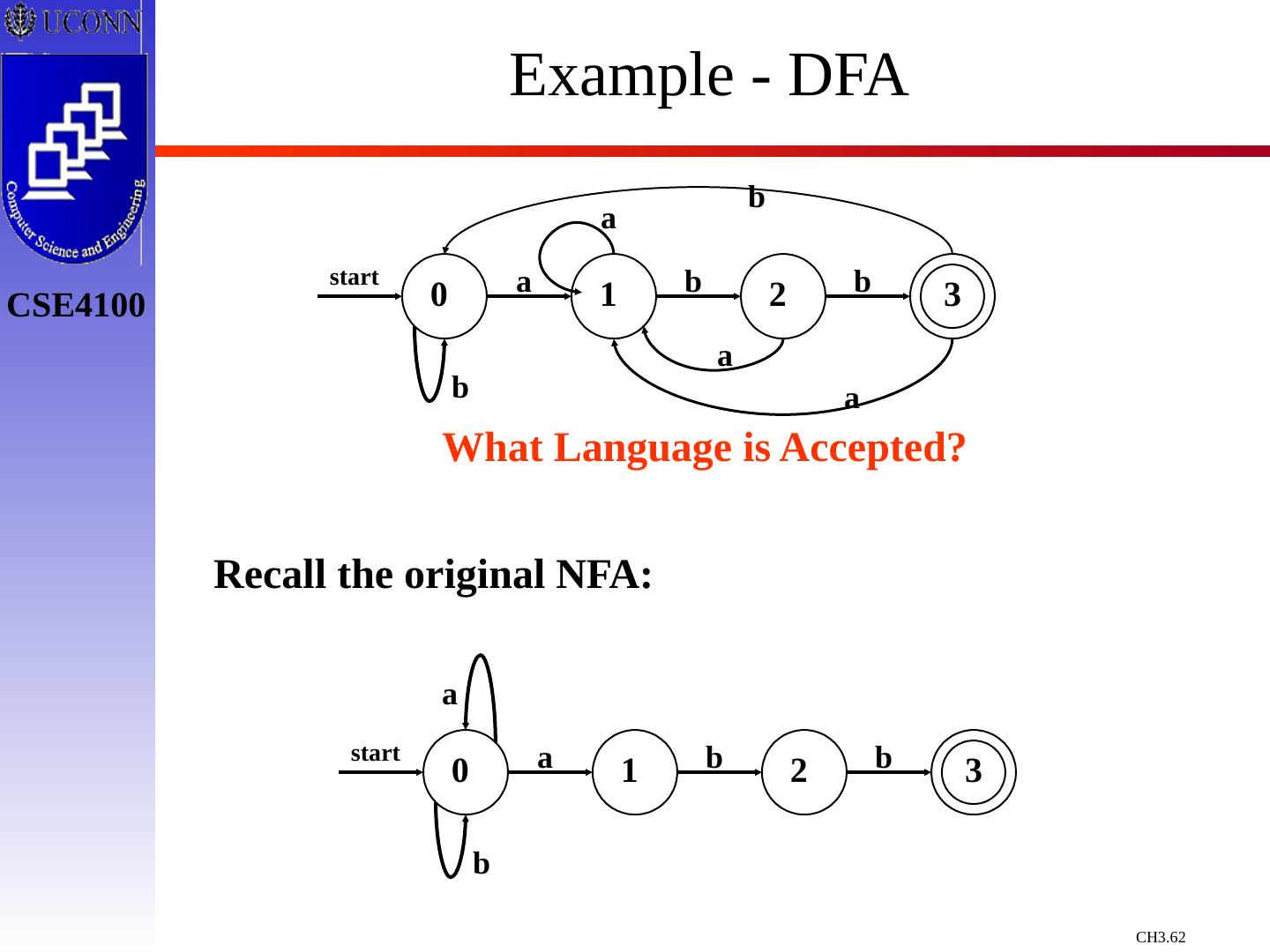
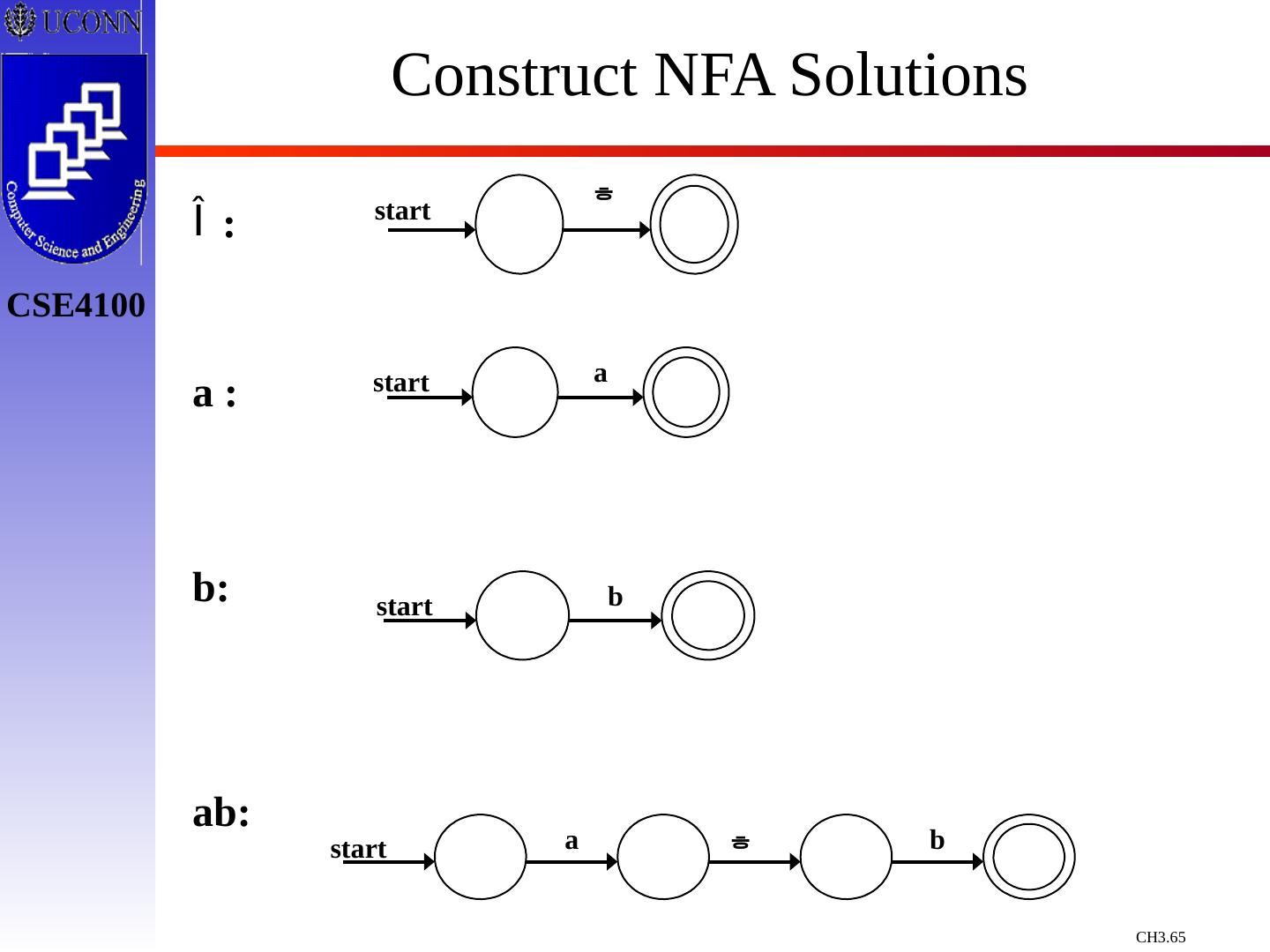
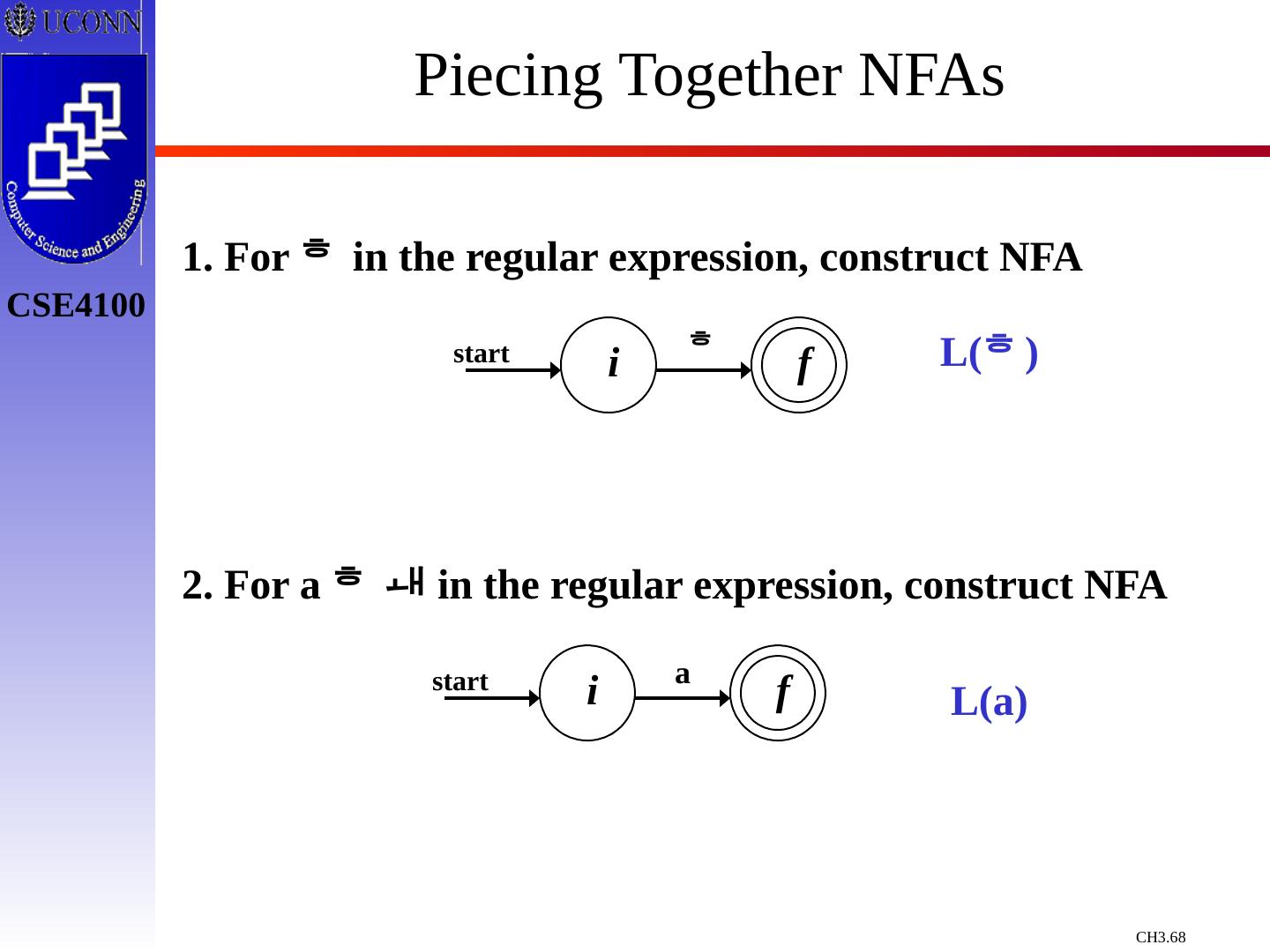
词法分析
展开查看详情
1 .Chapter 3: Lexical Analysis and Flex Prof. Steven A. Demurjian Computer Science & Engineering Department The University of Connecticut 371 Fairfield Way, Unit 2155 Storrs, CT 06269-3155 steve@engr.uconn.edu http://www.engr.uconn.edu/~steve (860) 486 - 4818 Material for course thanks to: Laurent Michel Aggelos Kiayias Robert LeBarre
2 .Overview of Chapter 3 Basic Concepts & Regular Expressions What does a Lexical Analyzer do? How does it Work? Formalizing Token Definition & Recognition Regular Expressions and Languages Reviewing Finite Automata Concepts Non-Deterministic and Deterministic FA Conversion Process Regular Expressions to NFA NFA to DFA Relating NFAs/DFAs /Conversion to Lexical Analysis – Tools Lex/Flex/ JFlex /ANTLR Detailed Discussion of Lex/Flex First portion of: www.engr.uconn.edu/~steve/CSE4100/lexandyacc.pptx Concluding Remarks /Looking Ahead
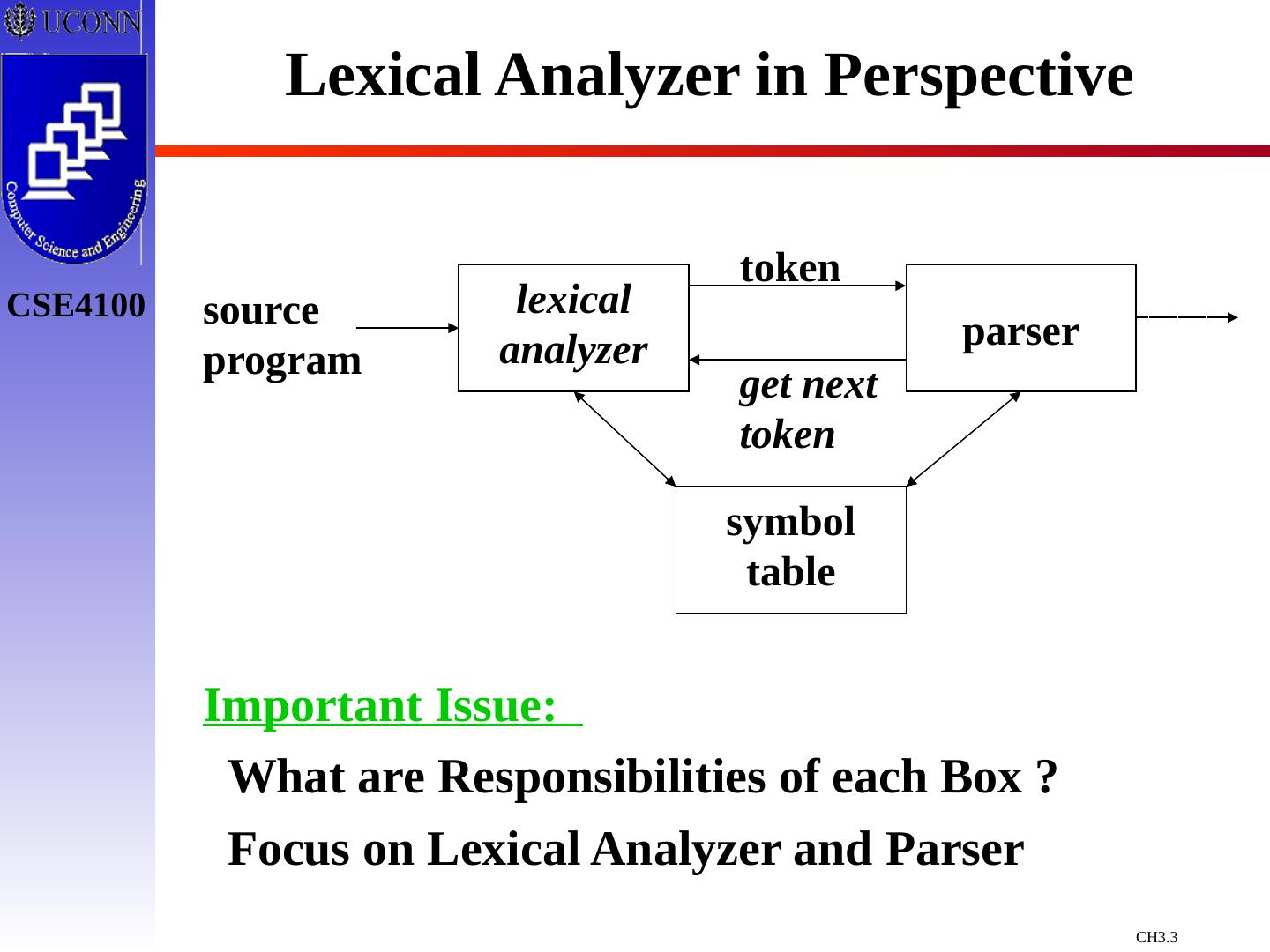
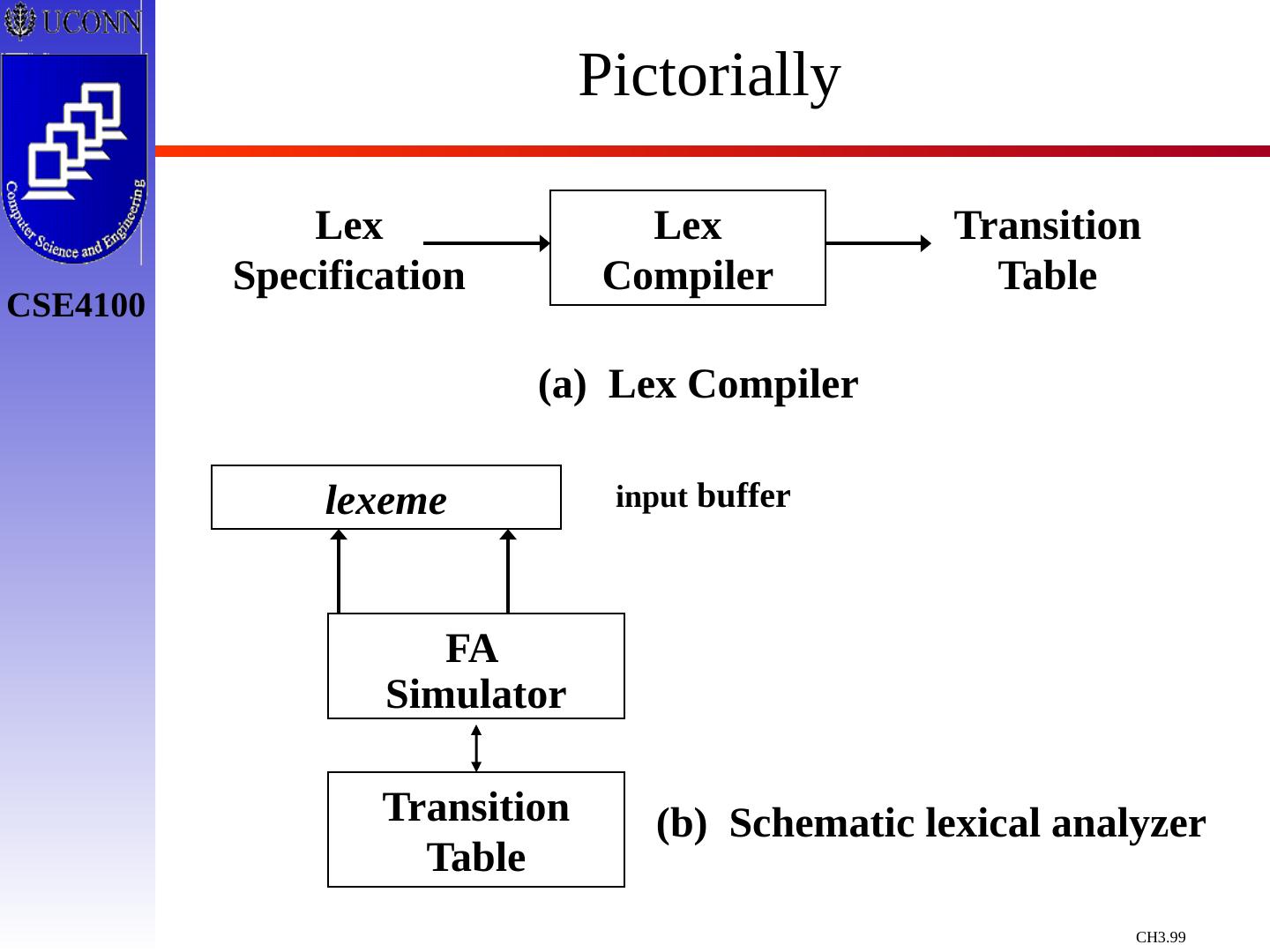
3 .Lexical Analyzer in Perspective lexical analyzer parser symbol table source program token get next token Important Issue: What are Responsibilities of each Box ? Focus on Lexical Analyzer and Parser
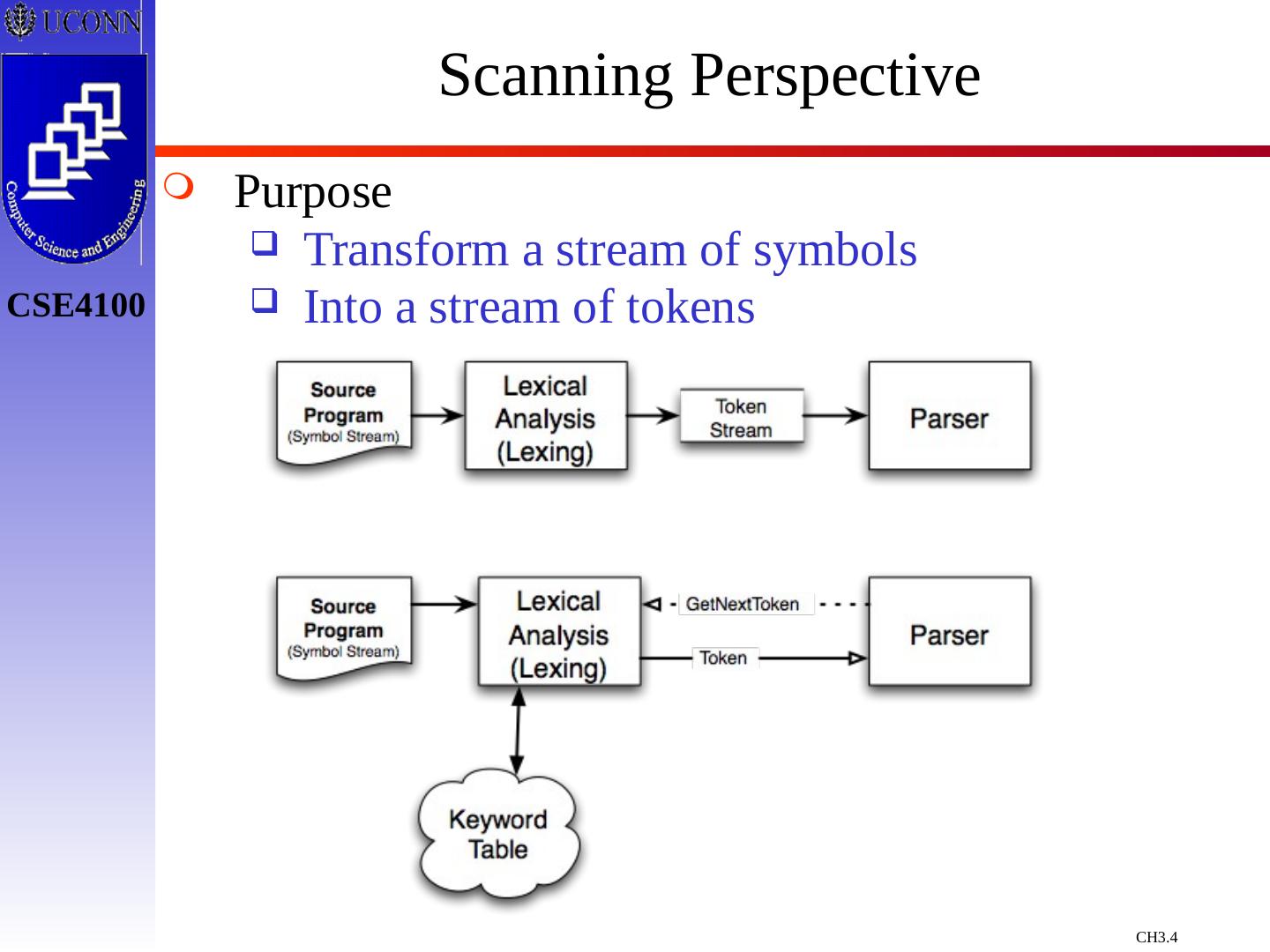
4 .Scanning Perspective Purpose Transform a stream of symbols Into a stream of tokens
5 .Lexical Analyzer in Perspective LEXICAL ANALYZER Scan Input Remove WS, NL, … Identify Tokens Create Symbol Table Insert Tokens into ST Generate Errors Send Tokens to Parser PARSER Perform Syntax Analysis Actions Dictated by Token Order Update Symbol Table Entries Create Abstract Rep. of Source Generate Errors And More…. (We’ll see later)
6 .What Factors Have Influenced the Functional Division of Labor ? Separation of Lexical Analysis From Parsing Presents a Simpler Conceptual Model From a Software Engineering Perspective Division Emphasizes High Cohesion and Low Coupling Implies Well Specified Parallel Implementation Separation Increases Compiler Efficiency (I/O Techniques to Enhance Lexical Analysis) Separation Promotes Portability . This is critical today, when platforms (OSs and Hardware) are numerous and varied! Emergence of Platform Independence - Java
7 .Introducing Basic Terminology What are Major Terms for Lexical Analysis? TOKEN A classification for a common set of strings Examples Include Identifier, Integer, Float, Assign, LParen, RParen, etc. PATTERN The rules which characterize the set of strings for a token – integers [0-9]+ Recall File and OS Wildcards ([A-Z]*.*) LEXEME Actual sequence of characters that matches pattern and is classified by a token Identifiers: x, count, name, etc… Integers: 345, 20 -12, etc.
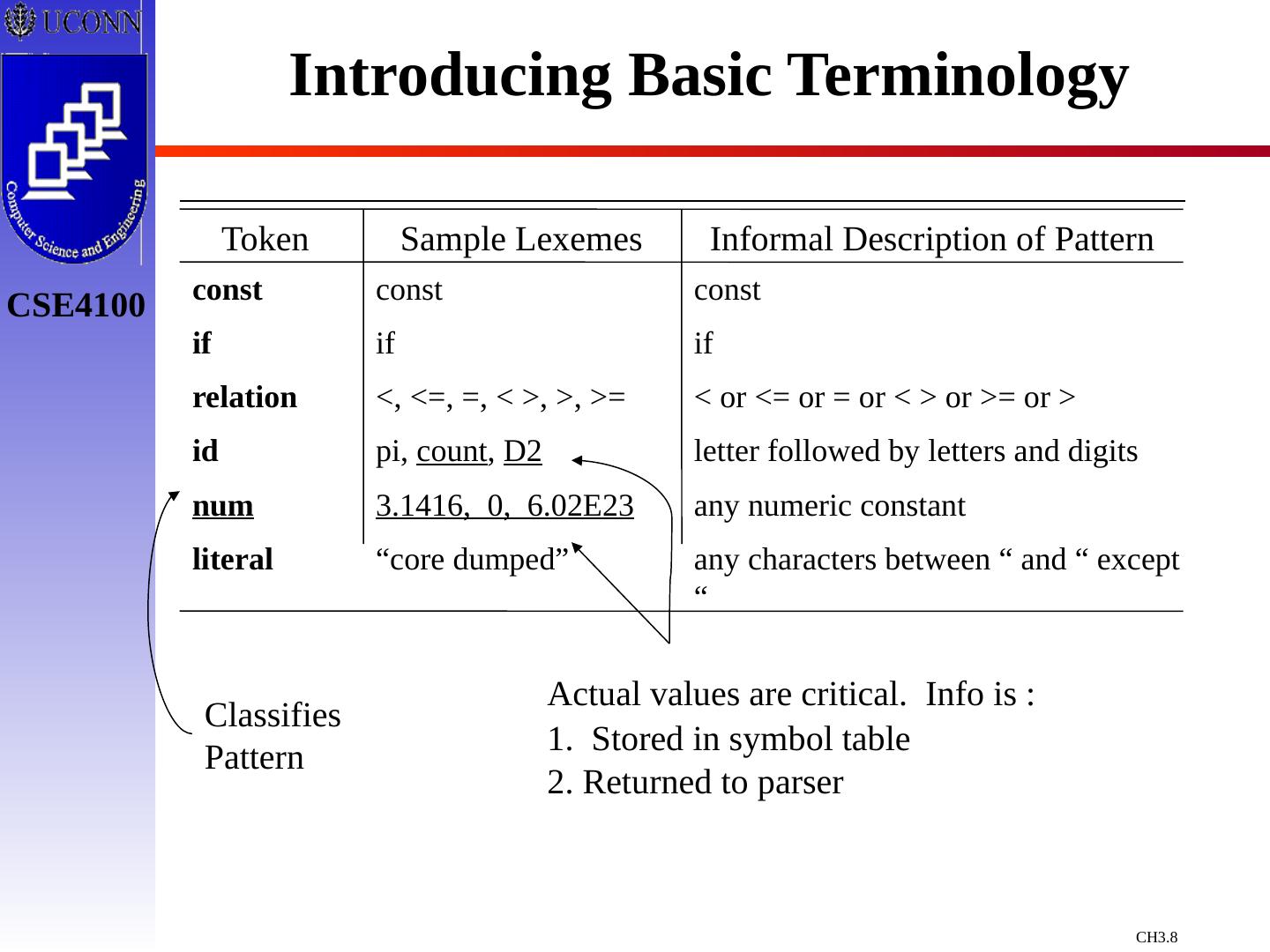
8 .Introducing Basic Terminology Token Sample Lexemes Informal Description of Pattern const if relation id num literal const if <, <=, =, < >, >, >= pi, count , D2 3.1416, 0, 6.02E23 “core dumped” const if < or <= or = or < > or >= or > letter followed by letters and digits any numeric constant any characters between “ and “ except “ Classifies Pattern Actual values are critical. Info is : 1. Stored in symbol table 2. Returned to parser
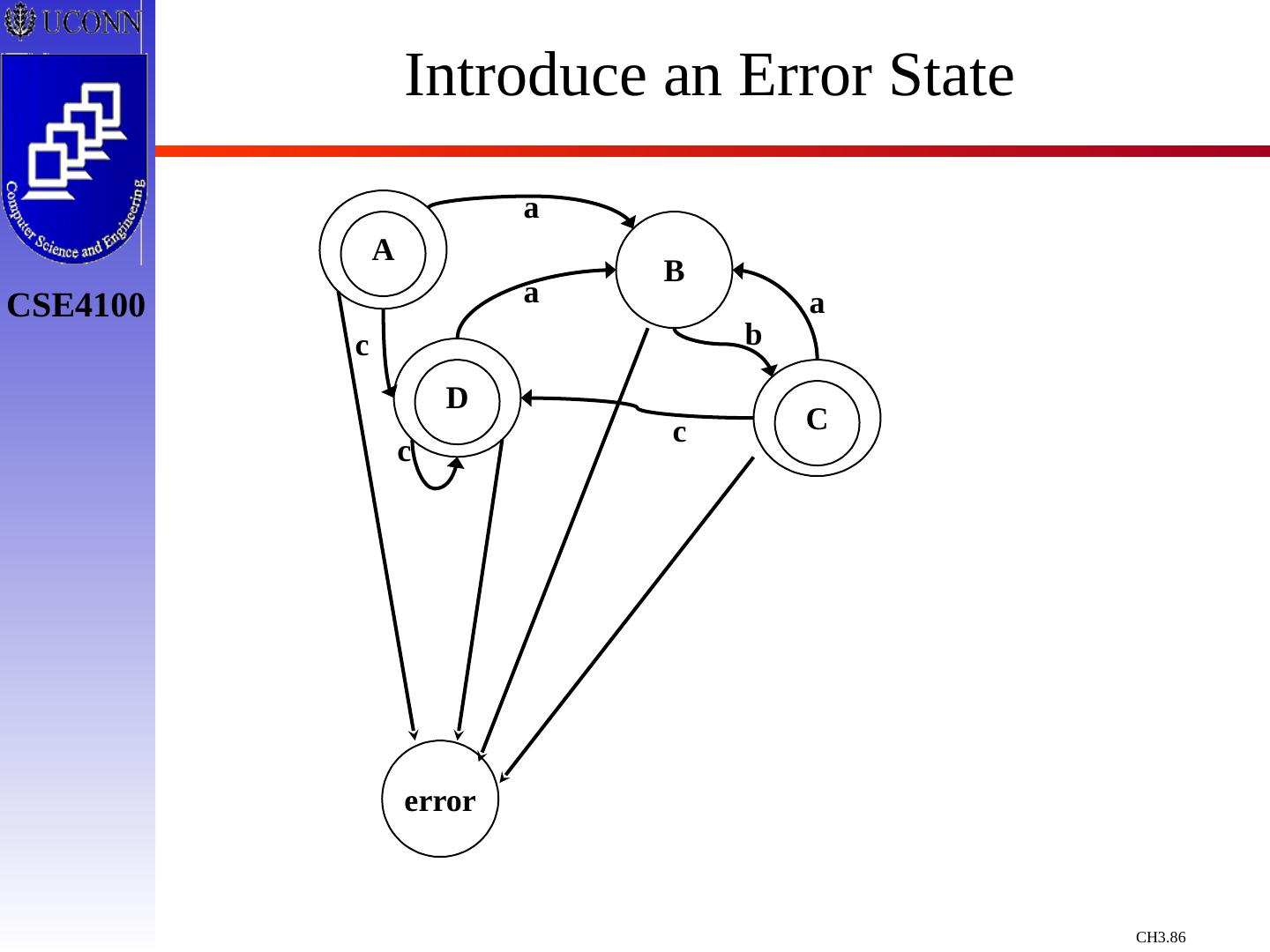
9 .Handling Lexical Errors Error Handling is very localized , with Respect to Input Source For example: whil ( x := 0 ) do generates no lexical errors in PASCAL In what Situations do Errors Occur? Prefix of remaining input doesn’t match any defined token Possible error recovery actions: Deleting or Inserting Input Characters Replacing or Transposing Characters Or, skip over to next separator to “ignore” problem
10 .How Does Lexical Analysis Work ? Question is related to efficiency Where is potential performance bottleneck? 3 Techniques to Address Efficiency : Lexical Analyzer Generator Hand-Code / High Level Language Hand-Code / Assembly Language In Each Technique … Who handles efficiency ? How is it handled ?
11 .Efficiency issues Is efficiency an issue? Three Lexical Analyzer construction techniques How they address efficiency? Lexical Analyzer Generator Hand-Code / High Level Language (I/O facilitated by the language) Hand-Code / Assembly Language (explicitly manage I/O). In Each Technique … Who handles efficiency ? How is it handled ?
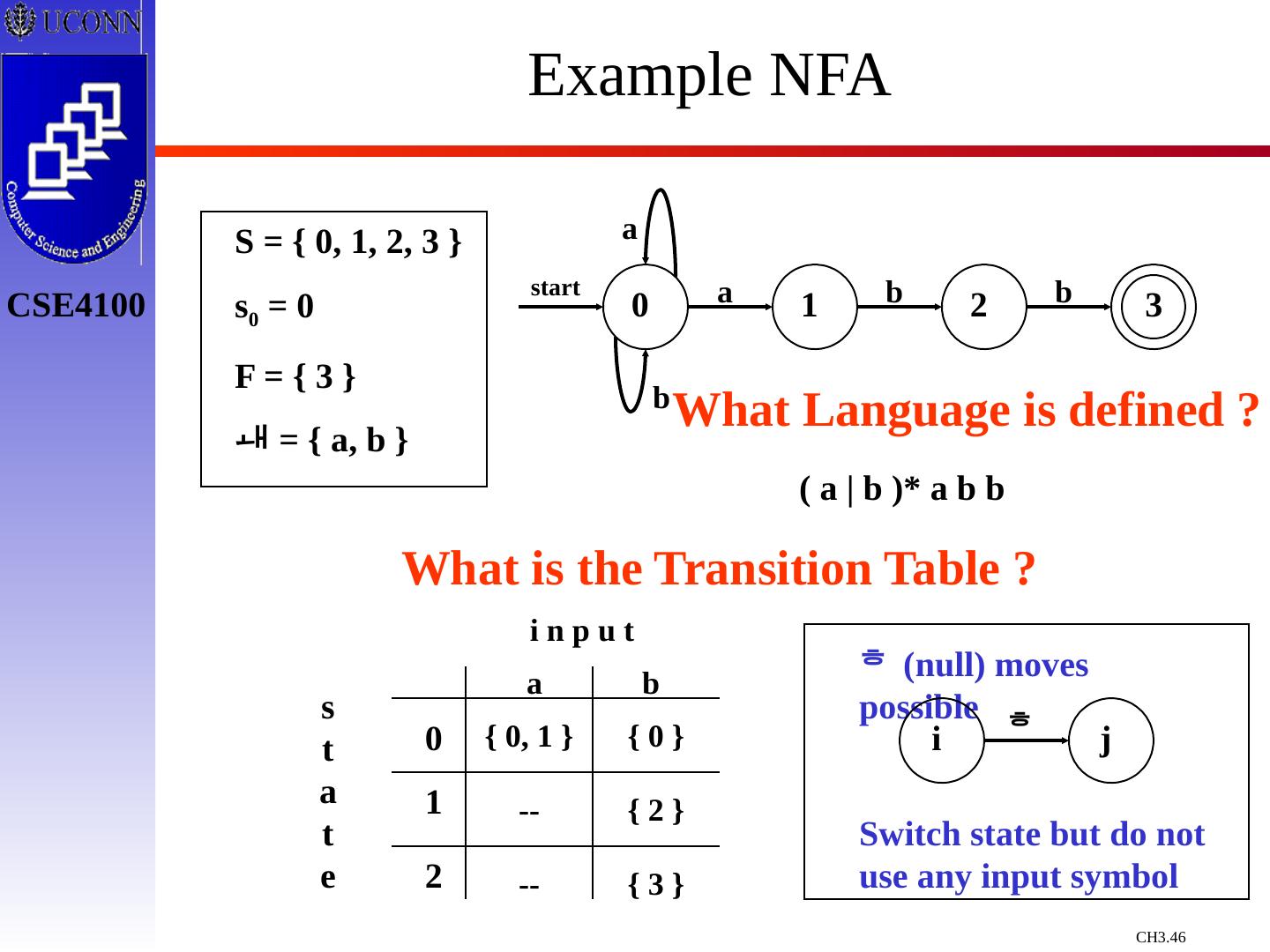
12 .Basic Scanning technique Use 1 character of look-ahead Obtain char with getc() Do a case analysis Based on lookahead char Based on current lexeme Outcome If char can extend lexeme, all is well, go on. If char cannot extend lexeme: Figure out what the complete lexeme is and return its token Put the lookahead back into the symbol stream
13 .Formalization How to formalize this pseudo-algorithm ? Idea Lexemes are simple Tokens are sets of lexemes.... So: Tokens form a LANGUAGE Question What languages do we know ? Regular Context Free Context Sensitive Natural
14 .Formalizing Token Definition ALPHABET : Finite set of symbols {0,1}, or {a,b,c}, or {n,m, … , z} DEFINITIONS: STRING : Finite sequence of symbols from an alphabet. 0011 or abbca or AABBC … A.K.A. word / sentence If S is a string, then |S| is the length of S, i.e. the number of symbols in the string S. : Empty String , with | | = 0
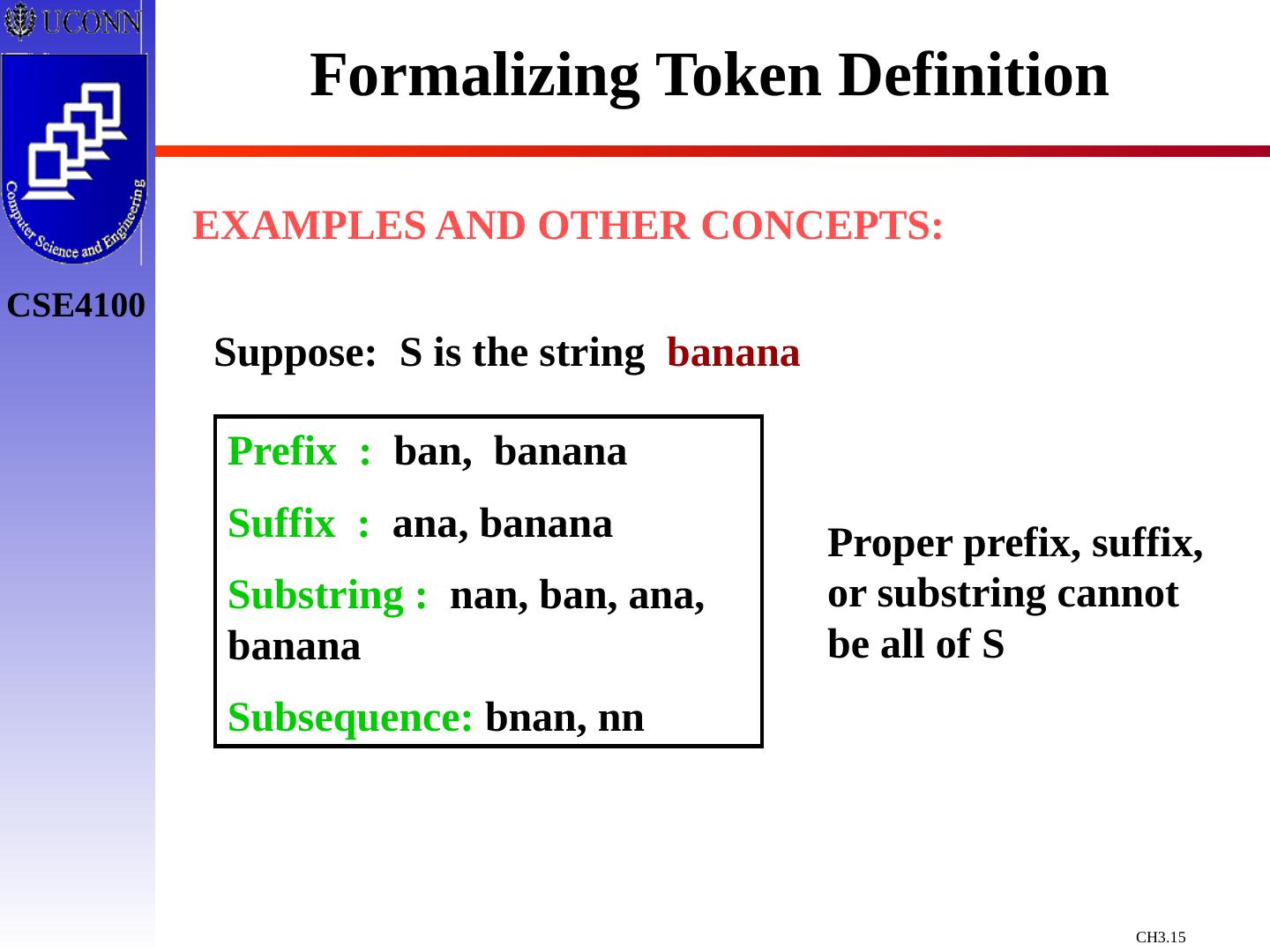
15 .Formalizing Token Definition EXAMPLES AND OTHER CONCEPTS: Suppose: S is the string banana Prefix : ban, banana Suffix : ana, banana Substring : nan, ban, ana, banana Subsequence: bnan, nn Proper prefix, suffix, or substring cannot be all of S
16 .Language Concepts A language, L , is simply any set of strings over a fixed alphabet. Alphabet Languages {0,1} {0,10,100,1000,100000…} {0,1,00,11,000,111,…} {a,b,c} {abc,aabbcc,aaabbbccc,…} {A, … ,Z} {TEE,FORE,BALL,…} {FOR,WHILE,GOTO,…} {A,…,Z,a,…,z,0,…9, { All legal PASCAL progs} +,-,…,<,>,…} { All grammatically correct English sentences } Special Languages: - EMPTY LANGUAGE - contains string only
17 .Formal Language Operations OPERATION DEFINITION union of L and M written L M concatenation o f L and M written LM Kleene closure of L written L* positive closure of L written L + L M = {s | s is in L or s is in M} L M = {st | s is in L and t is in M} L + = L* denotes “zero or more concatenations of “ L L* = L + denotes “one or more concatenations of “ L
18 .Formal Language Operations Examples L = {A, B, C, D } D = {1, 2, 3} L D = {A, B, C, D, 1, 2, 3 } LD = {A1, A2, A3, B1, B2, B3, C1, C2, C3, D1, D2, D3 } L 2 = { AA, AB, AC, AD, BA, BB, BC, BD, CA, … DD} L 4 = L 2 L 2 = ?? L* = { All possible strings of L plus } L + = L* - L ( L D ) = ?? L ( L D )* = ?? { A, B, C, D } ({A, B, C, D } { 1, 2, 3 }) L (L ( L D ))
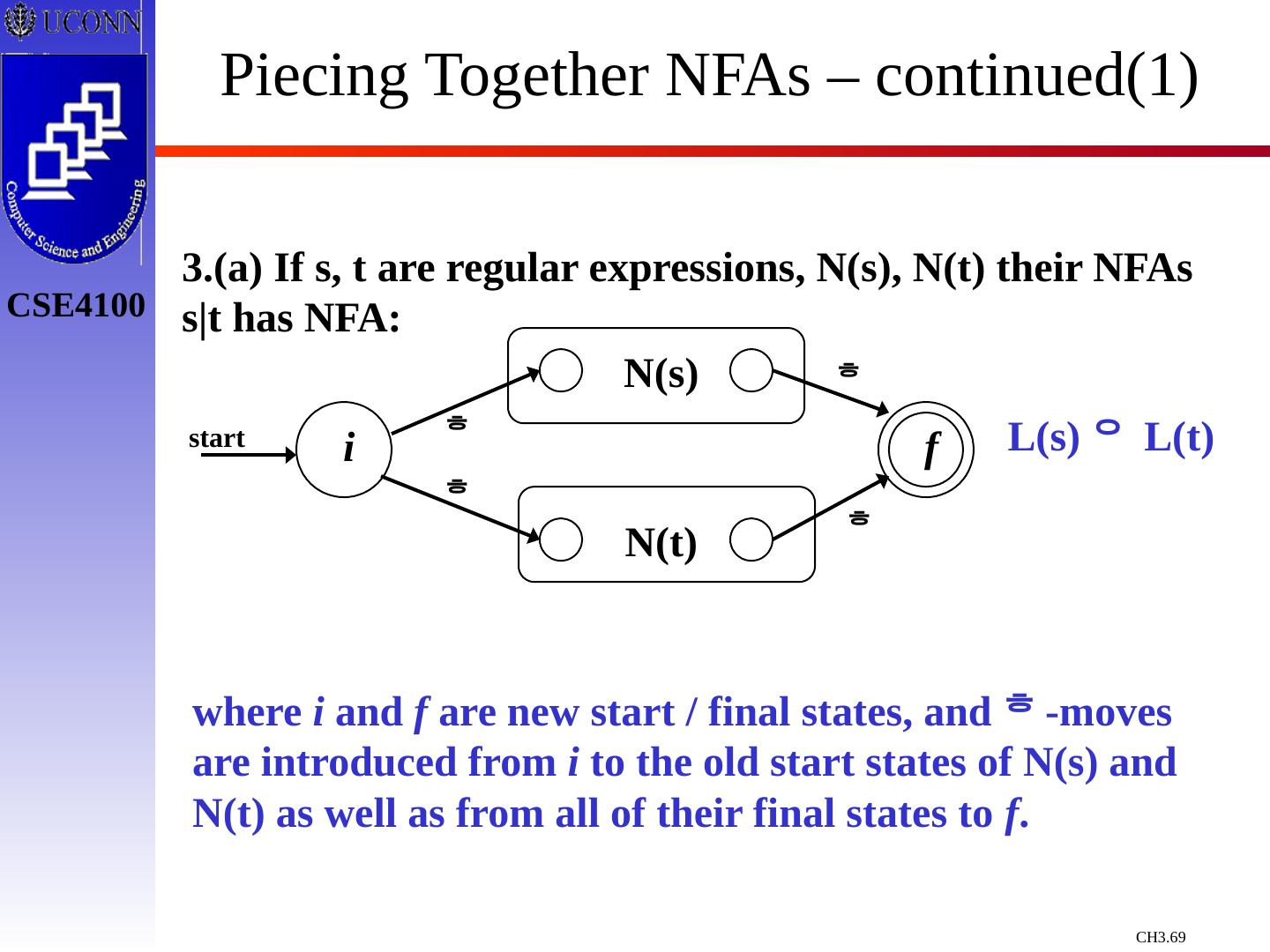
19 . A Regular Expression is a Set of Rules / Techniques for Constructing Sequences of Symbols (Strings) From an Alphabet. Let Be an Alphabet, r a Regular Expression Then L(r) is the Language That is Characterized by the Rules of R Language & Regular Expressions
20 .precedence Rules for Specifying Regular Expressions: is a regular expression denoting { } If a is in , a is a regular expression that denotes {a} Let r and s be regular expressions with languages L(r) and L(s). Then (a) (r) | (s) is a regular expression L(r) L(s) (b) (r)(s) is a regular expression L(r) L(s) (c) (r)* is a regular expression (L(r))* (d) (r) is a regular expression L(r) All are Left-Associative.
21 .EXAMPLES of Regular Expressions L = {A, B, C, D } D = {1, 2, 3} A | B | C | D = L (A | B | C | D ) (A | B | C | D ) = L 2 (A | B | C | D )* = L* (A | B | C | D ) ((A | B | C | D ) | ( 1 | 2 | 3 )) = L (L D)
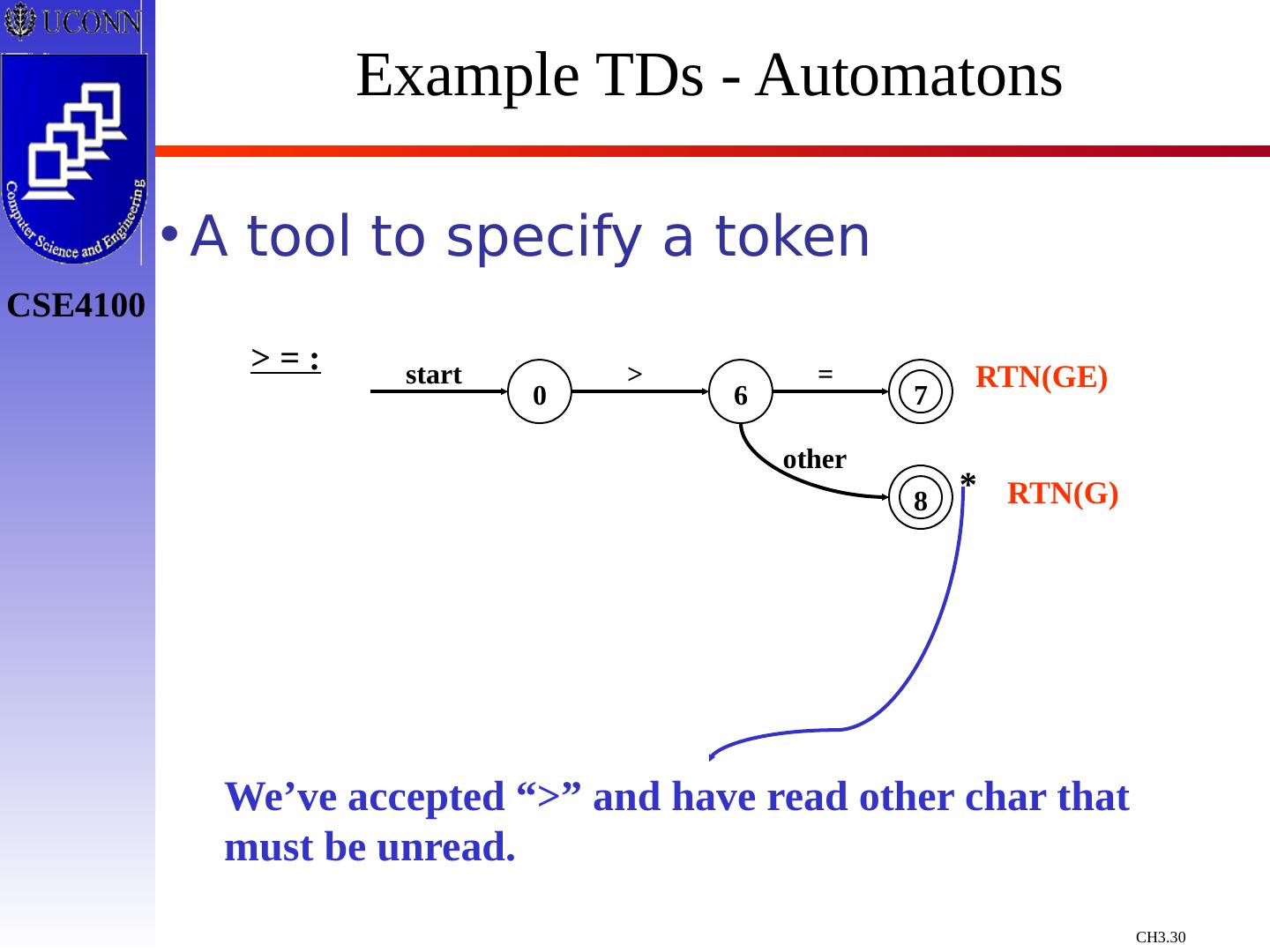
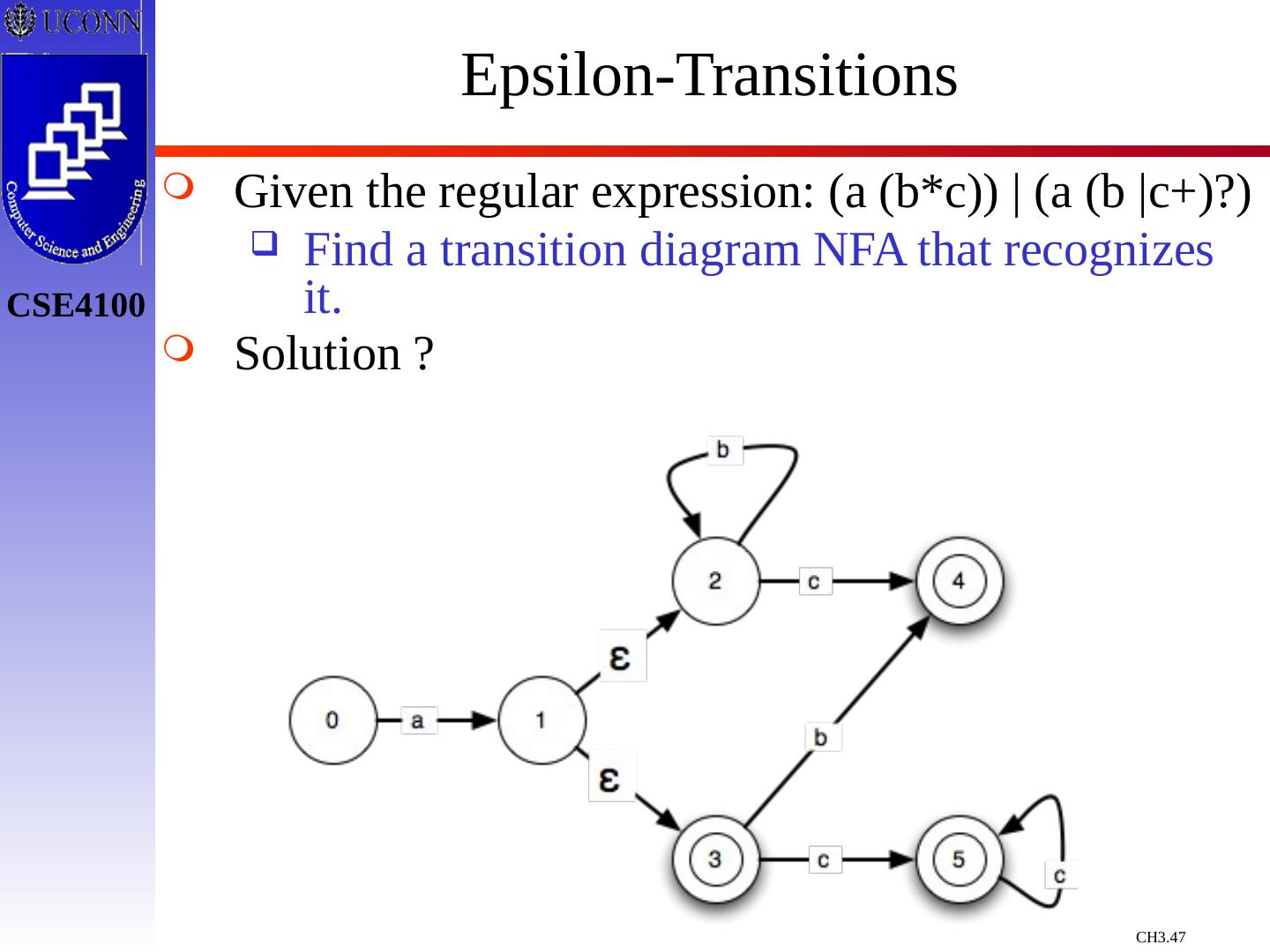
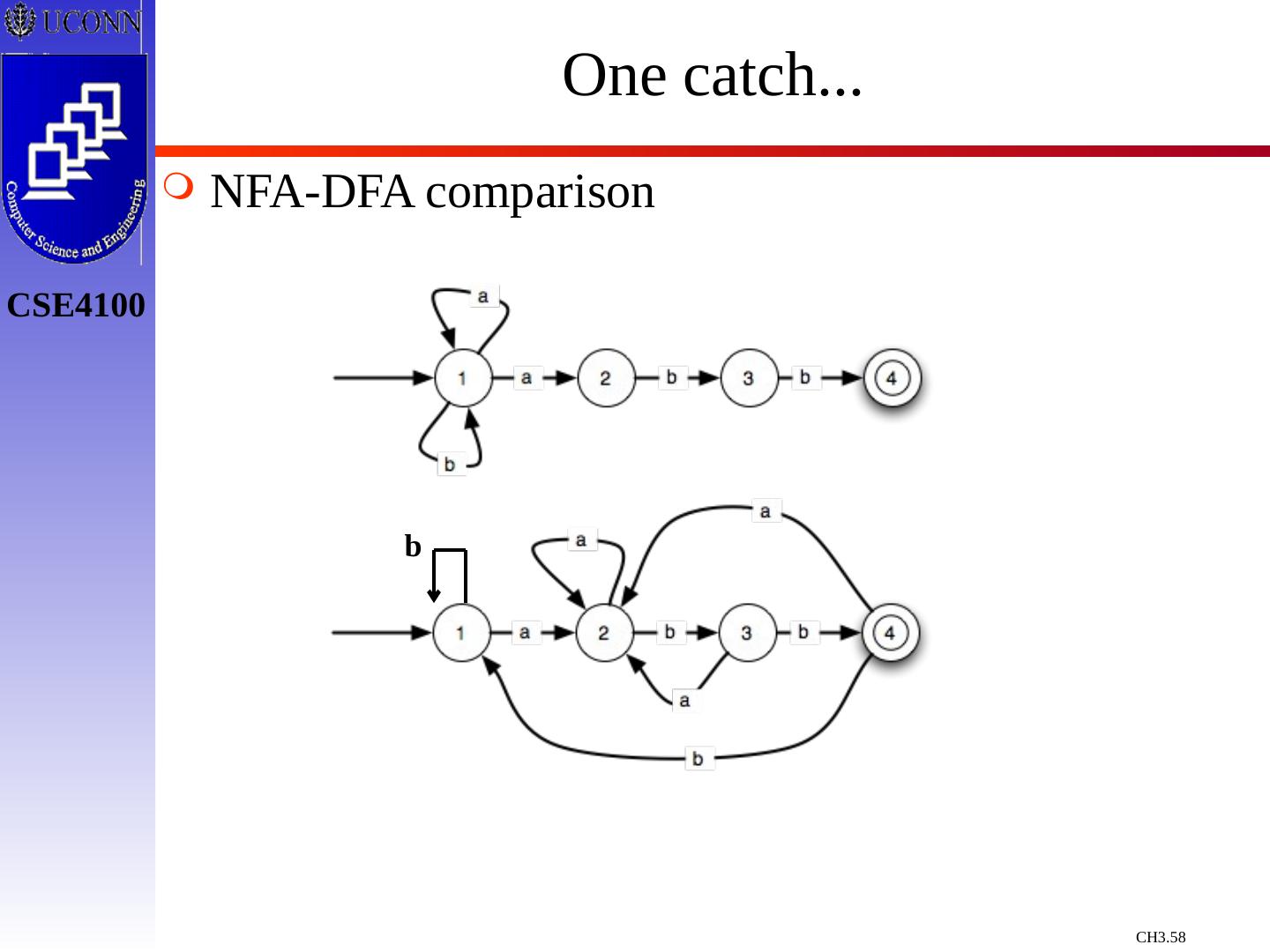
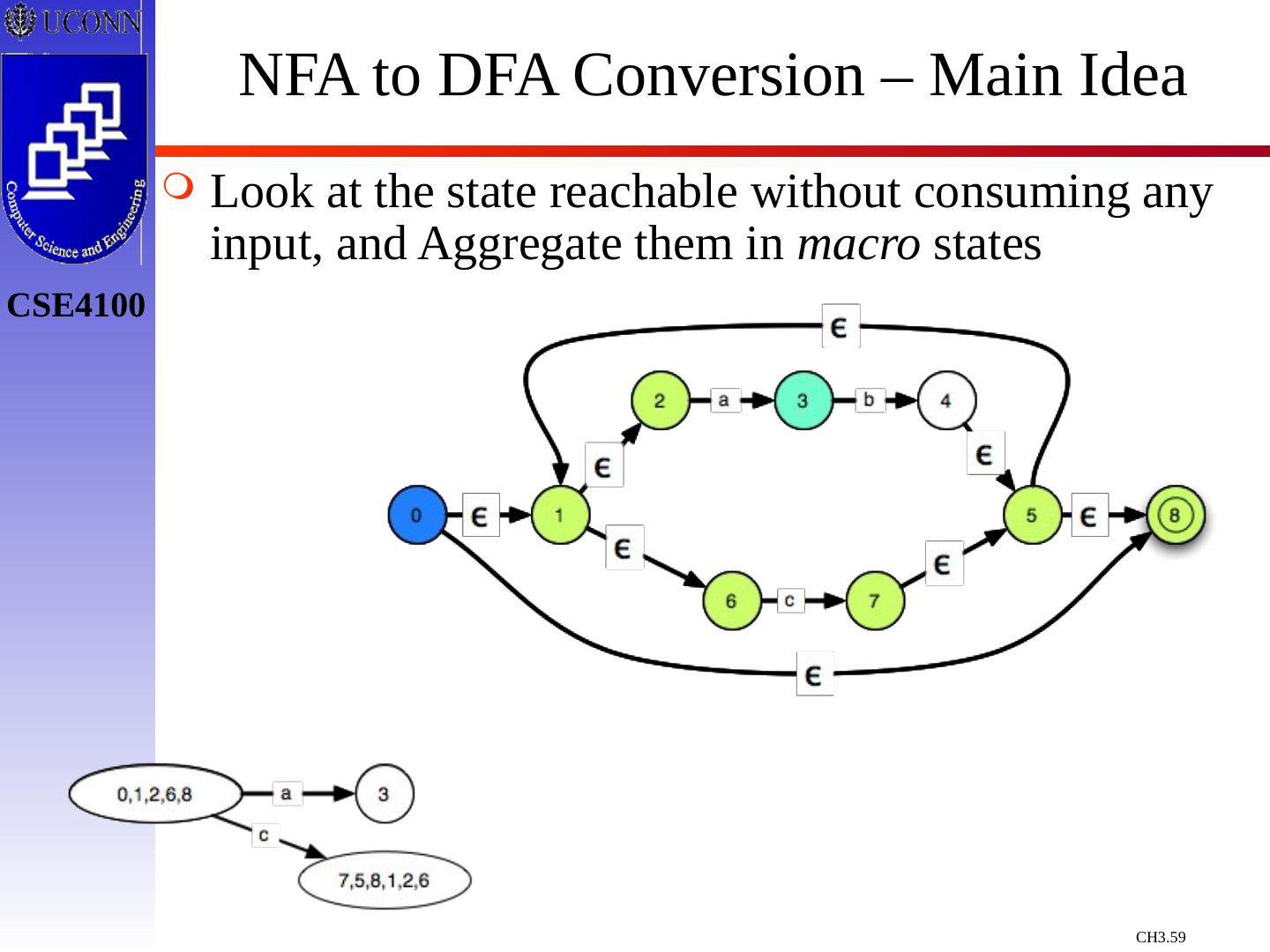
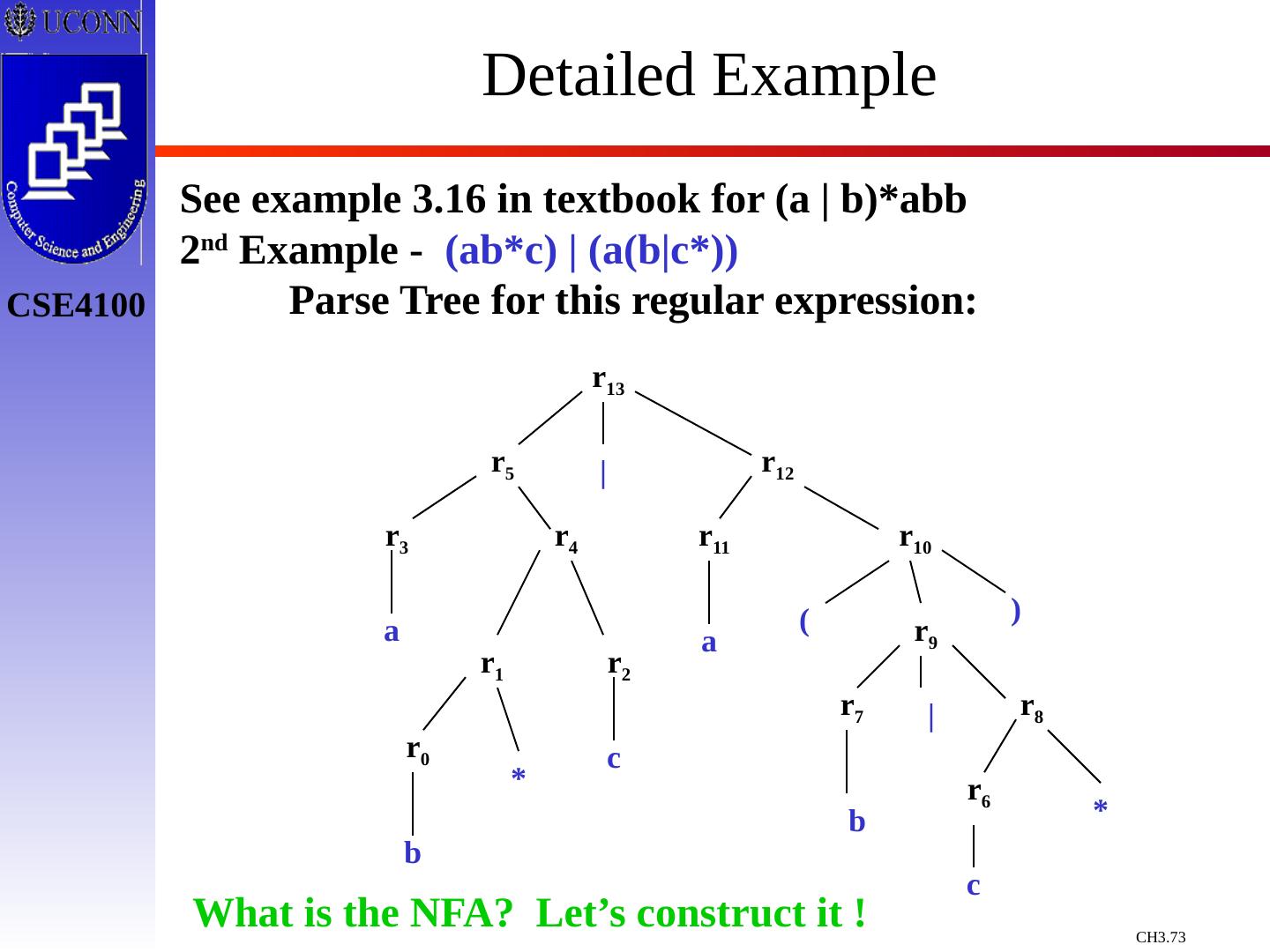
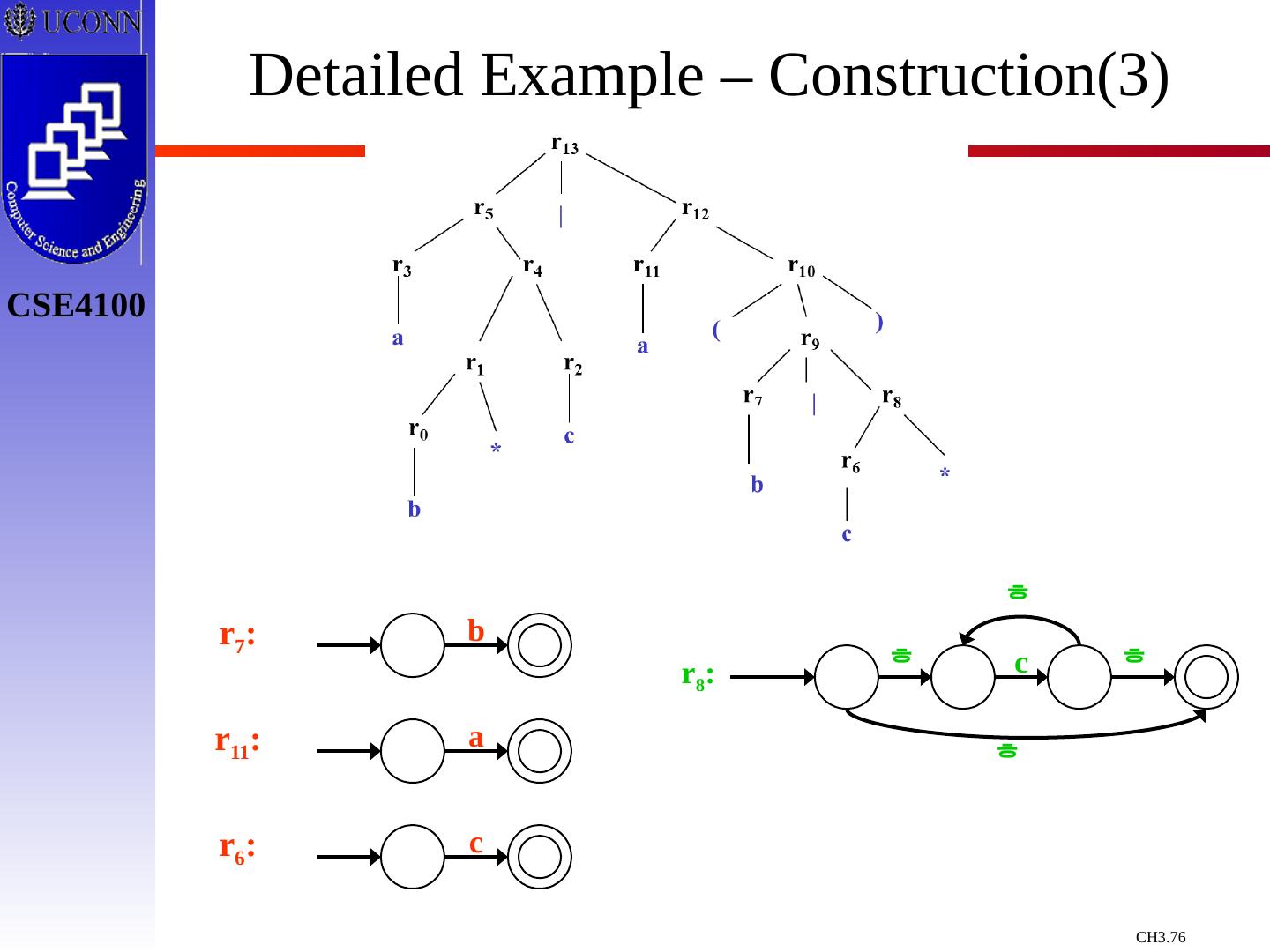
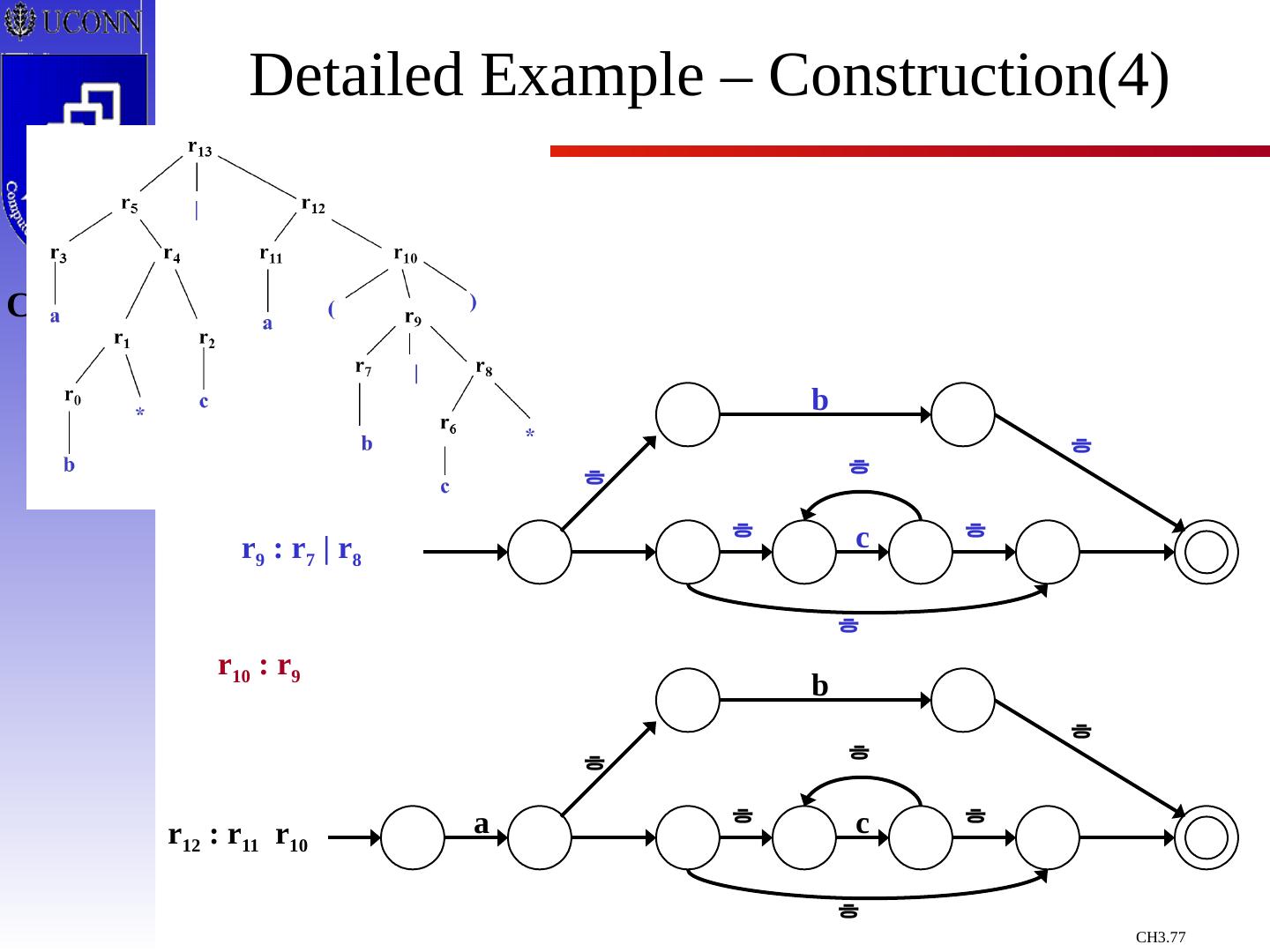
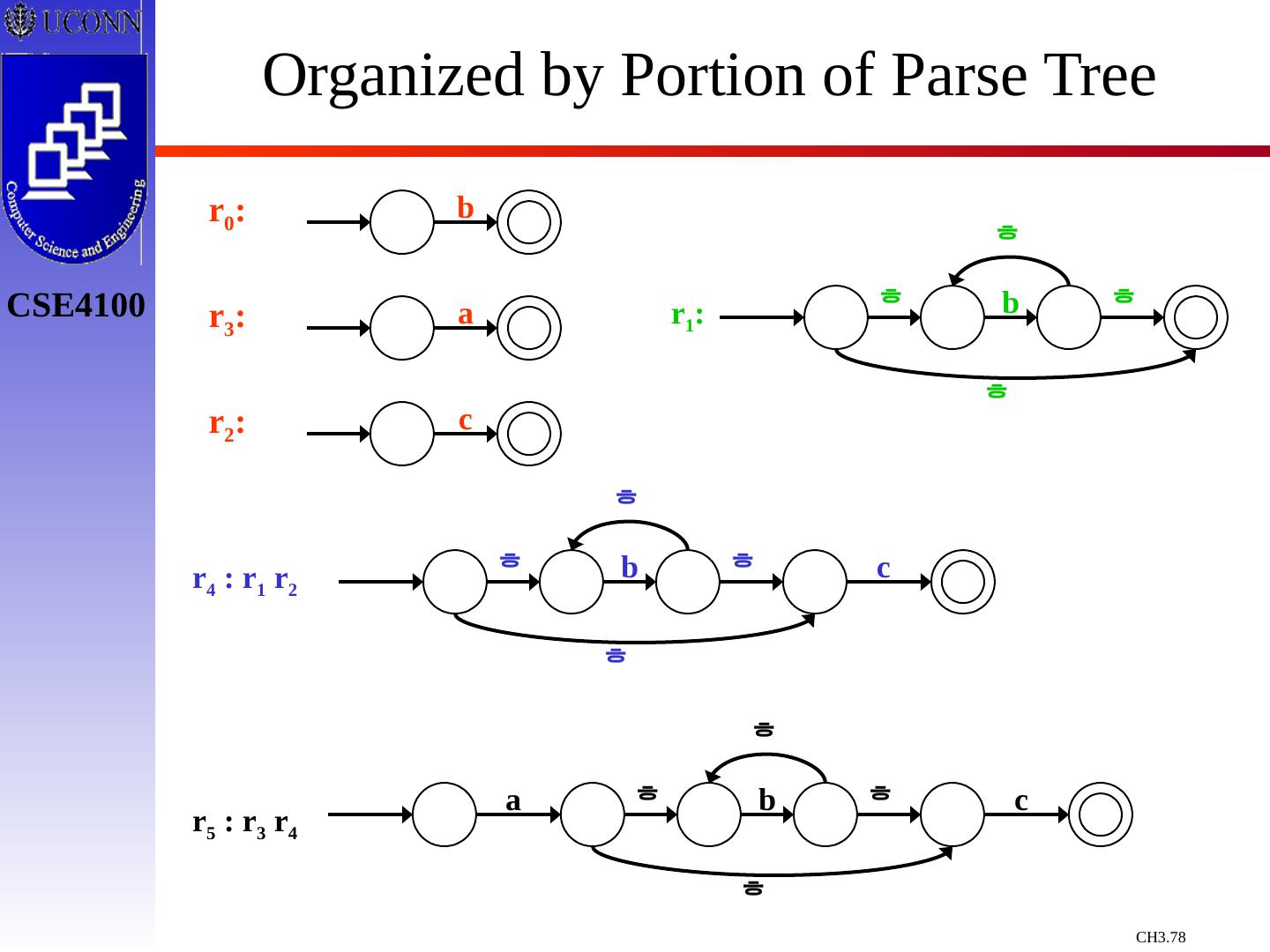
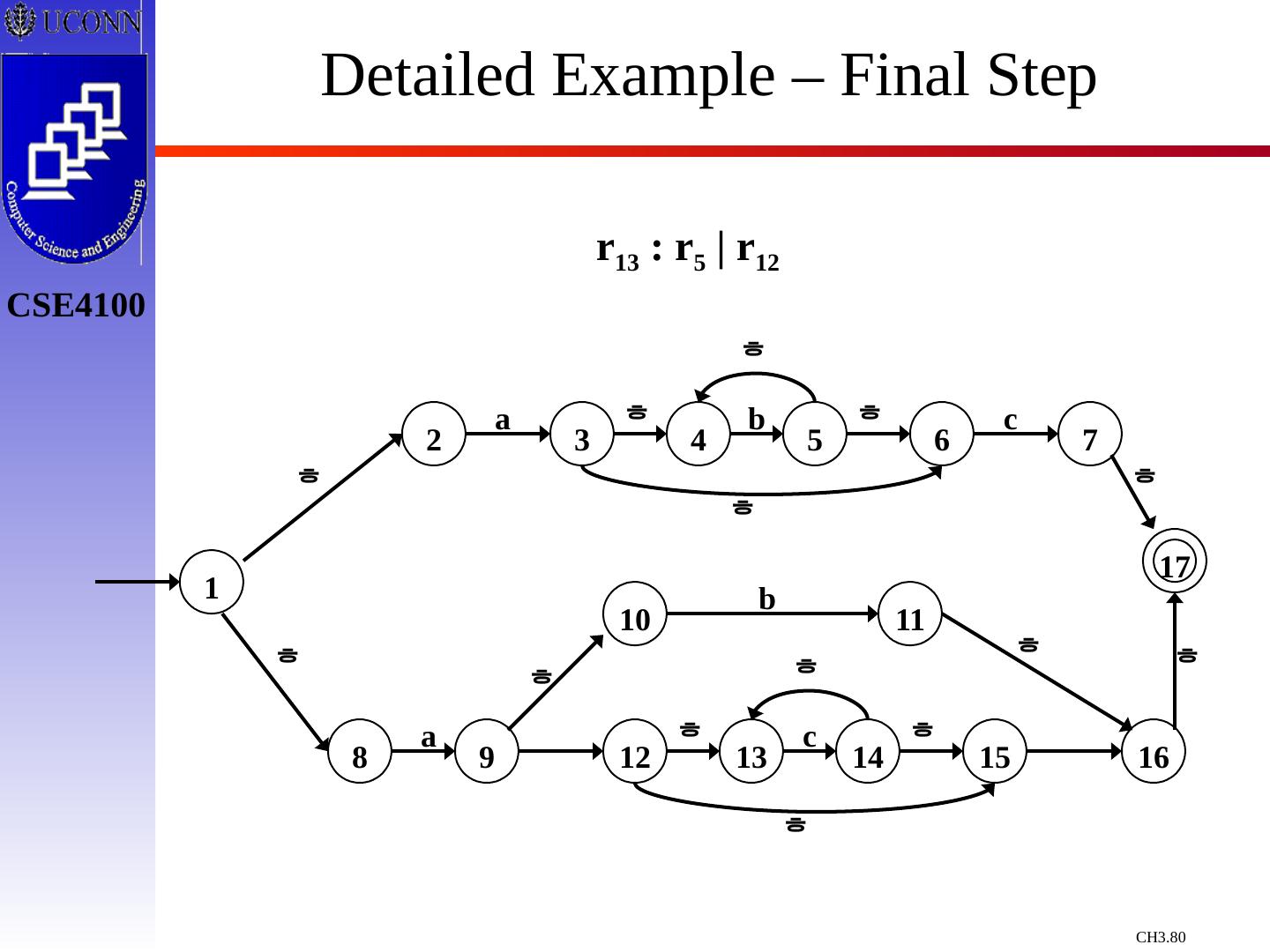
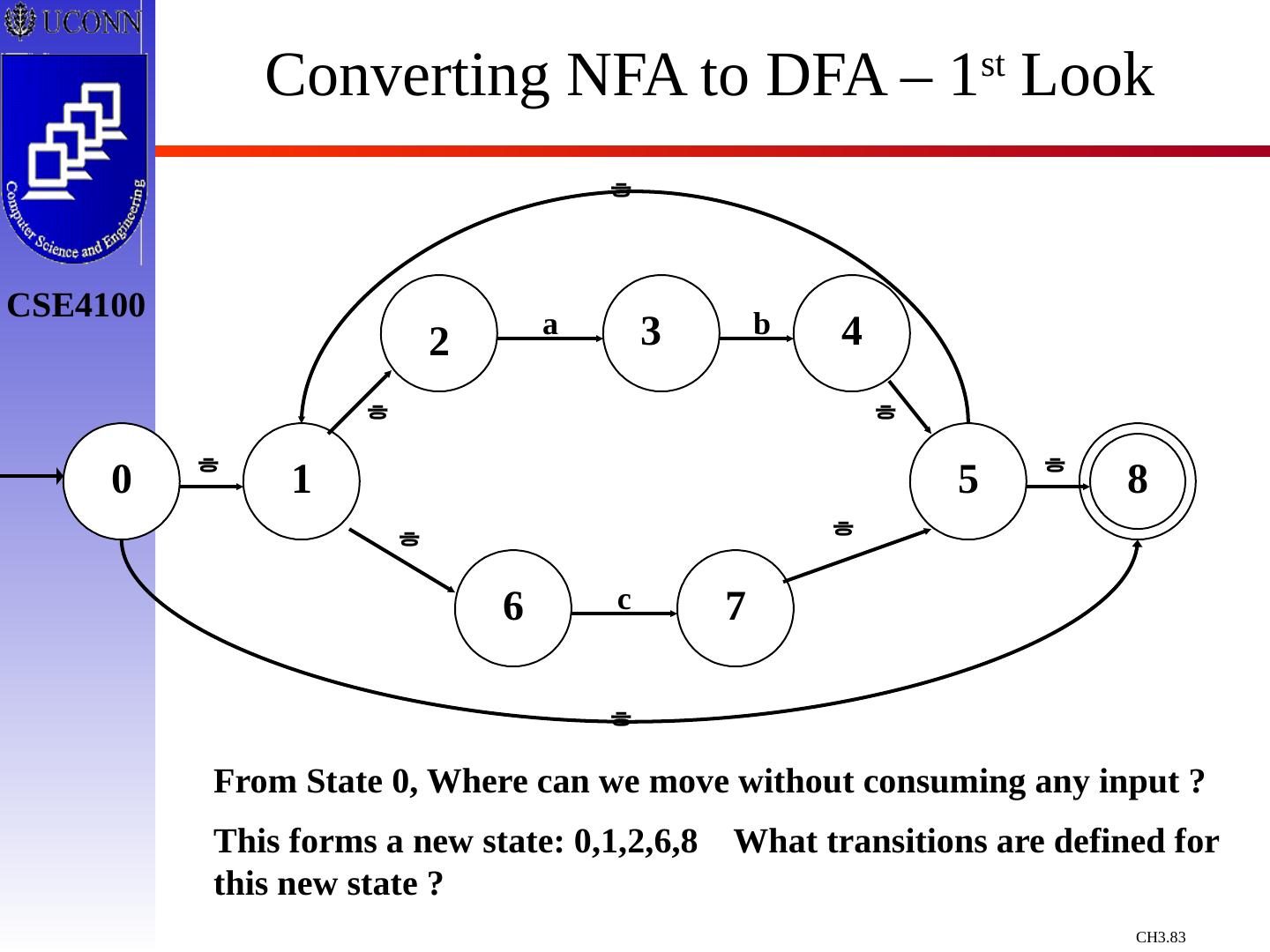
22 .Algebraic Properties of Regular Expressions AXIOM DESCRIPTION r | s = s | r r | (s | t) = (r | s) | t (r s) t = r (s t) r = r r = r r* = ( r | )* r ( s | t ) = r s | r t ( s | t ) r = s r | t r r** = r* | is commutative | is associative concatenation is associative concatenation distributes over | relation between * and Is the identity element for concatenation * is idempotent
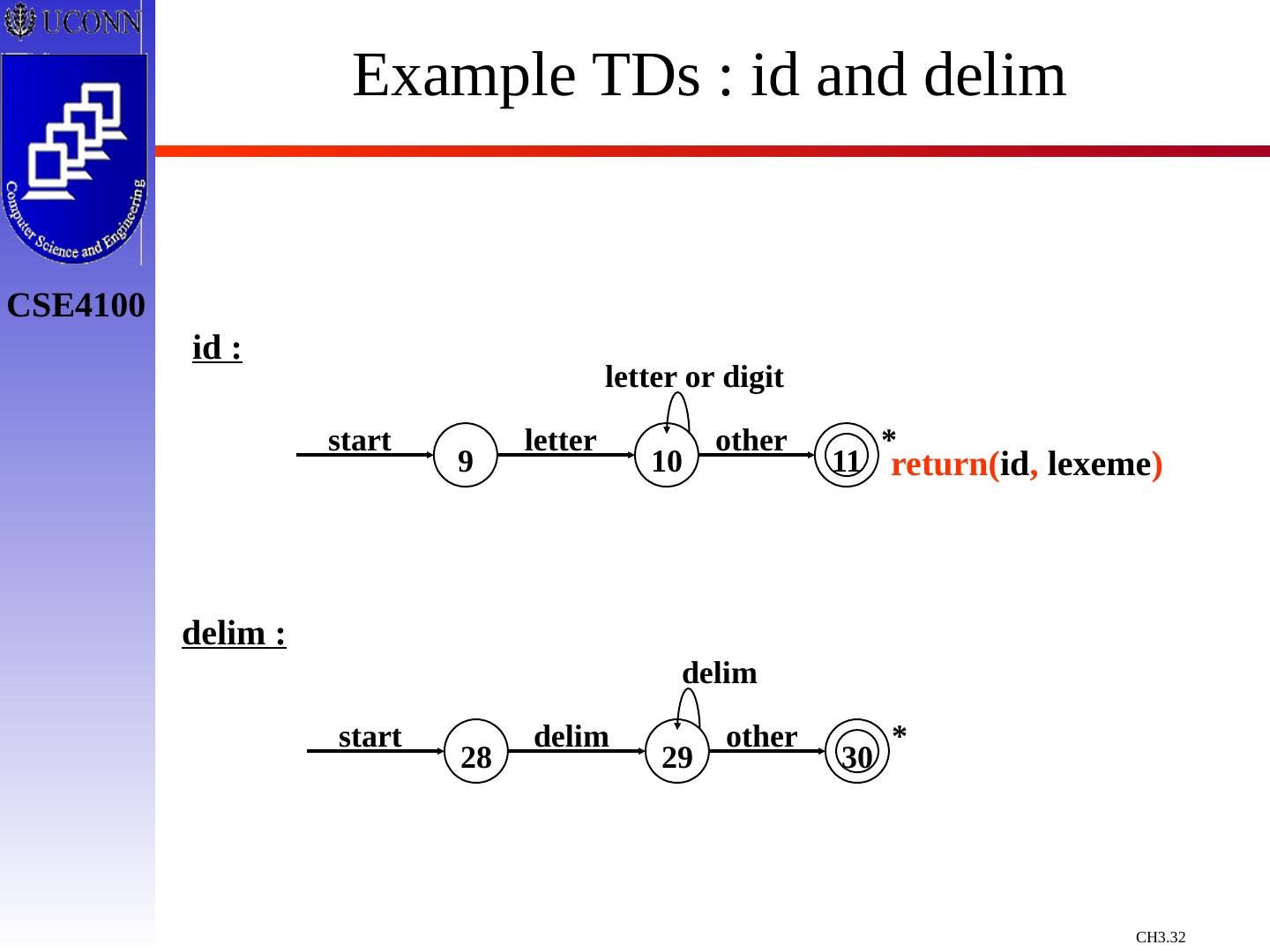
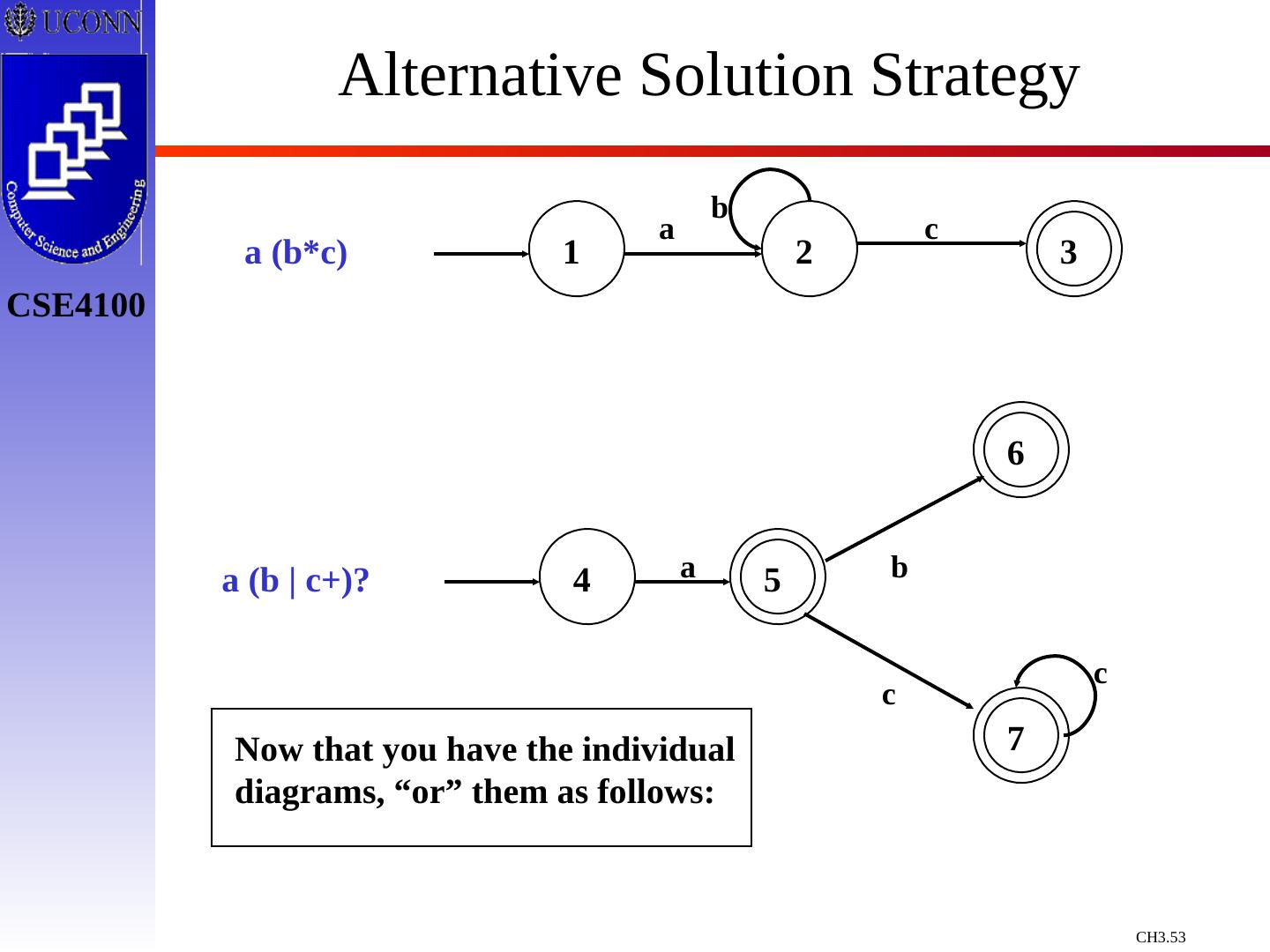
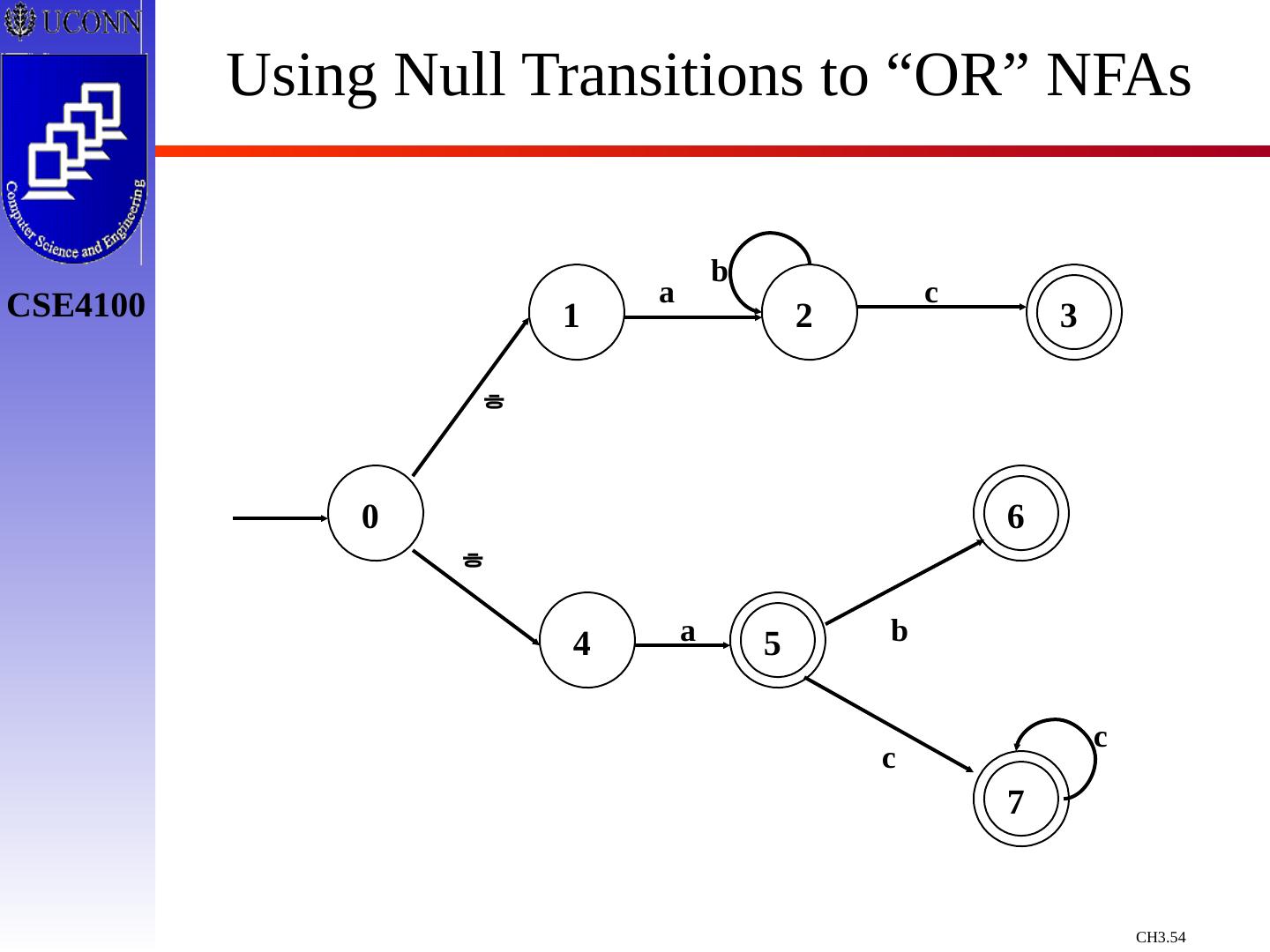
23 .Towards Token Definition Regular Definitions: Associate names with Regular Expressions For Example : PASCAL IDs letter A | B | C | … | Z | a | b | … | z digit 0 | 1 | 2 | … | 9 id letter ( letter | digit )* Shorthand Notation: “+” : one or more r* = r + | & r + = r r* “?” : zero or one [range] : set range of characters (replaces “|” ) [A-Z] = A | B | C | … | Z Using Shorthand : PASCAL IDs id [A-Za-z][A-Za-z0-9]* We’ll Use Both Techniques
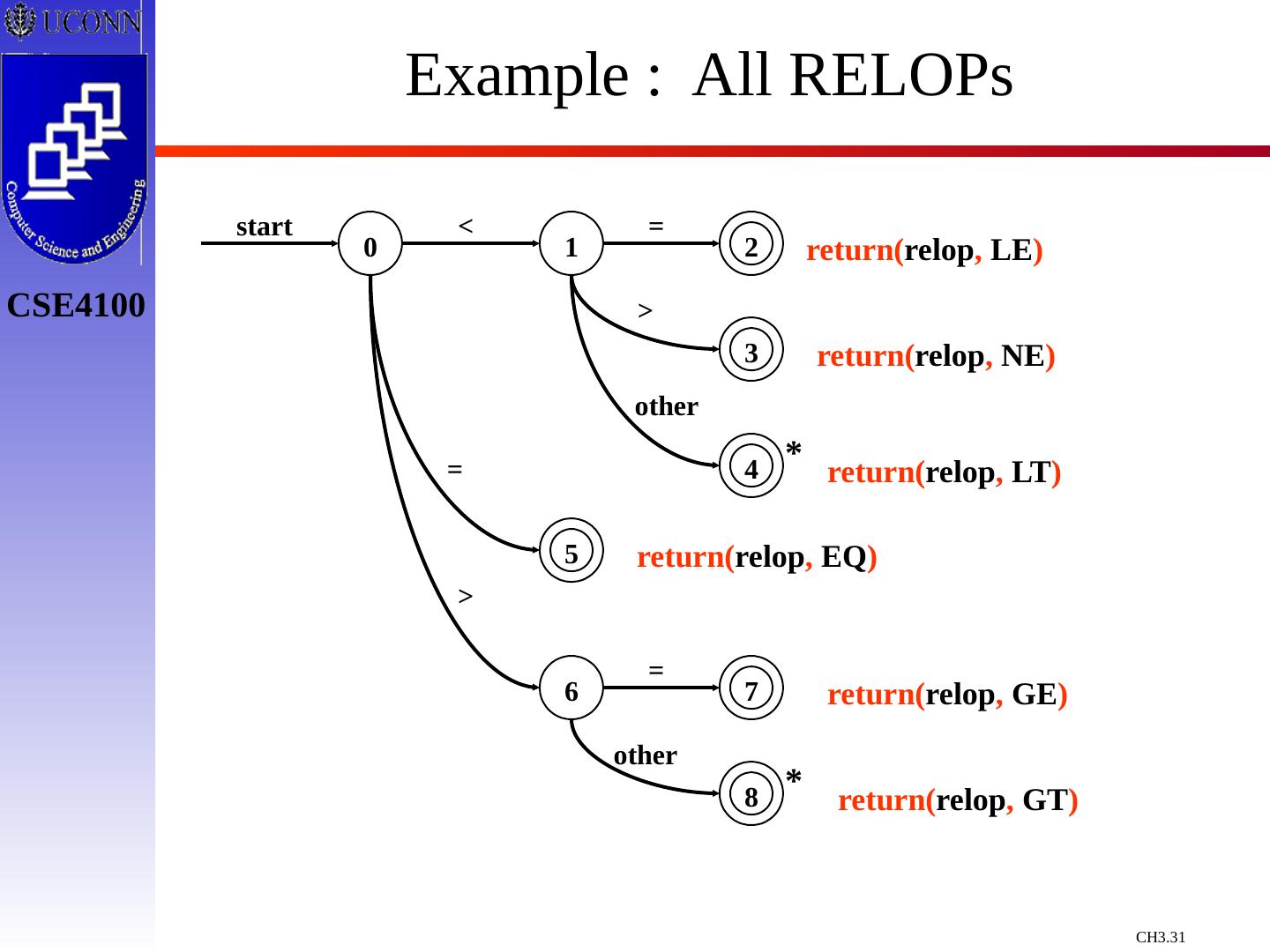
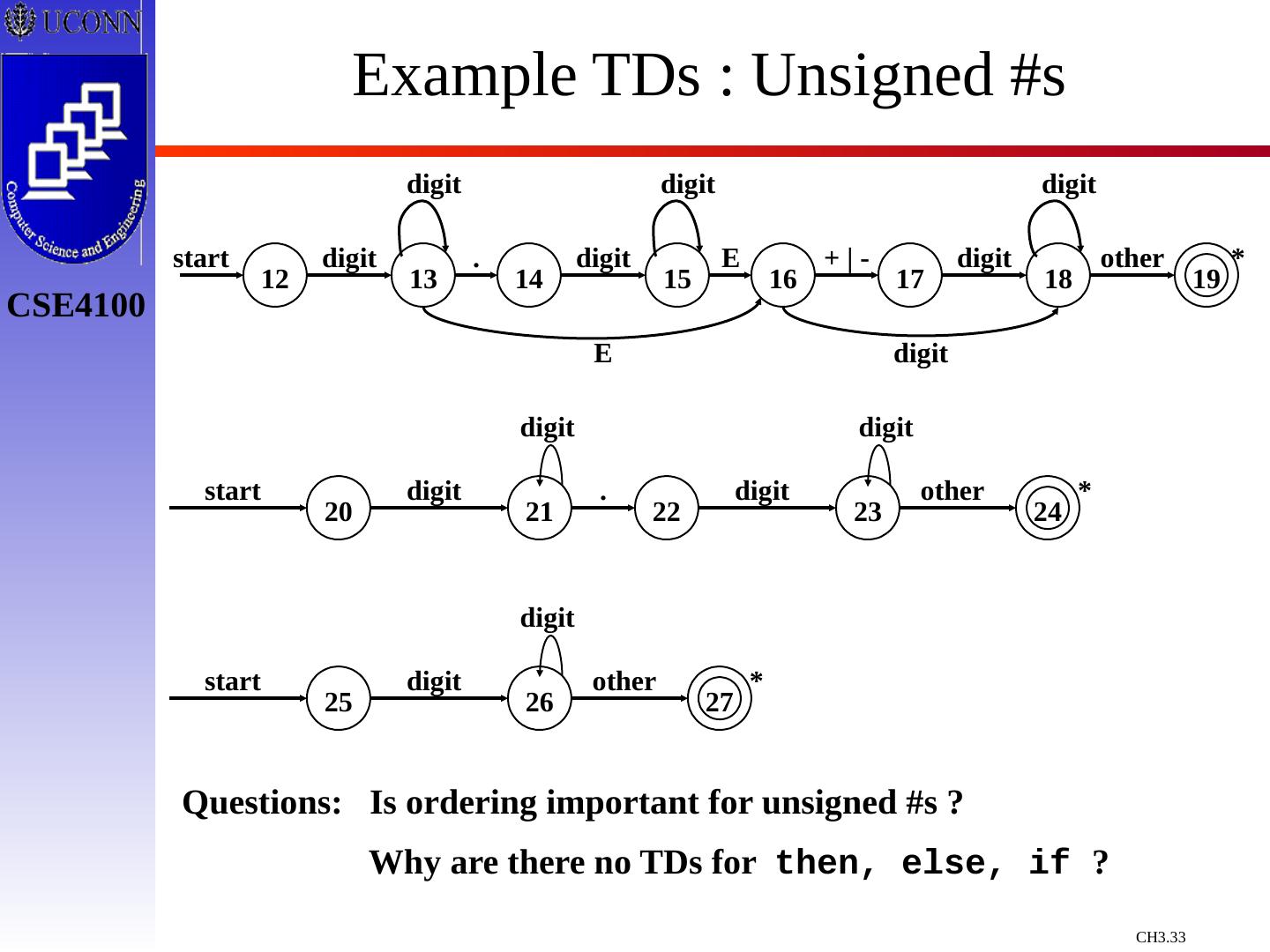
24 .Token Recognition Tokens as Patterns How can we use concepts developed so far to assist in recognizing tokens of a source language ? Assume Following Tokens: if, then, else, relop, id, num What language construct are they used for ? Given Tokens, What are Patterns ? if if then then else else relop < | <= | > | >= | = | <> id letter ( letter | digit )* num digit + (. digit + ) ? ( E(+ | -) ? digit + ) ? What does this represent ? What is ?
25 .What Else Does Lexical Analyzer Do? Throw Away Tokens Fact Some languages define tokens as useless Example: C whitespace, tabulations, carriage return, and comments can be discarded without affecting the program’s meaning. blank b tab ^T newline ^M delim blank | tab | newline ws delim +
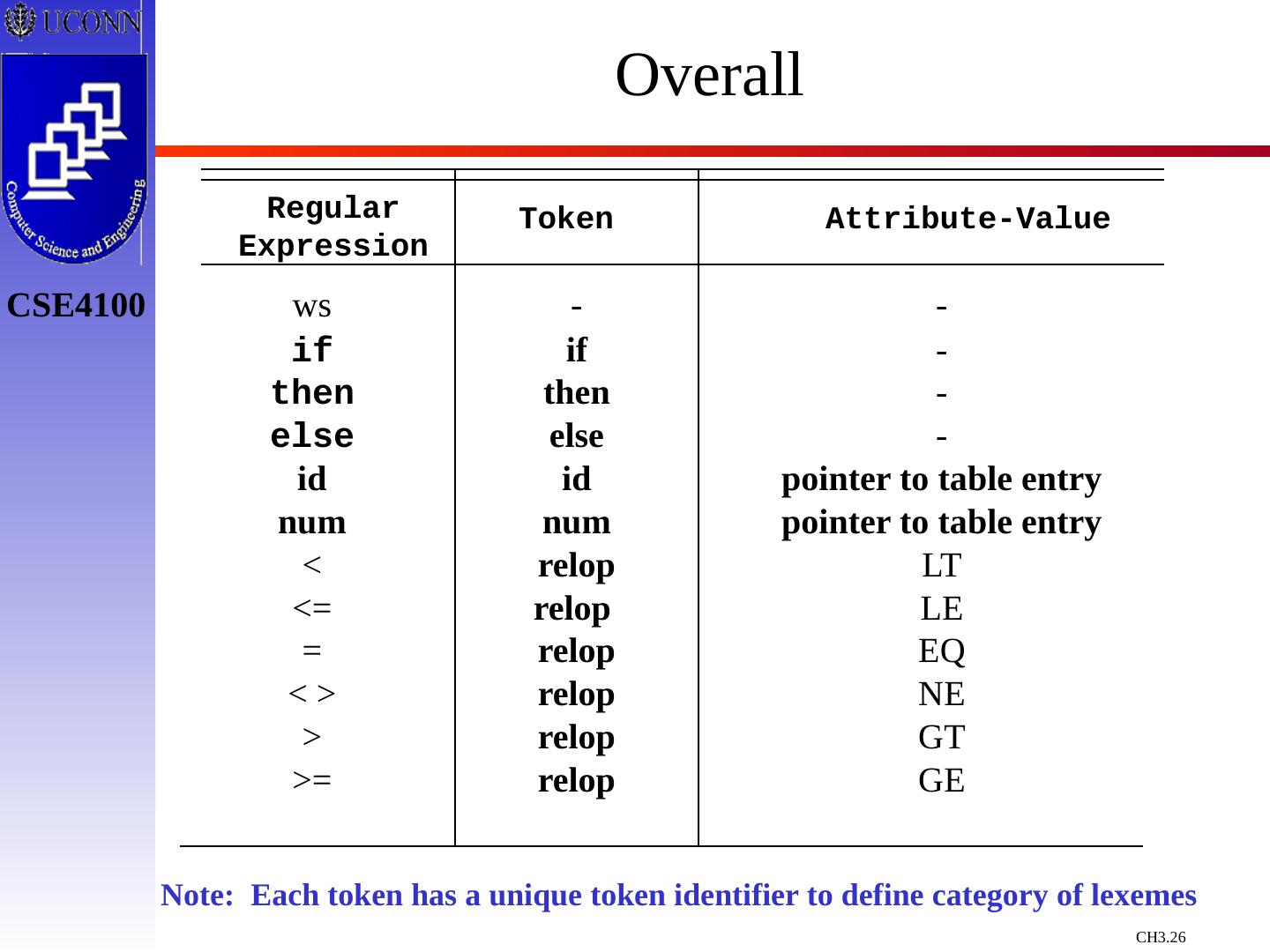
26 .Overall Regular Expression Token Attribute-Value ws if then else id num < <= = < > > >= - if then else id num relop relop relop relop relop relop - - - - pointer to table entry pointer to table entry LT LE EQ NE GT GE Note: Each token has a unique token identifier to define category of lexemes
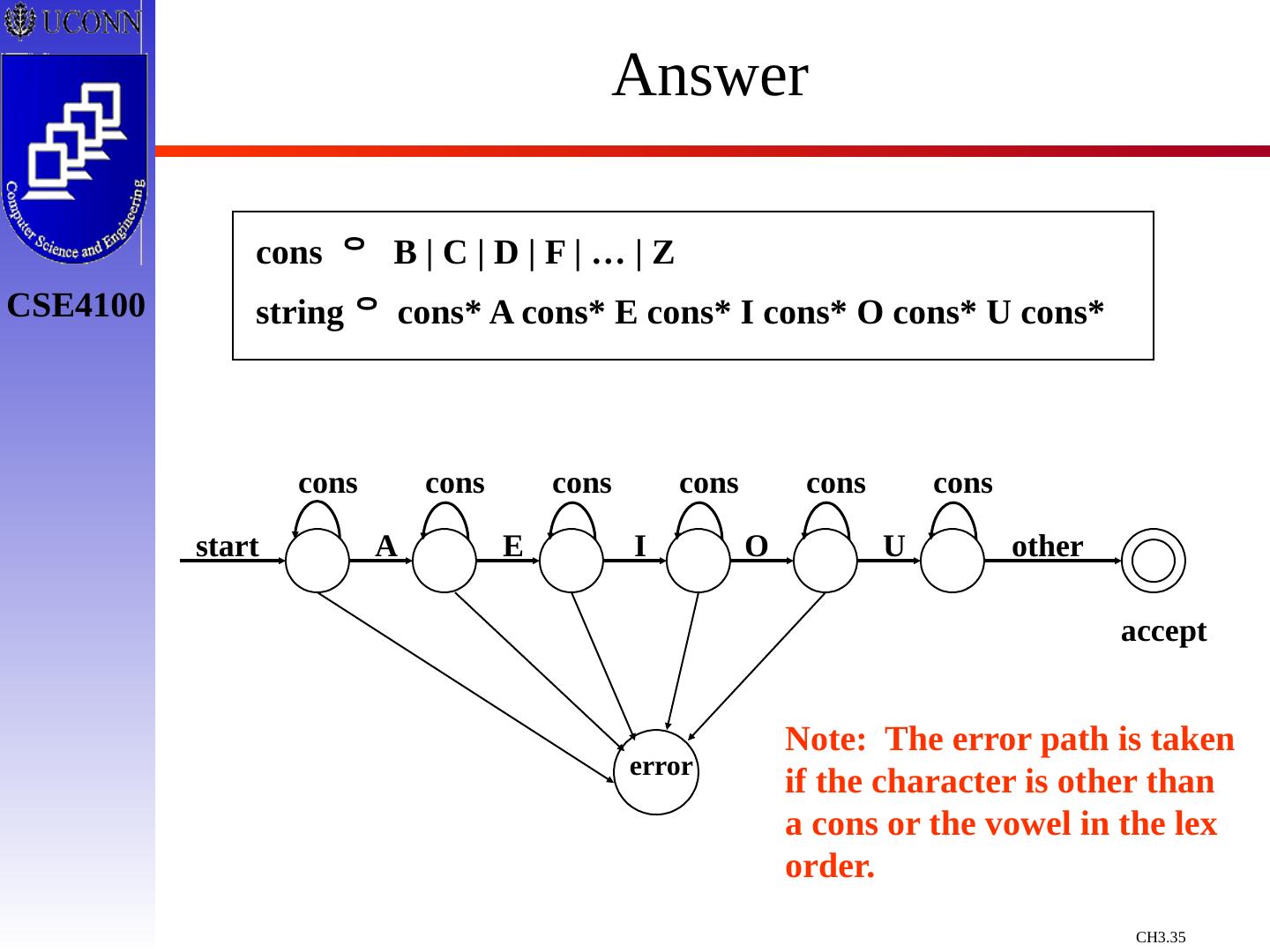
27 .Regular Expression Examples All Strings of Upper Case Characters That Contain Five Vowels in Order All Strings of Lower Case Characters start with “tab” or end with “bat” cons B | C | D | F | … | Z string cons* A cons* E cons* I cons* O cons* U cons* lowers a | b | … | z string ( tab lowers* ) |( lowers* bat )
28 .Regular Expression Examples All Strings of {1,2,3} where {1,2,3} exist in descending order All Strings of {0,1, …, 9} in which Digits are in Ascending Numerical Order string 3* 2* 1* string 0* 1* 2* 3* 4* 5* 6* 7* 8* 9*
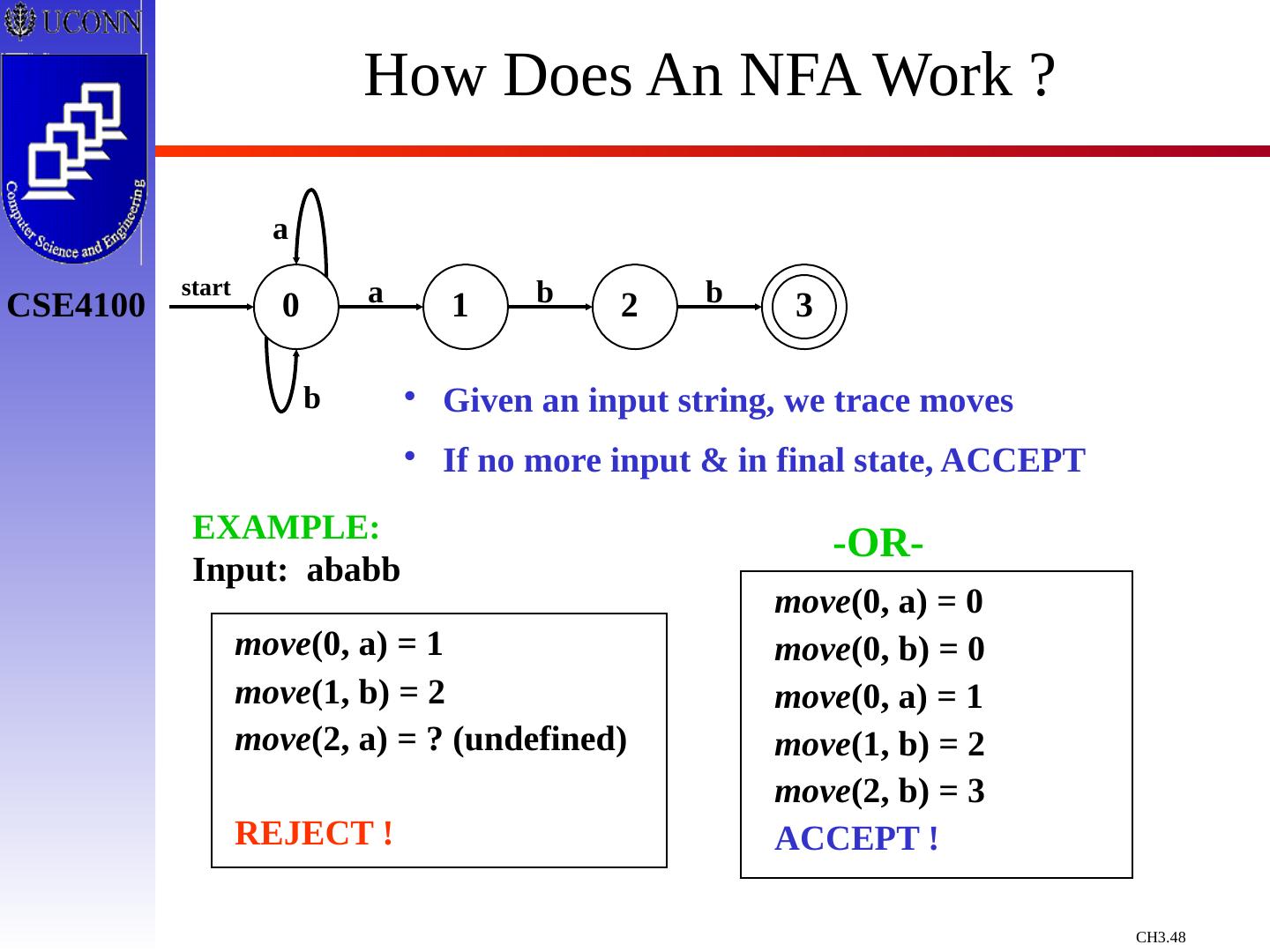
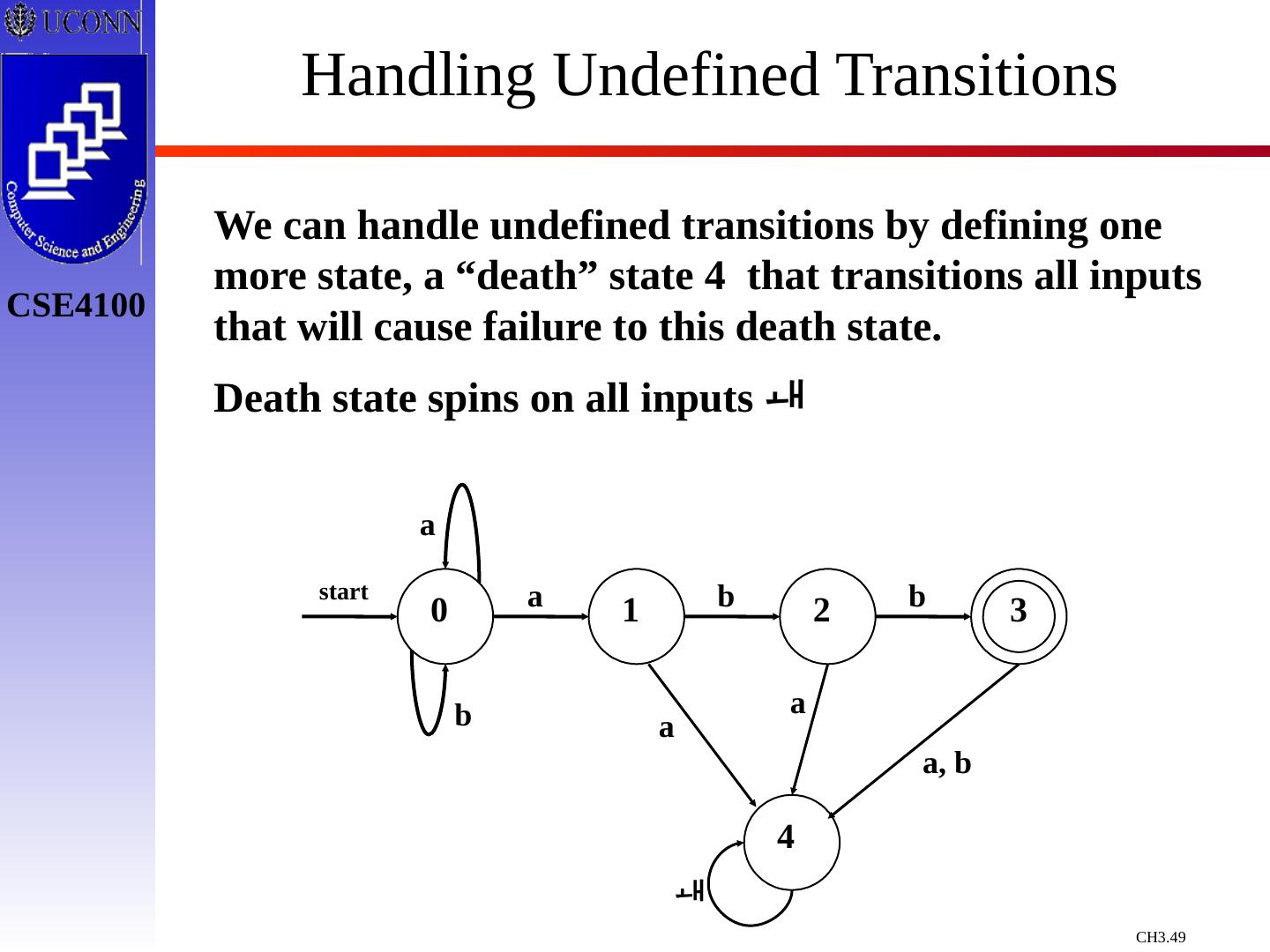
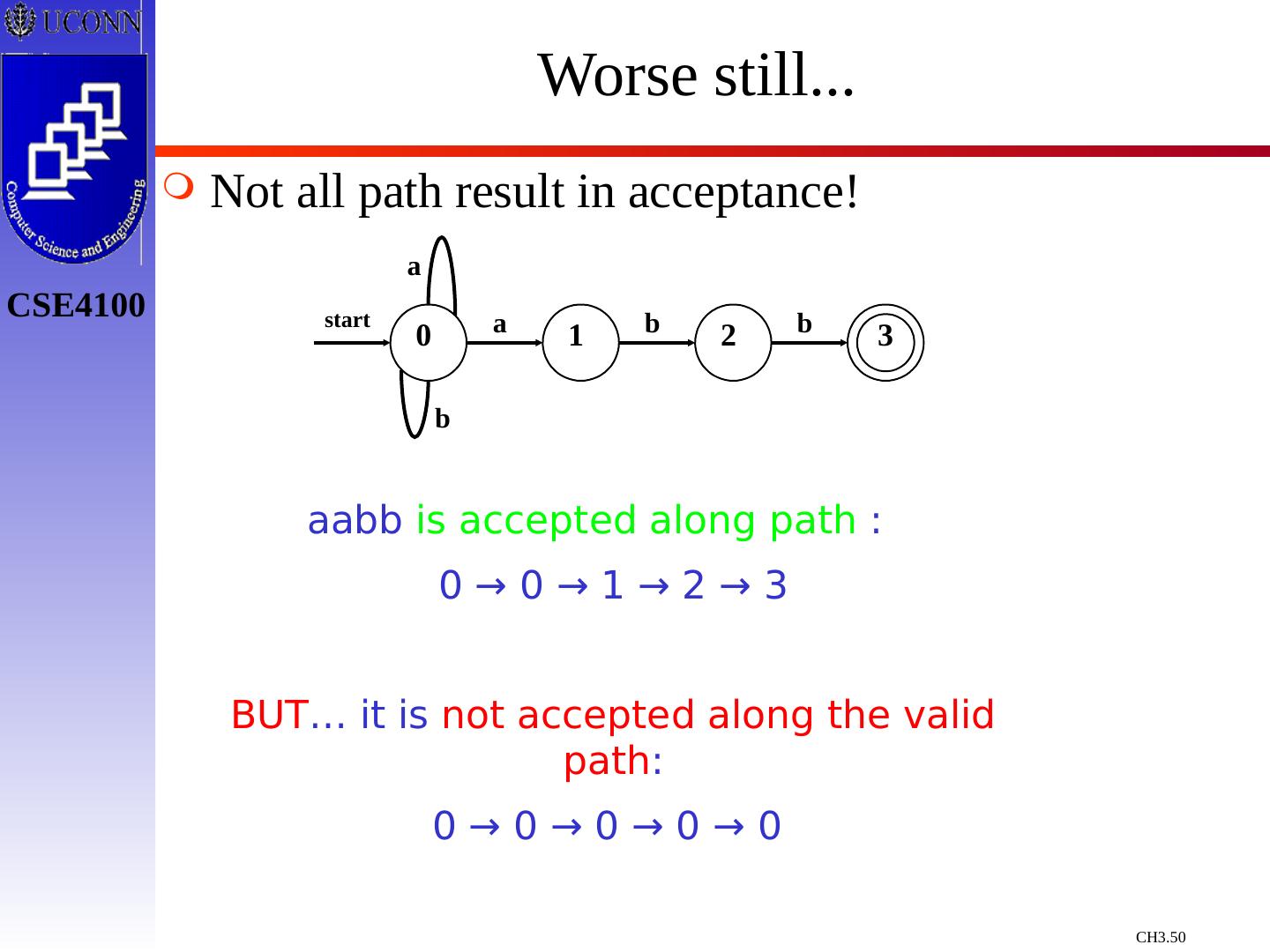
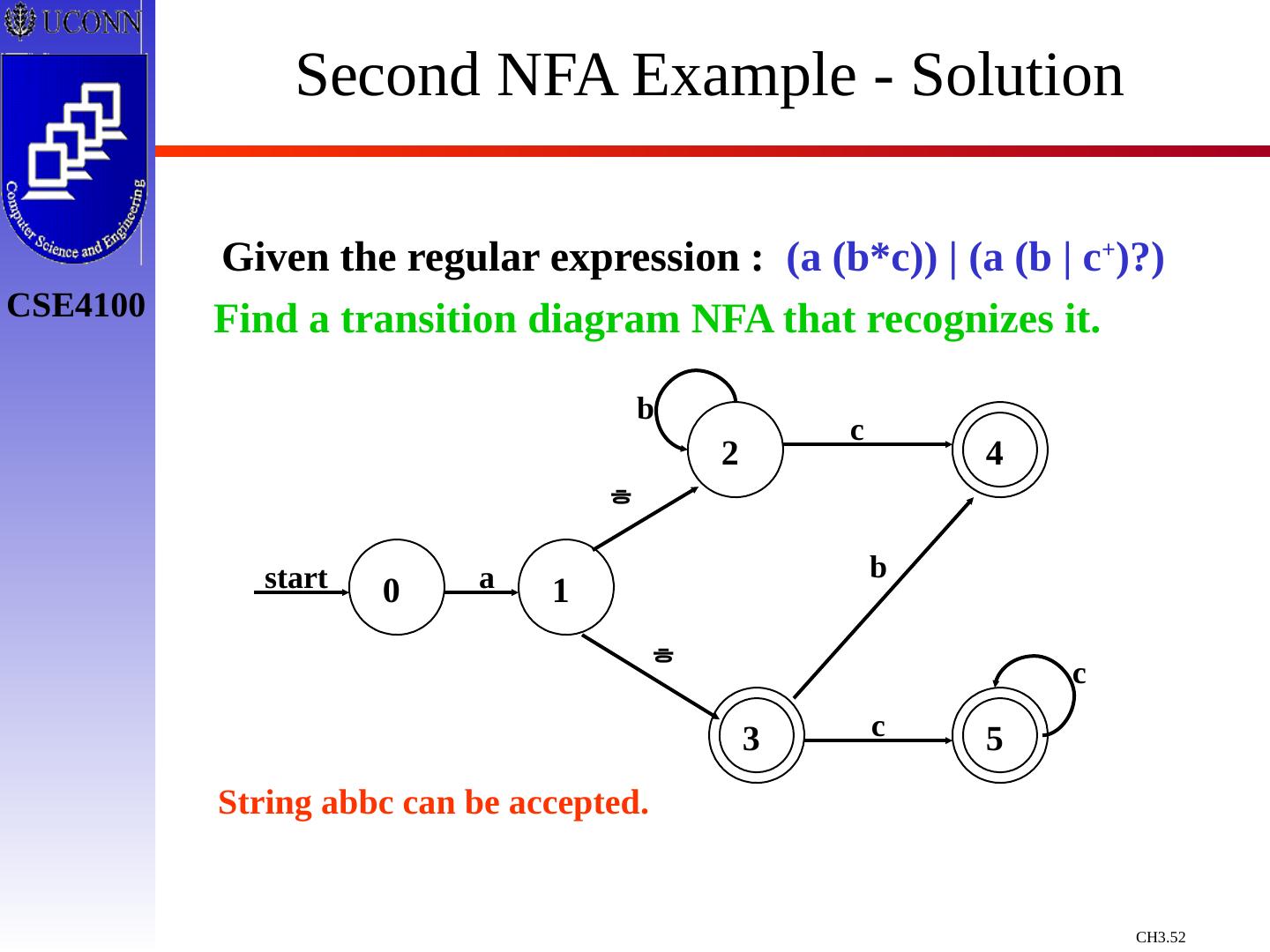
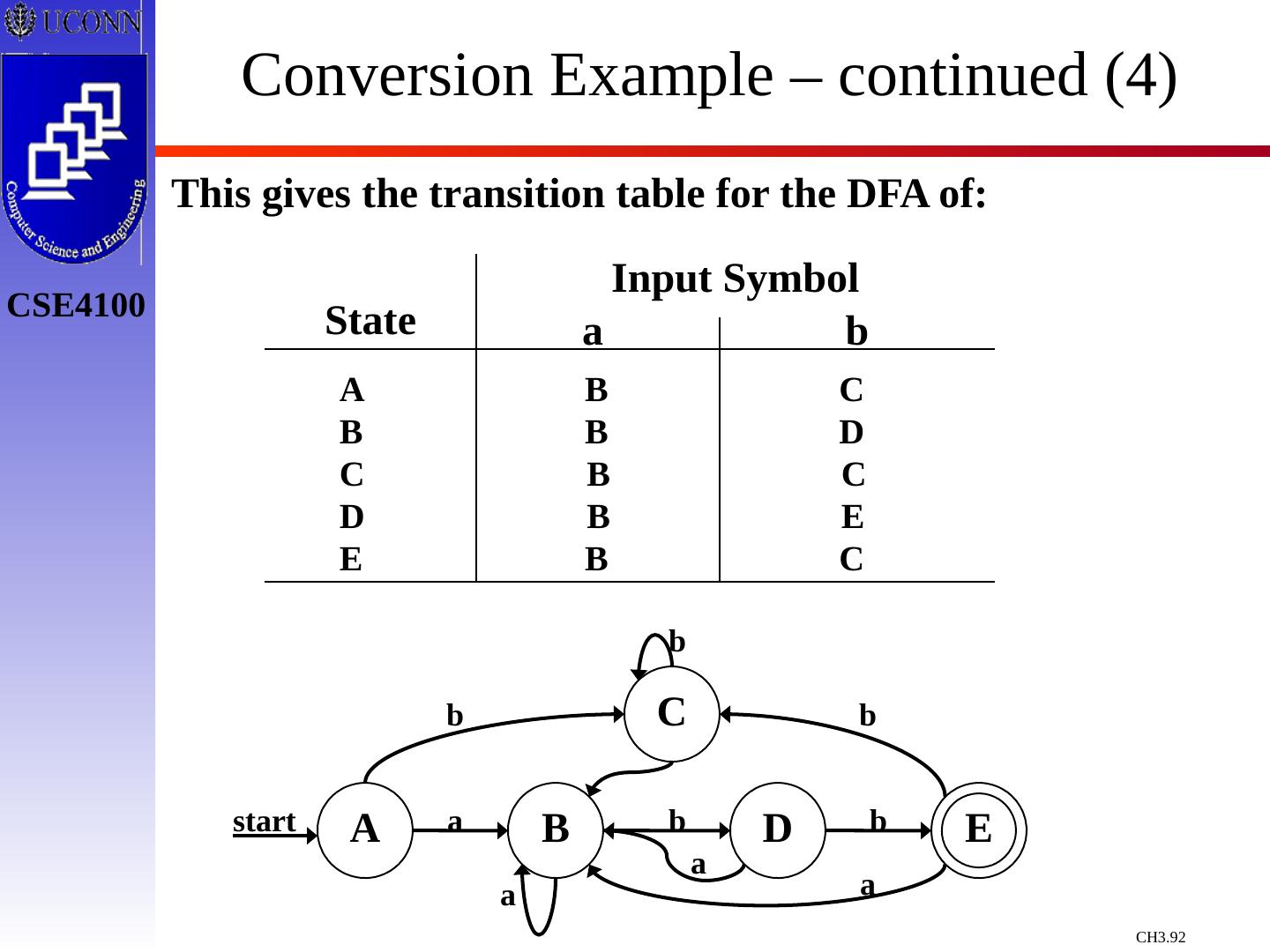
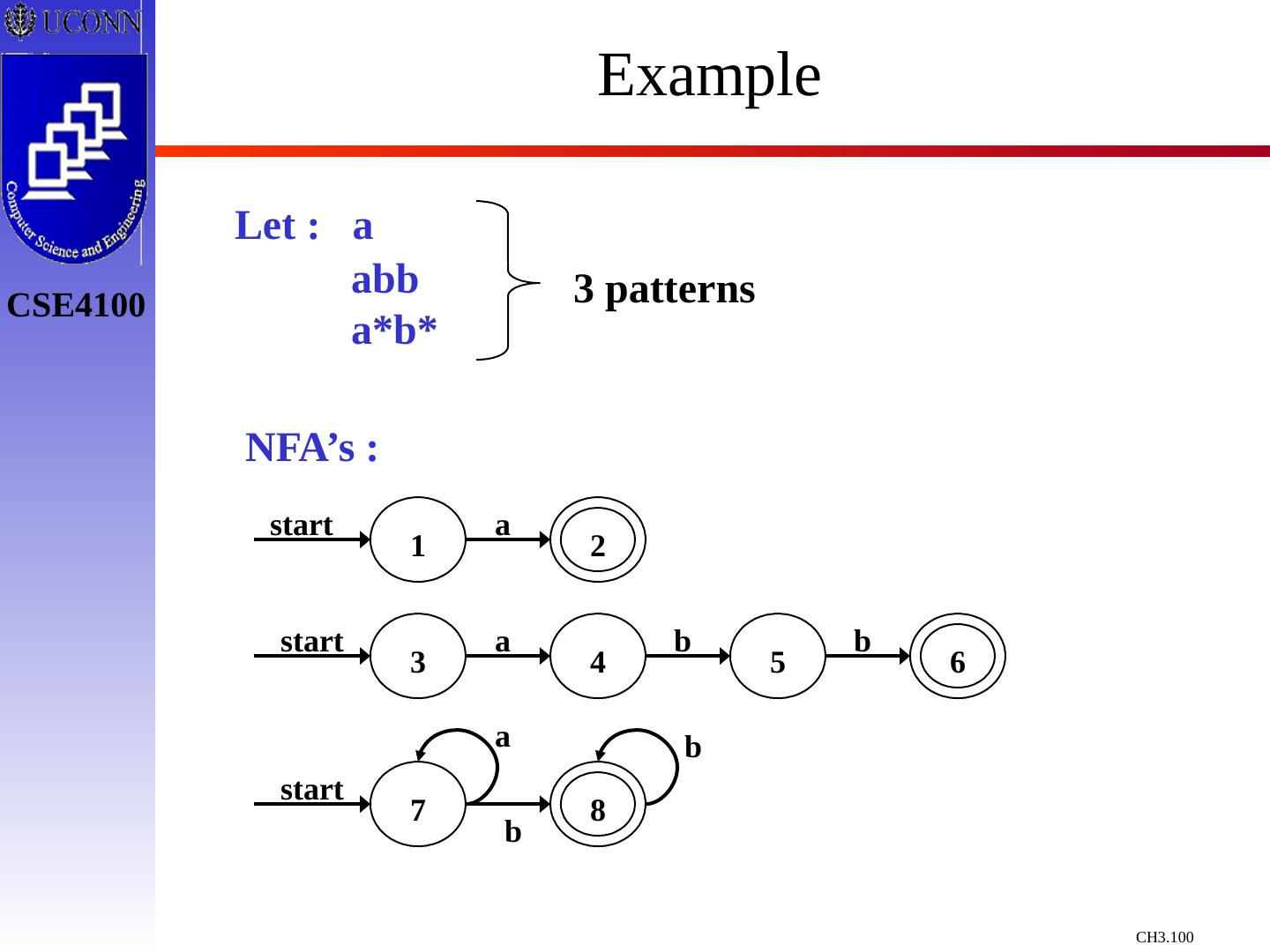
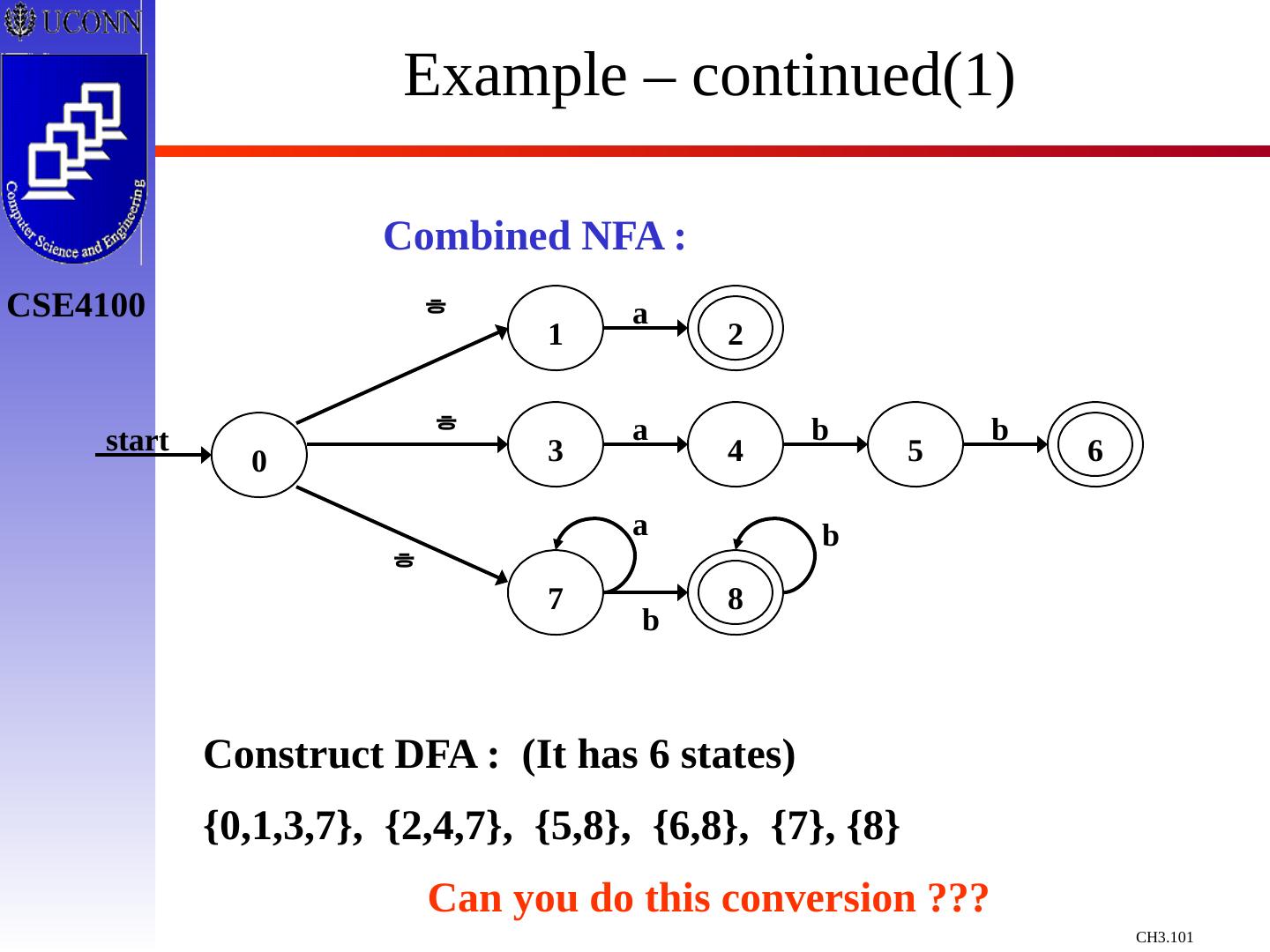
29 .Constructing Transition Diagrams for Tokens Transition Diagrams (TD) are used to represent the tokens – these are automatons! As characters are read, the relevant TDs are used to attempt to match lexeme to a pattern Each TD has: States : Represented by Circles Actions : Represented by Arrows between states Start State : Beginning of a pattern ( Arrowhead ) Final State (s) : End of pattern ( Concentric Circles ) Each TD is Deterministic - No need to choose between 2 different actions !