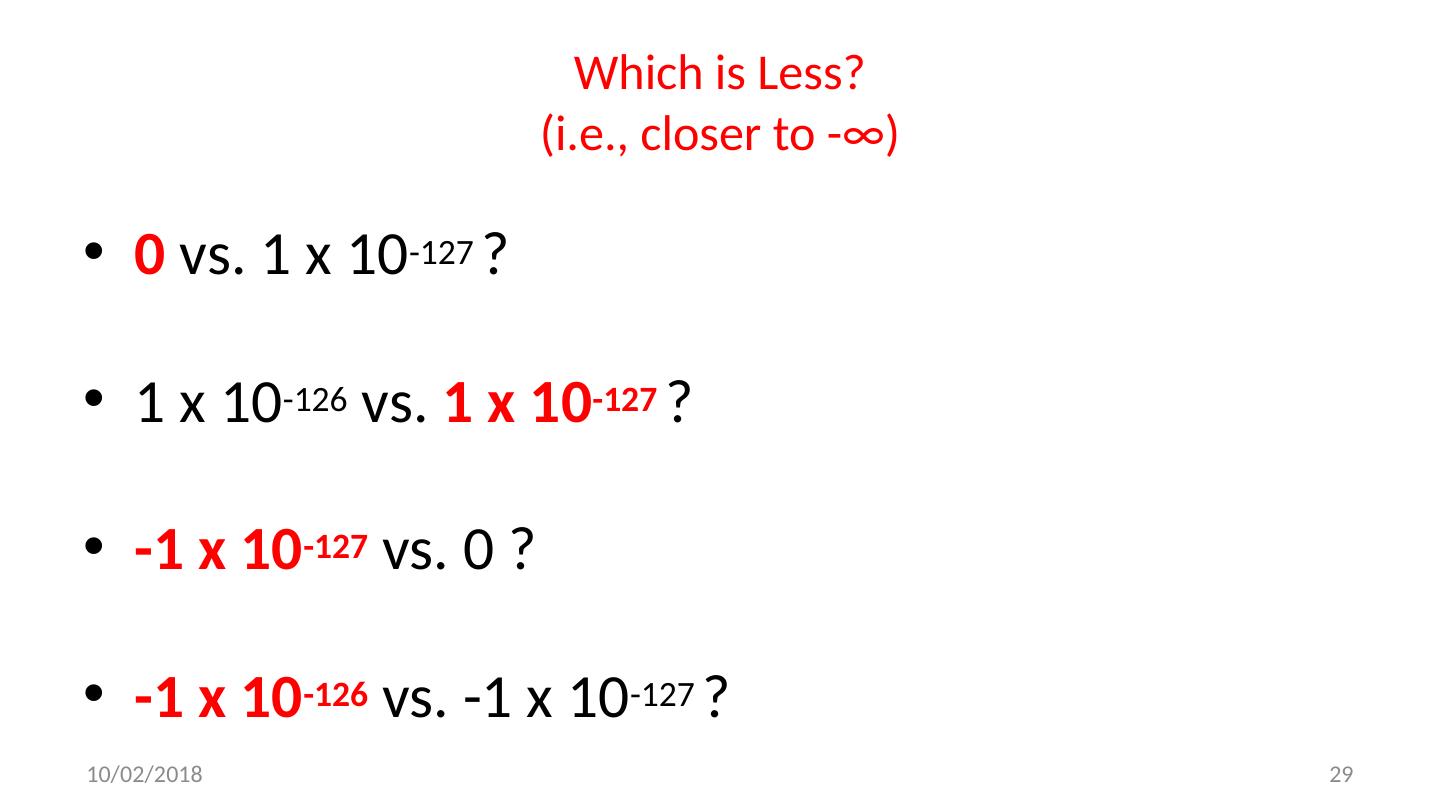- 快召唤伙伴们来围观吧
- 微博 QQ QQ空间 贴吧
- 文档嵌入链接
- 复制
- 微信扫一扫分享
- 已成功复制到剪贴板
性能和浮点运算
展开查看详情
1 .CS 61C: Great Ideas in Computer Architecture Performance and Floating-Point Arithmetic Instructors: Krste Asanović & Randy H. Katz http:// inst.eecs.berkeley.edu /~cs61c/fa17 10/24/17 Fall 2017-- Lecture #17 1
2 .Outline Defining Performance Floating-Point Standard And in Conclusion … 10/24/17 2
3 .What is Performance? Latency (or response time or execution time ) Time to complete one task Bandwidth (or throughput ) Tasks completed per unit time 10/24/17 3
4 .Cloud Performance: Why Application Latency Matters Key figure of merit: application responsiveness Longer the delay, the fewer the user clicks, the less the user happiness, and the lower the revenue per user 10/24/17 4
5 .CPU Performance Factors A program executes instructions CPU Time/Program = Clock Cycles/Program x Clock Cycle Time = Instructions/Program x Average Clock Cycles/Instruction x Clock Cycle Time 1 st term called Instruction Count 2 nd term abbreviated CPI for average Clock C ycles P er I nstruction 3rd term is 1 / Clock rate 10/24/17 5
6 .Restating Performance Equation Time = Seconds Program Instructions Clock cycles Seconds Program Instruction Clock Cycle × × = 10/24/17 6 CPU Iron Law!
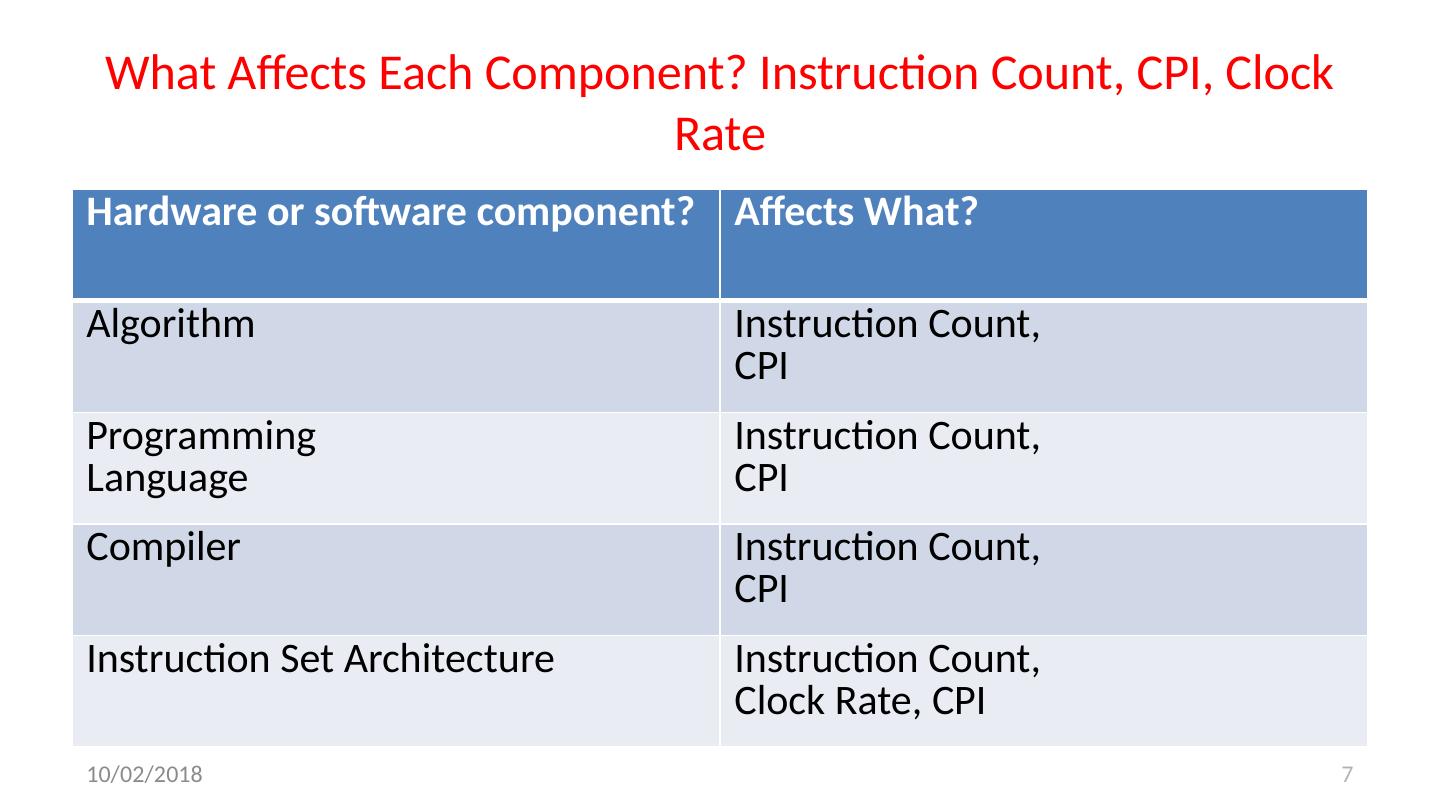
7 .What Affects Each Component? Instruction Count, CPI, Clock Rate Hardware or software component? Affects What? Algorithm Instruction Count, CPI Programming Language Instruction Count, CPI Compiler Instruction Count, CPI Instruction Set Architecture Instruction Count, Clock Rate, CPI 10/24/17 7
8 .Peer Instruction Which computer has the highest performance for a given program? Computer Clock frequency Clock cycles per instruction #instructions per program RED 1.0 GHz 2 1000 GREEN 2.0 GHz 5 800 ORANGE 0.5 GHz 1.25 400 YELLOW 5.0 GHz 10 2000 10/24/17 8
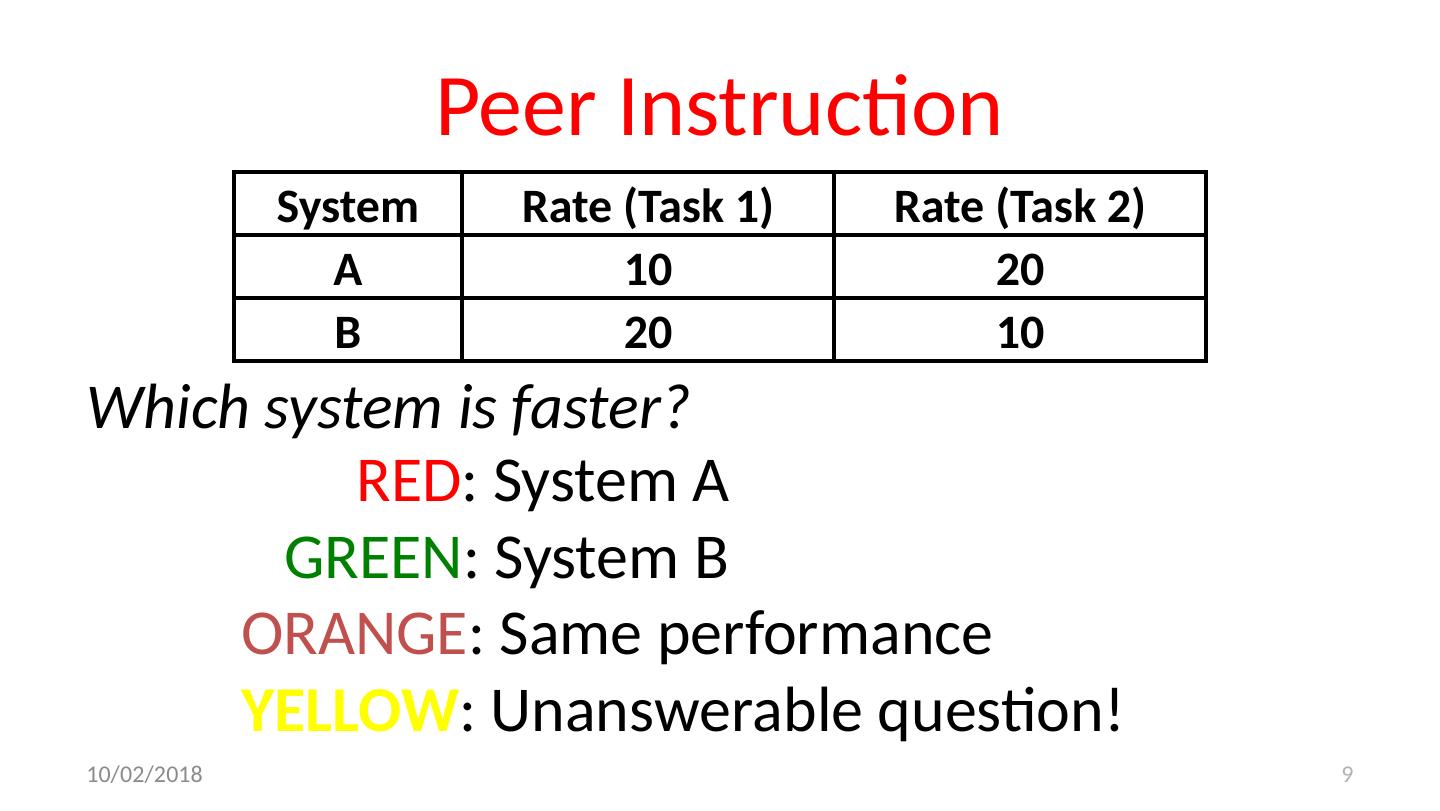
9 .Peer Instruction Which system is faster? 9 System Rate (Task 1) Rate (Task 2) A 10 20 B 20 10 RED : System A GREEN : System B ORANGE : Same performance YELLOW : Unanswerable question! 10/24/17
10 .Workload and Benchmark Workload : Set of programs run on a computer Actual collection of applications run or made from real programs to approximate such a mix Specifies both programs and relative frequencies Benchmark: Program selected for use in comparing computer performance Benchmarks form a workload Usually standardized so that many use them 10/24/17 10
11 .SPEC (System Performance Evaluation Cooperative) Computer Vendor cooperative for benchmarks, started in 1989 SPECCPU2006 12 Integer Programs 17 Floating-Point Programs Often turn into number where bigger is faster SPECratio : reference execution time on old reference computer divided by execution time on new computer, reported as speed-up (SPEC 2017 just released) 10/24/17 11
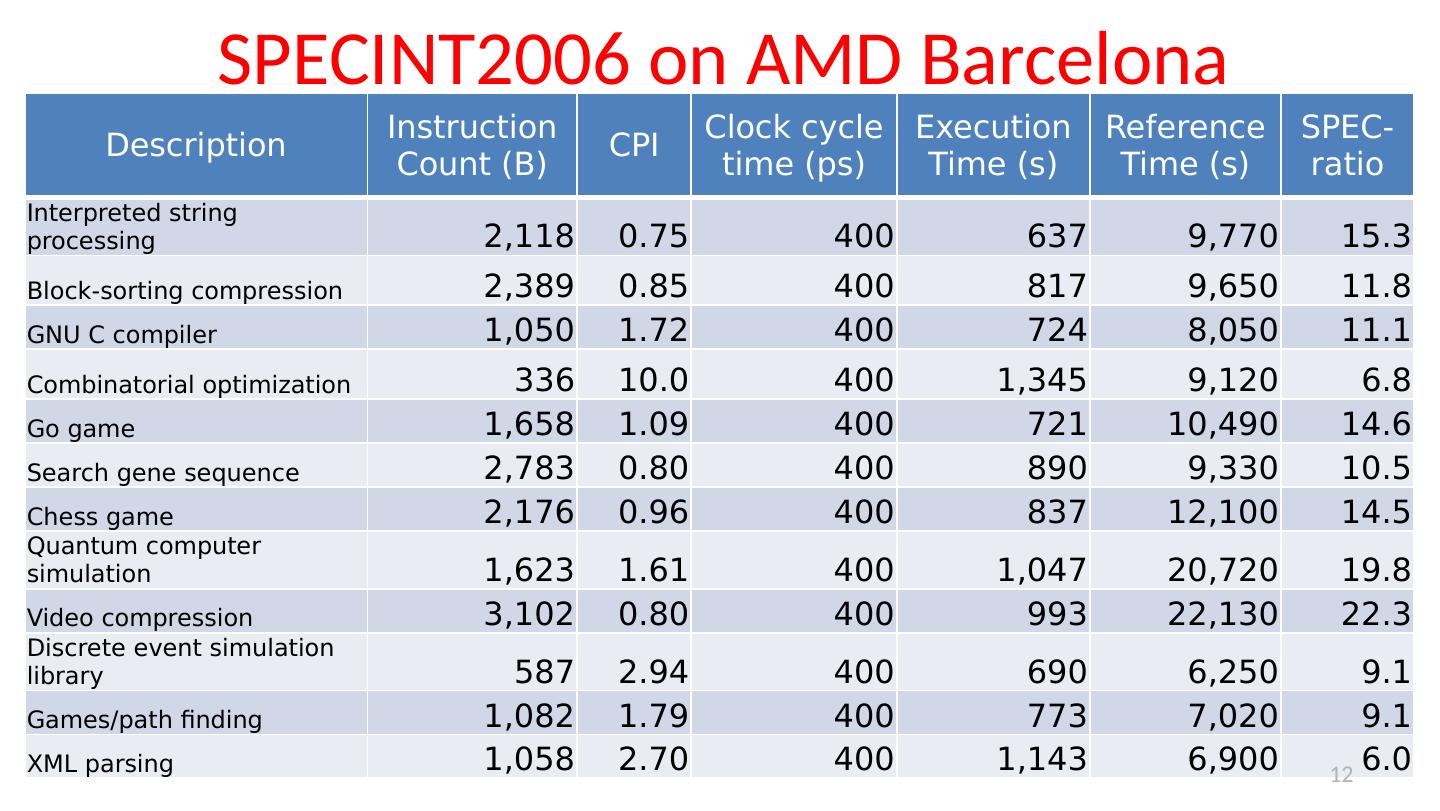
12 .SPECINT2006 on AMD Barcelona Description Instruction Count (B) CPI Clock cycle time ( ps ) Execution Time (s) Reference Time (s) SPEC-ratio Interpreted string processing 2,118 0.75 400 637 9,770 15.3 Block-sorting compression 2,389 0.85 400 817 9,650 11.8 GNU C compiler 1,050 1.72 400 724 8,050 11.1 Combinatorial optimization 336 10.0 400 1,345 9,120 6.8 Go game 1,658 1.09 400 721 10,490 14.6 Search gene sequence 2,783 0.80 400 890 9,330 10.5 Chess game 2,176 0.96 400 837 12,100 14.5 Quantum computer simulation 1,623 1.61 400 1,047 20,720 19.8 Video compression 3,102 0.80 400 993 22,130 22.3 Discrete event simulation library 587 2.94 400 690 6,250 9.1 Games/path finding 1,082 1.79 400 773 7,020 9.1 XML parsing 1,058 2.70 400 1,143 6,900 6.0 12
13 .Summarizing SPEC Performance Varies from 6x to 22x faster than reference computer Geometric mean of ratios: N- th root of product of N ratios Geometric Mean gives same relative answer no matter what computer is used as reference Geometric Mean for Barcelona is 11.7 10/24/17 13
14 .Administrivia 14 10/24/17 Midterm 2 in one week! Guerrilla Session tonight 7-9pm in Cory 293 ONE double sided cheat sheet Stay tuned for room assignments Review session: Saturday 10-12pm in Hearst Annex A1 Homework 4 released! Caches and Floating Point Due after the midterm Still good cache practice! Proj2-Part2 released Due after the midterm, but good to do before!
15 .Outline Defining Performance Floating-Point Standard And in Conclusion … 10/24/17 Fall 2016 – Lecture #17 15
16 .Quick Number Review Computers deal with numbers What can we represent in N bits? 2 N things, and no more! They could be… Unsigned integers: 0 to 2 N - 1 ( for N=32, 2 N – 1 = 4,294,967,295) Signed Integers (Two’s Complement) - 2 (N-1) to 2 (N-1) - 1 (for N=32, 2 (N-1) = 2,147,483,648) 10/24/17 16
17 .Other Numbers Very large numbers? (seconds/millennium) 31,556,926,000 10 (3.1556926 10 x 10 10 ) Very small numbers? (Bohr radius) 0.0000000000529177 10 m (5.29177 10 x 10 -11 ) Numbers with both integer & fractional parts? 1.5 First consider # 3 …our solution will also help with #1 and # 2 10/24/17 17
18 .Goals for Floating Point Standard arithmetic for reals for all computers Like two’s complement Keep as much precision as possible in formats Help programmer with errors in real arithmetic +∞, -∞, Not-A-Number ( NaN ), exponent overflow, exponent underflow Keep encoding that is somewhat compatible with two’s complement E.g., 0 in Fl. Pt. is 0 in two’s complement Make it possible to sort without needing to do floating-point comparison 10/24/17 18
19 .Representation of Fractions “Binary Point” like decimal point signifies boundary between integer and fractional parts: xx . yyyy 2 1 2 0 2 -1 2 -2 2 -3 2 -4 Example 6-bit representation: 10.1010 two = 1x2 1 + 1x2 -1 + 1x2 -3 = 2.625 ten If we assume “fixed binary point”, range of 6-bit representations with this format: 0 to 3.9375 (almost 4) 10/24/17 19
20 .Fractional Powers of 2 10/24/17 20 0 1.0 1 0.5 1 /2 0.25 1/4 0.125 1/8 0.0625 1/16 0.03125 1/32 0.015625 0.0078125 0.00390625 0.001953125 0.0009765625 0.00048828125 0.000244140625 0.0001220703125 0.00006103515625 0.000030517578125 i 2 -i
21 .Representation of Fractions with Fixed Pt. What about addition and multiplication? Addition is straightforward: 01.100 1.5 ten + 00.100 0.5 ten 10.000 2.0 ten Multiplication a bit more complex: 01.100 1.5 ten 00.100 0.5 ten 00 000 000 00 0110 0 00000 00000 0000110000 Where’s the answer, 0.11 ? (e.g., 0.5 + 0.25; Need to remember where point is!) 10/24/17 21
22 .Representation of Fractions O ur examples used a “fixed” binary point. What we really want is to “float” the binary point to make most effecitve use of limited bits … 000000.001010100000… Any other solution would lose accuracy! example: put 0.1640625 ten into binary . Represent with 5-bits choosing where to put the binary point. Store these bits and keep track of the binary point 2 places to the left of the MSB With floating-point representation, each numeral carries an exponent field recording the whereabouts of its binary point B inary point can be outside the stored bits, so very large and small numbers can be represented 10/24/17 22
23 .Scientific Notation (in Decimal) Normalized form: no leadings 0s (exactly one digit to left of decimal point) Alternatives to representing 1/1,000,000,000 Normalized: 1.0 x 10 -9 Not normalized: 0.1 x 10 -8 , 10.0 x 10 -10 6.02 ten x 10 23 radix (base) decimal point mantissa exponent 10/24/17 23
24 .Scientific Notation (in Binary) Computer arithmetic that supports it is called floating point , because it represents numbers where the binary point is not fixed, as it is for integers Declare such variable in C as float double for double precision 1.01 two x 2 -1 radix (base) “ binary point ” exponent mantissa 10/24/17 24
25 .Floating-Point Representation (1/4) 32-bit word has 2 32 patterns, so must be approximation of real numbers ≥ 1.0, < 2 IEEE 754 Floating-Point Standard: 1 bit for sign ( s ) of floating point number 8 bits for exponent (E) 23 bits for fraction (F) (get 1 extra bit of precision if leading 1 is implicit) (-1) s x (1 + F) x 2 E Can represent from 2.0 x 10 -38 to 2.0 x 10 38 10/24/17 25
26 .Floating-Point Representation (2/4) Normal format: + 1 . xxx… x two *2 yyy… y two Multiple of Word Size (32 bits) 0 31 S Exponent 30 23 22 Significand 1 bit 8 bits 23 bits S represents Sign Exponent represents y ’s Significand represents x ’s Represent numbers as small as 2.0 ten x 10 -38 to as large as 2.0 ten x 10 38 10/24/17 26
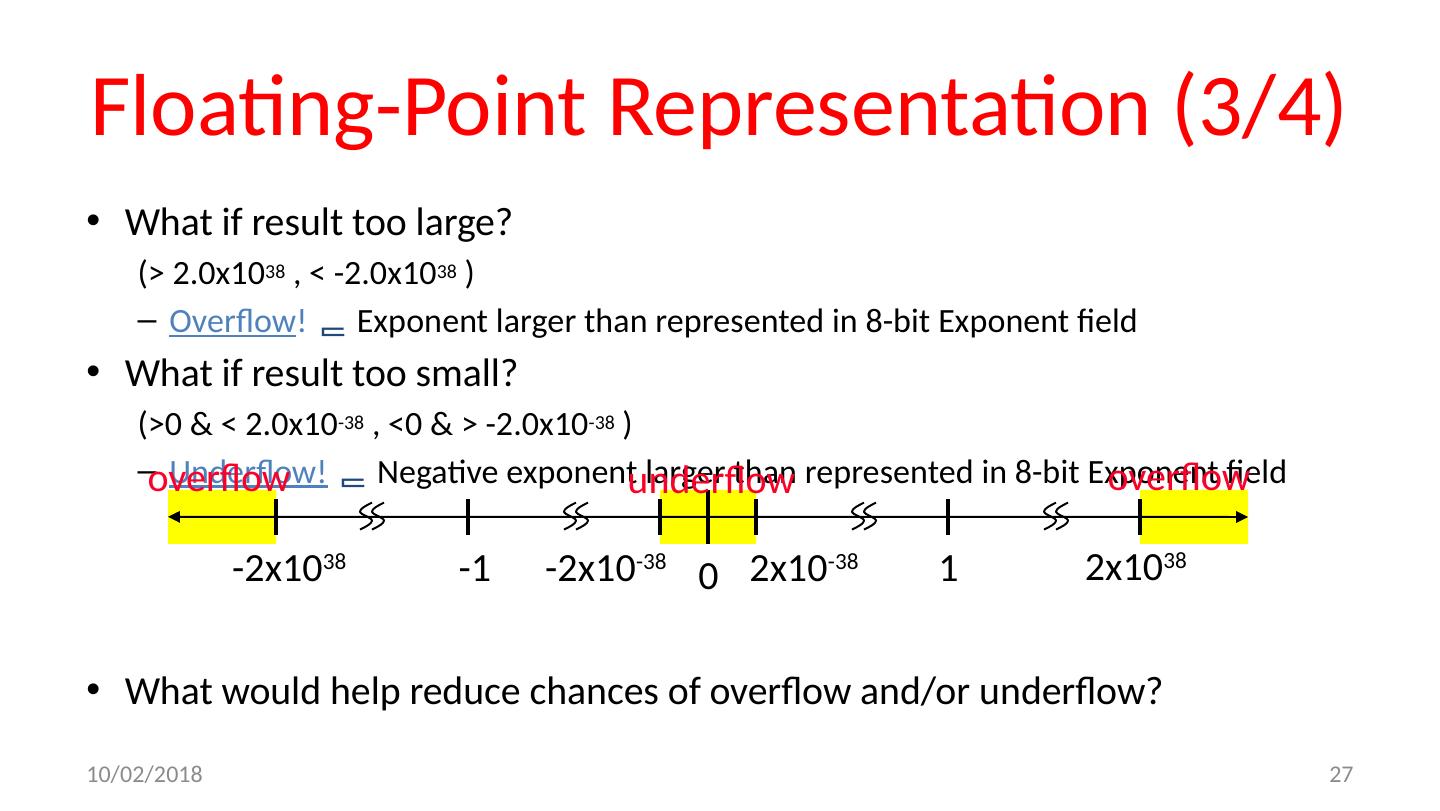
27 .Floating-Point Representation (3/4) What if result too large? (> 2.0x10 38 , < -2.0x10 38 ) Overflow ! Exponent larger than represented in 8-bit Exponent field What if result too small? (>0 & < 2.0x10 -38 , <0 & > -2.0x10 -38 ) Underflow! Negative exponent larger than represented in 8-bit Exponent field What would help reduce chances of overflow and/or underflow? 0 2x10 -38 2x10 38 1 -1 -2x10 -38 -2x10 38 underflow overflow overflow 10/24/17 27
28 .Floating-Point Representation (4/4) What about bigger or smaller numbers? IEEE 754 Floating-Point Standard: Double Precision (64 bits) 1 bit for sign (s) of floating-point number 11 bits for exponent (E) 52 bits for fraction (F) (get 1 extra bit of precision if leading 1 is implicit) (-1) s x (1 + F) x 2 E Can represent from 2.0 x 10 -308 to 2.0 x 10 308 32-bit format called Single Precision 10/24/17 28
29 .Which is Less? (i.e., closer to -∞) 0 vs. 1 x 10 -127 ? 1 x 10 -126 vs. 1 x 10 -127 ? -1 x 10 -127 vs. 0 ? -1 x 10 -126 vs. -1 x 10 -127 ? 10/24/17 29