more-analysis and heaps

1 .CSE 373 : Data Structures and Algorithms More A symptotic Analysis; More Heaps Riley Porter Winter 2017 Winter 2017 CSE373: Data Structure & Algorithms 1

2 .Course Logistics HW 1 posted. Due next Tuesday, January 17 th at 11 pm. Dropbox not on catalyst, will be through the Canvas for the course. TA office hour rooms and times are all posted and finalized. Please go visit the TAs so they aren’t lonely. Java Review Session materials from yesterday posted in the Announcements section of the website. 2 CSE373: Data Structures & Algorithms Winter 2017

3 .Review from last time (what did we learn?) Analyze algorithms without specific implementations through space and time (what we focused on). We only care about asymptotic runtimes, we want to know what will happen to the runtime proportionally as the size of input increases Big-O is an upper bound and you can prove that a runtime has a Big-O upper bound by computing two values: c and n 0 3 CSE373: Data Structures & Algorithms Winter 2017

4 .Review: Formally Big- O Definition: g( n ) is in O( f( n ) ) if there exist constants c and n 0 such that g( n )  c f( n ) for all n  n 0 To show g( n ) is in O( f( n ) ) , pick a c large enough to “cover the constant factors” and n 0 large enough to “cover the lower-order terms” Example: Let g( n ) = 3 n 2 +17 and f( n ) = n 2 c =5 and n 0 =10 is more than good enough This is “less than or equal to” So 3 n 2 +17 is also O ( n 5 ) and O (2 n ) etc. 4 CSE373: Data Structure & Algorithms Winter 2017

5 .Big-O: Common Names O (1) constant (same as O ( k ) for constant k ) O ( log n ) logarithmic O ( n ) linear O(n log n ) “ n log n ” O ( n 2 ) quadratic O ( n 3 ) cubic O ( n k ) polynomial (where is k is any constant: linear, quadratic and cubic all fit here too.) O ( k n ) exponential (where k is any constant > 1) Note : “exponential” does not mean “grows really fast”, it means “grows at rate proportional to k n for some k >1 ”. Example: a savings account accrues interest exponentially ( k =1.01? ). 5 CSE373: Data Structures & Algorithms Winter 2017

6 .More Asymptotic Notation Big-O Upper bound: O ( f( n ) ) is the set of all functions asymptotically less than or equal to f( n ) g( n ) is in O ( f( n ) ) if there exist constants c and n 0 such that g( n )  c f( n ) for all n  n 0 Big- Omega Lower bound: ( f( n ) ) is the set of all functions asymptotically greater than or equal to f( n ) g( n ) is in ( f( n ) ) if there exist constants c and n 0 such that g( n )  c f( n ) for all n  n 0 Big-Theta Tight bound:  ( f( n ) ) is the set of all functions asymptotically equal to f( n ) Intersection of O ( f( n ) ) and ( f( n ) ) (use different c values ) 6 CSE373: Data Structure & Algorithms Winter 2017

7 .A Note on Big-O Terms A common error is to say O( function ) when you mean ( function ) : People often say Big-O to mean a tight bound Say we have f(n)=n; we could say f(n) is in O(n), which is true , but only conveys the upper- bound Since f(n)=n is also O( n 5 ) , it’s tempting to say “this algorithm is exactly O(n) ” Somewhat incomplete; instead say it is (n ) That means that it is not, for example O(log n) 7 CSE373: Data Structures & Algorithms Winter 2017

8 .What We’re Analyzing The most common thing to do is give an O or  bound to the worst -case running time of an algorithm • Example: True statements about binary- search algorithm Common : (log n) running-time in the worst- case Less common: (1) in the best-case (item is in the middle ) Less common (but very good to know): the find-in- sorted array problem is (log n) in the worst- case No algorithm can do better (without parallelism ) 8 CSE373: Data Structures & Algorithms Winter 2017

9 .Intuition / Math on O( logN ) If you’re dividing your input in half (or any other constant) each iteration of an algorithm, that’s O( logN ). Binary Search Example: If you divide your input in half each time and discard half the values, to figure out the worst-case runtime you need to figure out how many “halves” you have in your input. So you’re solving: N / 2 x = 1 where N is size of input, X is “number of halves”, because 1 is the desired number of elements you’re trying to get to. log (2 x ) = X*log(2) = log(N) X = log(N) / log(2) X = log 2 (N) 9 CSE373: Data Structures & Algorithms Winter 2017

10 .Other things to analyze Remember we can often use space to gain time Average case Sometimes only if you assume something about the probability distribution of inputs Usually the way we think about Hashing Will discuss in two weeks Sometimes uses randomization in the algorithm Will see an example with sorting Sometimes an amortized guarantee Average time over any sequence of operations Will discuss next week 10 CSE373: Data Structure & Algorithms Winter 2017

11 .Usually asymptotic is valuable Asymptotic complexity focuses on behavior for large n and is independent of any computer / coding trick But you can “abuse” it to be misled about trade-offs Example: n 1/10 vs. log n Asymptotically n 1/10 grows more quickly But the “cross-over” point is around 5 * 10 17 So if you have input size less than 2 58 , prefer n 1/10 For small n , an algorithm with worse asymptotic complexity might be faster Here the constant factors can matter, if you care about performance for small n 11 CSE373: Data Structure & Algorithms Winter 2017

12 .Summary of Asymptotic Analysis Analysis can be about: The problem or the algorithm (usually algorithm) Time or space (usually time) Best -, worst-, or average-case (usually worst) Upper-, lower-, or tight-bound (usually upper) The most common thing we will do is give an O upper bound to the worst-case running time of an algorithm. 12 Winter 2017

13 .Let’s use our new skills! Here’s a picture of a kitten as a segue to analyzing an ADT 13 Winter 2017

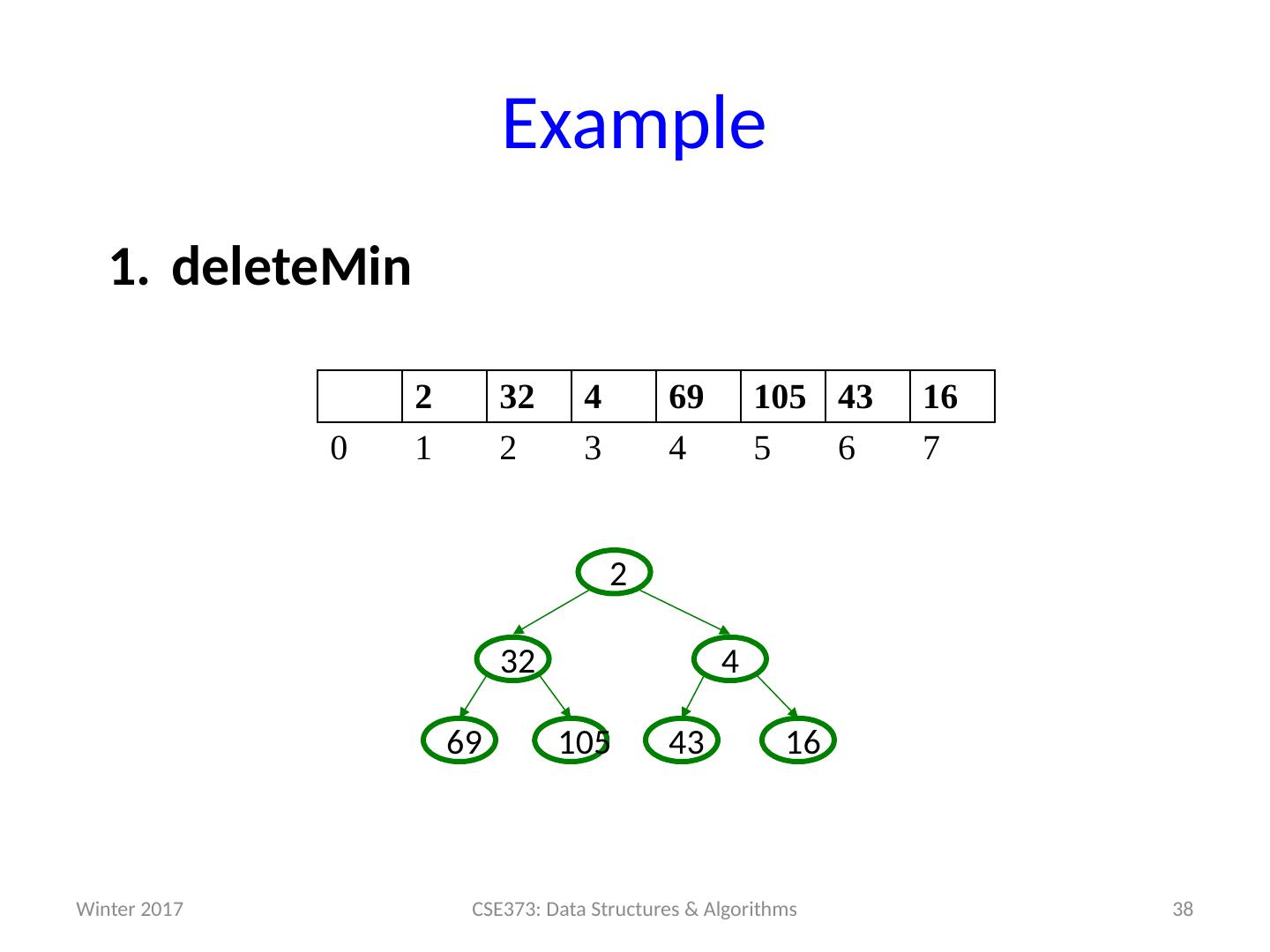
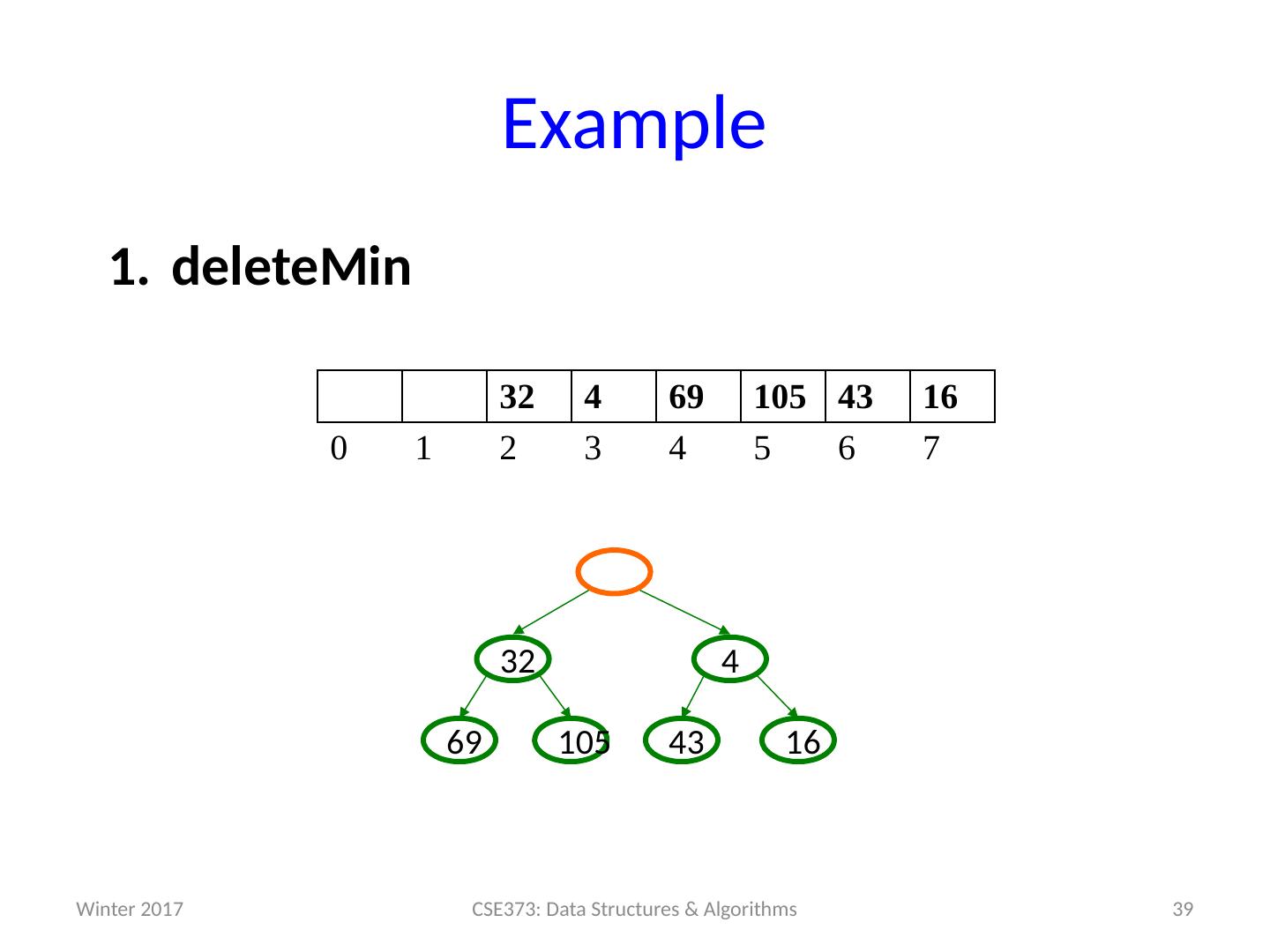
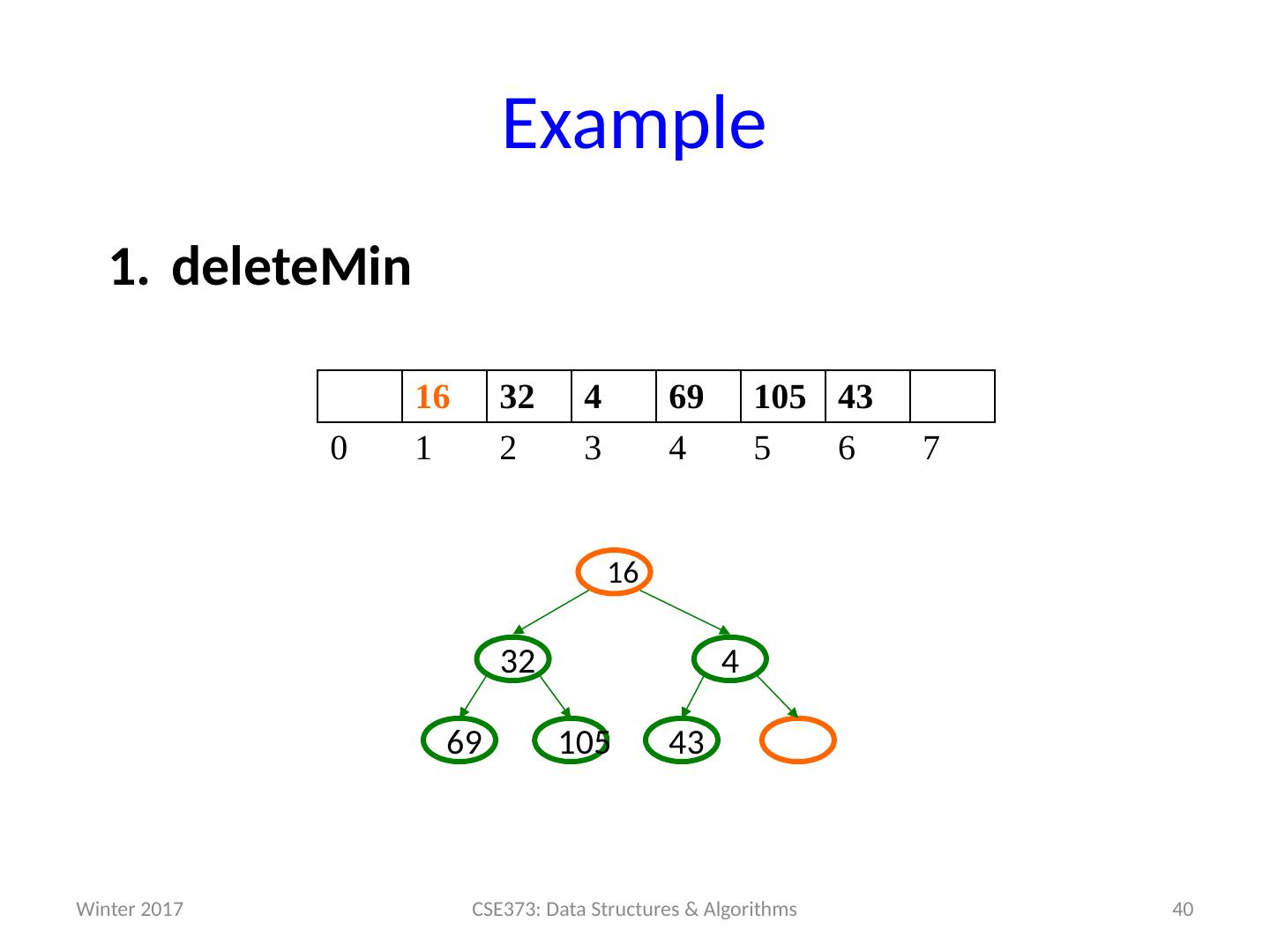
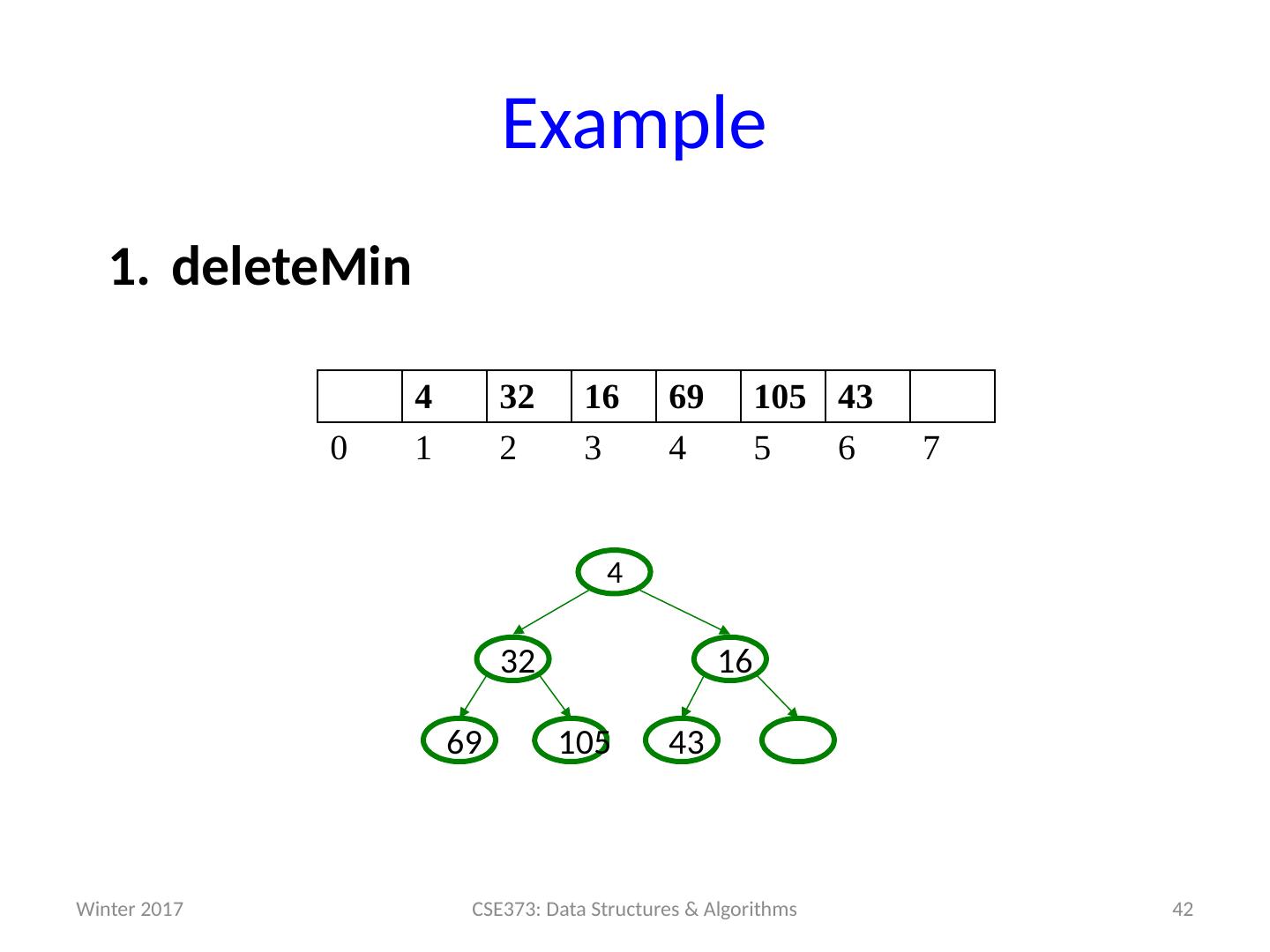
14 .Analysis of Priority Queue ADT Let’s compare some options for implementing Priority Queues. All runtimes worst-case, but assume arrays have room for new elements. We’ll look at the binary search tree operations and runtimes more on Friday. data structure insert deleteMin unsorted array add at end O (1) search O ( n ) unsorted linked list add at front O (1) search O ( n ) s orted array search / shift O ( n ) stored in reverse O (1) sorted linked list put in right place O ( n ) remove at front O (1) binary search tree put in right place O ( n ) leftmost O ( n ) h eaps ??? ??? 14 CSE373: Data Structures & Algorithms Winter 2017

15 .Review of last time: Heaps Heaps follow the following two properties: Structure property: A complet e binary tree Heap order property : The priority of the children is always a greater value than the parents (greater value means less priority / less importance) Winter 2017 15 CSE373: Data Structures & Algorithms 15 30 80 20 10 99 60 40 80 20 10 50 700 85 not a heap a heap 450 3 1 75 50 8 6 0 n ot a hea p 10 10

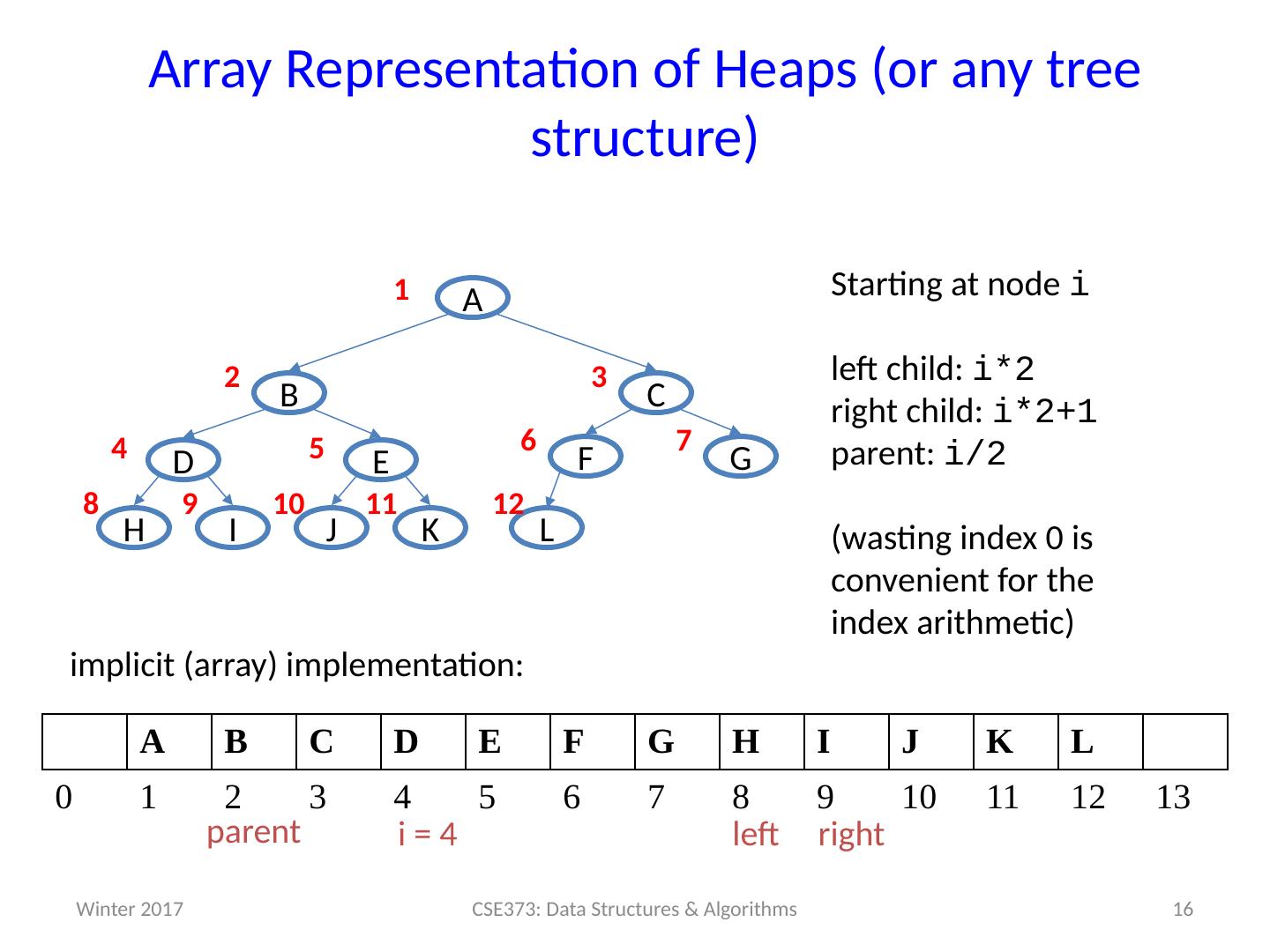
16 .16 Array Representation of Heaps (or any tree structure) G E D C B A J K H I F L Starting at node i left child : i *2 right child : i *2+1 parent : i /2 (wasting index 0 is convenient for the index arithmetic) 7 1 2 3 4 5 6 9 8 10 11 12 A B C D E F G H I J K L 0 1 2 3 4 5 6 7 8 9 10 11 12 13 implicit (array) implementation: 2 * i (2 * i)+1 └ i / 2 ┘ CSE373: Data Structures & Algorithms i = 4 left right parent Winter 2017

17 .Judging the array implementation Positives: Non-data space is minimized: just index 0 and unused space on right In conventional tree representation, one edge per node (except for root), so n -1 wasted space (like linked lists) Array would waste more space if tree were not complete Multiplying and dividing by 2 is very fast (shift operations in hardware) Last used position is just index size Negatives: Same might-by-empty or might-get-full problems we saw with stacks and queues (resize by doubling as necessary) Plusses outweigh minuses: “this is how people do it” 17 CSE373: Data Structures & Algorithms Winter 2017

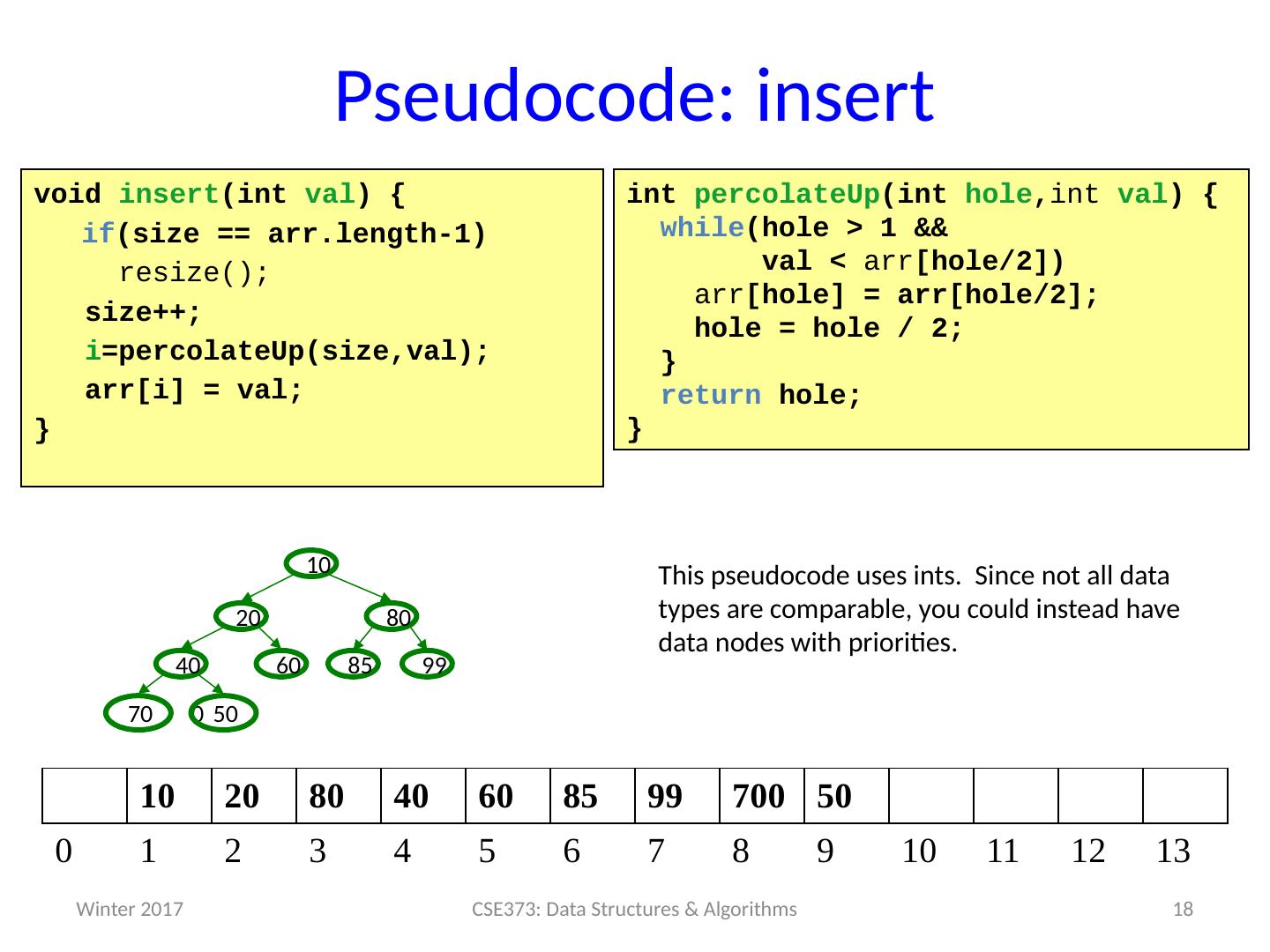
18 .Pseudocode : insert 18 CSE373: Data Structures & Algorithms void insert ( int val ) { if (size == arr.length-1) resize(); size++; i = percolateUp ( size,val ); arr [ i ] = val ; } int percolateUp ( int hole , int val ) { while (hole > 1 & & val < arr [hole/2]) arr [hole ] = arr [hole/2 ]; hole = hole / 2 ; } return hole; } 99 60 40 80 20 10 70 0 50 85 10 20 80 40 60 85 99 700 50 0 1 2 3 4 5 6 7 8 9 10 11 12 13 This pseudocode uses ints . Since not all data types are comparable , you could instead have data nodes with priorities. Winter 2017

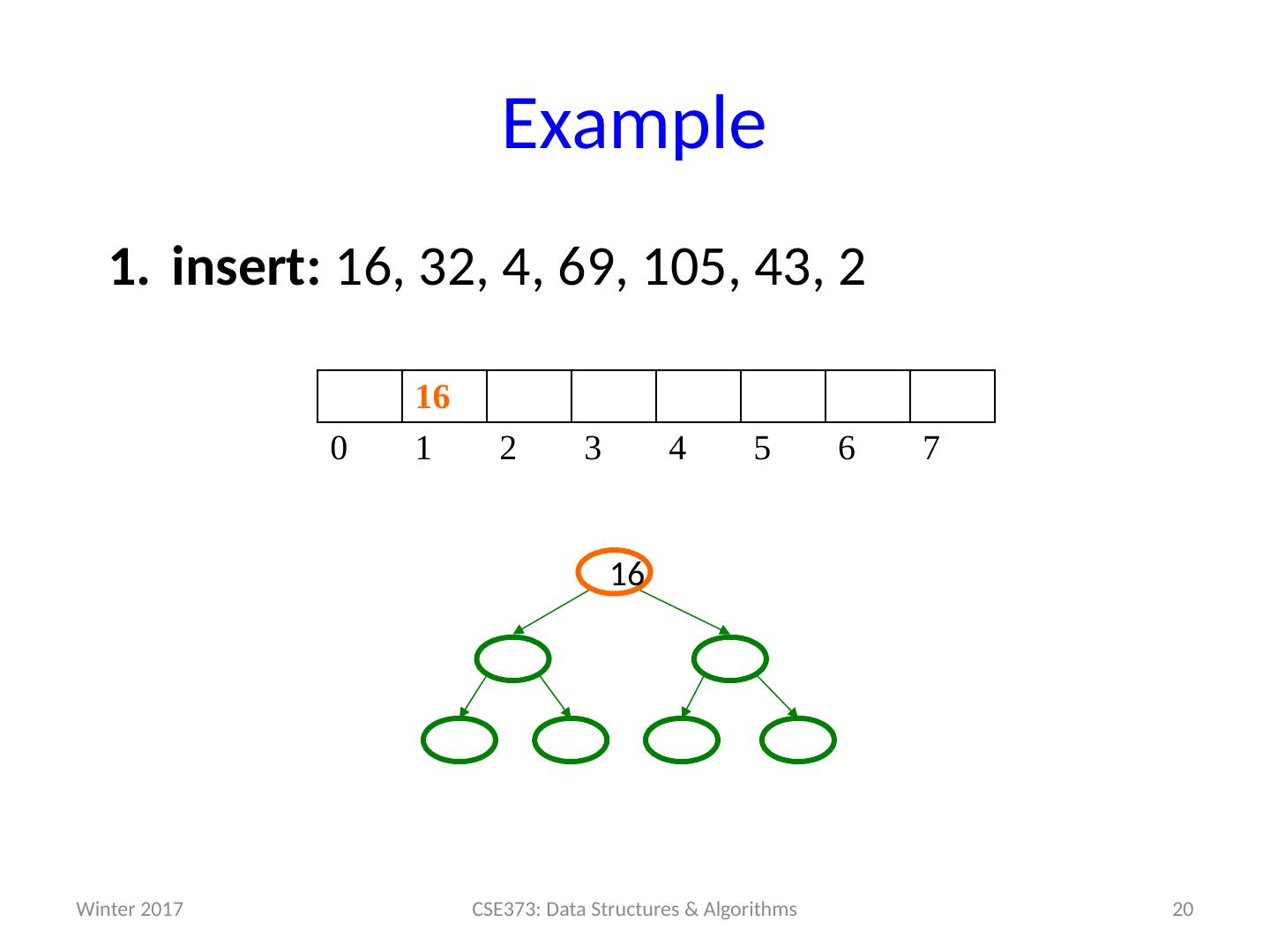
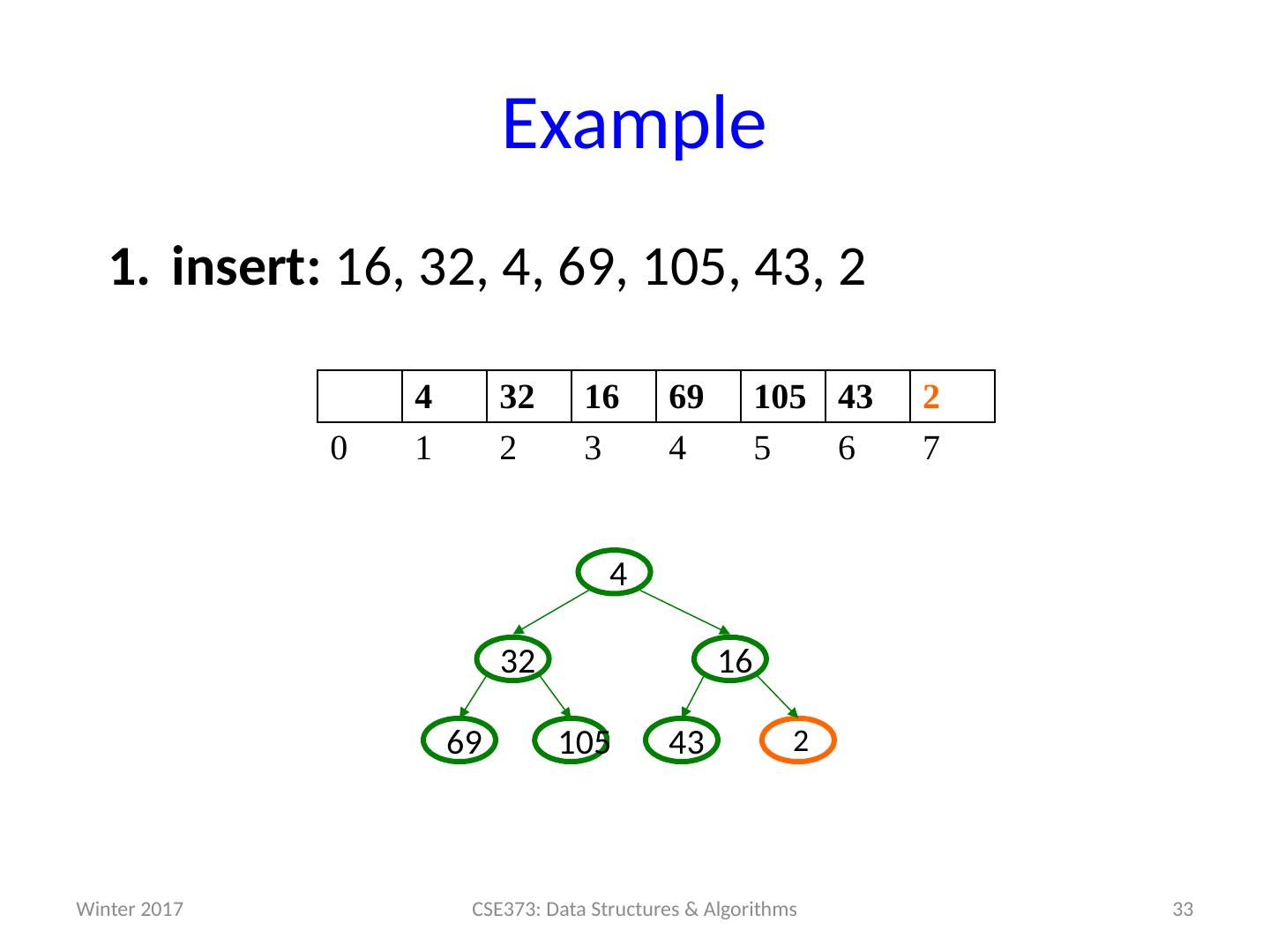
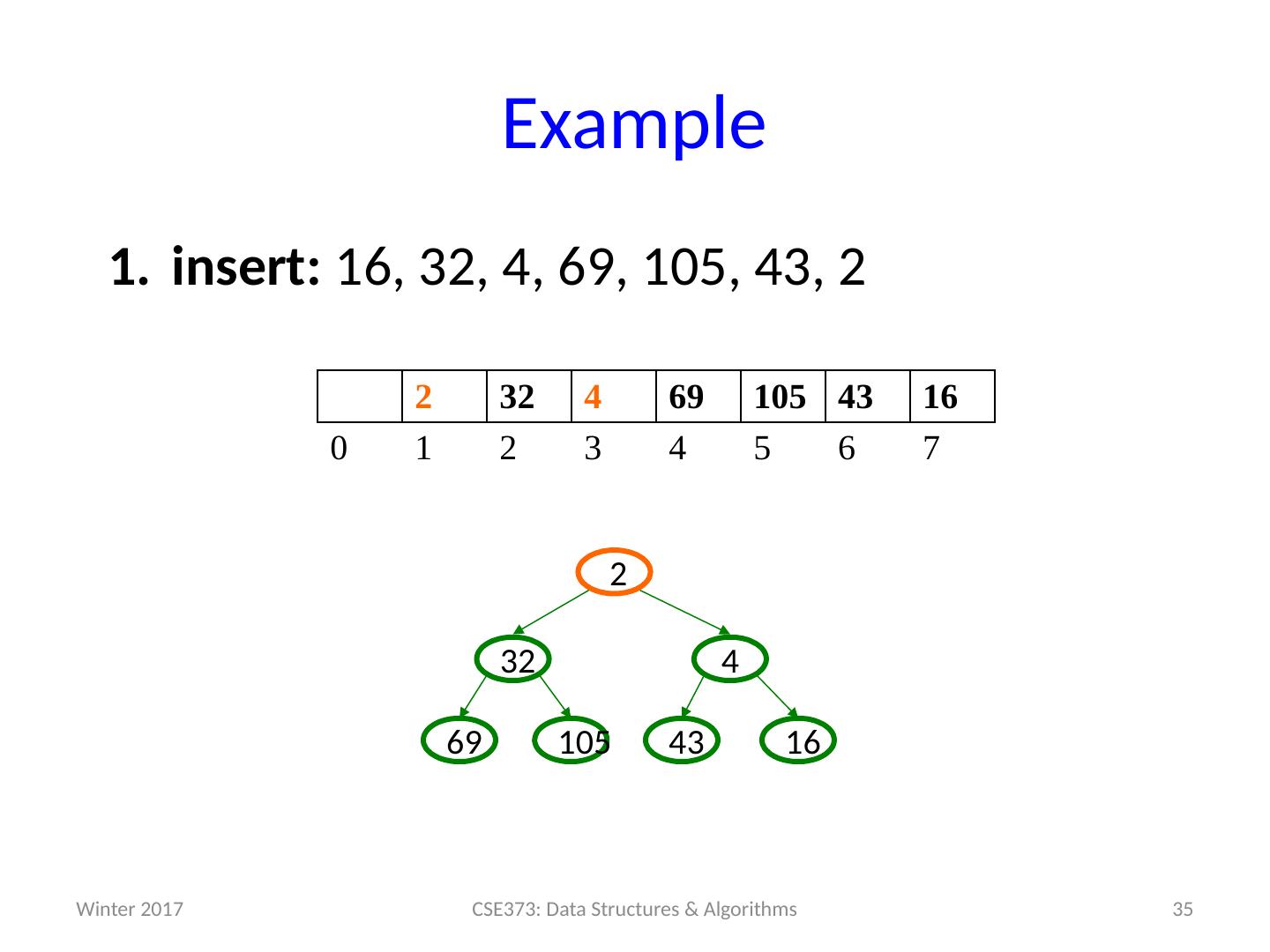
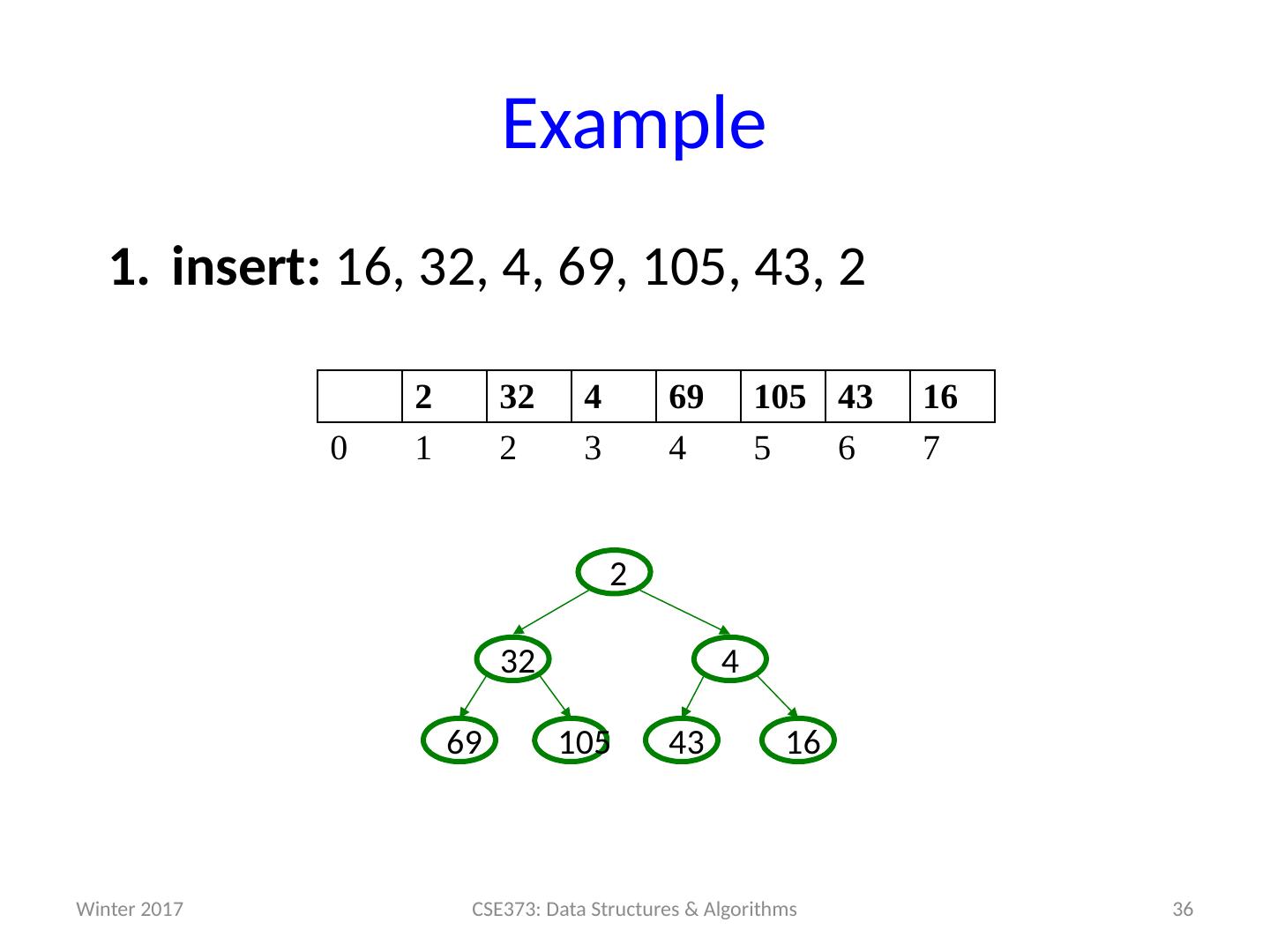
19 .Example insert: 16, 32, 4, 69, 105, 43, 2 19 CSE373: Data Structures & Algorithms 0 1 2 3 4 5 6 7 Winter 2017

20 .Example insert: 16, 32, 4, 69, 105, 43, 2 20 CSE373: Data Structures & Algorithms 16 0 1 2 3 4 5 6 7 16 Winter 2017

21 .Example insert: 16, 32, 4, 69, 105, 43, 2 21 CSE373: Data Structures & Algorithms 16 0 1 2 3 4 5 6 7 16 Winter 2017

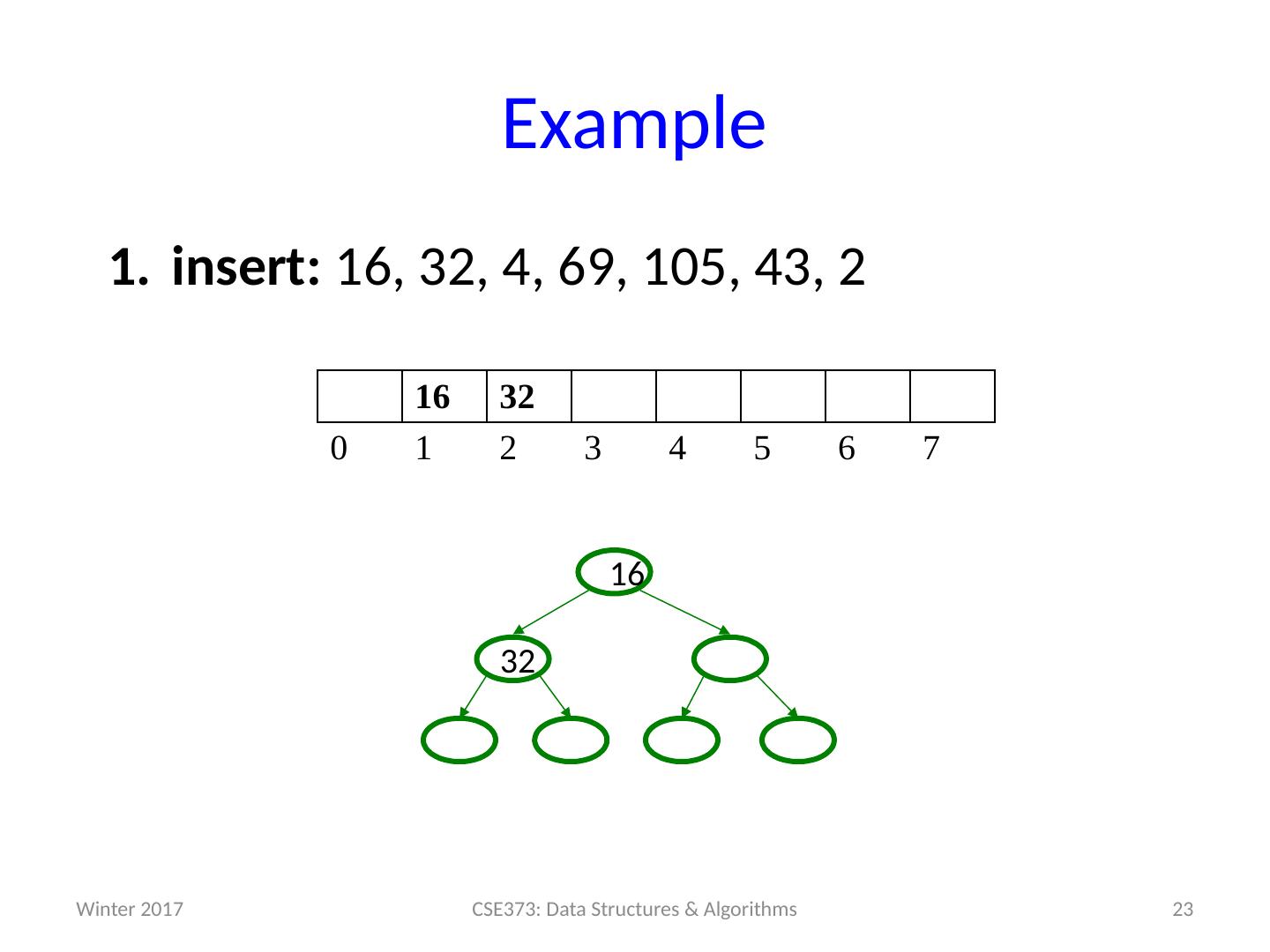
22 .Example insert: 16, 32, 4, 69, 105, 43, 2 22 CSE373: Data Structures & Algorithms 16 32 0 1 2 3 4 5 6 7 32 16 Winter 2017

23 .Example insert: 16, 32, 4, 69, 105, 43, 2 23 CSE373: Data Structures & Algorithms 16 32 0 1 2 3 4 5 6 7 32 16 Winter 2017

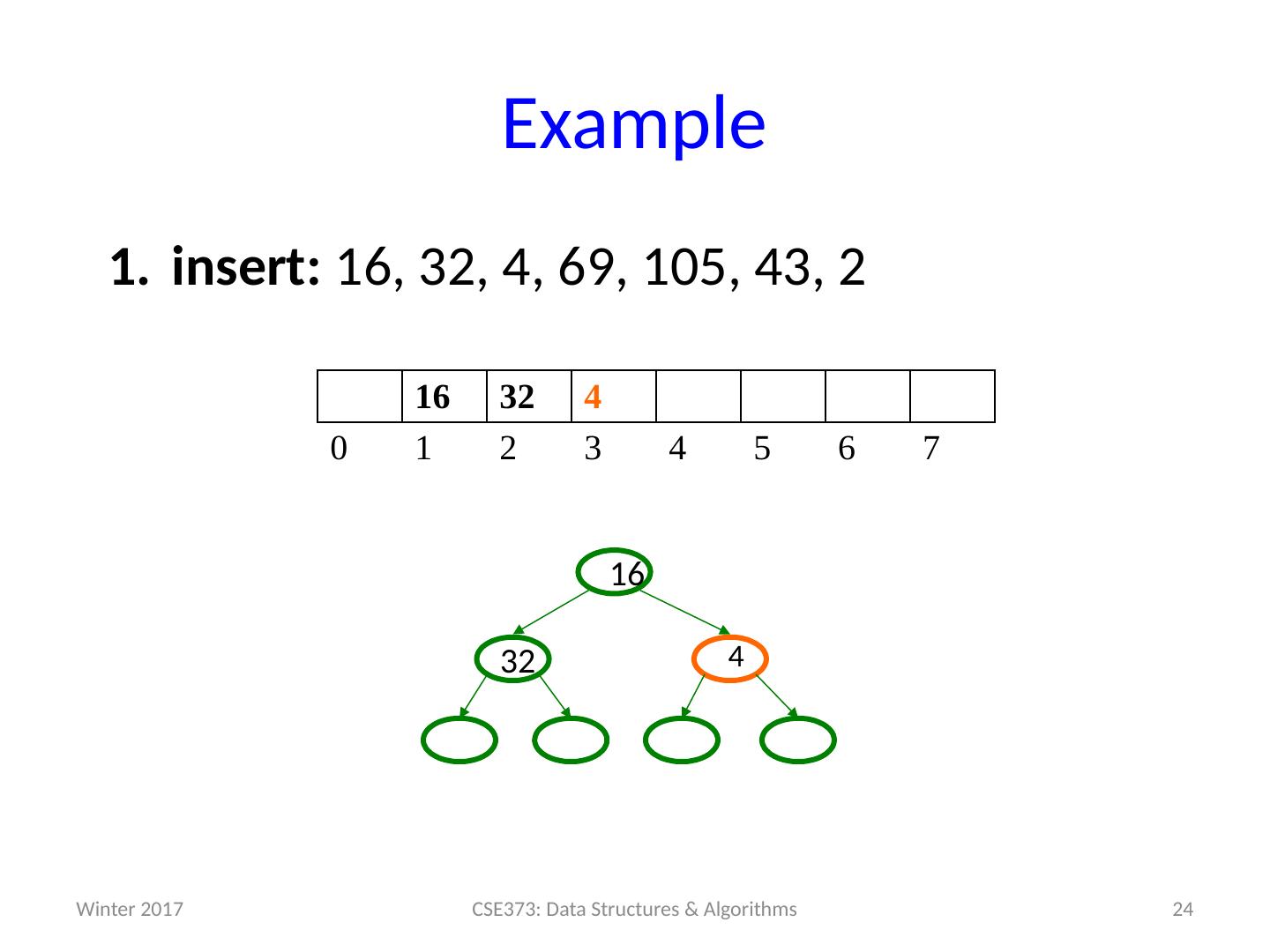
24 .Example insert: 16, 32, 4, 69, 105, 43, 2 24 CSE373: Data Structures & Algorithms 16 32 4 0 1 2 3 4 5 6 7 32 16 4 Winter 2017

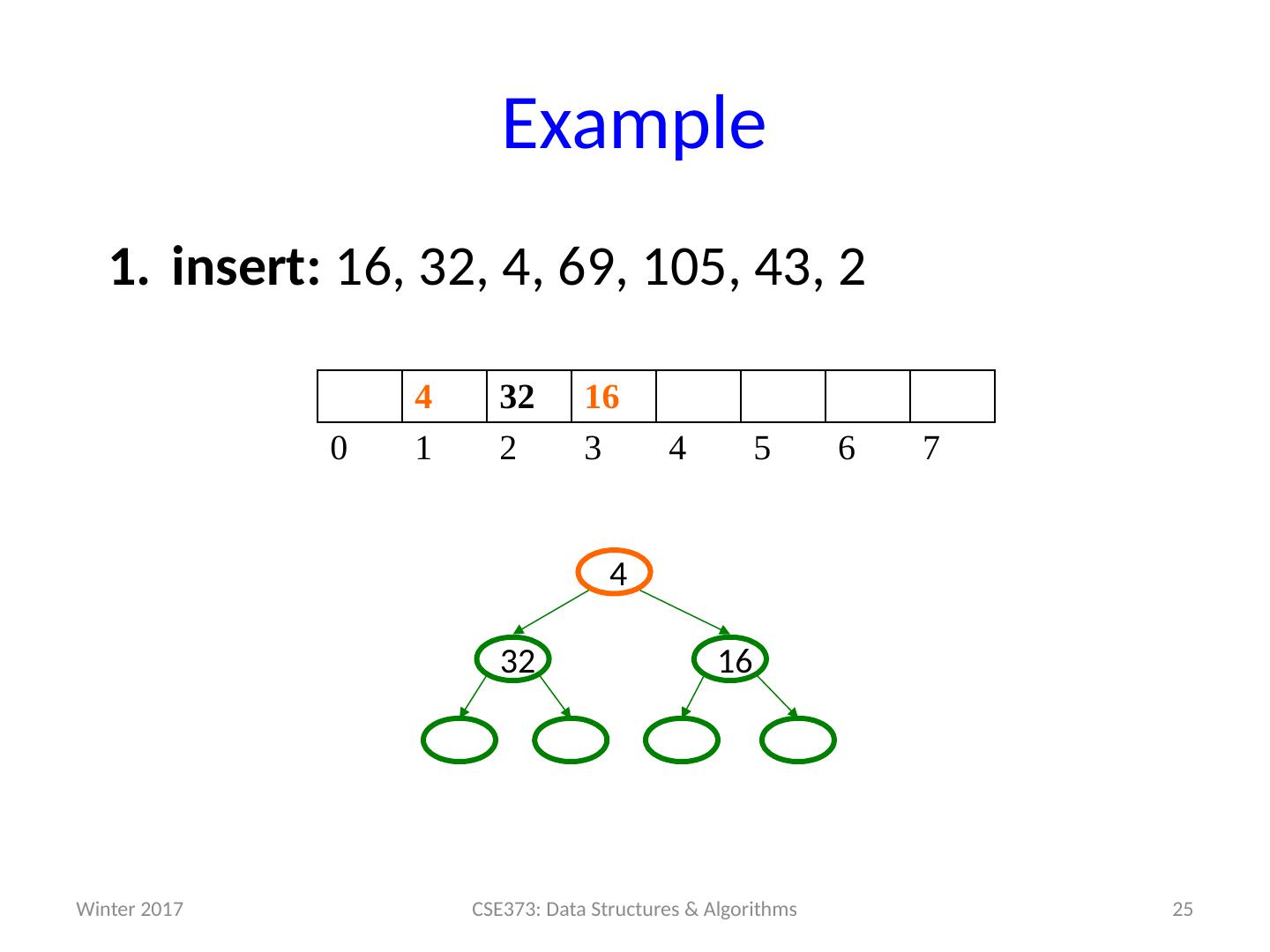
25 .Example insert: 16, 32, 4, 69, 105, 43, 2 25 CSE373: Data Structures & Algorithms 4 32 16 0 1 2 3 4 5 6 7 16 32 4 Winter 2017

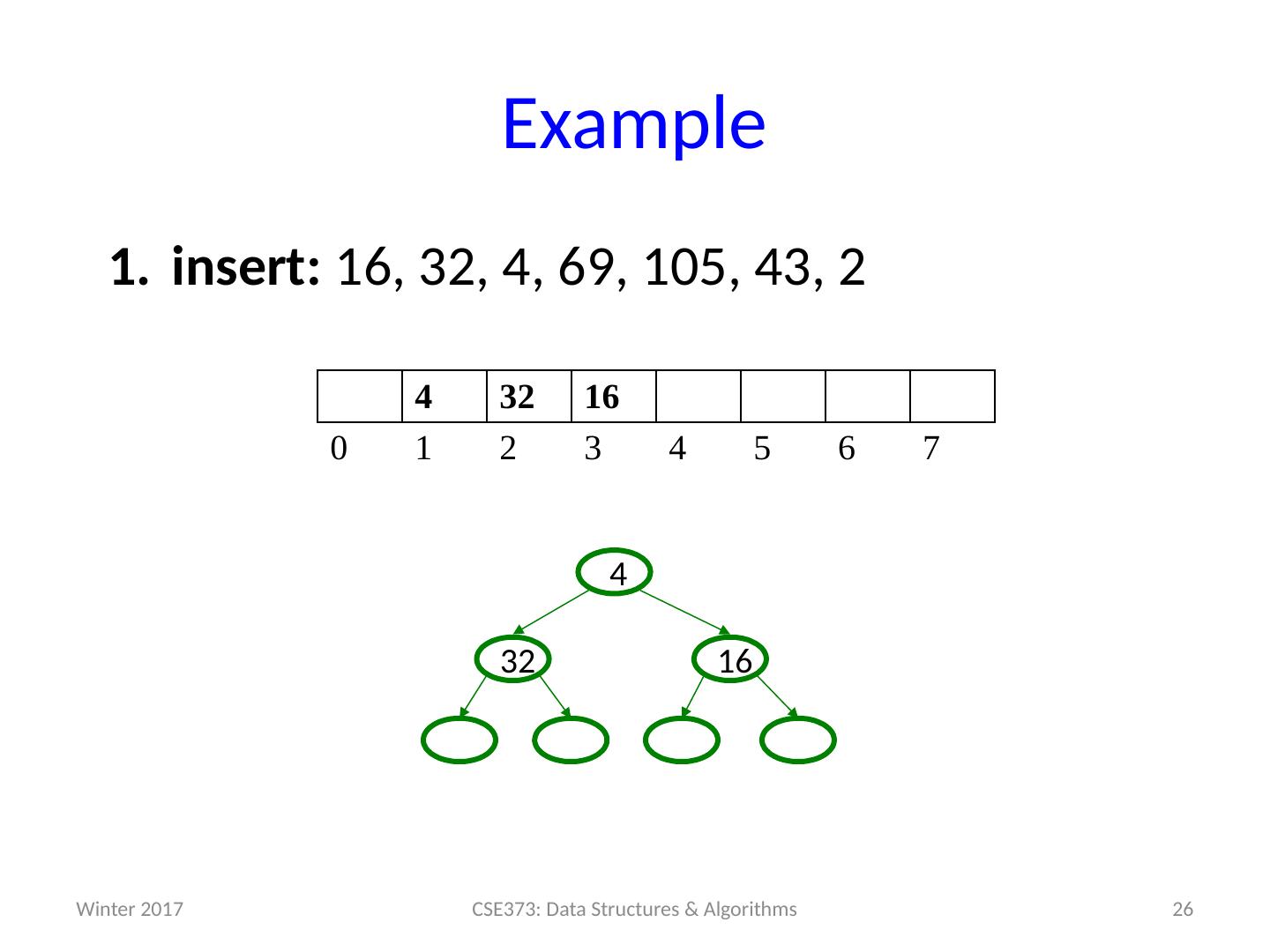
26 .Example insert: 16, 32, 4, 69, 105, 43, 2 26 CSE373: Data Structures & Algorithms 4 32 16 0 1 2 3 4 5 6 7 16 32 4 Winter 2017

27 .Example insert: 16, 32, 4, 69, 105, 43, 2 27 CSE373: Data Structures & Algorithms 4 32 16 69 0 1 2 3 4 5 6 7 69 16 32 4 Winter 2017

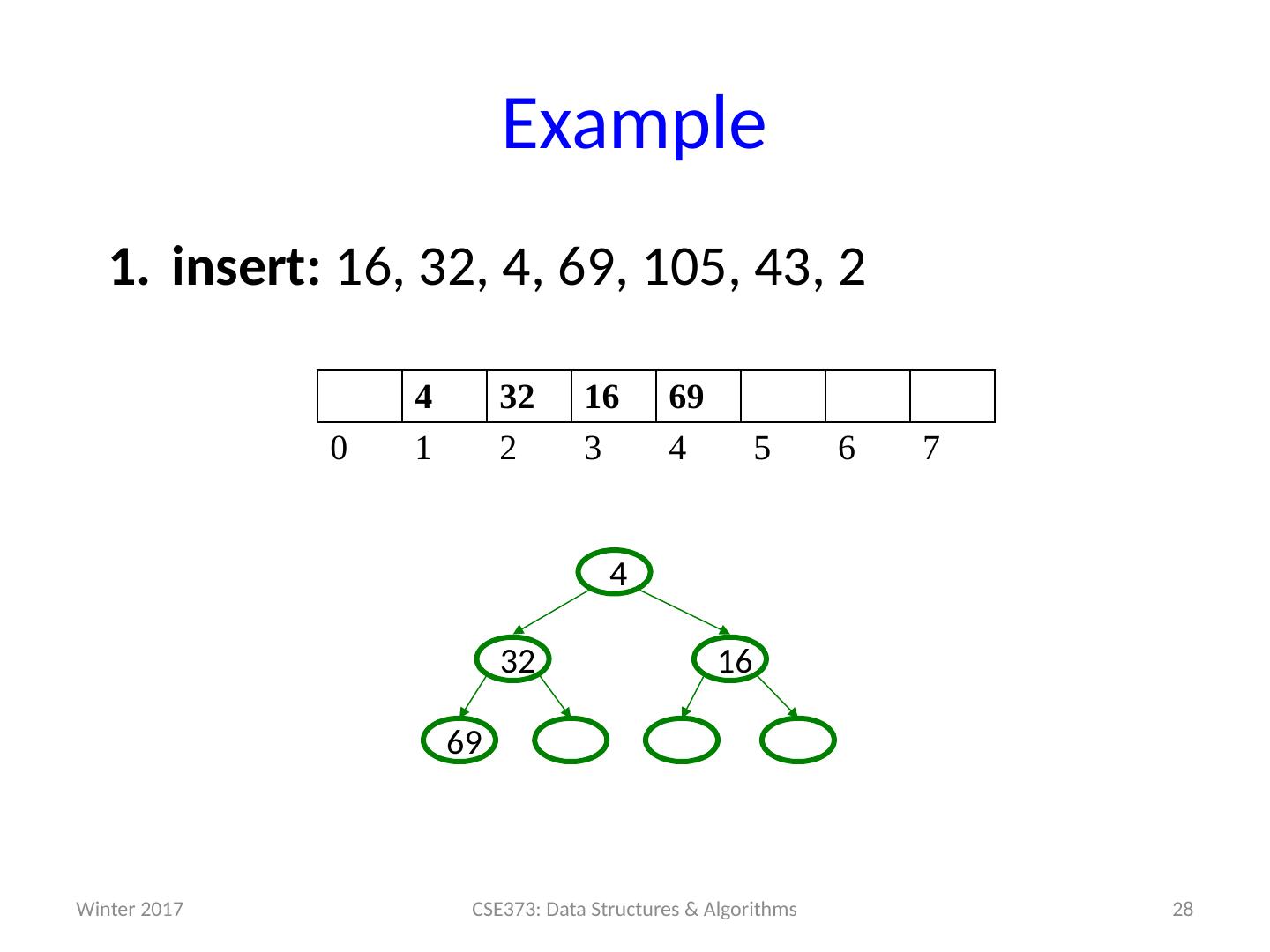
28 .Example insert: 16, 32, 4, 69, 105, 43, 2 28 CSE373: Data Structures & Algorithms 4 32 16 69 0 1 2 3 4 5 6 7 69 16 32 4 Winter 2017

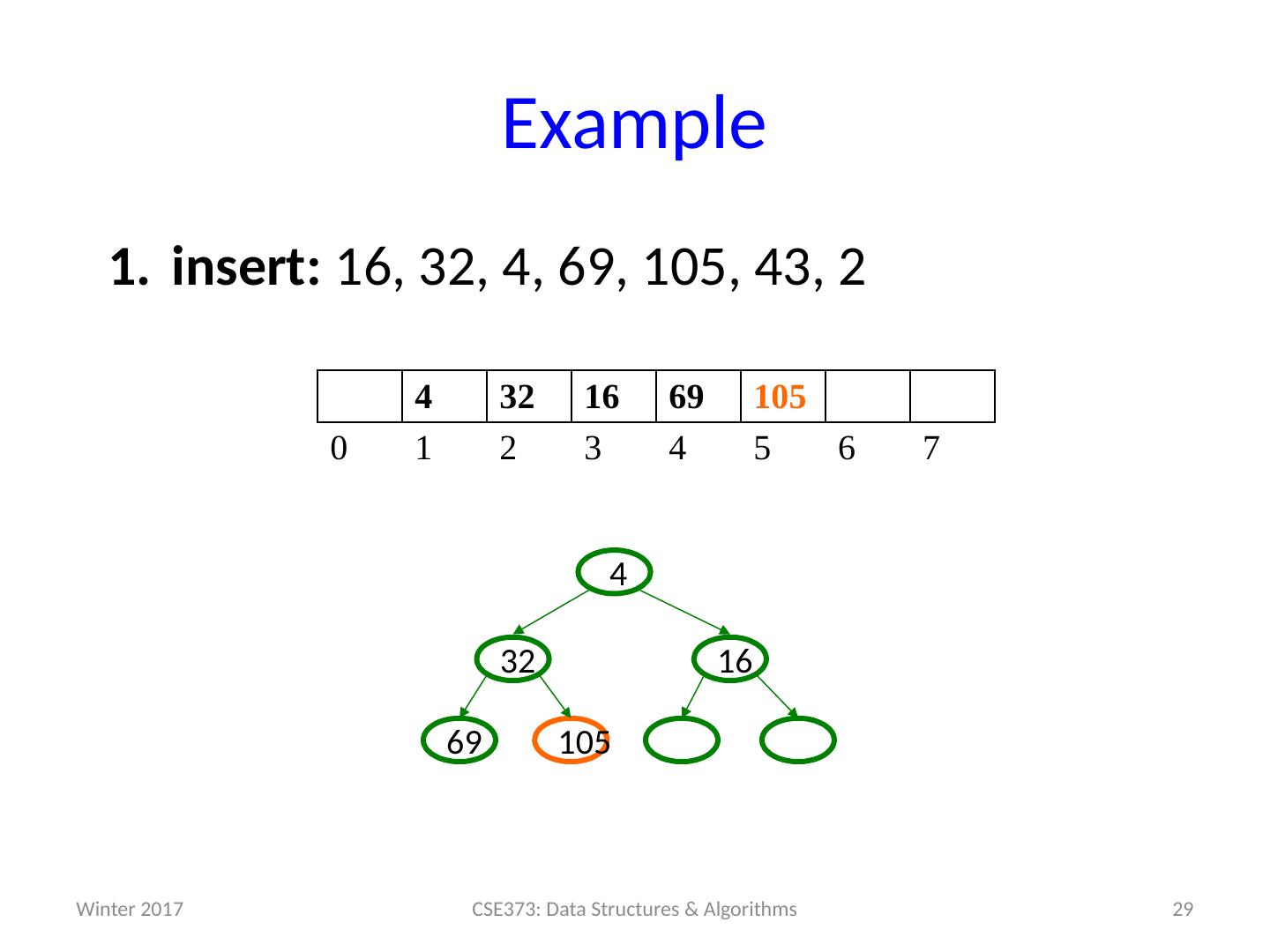
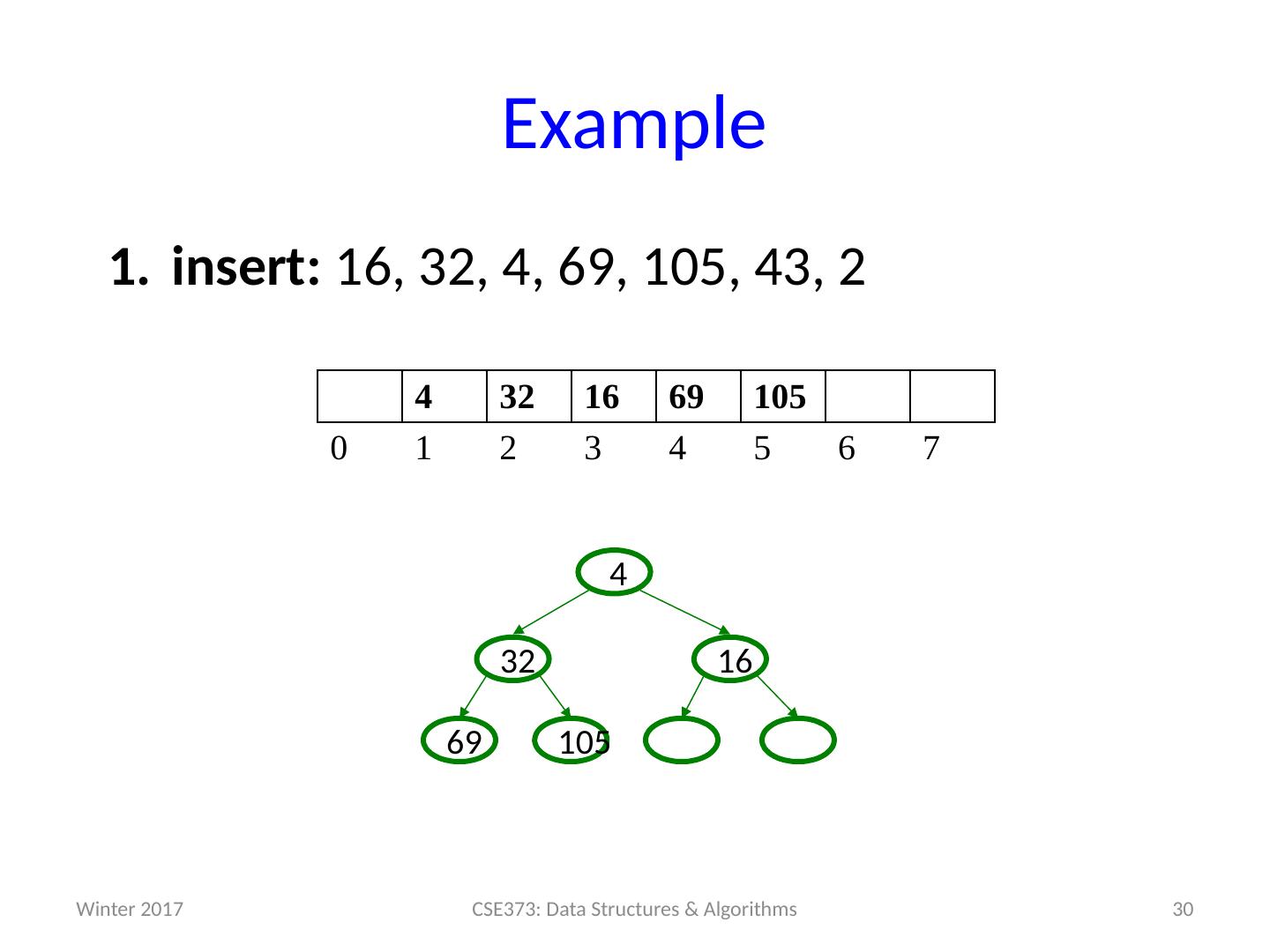
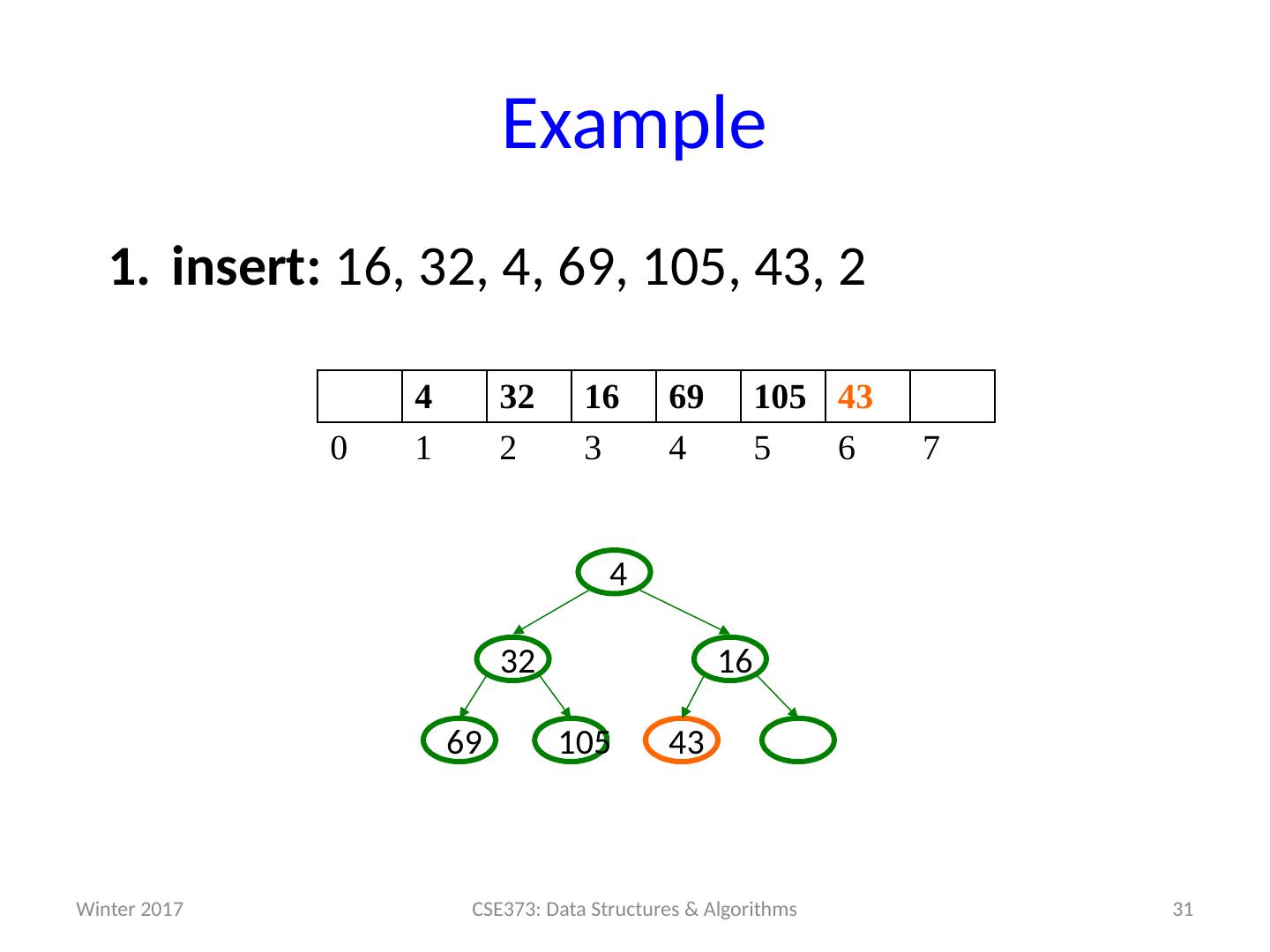
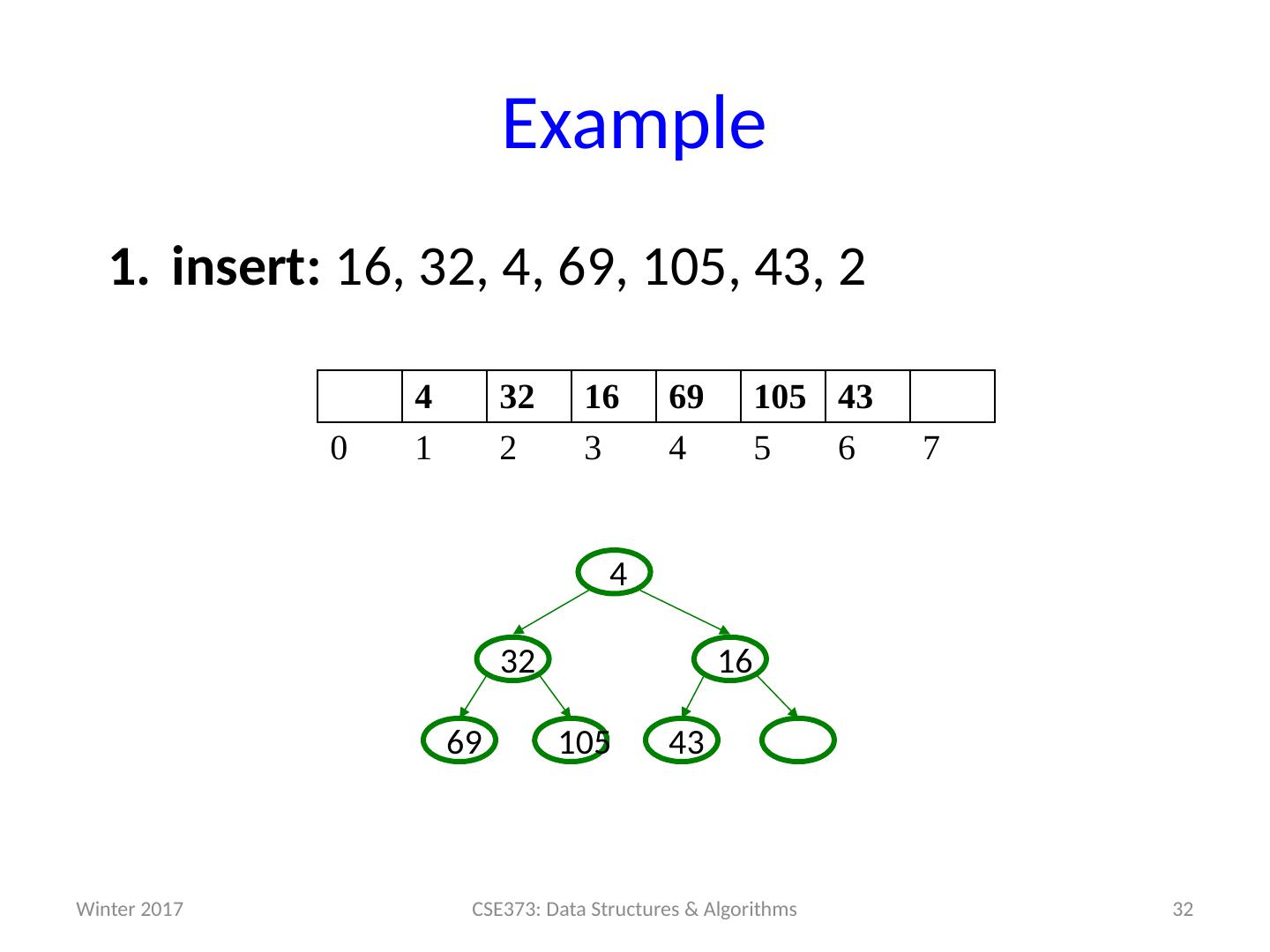
29 .Example insert: 16, 32, 4, 69, 105, 43, 2 29 CSE373: Data Structures & Algorithms 4 32 16 69 105 0 1 2 3 4 5 6 7 105 69 16 32 4 Winter 2017