amortized-analysis

1 .CSE 373 : Data Structures & Algorithms Balancing BSTs; Lazy D eletion; Amortized Analysis Riley Porter Winter 2017 Winter 2017 CSE373: Data Structures & Algorithms 1

2 .Course Logistics HW1 due last night, HW2 (Asymptotic Runtime Analysis (Big-O ) and Implementing Heaps) released tomorrow and due a week from Friday. Canvas does weird name things with resubmission, don’t worry about it. We’ll make future HW submissions a zip to avoid it. If you have weird technical issues with submitting HW, you can email your TA an attachment of your files. This shouldn’t be the norm, but we can accept an email with that timestamp as a submission. C ourse message board will be better monitored, we have a schedule now. We’ll be posting weekly summaries / self checks. Expect the first two week’s posted tomorrow. They’re just extra material for you to gauge how you’re doing, feel free to ask questions about them in office hours or on the discussion board. This is hopefully to supplement not recording lectures in case you are nervous about what you need to have learned each week. Section materials will be posted online, the day before section, but solutions only available in section. If you have to miss a day, talk to your TA. CSE373: Data Structures & Algorithms 2 Winter 2017

3 .Topics from Last Lecture Floyd’s algorithm for building a heap proof of O(N) for buildHeap , which is faster than N inserts which would be O( NlogN ) Review from 143 Dictionaries /Maps/Sets: understand how to be a client of them and the ADT, think about tradeoffs for implementations. implementations all assuming non-hash structure Review from 143 Binary Search Trees: structure, insert, evaluate the runtime of operations. New thing: deleting from a BST . ( findMin and findMax for node replacement) CSE373: Data Structures & Algorithms 3 Winter 2017

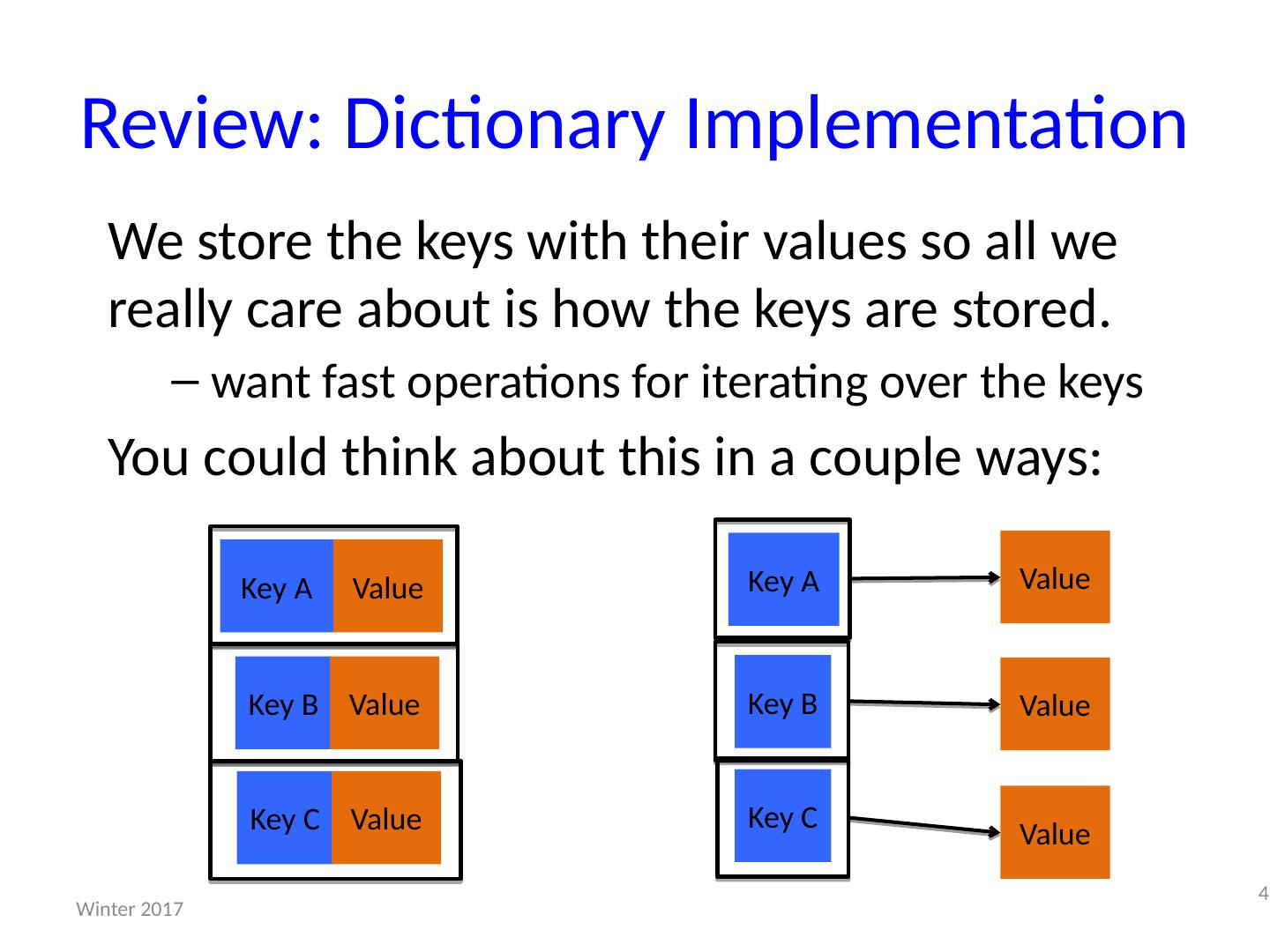
4 .Review: Dictionary Implementation We store the keys with their values so all we really care about is how the keys are stored. want fast operations for iterating over the keys You could think about this in a couple ways: 4 Winter 2017 Key A Value Key B Value Key C Value Key A Value Key B Value Key C Value

5 .Review: Simple Dictionary Implementations; Operation Analysis For dictionary with n key/value pairs insert find delete Unsorted linked-list Unsorted array Sorted linked list Sorted array * Unless we need to check for duplicates 5 O(1)* O (N) O (N) O(1)* O (N) O (N) O (N) O (N) O (N) O (N) O( logN ) O (N) We’ll see a Binary Search Tree (BST) probably does better, but not in the worst case unless we keep it balanced Winter 2017

6 .Sorted Array: Lazy Deletion A general technique for making delete as fast as find : Instead of actually removing the item just mark it deleted Plusses: Simpler to delete (no shifting). If element is re-added soon afterwards, simple to insert it again (no shifting) Can control removals and do them later in batches ( amortized cost , we’ll talk about this later today) Minuses: Extra space for the “is-it-deleted” flag Data structure full of deleted nodes wastes space Now we can’t use N in runtime: find O ( log m ) time where m is data-structure size (okay ) 6 10 12 24 30 41 42 44 45 50          Winter 2017

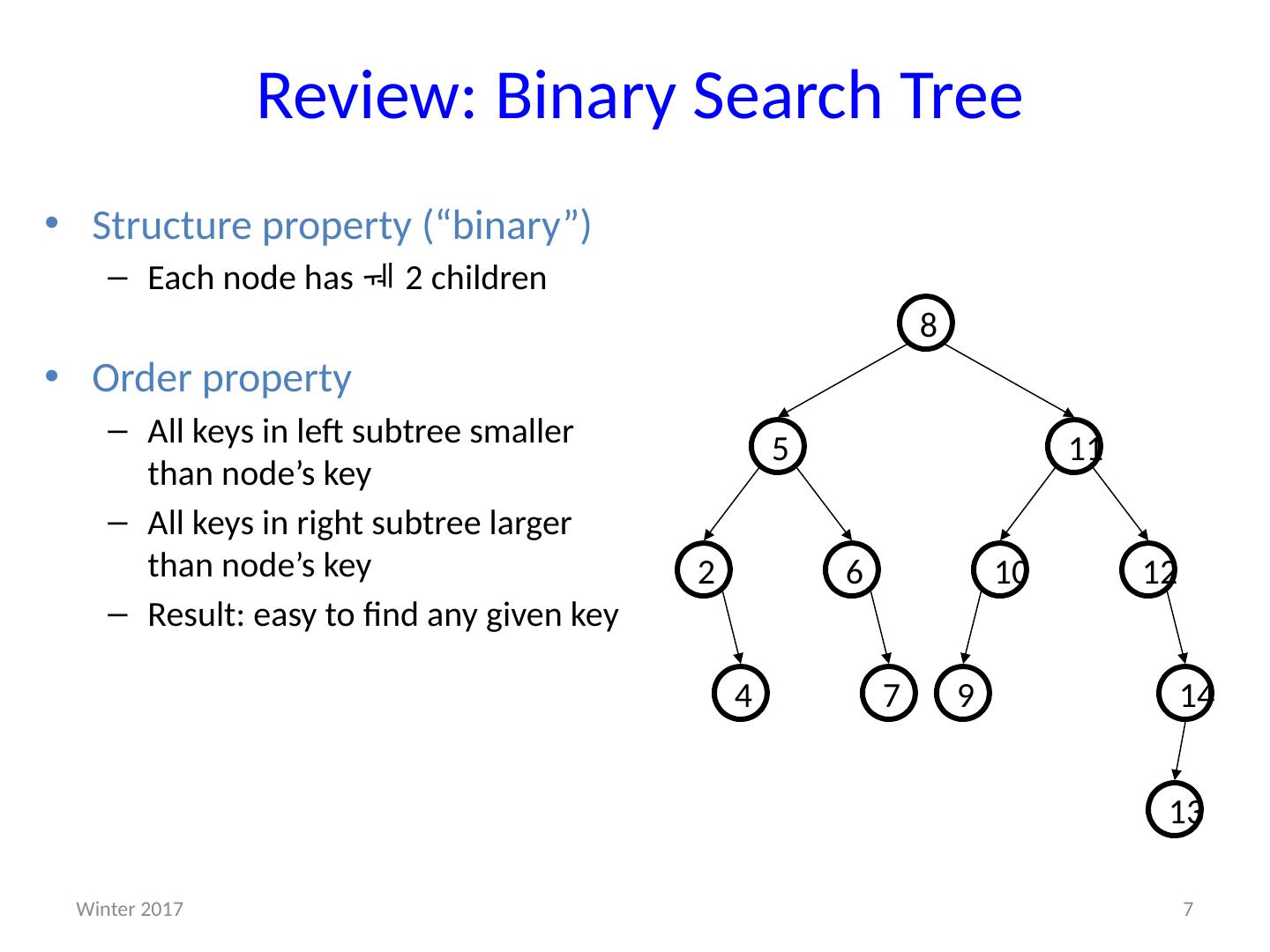
7 .Review: Binary Search Tree 4 12 10 6 2 11 5 8 14 13 7 9 Structure property (“binary”) E ach node has  2 children Order property A ll keys in left subtree smaller than node’s key A ll keys in right subtree larger than node’s key R esult: easy to find any given key 7 Winter 2017

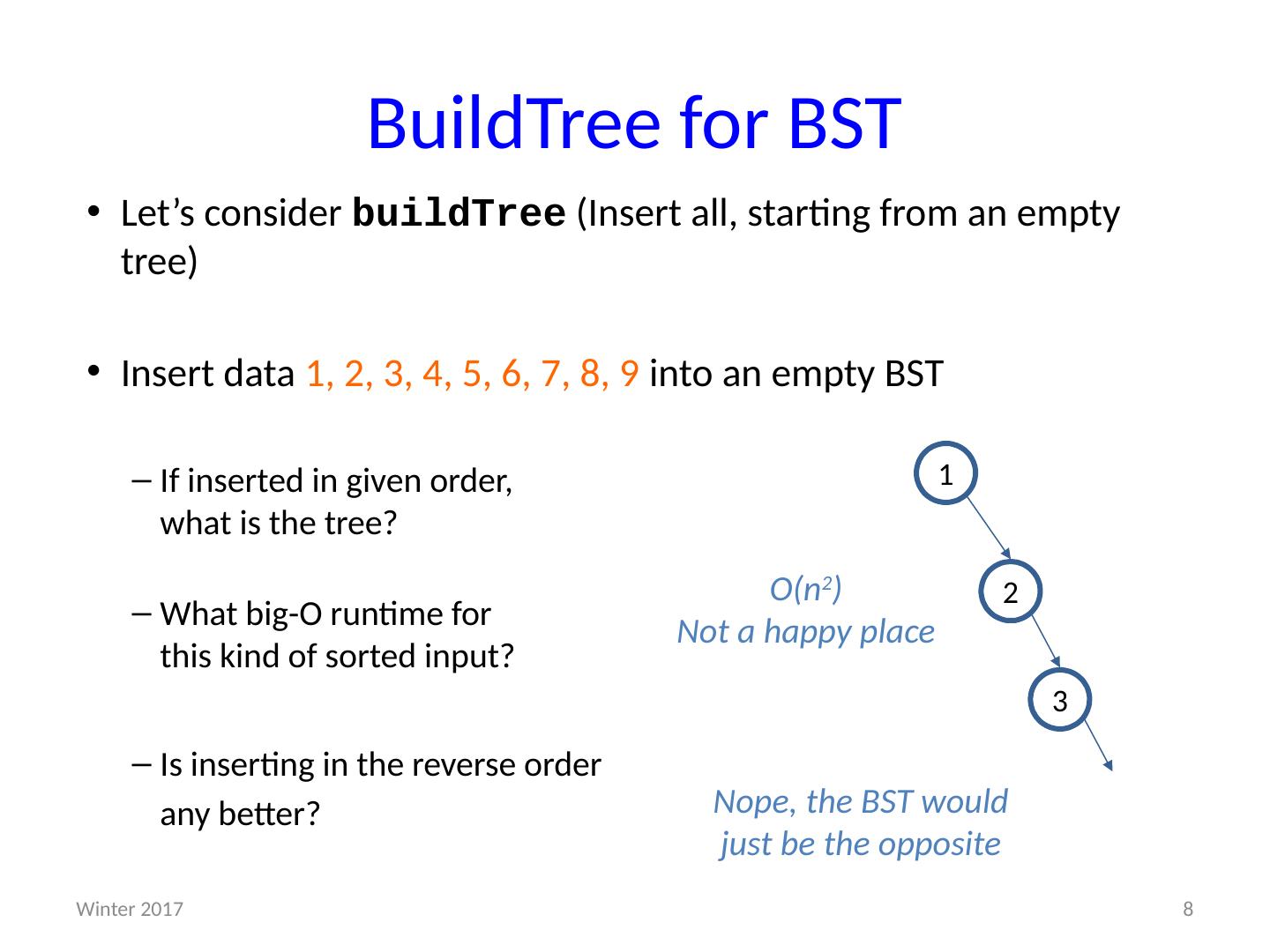
8 .BuildTree for BST Let’s consider buildTree ( Insert all, starting from an empty tree) Insert data 1 , 2, 3, 4, 5, 6, 7, 8, 9 into an empty BST If inserted in given order, what is the tree? What big-O runtime for this kind of sorted input? Is inserting in the reverse order any better? Θ ( n 2 ) Θ ( n 2 ) 1 2 3 O(n 2 ) Not a happy place 8 Winter 2017 Nope, the BST would just be the opposite

9 .Intuition: Balanced BSTs are good What if we re -arrange the data when inserting median first, then left median, right median, etc. 5, 3, 7, 2, 1, 4, 8, 6, 9 What tree does that give us? What big-O runtime? 5, 3, 7, 2, 1, 6, 8, 9 better: n log n 8 4 2 7 3 5 9 6 1 O (N log N ) , definitely better 9 Winter 2017

10 .Intuition: Unbalanced BSTs are bad Even if we balance a BST during buildTree , a series of sorted data insertions can mess up our structure badly With a bad structure, all operations are O(N): find insert delete 1 2 3 10 Winter 2017

11 .BST Operations Analysis For BST with n nodes insert find delete Worst Case (unbalanced) Average Case (balanced) 11 O ( N ) O (N) O (N) O ( logN ) O ( logN ) O ( logN ) Winter 2017 Hard to keep a BST balanced, so BSTs are only “probably” better as implementations than a sorted array. We’ll see how to keep them balanced on Friday

12 .Lazy Deletion for BSTs: Plusses: Simpler: delete with findMin and findMax are difficult operations, this minimizes those traversals Can do “real deletions” later as a batch Some inserts can just “undelete” a tree node Minuses: Can waste space and slow down find operations Makes some operations more complicated with extra nodes in the tree 12 Winter 2017

13 .Keeping BSTs Balanced For a BST with N nodes inserted in arbitrary order Average height is O ( log N ) – intuition on Friday’s slides, proof in text Worst case height is O ( N ) Simple, commonly occurring cases, such as inserting in key order, lead to the worst-case scenario Solution : Require a Balance Condition that maintains a nice structure: E nsures depth is always O ( log N ) – strong enough! I s efficient to maintain – not too strong! 13 Winter 2017

14 .Potential Balance Conditions Left and right subtrees of every node have equal number of nodes Left and right subtrees of every node have equal height Too strong! Only perfect trees (2 n – 1 nodes) Too strong! Only perfect trees (2 n – 1 nodes) 14 Winter 2017

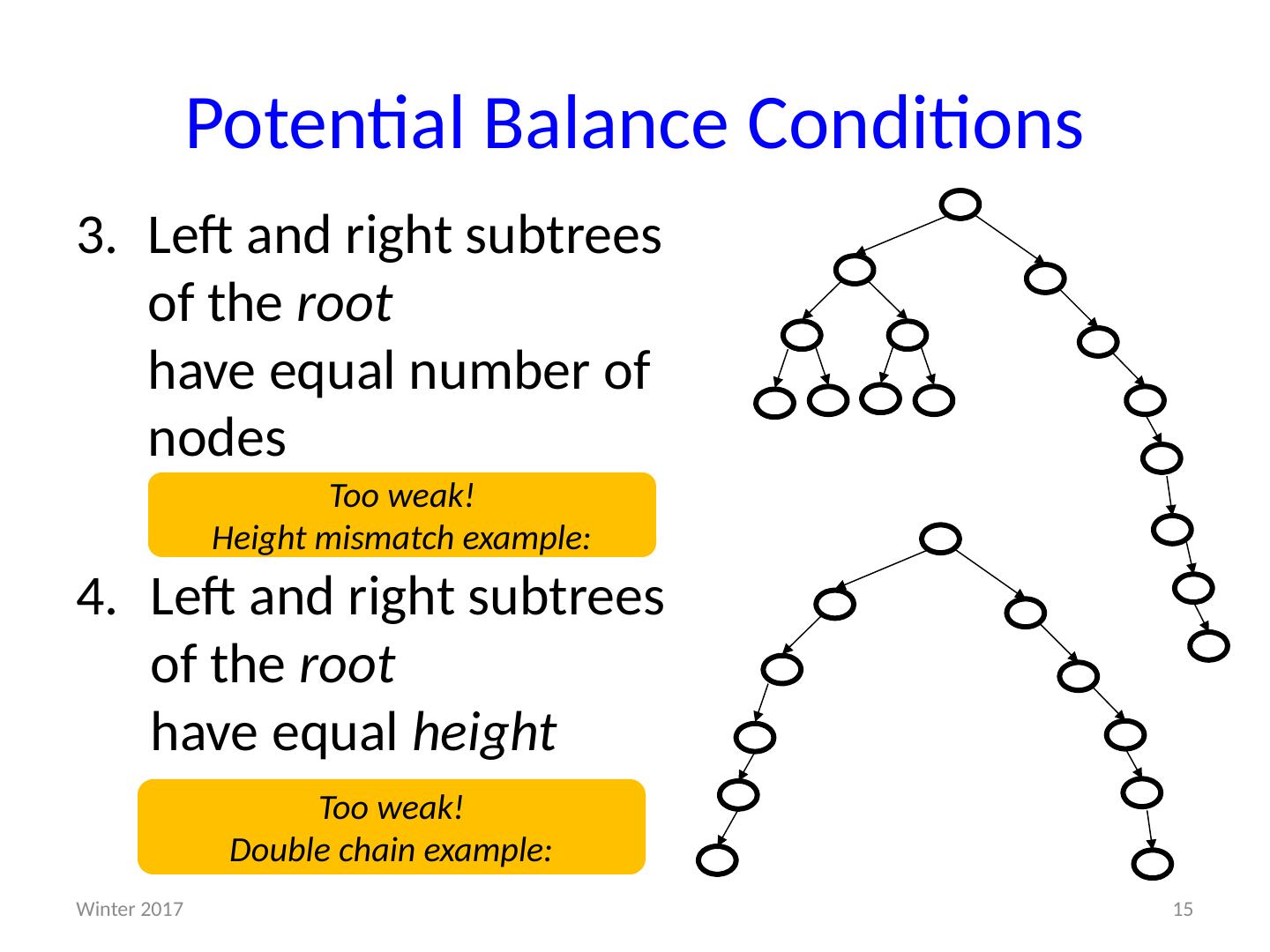
15 .Potential Balance Conditions Left and right subtrees of the root have equal number of nodes 4 . Left and right subtrees of the root have equal height Too weak! Height mismatch example: Too weak! Double chain example: 15 Winter 2017

16 .16 The AVL Balance Condition Left and right subtrees of every node have heights differing by at most 1 Definition : balance ( node ) = height( node .left ) – height( node .right ) AVL property : for every node x, –1  balance( x )  1 Ensures small depth Will prove this by showing that an AVL tree of height h must have a number of nodes exponential in h Efficient to maintain Using single and double rotations Adelson-Velskii and Landis Winter 2017

17 .Any questions on Dictionaries or BSTs? We’ll explore the AVL balance condition and AVL trees more on Friday. For now let’s consider something we skipped when talking about asymptotic runtime analysis 17 CSE373: Data Structures & Algorithms Winter 2017

18 .Amortized Runtime Complexity Recall our plain-old stack implemented as an array that doubles its size if it runs out of room How can we claim push is O ( 1 ) time if resizing is O ( n ) time? We can’t , but we can claim it’s an O ( 1 ) amortized operation What does amortized mean? When are amortized bounds good enough? How can we prove an amortized bound? Will just do two simple examples Text has more sophisticated examples and proof techniques Idea of how amortized describes average cost is essential 18 CSE373: Data Structures & Algorithms Winter 2017

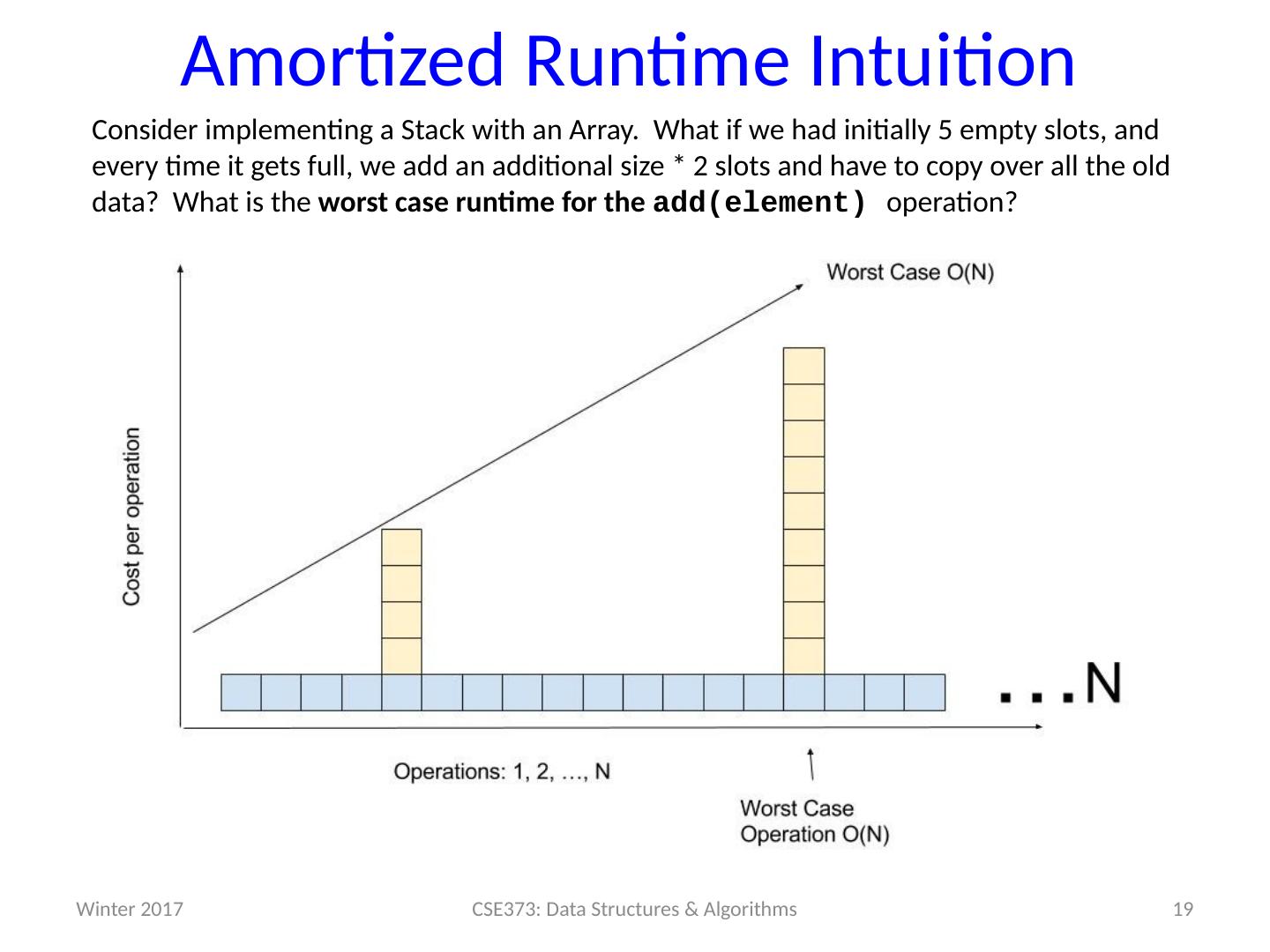
19 .Amortized Runtime Intuition Consider implementing a Stack with an Array. What if w e had initially 5 empty slots, and every time it gets full, we add an additional size * 2 slots and have to copy over all the old data? What is the worst case runtime for the add(element) operation? 19 CSE373: Data Structures & Algorithms Winter 2017

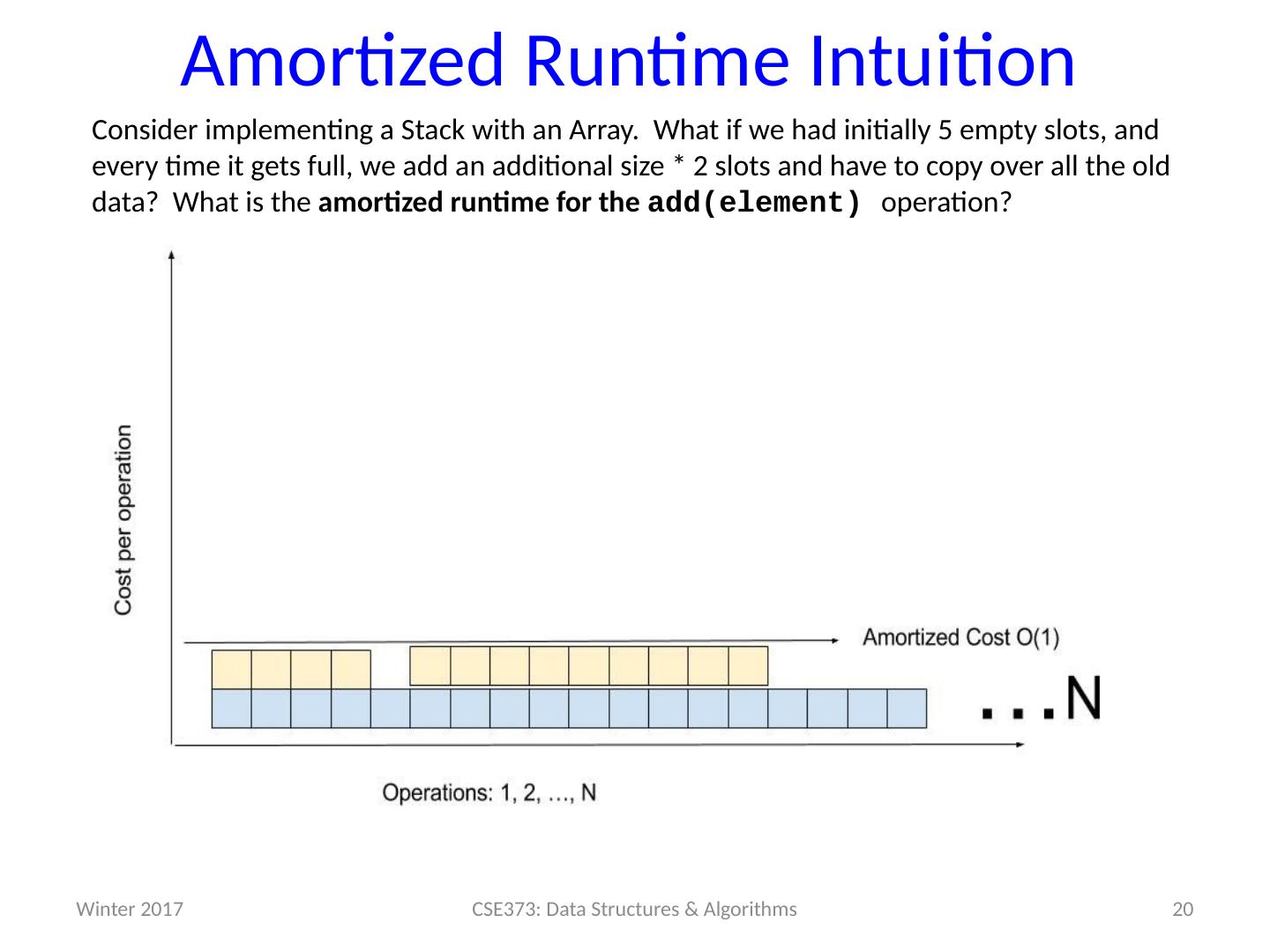
20 .Amortized Runtime Intuition Consider implementing a Stack with an Array. What if w e had initially 5 empty slots, and every time it gets full, we add an additional size * 2 slots and have to copy over all the old data? What is the amortized runtime for the add(element) operation? 20 CSE373: Data Structures & Algorithms Winter 2017

21 .“Building Up Credit ” Intuition Can think of preceding “cheap” operations as building up “credit” that can be used to “pay for” later “expensive” operations Because any sequence of operations must be under the bound, enough “cheap” operations must come first Else a prefix of the sequence, which is also a sequence, would violate the bound 21 CSE373: Data Structures & Algorithms Winter 2017

22 .Amortized Runtime Complexity If a sequence of M operations takes O ( M f(n) ) time, we say the amortized runtime is O ( f(n) ) Amortized bound: worst-case guarantee over sequences of operations Example: If any n operations take O ( n ), then amortized O ( 1 ) Example: If any n operations take O ( n 3 ), then amortized O ( n 2 ) The worst case time per operation can be larger than f(n) As long as the worst case is always “rare enough” in any sequence of operations Amortized guarantee ensures the average time per operation for any sequence is O ( f(n) ) 22 CSE373: Data Structures & Algorithms Winter 2017

23 .Example #1: Resizing stack A stack implemented with an array where we double the size of the array if it becomes full Claim: Any sequence of push / pop / isEmpty is amortized O ( 1 ) Need to show any sequence of M operations takes time O ( M ) Recall the non-resizing work is O ( M ) (i.e., M* O ( 1 )) The resizing work is proportional to the total number of element copies we do for the resizing So it suffices to show that: After M operations, we have done < 2M total element copies (So average number of copies per operation is bounded by a constant) 23 CSE373: Data Structures & Algorithms Winter 2017

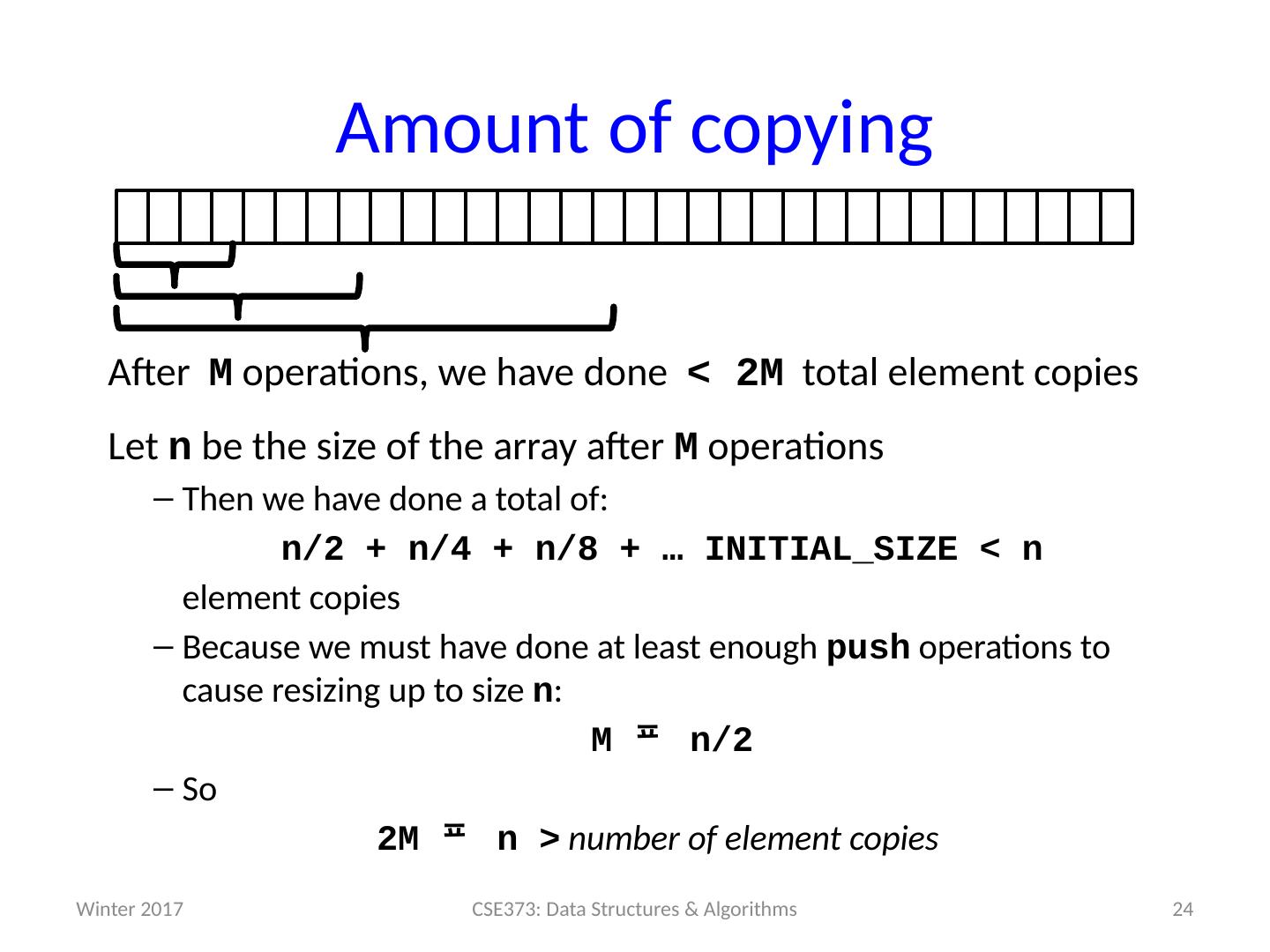
24 .Amount of copying After M operations, we have done < 2M total element copies Let n be the size of the array after M operations Then we have done a total of: n/2 + n/4 + n/8 + … INITIAL_SIZE < n element copies Because we must have done at least enough push operations to cause resizing up to size n : M  n/2 So 2M  n > number of element copies 24 CSE373: Data Structures & Algorithms Winter 2017

25 .Other approaches If array grows by a constant amount (say 1000), operations are not amortized O ( 1 ) After O ( M ) operations, you may have done  ( M 2 ) copies If array doubles when full and shrinks when 1/2 empty, operations are not amortized O ( 1 ) Terrible case : pop once and shrink, push once and grow, pop once and shrink, … If array doubles when full and shrinks when 3/4 empty, it is amortized O ( 1 ) Proof is more complicated, but basic idea remains: by the time an expensive operation occurs, many cheap ones occurred 25 CSE373: Data Structures & Algorithms Winter 2017

26 .Example #2: Queue with two stacks A clever and simple queue implementation using only stacks 26 CSE373: Data Structures & Algorithms class Queue < E > { Stack<E> in = new Stack<E>(); Stack<E> out = new Stack<E>(); void enqueue (E x ){ in.push (x); } E dequeue (){ if ( out.isEmpty ()) { while (! in.isEmpty ()) { out.push (in.pop()); } } return out.pop(); } } C B A in out enqueue : A, B, C Winter 2017

27 .Example #2: Queue with two stacks A clever and simple queue implementation using only stacks 27 CSE373: Data Structures & Algorithms class Queue < E > { Stack<E> in = new Stack<E>(); Stack<E> out = new Stack<E>(); void enqueue (E x ){ in.push (x); } E dequeue (){ if ( out.isEmpty ()) { while (! in.isEmpty ()) { out.push (in.pop()); } } return out.pop(); } } in out dequeue B C A Winter 2017

28 .Example #2: Queue with two stacks A clever and simple queue implementation using only stacks 28 CSE373: Data Structures & Algorithms class Queue < E > { Stack<E> in = new Stack<E>(); Stack<E> out = new Stack<E>(); void enqueue (E x ){ in.push (x); } E dequeue (){ if ( out.isEmpty ()) { while (! in.isEmpty ()) { out.push (in.pop()); } } return out.pop(); } } in out enqueue D, E B C A E D Winter 2017

29 .Example #2: Queue with two stacks A clever and simple queue implementation using only stacks 29 CSE373: Data Structures & Algorithms class Queue < E > { Stack<E> in = new Stack<E>(); Stack<E> out = new Stack<E>(); void enqueue (E x ){ in.push (x); } E dequeue (){ if ( out.isEmpty ()) { while (! in.isEmpty ()) { out.push (in.pop()); } } return out.pop(); } } in out dequeue twice C B A E D Winter 2017