Antialiasing

1 .Antialiasing CMSC 435/634

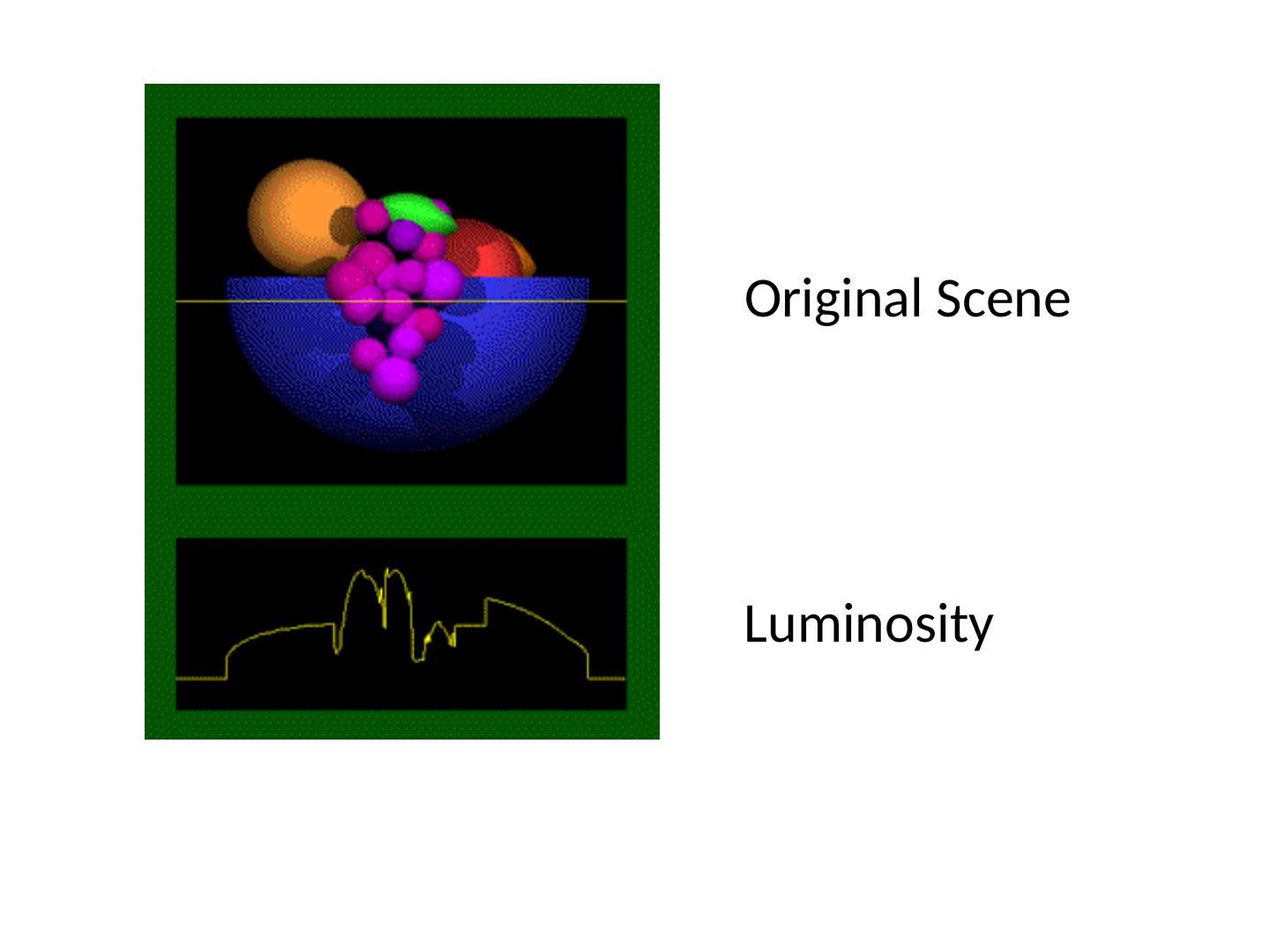
2 .Original Scene Luminosity

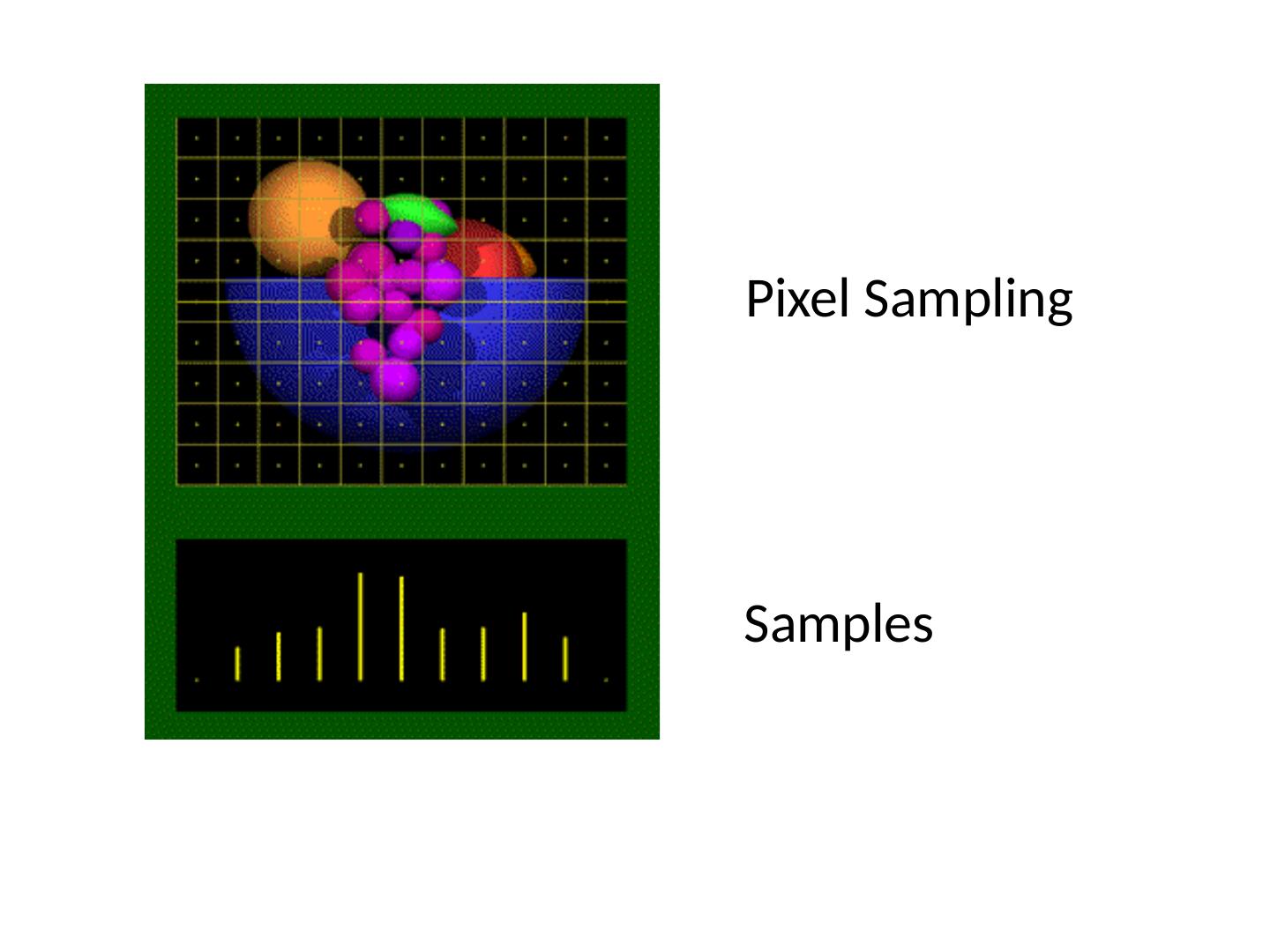
3 .Pixel Sampling Samples

4 .Displayed Image Luminosity

5 .What went wrong?

6 .Aliasing Visual artifacts Jagged lines and edges High frequencies appearing as low Small objects missed T exture distortions Strobing and popping Backward movement

7 .Jagged Lines

8 .Jagged Edges

9 .Frequency Aliasing

10 .Missed Detail

11 .Missed Detail

12 .

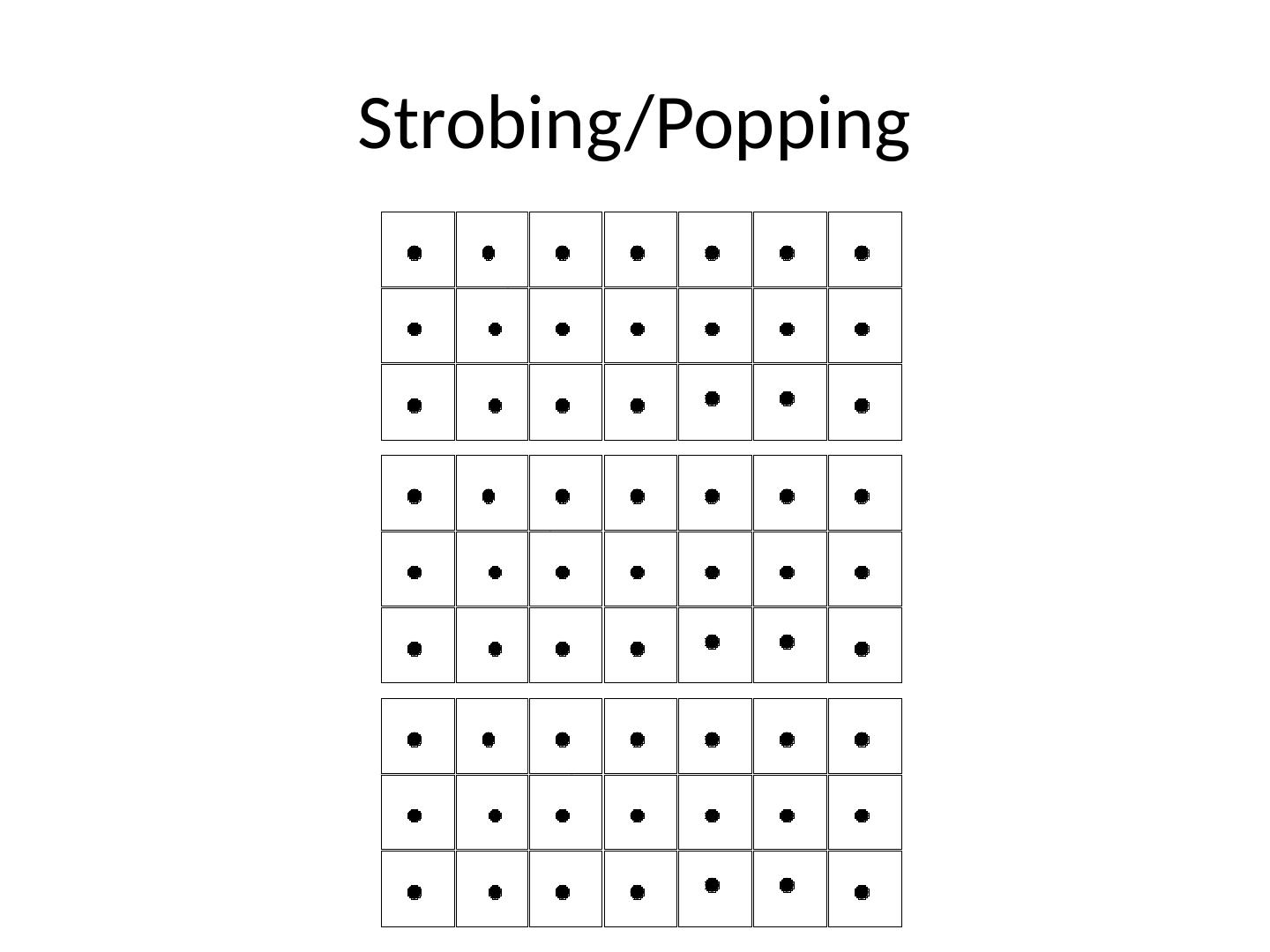
13 .Strobing /Popping

14 .How might you fix aliasing?

15 .How might you fix aliasing?

16 .How might you fix aliasing?

17 .How might you fix aliasing?

18 .How might you fix aliasing?

19 .Sampling Theory Shannon ’ s sampling theory (1D): A band limited signal f(t) with cut off frequency w F may be perfectly reconstructed from its samples f(nT 0 ) if 2 p /T 0 >= 2w F w F == Nyquist limit Alternatively: a signal can be reconstructed exactly from samples only if the highest frequency is less than half the sampling rate

20 .Sampling a Sine Wave

21 .What Will Alias? Plot based on frequency Like audio equalizer Fourier transform

22 .What Will Alias? Sampling replicates spectrum in a grid Aliasing when they overlap

23 .How to Fix It? Filter Blur away high frequency Blur is better than aliasing

24 .Filters 24

25 .Using a Filter to Compute Pixel Color 25

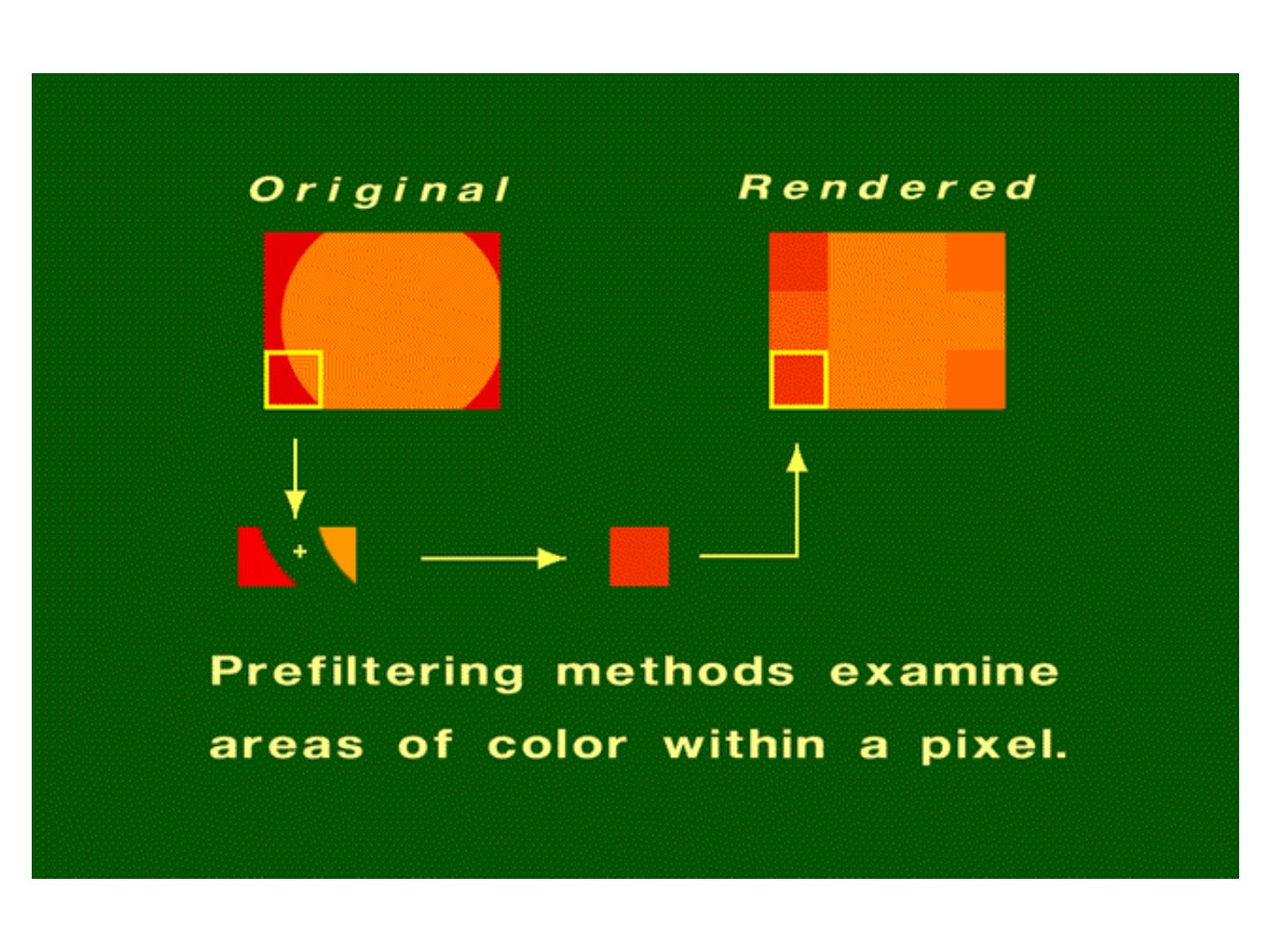
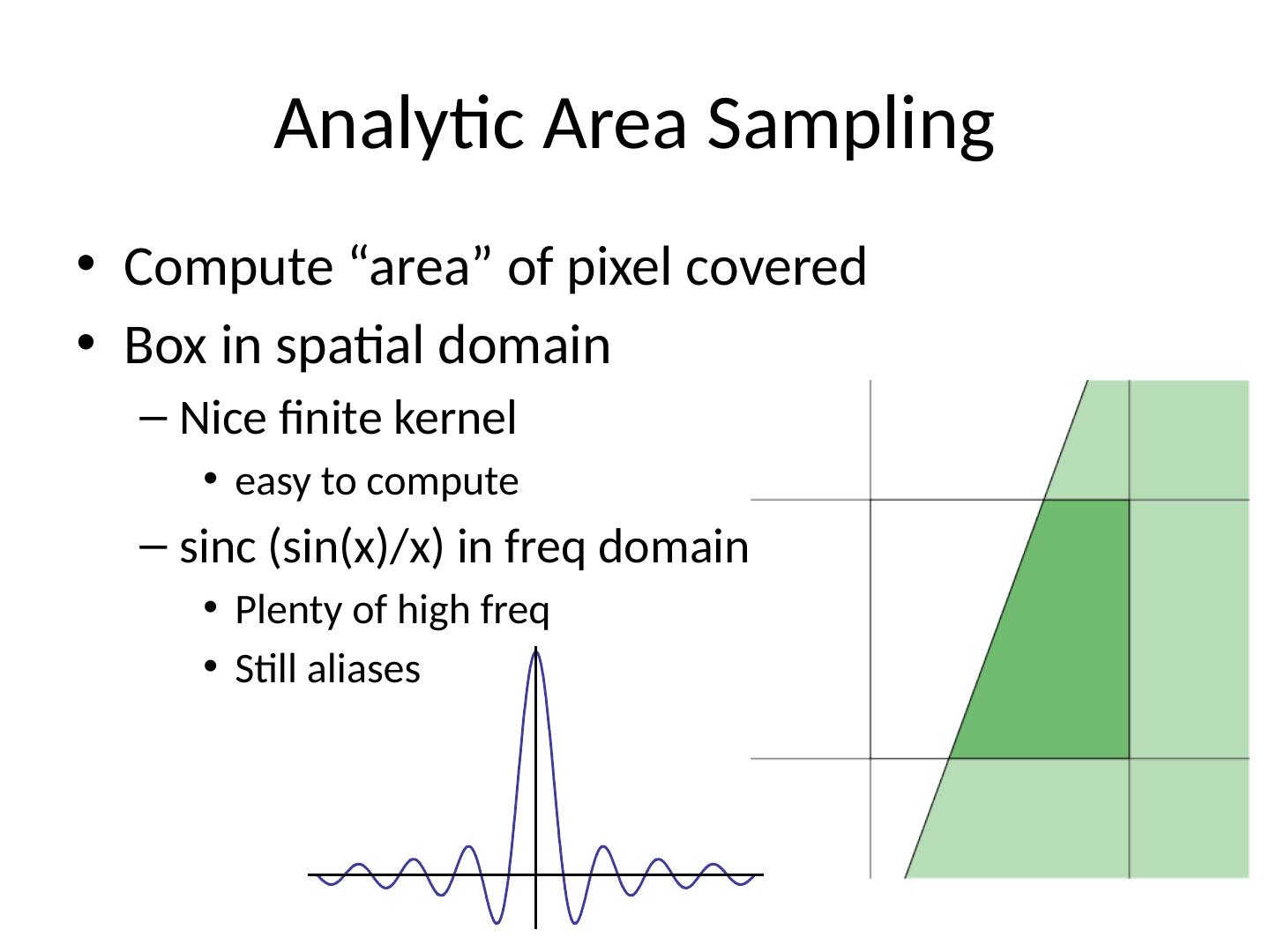
26 .Analytic Area Sampling Compute “area” of pixel covered Box in spatial domain Nice finite kernel easy to compute sinc (sin(x)/x) in freq domain Plenty of high freq Still aliases

27 .Analytic higher order filtering Fold better filter into rasterization Can make rasterization much harder Usually just done for lines Draw with filter kernel “paintbrush” Only practical for finite filters

28 .Supersampling Numeric integration of filter Grid with equal weight = box filter Push up Nyquist frequency Edges: ∞ frequency, still alias Other filters: Grid with unequal weights Priority sampling

29 .Adaptive sampling Vary numerical integration step More samples in high contrast areas Easy with ray tracing, harder for others Possible bias