排序算法的种类

1 .CSE 373 : Data Structures & Algorithms M ore Sorting and Beyond Comparison Sorting Riley Porter Winter 2017 Summer 2016 CSE373: Data Structures & Algorithms 1

2 .Course Logistics HW5 due in a couple days  more graphs! Don’t forget about the write-up! HW6 out later today  sorting (and to a lesser degree reading specs/other files/tests). Final exam in 2 weeks! 2 CSE373: Data Structures & Algorithms

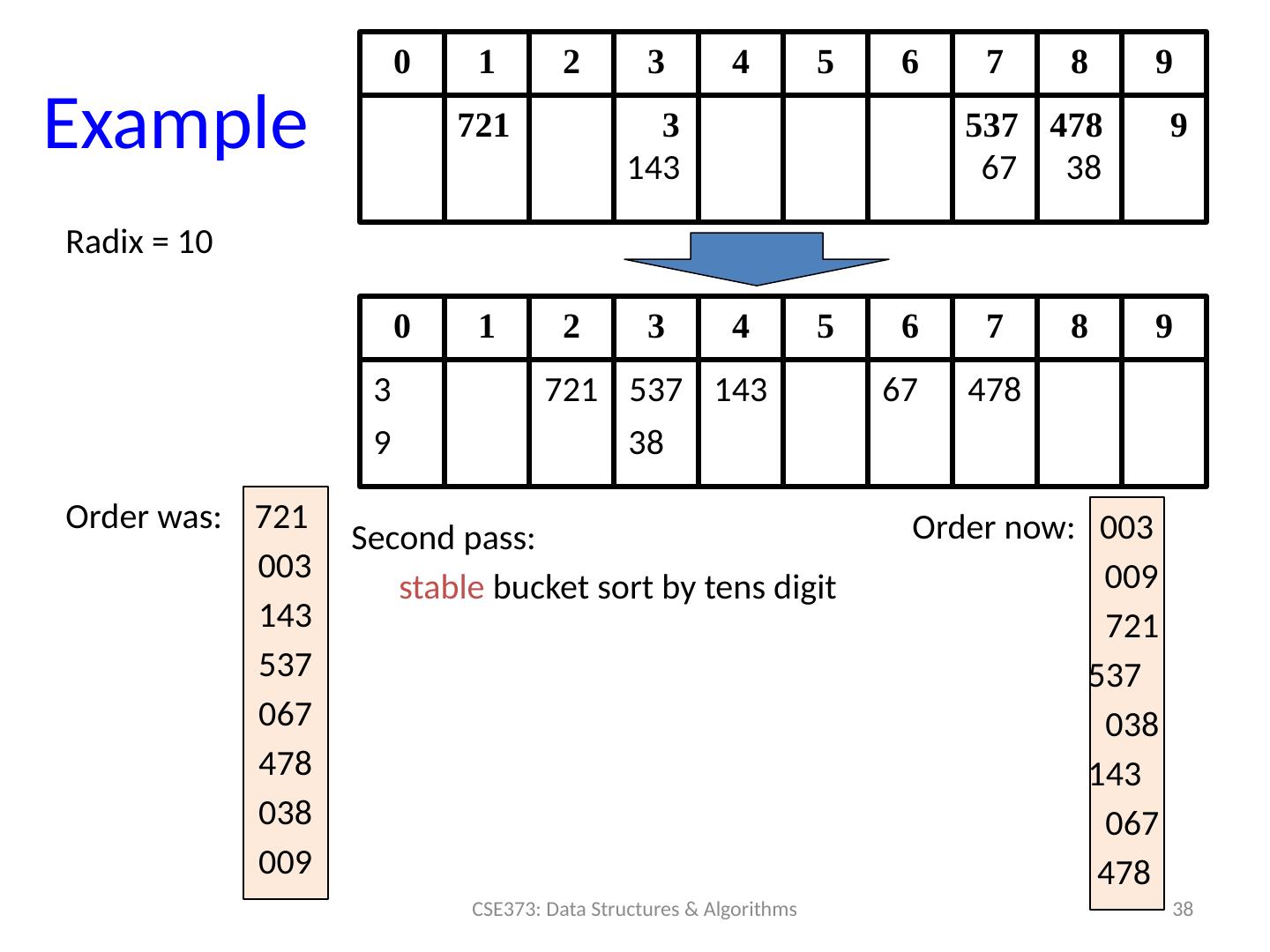
3 .Review: Sorting : The Big Picture 3 CSE373: Data Structures & Algorithms Simple algorithms: O( n 2 ) Fancier algorithms: O( n log n ) Comparison lower bound: ( n log n ) Specialized algorithms: O( n ) Handling huge data sets Insertion sort Selection sort Bubble sort Shell sort … Heap sort Merge sort Quick sort ( avg ) … Bucket sort Radix sort External sorting O(n 2 ) O(n)

4 .Quick Sort 4 CSE373: Data Structures & Algorithms 5 2 8 4 7 3 1 6 Divide : Split array around a ‘pivot’ 5 2 4 3 7 6 8 1 numbers <= pivot numbers > pivot pivot

5 .Quick Sort 5 CSE373: Data Structures & Algorithms Unsorted <= P > P Divide : Pick a pivot, partition into groups S orted <= P > P Conquer : Return array when length ≤ 1 Combine: Combine sorted partitions and pivot P P

6 .Quick Sort Pseudocode Core idea: Pick some item from the array and call it the pivot. Put all items smaller in the pivot into one group and all items larger in the other and recursively sort. If the array has size 0 or 1, just return it unchanged. 6 CSE373: Data Structures & Algorithms quicksort (input) { if ( input.length < 2) { return input; } else { pivot = getPivot (input); smallerHalf = sort( getSmaller (pivot, input)); largerHalf = sort( getBigger (pivot, input)); return smallerHalf + pivot + largerHalf ; } }

7 .Think in Terms of Sets 7 CSE373: Data Structures & Algorithms 13 81 92 43 65 31 57 26 75 0 S select pivot value 13 81 92 43 65 31 57 26 75 0 S 1 S 2 partition S 13 43 31 57 26 0 S 1 81 92 75 65 S 2 Quicksort(S 1 ) and Quicksort(S 2 ) 13 43 31 57 26 0 65 81 92 75 S Presto! S is sorted [Weiss]

8 .Quick S ort Example: Divide 8 CSE373: Data Structures & Algorithms 7 3 8 4 5 2 1 6 Pivot rule : pick the element at index 0 7 3 8 4 5 2 1 3 4 5 2 1 6 6 2 1 4 5 6 5 6

9 .Quick S ort Example: Combine 9 CSE373: Data Structures & Algorithms 7 3 8 4 5 2 1 6 Combine: this is the order of the elements we’ll care about when combining 7 3 8 4 5 2 1 3 4 5 2 1 6 6 2 1 4 5 6 5 6

10 .Quick S ort Example: Combine 10 CSE373: Data Structures & Algorithms 1 2 3 4 5 6 7 8 Combine : put left partition < pivot < right partition 7 1 8 2 3 4 5 3 4 5 1 2 6 6 2 1 4 5 6 5 6

11 .Details Have not yet explained: How to pick the pivot element Any choice is correct: data will end up sorted But as analysis will show, want the two partitions to be about equal in size How to implement partitioning In linear time In place 11 CSE373: Data Structures & Algorithms

12 .Pivots Worst pivot? Greatest/least element Recurse on p roblem of size n – 1 Best pivot? Median Halve each time 8 2 9 4 5 3 6 8 2 9 4 5 3 1 6 1 CSE373: Data Structures & Algorithms 12 2 4 3 1 8 9 6 8 2 9 4 5 3 1 6 5

13 .Potential pivot rules Pick first or last element : f ast , but worst-case occurs with mostly sorted input (as we’ve seen) Try looping through the array: we’ll get a good value, but that’s slow and hard to implement Pick random element: cool, does as well as any technique, but (pseudo)random number generation can be slow P ick the median of first, middle, and last: Easy to implement and is a common heuristic that tends to work well e.g ., arr [lo], arr [hi-1], arr [( hi+lo )/2 ] 13 CSE373: Data Structures & Algorithms

14 .Median Pivot Example 14 CSE373: Data Structures & Algorithms 2 8 4 5 3 1 6 Pick the median of first, middle, and last 7 Median = 6 Swap the median with the first value 2 8 4 5 3 1 6 7 2 8 4 5 3 1 7 6 Pivot is now at index 0, and we’re ready to go

15 .Partitioning Conceptually simple, but hardest part to code up correctly After picking pivot, need to partition in linear time in place One approach (there are slightly fancier ones): Put pivot in index lo Use two pointers i and j , starting at lo+1 and hi-1 while ( i < j) if ( arr [j] > pivot) j-- else if ( arr [ i ] < pivot) i ++ else swap arr [ i ] with arr [j] Swap pivot with arr [ i ] * *skip step 4 if pivot ends up being least element 15 CSE373: Data Structures & Algorithms

16 .Example Step one : pick pivot as median of 3 lo = 0, hi = 10 16 CSE373: Data Structures & Algorithms 6 1 4 9 0 3 5 2 7 8 0 1 2 3 4 5 6 7 8 9 Step two : move pivot to the lo position 8 1 4 9 0 3 5 2 7 6 0 1 2 3 4 5 6 7 8 9

17 .Quick Sort Partition Example 17 CSE373: Data Structures & Algorithms 6 1 4 9 0 3 5 7 2 8 6 1 4 2 0 3 5 7 9 8 5 1 4 2 0 3 6 7 9 8 6 1 4 9 0 3 5 7 2 8 6 1 4 9 0 3 5 7 2 8 6 1 4 9 0 3 5 7 2 8 6 1 4 2 0 3 5 7 9 8

18 .Quick Sort Analysis Best-case : Pivot is always the median, split data in half Same as mergesort : O ( n log n ), O(n) partition work for O(log(n)) levels Worst-case : Pivot is always smallest or largest element Basically same as selection sort: O ( n 2 ) Average-case (e.g., with random pivot) O( n log n ), you’re not responsible for proof (in text) 18 CSE373: Data Structures & Algorithms

19 .Quick Sort Analysis In-place: Yep! We can use a couple pointers and partition the array in place, recursing on differe nt lo and hi indices Stable : Not necessarily. Depends on how you handle equal values when partitioning. A stable version of quick sor t uses some extra storage for partitioning. 19 CSE373: Data Structures & Algorithms

20 .Divide and Conquer: Cutoffs For small n , all that recursion tends to cost more than doing a simple, quadratic sort Remember asymptotic complexity is for large n Common engineering technique: switch algorithm below a cutoff Reasonable rule of thumb: use insertion sort for n < 10 Notes: Cutoffs are also the norm with parallel algorithms Switch to sequential algorithm None of this affects asymptotic complexity 20 CSE373: Data Structures & Algorithms

21 .Cutoff Pseudocode 21 CSE373: Data Structures & Algorithms void quicksort ( int [] arr , int lo , int hi ) { if (hi – lo < CUTOFF) insertionSort ( arr,lo,hi ); else … } Notice how this cuts out the vast majority of the recursive calls Think of the recursive calls to quicksort as a tree Trims out the bottom layers of the tree

22 .Cool Comparison Sorting Links Visualization of sorts on different inputs: http ://www.sorting-algorithms.com / Visualization of sorting with sound: https ://www.youtube.com/watch?v=t8g- iYGHpEA Sorting via dance: https ://www.youtube.com/watch?v= XaqR3G_NVoo XKCD Ineffective sorts: https://xkcd.com/1185/ 22 CSE373: Data Structures & Algorithms

23 .Sorting: The Big Picture 23 CSE373: Data Structures & Algorithms Simple algorithms: O( n 2 ) Fancier algorithms: O( n log n ) Comparison lower bound: ( n log n ) Specialized algorithms: O( n ) Handling huge data sets Insertion sort Selection sort Shell sort … Heap sort Merge sort Quick sort ( avg ) … Bucket sort Radix sort External sorting

24 .How Fast Can We Sort? Heapsort & mergesort have O ( n log n ) worst-case running time Quicksort has O ( n log n ) average-case running time These bounds are all tight, actually  ( n log n ) Assuming our comparison model : The only operation an algorithm can perform on data items is a 2-element comparison. There is no lower asymptotic complexity, such as O ( n ) or O ( n log log n ) 24 CSE373: Data Structures & Algorithms

25 .Counting Comparisons No matter what the algorithm is, it cannot make progress without doing comparisons Intuition : Each comparison can at best eliminate half the remaining possibilities of possible orderings Can represent this process as a decision tree Nodes contain “set of remaining possibilities” Edges are “answers from a comparison” The algorithm does not actually build the tree; it’s what our proof uses to represent “the most the algorithm could know so far” as the algorithm progresses 25 CSE373: Data Structures & Algorithms

26 .Decision Tree for n = 3 26 CSE373: Data Structures & Algorithms a < b < c, b < c < a, a < c < b, c < a < b, b < a < c, c < b < a a < b < c a < c < b c < a < b b < a < c b < c < a c < b < a a < b < c a < c < b c < a < b a < b < c a < c < b b < a < c b < c < a c < b < a b < c < a b < a < c a < b a > b a > c a < c b < c b > c b < c b > c c < a c > a The leaves contain all the possible orderings of a, b, c

27 .Example if a < c < b 27 CSE373: Data Structures & Algorithms a < b < c, b < c < a, a < c < b, c < a < b, b < a < c, c < b < a a < b < c a < c < b c < a < b b < a < c b < c < a c < b < a a < b < c a < c < b c < a < b a < b < c a < c < b b < a < c b < c < a c < b < a b < c < a b < a < c a < b a > b a > c a < c b < c b > c b < c b > c c < a c > a possible orders actual order

28 .What the Decision Tree Tells Us A binary tree because each comparison has 2 outcomes (we’re comparing 2 elements at a time) Because any data is possible, any algorithm needs to ask enough questions to produce all orderings. The facts we can get from that: Each ordering is a different leaf (only one is correct) Running any algorithm on any input will at best correspond to a root-to-leaf path in some decision tree. Worst number of comparisons is the longest path from root-to-leaf in the decision tree for input size n There is no worst -case running time better than the height of a tree with < num possible orderings> leaves CSE373: Data Structures & Algorithms 28

29 .How many possible orderings? Assume we have n elements to sort. How many permutations of the elements (possible orderings) ? For simplicity, assume none are equal (no duplicates ) Example, n =3 a[0]<a[1]<a[2 ] a [0]<a[2]<a[1] a [1]<a[0]<a[2] a [1]<a[2]<a[0] a [2]<a[0]<a[1] a [2]<a[1]<a[0] In general, n choices for least element, n -1 for next, n -2 for next, … n ( n -1)( n -2)…(2)(1) = n ! possible orderings That means with n! possible leaves, best height for tree is log(n!) , given that best case tree splits leaves in half at each branch 29 CSE373: Data Structures & Algorithms