Graphics Pipeline Rasterization

1 .Graphics Pipeline Rasterization CMSC 435/634

2 .Drawing Terms Primitive Basic shape, drawn directly Compare to building from simpler shapes Rasterization or Scan Conversion Find pixels for a primitive Usually for algorithms that generate all pixels for one primitive at a time Compare to ray tracing: all primitives for one pixel

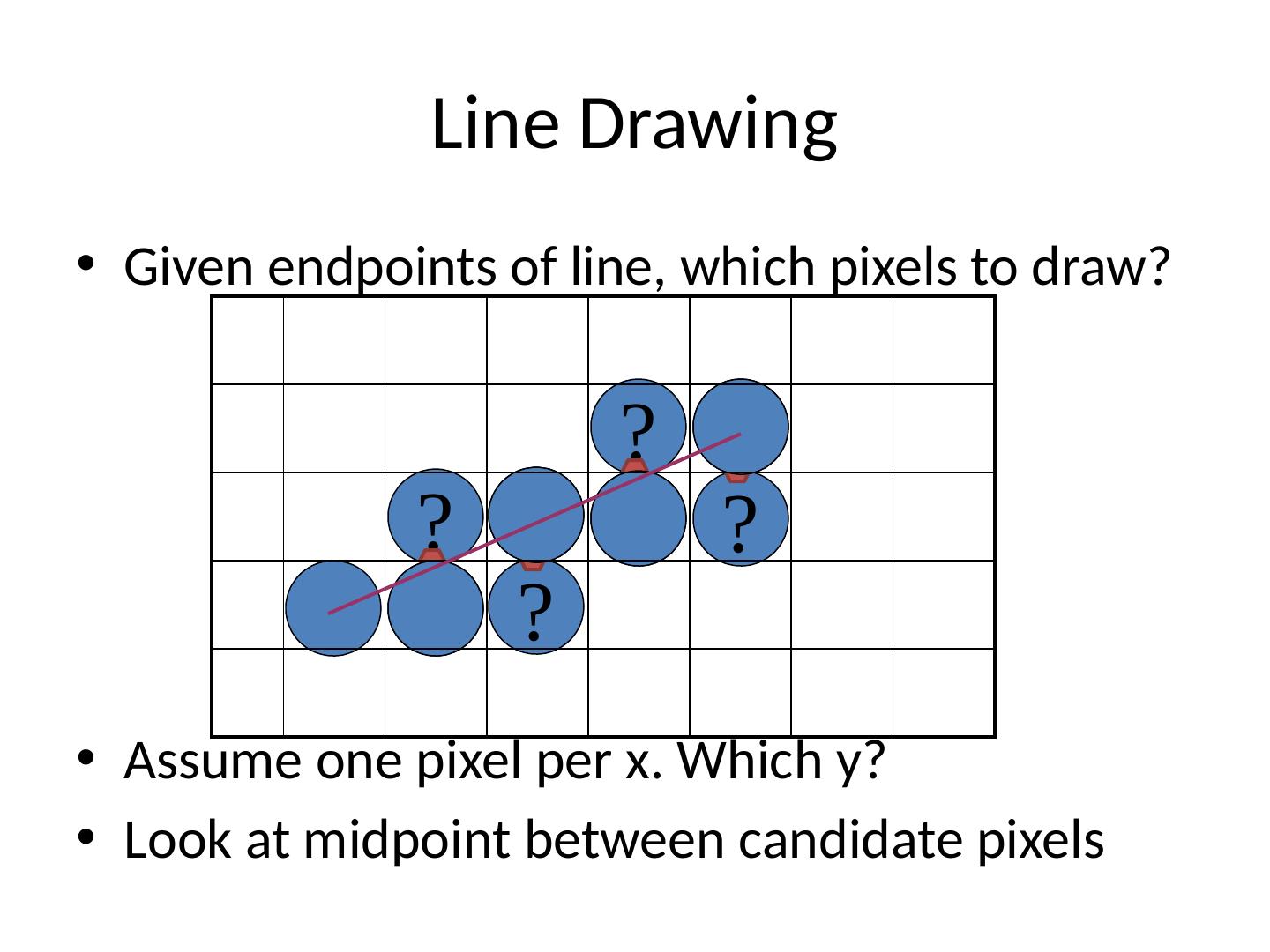
3 .Line Drawing Given endpoints of line, which pixels to draw?

4 .Line Drawing Given endpoints of line, which pixels to draw?

5 .Line Drawing Given endpoints of line, which pixels to draw? Assume one pixel per x. Which y? Look at midpoint between candidate pixels ? ? ? ? ? ? ? ?

6 .Line Drawing Plug midpoint into implicit line equation Sign decides: called a decision variable Incremental update

7 .Line Drawing Implicit line equation Midpoint algorithm y = y 0 d = f(x 0 +1, y 0 +0.5) for x = x 0 to x 1 draw( x,y ) if (d < 0) then y = y+1 d = d + (x 1 - x 0 ) + (y 0 - y 1 ) else d = d + (y 0 - y 1 )

8 .Polygon Rasterization Problem How to generate filled polygons (by determining which pixel positions are inside the polygon) Conversion from continuous to discrete domain Concepts Spatial coherence Span coherence Edge coherence

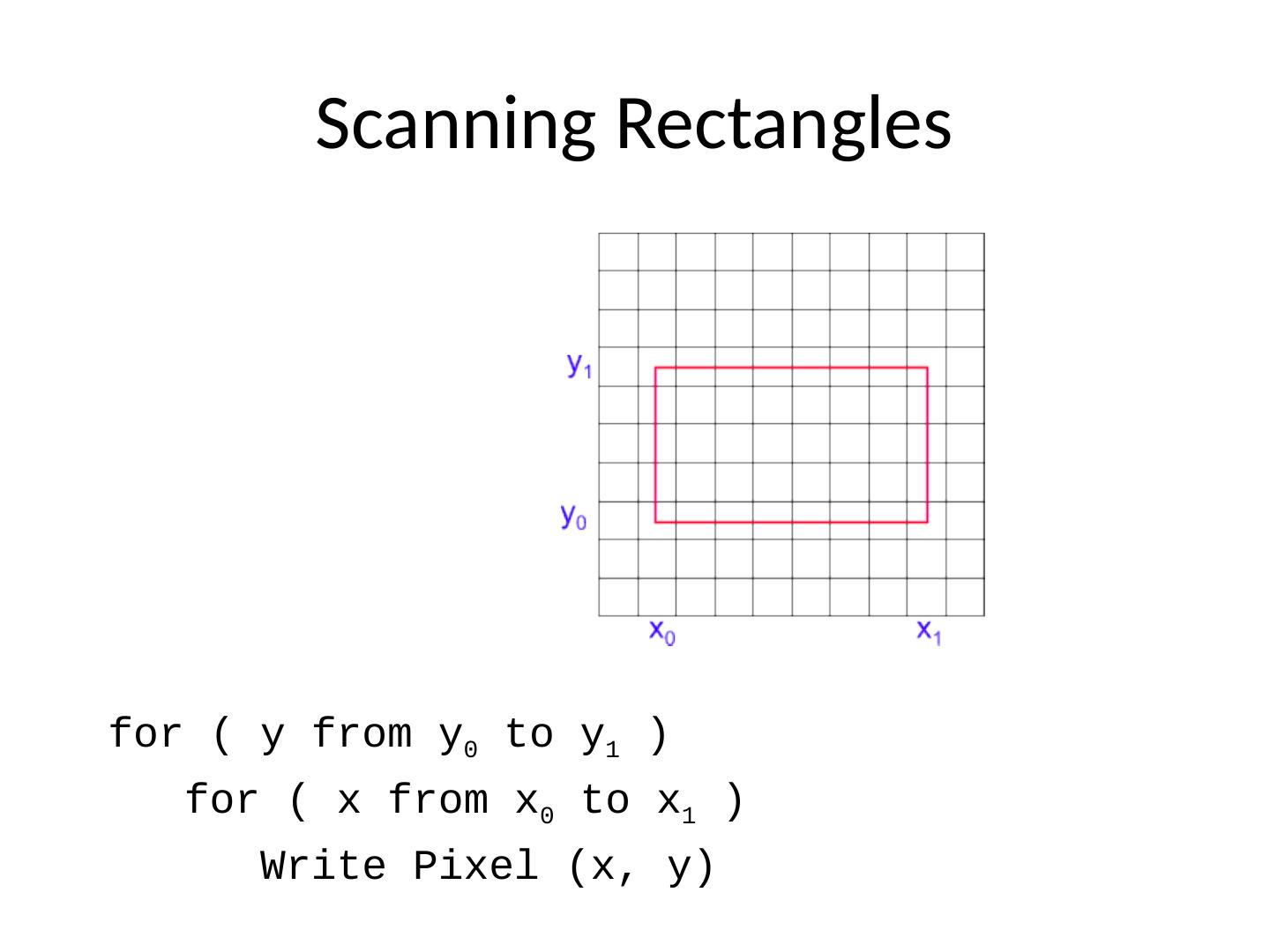
9 .Scanning Rectangles for ( y from y 0 to y 1 ) for ( x from x 0 to x 1 ) Write Pixel (x, y)

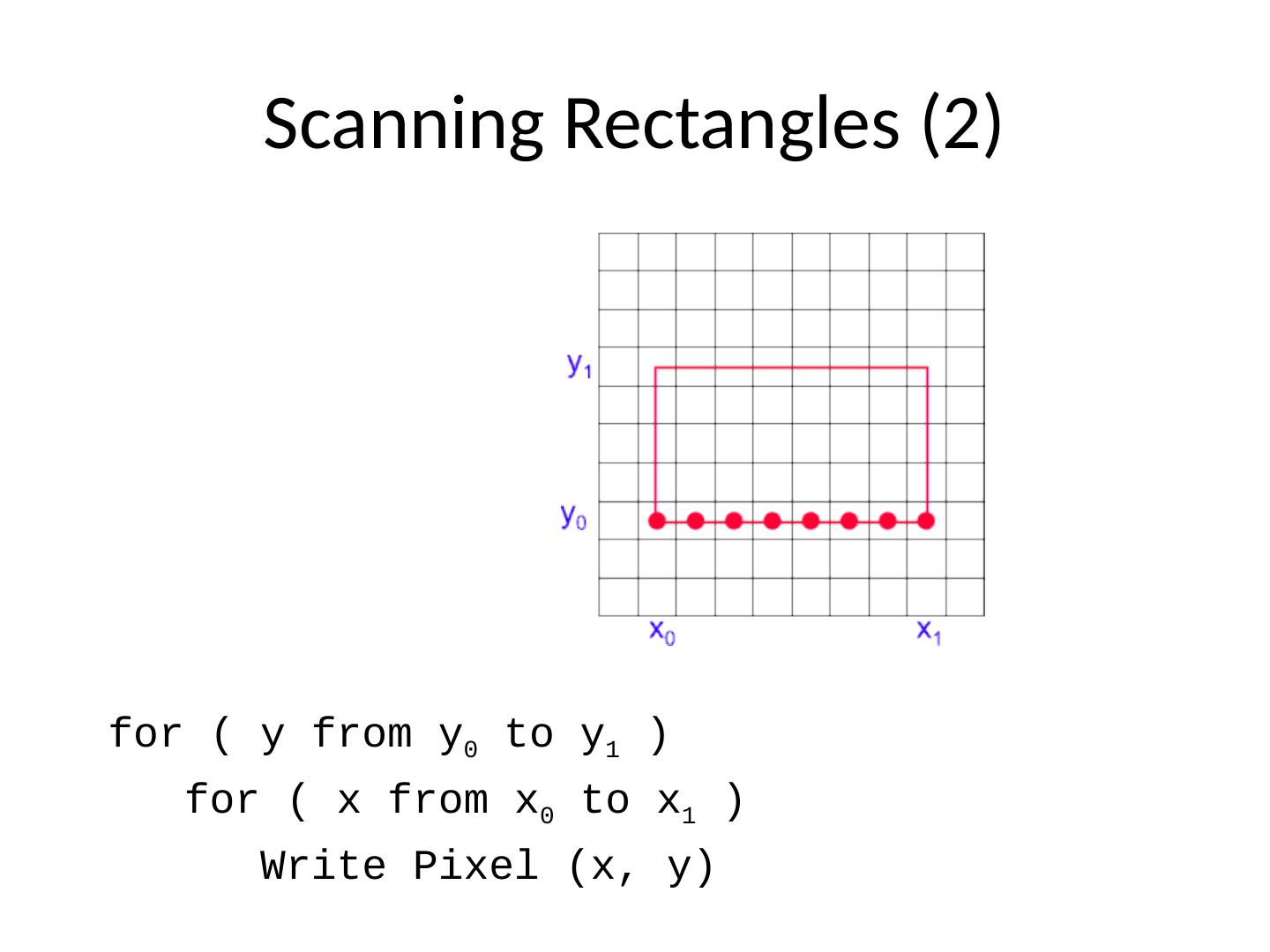
10 .Scanning Rectangles (2) for ( y from y 0 to y 1 ) for ( x from x 0 to x 1 ) Write Pixel (x, y)

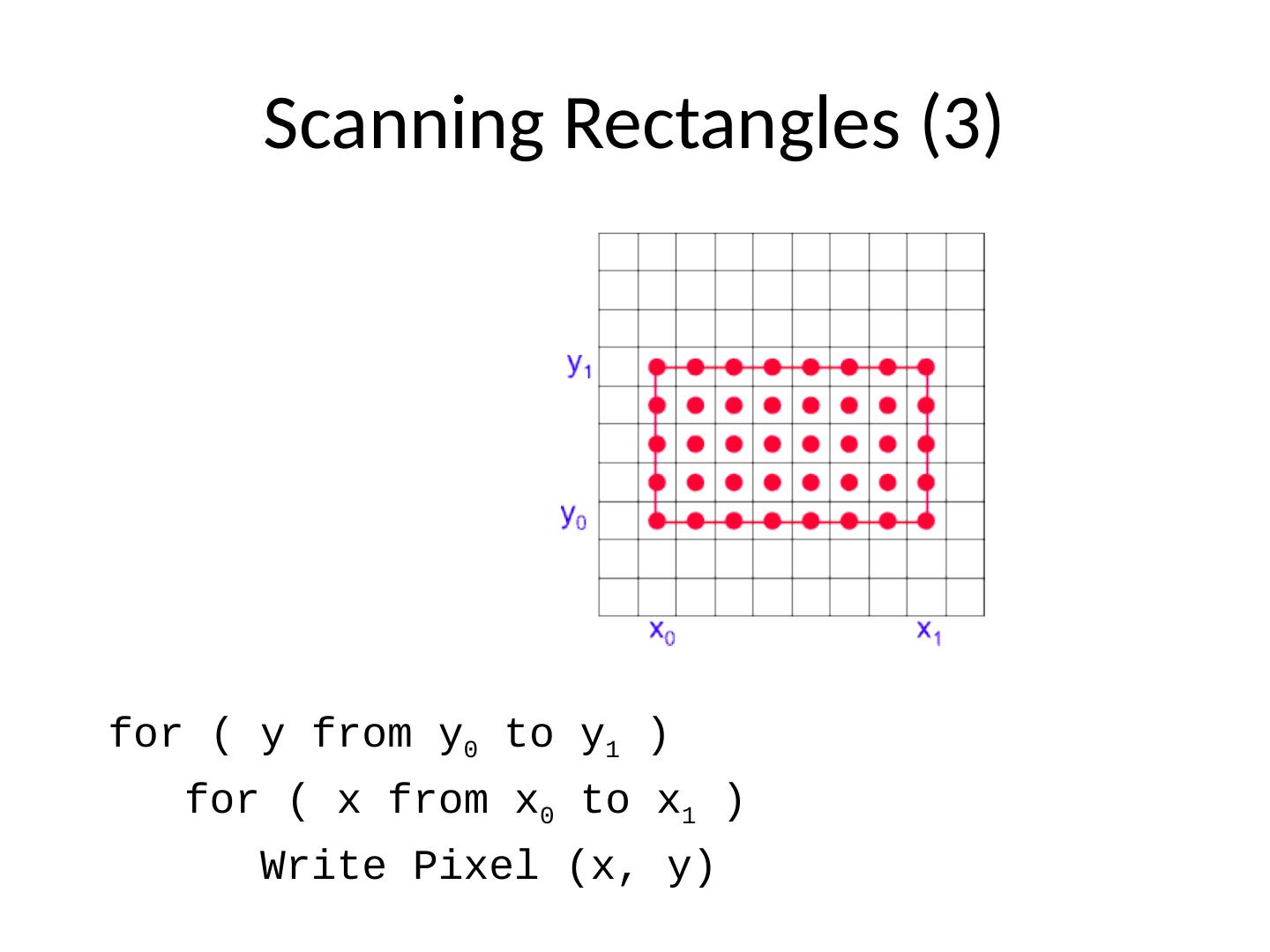
11 .Scanning Rectangles (3) for ( y from y 0 to y 1 ) for ( x from x 0 to x 1 ) Write Pixel (x, y)

12 .Triangle Rasterization Barycentric coordinates are decision variables

13 .Barycentric Triangle Rasterization For all y in y min to y max do For all x in x min to x max do Compute ( a , b , g ) for ( x,y ) If ( a ≥ 0 and b ≥ 0 and g ≥ 0) then c = a c 0 + b c 1 + g c 2 Draw pixel( x,y ) with color c

14 .Incremental Computation a , b , and g are linear in X and Y What about pixel-to-pixel updates?

15 .“ Clipless ” Homogeneous Rasterization Compute barycentrics using homogeneous coordinates Extra edge equations for clip edges Compute t for clip plane at each vertex Only visible (w>near) pixels will be drawn Adds computation Divide by w per pixel instead of per vertex But avoids branching and extra triangles Good for hardware

16 .Homogeneous Barycentrics Each barycentric is Equal to 1 at one vertex Equal to 0 at the other two

17 .Homogeneous Barycentrics Write formula for barycentric coordinate in homogeneous form

18 .Homogeneous Barycentrics This defines a system of three equations or

19 .Homogeneous Barycentrics Equation (again) Which we can solve:

20 .Homogeneous Barycentrics Coefficients for all three:

21 .Changes to Rasterization NONE! Coefficients computed with homogeneous coords But they’re the same coefficients!

22 .Homogenous Clip Plane Clip parameter at each vertex Clipping decision variable coefficients