- 快召唤伙伴们来围观吧
- 微博 QQ QQ空间 贴吧
- 文档嵌入链接
- 复制
- 微信扫一扫分享
- 已成功复制到剪贴板
Graphics Pipeline Clipping
展开查看详情
1 .Graphics Pipeline Clipping CMSC 435/634
2 .Graphics Pipeline Object-order approach to rendering Vertex Processing Clipping Rasterization Fragment Processing Visibility & Blending Transformations Vertex components of shading Find the visible parts of primitives Break primitives into fragments/pixels Fragment components of shading Which do we see, how do they combine?
3 .Why Clip? Window sides Draw less Some rasterization algorithms need everything on screen Near Draw less Don’t divide by 0 Don’t divide by negative z Far Draw less Constrain Z range
4 .Clipping & Culling Cull: decide not to draw an object at all Clip: slice to keep just the visible parts Trivial Reject: Entirely off-screen Trivial Accept: Entirely on screen 4
5 .Clipping Lines Lines intersecting a rectangular clip region are always clipped into a single line segment Clip against one window edge at a time 5 Clip Rectangle A B A B C D D’ C D’ E F G H G’ H’ H’ G’ I J I’ J’
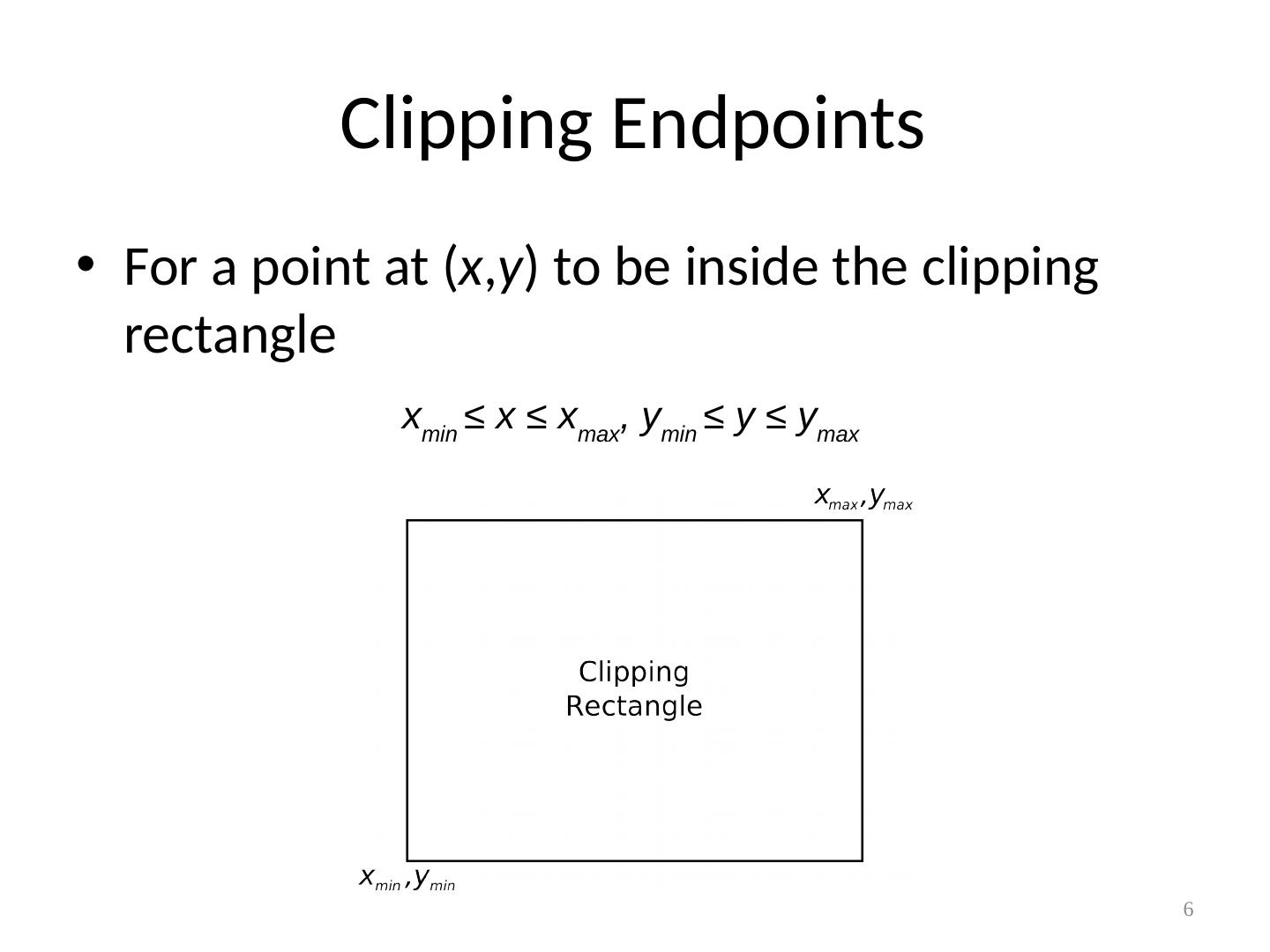
6 .Clipping Endpoints For a point at ( x , y ) to be inside the clipping rectangle 6 x min ≤ x ≤ x max , y min ≤ y ≤ y max
7 .Clipping Conditions Both endpoints are inside (AB) One endpoint in, another end outside (CD) Both outside (EF, GH, IJ) May or may not be in, further calculations needed 7
8 .Cohen-Sutherland Line Clipping First, endpoint pairs are checked for trivial acceptance If not, region checks are performed in order to trivially reject certain lines If both x pairs are <0 or >1, then it lies outside (EF) If both y pairs are <0 or >1, then it too lies outside 8
9 .Cohen-Sutherland Line Clipping Create bit code for each endopint Each region is assigned a 4-bit code ( outcode ) 1 st bit – above top edge y > y max 2 nd bit – below bottom edge y < y min 3 rd bit – right of right edge x > x max 4 th bit – left of left edge x < x min 9
10 .Efficient Computation of Bit-Code Compute each bit First bit is the sign bit of y max – y Second bit is y – y min Third bit is the sign bit of x max – x Forth bit is x – x min 10
11 .Bit-Code Trivial Rejects and Accepts If both bit codes are zero – trivial accept If endpoints are both outside of same edge, they will share that bit This can easily be computed as a logical and operation – trivial reject if non-zero result If not, then need to split line at clip edge, discard portion outside, continue testing 11
12 .Cohen-Sutherland Line Clipping Algorithm 12 code1 = outcode from endpoint1 code2 = outcode from endpoint2 if ( code1 == 0 && code2 == 0) then trivial_accept else if ( code1 & code2 != 0) then trivial_reject else clip against left clip against right clip against bottom clip against top if (anything is left) then accept clipped segment
13 .Homogeneous Clipping Works for 3D planes If point is inside clipping plane: Point on line: Intersection:
14 .Polygon Clipping Many cases (new edges, discarded edges) Multiple polygons may result after clipping a single polygon 14
15 .Sutherland-Hodgman Polygon Clipping Divide and conquer Simple problem is to clip polygon against a single infinite clip edge Sequence of 4 clips against clipping rectangle 15
16 .Sutherland-Hodgman Polygon Clipping Algorithm moves around the polygon from v n to v 1 and then on back to v n At each step Check (v i to v i+1 ) line against the clip edge Add zero, one, or two vertices to the output 16
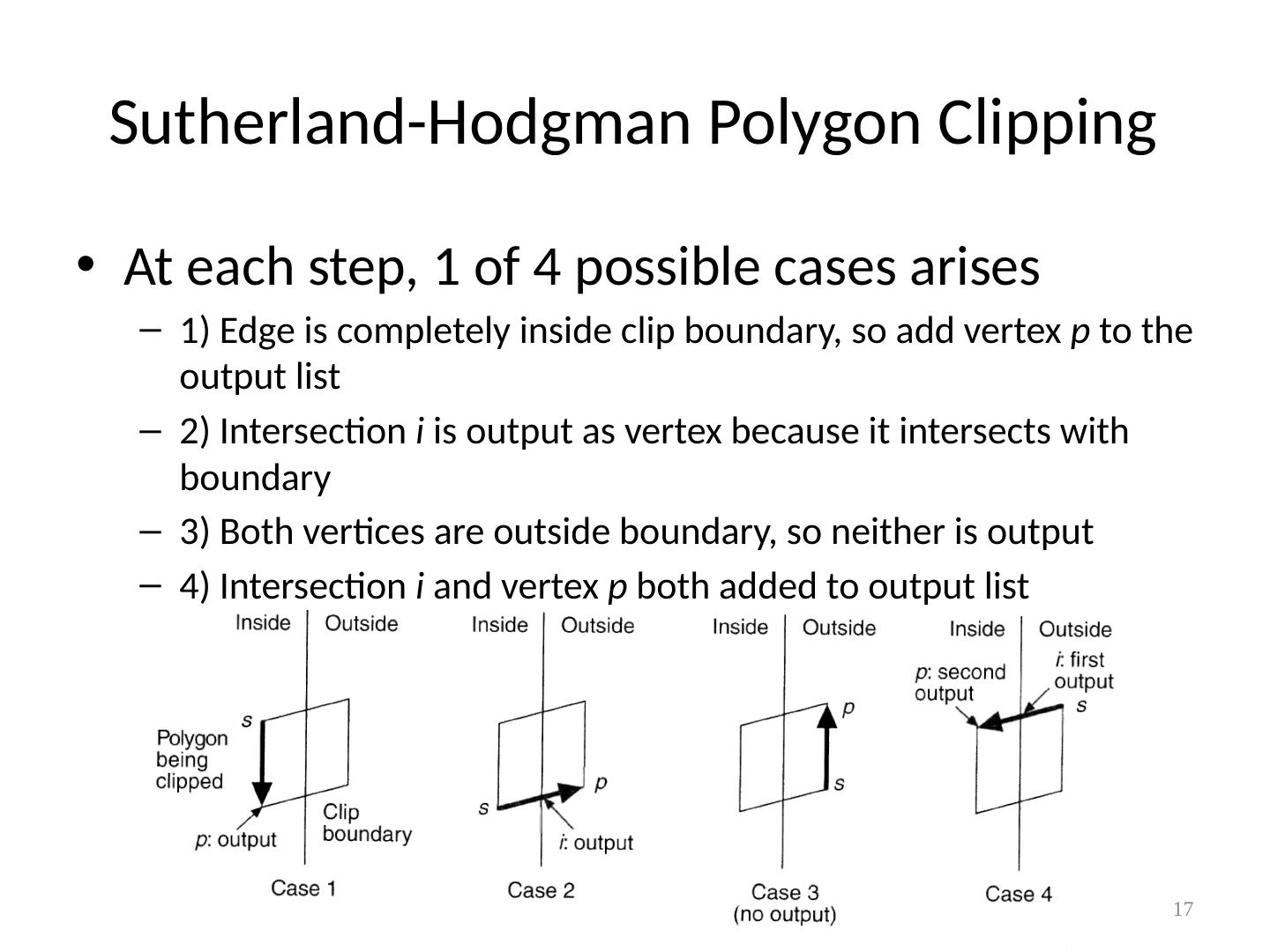
17 .Sutherland-Hodgman Polygon Clipping At each step, 1 of 4 possible cases arises 1) Edge is completely inside clip boundary, so add vertex p to the output list 2) Intersection i is output as vertex because it intersects with boundary 3) Both vertices are outside boundary, so neither is output 4) Intersection i and vertex p both added to output list 17
18 .Sutherland-Hodgman Algorithm 18 Sutherland-Hodgman( array ) vertex S = array [ length( array ) - 1 ] for ( j = 0 ; j < length(array) ; j++ ) do vertex P = array [ j ] if ( P is inside clip plane ) then if ( S is inside clip plane ) then /* case 1 */ Output( P ) else /* case 2 */ Output( ComputeIntersection( S , P , clip plane ) ) Output( P ) else if ( S is inside clip plane ) then /* case 2 */ Output( ComputeIntersection( P, S, clip plane ) ) else /* case 3 */ no op S = P