算法设计范例

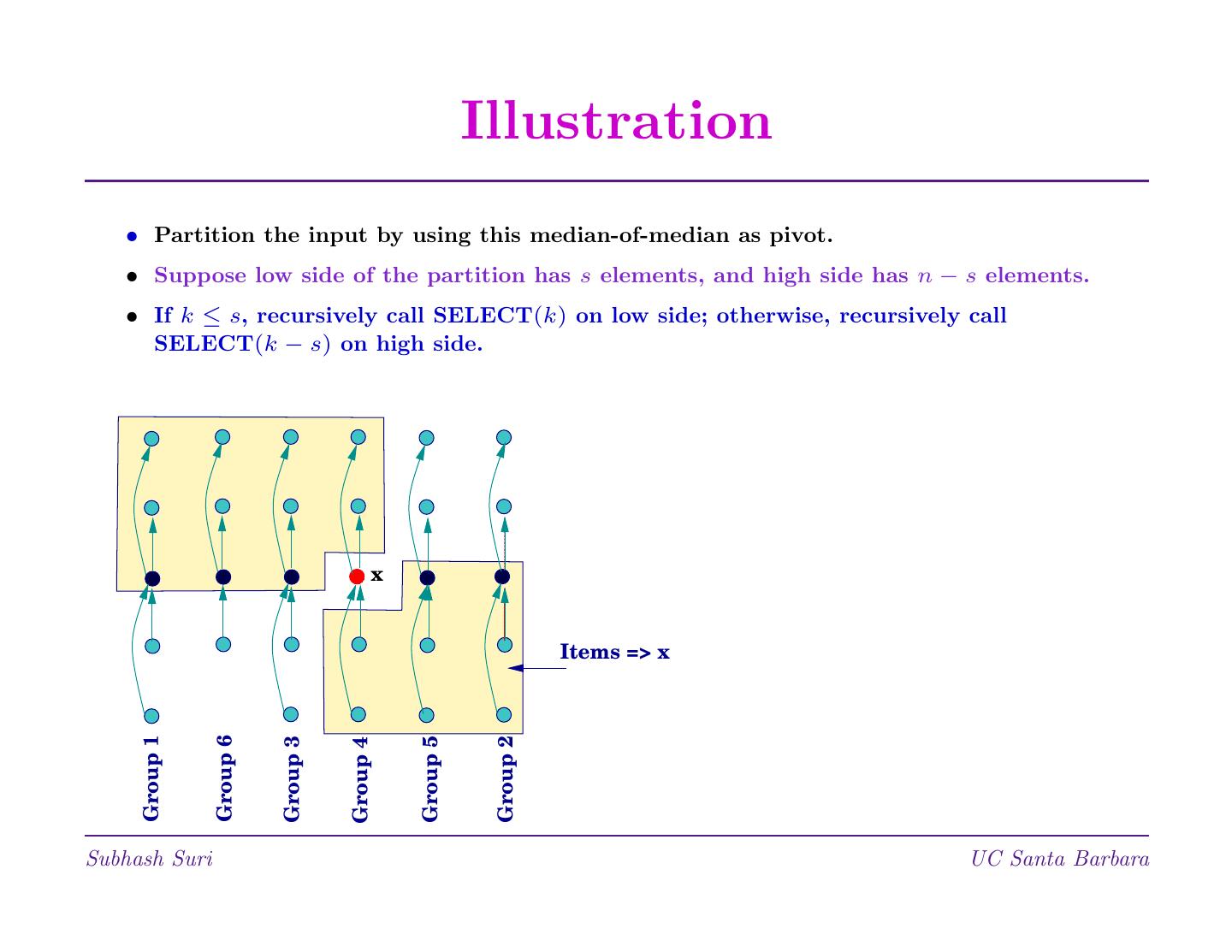
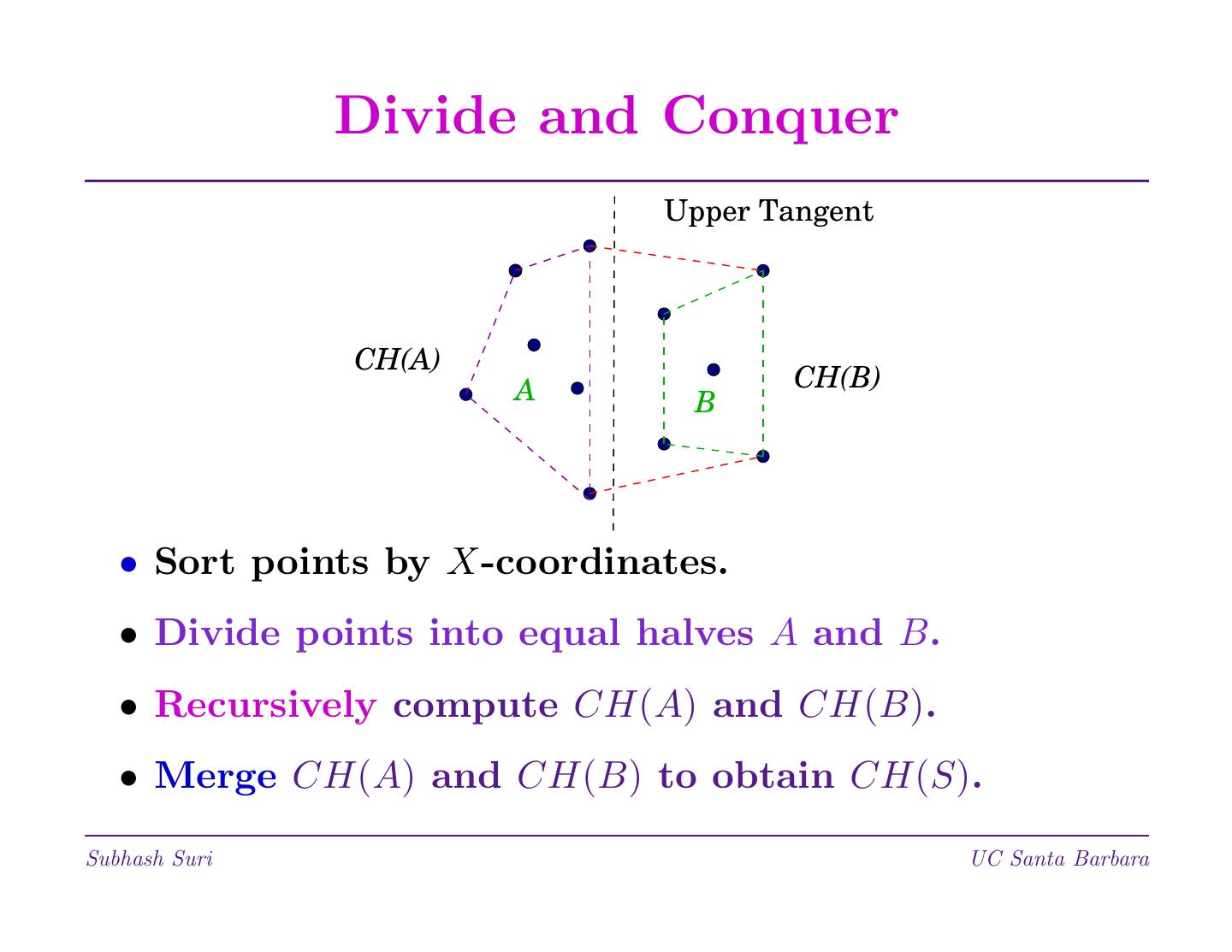
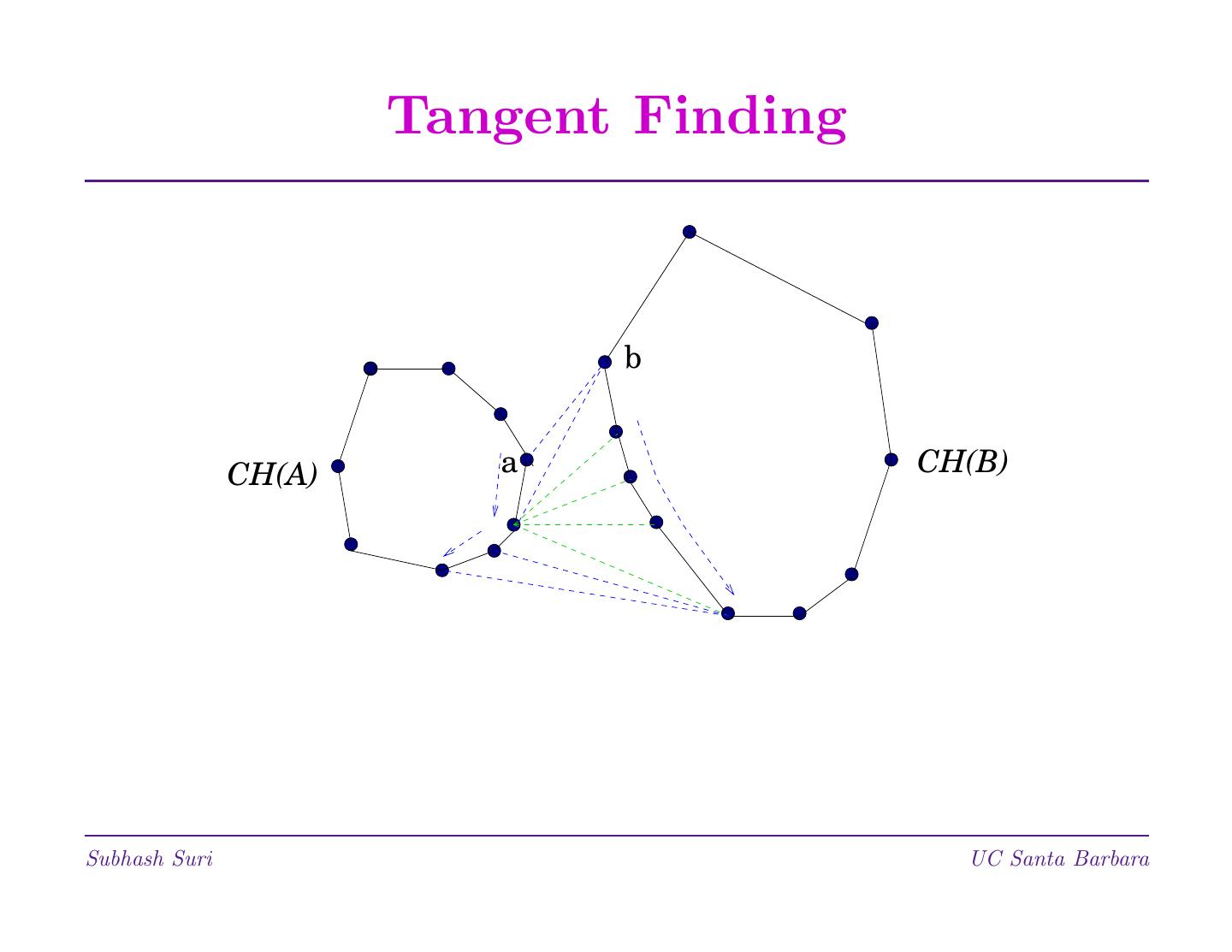
1 . Divide and Conquer • A general paradigm for algorithm design; inspired by emperors and colonizers. • Three-step process: 1. Divide the problem into smaller problems. 2. Conquer by solving these problems. 3. Combine these results together. • Examples: Binary Search, Merge sort, Quicksort etc. Matrix multiplication, Selection, Convex Hulls. Subhash Suri UC Santa Barbara 

2 . Binary Search • Search for x in a sorted array A. Binary-Search (A, p, q, x) 1. if p > q return -1; 2. r = (p + q)/2 3. if x = A[r] return r 4. else if x < A[r] Binary-Search(A, p, r, x) 5. else Binary-Search(A, r + 1, q, x) • The initial call is Binary-Search(A, 1, n, x). Subhash Suri UC Santa Barbara 

3 . Binary Search • Let T (n) denote the worst-case time to binary search in an array of length n. • Recurrence is T (n) = T (n/2) + O(1). • T (n) = O(log n). Subhash Suri UC Santa Barbara 

4 . Merge Sort • Sort an unordered array of numbers A. Merge-Sort (A, p, q) 1. if p ≥ q return A; 2. r = (p + q)/2 3. Merge-Sort (A, p, r) 4. Merge-Sort (A, r + 1, q) 5. MERGE (A, p, q, r) • The initial call is Merge-Sort (A, 1, n). Subhash Suri UC Santa Barbara 

5 . Merge Sort • Let T (n) denote the worst-case time to merge sort an array of length n. • Recurrence is T (n) = 2T (n/2) + O(n). • T (n) = O(n log n). Subhash Suri UC Santa Barbara 

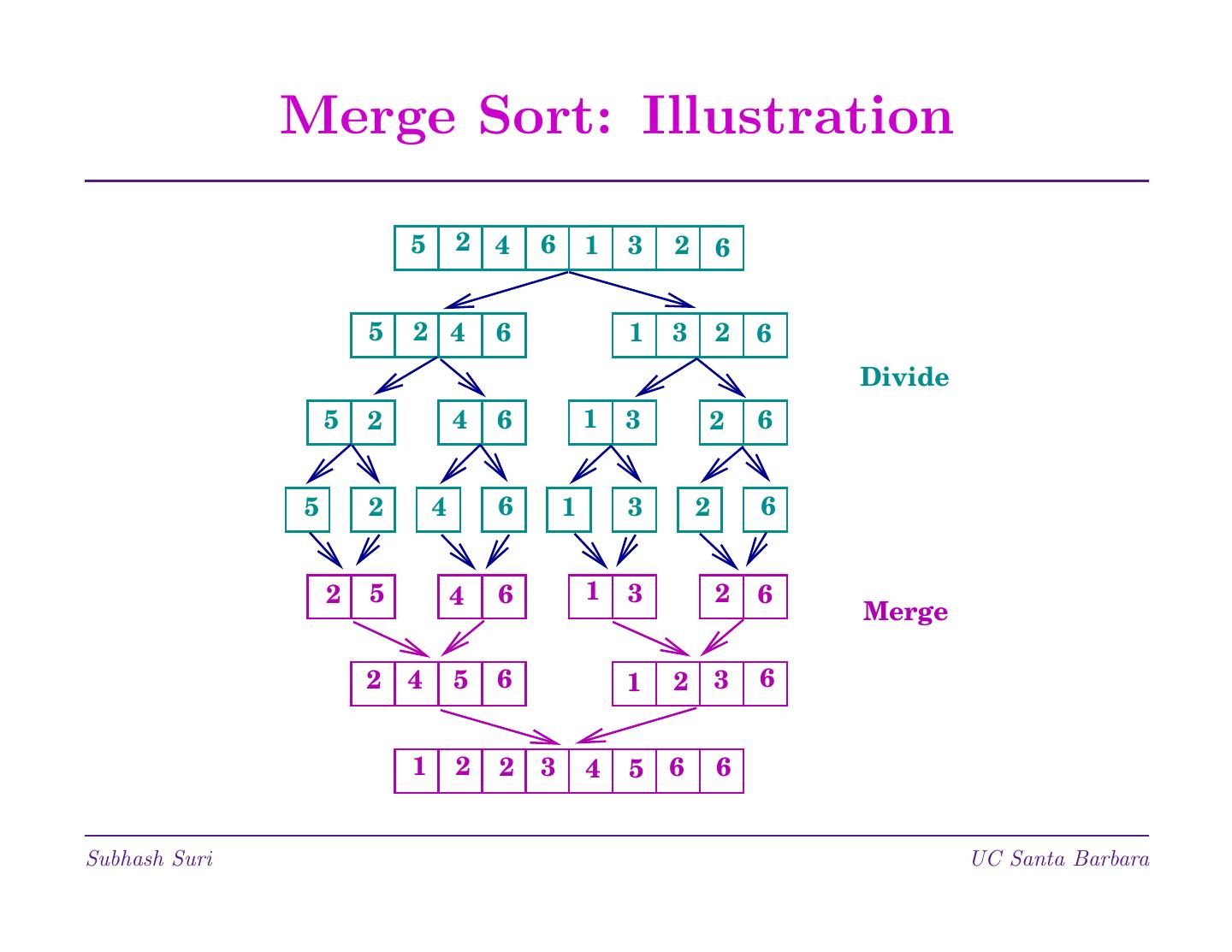
6 . Merge Sort: Illustration 5 2 4 6 1 3 2 6 5 2 4 6 1 3 2 6 Divide 5 2 4 6 1 3 2 6 5 2 4 6 1 3 2 6 2 5 4 6 1 3 2 6 Merge 2 4 5 6 1 2 3 6 1 2 2 3 4 5 6 6 Subhash Suri UC Santa Barbara 

7 . Multiplying Numbers • We want to multiply two n-bit numbers. Cost is number of elementary bit steps. • Grade school method has Θ(n2) cost.: xxxxxxxx xxxxxxxx xxxxxxxxx xxxxxxxxx . . . xxxxxxxxx xxxxxxxxxxxxxxxx • n2 multiplies, n2/2 additions, plus some carries. Subhash Suri UC Santa Barbara 

8 . Why Bother? • Doesn’t hardware provide multiply? It is fast, optimized, and free. So, why bother? • True for numbers that fit in one computer word. But what if numbers are very large. • Cryptography (encryption, digital signatures) uses big number “keys.” Typically 256 to 1024 bits long! • n2 multiplication too slow for such large numbers. • Karatsuba’s (1962) divide-and-conquer scheme multiplies two n bit numbers in O(n1.59) steps. Subhash Suri UC Santa Barbara 

9 . Karatsuba’s Algorithm • Let X and Y be two n-bit numbers. Write X = ab Y = cd • a, b, c, d are n/2 bit numbers. (Assume n = 2k .) XY = (a2n/2 + b)(c2n/2 + d) = ac2n + (ad + bc)2n/2 + bd Subhash Suri UC Santa Barbara 

10 . An Example • X = 4729 Y = 1326. • a = 47; b = 29 c = 13; d = 26. • ac = 47 ∗ 13 = 611 • ad = 47 ∗ 26 = 1222 • bc = 29 ∗ 13 = 377 • bd = 29 ∗ 26 = 754 • XY = 6110000 + 159900 + 754 • XY = 6270654 Subhash Suri UC Santa Barbara 

11 . Karatsuba’s Algorithm • This is D&C: Solve 4 problems, each of size n/2; then perform O(n) shifts to multiply the terms by 2n and 2n/2. • We can write the recurrence as T (n) = 4T (n/2) + O(n) • But this solves to T (n) = O(n2)! Subhash Suri UC Santa Barbara 

12 . Karatsuba’s Algorithm • XY = ac2n + (ad + bc)2n/2 + bd. • Note that (a − b)(c − d) = (ac + bd) − (ad + bc). • Solve 3 subproblems: ac, bd, (a − b)(c − d). • We can get all the terms needed for XY by addition and subtraction! • The recurrence for this algorithm is T (n) = 3T (n/2) + O(n) = O(nlog2 3). • The complexity is O(nlog2 3) ≈ O(n1.59). Subhash Suri UC Santa Barbara 

13 . Recurrence Solving: Review • T (n) = 2T (n/2) + cn, with T (1) = 1. • By term expansion. T (n) = 2T (n/2) + cn = 2 2T (n/22) + cn/2 + cn = 22T (n/22) + 2cn = 22 2T (n/23) + cn/22 + 2cn = 23T (n/23) + 3cn .. = 2iT (n/2i) + icn • Set i = log2 n. Use T (1) = 1. • We get T (n) = n + cn(log n) = O(n log n). Subhash Suri UC Santa Barbara 

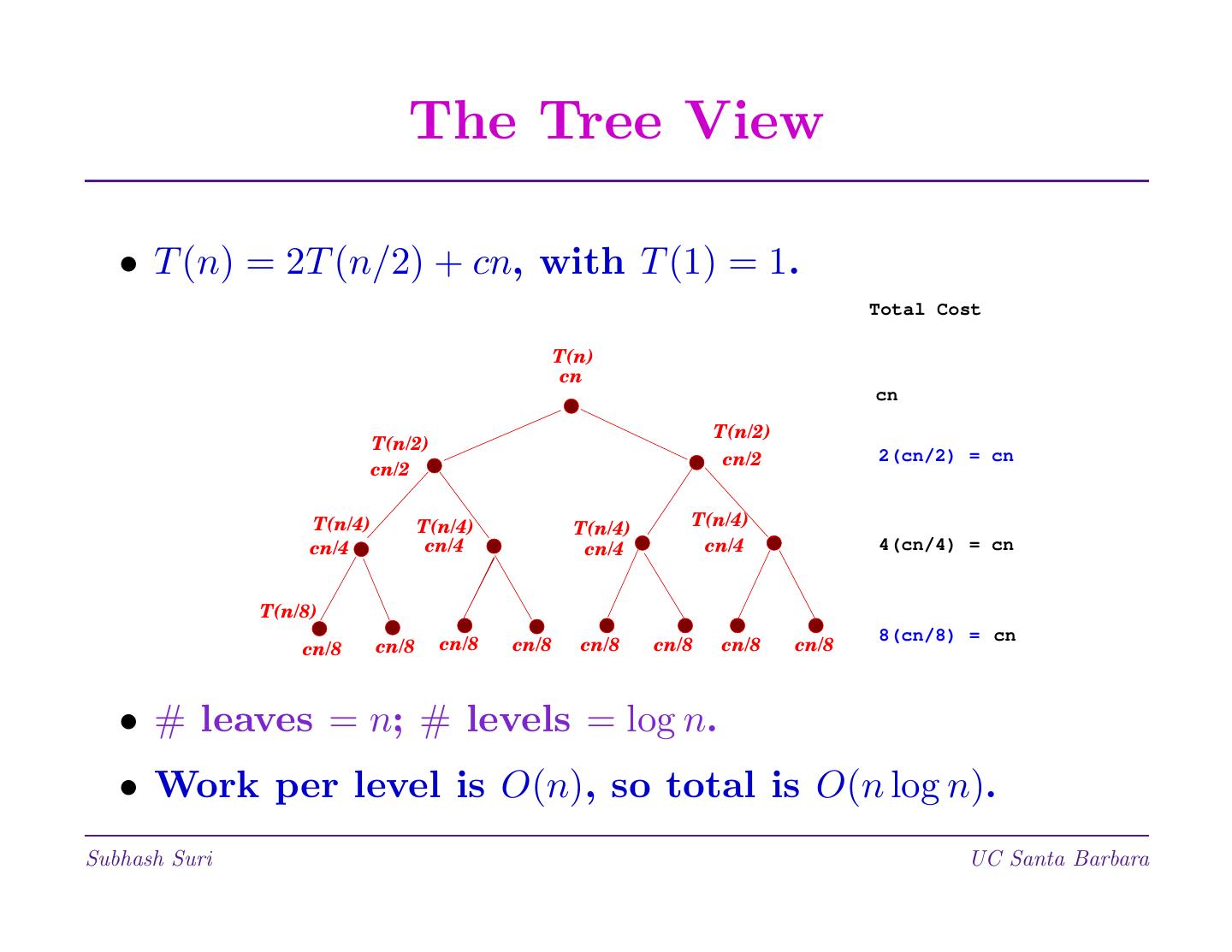
14 . The Tree View • T (n) = 2T (n/2) + cn, with T (1) = 1. Total Cost T(n) cn cn T(n/2) T(n/2) cn/2 2(cn/2) = cn cn/2 T(n/4) T(n/4) T(n/4) T(n/4) cn/4 cn/4 cn/4 cn/4 4(cn/4) = cn T(n/8) 8(cn/8) = cn cn/8 cn/8 cn/8 cn/8 cn/8 cn/8 cn/8 cn/8 • # leaves = n; # levels = log n. • Work per level is O(n), so total is O(n log n). Subhash Suri UC Santa Barbara 

15 . Solving By Induction • Recurrence: T (n) = 2T (n/2) + cn. • Base case: T (1) = 1. • Claim: T (n) = cn log n + cn. T (n) = 2T (n/2) + cn = 2 (c(n/2) log(n/2) + cn/2) + cn = cn (log n − 1 + 1) + cn = cn log n + cn Subhash Suri UC Santa Barbara 

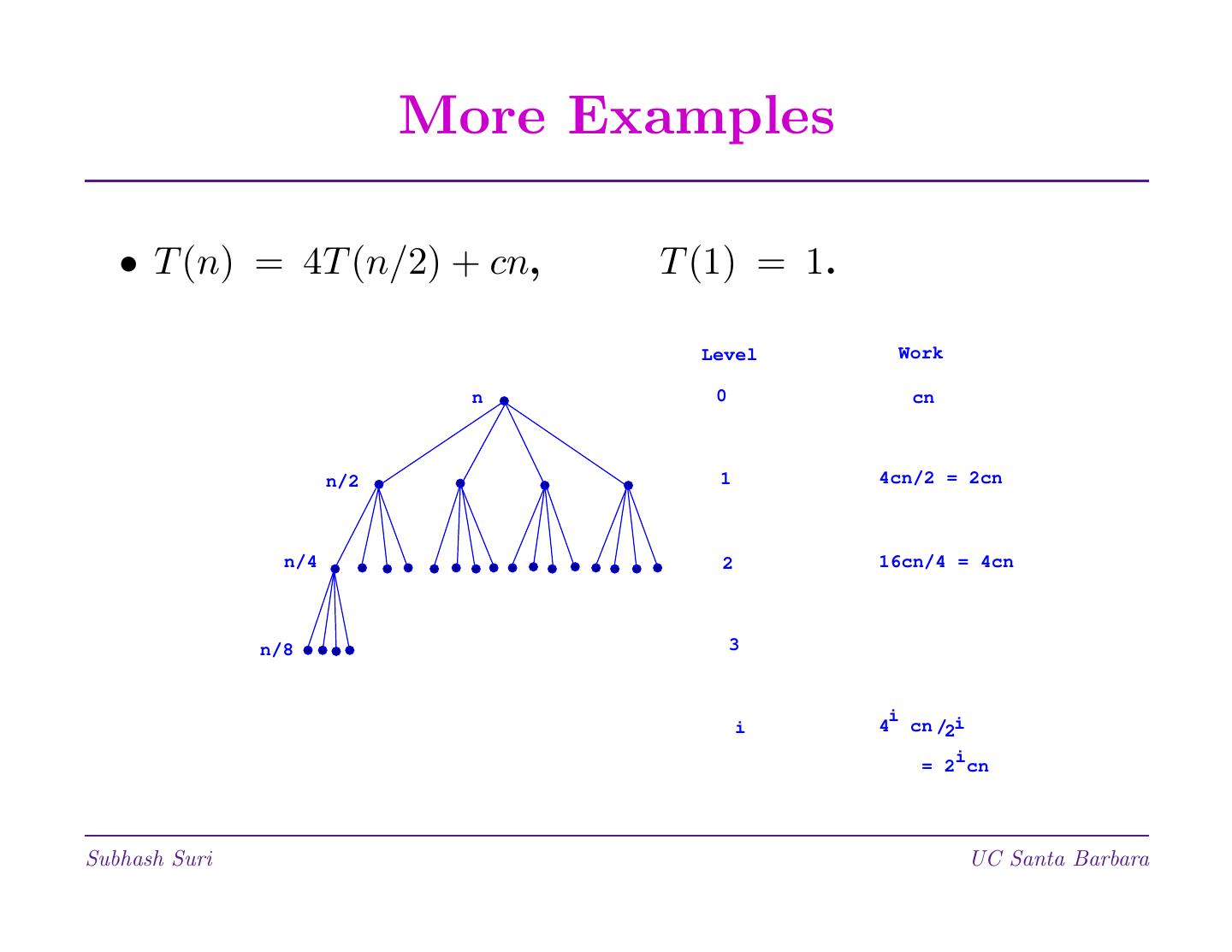
16 . More Examples • T (n) = 4T (n/2) + cn, T (1) = 1. Level Work n 0 cn n/2 1 4cn/2 = 2cn n/4 2 16cn/4 = 4cn n/8 3 i i 4 cn /2i i = 2 cn Subhash Suri UC Santa Barbara 

17 . More Examples Level Work n 0 cn n/2 1 4cn/2 = 2cn n/4 2 16cn/4 = 4cn n/8 3 i i 4 cn /2i i = 2 cn • Stops when n/2i = 1, and i = log n. • Recurrence solves to T (n) = O(n2). Subhash Suri UC Santa Barbara 

18 . By Term Expansion T (n) = 4T (n/2) + cn = 42T (n/22) + 2cn + cn = 43T (n/23) + 22cn + 2cn + cn .. = 4iT (n/2i) + cn 2i−1 + 2i−2 + . . . + 2 + 1 = 4iT (n/2i) + 2icn • Terminates when 2i = n, or i = log n. • 4i = 2i × 2i = n × n = n2. • T (n) = n2 + cn2 = O(n2). Subhash Suri UC Santa Barbara 

19 . More Examples √ T (n) = 2T (n/4) + n, T (1) = 1. √ T (n) = 2T (n/4) + n 2 √ = 2 2T (n/4 ) + n/4 + n 2 2 √ = 2 T (n/4 ) + 2 n 2 3 √ = 2 2T (n/4 ) + n/42 +2 n 3 3 √ = 2 T (n/4 ) + 3 n .. i i √ = 2 T (n/4 ) + i n Subhash Suri UC Santa Barbara 

20 . More Examples • Terminates when 4i = n, or when i = log4 n = log 2n log 4 = 1 2 log n. 2 1 log n √ T (n) = 2 2 + n log4 n √ = n(log4 n + 1) √ = O( n log n) Subhash Suri UC Santa Barbara 

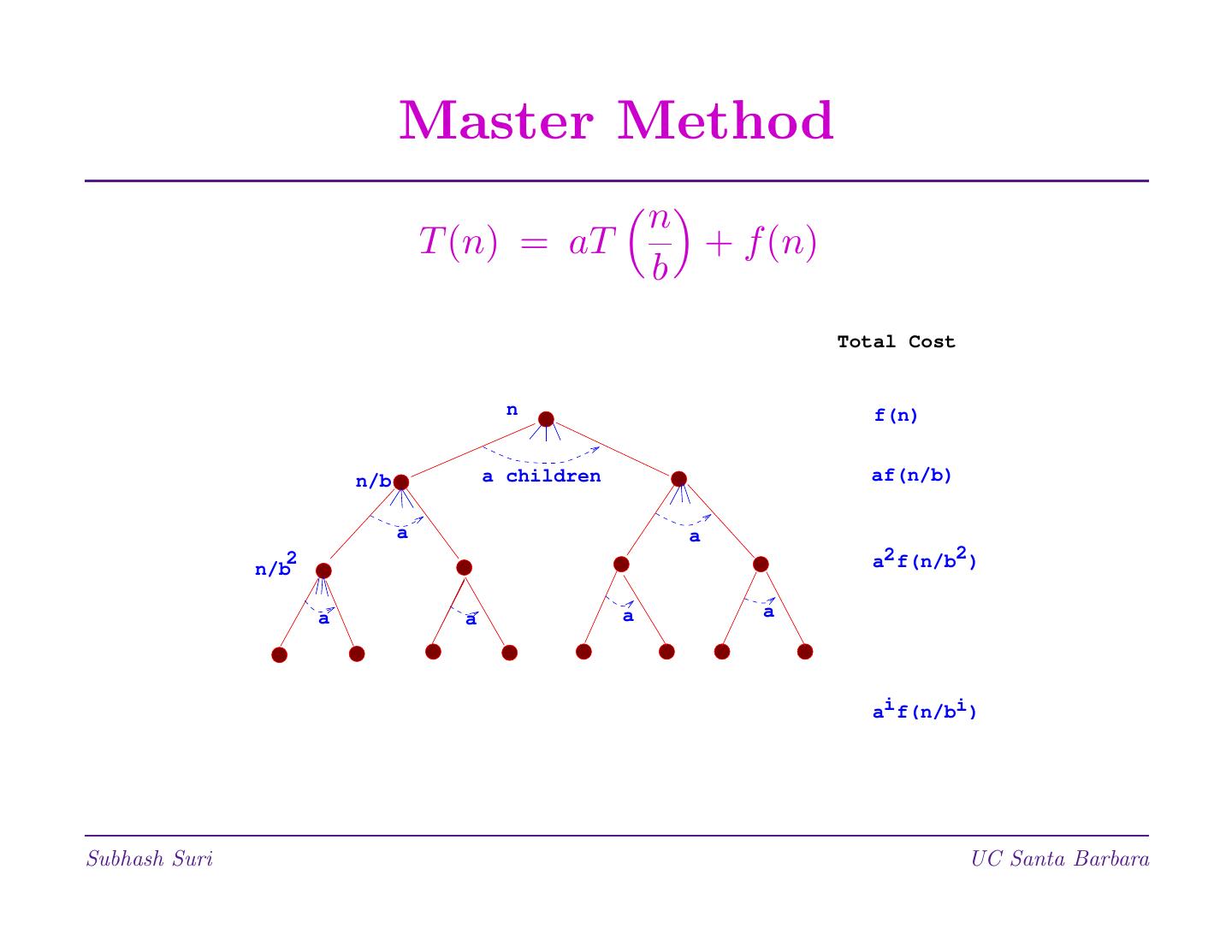
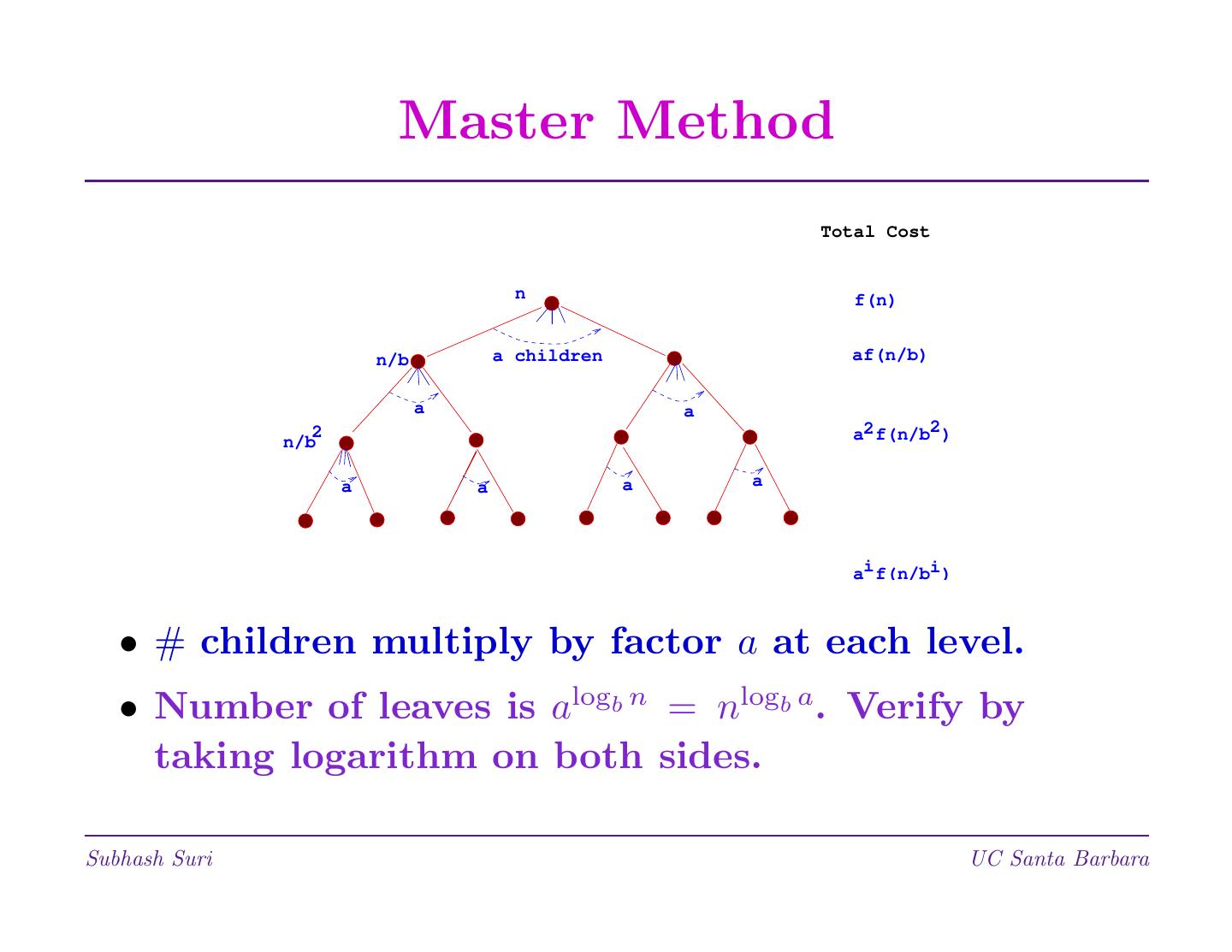
21 . Master Method n T (n) = aT + f (n) b Total Cost n f(n) n/b a children af(n/b) a a n/b 2 a2 f(n/b2 ) a a a a ai f(n/bi ) Subhash Suri UC Santa Barbara 

22 . Master Method Total Cost n f(n) n/b a children af(n/b) a a n/b 2 a2 f(n/b2 ) a a a a ai f(n/bi ) • # children multiply by factor a at each level. • Number of leaves is alogb n = nlogb a. Verify by taking logarithm on both sides. Subhash Suri UC Santa Barbara 

23 . Master Method • By recursion tree, we get logb n−1 logb a i n T (n) = Θ(n ) + af i i=0 b • Let f (n) = Θ(np logk n), where p, k ≥ 0. • Important: a ≥ 1 and b > 1 are constants. • Case I: p < logb a. nlogb a grows faster than f (n). T (n) = Θ(nlogb a) Subhash Suri UC Santa Barbara 

24 . Master Method • By recursion tree, we get logb n−1 logb a i n T (n) = Θ(n ) + af i i=0 b • Let f (n) = Θ(np logk n), where p, k ≥ 0. • Case II: p = logb a. Both terms have same growth rates. T (n) = Θ(nlogb a logk+1 n) Subhash Suri UC Santa Barbara 

25 . Master Method • By recursion tree, we get logb n−1 logb a i n T (n) = Θ(n ) + af i i=0 b • Let f (n) = Θ(np logk n), where p, k ≥ 0. • Case III: p > logb a. nlogb a is slower than f (n). T (n) = Θ (f (n)) Subhash Suri UC Santa Barbara 

26 . Applying Master Method • Merge Sort: T (n) = 2T (n/2) + Θ(n). a = b = 2, p = 1, and k = 0. So logb a = 1, and p = logb a. Case II applies, giving us T (n) = Θ(n log n) • Binary Search: T (n) = T (n/2) + Θ(1). a = 1, b = 2, p = 0, and k = 0. So logb a = 0, and p = logb a. Case II applies, giving us T (n) = Θ(log n) Subhash Suri UC Santa Barbara 

27 . Applying Master Method • T (n) = 2T (n/2) + Θ(n log n). a = b = 2, p = 1, and k = 1. p = 1 = logb a, and Case II applies. T (n) = Θ(n log2 n) • T (n) = 7T (n/2) + Θ(n2). a = 7, b = 2, p = 2, and logb 2 = log 7 > 2. Case I applied, and we get T (n) = Θ(nlog 7) Subhash Suri UC Santa Barbara 

28 . Applying Master Method 2 √ • T (n) = 4T (n/2) + Θ(n n). a = 4, b = 2, p = 2.5, and k = 0. So logb a = 2, and p > logb a. Case III applies, giving us 2 √ T (n) = Θ(n n) n • T (n) = 2T (n/2) + Θ log n . a = 2, b = 2, p = 1. But k = −1, and so the Master Method does not apply! Subhash Suri UC Santa Barbara 

29 . Matrix Multiplication • Multiply two n × n matrices: C = A × B. n • Standard method: Cij = k=1 Aik × Bkj . • This takes O(n) time per element of C, for the total cost of O(n3) to compute C. • This method, known since Gauss’s time, seems hard to improve. • A very surprising discovery by Strassen (1969) broke the n3 asymptotic barrier. • Method is divide and conquer, with a clever choice of submatrices to multiply. Subhash Suri UC Santa Barbara