集合

1 .CSE 373 : Data Structures & Algorithms Disjoint Sets & Union-Find Riley Porter Winter 2017 CSE373: Data Structures & Algorithms 1

2 .Course Logistics Hashing topic summary out now (thanks Matthew!) HW3 still out. Some changes to clarify based on common confusion popping up: WordInfo objects now have a hashCode () some clarification in the Mutability paragrap h in implementation notes rehashing pseudocode on the topic summary AND in section tomorrow Midterm a week from Friday, we’ll do review in lecture next week 2 CSE373: Data Structures & Algorithms

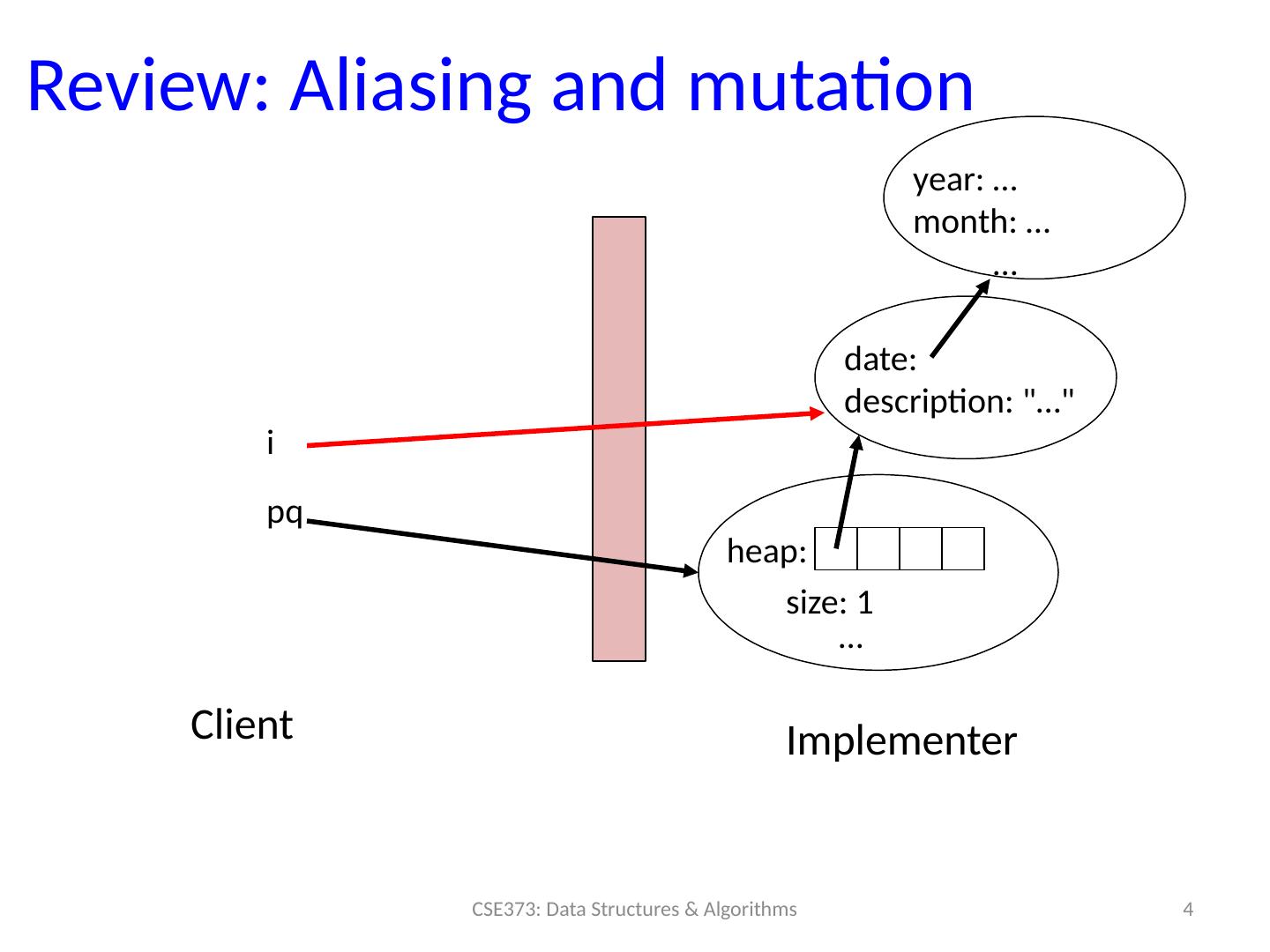
3 .Review: Abstractions from Monday 3 CSE373: Data Structures & Algorithms public class ToDoPQ { private ToDoItem [] heap; private int size; void insert ( ToDoItem t ) {…} ToDoItem deleteMin () {…} / / more methods } public class ToDoItem { private Date date; private String description; / / methods } public class Date { private int day; private int month ; private int year; / / methods } What could go wrong with these classes depending on their implementation? Think of some client code that might break abstraction through aliases.

4 .Review: Aliasing and mutation 4 CSE373: Data Structures & Algorithms pq h eap: size: 1 … date: d escription: "…" year: … month: … … i Client Implementer

5 .Review: The Fix How do we protect against aliases getting passed back to the client? Copy-in and Copy-out: whenever the client gives us a new object to store or whenever we’re giving the client a reference to an object, we better copy it. Deep copying: copy the objects all the way down Immutability: protect by only storing things that can’t change. Deep copy down to the level of immutability 5 CSE373: Data Structures & Algorithms

6 .New Topic! C onsider this problem. How would you implement a solution ? Given : Set<Set<String>> friendGroups representing groups of friends. You can assume unique names for each person and each person is only in one group. Example input: [ ["Riley", "Pascale", "Matthew", "Hunter"], [ "Chloe", "Paul", " Zelina "], [ "Rebecca", "Raquel", " Trung ", "Kyle", "Josh"] ] Problem : Given two Strings "Pascale" and "Raquel" determine if they are in the same group of friends. 6 CSE373: Data Structures & Algorithms

7 .Solution Ideas Traverse each Set until you find the Set containing the first name, then see if it also contains the second name. Store a map of people to the set of people they are friends with. Then find the Set of friends for the first name and see if it contains the second name . Note, this works for friends in multiple groups as well. [ "Riley”  [ "Pascale", "Matthew", "Hunter"], "Pascale”  [ ”Riley", "Matthew", "Hunter"], ... ] Store friendship in a Graph. A lot like solution 2 actually. We ’ re not there yet , but we’ll get there soon . Disjoint Sets and Union- Find (new today and Friday!) Others ? 7 CSE373: Data Structures & Algorithms

8 .Disjoint Sets and Union Find: the plan What are sets and disjoint sets The union-find ADT for disjoint sets Friday: Basic implementation with "up trees" Optimizations that make the implementation much faster 8 CSE373: Data Structures & Algorithms

9 .Terminology CSE373: Data Structures & Algorithms 9 Intersection  Union  Empty set:  Set S containin g e1, e2 and e3: {e1, e2, el3} e1 is an element of S: e1 ∈ S Notation for elements in a set:

10 .Disjoint sets A set is a collection of elements (no-repeats) Every set contains the empty set by default Two sets are disjoint if they have no elements in common S 1  S 2 =  Examples: { a, e, c} and {d, b} { x, y, z} and {t, u, x } 10 CSE373: Data Structures & Algorithms Disjoint Not disjoint

11 .Partitions A partition P of a set S is a set of sets { S 1 , S 2 ,…, S n } such that every element of S is in exactly one S i Put another way: S 1  S 2  . . .  S k = S For all i and j, i  j implies S i  S j =  (sets are disjoint with each other) Example: Let S be { a,b,c,d,e } { a}, { d,e }, { b,c } { a,b,c }, , {d}, {e} { a,b,c,d,e } { a,b,d }, { c,d,e } { a,b }, { e,c } 11 CSE373: Data Structures & Algorithms Partition Partition Partition Not a partition, not disjoint, both sets have d Not a partition of S (doesn’t have d)

12 .Union Find ADT: Operations Given an unchanging set S , create an initial partition of a set Typically each item in its own subset: {a}, {b}, {c}, … Give each subset a "name" by choosing a representative element Operation find takes an element of S and returns the representative element of the subset it is in Operation union takes two subsets and (permanently) makes one larger subset A different partition with one fewer set Affects result of subsequent find operations Choice of representative element up to implementation 12 CSE373: Data Structures & Algorithms

13 .Subset Find for our problem Given an unchanging set S , create an initial partition of a set “Riley” -> [ "Riley", "Pascale", "Matthew", "Hunter"], “Chloe” -> [ "Chloe", "Paul", " Zelina "], “Rebecca” -> [ "Rebecca", "Raquel", " Trung ", "Kyle", "Josh"] Operation find takes an element of S and returns the representative element of the subset it is in find(“Pascale”) returns “Riley” find(“Chloe”) returns “Chloe” Not the same subset since not the same representative 13 CSE373: Data Structures & Algorithms

14 .Union of two subsets for our problem Operation union takes two subsets and (permanently) makes one larger subset Chloe and Riley become friends, merging their two groups. Now those to subsets become one subset. We can represent that in two ways: Merge the sets: “Chloe” -> [ "Chloe", "Paul", " Zelina ”, "Riley”, " Pascale", "Matthew", "Hunter" ] Or tell Riley that her representative is now Chloe, and on find anyone in Riley’s old subset like find(“Pascale”) see what group Riley is in: “Riley” -> [" Pascale", "Matthew", "Hunter"], “Chloe” -> [ "Chloe", "Paul", " Zelina ”, "Riley” ] Either way, find(“Pascale”) returns “Chloe” 14 CSE373: Data Structures & Algorithms

15 .Another Example Let S = {1,2,3,4,5,6,7,8,9} Let initial partition be (will highlight representative elements red ) { 1 }, { 2 }, { 3 }, { 4 }, { 5 }, { 6 }, { 7 }, { 8 }, { 9 } union (2,5): { 1 }, { 2 , 5}, { 3 }, { 4 }, { 6 }, { 7 }, { 8 }, { 9 } find (4) = 4, find (2) = 2, find (5) = 2 union (4,6), union (2,7) { 1 }, { 2 , 5, 7}, { 3 }, {4, 6 }, { 8 }, { 9 } find (4) = 6, find (2) = 2, find (5) = 2 union (2,6) { 1 }, { 2 , 4, 5 , 6, 7 }, { 3 }, { 8 }, { 9 } 15 CSE373: Data Structures & Algorithms

16 .No other operations All that can "happen" is sets get unioned No "un - union" or "create new set" or … As always: trade-offs – implementations are different ideas? How do we maintain “representative” of a subset? Surprisingly useful ADT , b ut not as common as dictionaries, priority queues / heaps, AVL trees or hashing 16 CSE373: Data Structures & Algorithms

17 .Example application: maze-building Build a random maze by erasing edges Criteria: Possible to get from anywhere to anywhere No loops possible without backtracking After a "bad turn" have to "undo" 17 CSE373: Data Structures & Algorithms

18 .Maze building Pick start edge and end edge 18 CSE373: Data Structures & Algorithms Start End

19 .Repeatedly pick random edges to delete One approach: just keep deleting random edges until you can get from start to finish 19 CSE373: Data Structures & Algorithms Start End

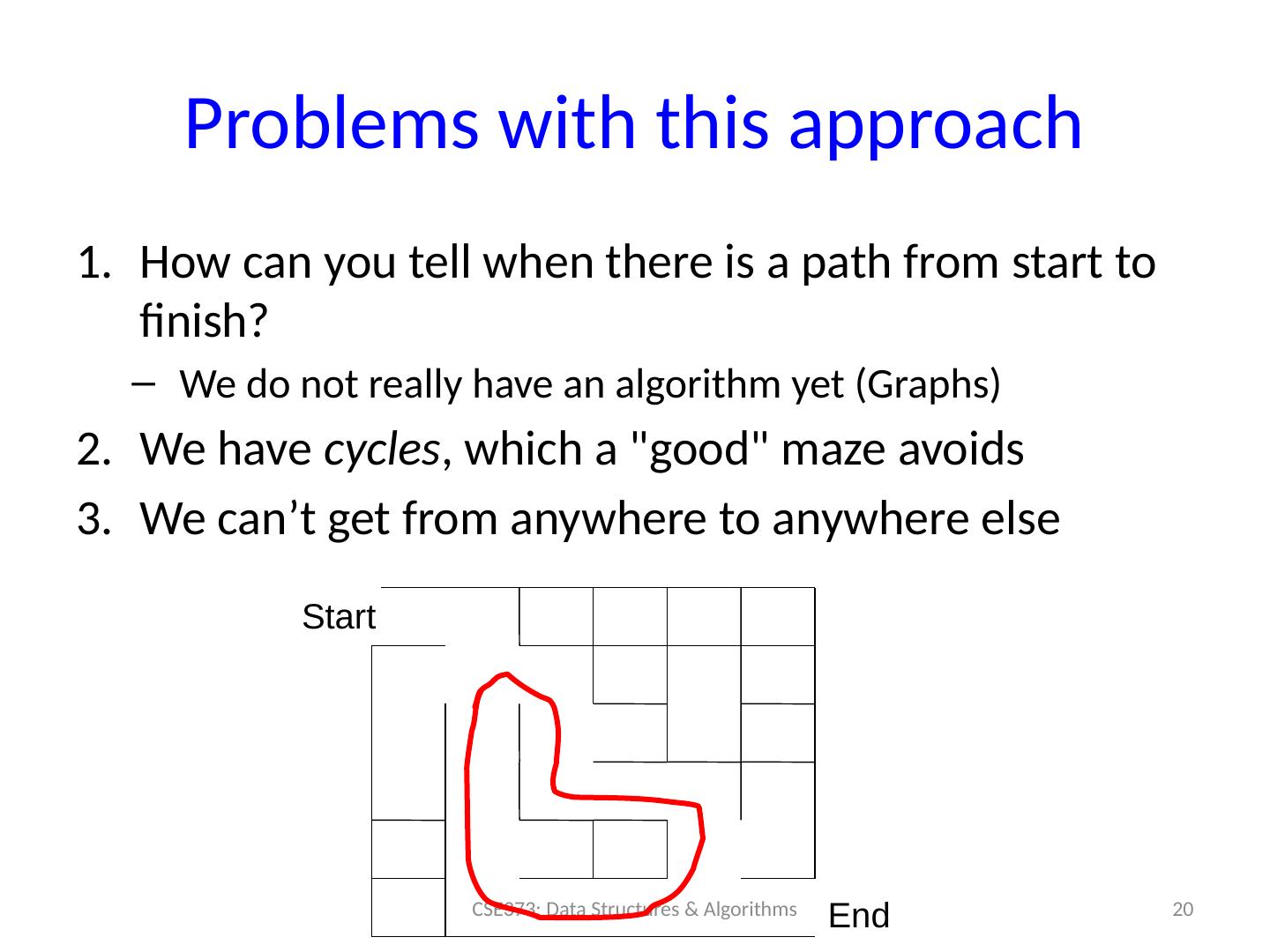
20 .Problems with this approach How can you tell when there is a path from start to finish? We do not really have an algorithm yet (Graphs) We have cycles , which a "good" maze avoids We can’t get from anywhere to anywhere else 20 CSE373: Data Structures & Algorithms Start End

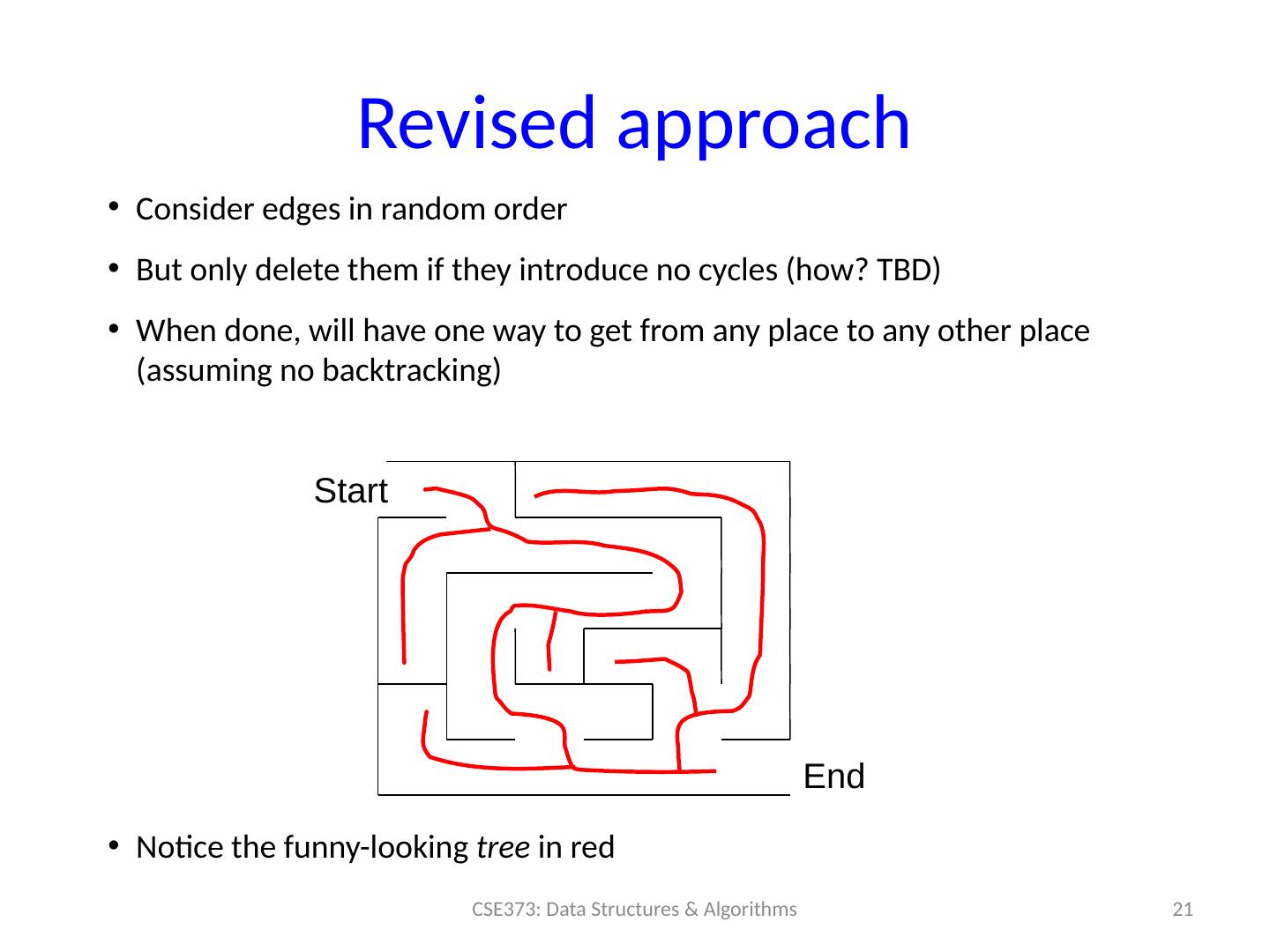
21 .Revised approach Consider edges in random order But only delete them if they introduce no cycles (how? TBD) When done, will have one way to get from any place to any other place (assuming no backtracking) Notice the funny-looking tree in red 21 CSE373: Data Structures & Algorithms Start End

22 .Cells and edges Let’s number each cell 36 total for 6 x 6 An (internal) edge ( x,y ) is the line between cells x and y 60 total for 6x6: (1,2), (2,3), …, (1,7), (2,8), … 22 CSE373: Data Structures & Algorithms Start End 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36

23 .The trick Partition the cells into disjoint sets : "are they connected" Initially every cell is in its own subset If an edge would connect two different subsets: then remove the edge and union the subsets e lse leave the edge because removing it makes a cycle 23 CSE373: Data Structures & Algorithms Start End 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 Start End 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36

24 .Pseudocode of the algorithm Partition = disjoint sets of connected cells, initially each cell in its own 1 - element set Edges = set of edges not yet processed, initially all (internal) edges Maze = set of edges kept in maze (initially empty ) / / stop when possible to get anywhere while Partition has more than one set { p ick a random edge ( c ell_1, cell_2 ) to remove from Edges set_1 = find (cell_1) set_2 = find (cell_2) if set_1 == set_2: / / same subset, do not create cycle add ( cell_1 , cell_2 ) to Maze else: / / do not put edge in Maze, connect subsets union ( set_1 , set_2) } Add remaining members of Edges to Maze, then output Maze 24 CSE373: Data Structures & Algorithms

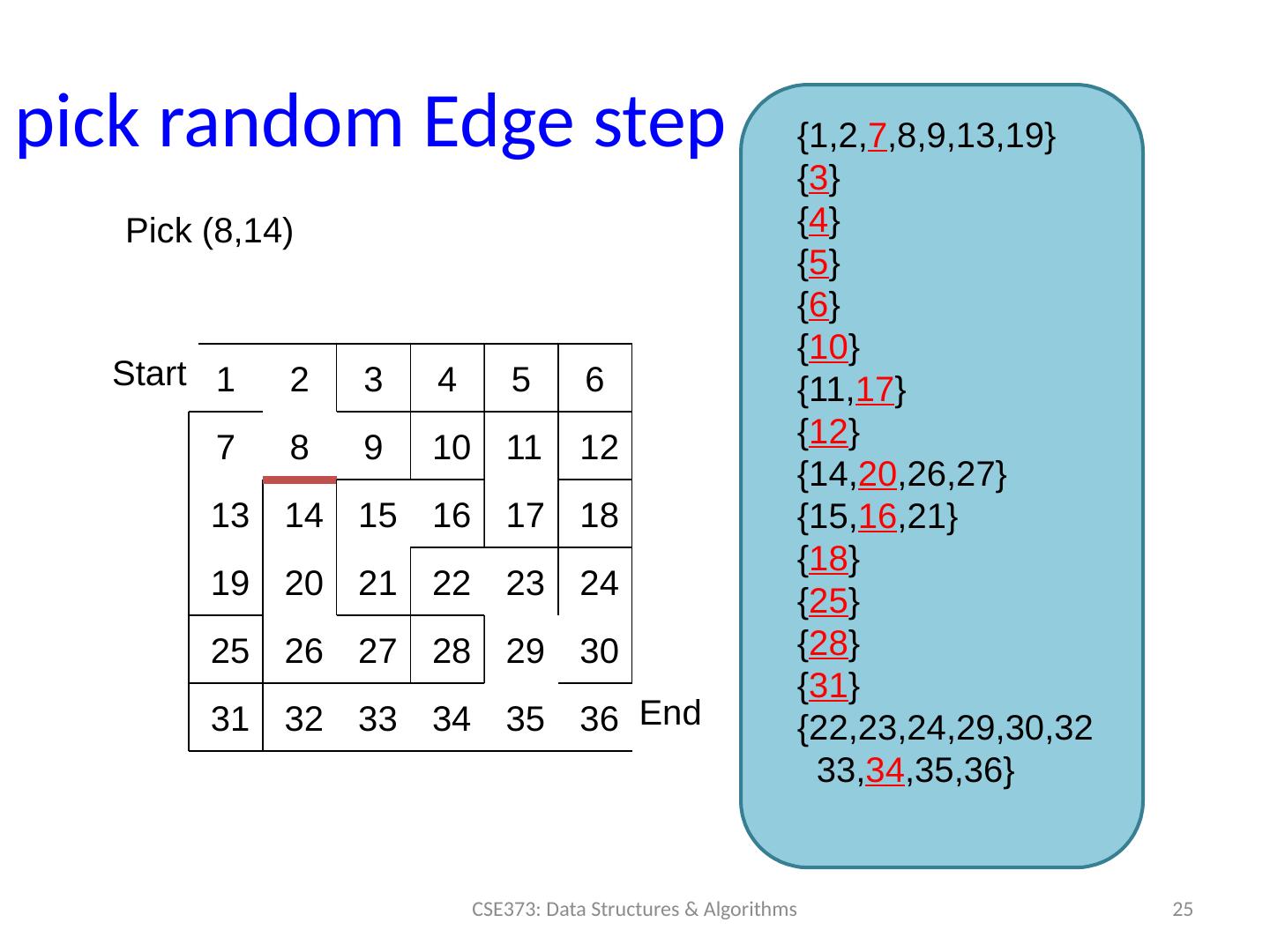
25 .pick random Edge step 25 CSE373: Data Structures & Algorithms Start End 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 Pick (8,14) { 1,2, 7 ,8,9,13,19} { 3 } { 4 } { 5 } { 6 } { 10 } {11, 17 } { 12 } {14, 20 ,26,27} {15, 16 ,21} { 18 } { 25 } { 28 } { 31 } { 22,23,24,29,30,32 33, 34 ,35,36}

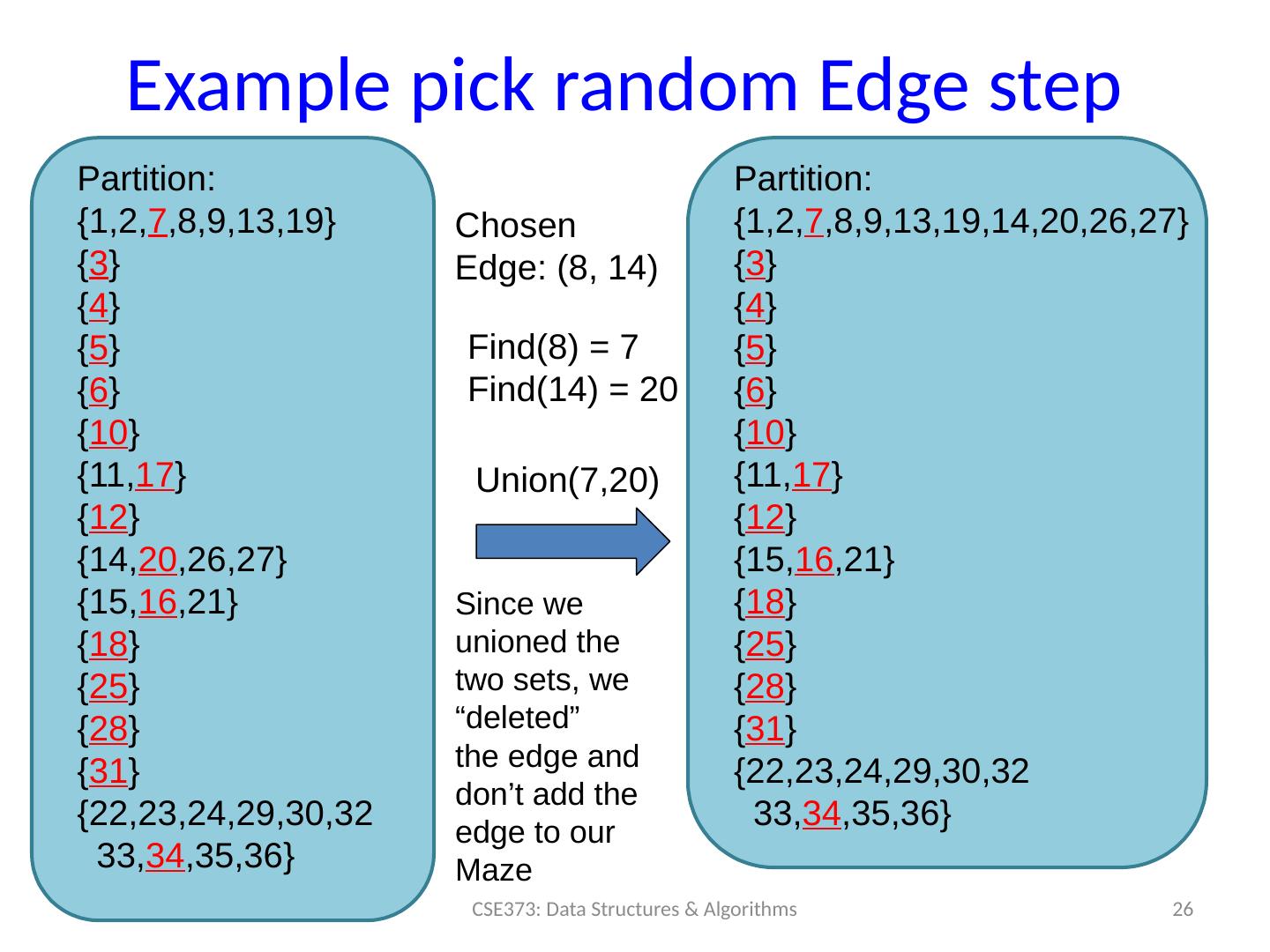
26 .Example pick random Edge step Partition: {1,2, 7 ,8,9,13,19} { 3 } { 4 } { 5 } { 6 } { 10 } {11, 17 } { 12 } {14, 20 ,26,27} {15, 16 ,21} { 18 } { 25 } { 28 } { 31 } { 22,23,24,29,30,32 33, 34 ,35,36} Find(8) = 7 Find (14) = 20 Union(7,20) Partition: { 1,2, 7 ,8,9,13,19,14,20,26,27} { 3 } { 4 } { 5 } { 6 } { 10 } {11, 17 } { 12 } { 15, 16 ,21} { 18 } { 25 } { 28 } { 31 } { 22,23,24,29,30,32 33, 34 ,35,36} CSE373: Data Structures & Algorithms 26 Chosen Edge: (8, 14) Since we unioned the two sets, we “deleted” the edge and don’t add the edge to our Maze

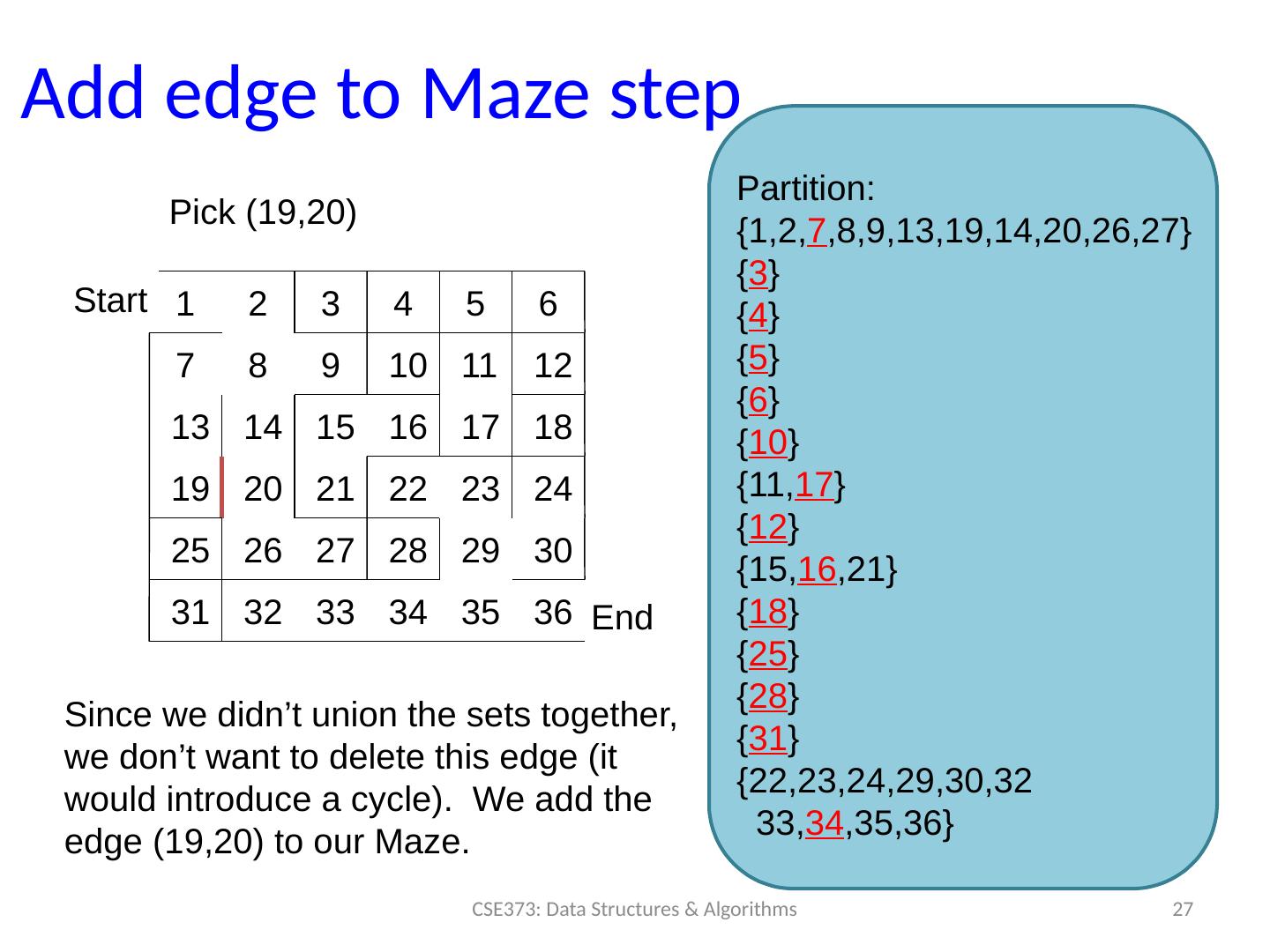
27 .Add edge to Maze step 27 CSE373: Data Structures & Algorithms Partition: { 1,2, 7 ,8,9,13,19,14,20,26,27} { 3 } { 4 } { 5 } { 6 } { 10 } {11, 17 } { 12 } { 15, 16 ,21} { 18 } { 25 } { 28 } { 31 } { 22,23,24,29,30,32 33, 34 ,35,36} Pick (19,20) Start End 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 Since we didn’t union the sets together, we don’t want to delete this edge (it would introduce a cycle). We add the edge (19,20) to our Maze.

28 .At the end Stop when Partition has one set Suppose green edges are already in Maze and black edges were not yet picked Add all black edges to Maze 28 CSE373: Data Structures & Algorithms Start End 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 Partition: {1,2,3,4,5,6, 7 ,… 36}

29 .Applications / Thoughts on Union-Find Maze-building is cute  and a surprising use of the union-find ADT Many other uses: Road/network/graph connectivity (will see this again) "connected components" e.g., in social network Partition an image by connected-pixels-of-similar-color Type inference in programming languages Our friend group example could be done with Graphs (we’ll learn about them later) but we can use Union-Find for a much less storage intense implementation. Cool!  Union-Find is n ot as common as dictionaries, queues, and stacks, but valuable because implementations are very fast, so when applicable can provide big improvements 29 CSE373: Data Structures & Algorithms