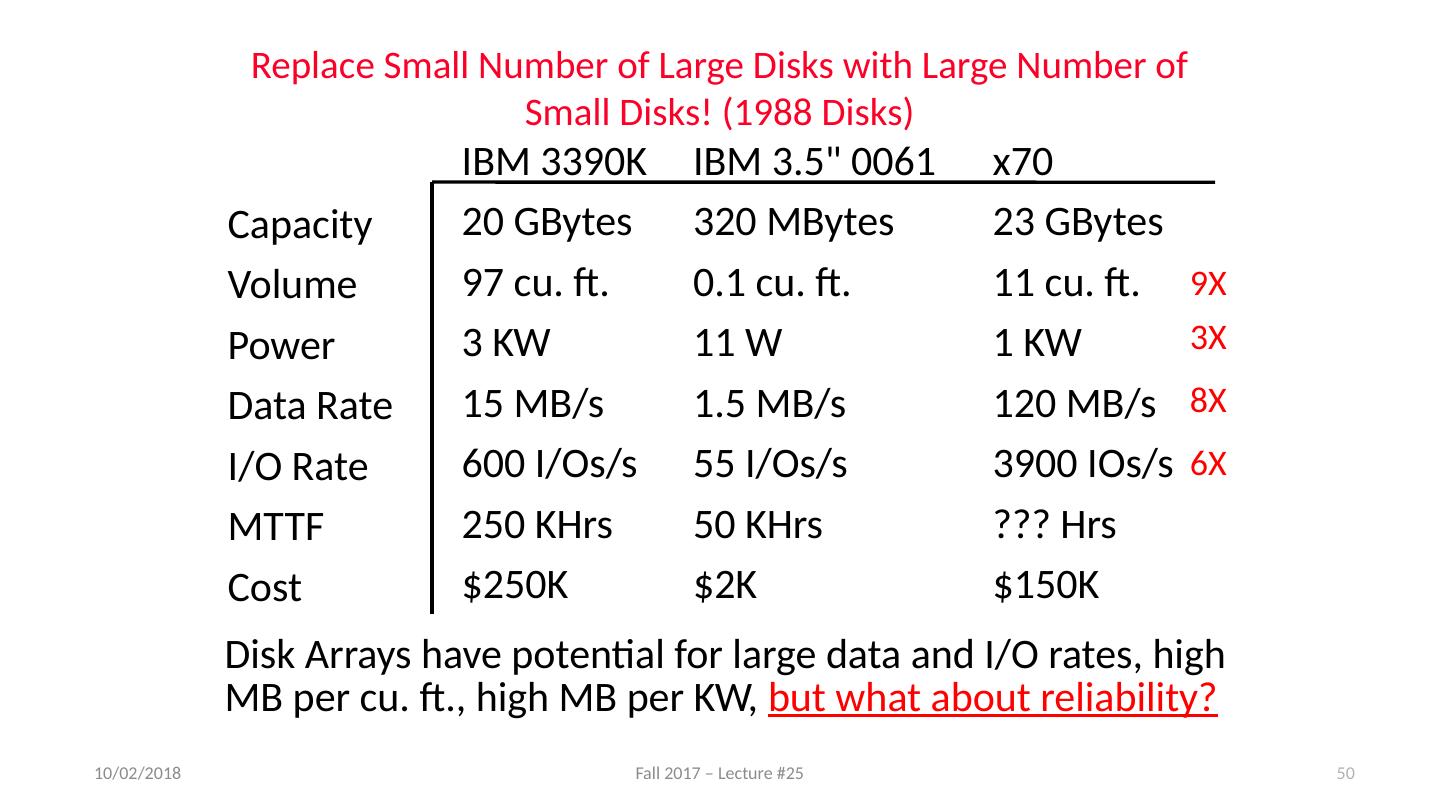
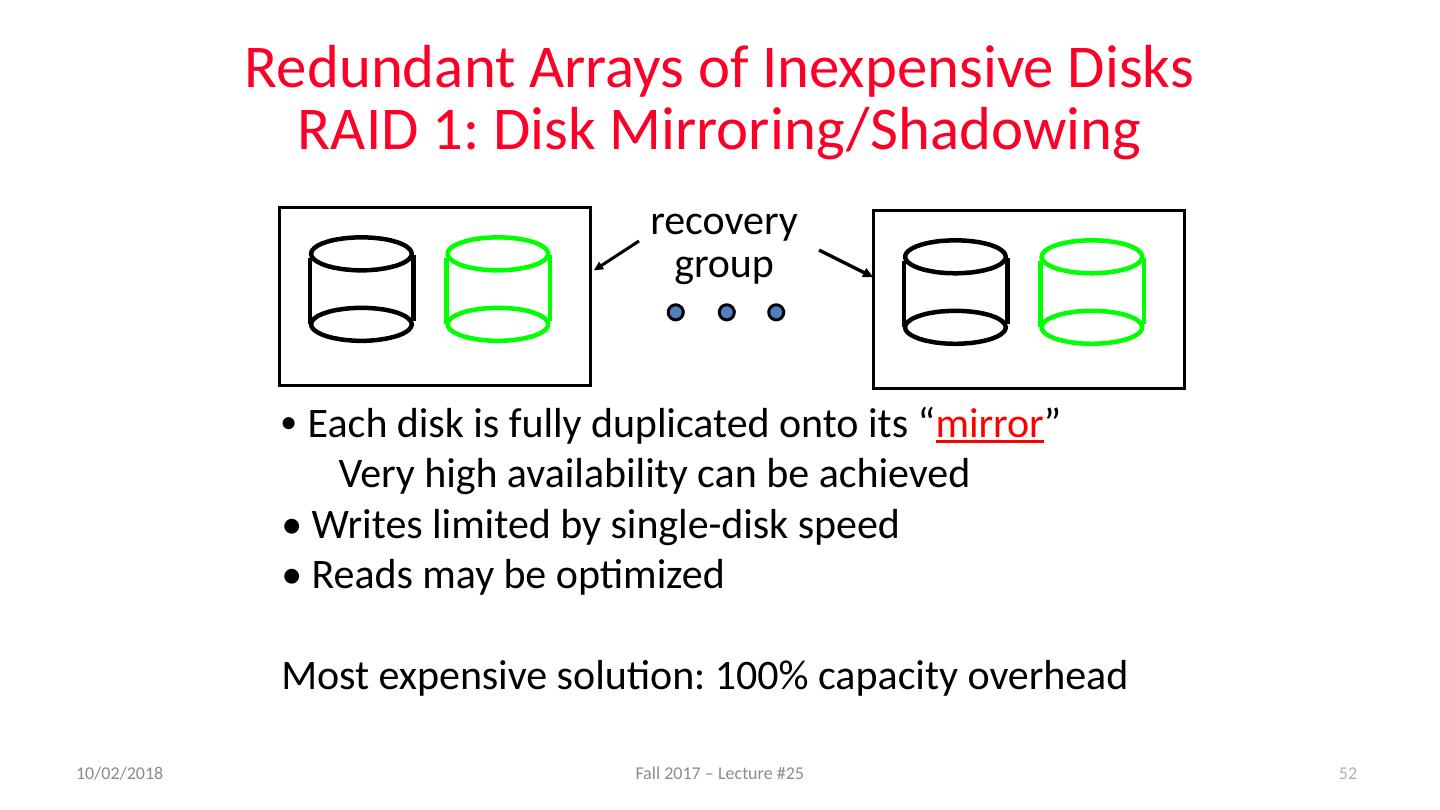
可靠性和RAID

1 .CS 61C: Great Ideas in Computer Architecture Lecture 25: Dependability and RAID Krste Asanović & Randy H. Katz http://inst.eecs.berkeley.edu/~ cs61c/fa17 11/27/17 Fall 2017 – Lecture #25 1

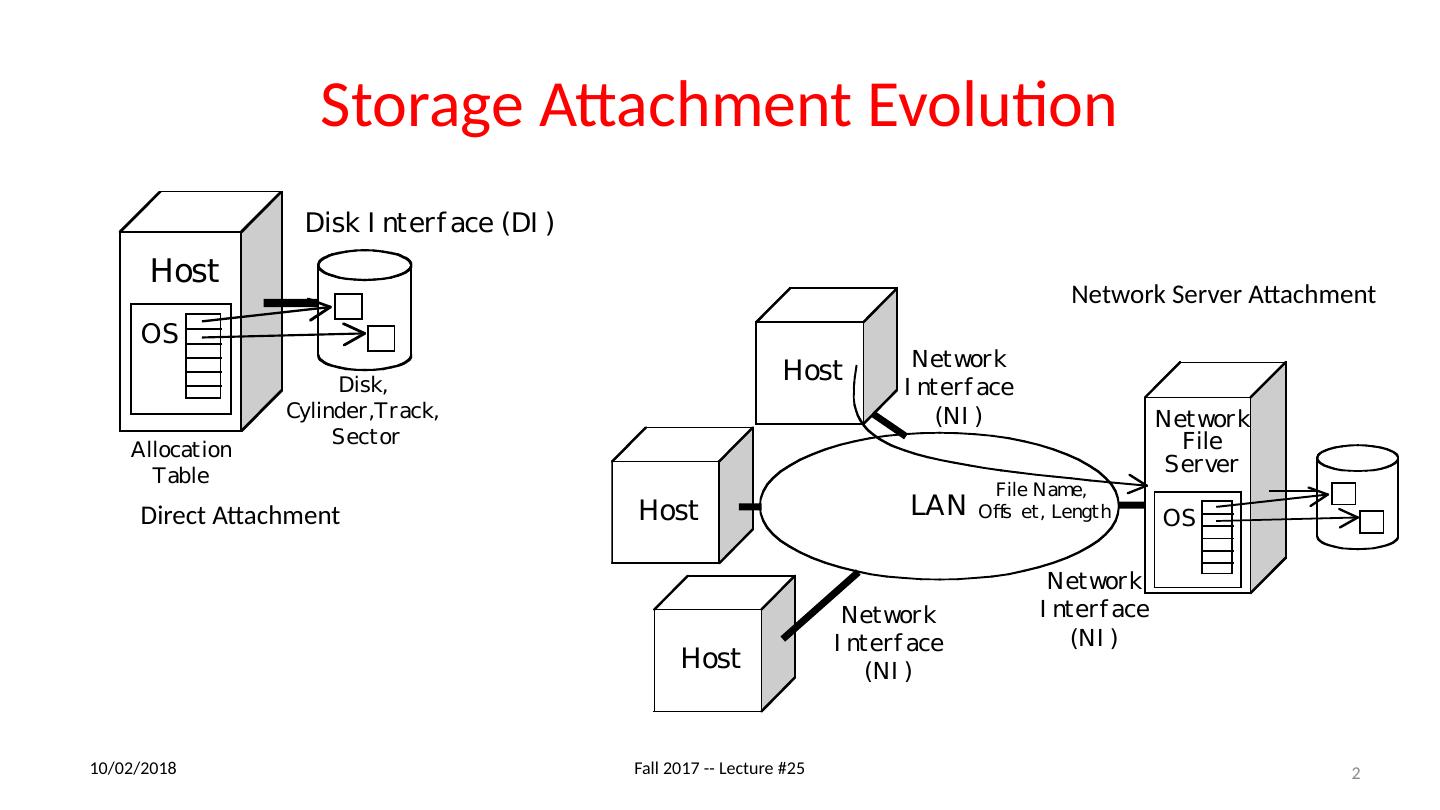
2 .Storage Attachment Evolution Direct Attachment Network Server Attachment 11/27/17 Fall 2017 -- Lecture #25 2

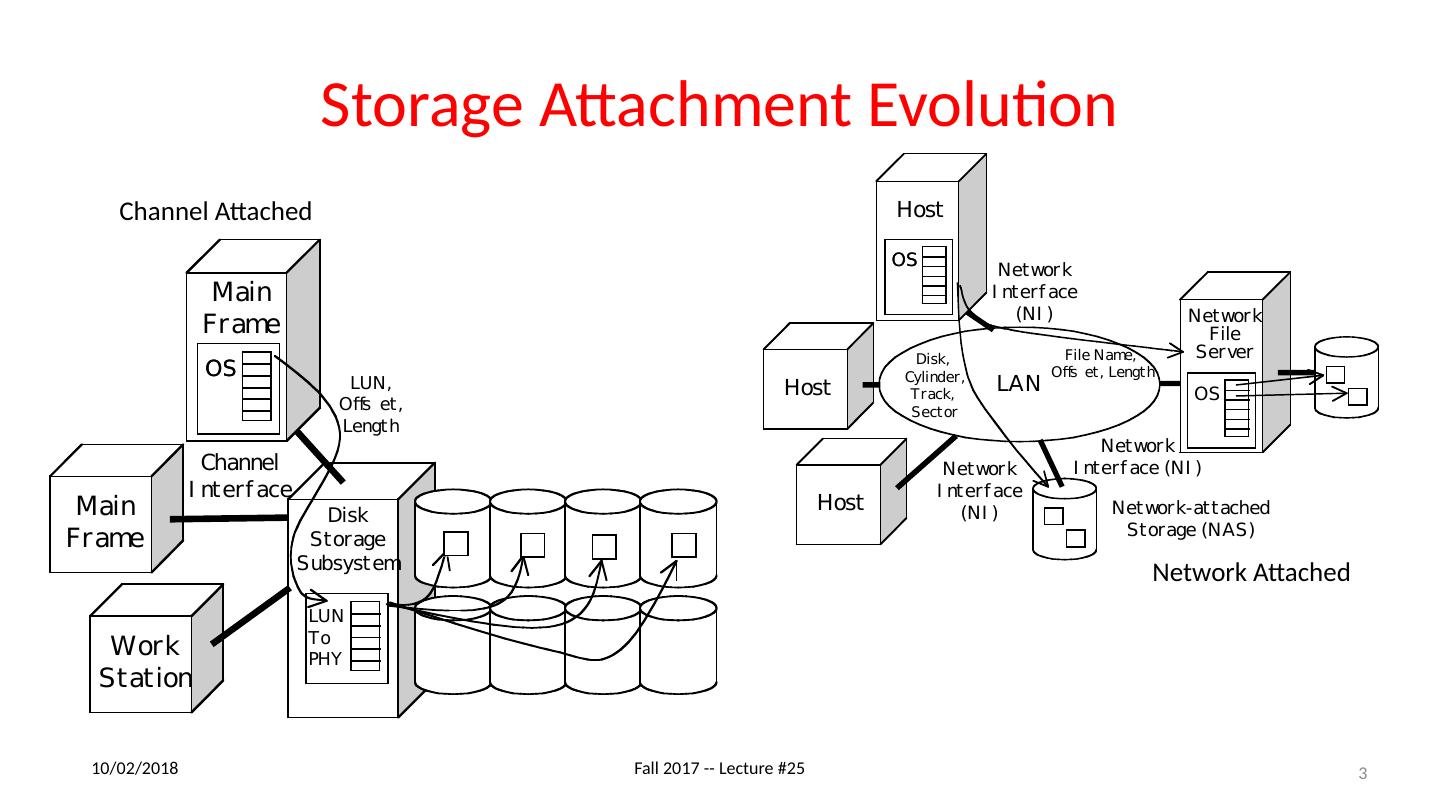
3 .Storage Attachment Evolution 11/27/17 Fall 2017 -- Lecture #25 3 Network Attached Channel Attached

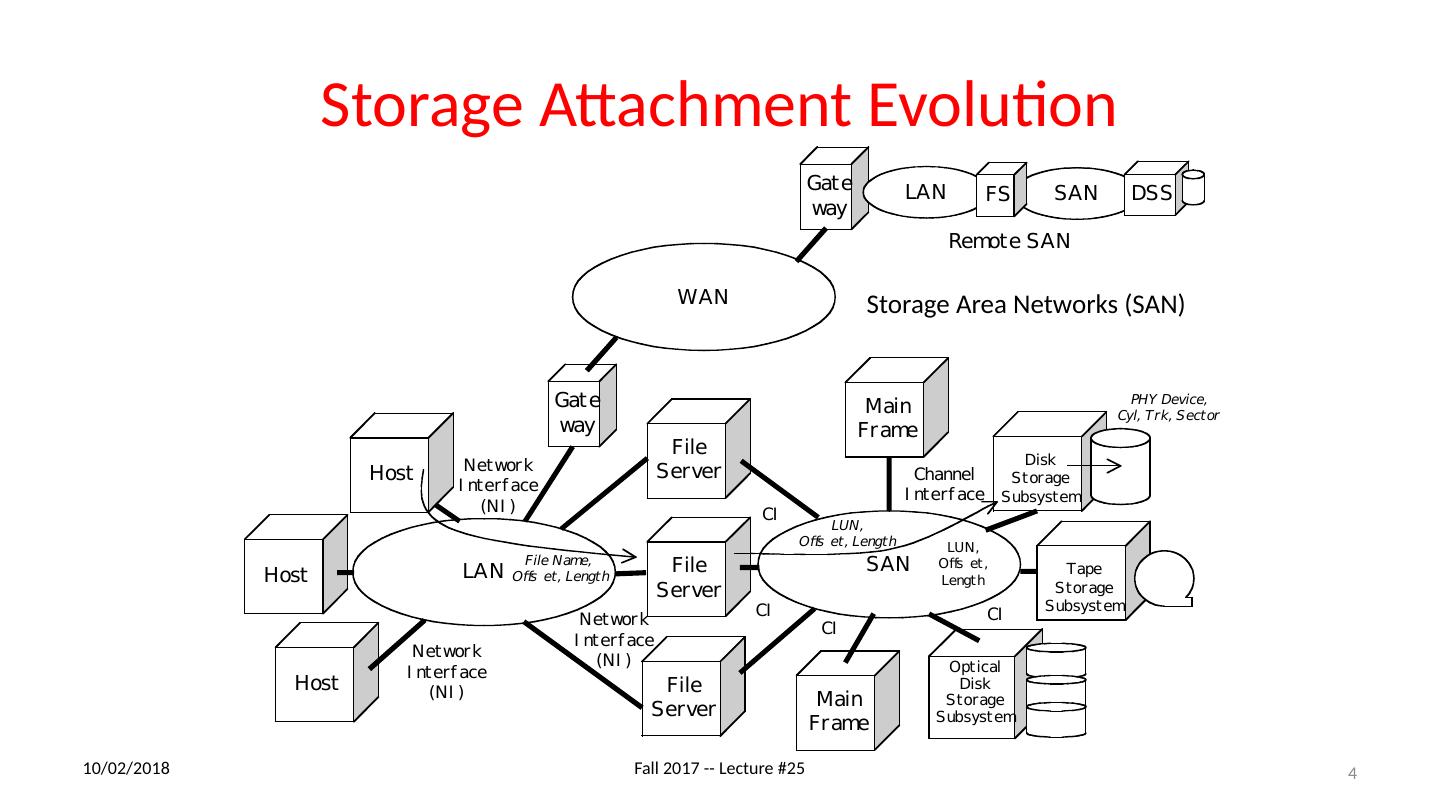
4 .Storage Attachment Evolution 11/27/17 Fall 2017 -- Lecture #25 4 Storage Area Networks (SAN)

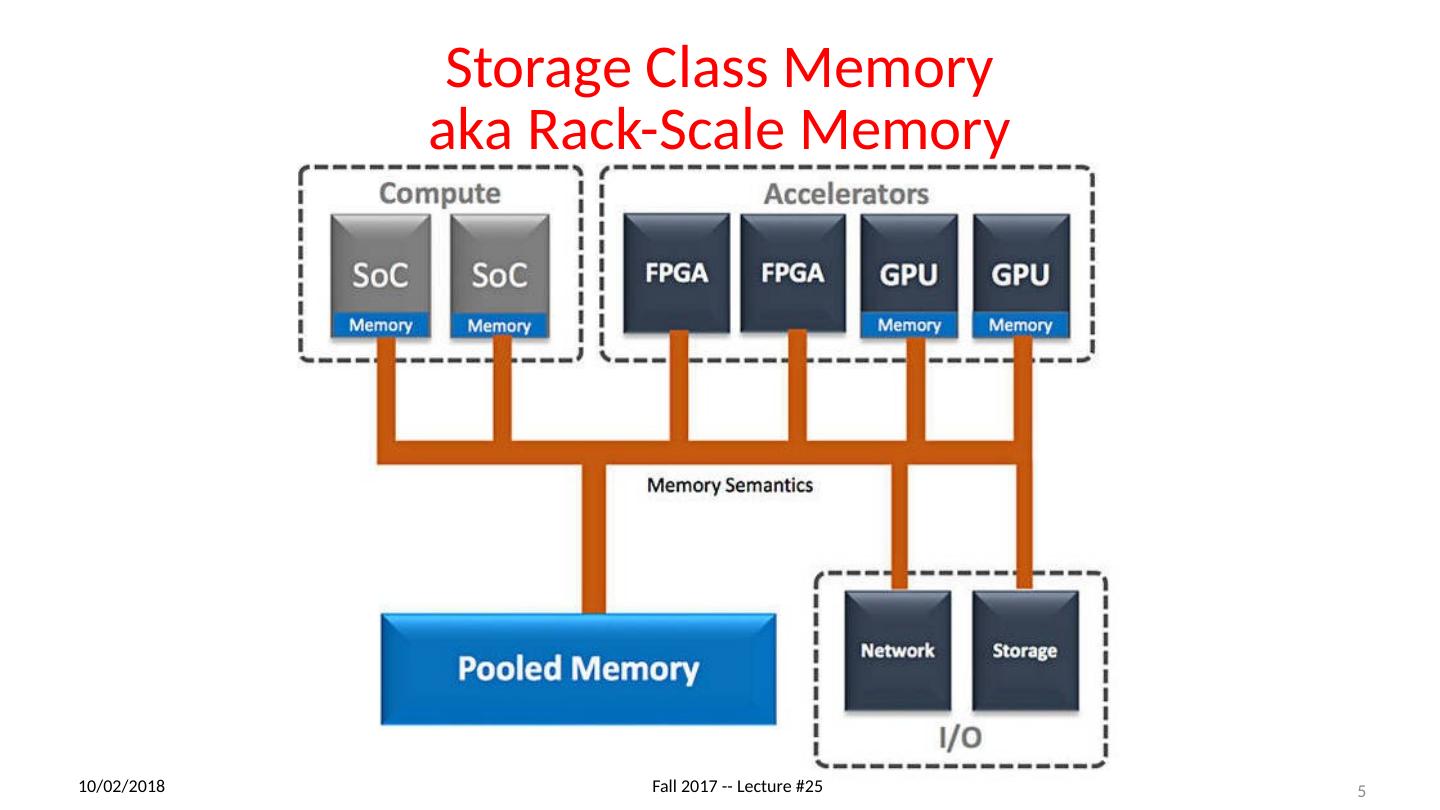
5 .Storage Class Memory aka Rack-Scale Memory 11/27/17 Fall 2017 -- Lecture #25 5

6 .Storage Class Memory aka Rack-Scale Memory 11/27/17 Fall 2017 -- Lecture #25 6 Cheaper than DRAM More expensive than disk Non-Volatile and faster than disk

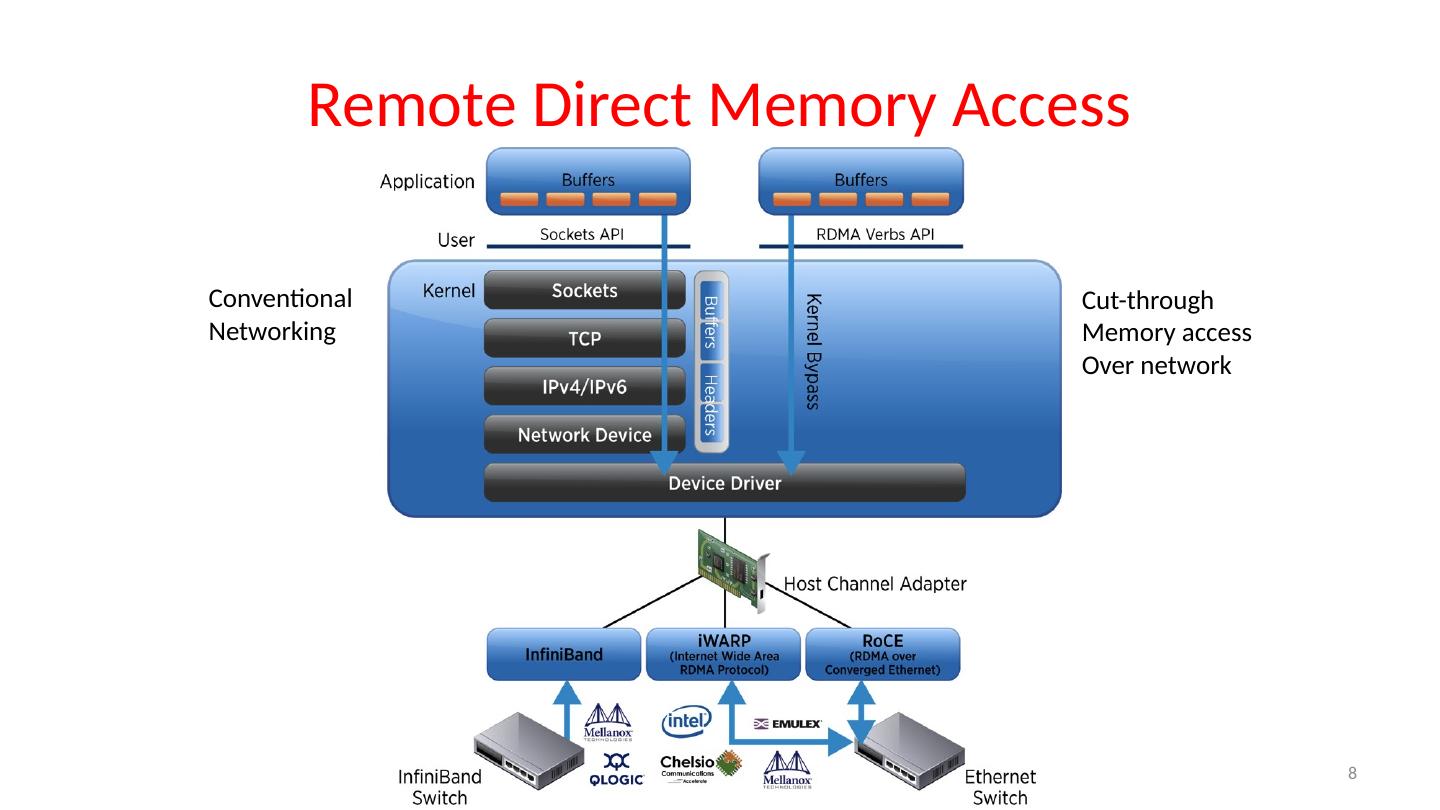
7 .Remote Direct Memory Access 7 11/27/17 Fall 2017 -- Lecture #25

8 .Remote Direct Memory Access 8 Conventional Networking Cut-through Memory access Over network

9 .Outline Dependability via Redundancy Error Correction/Detection RAID And, in Conclusion … 11/27/17 Fall 2017 – Lecture #25 9

10 .Outline Dependability via Redundancy Error Correction/Detection RAID And, in Conclusion … 11/27/17 Fall 2017 – Lecture #25 10

11 .Six Great Ideas in Computer Architecture Design for Moore’s Law (Multicore, Parallelism, OpenMP , Project #3) Abstraction to Simplify Design (Everything a number, Machine/Assembler Language, C, Project #1; Logic Gates, Datapaths , Project #2) Make the Common Case Fast (RISC Architecture, Instruction Pipelining, Project #2) Memory Hierarchy (Locality, Consistency, False Sharing, Project #3) Performance via Parallelism/Pipelining/Prediction (the five kinds of parallelism, Project #3, #4) Dependability via Redundancy (ECC, RAID) 11/27/17 Fall 2017 – Lecture #25 11

12 .Great Idea #6: Dependability via Redundancy Redundancy so that a failing piece doesn’t make the whole system fail 1+1=2 1+1=2 1+1=1 1+1=2 2 of 3 agree FAIL! Increasing transistor density reduces the cost of redundancy 11/27/17 Fall 2017 – Lecture #25 12

13 .Great Idea #6: Dependability via Redundancy Applies to everything from datacenters to memory Redundant datacenters so that can lose one datacenter but Internet service stays online Redundant routes so can lose nodes but Internet doesn’t fail Redundant disks so that can lose one disk but not lose data (Redundant Arrays of Independent Disks/RAID) Redundant memory bits of so that can lose 1 bit but no data (Error Correcting Code/ECC Memory) 11/27/17 Fall 2017 – Lecture #25 13

14 .Dependability Fault: failure of a component May or may not lead to system failure Service accomplishment Service delivered as specified Service interruption Deviation from specified service Failure Restoration 11/27/17 Fall 2017 – Lecture #25 14

15 .Dependability via Redundancy: Time vs. Space Spatial Redundancy – replicated data or check information or hardware to handle hard and soft (transient) failures Temporal Redundancy – redundancy in time (retry) to handle soft (transient) failures 11/27/17 Fall 2017 – Lecture #25 15

16 .Dependability Measures Reliability: Mean Time To Failure ( MTTF ) Service interruption: Mean Time To Repair ( MTTR ) Mean time between failures ( MTBF ) MTBF = MTTF + MTTR Availability = MTTF / (MTTF + MTTR) Improving Availability Increase MTTF: More reliable hardware/software + Fault Tolerance Reduce MTTR: improved tools and processes for diagnosis and repair 11/27/17 Fall 2017 – Lecture #25 16

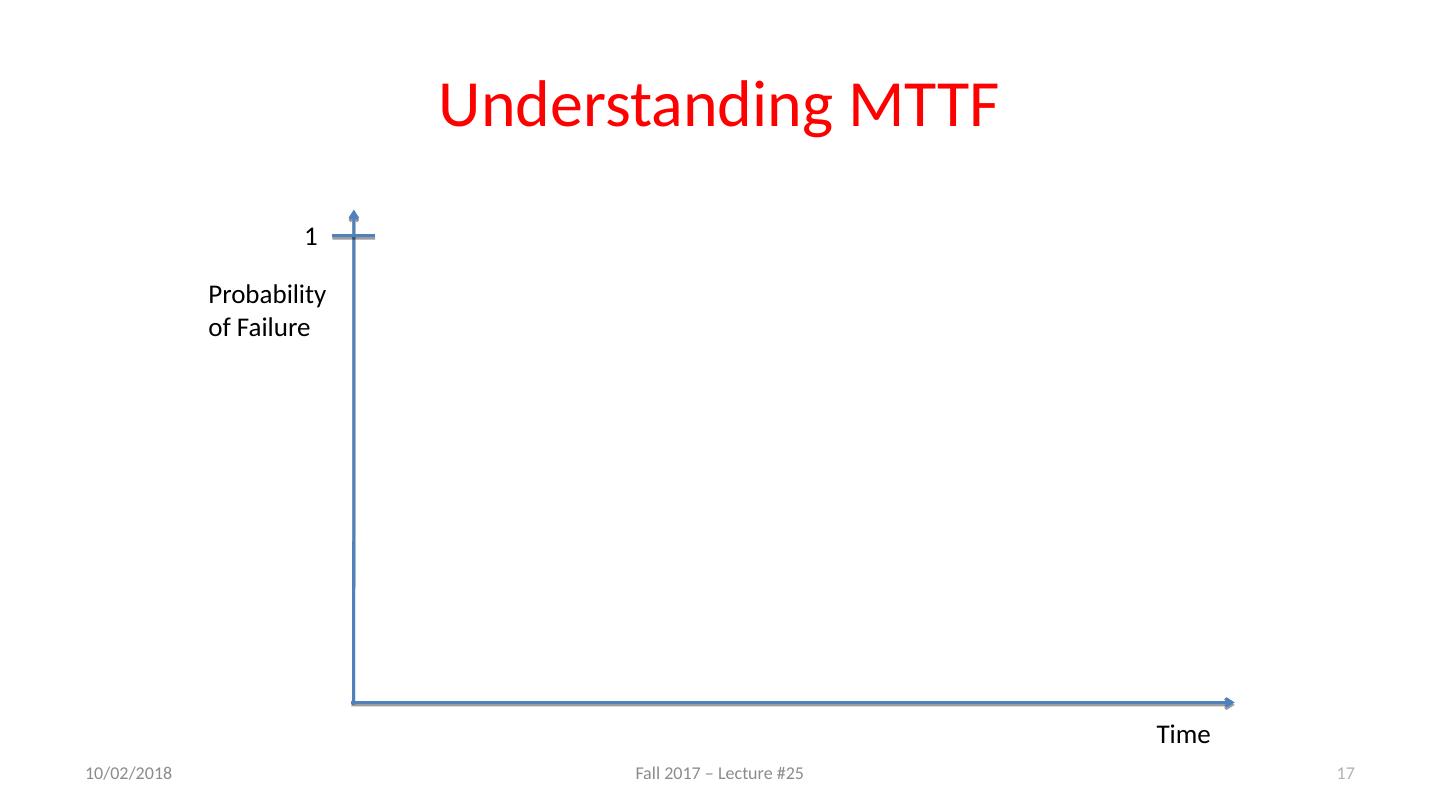
17 .Understanding MTTF Probability of Failure 1 Time 11/27/17 Fall 2017 – Lecture #25 17

18 .Availability Measures Availability = MTTF / (MTTF + MTTR) as % MTTF, MTBF usually measured in hours Since hope rarely down, shorthand is “number of 9s of availability per year” 1 nine: 90% => 36 days of repair/year 2 nines: 99% => 3.6 days of repair/year 3 nines: 99.9% => 526 minutes of repair/year 4 nines: 99.99% => 53 minutes of repair/year 5 nines: 99.999% => 5 minutes of repair/year 11/27/17 Fall 2017 – Lecture #25 18

19 .Reliability Measures Another is average number of failures per year: Annualized Failure Rate ( AFR ) E.g., 1000 disks with 100,000 hour MTTF 365 days * 24 hours = 8760 hours (1000 disks * 8760 hrs/year) / 100,000 = 87.6 failed disks per year on average 87.6/1000 = 8.76% annual failure rate Google’s 2007 study* found that actual AFRs for individual drives ranged from 1.7% for first year drives to over 8.6% for three-year old drives * research. google .com/archive/disk_failures.pdf 11/27/17 Fall 2017 – Lecture #25 19

20 .Breaking News, 1Q17, BackBlaze https://www.backblaze.com/blog/hard-drive-failure-rates-q1-2017 / 11/27/17 Fall 2017 – Lecture #25 20

21 .Dependability Design Principle Design Principle: No single points of failure “Chain is only as strong as its weakest link” Dependability Corollary of Amdahl’s Law Doesn’t matter how dependable you make one portion of system Dependability limited by part you do not improve 11/27/17 Fall 2017 – Lecture #25 21

22 .Outline Dependability via Redundancy Error Correction/Detection RAID And, in Conclusion … 11/27/17 Fall 2017 – Lecture #25 22

23 .Error Detection/Correction Codes Memory systems generate errors (accidentally flipped-bits) DRAMs store very little charge per bit “Soft” errors occur occasionally when cells are struck by alpha particles or other environmental upsets “Hard ” errors can occur when chips permanently fail Problem gets worse as memories get denser and larger Memories protected against failures with EDC/ECC Extra bits are added to each data-word U sed to detect and/or correct faults in the memory system Each data word value mapped to unique code word A fault changes valid code word to invalid one, which can be detected 11/27/17 Fall 2017 – Lecture #25 23

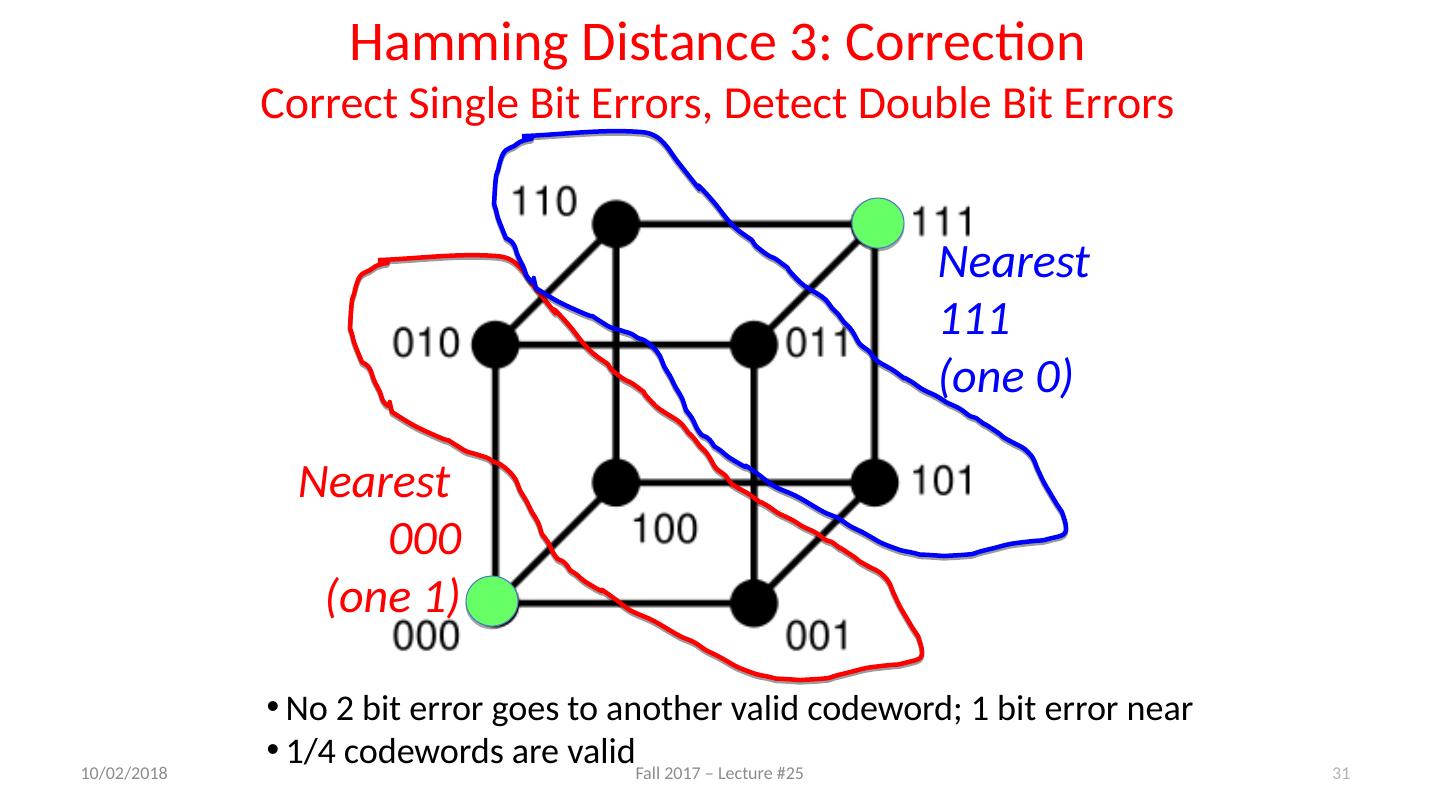
24 .Block Code Principles Hamming distance = difference in # of bits p = 0 1 1 0 11, q = 0 0 1 1 11, Ham. distance ( p,q ) = 2 p = 011011, q = 110001, distance ( p,q ) = ? Can think of extra bits as creating a code with the data What if minimum distance between members of code is 2 and get a 1-bit error? Richard Hamming, 1915-98 Turing Award Winner 11/27/17 Fall 2017 – Lecture #25 24

25 .Parity: Simple Error-Detection Coding Each data value, before it is written to memory is “tagged” with an extra bit to force the stored word to have even parity : Each word, as it is read from memory is “checked” by finding its parity (including the parity bit). b 7 b 6 b 5 b 4 b 3 b 2 b 1 b 0 + b 7 b 6 b 5 b 4 b 3 b 2 b 1 b 0 p + c Minimum Hamming distance of parity code is 2 A non-zero parity check indicates an error occurred: 2 errors (on different bits) are not detected Nor any even number of errors, just odd numbers of errors are detected p 11/27/17 Fall 2017 – Lecture #25 25

26 .Parity Example Data 0101 0101 4 ones, even parity now Write to memory: 0101 0101 0 to keep parity even Data 0101 0111 5 ones, odd parity now Write to memory: 0101 0111 1 to make parity even Read from memory 0101 0101 0 4 ones => even parity, so no error Read from memory 1101 0101 0 5 ones => odd parity, so error What if error in parity bit? 11/27/17 Fall 2017 – Lecture #25 26

27 .Suppose Want to Correct One Error? Hamming came up with simple to understand mapping to allow Error Correction at minimum distance of three Single error correction, double error detection Called “Hamming ECC” Worked weekends on relay computer with unreliable card reader, frustrated with manual restarting Got interested in error correction; published 1950 R . W. Hamming , “Error Detecting and Correcting Codes,” The Bell System Technical Journal , Vol. XXVI, No 2 (April 1950) pp 147-160 . 11/27/17 Fall 2017 – Lecture #25 27

28 .Detecting/Correcting Code Concept Detection : bit pattern fails codeword check Correction : map to nearest valid code word 11/27/17 Fall 2017 – Lecture #25 28 Space of possible bit patterns (2 N ) Sparse population of code words (2 M << 2 N ) - with identifiable signature Error changes bit pattern to non-code

29 .Hamming Distance: Eight Code Words 11/27/17 Fall 2017 – Lecture #25 29