- 快召唤伙伴们来围观吧
- 微博 QQ QQ空间 贴吧
- 文档嵌入链接
- 复制
- 微信扫一扫分享
- 已成功复制到剪贴板
排序算法比较
展开查看详情
1 .CSE 373 : Data Structure & Algorithms Comparison Sorting Riley Porter Winter 2017 CSE373: Data Structures & Algorithms 1
2 .Course Logistics HW4 preliminary scripts out HW5 out more graphs! Last main course topic this week: Sorting! Final exam in 2 weeks! 2 CSE373: Data Structures & Algorithms
3 .Introduction to Sorting Why study sorting? It uses information theory and is good algorithm practice! Different sorting al gorithms have different trade -offs No single “best” sort for all scenarios Knowing one way to sort just isn’t enough Not usually asked about on tech interviews .. . but if it comes up, you look bad if you can’t talk about it 3 CSE373: Data Structures & Algorithms
4 .More Reasons to Sort General technique in computing: Preprocess data to make subsequent operations faster Example: Sort the data so that you can Find the k th largest in constant time for any k Perform binary search to find elements in logarithmic time Whether the performance of the preprocessing matters depends on How often the data will change (and how much it will change) How much data there is 4 CSE373: Data Structures & Algorithms
5 .Definition: Comparison Sort A computational problem with the following input and output Input: An array A of length n comparable elements Output : The same array A, containing the same elements where: for any i and j where 0 i < j < n then A[ i ] A[j] 5 CSE373: Data Structures & Algorithms
6 .More Definitions In-Place Sort: A sorting algorithm is in-place if it requires only O(1) extra space to sort the array. Usually modifies input array Can be useful: lets us minimize memory Stable Sort : A sorting algorithm is stable if any equal items remain in the same relative order before and after the sort. Items that ’compare’ the same might not be exact duplicates Might want to sort on some, but not all attributes of an item Can be useful to sort on one attribute first, then another one 6 CSE373: Data Structures & Algorithms
7 .Stable Sort Example Input : [ (8, "fox"), (9, "dog"), (4, "wolf"), (8, "cow")] Compare function: compare pairs by number only Output ( stable sort): [(4, "wolf"), (8, "fox") , (8, "cow") , (9, "dog") ] Output ( unstable sort): [(4, "wolf") , (8, "cow") , (8, "fox") , (9, "dog")] 7 CSE373: Data Structures & Algorithms
8 .Lots of algorithms for sorting... 8 CSE373: Data Structures & Algorithms Quicksort, Merge sort, In-place merge sort, Heap sort, Insertion sort , Intro sort, Selection sort, Timsort , Cubesort , Shell sort , Bubble sort, Binary tree sort, Cycle sort, Library sort, Patience sorting , Smoothsort , Strand sort, Tournament sort, Cocktail sort , Comb sort, Gnome sort, Block sort, Stackoverflow sort , Odd -even sort, Pigeonhole sort, Bucket sort, Counting sort , Radix sort, Spreadsort , Burstsort , Flashsort , Postman sort, Bead sort , Simple pancake sort, Spaghetti sort, Sorting network , Bitonic sort, Bogosort , Stooge sort, Insertion sort, Slow sort , Rainbow sort...
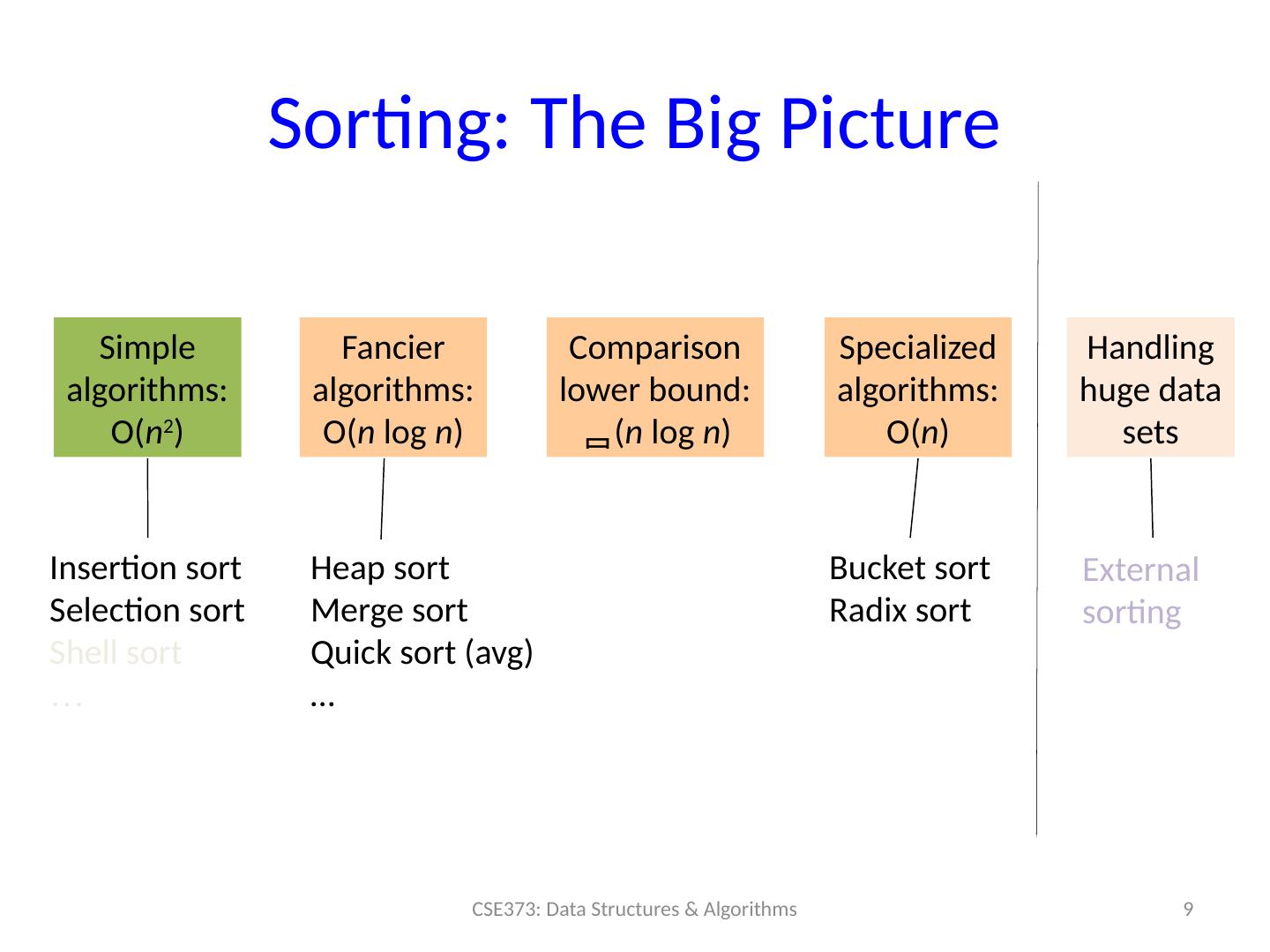
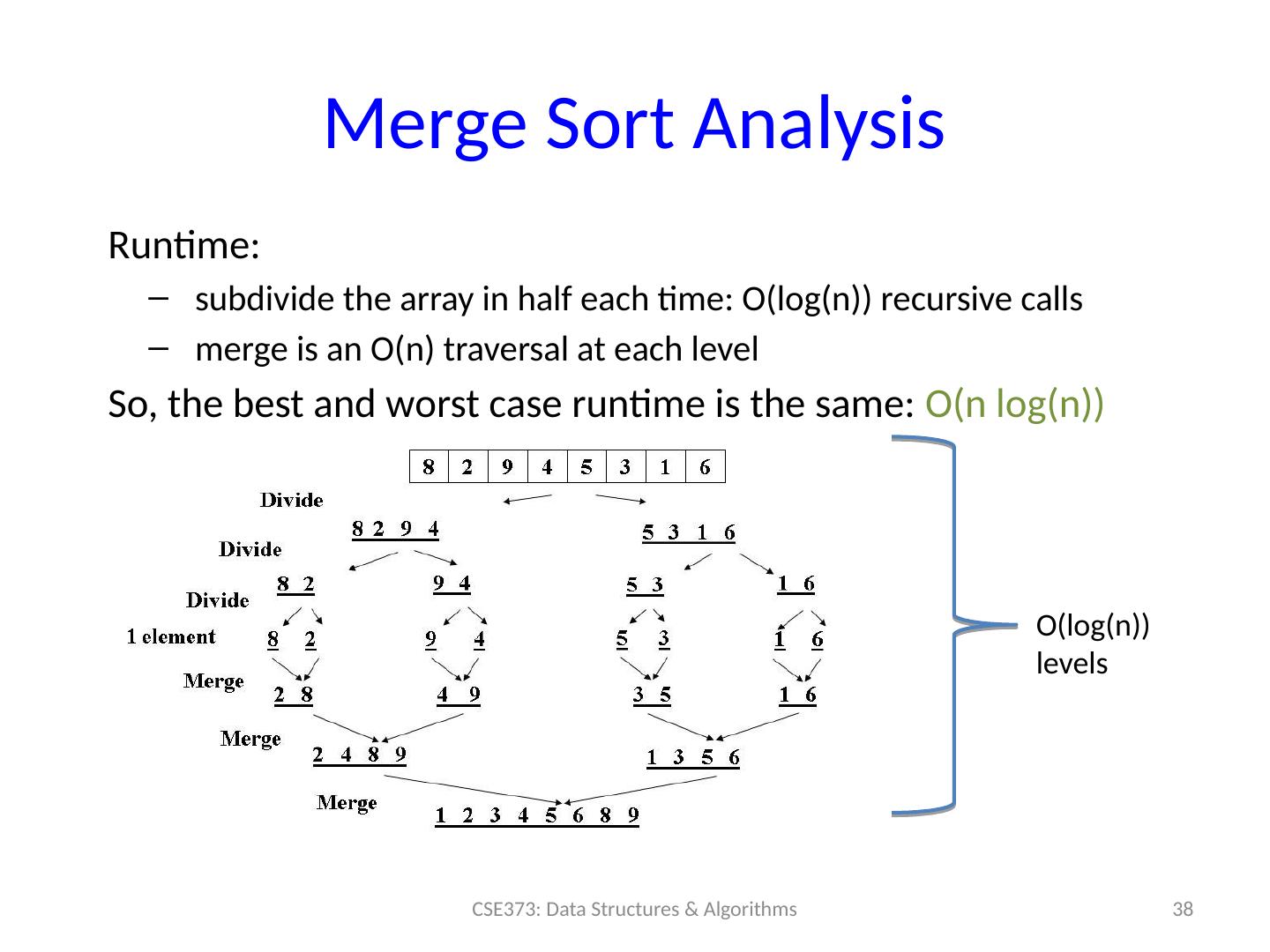
9 .Sorting: The Big Picture 9 CSE373: Data Structures & Algorithms Simple algorithms: O( n 2 ) Fancier algorithms: O( n log n ) Comparison lower bound: ( n log n ) Specialized algorithms: O( n ) Handling huge data sets Insertion sort Selection sort Shell sort … Heap sort Merge sort Quick sort ( avg ) … Bucket sort Radix sort External sorting
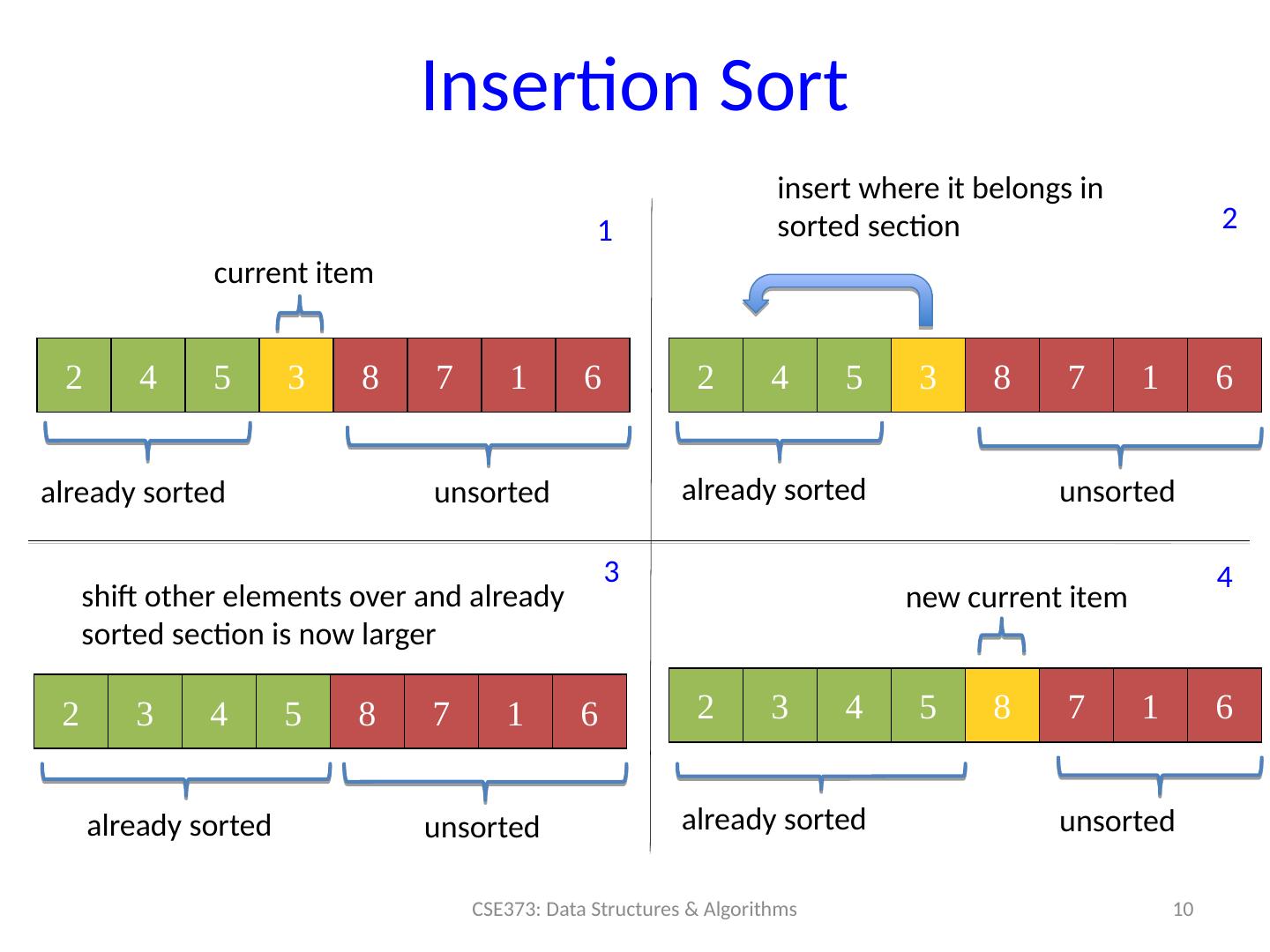
10 .Insertion Sort 10 CSE373: Data Structures & Algorithms 2 4 5 3 8 7 1 6 already sorted unsorted current item 2 4 5 3 8 7 1 6 already sorted unsorted 2 3 4 5 8 7 1 6 already sorted unsorted 2 3 4 5 8 7 1 6 already sorted unsorted insert where it belongs in sorted section shift other elements over and already sorted section is now larger new current item 1 2 3 4
11 .Insertion Sort Idea: At step k , put the k th element in the correct position among the first k elements for ( int i = 0; i < n; i ++) { / / Find index to insert into int newIndex = findPlace ( i ); / / Insert and shift nodes over shift ( newIndex , i ); } Loop invariant : when loop index is i , first i elements are sorted Runt ime ? Best-case _____ Worst-case _____ Average - case ____ Stable? _____ In- place? _____ 11 CSE373: Data Structures & Algorithms
12 .Insertion Sort Idea: At step k , put the k th element in the correct position among the first k elements for ( int i = 0; i < n; i ++) { / / Find index to insert into int newIndex = findPlace ( i ); / / Insert and shift nodes over shift ( newIndex , i ); } Loop invariant : when loop index is i , first i elements are sorted Runt ime ? Best-case O(n) Worst-case O(n 2 ) Average-case O(n 2 ) start sorted start reverse sorted ( see text) Stable? Depends on implementation. Usually. In-place? Yes 12 CSE373: Data Structures & Algorithms
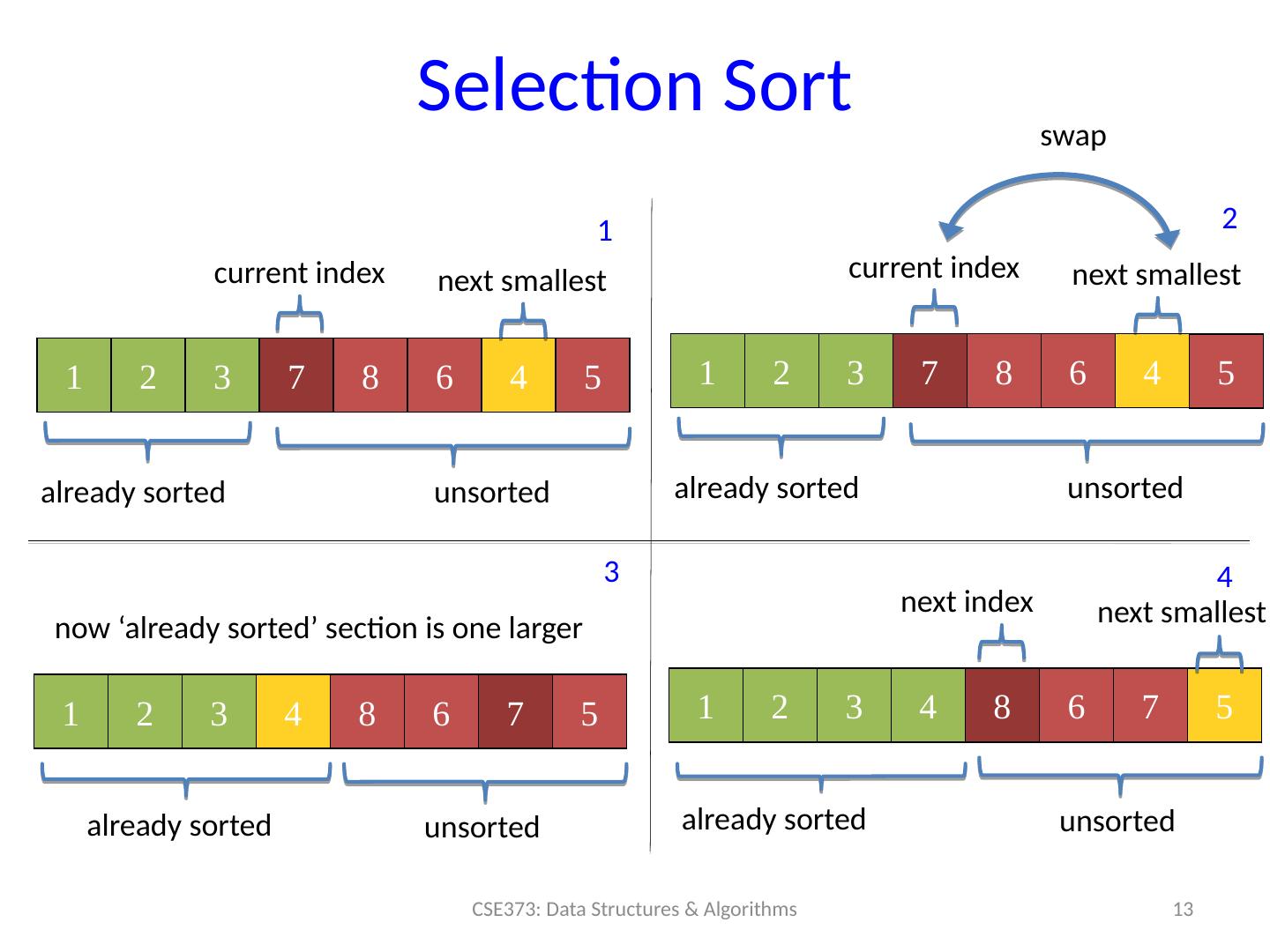
13 .Selection Sort 13 CSE373: Data Structures & Algorithms 1 2 3 7 8 6 4 5 already sorted unsorted current index 1 2 3 4 8 6 7 5 already sorted unsorted 1 2 3 4 8 6 7 5 already sorted unsorted now ‘already sorted’ section is one larger next index 1 2 3 4 next smallest 1 2 3 7 8 6 4 already sorted unsorted 5 current index next smallest swap next smallest
14 .Selection Sort Idea: At step k , find the smallest element among the not-yet-sorted elements and put it at position k for ( int i = 0; i < n; i ++) { / / Find next smallest int newIndex = findNextMin ( i ); / / Swap current and next smallest swap ( newIndex , i ); } Loop invariant : when loop index is i , first i elements are sorted Runt ime ? Best-case _____ Worst-case _____ Average-case ____ Stable? _____ In- place? _____ 14 CSE373: Data Structures & Algorithms
15 .Selection Sort Idea: At step k , find the smallest element among the not-yet-sorted elements and put it at position k for ( int i = 0; i < n; i ++) { / / Find next smallest int newIndex = findNextMin ( i ); / / Swap current and next smallest swap ( newIndex , i ); } Loop invariant : when loop index is i , first i elements are sorted Runt ime ? Best- case, Worst - case, and Average - case O(n 2 ) Stable? Depends on implementation. Usually. In- place? Yes 15 CSE373: Data Structures & Algorithms
16 .Insertion Sort vs. Selection Sort Have the same worst-case and average-case asymptotic complexity Insertion-sort has better best-case complexity; preferable when input is “mostly sorted” Useful for small arrays or for mostly sorted input 16 CSE373: Data Structures & Algorithms
17 .Bubble Sort for n iterations: ‘bubble’ next largest element to the end of the unsorted section, by doing a series of swaps Not intuitive – It’s unlikely that you’d come up with bubble sort Not good asymptotic complexity: O ( n 2 ) It’s not particularly efficient with respect to common factors Basically, almost never is better than insertion or selection sort. 17 CSE373: Data Structures & Algorithms
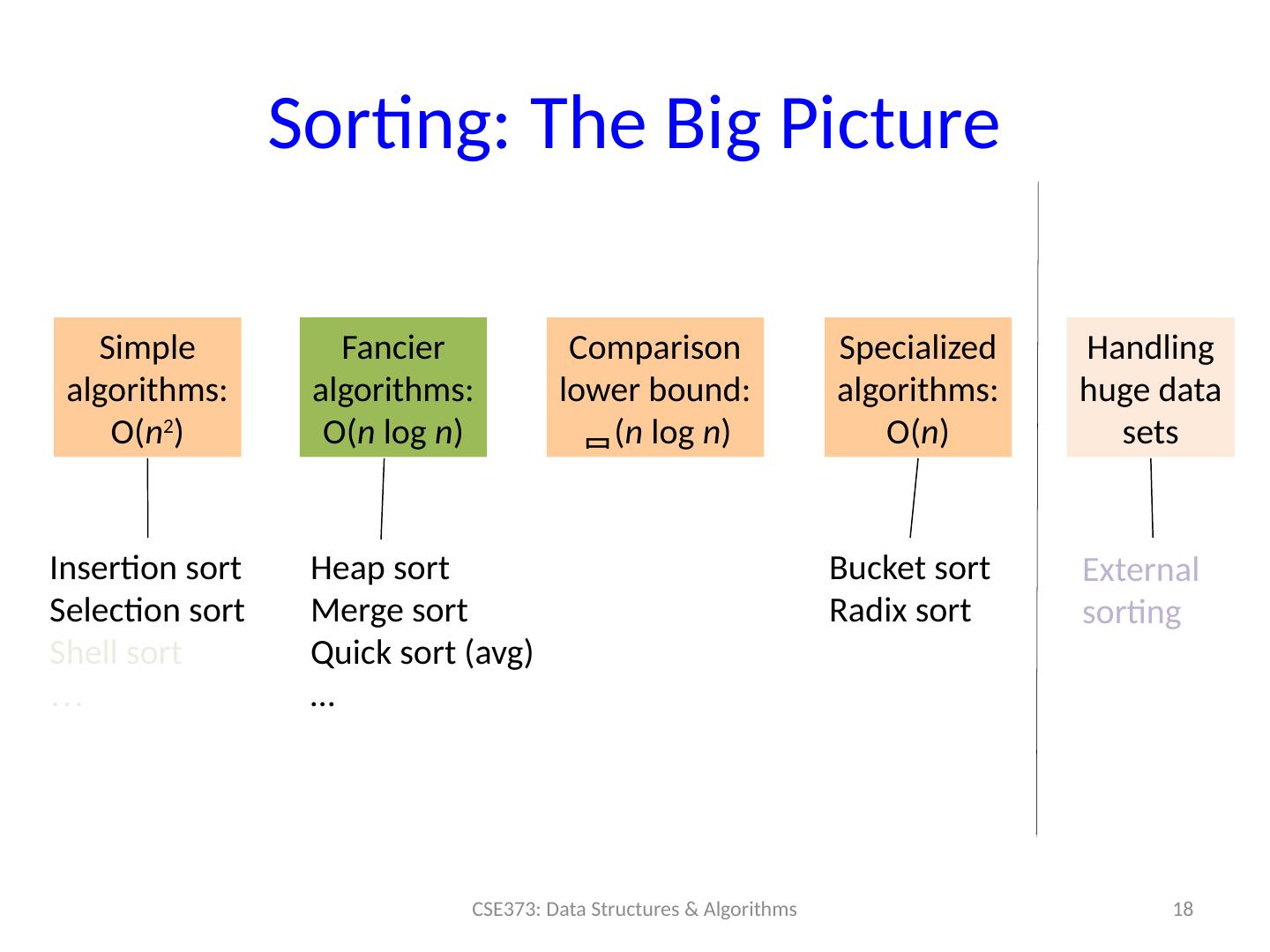
18 .Sorting: The Big Picture 18 CSE373: Data Structures & Algorithms Simple algorithms: O( n 2 ) Fancier algorithms: O( n log n ) Comparison lower bound: ( n log n ) Specialized algorithms: O( n ) Handling huge data sets Insertion sort Selection sort Shell sort … Heap sort Merge sort Quick sort ( avg ) … Bucket sort Radix sort External sorting
19 .Heap Sort Idea: buildHeap then call deleteMin n times E[] input = buildHeap (...); E[] output = new E[n]; for ( int i = 0; i < n; i ++) { output [ i ] = deleteMin ( input); } Runt ime ? Best -case ___ Worst - case ___ Average-case ___ Stable? _____ In- place? _____ 19 CSE373: Data Structures & Algorithms
20 .Heap Sort Idea: buildHeap then call deleteMin n times E[] input = buildHeap (...); E[] output = new E[n]; for ( int i = 0; i < n; i ++) { output [ i ] = deleteMin ( input); } Runt ime ? Best-case, Worst-case, and Average-case : O ( n log (n)) Stable? No In- place? No. But it could be, with a slight trick... 20 CSE373: Data Structures & Algorithms
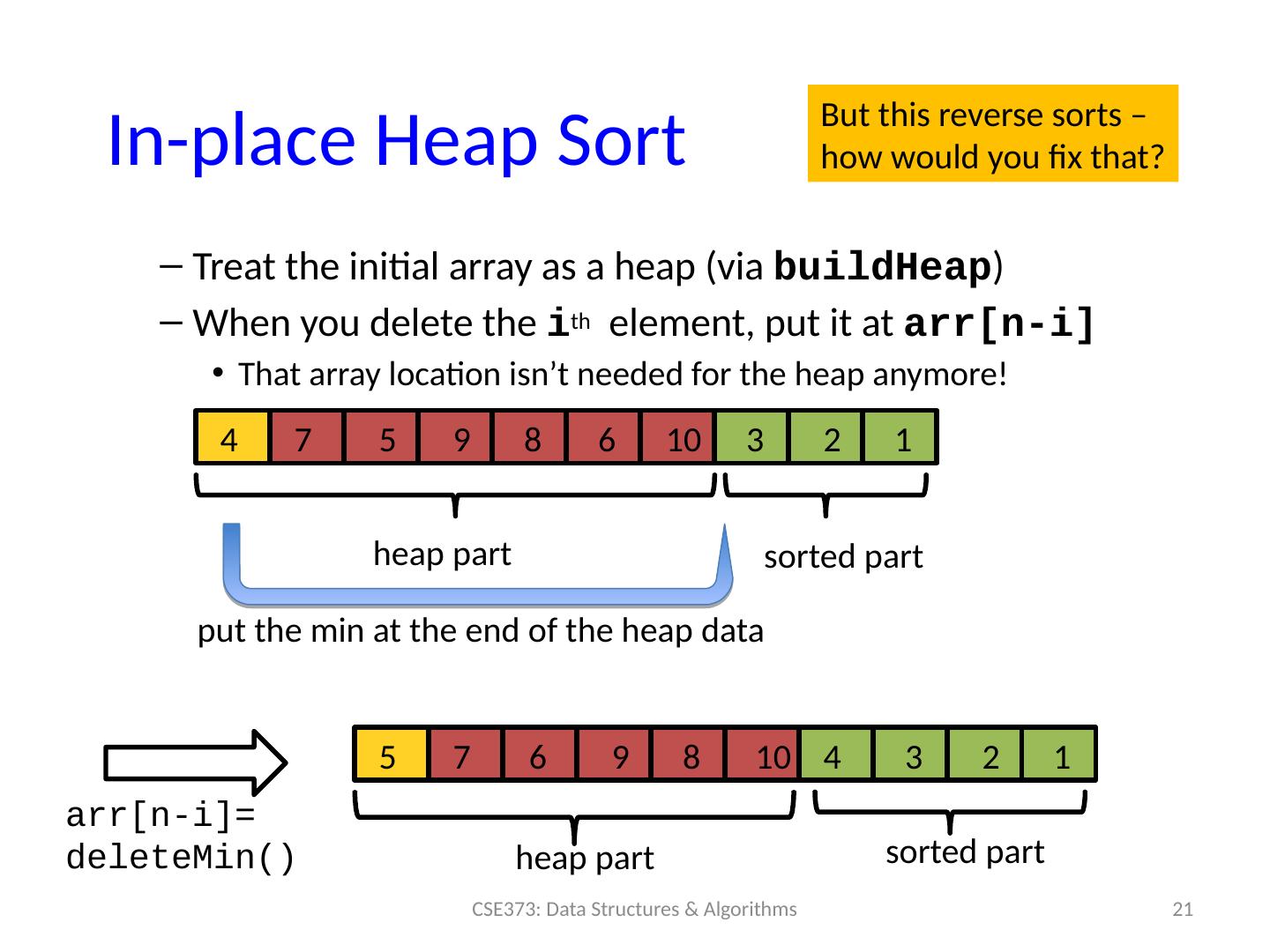
21 .In-place Heap S ort Treat the initial array as a heap (via buildHeap ) When you delete the i th element, put it at arr [n- i ] That array location isn’t needed for the heap anymore! 21 CSE373: Data Structures & Algorithms 4 7 5 9 8 6 10 3 2 1 sorted part heap part arr [n- i ]= deleteMin () 5 7 6 9 8 10 4 3 2 1 sorted part heap part But this reverse sorts – how would you fix that? put the min at the end of the heap data
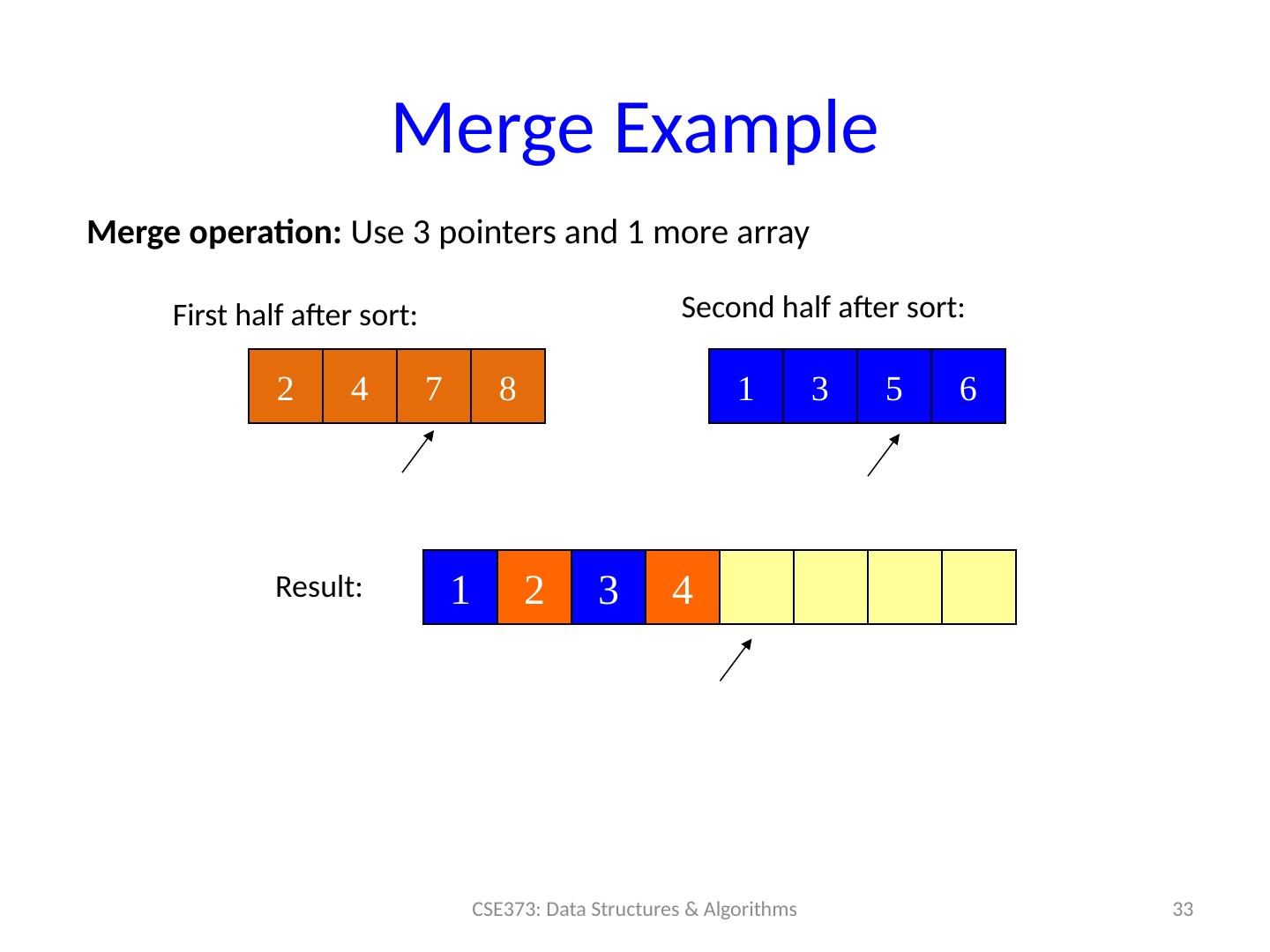
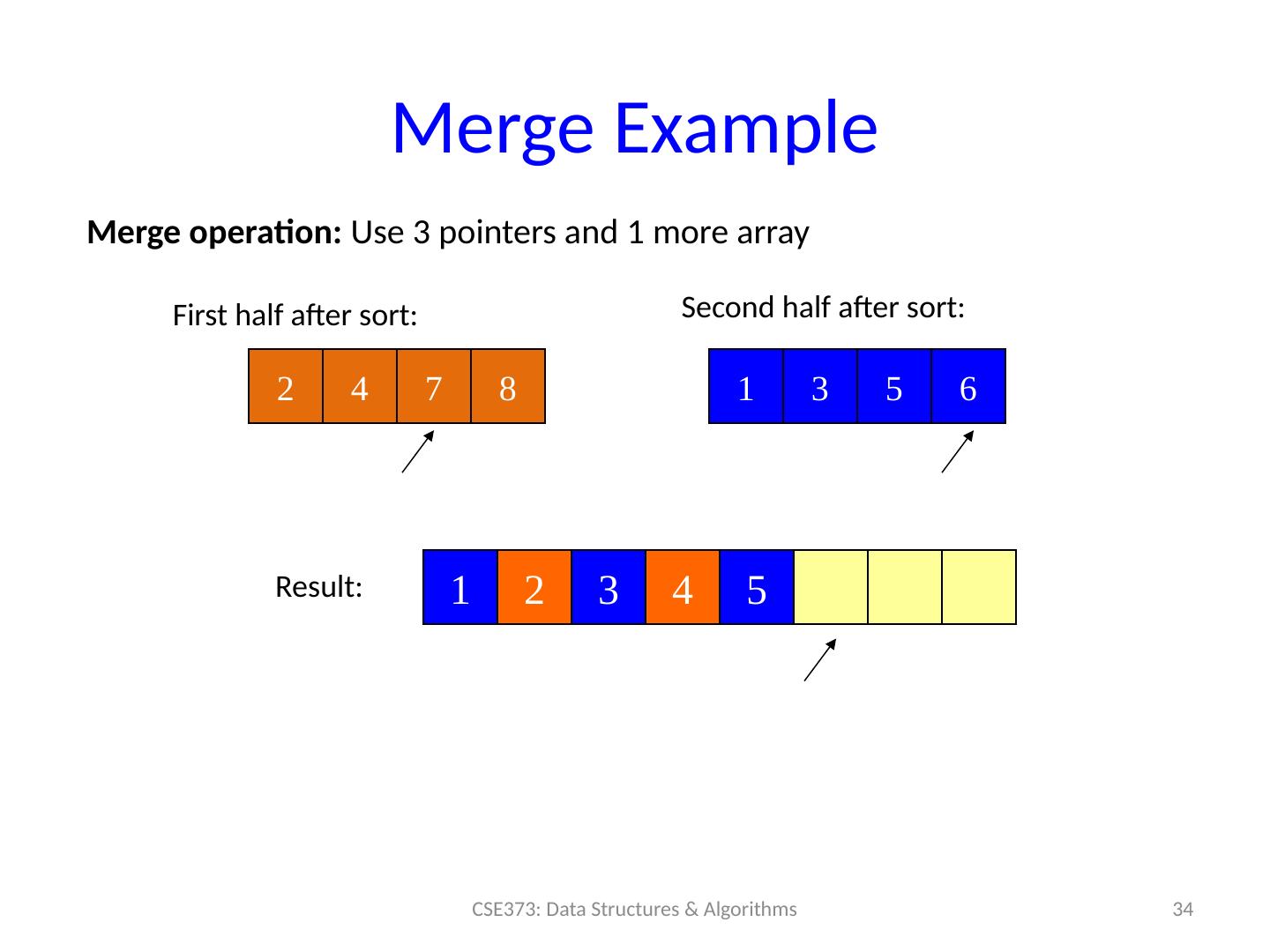
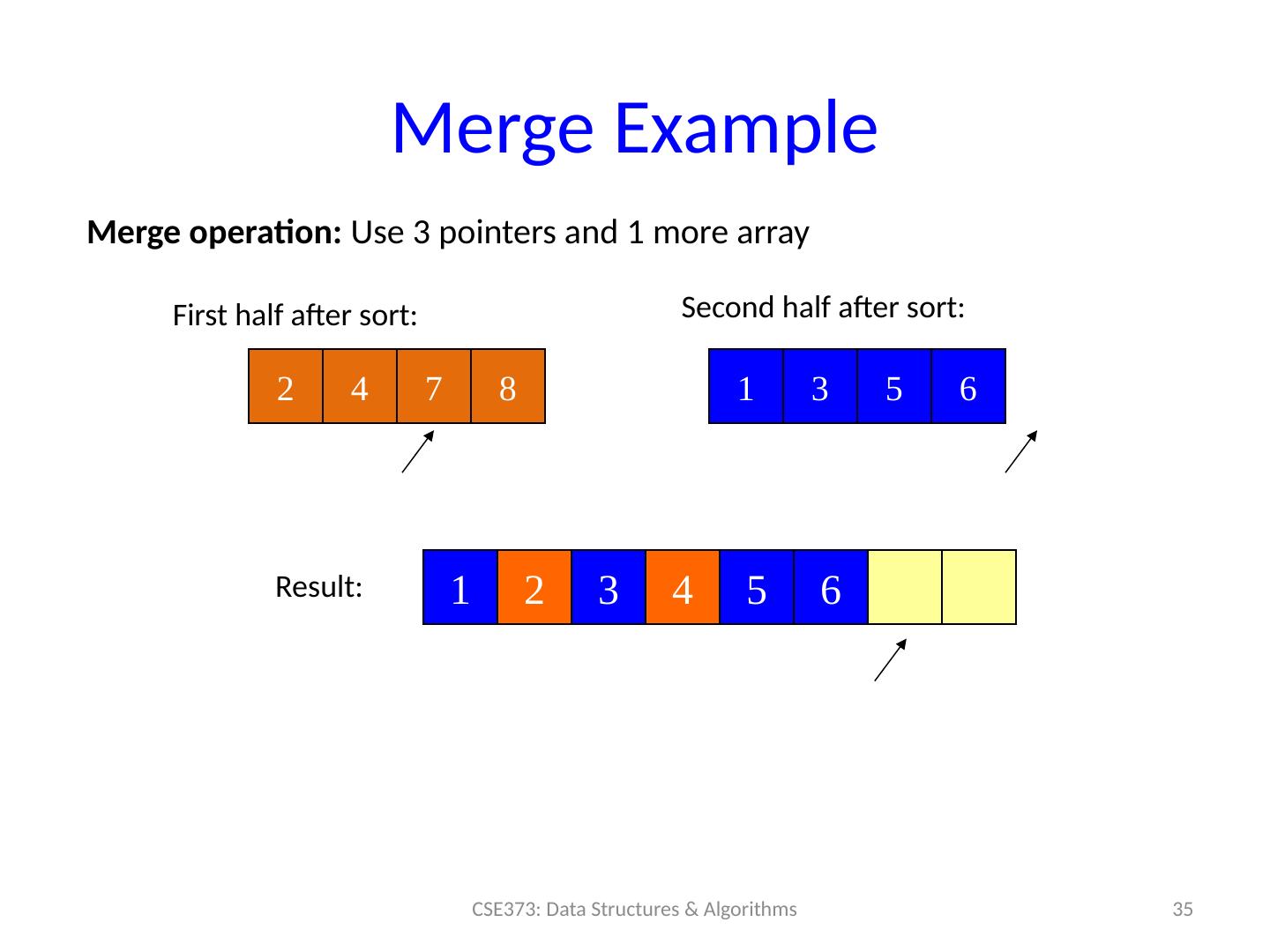
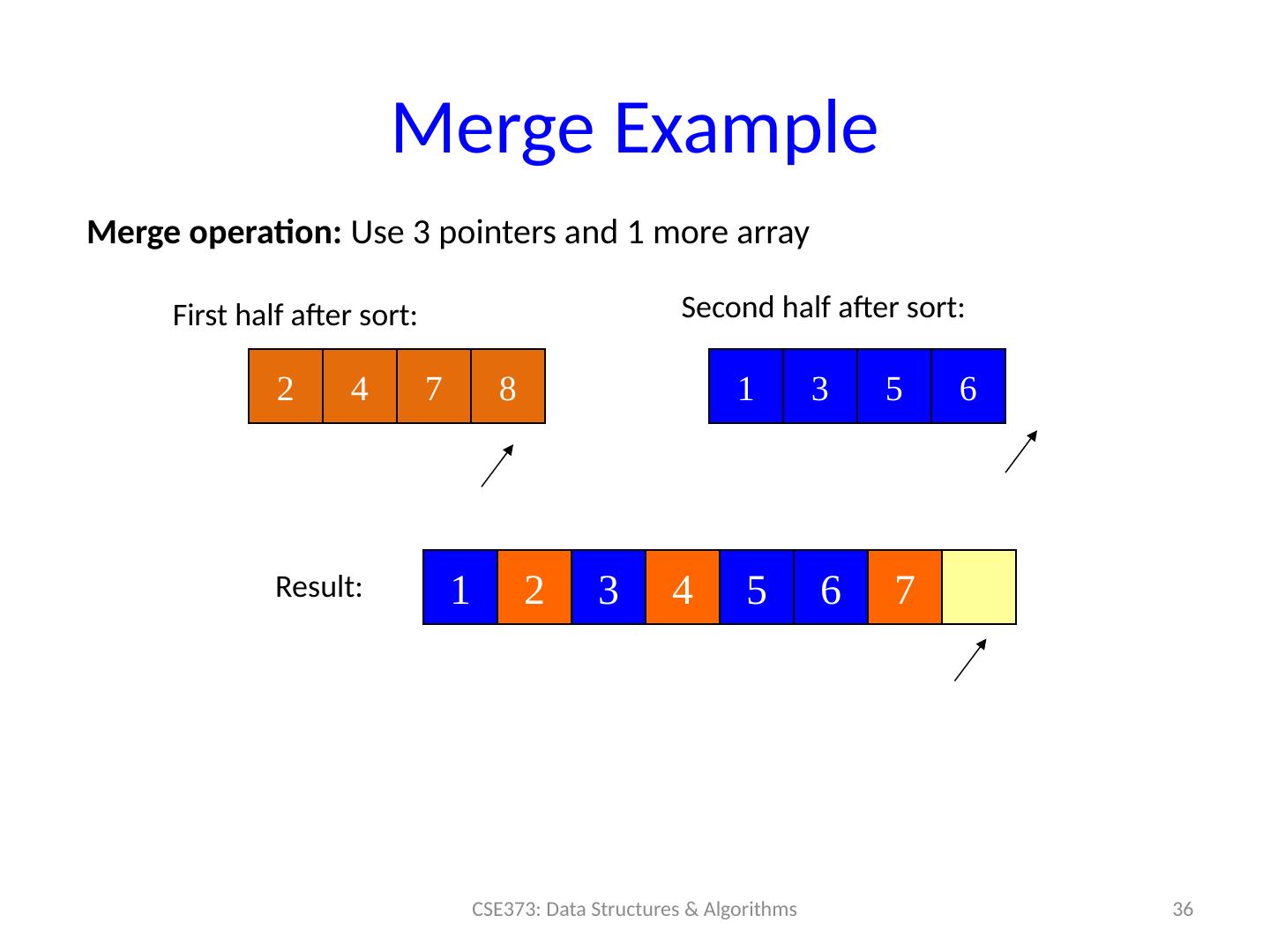
22 .“AVL sort”? “ Hash sort” ? AVL Tree : sure, we can also use an AVL tree to: insert each element: total time O ( n log n ) Repeatedly deleteMin : total time O ( n log n ) Better: in-order traversal O ( n ), but still O ( n log n ) overall But this cannot be done in-place and has worse constant factors than heap sort Hash Structure : don’t even think about trying to sort with a hash table ! Finding min item in a hashtable is O (n), so this would be a slower, more complicated selection sort 22 CSE373: Data Structures & Algorithms
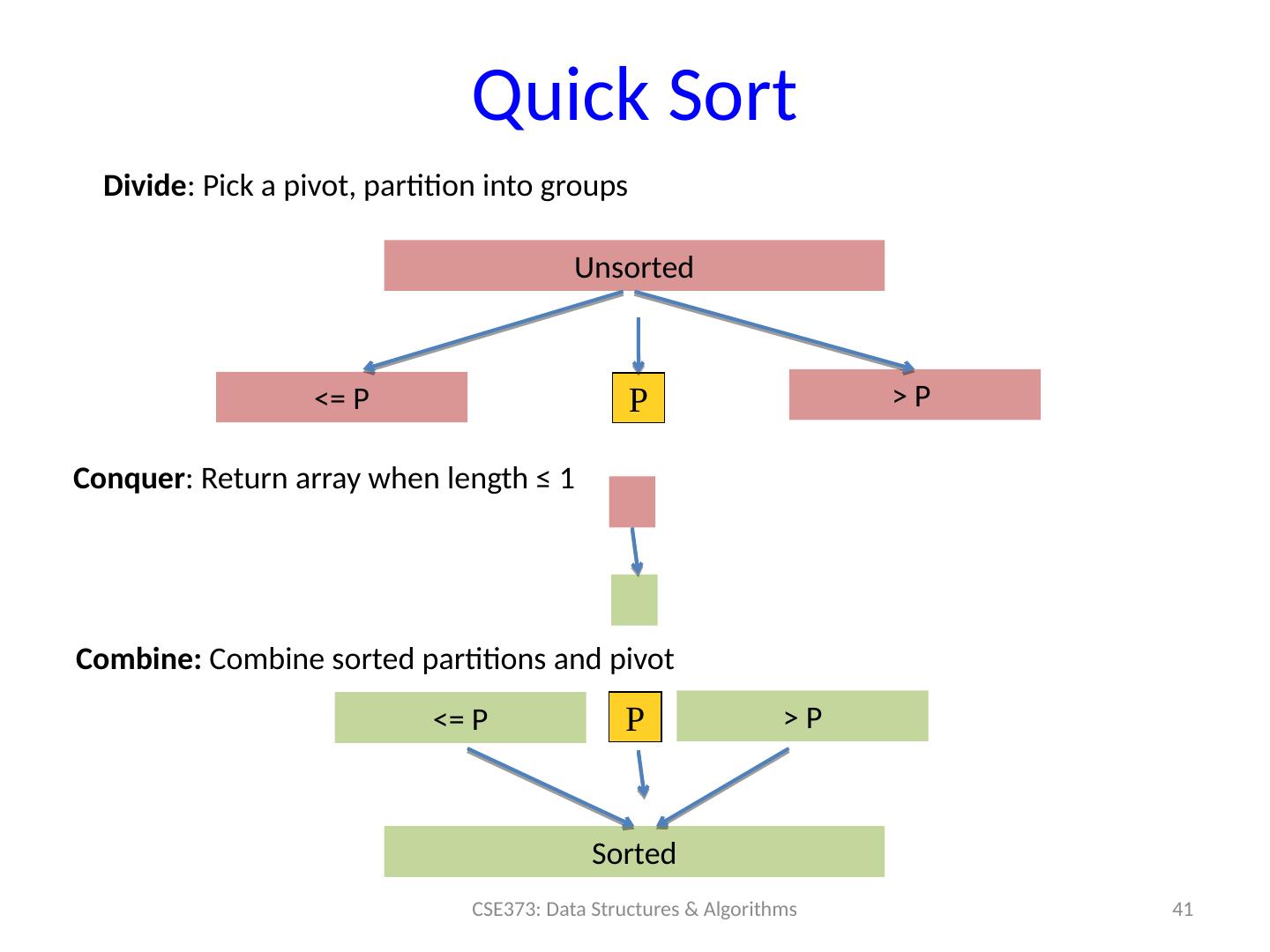
23 .Divide and conquer Divide-and-conquer is a useful technique for solving many kinds of problems (not just sorting). It consists of the following steps: 1. Divide your work up into smaller pieces (recursively) 2. Conquer the individual pieces (as base cases) 3. Combine the results together (recursively) 23 CSE373: Data Structures & Algorithms algorithm (input) { if (small enough) { CONQUER , solve, and return input } else { DIVIDE input into multiple pieces RECURSE on each piece COMBINE and return results } }
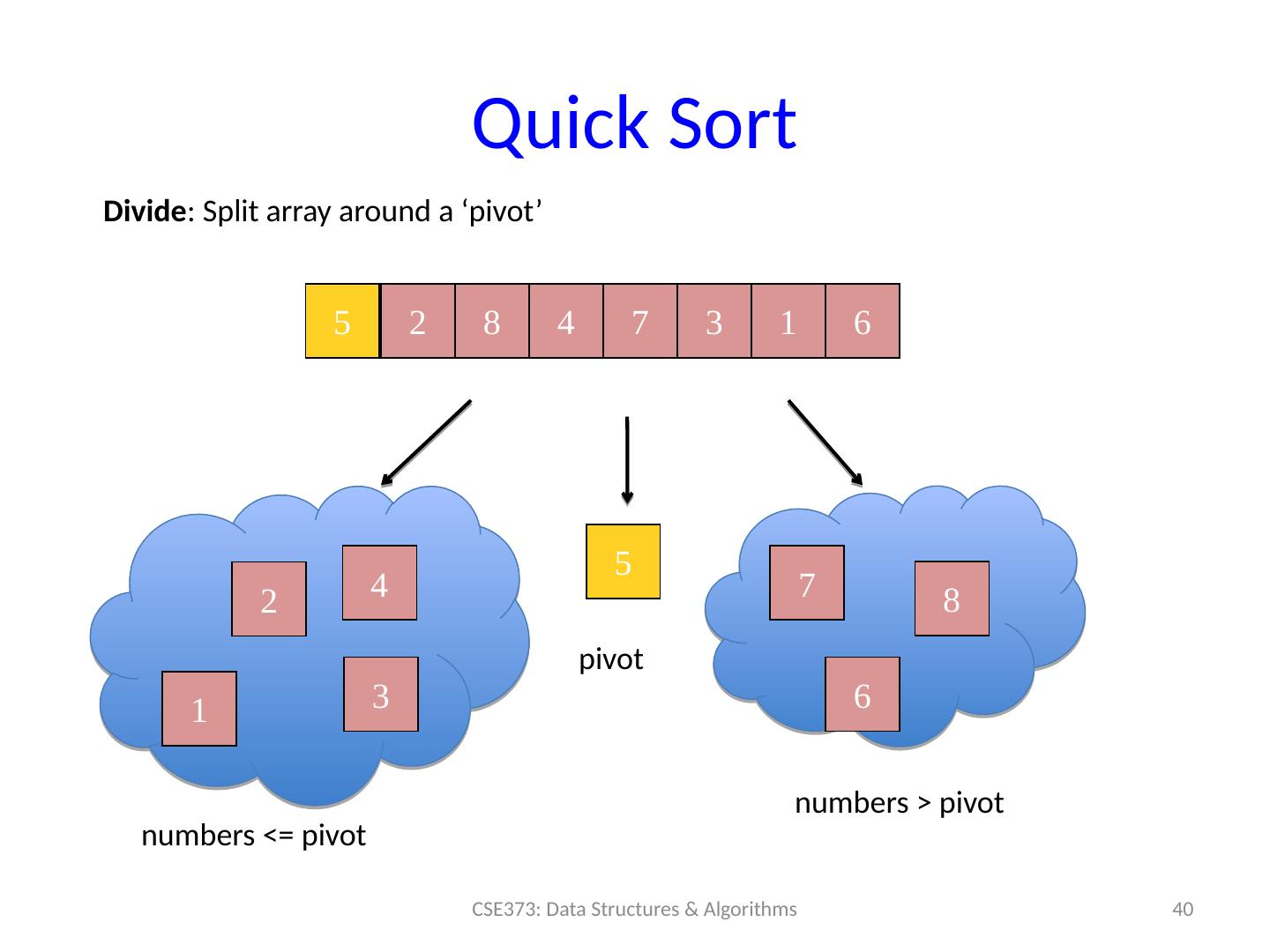
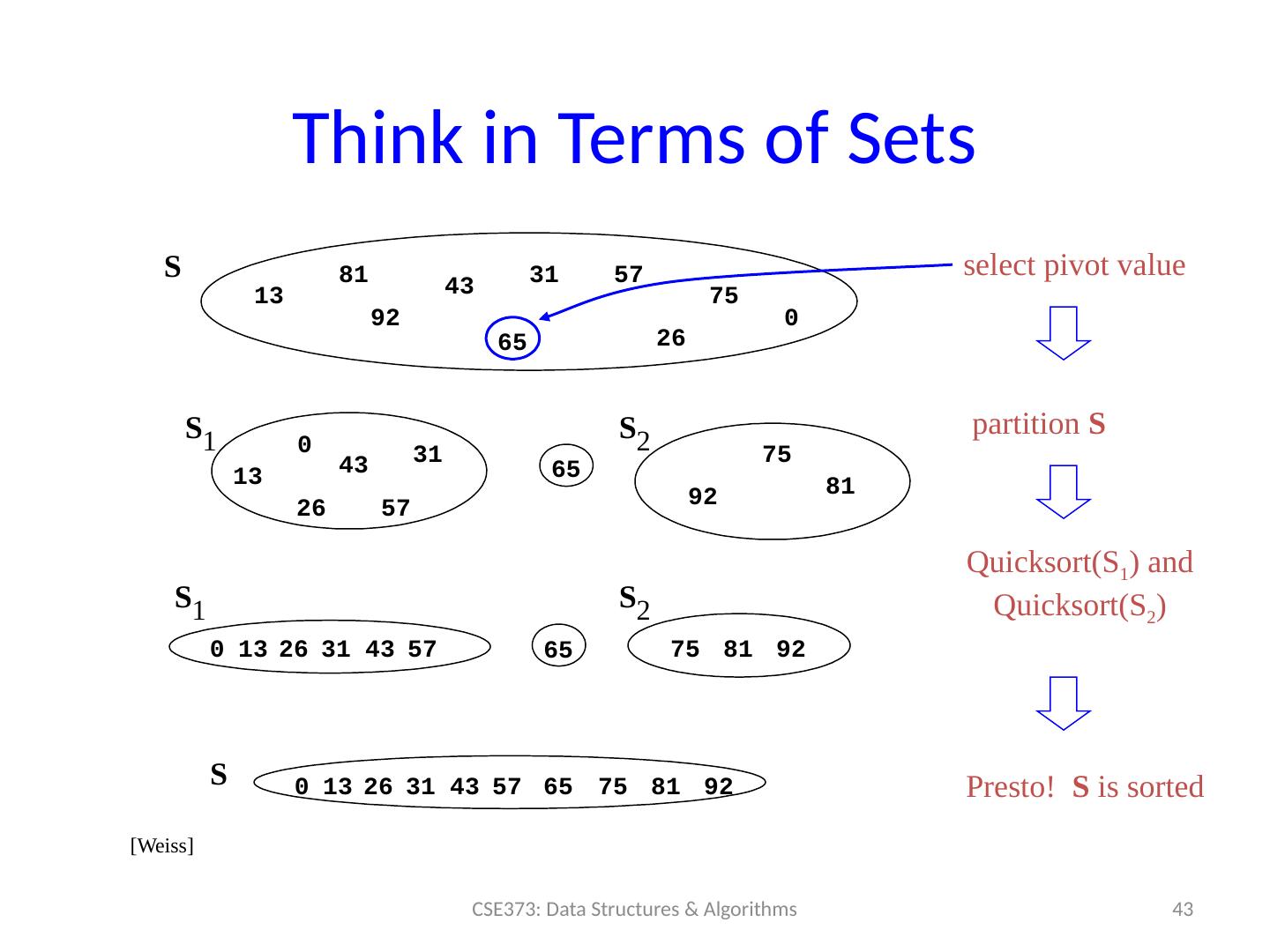
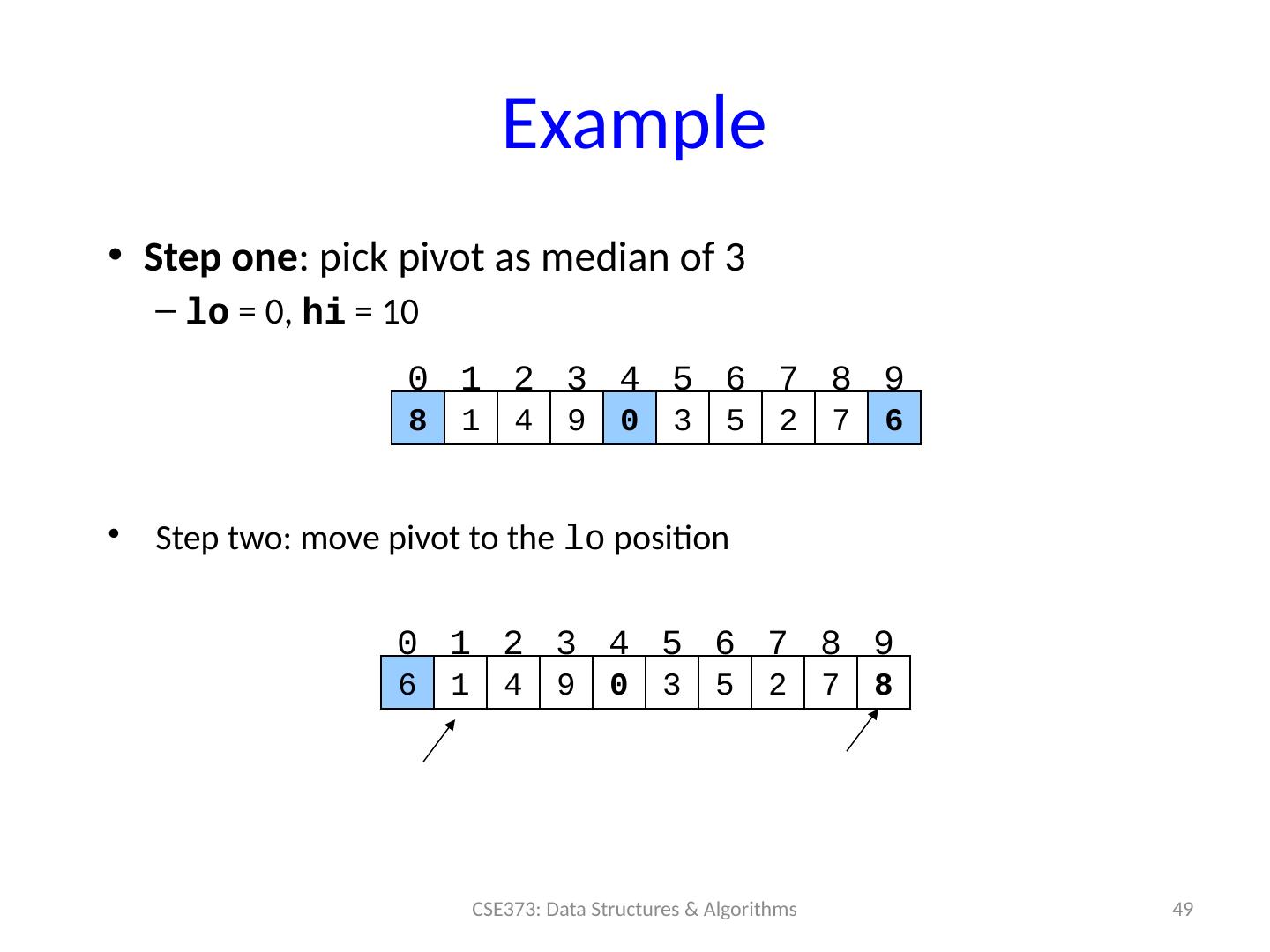
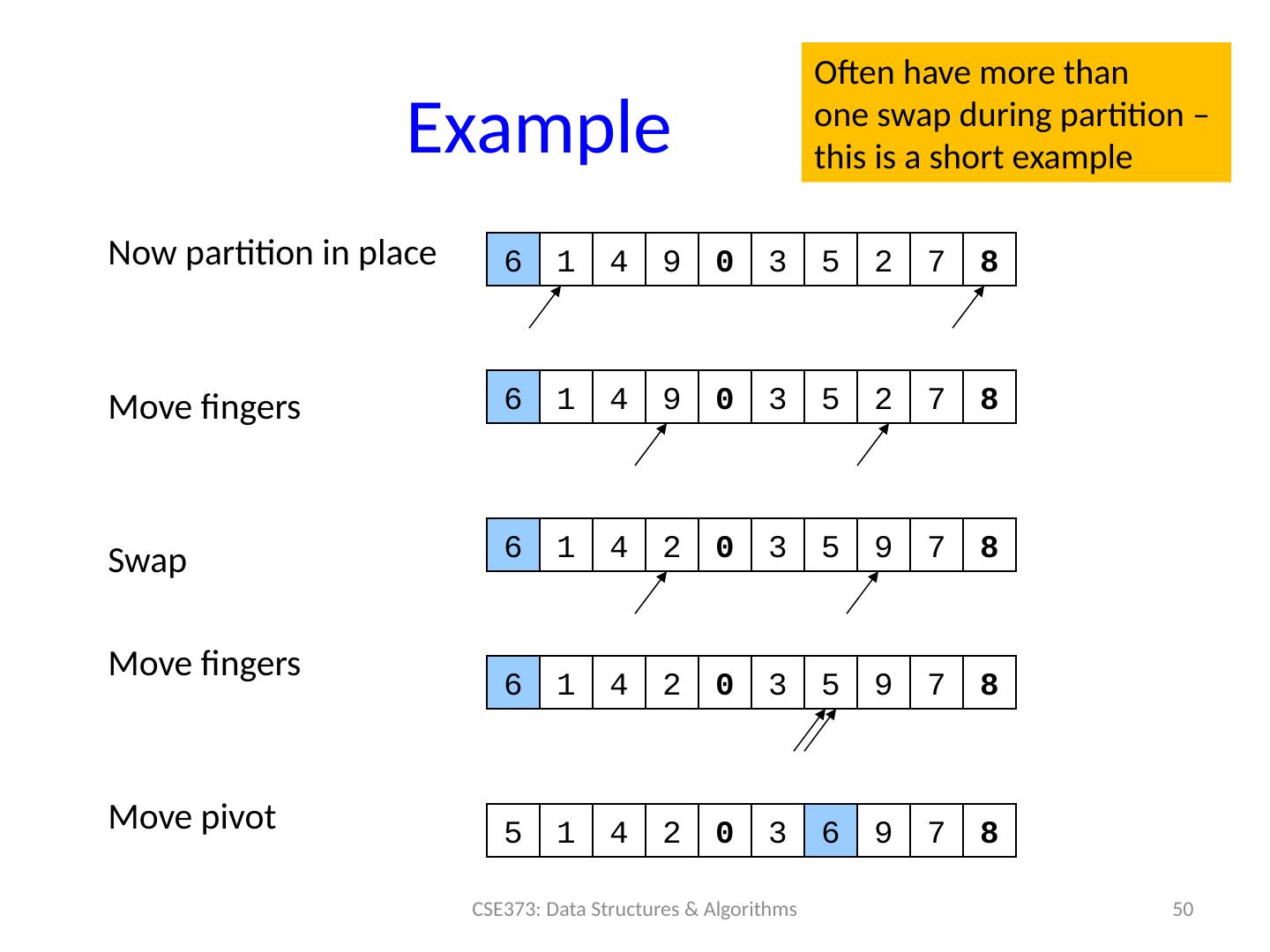
24 .Divide-and-Conquer Sorting Two great sorting methods are fundamentally divide-and- conquer Mergesort : Sort the left half of the elements (recursively) Sort the right half of the elements (recursively) Merge the two sorted halves into a sorted whole Quicksort: Pick a “pivot” element Divide elements into less-than pivot and greater-than pivot Sort the two divisions (recursively on each) Answer is: sorted -less- than....pivot....sorted -greater-than 24 CSE373: Data Structures & Algorithms
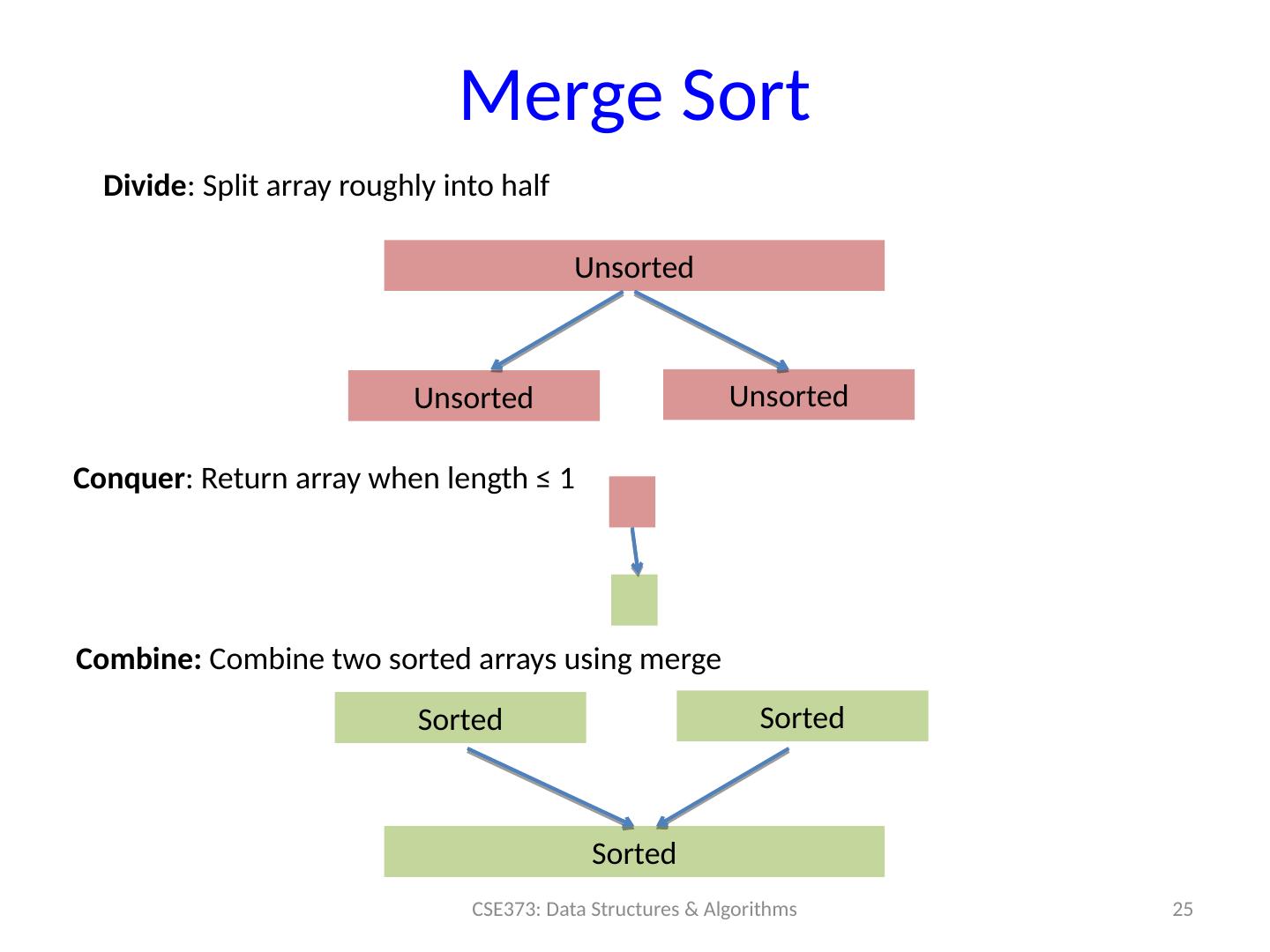
25 .Merge Sort 25 CSE373: Data Structures & Algorithms Unsorted Unsorted Unsorted Divide : Split array roughly into half S orted S orted Sorted Conquer : Return array when length ≤ 1 Combine: Combine two sorted arrays using merge
26 .Merge Sort: Pseudocode Core idea: split array in half, sort each half, merge back together . If the array has size 0 or 1, just return it unchanged 26 CSE373: Data Structures & Algorithms mergesort (input) { if ( input.length < 2) { return input; } else { smallerHalf = sort(input[0, ..., mid]); largerHalf = sort(input[mid + 1, ...]); return merge( smallerHalf , largerHalf ); } }
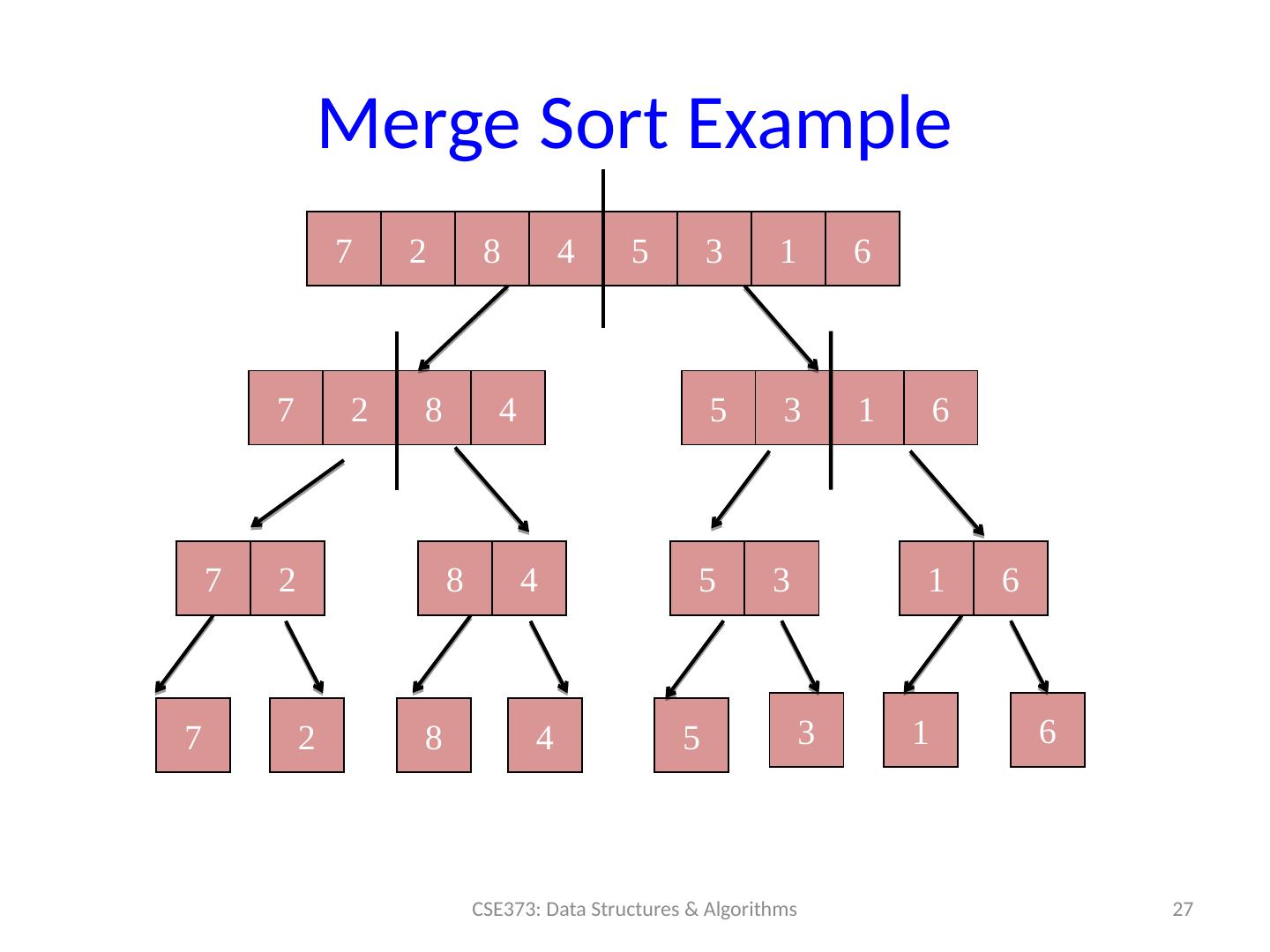
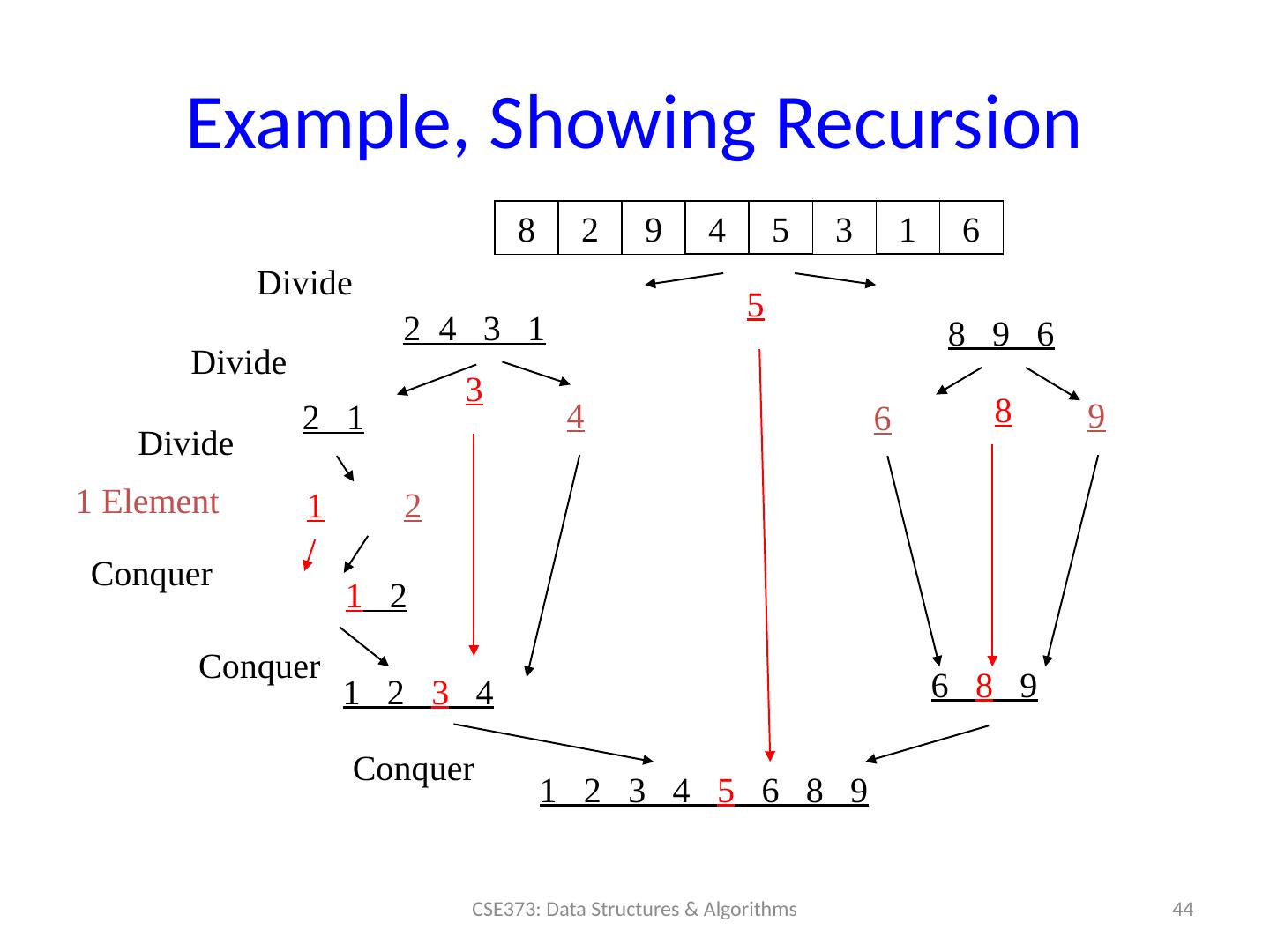
27 .Merge S ort Example 27 CSE373: Data Structures & Algorithms 7 2 8 4 5 3 1 6 7 2 8 4 7 2 7 2 8 4 8 4 5 3 1 6 5 3 1 6 5 3 1 6
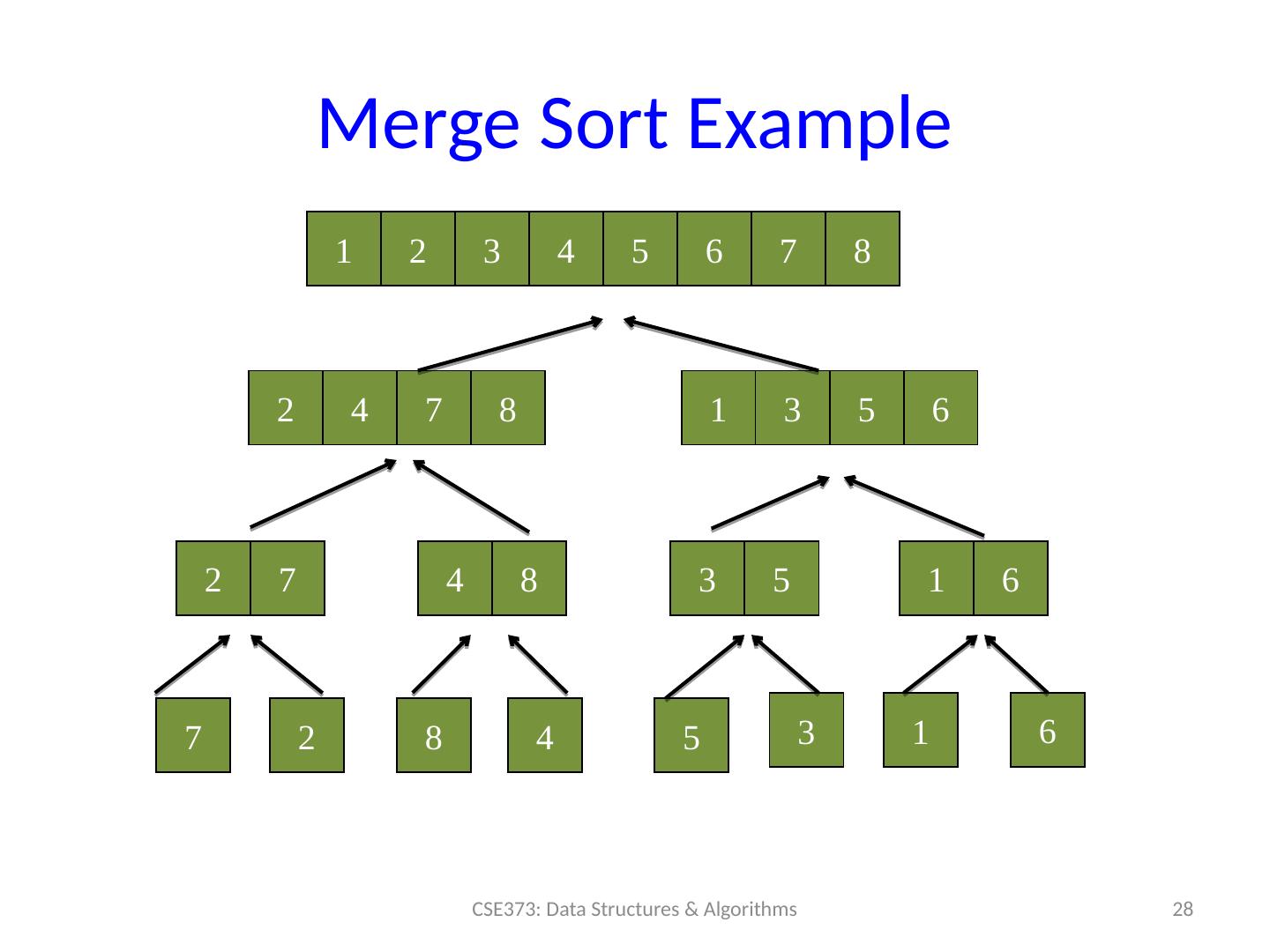
28 .Merge S ort Example 28 CSE373: Data Structures & Algorithms 1 2 3 4 5 6 7 8 2 4 7 8 2 7 7 2 4 8 8 4 1 3 5 6 3 5 1 6 5 3 1 6
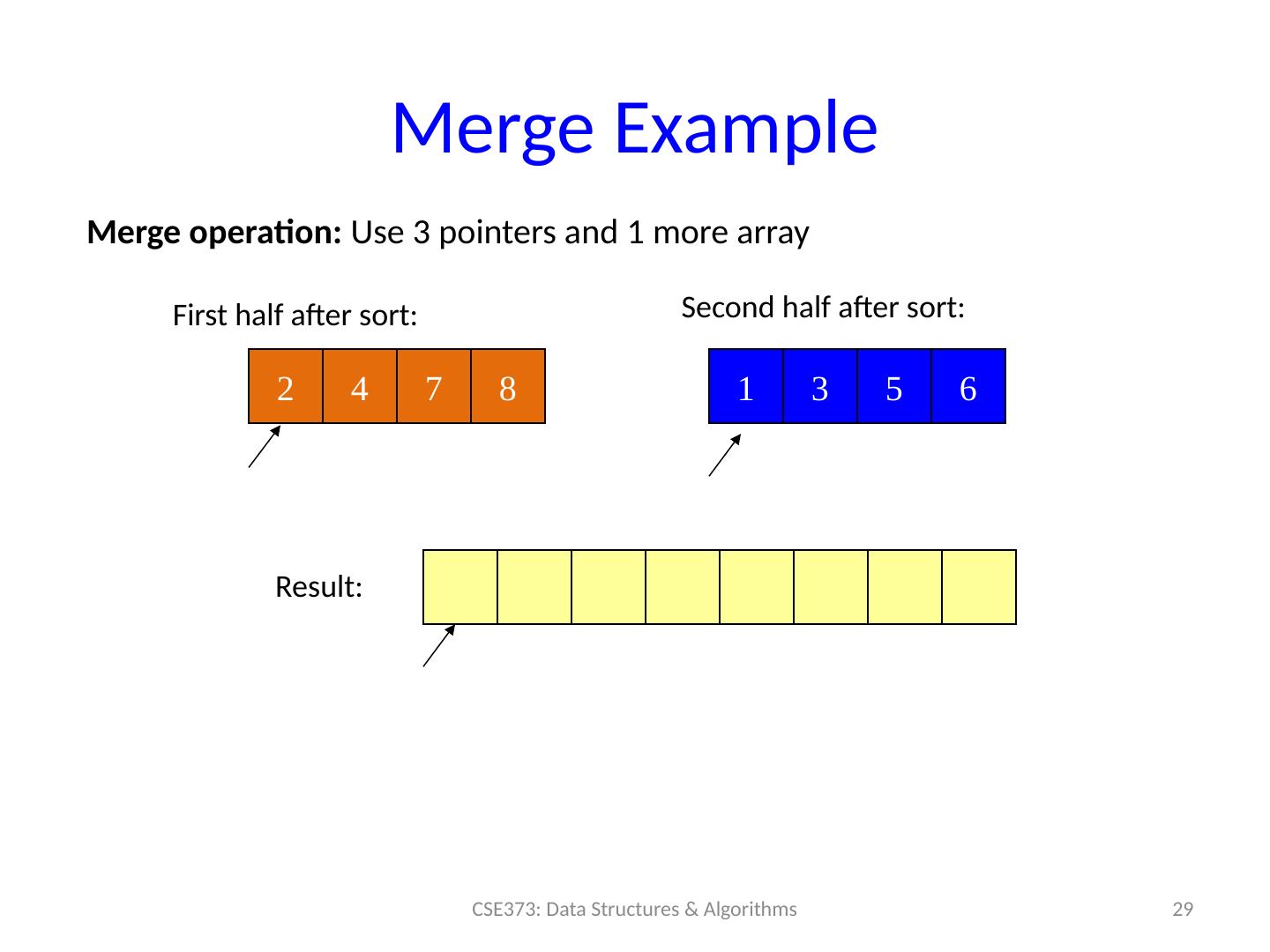
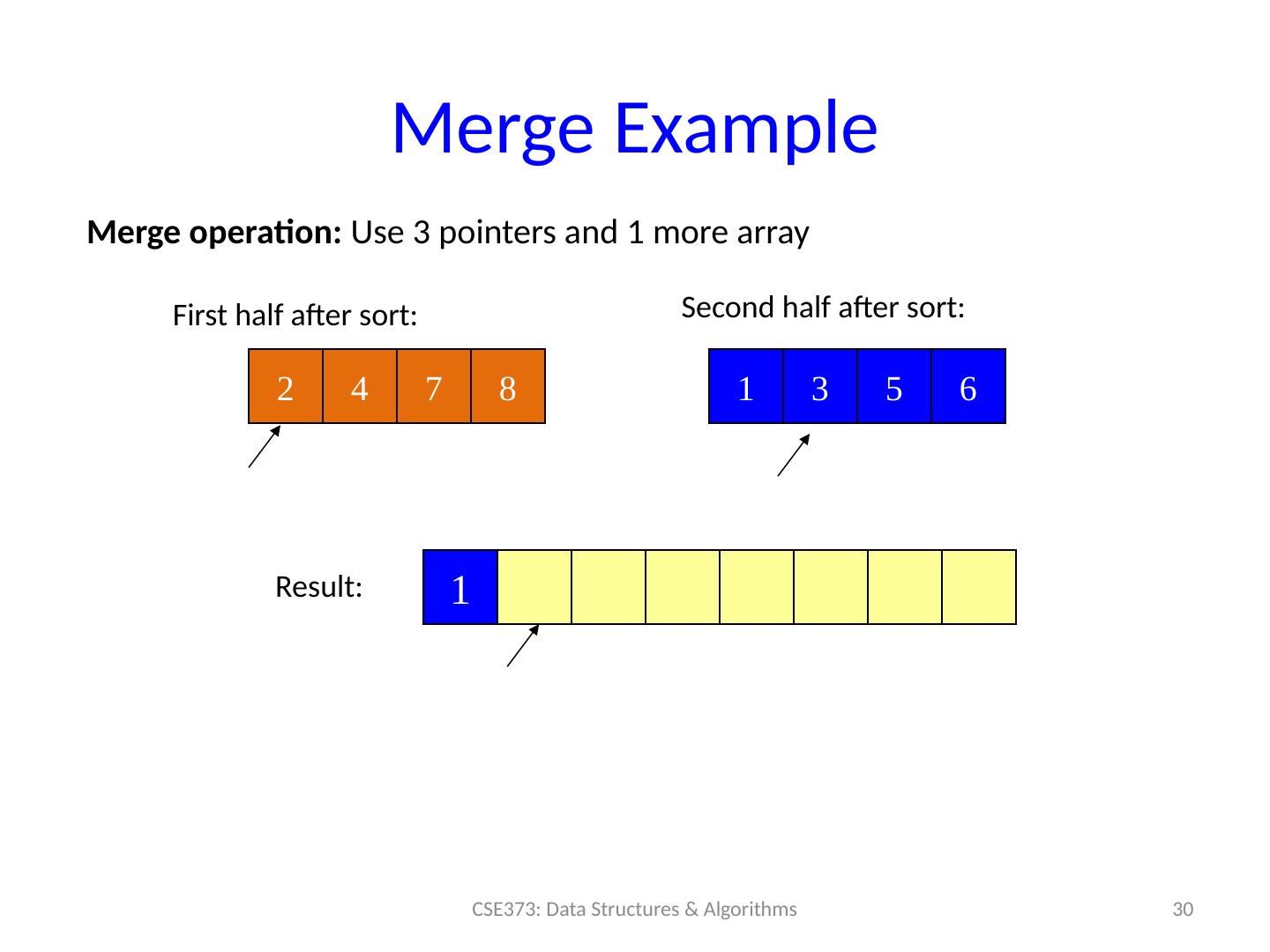
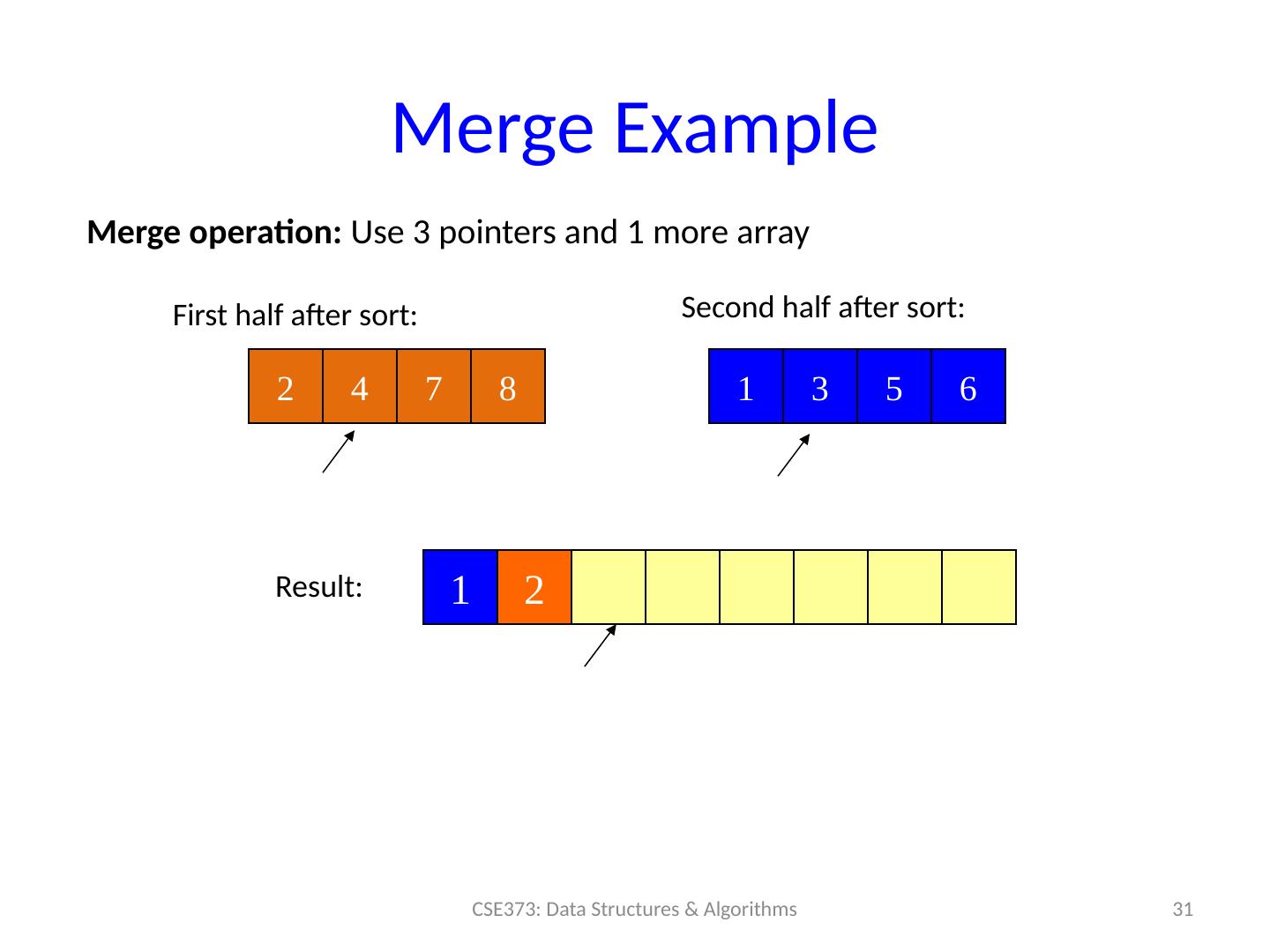
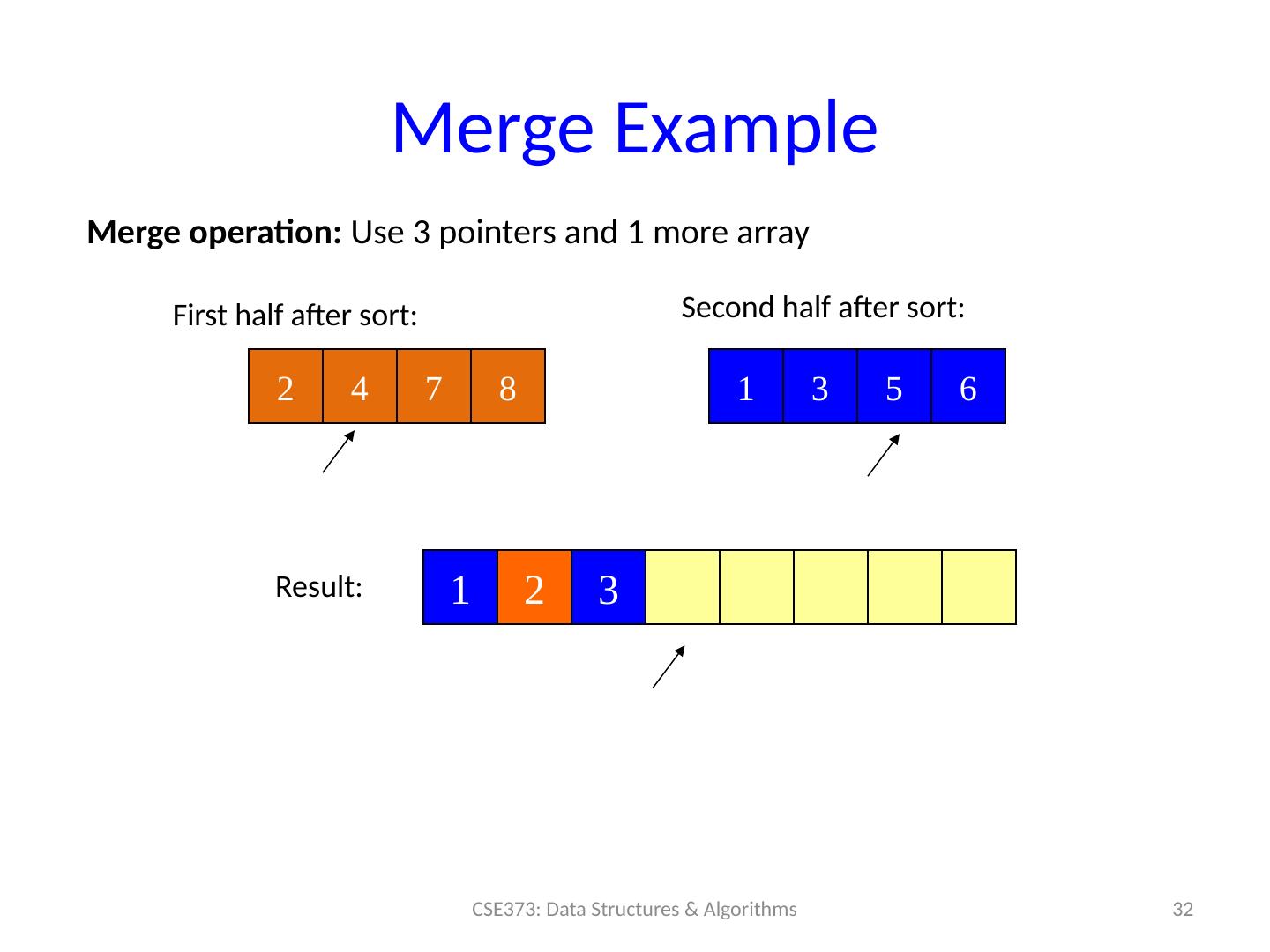
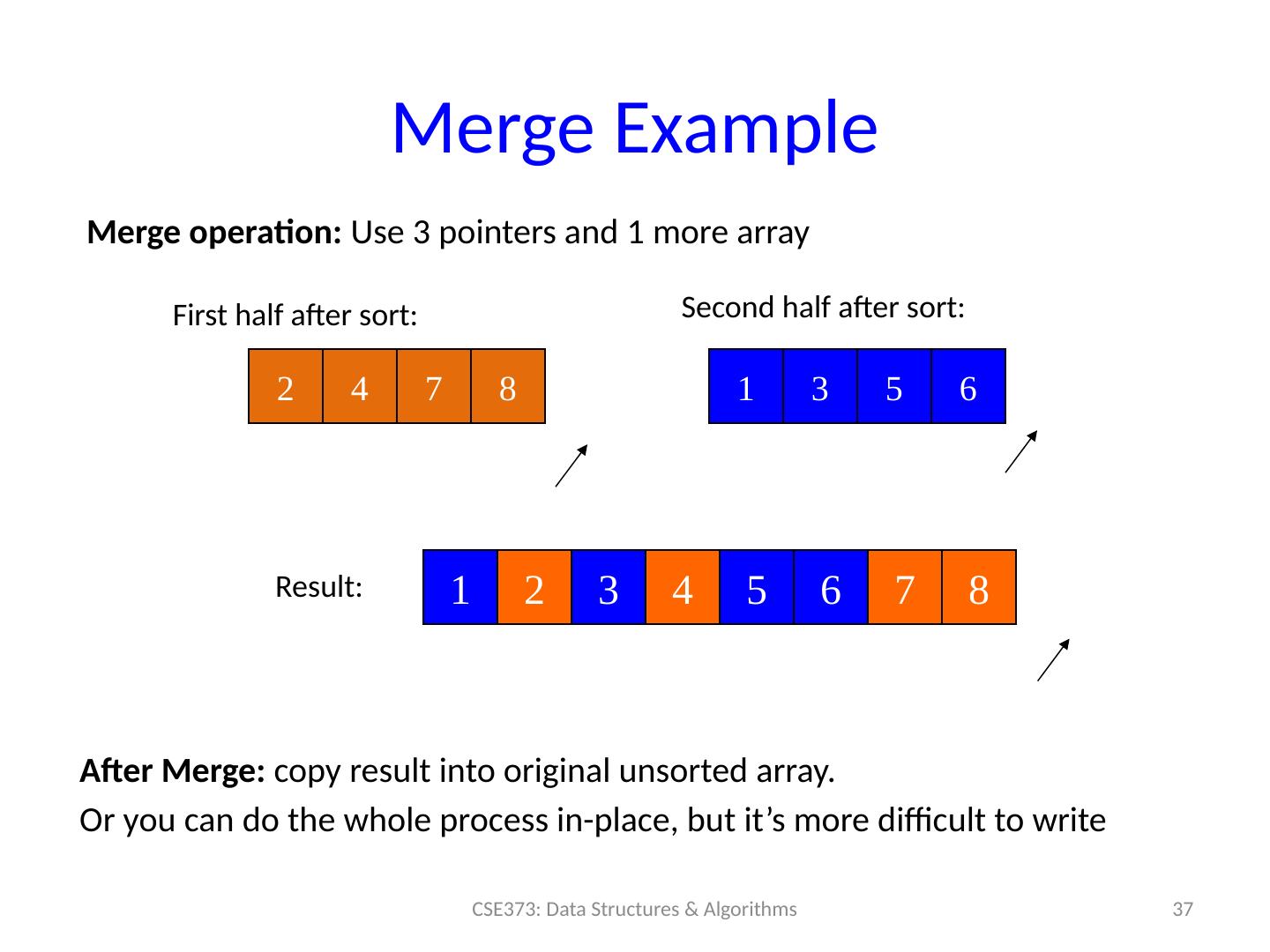
29 .Merge Example 29 CSE373: Data Structures & Algorithms 2 4 7 8 1 3 5 6 Merge operation: Use 3 pointers and 1 more array First half after sort: Second half after sort: Result: