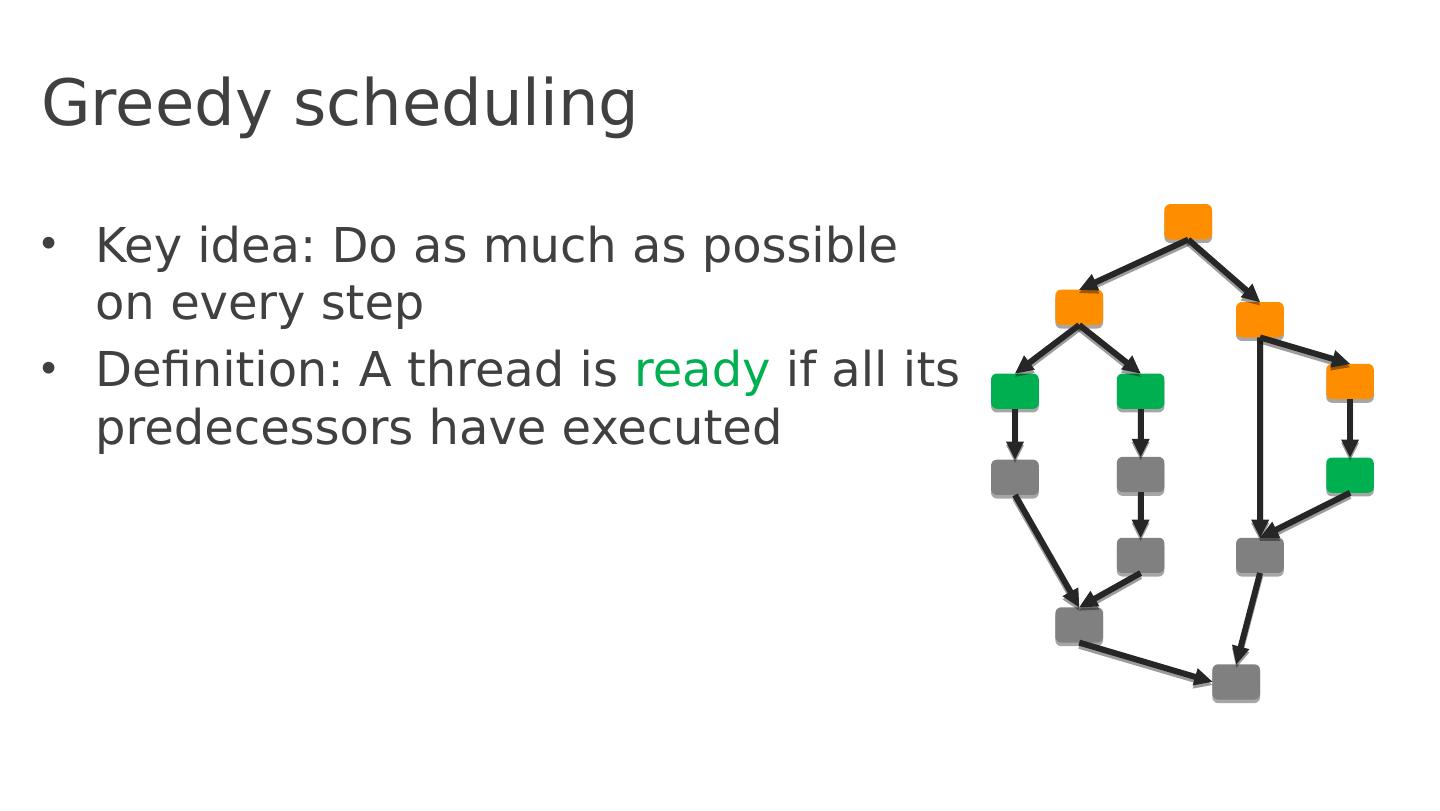
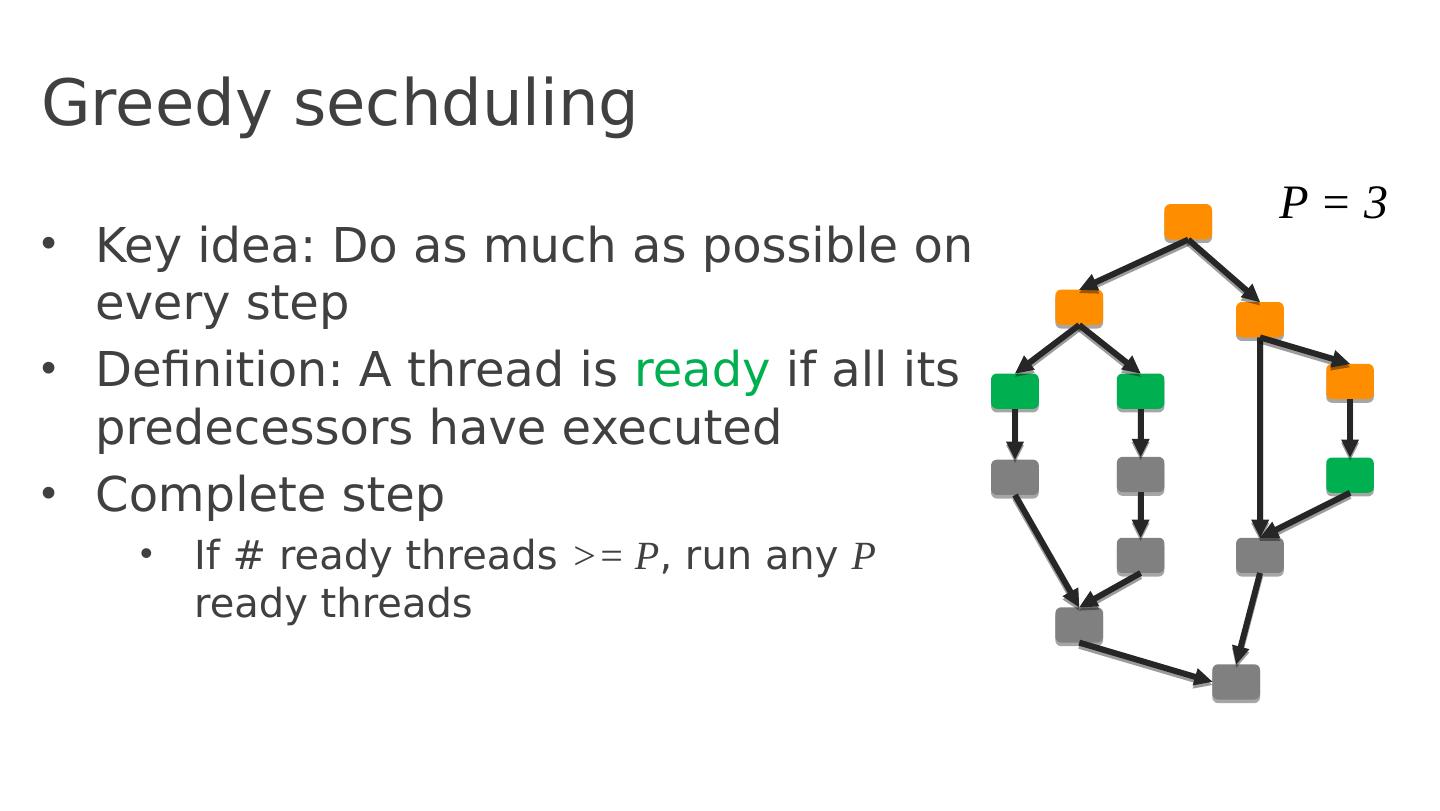
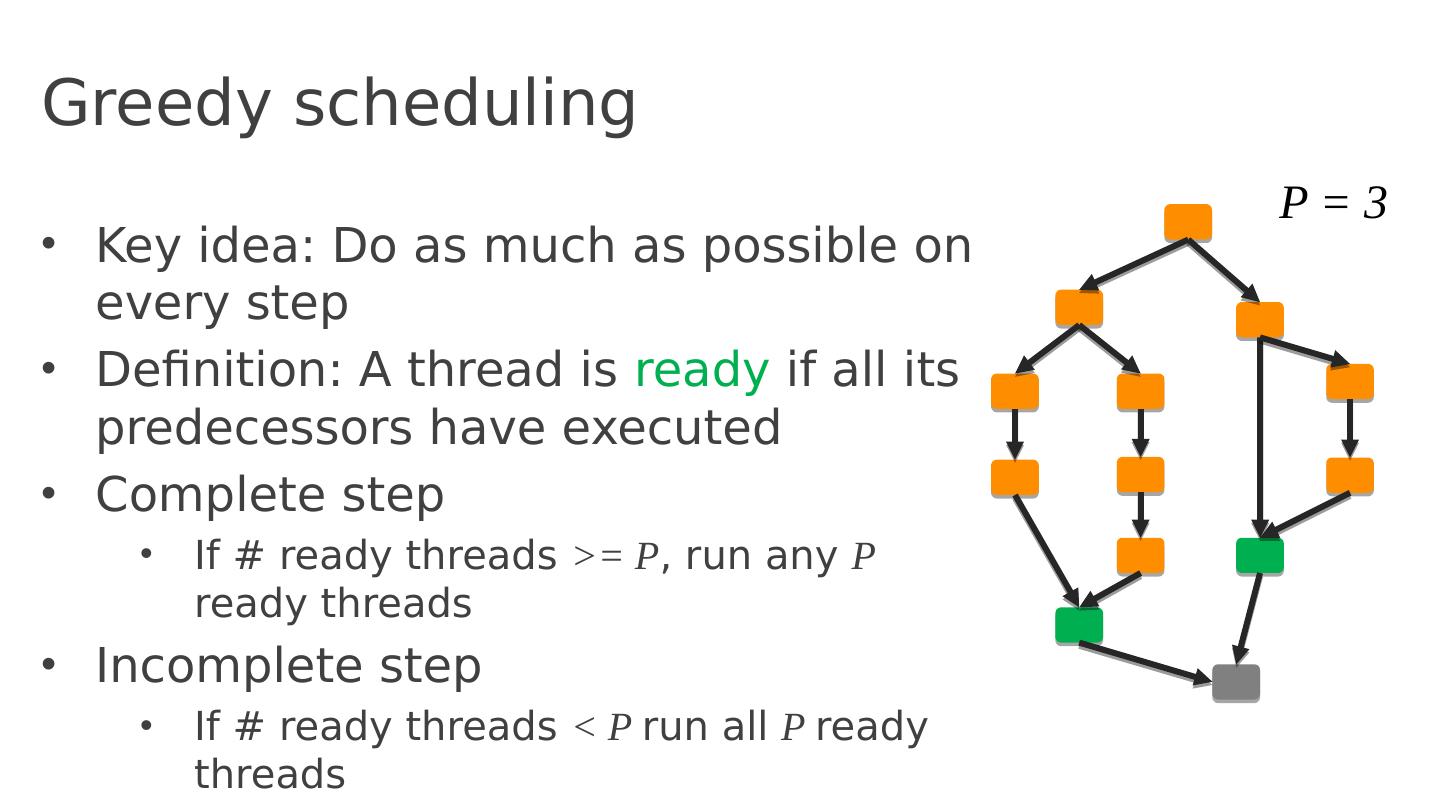
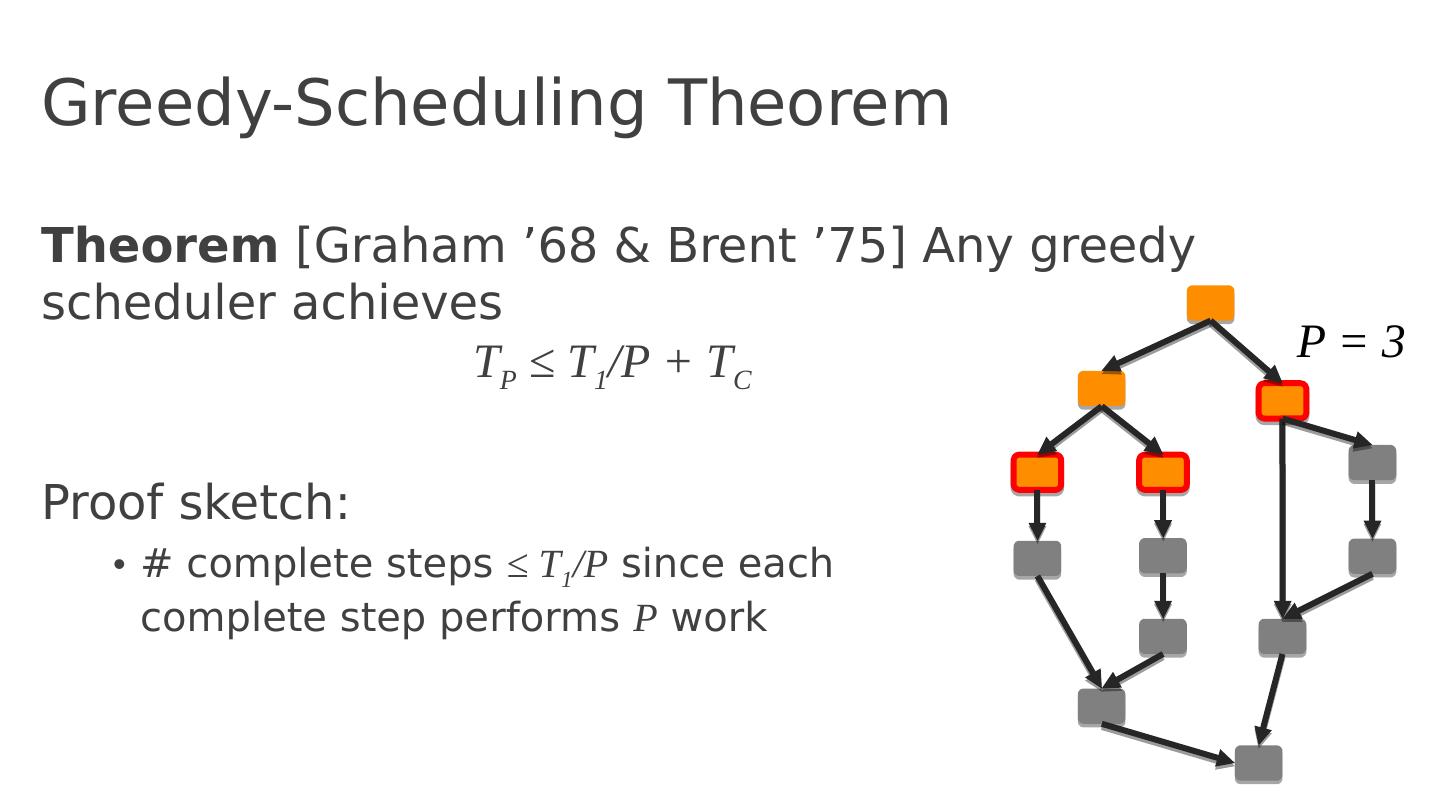
- 快召唤伙伴们来围观吧
- 微博 QQ QQ空间 贴吧
- 文档嵌入链接
- 复制
- 微信扫一扫分享
- 已成功复制到剪贴板
Cilk&OpenMP
展开查看详情
1 .Cilk and OpenMP (Lecture 20, cs262a) Ion Stoica, UC Berkeley April 4 , 2018
2 .Today’s papers “ Cilk : An Efficient Multithreaded Runtime System” by Robert D. Blumofe , Christopher F. Joerg , Bradley C. Kuszmaul , Charles E. Leiserson , Keith H. Randall and Yuli Zhou http:// supertech.csail.mit.edu/papers/PPoPP95.pdf “ OpenMP : An IndustryStandard API for SharedMemory Programming”, Leonardo Dagum and Ramesh Menon https://ucbrise.github.io/cs262a-spring2018 /
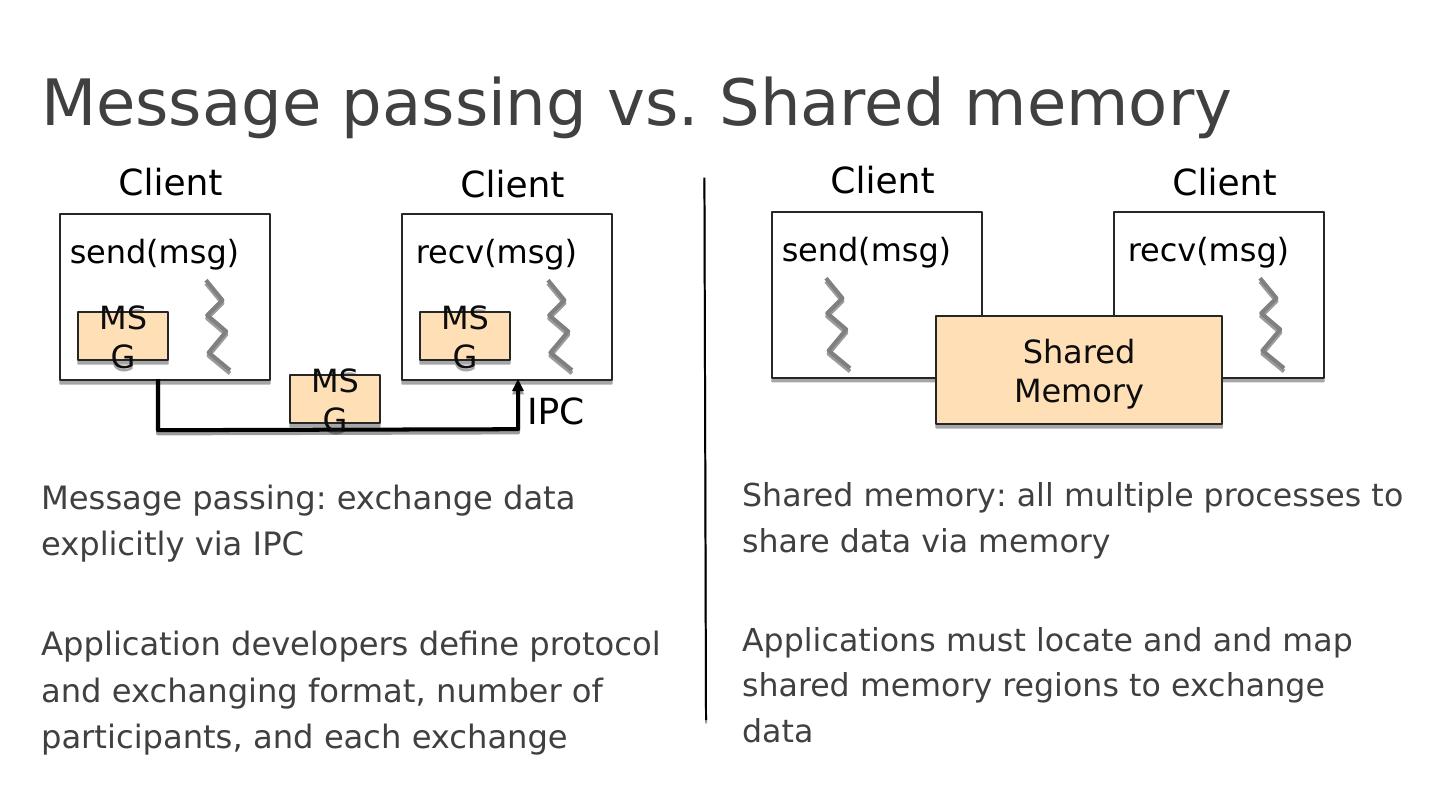
3 .Message passing vs. Shared memory Message passing : exchange data explicitly via IPC Application developers define protocol and exchanging format, number of participants, and each exchange Shared memory : all multiple processes to share data via memory Applications must locate and and map shared memory regions to exchange data Client s end( msg ) MSG Client recv ( msg ) MSG MSG IPC Client s end( msg ) Client recv ( msg ) Shared Memory
4 .Architectures Uniformed Shared Memory (UMA) Cray 2 Massively Parallel DistrBluegene /L Non-Uniformed Shared Memory (NUMA) SGI Altix 3700 Orthogonal to programming model
5 .Motivation Multicore CPUs are everywhere: Servers with over 100 cores today Even smartphone CPUs have 8 cores Multithreading, natural programming model All processors share the same memory Threads in a process see same address space Many shared -memory algorithms developed
6 .But … Multithreading is hard Lots of expertise necessary Deadlocks and race conditions Non-deterministic behavior makes it hard to debug
7 .Example Parallelize the following code using threads: for ( i =0; i <n; i ++) { sum = sum + sqrt (sin(data[ i ])); } Why hard? Need mutex to protect the accesses to sum Different code for serial and parallel version No built-in tuning (# of processors? )
8 .Cilk Based on slides available at http://supertech.csail.mit.edu/cilk/lecture-1.pdf
9 .Cilk A C language for programming dynamic multithreaded applications on shared-memory multiprocessors Examples: dense and sparse matrix computations n-body simulation heuristic search graphics rendering …
10 .Cilk in one slide Simple extension to C; just three basic keywords Cilk programs maintain serial semantics Abstracts away parallel execution, load balancing and scheduling Parallelism Processor-oblivious Speculative execution Provides performance “guarantees”
11 .Example: Fibonacci int fib ( int n ) { if ( n <2) return ( n ); else { int x,y ; x = fib (n-1); y = fib (n-2); return ( x+y ); } } cilk int fib ( int n ) { if ( n <2) return ( n ); else { int x,y ; x = spawn fib (n-1 ); y = spawn fib (n-2); sync return ( x+y ); } } A Cilk program’s serial elision is always a legal implementation of Cilk semantics Cilk provides no new data types . C (elision) Click
12 .Cilk basic kewords click int fib ( int n ) { if ( n <2) return ( n ); else { int x,y ; x = spawn fib (n-1); y = spawn fib (n-2); sync return ( x+y ); } } Identifies a function as a Cilk procedure , capable of being spawned in parallel . The named child Cilk procedure can execute in parallel with the parent caller Control cannot pass this point until all spawned children have returned
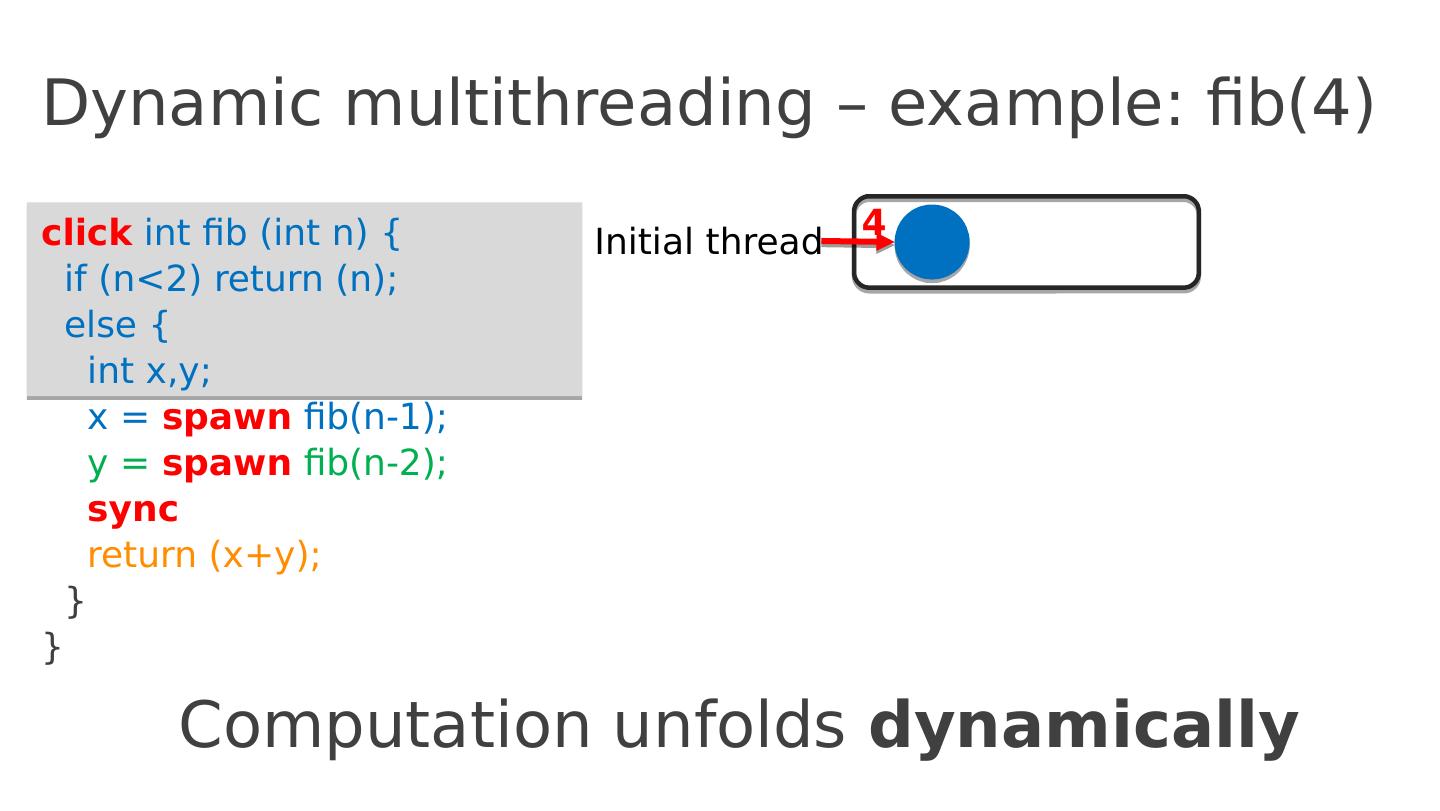
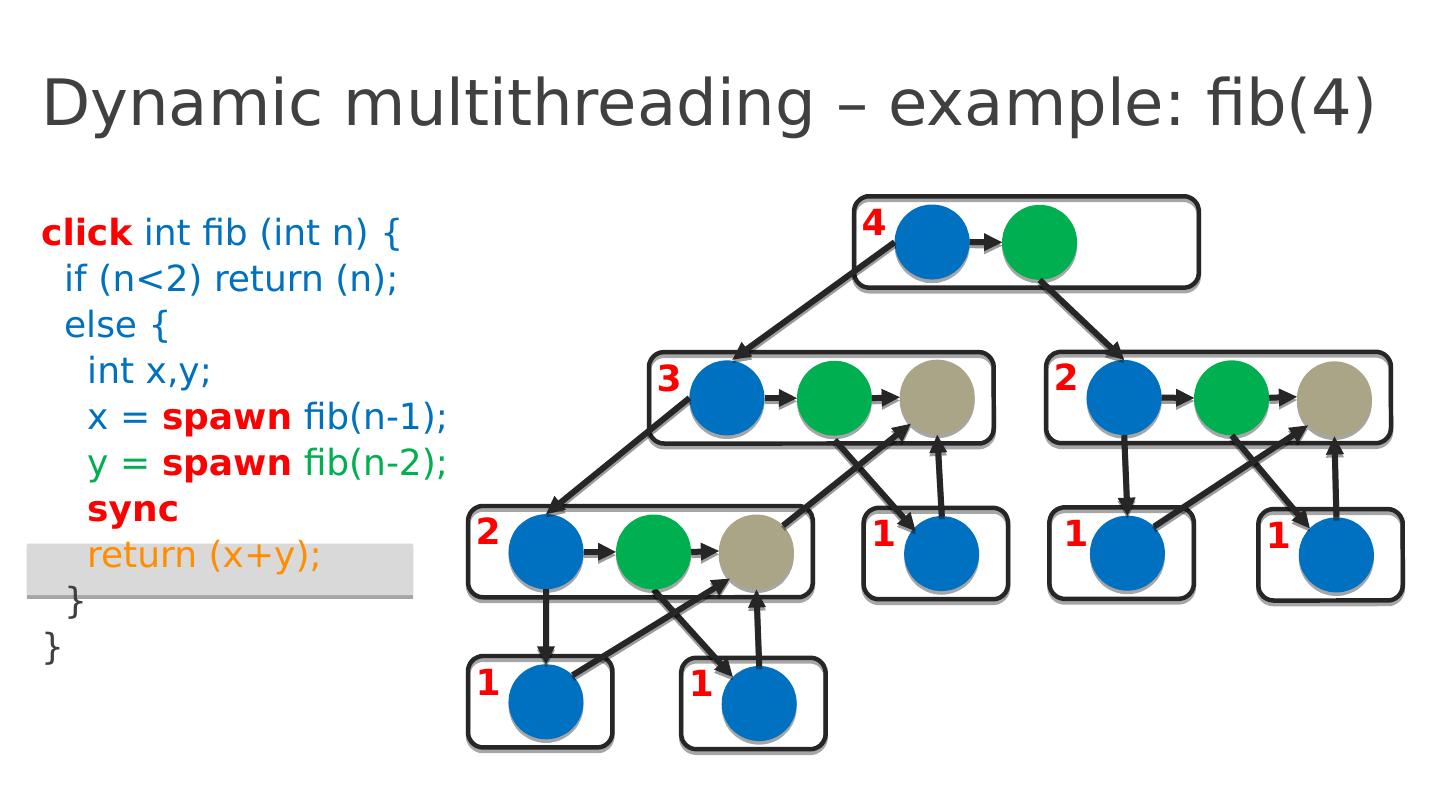
13 .Dynamic multithreading – example: fib(4) click int fib ( int n ) { if ( n <2) return ( n ); else { int x,y ; x = spawn fib (n-1); y = spawn fib (n-2); sync return ( x+y ); } } 4 Computation unfolds dynamically Initial thread
14 .Dynamic multithreading – example: fib(4) click int fib ( int n ) { if ( n <2) return ( n ); else { int x,y ; x = spawn fib (n-1); y = spawn fib (n-2); sync return ( x+y ); } } 4 Initial thread Execution represented as a graph, G = (V, E ) Each vertex v ∈ V represents a ( Cilk ) thread: a maximal sequence of instructions not containing parallel control ( spawn , sync , return ) Every edge e ∈ E is either a spawn , a return or a continue edge
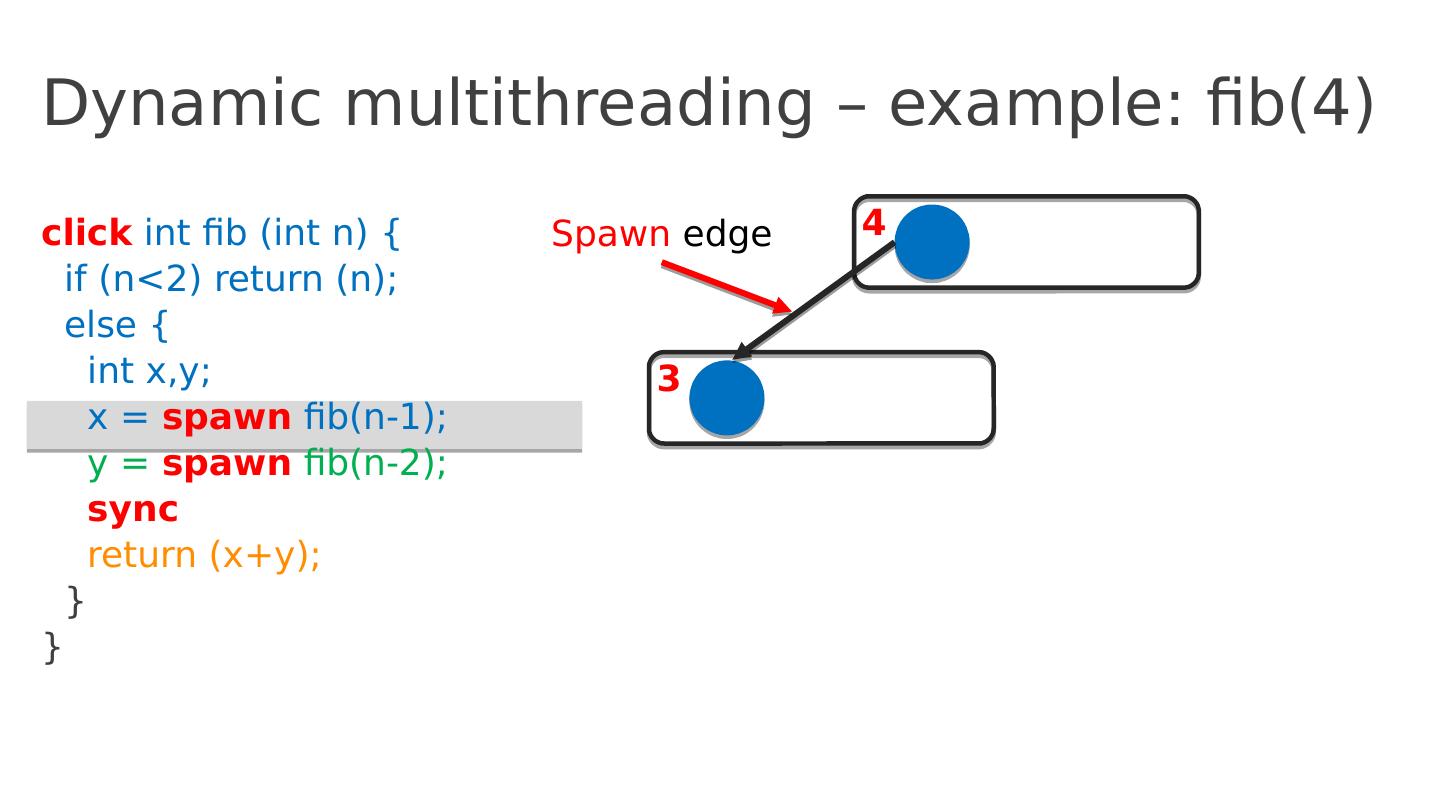
15 .Dynamic multithreading – example: fib(4) click int fib ( int n ) { if ( n <2) return ( n ); else { int x,y ; x = spawn fib (n-1); y = spawn fib (n-2); sync return ( x+y ); } } 4 3 Spawn edge
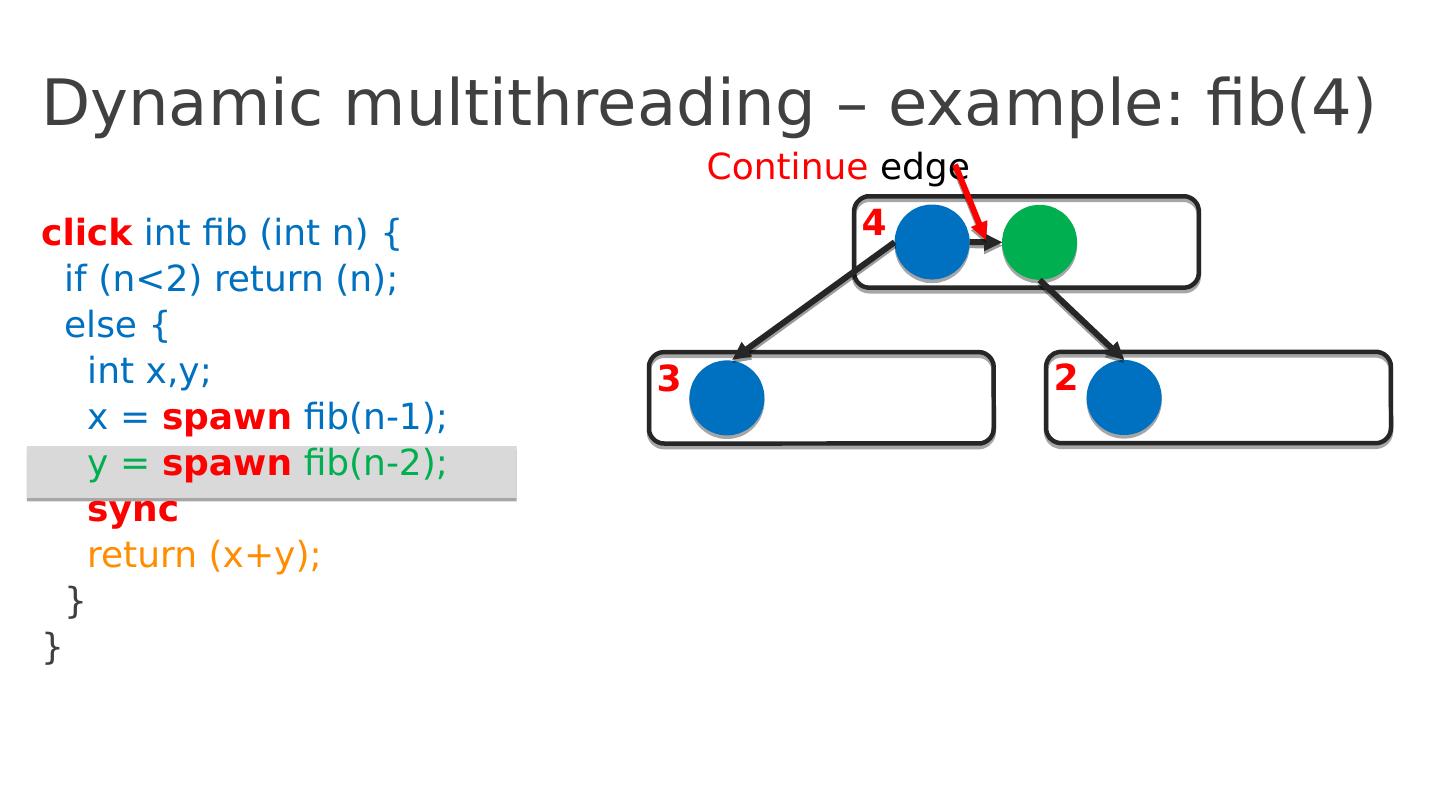
16 .Dynamic multithreading – example: fib(4) click int fib ( int n ) { if ( n <2) return ( n ); else { int x,y ; x = spawn fib (n-1); y = spawn fib (n-2); sync return ( x+y ); } } 4 3 2 Continue edge
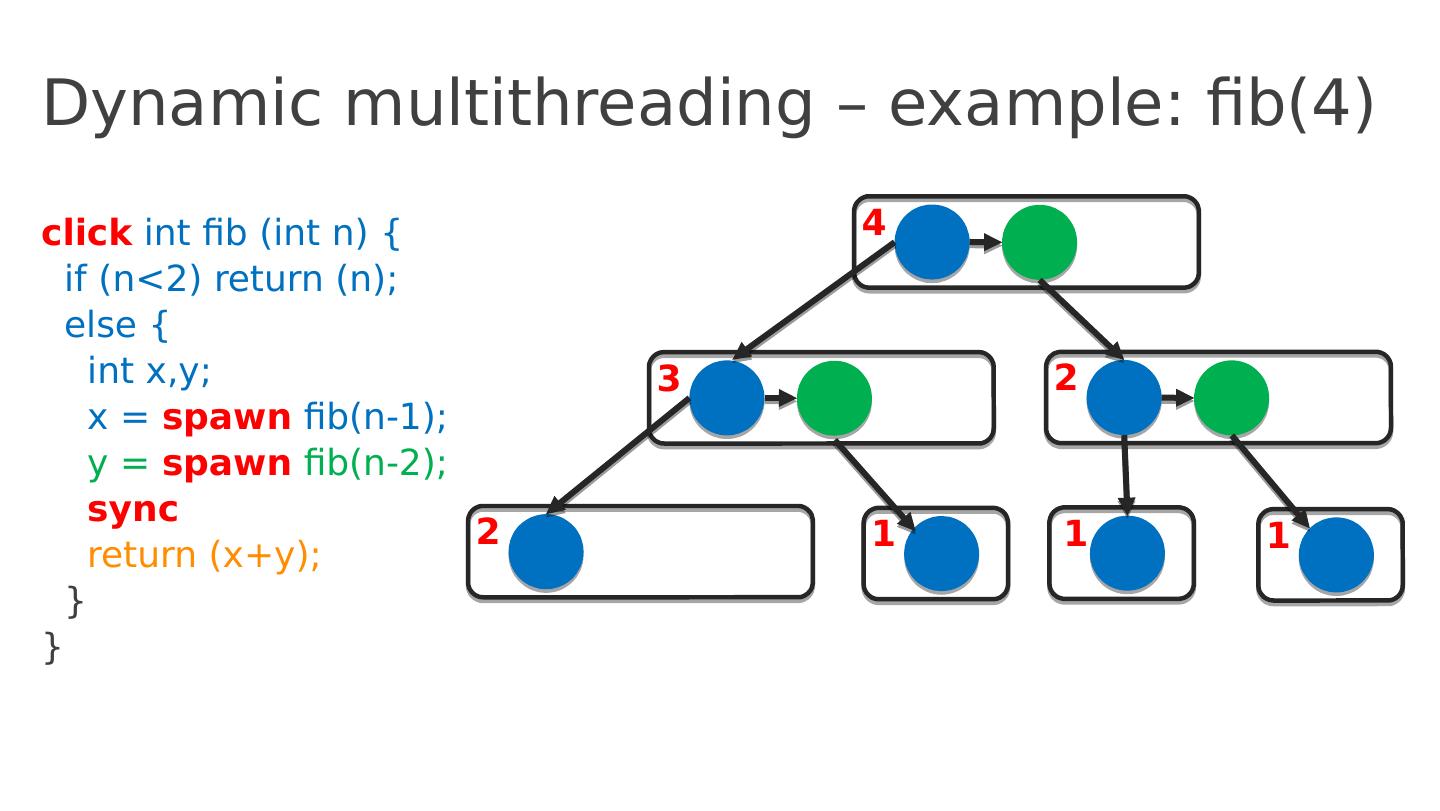
17 .Dynamic multithreading – example: fib(4) click int fib ( int n ) { if ( n <2) return ( n ); else { int x,y ; x = spawn fib (n-1); y = spawn fib (n-2); sync return ( x+y ); } } 4 3 2 2 1 1 1
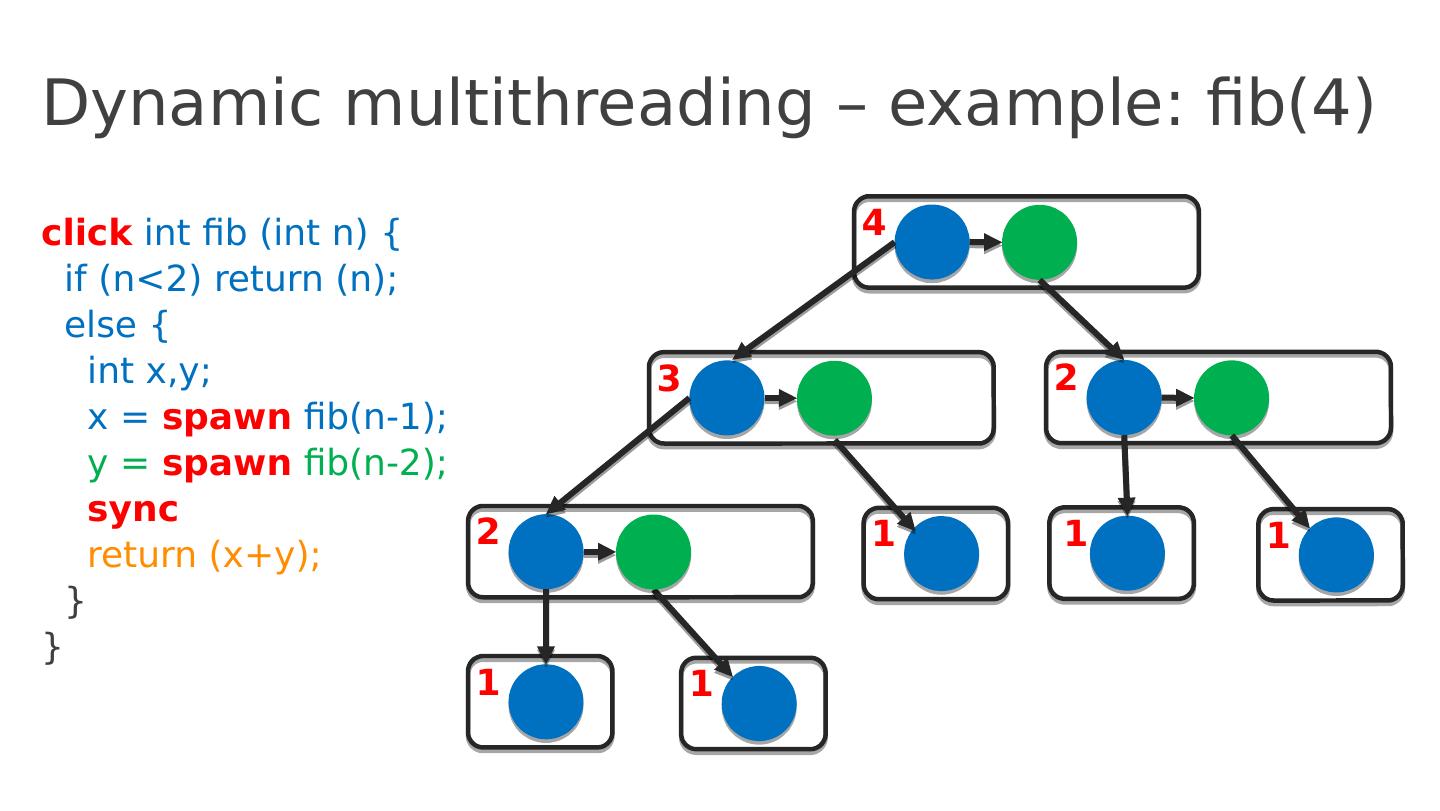
18 .Dynamic multithreading – example: fib(4) click int fib ( int n ) { if ( n <2) return ( n ); else { int x,y ; x = spawn fib (n-1); y = spawn fib (n-2); sync return ( x+y ); } } 4 3 2 2 1 1 1 1 1
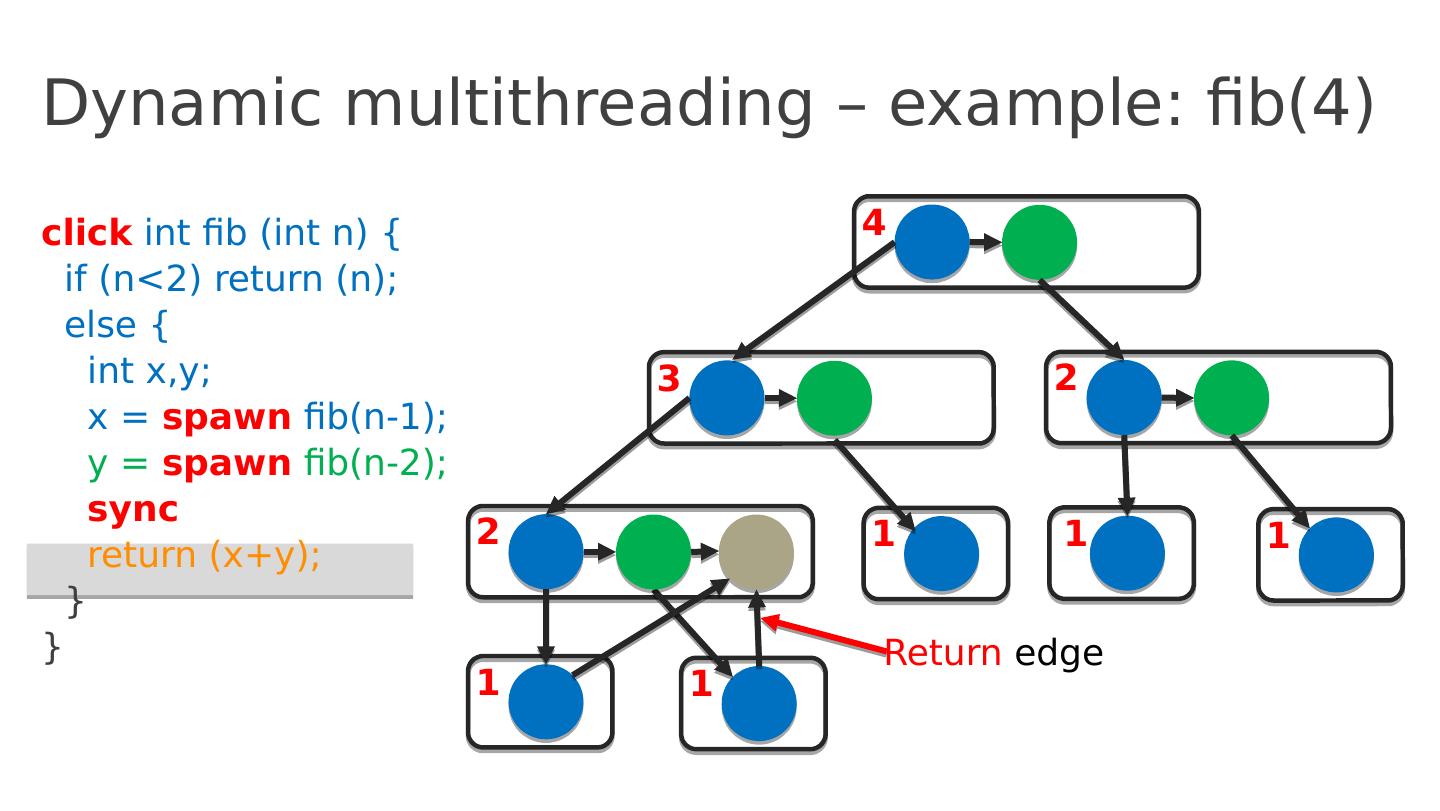
19 .Dynamic multithreading – example: fib(4) click int fib ( int n ) { if ( n <2) return ( n ); else { int x,y ; x = spawn fib (n-1); y = spawn fib (n-2); sync return ( x+y ); } } 4 3 2 2 1 1 1 1 1 Return edge
20 .Dynamic multithreading – example: fib(4) click int fib ( int n ) { if ( n <2) return ( n ); else { int x,y ; x = spawn fib (n-1); y = spawn fib (n-2); sync return ( x+y ); } } 4 3 2 2 1 1 1 1 1 Return edge
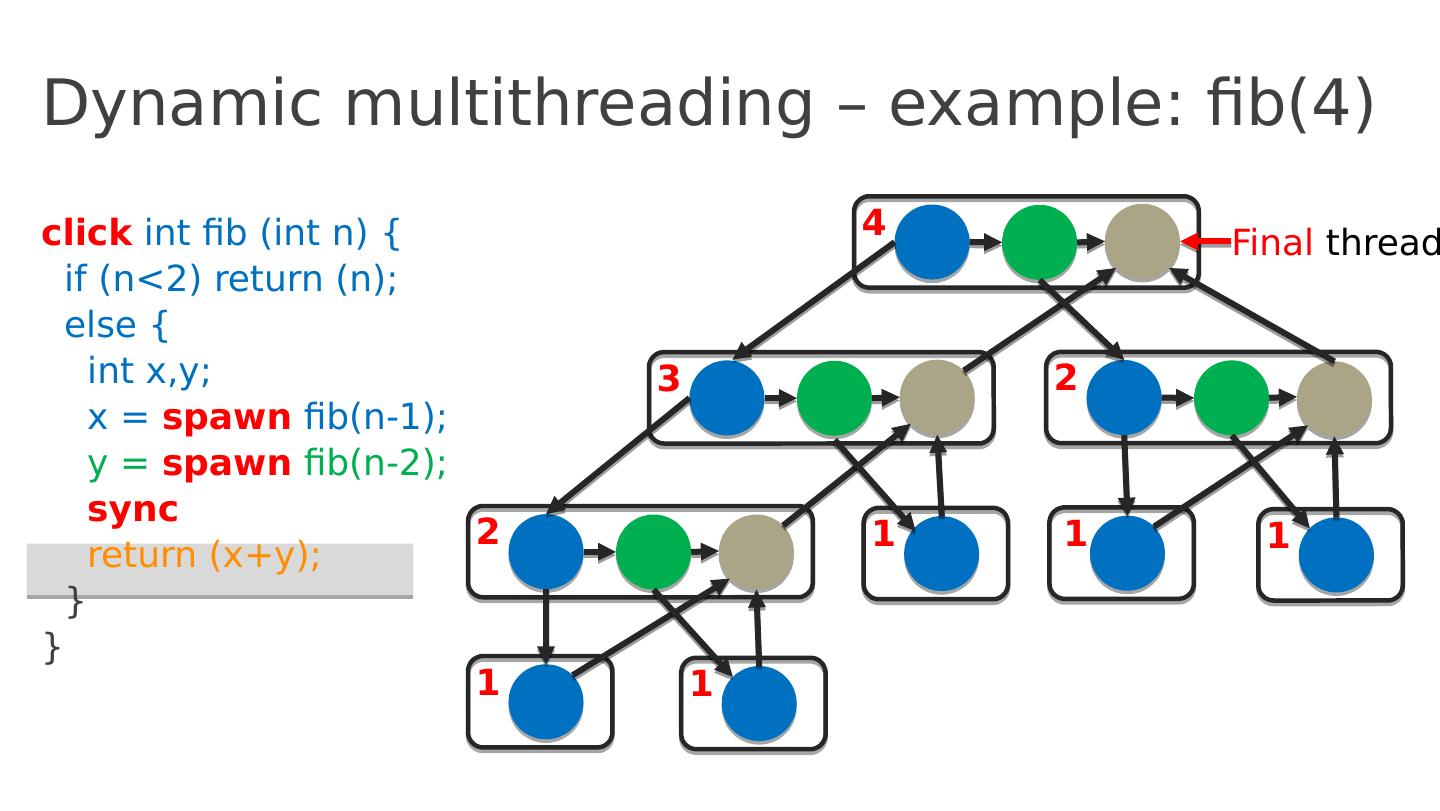
21 .Dynamic multithreading – example: fib(4) click int fib ( int n ) { if ( n <2) return ( n ); else { int x,y ; x = spawn fib (n-1); y = spawn fib (n-2); sync return ( x+y ); } } 4 3 2 2 1 1 1 1 1 Final thread
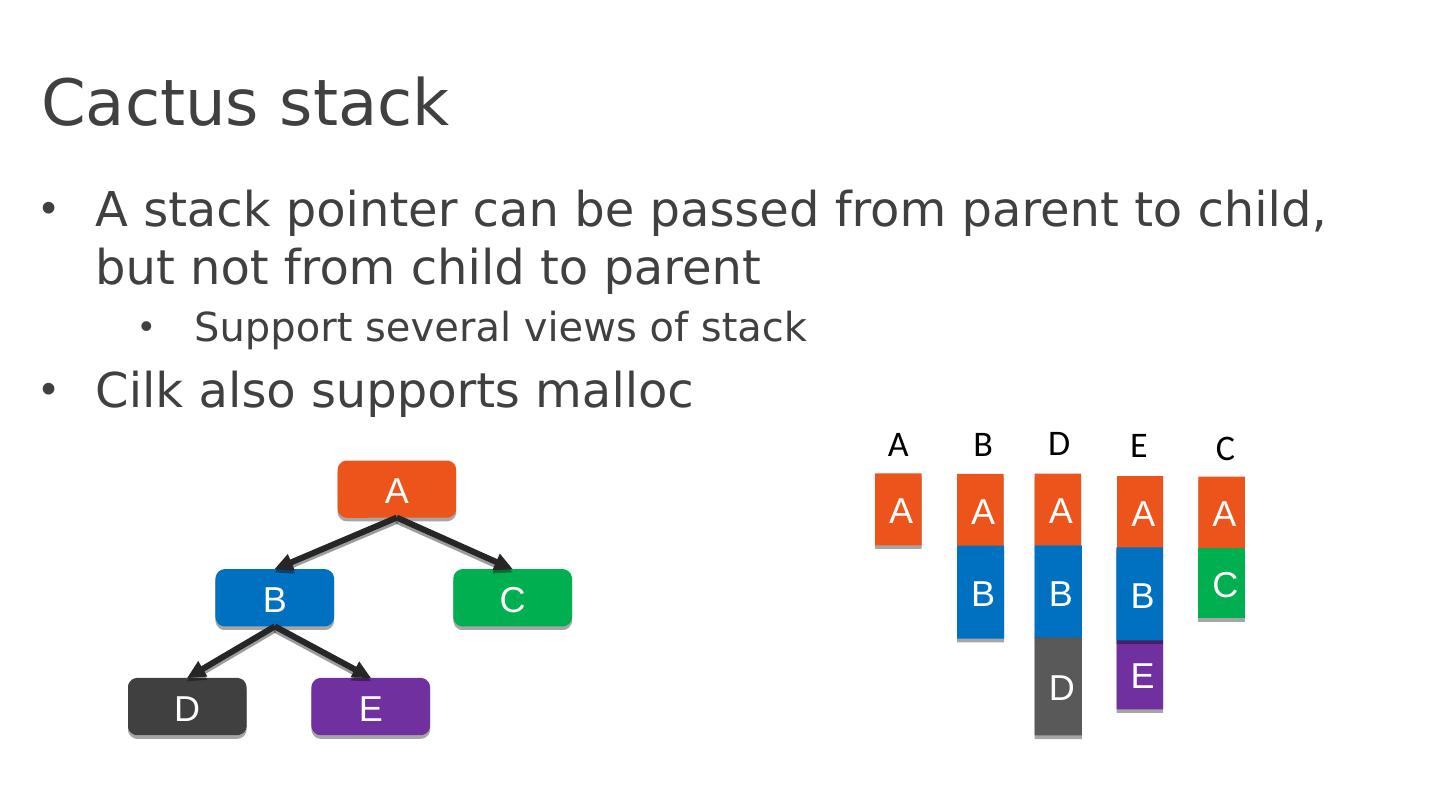
22 .Cactus stack A stack pointer can be passed from parent to child, but not from child to parent Support several views of stack Cilk also supports malloc A B C D E A A A A B C D E B A B A B D E C
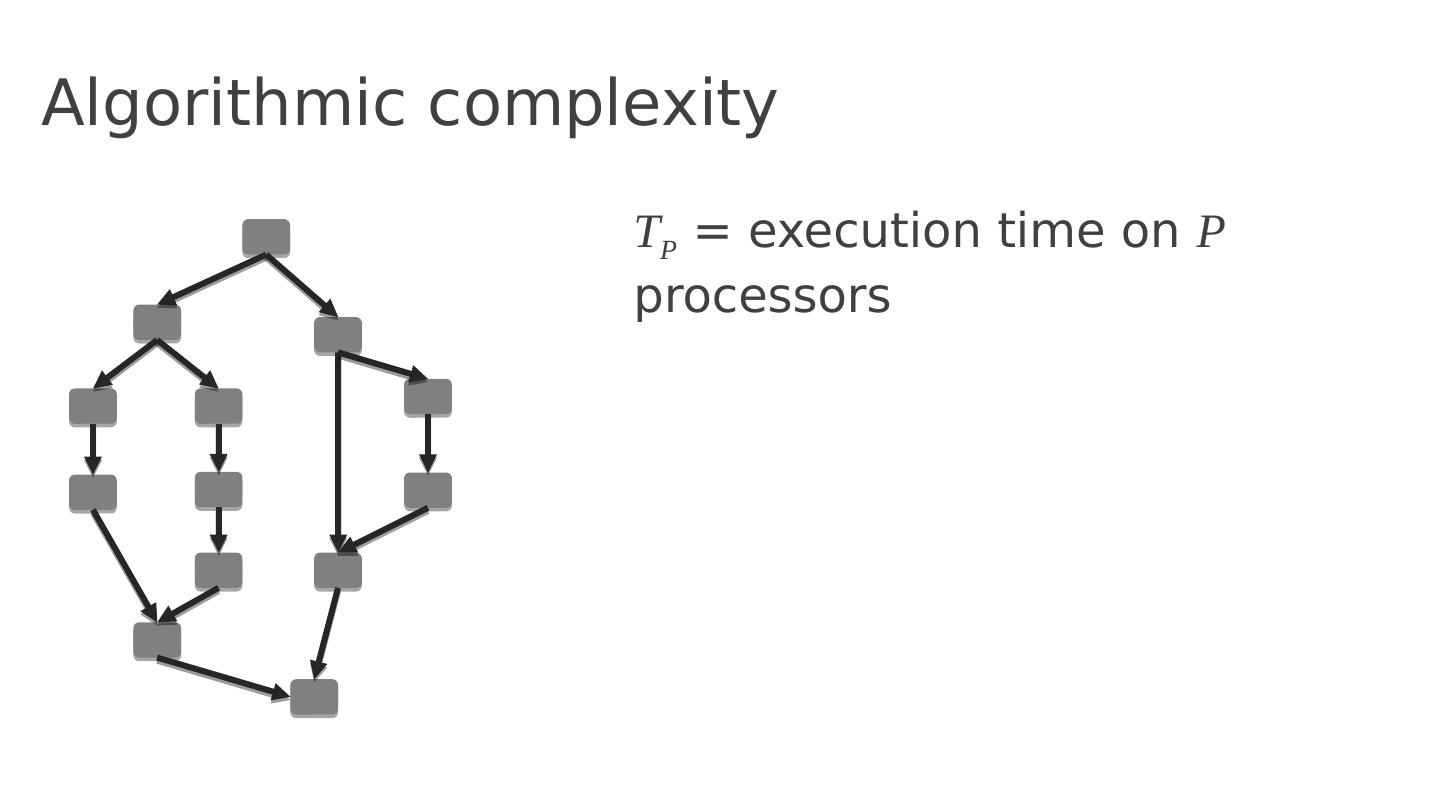
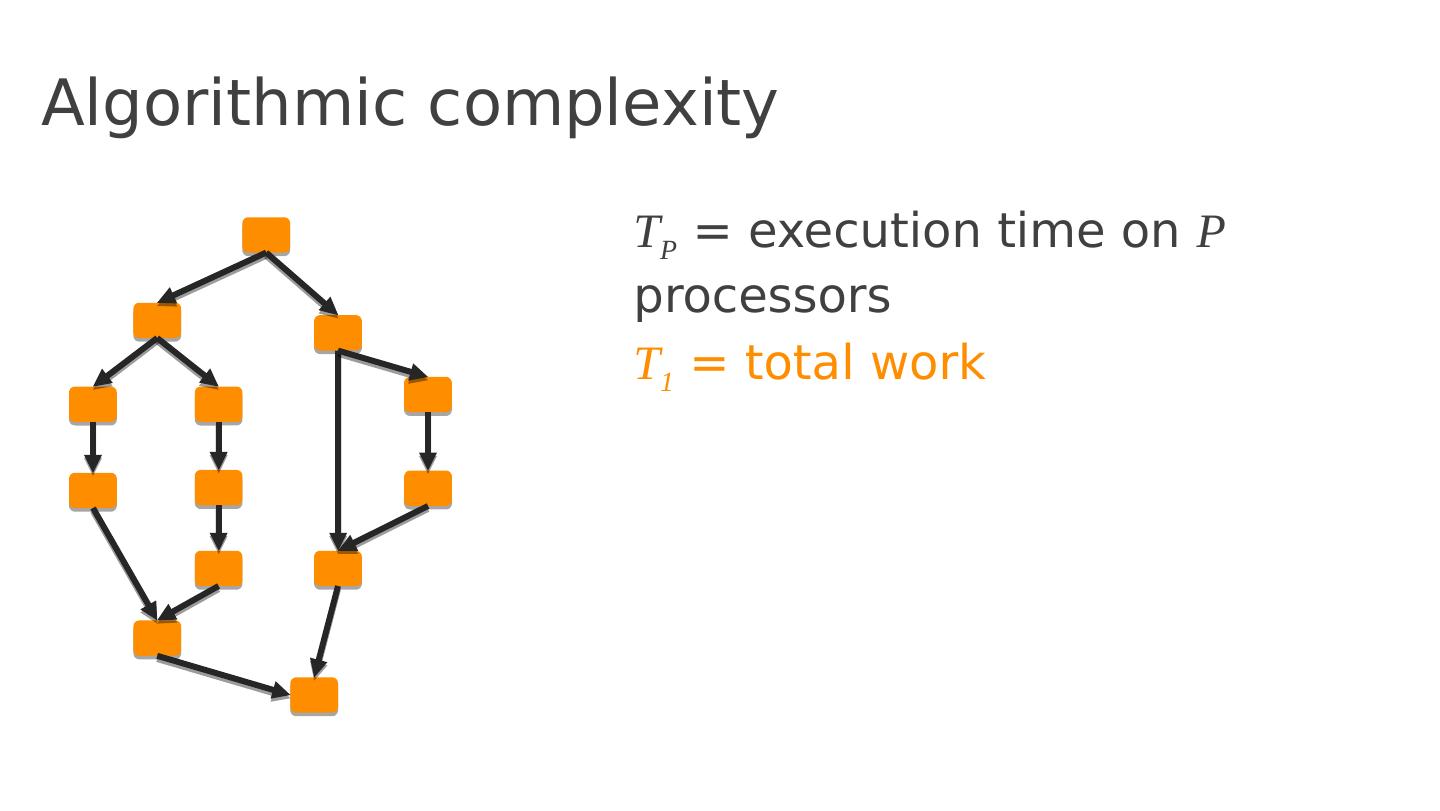
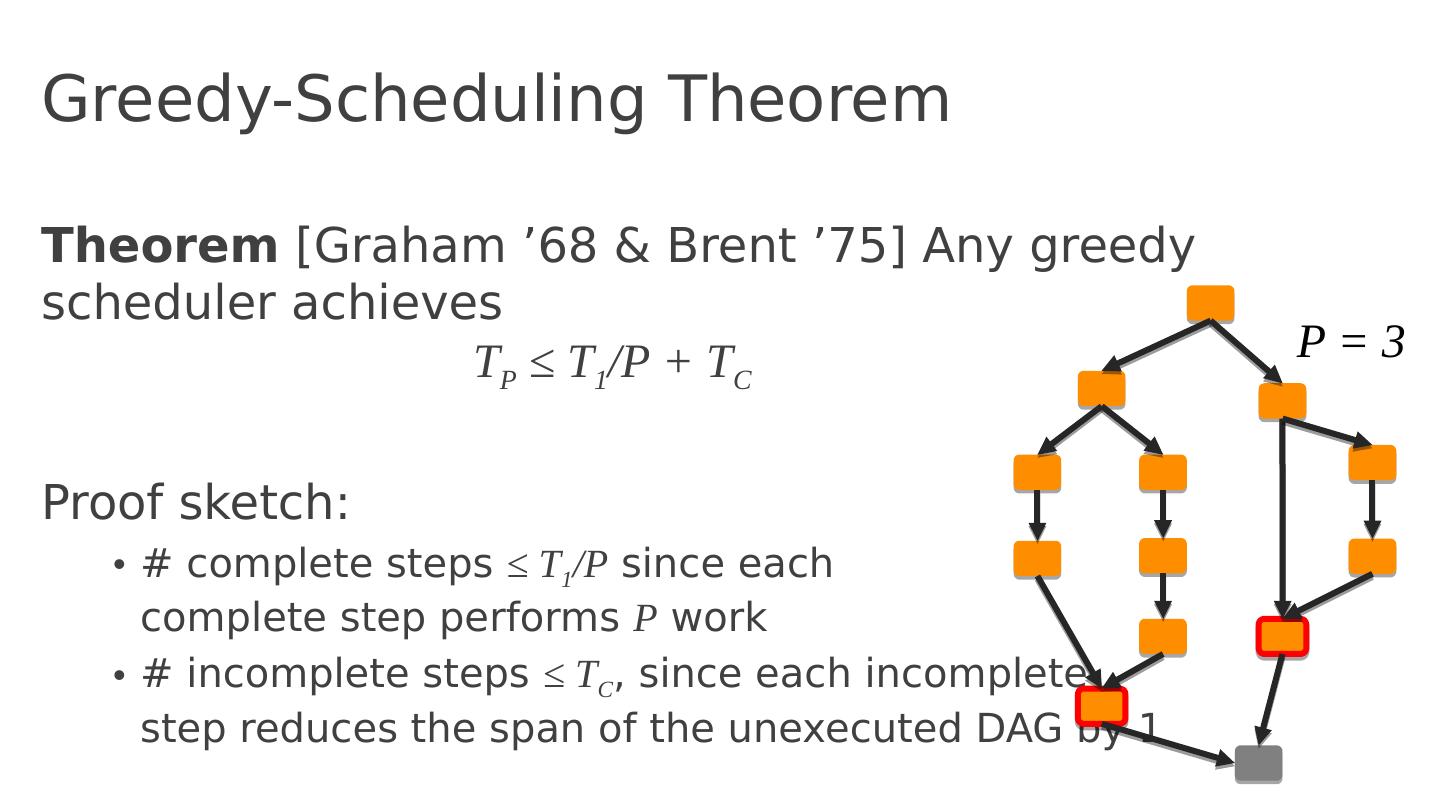
23 .Algorithmic complexity T P = execution time on P processors
24 .Algorithmic complexity T P = execution time on P processors T 1 = total work
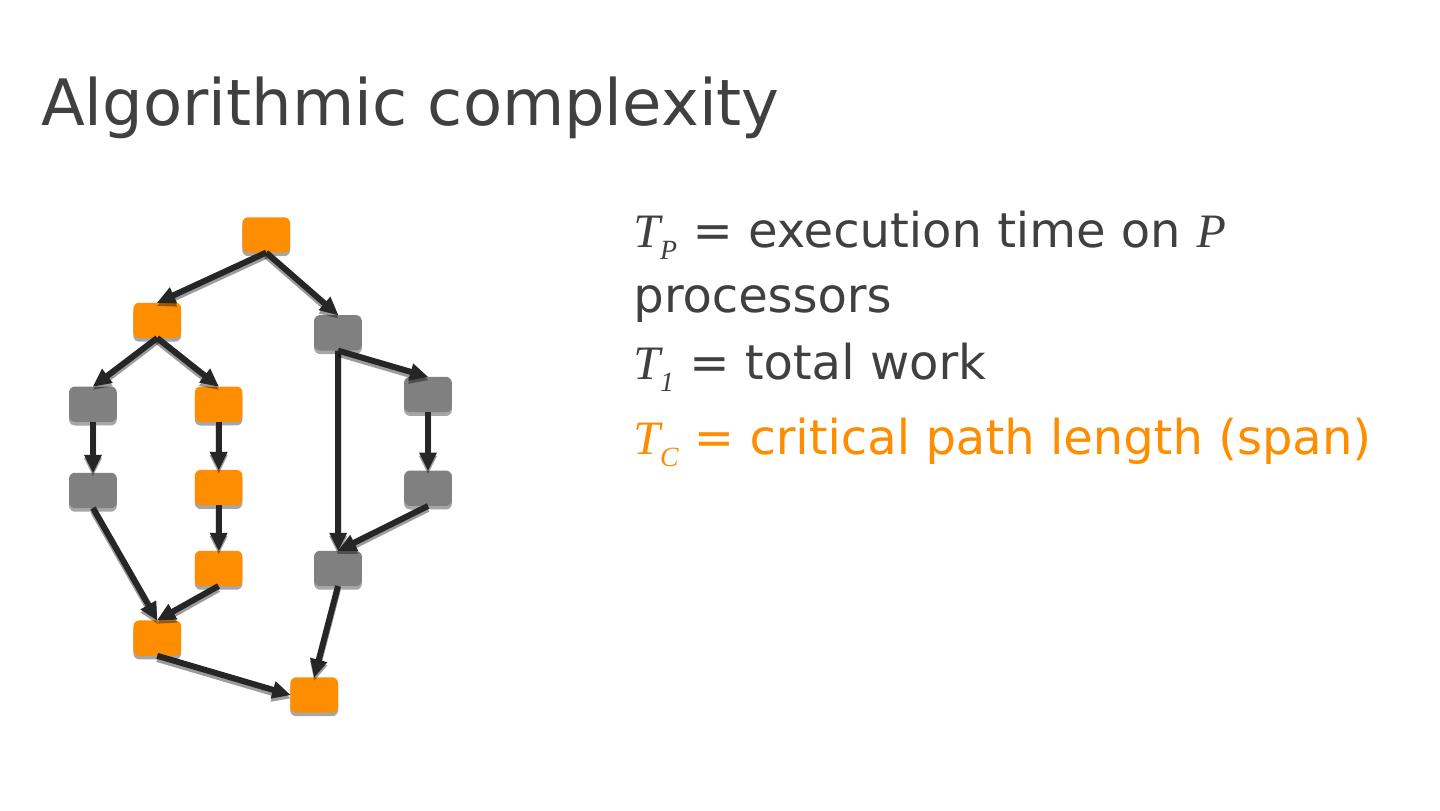
25 .Algorithmic complexity T P = execution time on P processors T 1 = total work T C = critical path length (span)
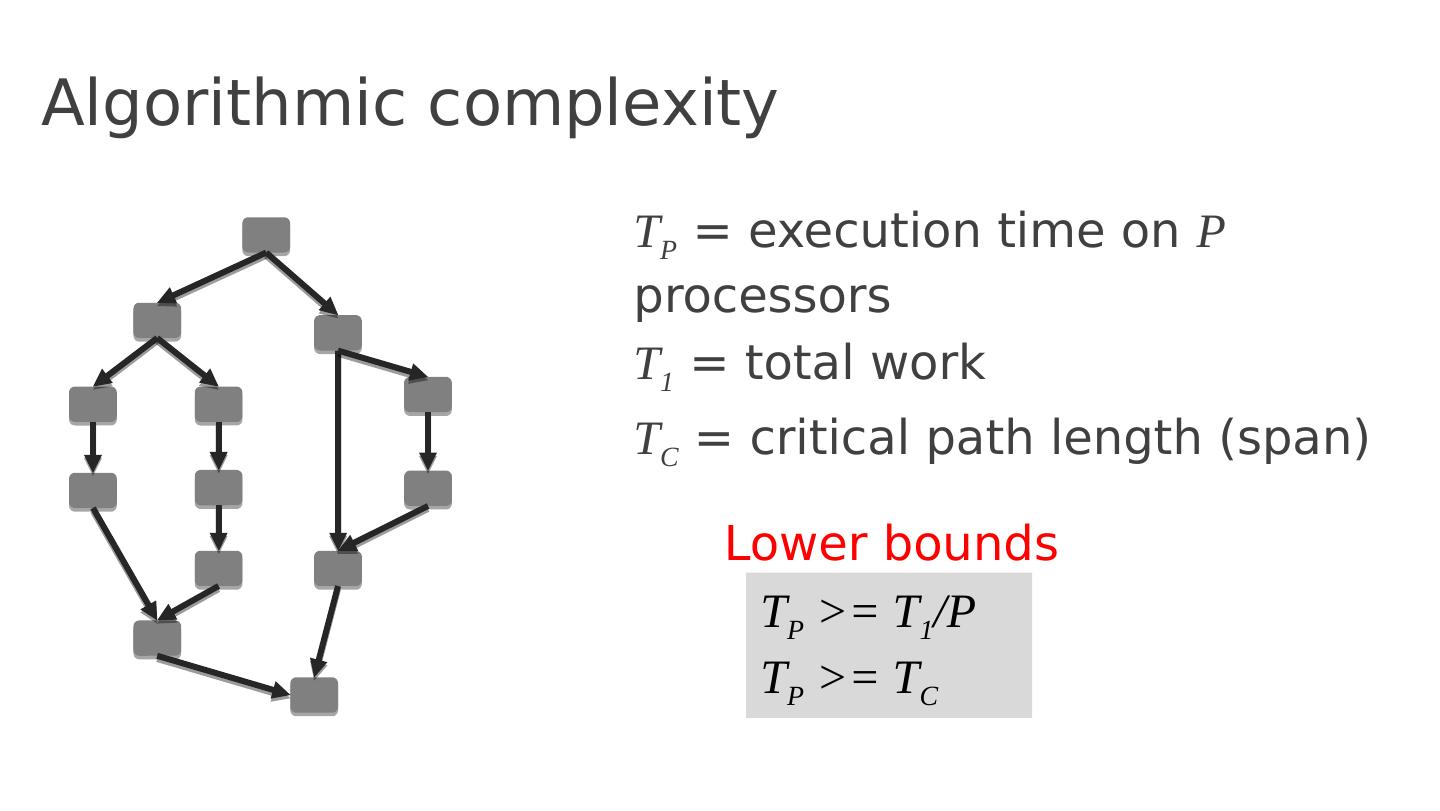
26 .Algorithmic complexity T P = execution time on P processors T 1 = total work T C = critical path length (span) T P >= T 1 /P T P >= T C Lower bounds
27 .Speedup T 1 /T P = speedup on P processors. If T 1 /T P = Θ (P) <= P , linear speedup If T 1 /T P = P , perfect linear speedup
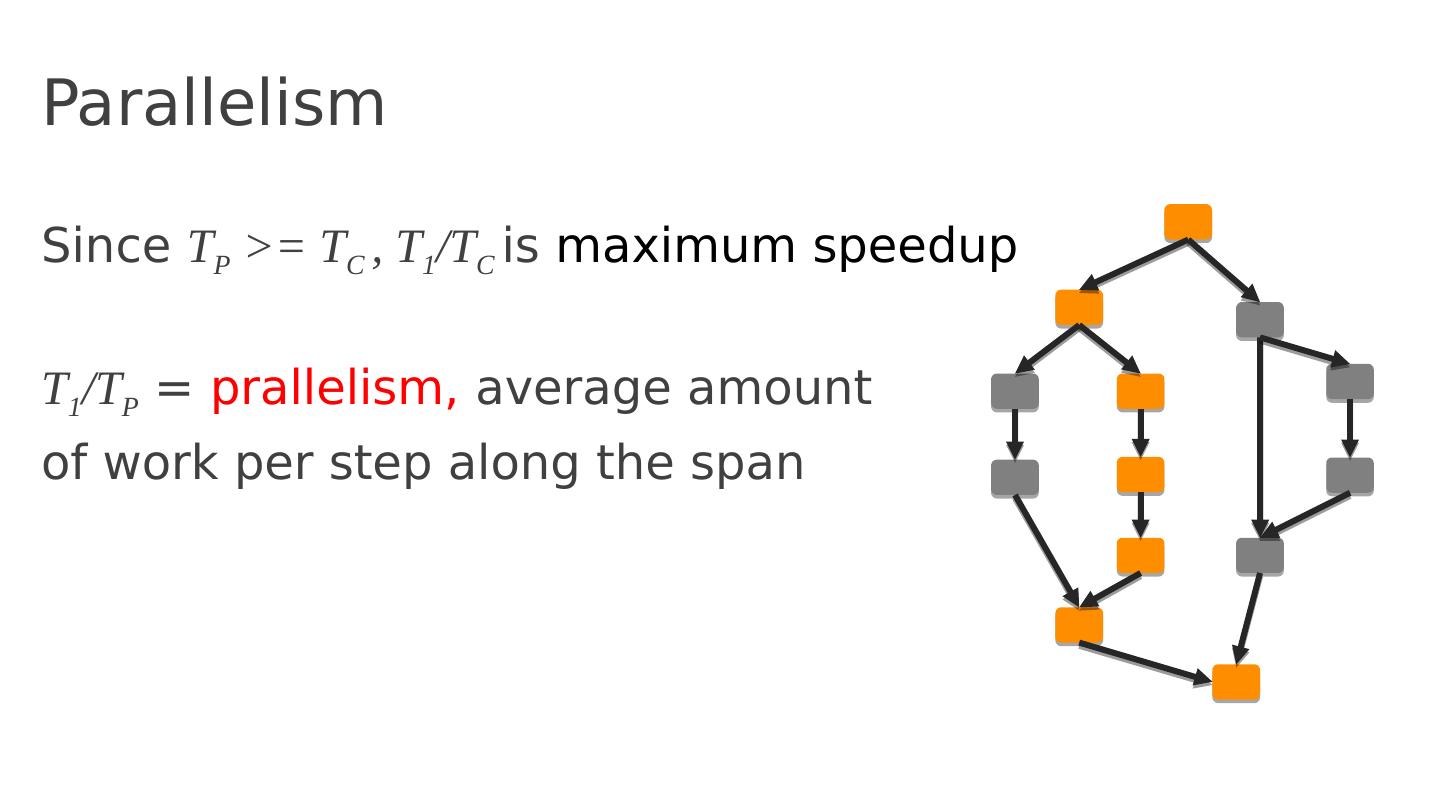
28 .Parallelism Since T P >= T C , T 1 /T C is maximum speedup T 1 /T P = prallelism , average amount of work per step along the span
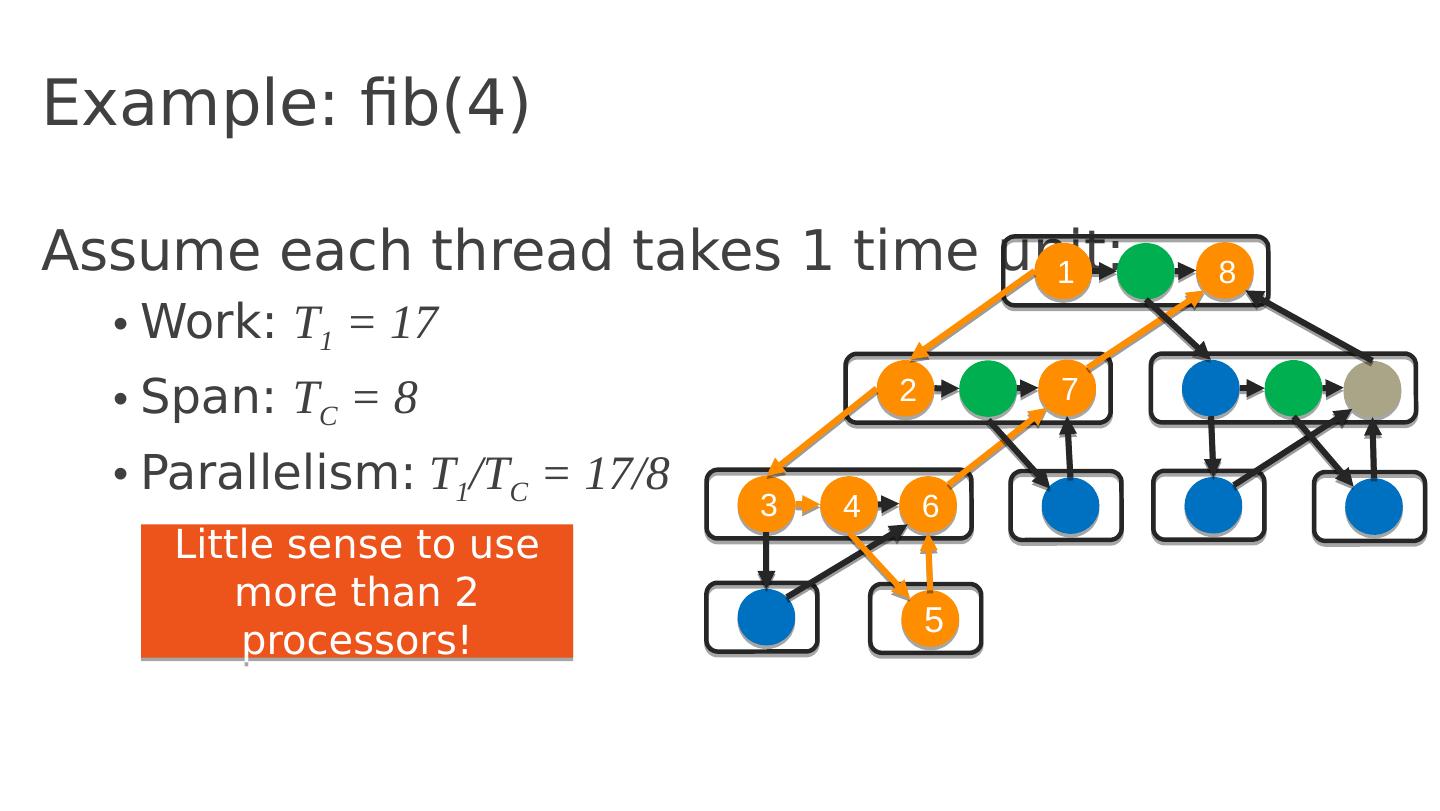
29 .Example: fib(4) Assume each thread takes 1 time unit: Work: T 1 = 17 Span: T C = 8 Parallelism: T 1 /T C = 17/8 1 8 2 7 3 4 6 5 Little sense to use more than 2 processors!