CRDTs

1 .CRDTs and Coordination Avoidance (Lecture 8, cs262a) Ion Stoica & Ali Ghodsi UC Berkeley February 12, 2018

2 .Today’s Papers CRDTs : Consistency without concurrency control, Marc Shapiro, Nuno Preguica , Carlos Baquero , Marek Zawirski Research Report, RR-6956, INRIA, 2009 ( https://hal.inria.fr/inria-00609399v1/ document ) Coordination Avoidance in Database Systems, Peter Bailis , Alan Fekete , Michael J. Franklin, Ali Ghodsi, Joseph M. Hellerstein , Ion Stoica , Proceedings of VLDB’14 ( http://www.vldb.org/pvldb/vol8/p185-bailis.pdf )

3 .Replicated Data Replicate data at many nodes P erformance : local reads Fault-tolerance: no data loss unless all replicas fail or become unreachable Availability: data still available unless all replicas fail or become unreachable Scalability : load balance across nodes for reads Updates Push to all replicas Consistency: expensive!

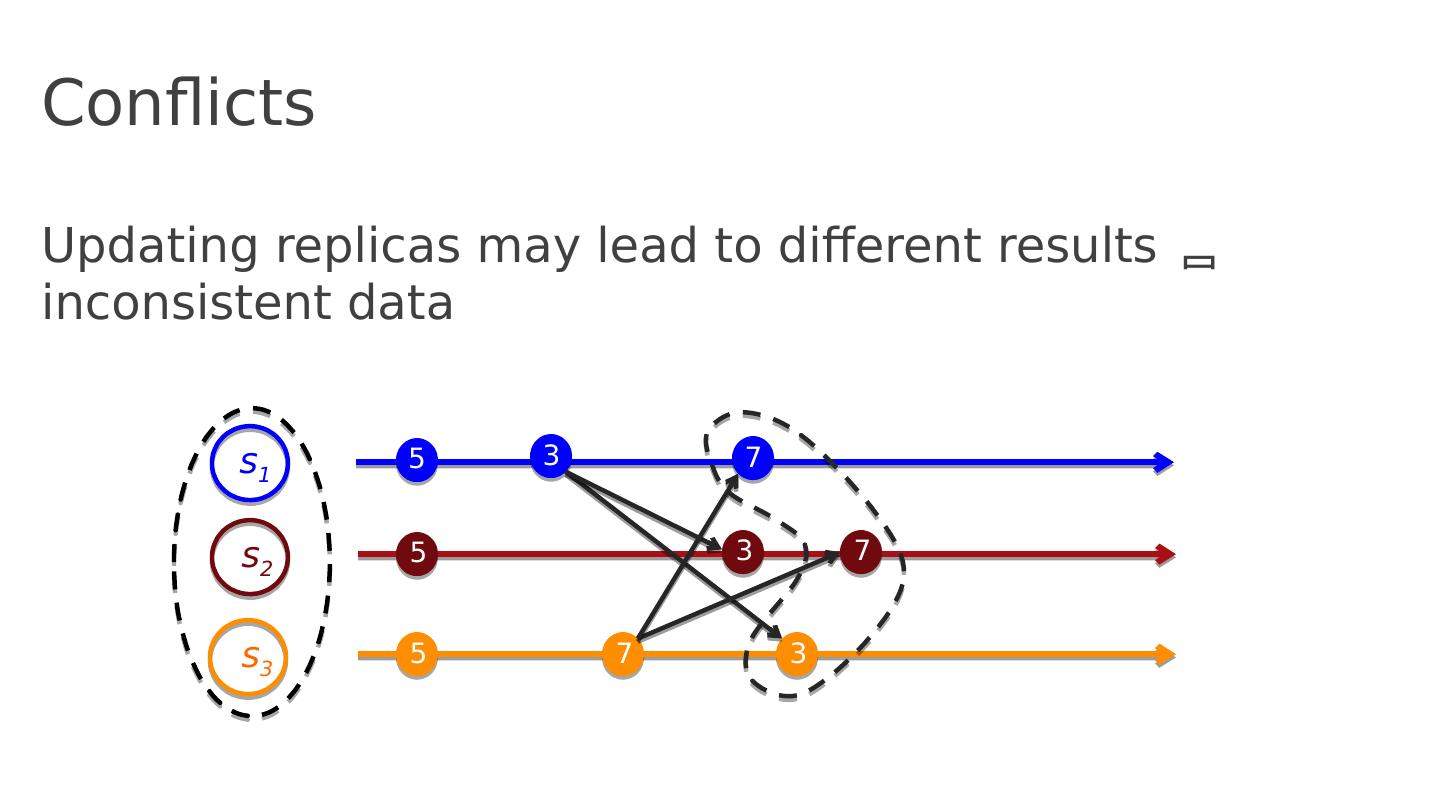
4 .Conflicts Updating replicas may lead to different results  inconsistent data s 1 s 2 s 3 5 5 5 7 3 3 7 3 7

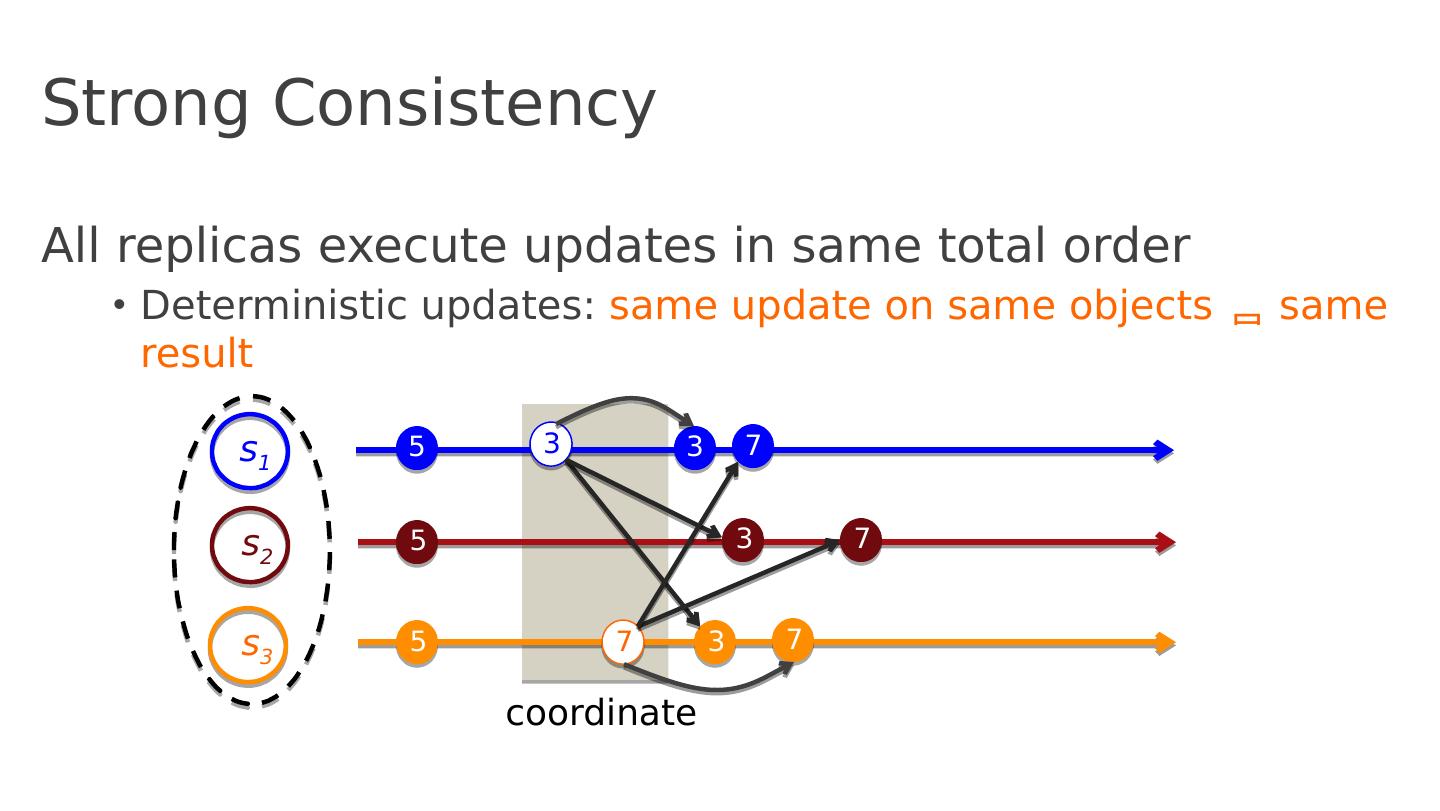
5 .Strong Consistency All replicas execute updates in same total order D eterministic updates: same update on same objects  same result s 1 s 2 s 3 5 5 5 7 3 3 7 3 7 3 7 coordinate

6 .Strong Consistency All replicas execute updates in same total order D eterministic updates: same update on same objects  same result Requires coordination and consensus to decide on total order of operations N-way agreement, basically serialize updates  very expensive!

7 .CAP theorem Can only have two of the three properties in a distributed system Consistency . Always return a consistent results ( linearizable ). As if there was only a single copy of the data. Availability . Always return an answer to requests (faster than really long lived partitions). Partition-tolerance . Continue operating correctly even if the network partitions.

8 .CAP theorem v2 When the networked is partitioned , you must chose one of these Consistency . Always return a consistent results ( linearizable ). As if there was only a single copy of the data. Availability . Always return an answer to requests (faster than really long lived partitions). How can we get around CAP?

9 .Eventual Consistency to the rescue If no new updates are made to an object all replicas will eventually converge to the same value Update local and propagate No consensus in the background  scale well for both reads and writes Expose intermediate state Assume, eventual , reliable delivery On conflict, applications Arbitrate & Rollback

10 .Eventual Consistency If no new updates are made to an object all replicas will eventually converge to the same value However High complexity Unclear semantics if application reads data and then we have a rollback!

11 .

12 .Must be available when partitions happen “For example, customers should be able to view and add items to their shopping cart even if disks are failing, network routes are flapping, or data centers are being destroyed by tornados. Therefore, the service responsible for managing shopping carts requires that it can always write to and read from its data store, and that its data needs to be available across multiple data centers .” Handles 3 million checkouts a day (2009). Availability!

13 .Must be available when partitions happen “Many traditional [ … ]. In such systems, writes may be rejected if the data store cannot reach all (or a majority of) the replicas at a given time. On the other hand, Dynamo targets the design space of an “always writeable” data store (i.e., a data store that is highly available for writes). [ … ] For instance, the shopping cart service must allow customers to add and remove items from their shopping cart even amidst network and server failures. This requirement forces us to push the complexity of conflict resolution to the reads in order to ensure that writes are never rejected”

14 .Must be available when partitions happen “There is a category of applications in Amazon’s platform that can tolerate such inconsistencies and can be constructed to operate under these conditions. For example, the shopping cart application requires that an “Add to Cart” operation can never be forgotten or rejected . If the most recent state of the cart is unavailable, and a user makes changes to an older version of the cart, that change is still meaningful and should be preserved. Note that both “add to cart” and “delete item from cart” operations are translated into put requests to Dynamo . When a customer wants to add an item to (or remove from) a shopping cart and the latest version is not available, the item is added to (or removed from) the older version and the divergent versions are reconciled later. .”

15 .Main idea of CRDTs How does CRDTs get around these consistency problems of eventual consistency ? Create many specialized APIs with custom semantics Shopping cart might need a SET instead of PUT/GET A search engine might need a distributed DAG CS Research Trick: assume more semantics. More limited applicability, but can do things that were impossible before!

16 .Strong Eventual Consistency Strong Eventual Consistency (SEC) is Eventual Consistency with the guarantee that correct replicas that have received the same updates (maybe in different order) have an equivalent correct state! Like eventual consistency but with deterministic outcomes of concurrent updates No need for background consensus No need to rollback Available, fault-tolerant, scalable

17 .Partial Order ( poset ) Set of objects S and an order relationship ≤ between them, such that for all a, b, c in S Reflexive : a ≤ a Antisymmetric : ( a ≤ b ∧ b ≤ a ) ⇒ ( a = b ) Transitive : ( a ≤ b ∧ b ≤ c ) ⇒ ( a ≤ c )

18 .Hesse diagram Simple way of describing posets , with a graph Read bottom to top (smaller to greater), no arrows, just links Remove self links Remove transitive links

19 .Semi-lattice Partial order ≤ set S with a least upper bound (LUB ), denoted ⊔ m = x ⊔ y is a LUB of {x , y} under ≤ iff ∀ m ′ ( x ≤ m ′ ∧ y ≤ m ′) ⇒ ( x ≤ m ∧ y ≤ m ∧ m ≤ m ′ ) The nice thing about semi-lattices is that it follows that ⊔ is: c ommutative : x ⊔ y = y ⊔ x idempotent : x ⊔ x = x associative : ( x ⊔ y ) ⊔ z = x ⊔ ( y ⊔ z )

20 .Example Partial order ≤ on set of integers ⊔: max( ) Then, we have: commutative : max(x, y) = max(y, x) idempotent : max(x, x) = x a ssociative : max(max(x, y), z) = max(x, max(y, z))

21 .Example Partial order ⊆ on sets ⊔: U (set union) Then, we have: commutative : A U B = B U A idempotent : A U A = A a ssociative : (A U B) U C = A U (B U C)

22 .Aha! How can this help us in building replicated distributed systems? Just use the LUB ⊔ to merge state between replicas For instance, could build a CRDT using Supports add(integer) Supports get  returns the maximum integer How? Always correct: available and strongly eventually consistent Can we support remove(integer)?

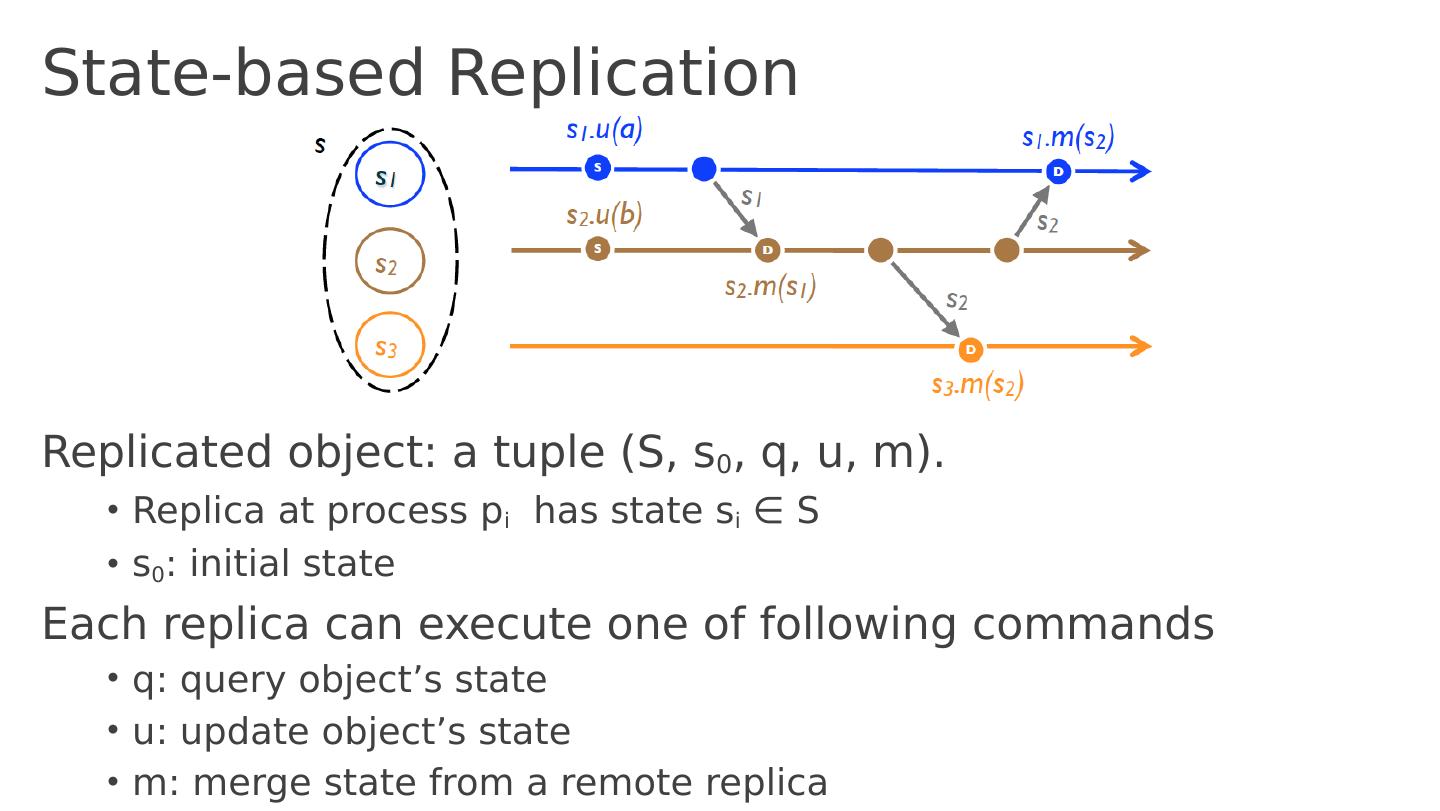
23 .State-based Replication Replicated object: a tuple ( S, s 0 , q, u , m) . Replica at process p i has state s i ∈ S s 0 : initial state Each replica can execute one of following commands q : query object’s state u : update object’s state m : merge state from a remote replica

24 .State-based Replication Algorithm Periodically, replica at p i sends its current state to p j R eplica p j merges received state into its local state by executing m After receiving all updates (irrespective of order), each replica will have same state

25 .Monotonic Semi-lattice Object A state-based object with partial order ≤, noted ( S,≤, s 0 , q, u , m) , that has following properties, is called a monotonic semi -lattice: Set S of values forms a semi-lattice ordered by ≤ Merging state s with remote state s′ computes the LUB of the two states, i.e., s •m (s′ ) = s⊔s ′ State is monotonically non-decreasing across updates, i.e., s ≤ s • u

26 . Convergent Replicated Data Type ( CvRDT ) Theorem : Assuming eventual delivery and termination, any state-based object that satisfies the monotonic semi-lattice property is SEC

27 .Why does it work? Don’t care about order: Merge is both commutative and associative Don’t care about delivering more than once Merge is idempotent

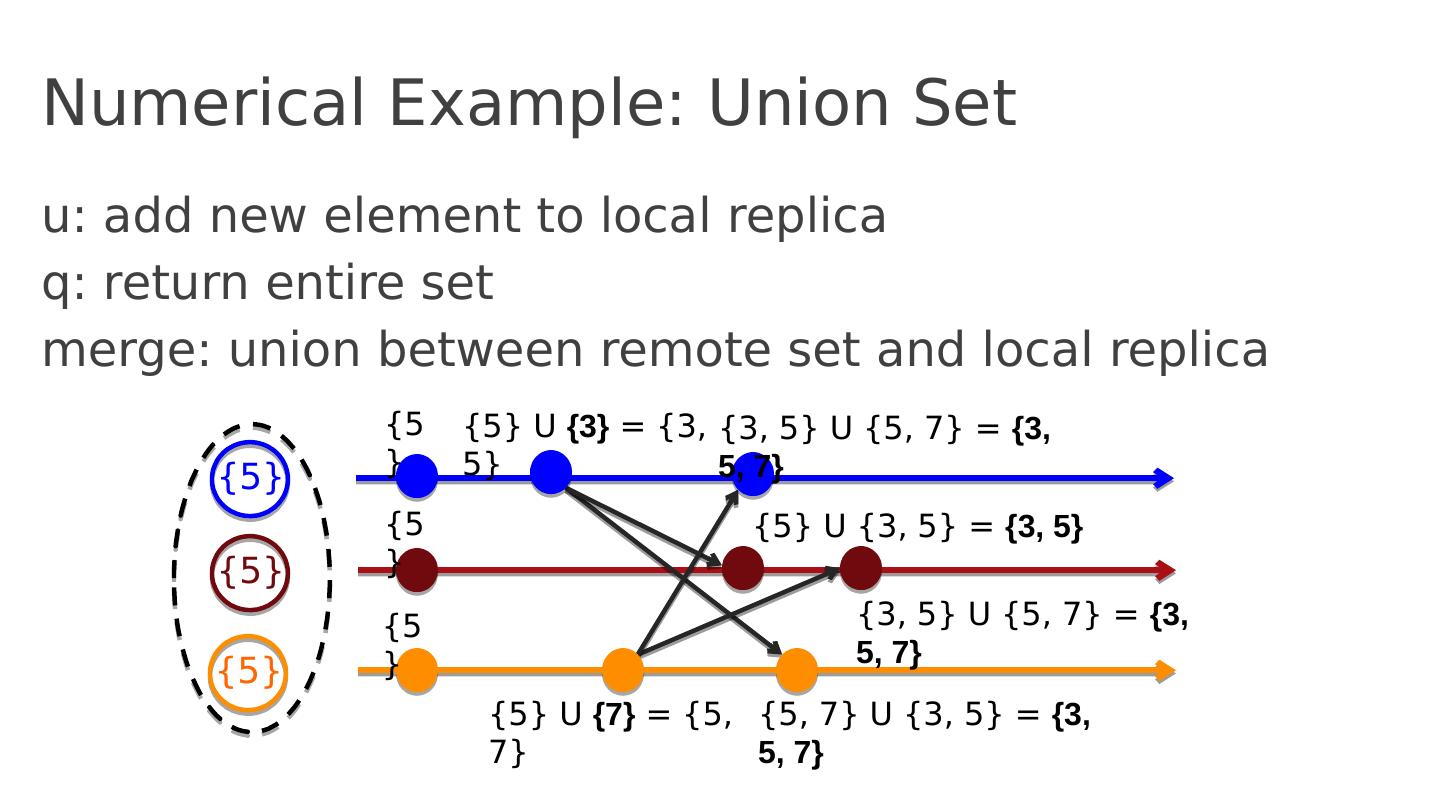
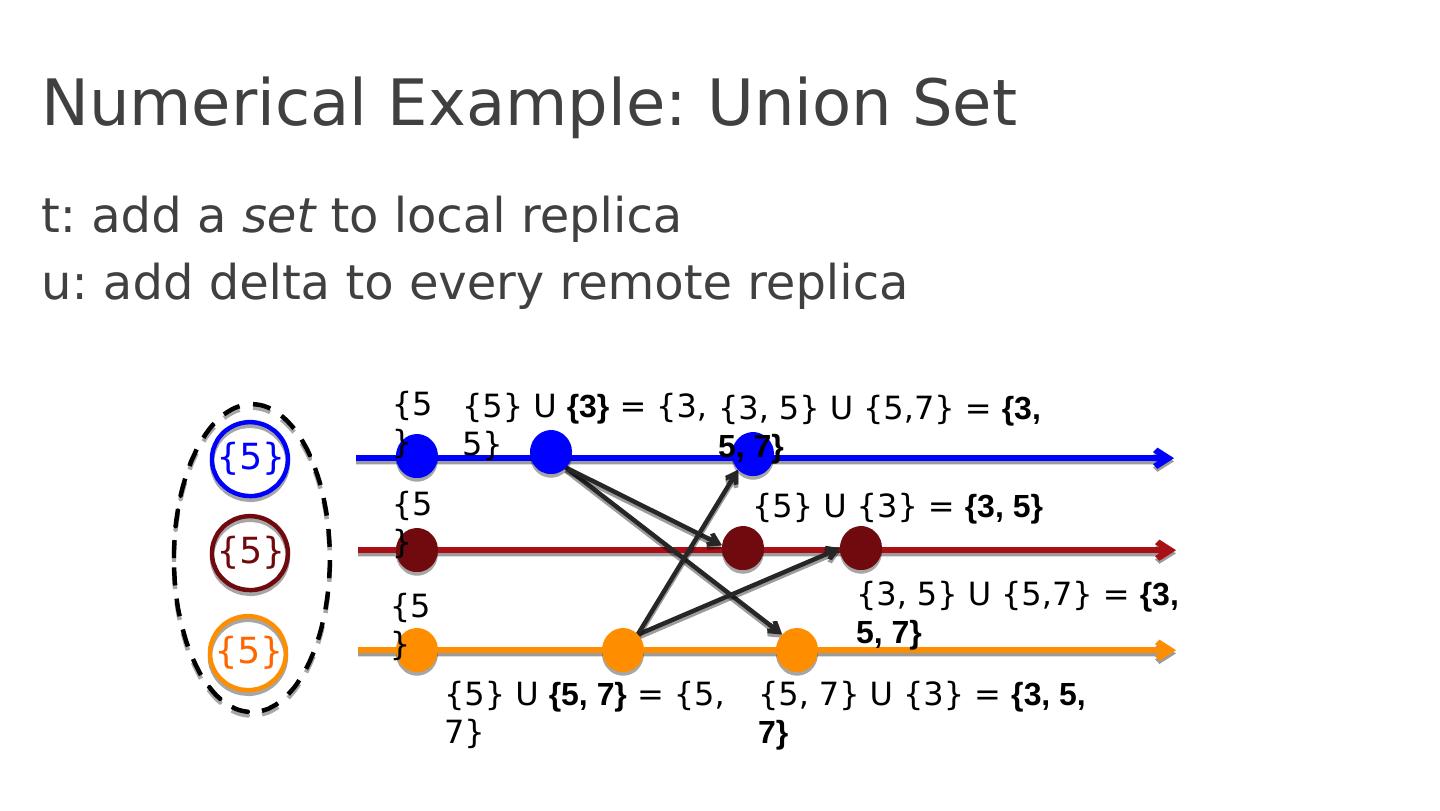
28 .Numerical Example: Union Set u : add new element to local replica q : return entire set m erge: union between remote set and local replica {5} {5} {5} {5} {5} {5} {5} U {3} = {3, 5} {5} U {7} = {5, 7} {3, 5} U {5, 7} = {3, 5, 7} {5, 7} U {3, 5} = {3, 5, 7} {5} U {3, 5 } = {3, 5 } {3, 5} U {5, 7} = {3, 5, 7}

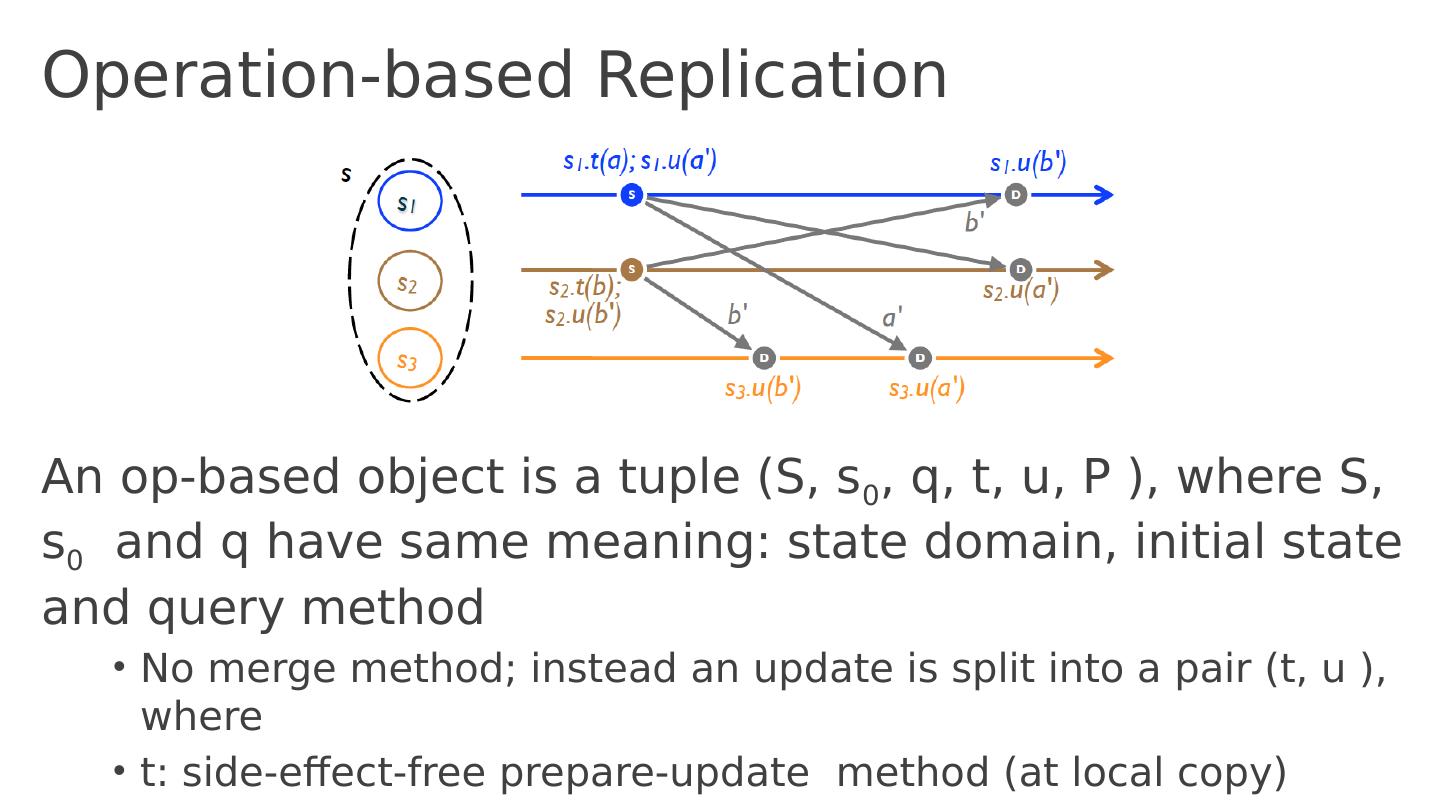
29 .Operation-based Replication An op-based object is a tuple (S, s 0 , q, t, u, P ), where S, s 0 and q have same meaning: state domain, initial state and query method No merge method; instead an update is split into a pair (t, u ) , where t : side -effect-free prepare-update method (at local copy) u : effect-free update method (at all copies) P: delivery precondition (see next)