Basic Ray Tracing

1 .Basic Ray Tracing CMSC 435/634

2 .Visibility Problem Rendering: converting a model to an image Visibility : deciding which objects (or parts) will appear in the image Object- order OpenGL (later) Image-order Ray Tracing (now)

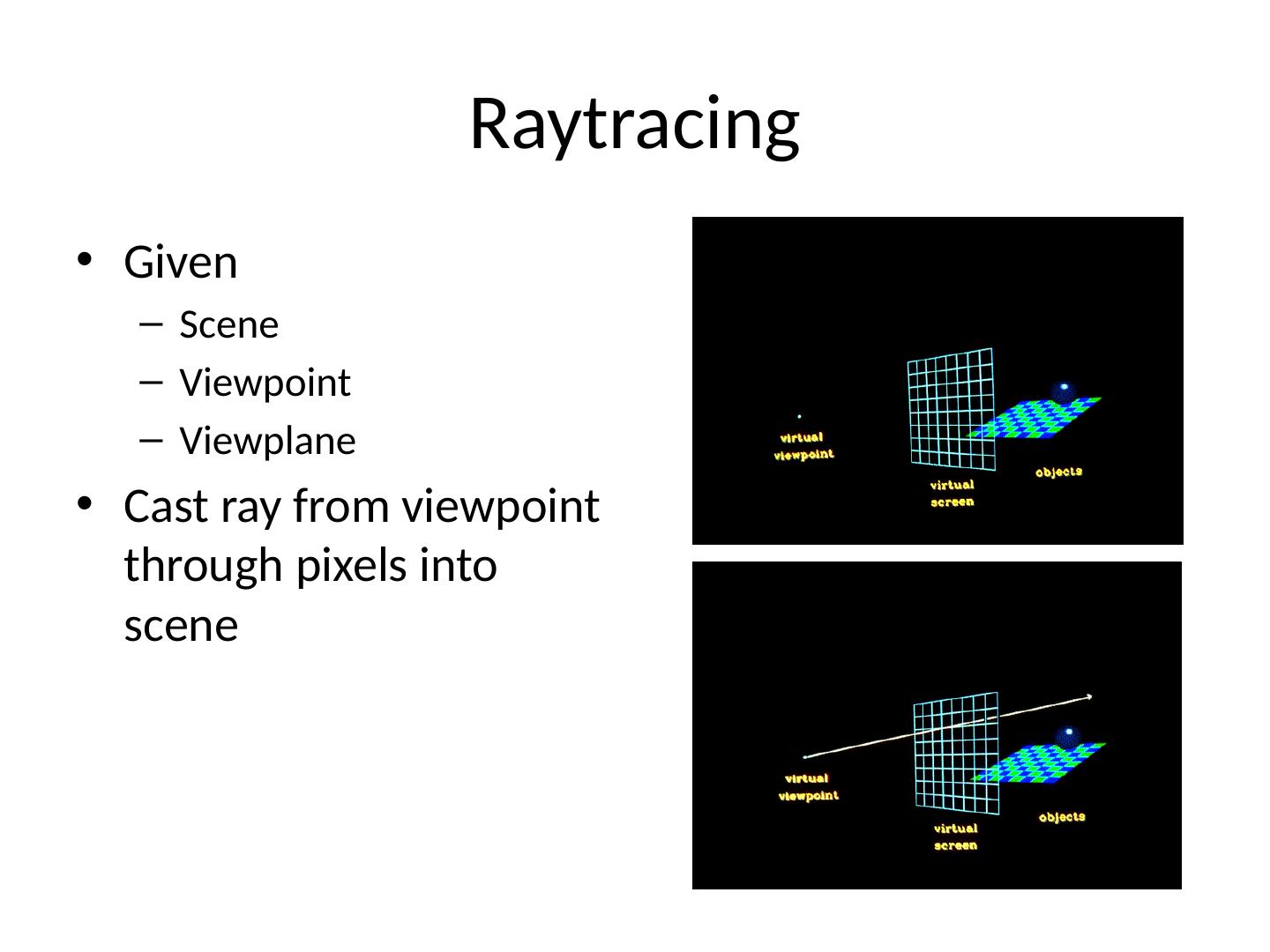
3 .Raytracing Given Scene Viewpoint Viewplane Cast ray from viewpoint through pixels into scene

4 .View

5 .Parametric and Implicit Forms Want to describe an object plane / sphere / triangle / ray / … Parametric: equation with parameters Varying parameters sweeps out object Implicit: equation(s) true on the object

6 .Parametric vs Implicit Object Parametric Implicit Plane Ray Triangle Sphere

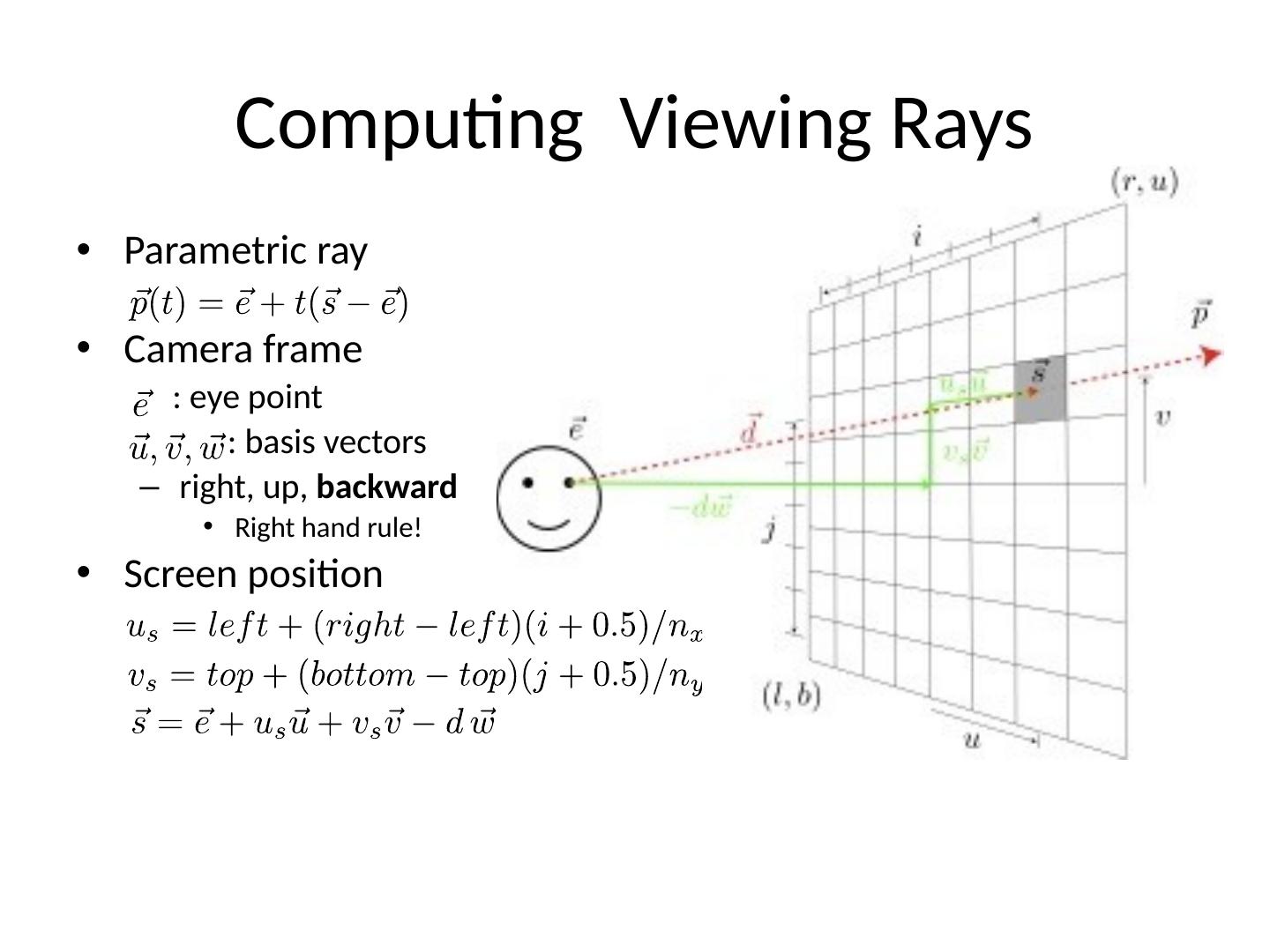
7 .Computing Viewing Rays Parametric ray Camera frame : eye point : basis vectors right, up, backward Right hand rule ! Screen position

8 .Calculating Intersections Define ray parametrically : If is center of projection and is center of pixel, then : points between those locations : points behind viewer : points beyond view window

9 .Ray-Sphere Intersection Sphere in vector form Ray Intersection when

10 .Ray-Sphere Problems When can go bad? Division by 0? Only if , aka ray direction = 0 No real intersections Happens when ray misses the sphere

11 .Ray-Triangle Intersection Intersection of ray with barycentric triangle 4 linear equations ( x,y,z and barycentric sum) in 4 unknowns In triangle if α ≥ 0,  ≥ 0,  ≥ 0 To avoid computing all three, can replace α ≥ 0 with  +  ≤ 1 boolean raytri (ray r, vector p0, p1 , p2, interval [t 0 ,t 1 ] ) { compute t if (( t < t 0 ) or (t > t 1 )) return ( false ) compute  if ((  < 0 ) or (  > 1)) return ( false ) compute  if ((  < 0 ) or ( + > 1)) return ( false ) return true }

12 .Ray-Polygon Intersection Given ray and plane containing polygon What is ray/plane intersection? Is intersection point inside polygon?

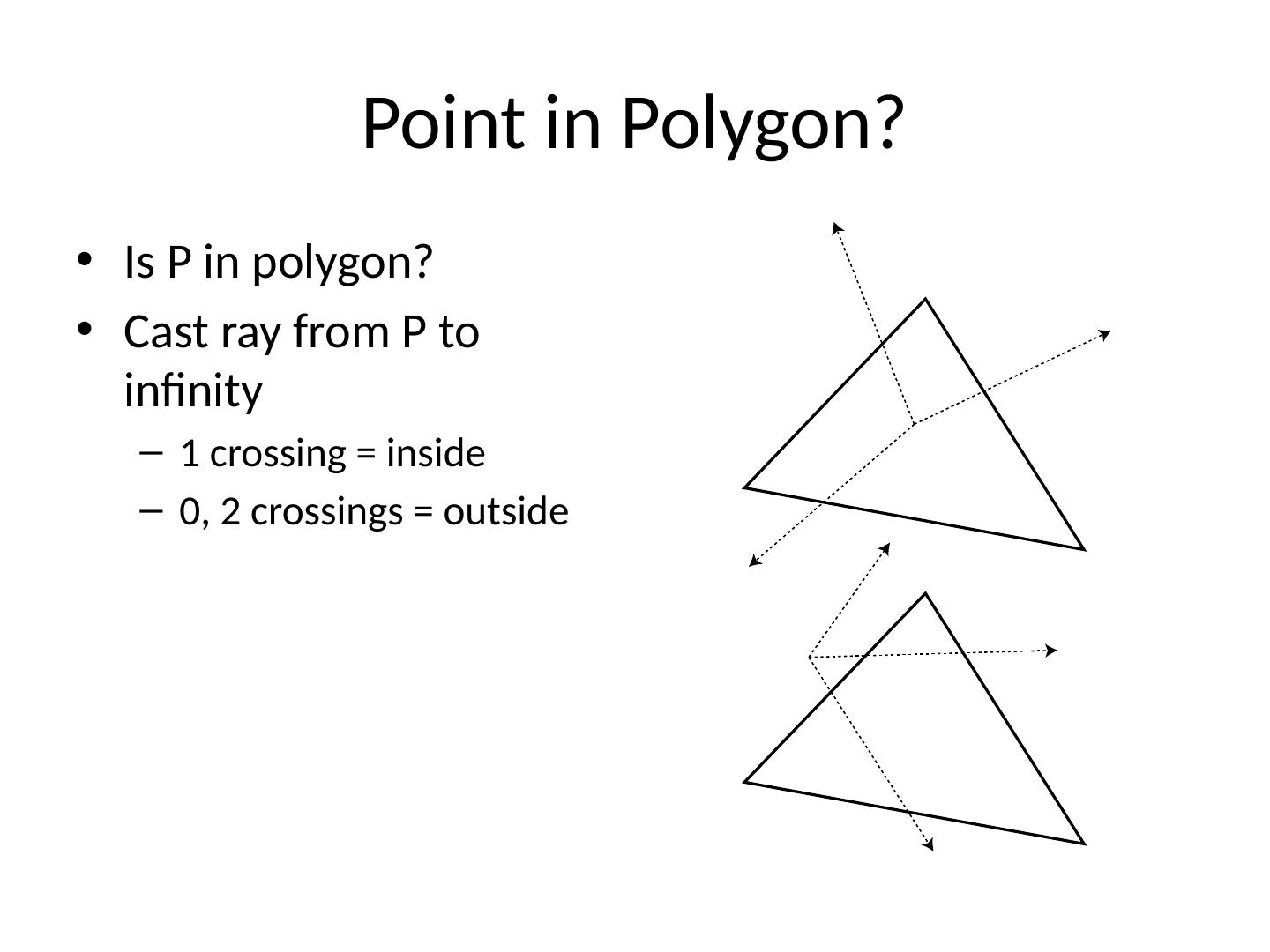
13 .Point in Polygon? Is P in polygon? Cast ray from P to infinity 1 crossing = inside 0 , 2 crossings = outside

14 .Point in Polygon? Is P in concave polygon? Cast ray from P to infinity Odd crossings = inside Even crossings = outside

15 .What Happens ?

16 .Raytracing Characteristics Good Simple to implement Minimal memory required Easy to extend Bad Aliasing Computationally intensive Intersections expensive (75-90% of rendering time) Lots of rays

17 .Basic Illumination Concepts Terms Illumination: calculating light intensity at a point (object space; equation) based loosely on physical laws Shading: algorithm for calculating intensities at pixels (image space; algorithm) Objects Light sources: light-emitting Other objects: light-reflecting Light sources Point (special case: at infinity) Area

18 .Lambert ’ s Law Intensity of reflected light related to orientation

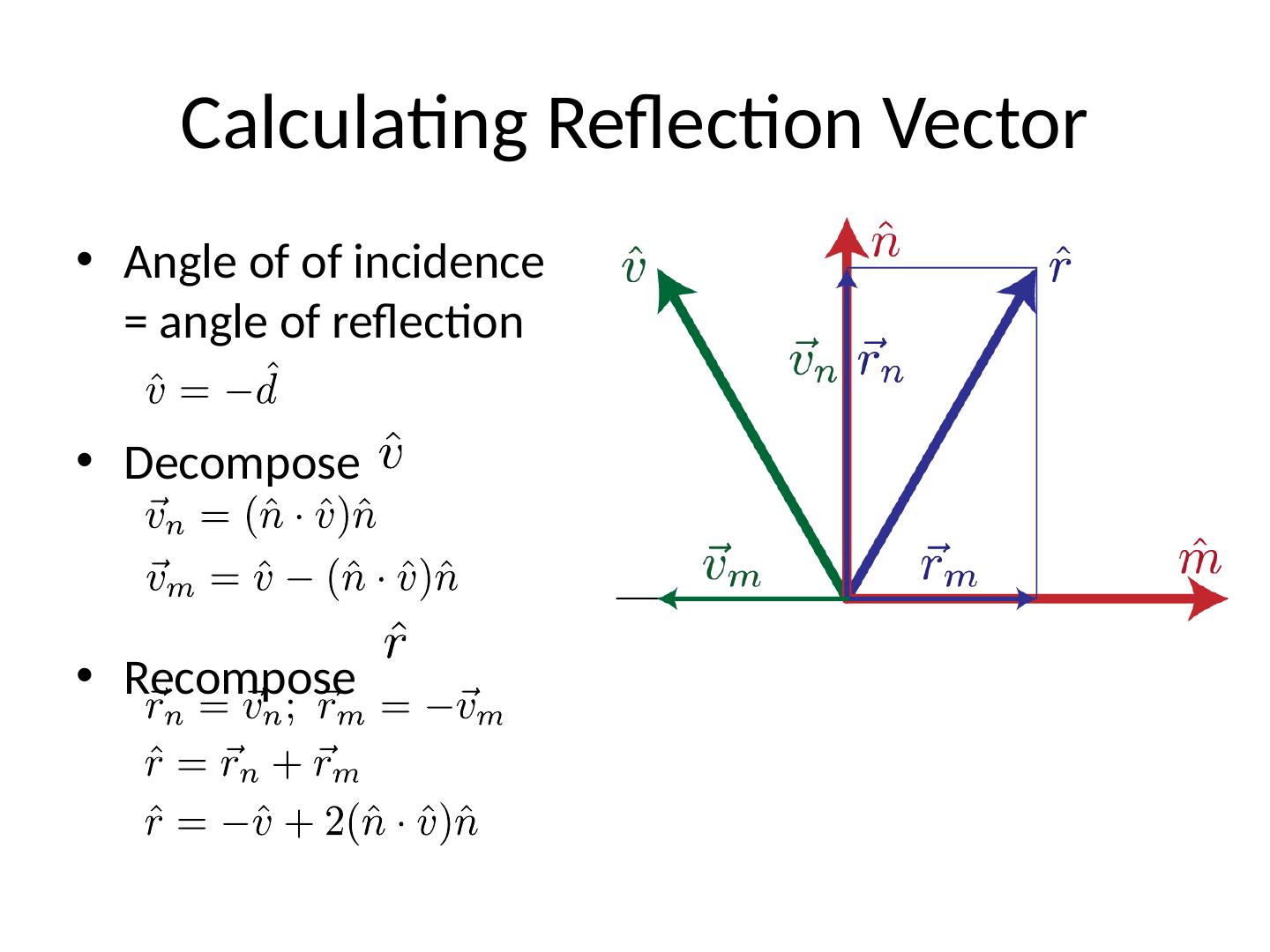
19 .Lambert ’ s Law Specifically: the radiant energy from any small surface area dA in any direction  relative to the surface normal is proportional to cos 

20 .Ambient Light Additional light bounces we’re not counting Approximate them as a constant = Amount of extra light coming into this surface = Amount that bounces off of this surface Total extra light bouncing off this surface

21 .Combined Model Adding color: For any wavelength :

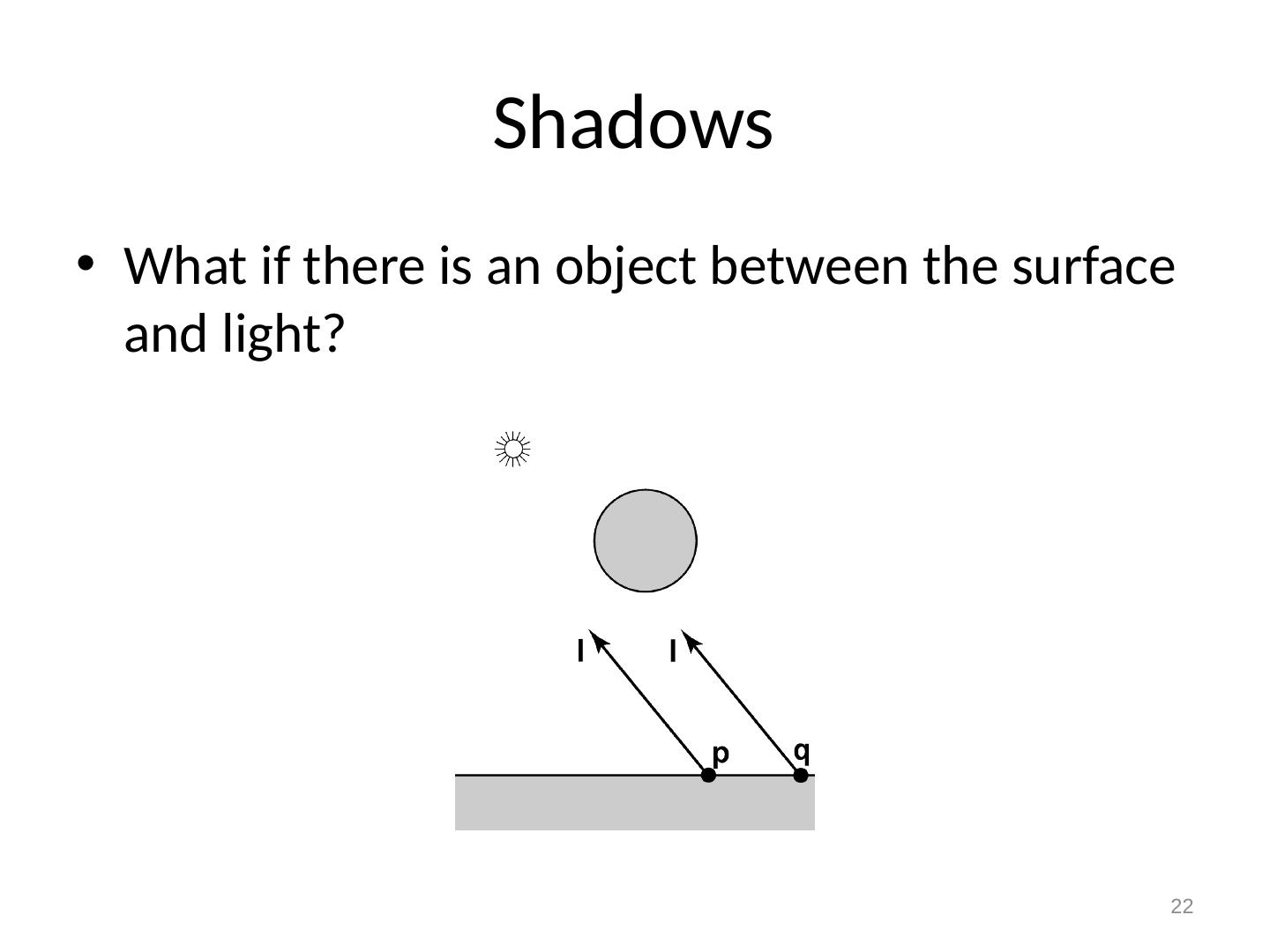
22 .22 Shadows What if there is an object between the surface and light?

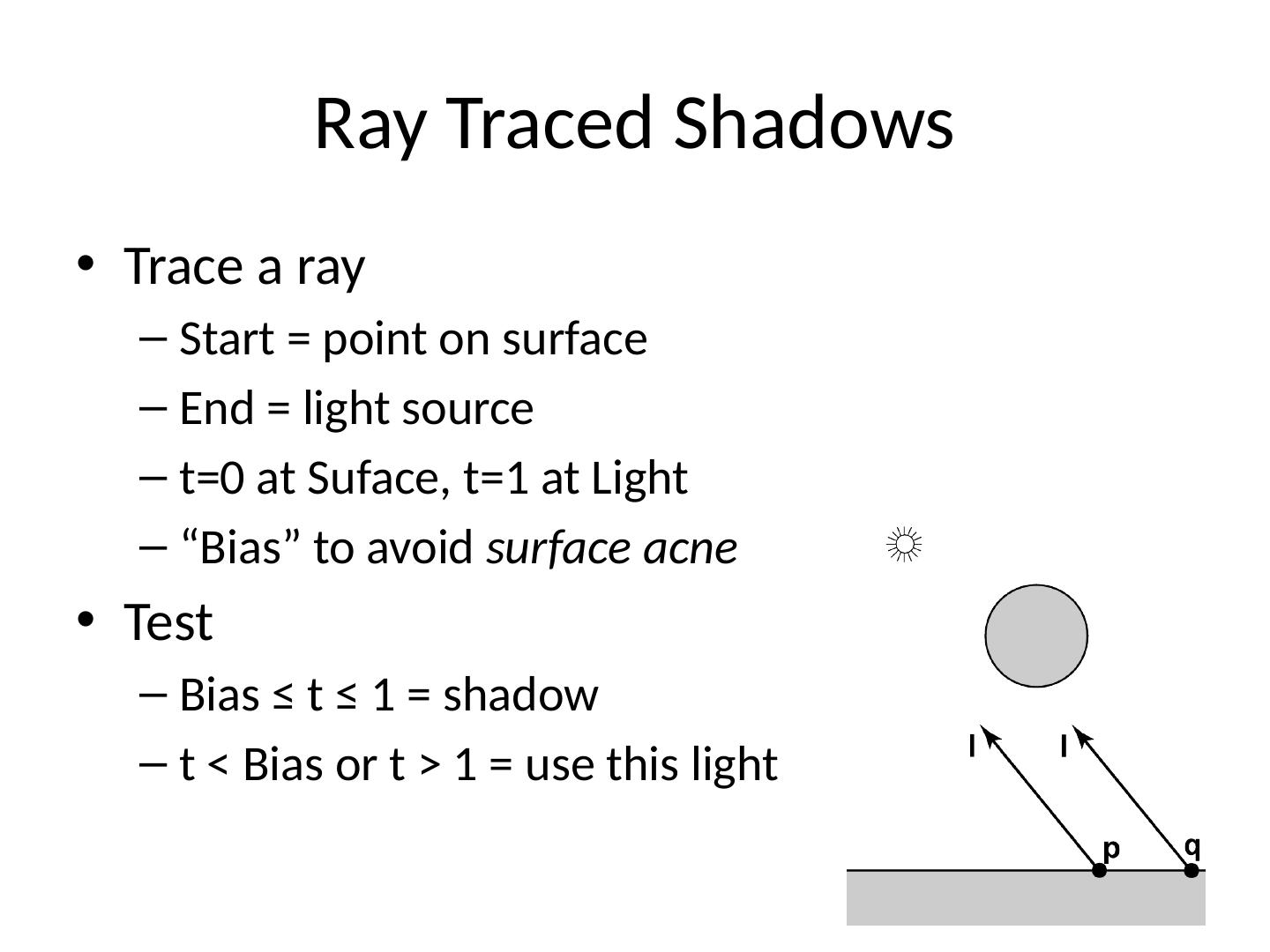
23 .Ray Traced Shadows Trace a ray Start = point on surface End = light source t=0 at Suface , t=1 at Light “Bias” to avoid surface acne Test Bias ≤ t ≤ 1 = shadow t < Bias or t > 1 = use this light

24 .Mirror Reflection The Dark Side of the Trees - Gilles Tran, Spheres - Martin K. B. 24

25 .25 Ray Tracing Reflection Viewer looking in direction d sees whatever the viewer “below” the surface sees looking in direction r In the real world Energy loss on the bounce Loss different for different colors New ray Start on surface, in reflection direction

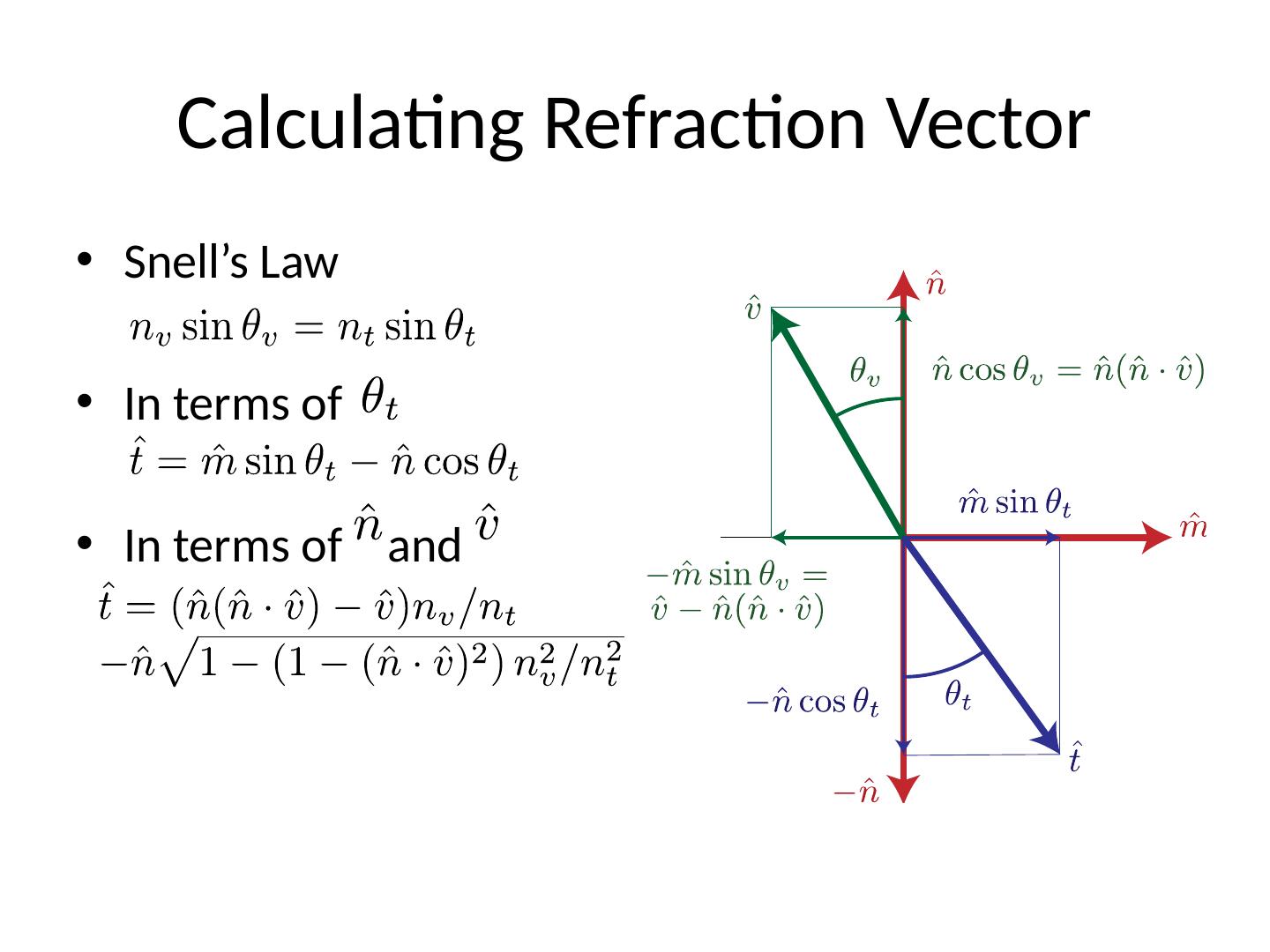
26 .Calculating Reflection Vector Angle of of incidence = angle of reflection Decompose R ecompose

27 .Ray Traced Reflection Avoid looping forever Stop after n bounces Stop when contribution to pixel gets too small

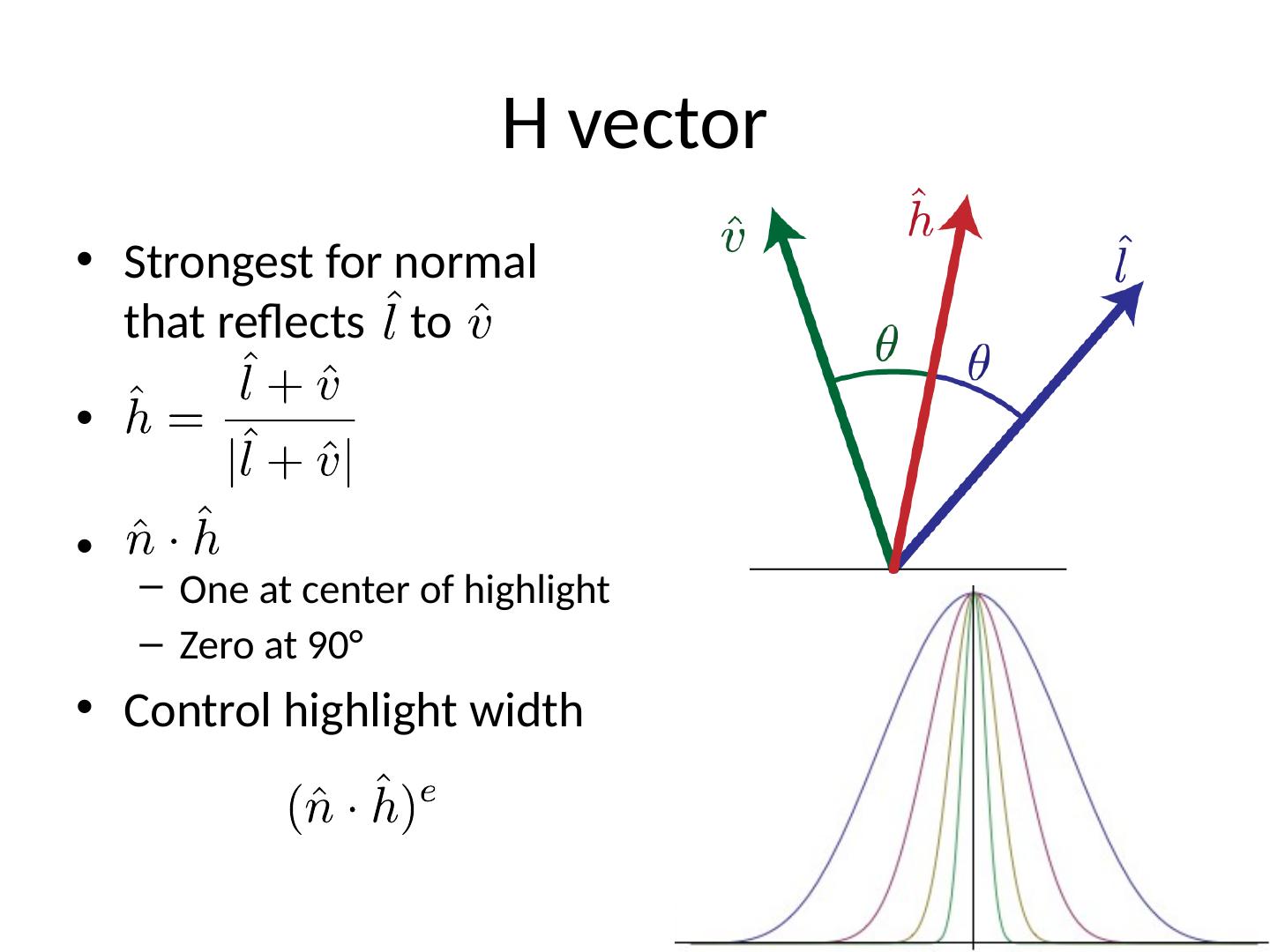
28 .Specular Reflection Shiny reflection from rough surface Centered around mirror reflection direction But more spread more, depending on roughness Easiest for individual light sources

29 .Specular vs. Mirror Reflection