- 快召唤伙伴们来围观吧
- 微博 QQ QQ空间 贴吧
- 文档嵌入链接
- 复制
- 微信扫一扫分享
- 已成功复制到剪贴板
算法分析
展开查看详情
1 .CSE 373 : Data Structures and Algorithms Pep Talk; Algorithm Analysis Riley Porter Winter 2017
2 .Announcements Optional Java Review Section: PAA A102 Tuesday, January 10 th , 3:30-4:30pm . Any materials covered will be posted online . TAs will be around after the session to answer questions. TA office hours will be posted on the website later today HW1 released after class today Extension: Due Tuesday, January 17 th at 11:00PM 2 CSE373: Data Structures & Algorithms Winter 2017
3 .Assumed Knowledge (Pep Talk) Objects in Java : fields, methods, encapsulation, inheritance, interfaces, classes Bein g the Client of Data Structures : List, Set, Stack, Queue, Map, Trees Being the implementer of Data Structures: ArrayList , LinkedList , Binary Trees, testing your objects Binary Search, and some awareness of how sorting works : merge sort, selection sort. Some basic analysis about above . Examples: when to use a HashSet vs a TreeSet ? when does adding into an ArrayList become expensive? why does sorting an array help for searching? Winter 2017 3 CSE373: Data Structures & Algorithms
4 .NOT Assumed Knowledge Full understanding of the difference between the definitions of ADTs vs Data Structures vs Implementations Big O analysis . Maybe you have some awareness, but we don’t expect mastery of Big O yet. Indepth analysis or mastery of sorting or hashing . Anything at all about Graphs, Heaps, AVL Trees, Union Find, Disjoint Sets, Hashing, Topological Sort, Parallelism Any advanced algorithms, dynamic programming, P vs NP, complexity theory, proofs, induction 4 CSE373: Data Structures & Algorithms Winter 2017
5 .Review of last time: Heaps Heaps follow the following two properties: Structure property: A complet e binary tree Heap order property : The priority of the children is always a greater value than the parents (greater value means less priority / less importance) Winter 2017 5 CSE373: Data Structures & Algorithms 15 30 80 20 10 99 60 40 80 20 10 50 700 85 not a heap a heap 450 3 1 75 50 8 6 0 n ot a hea p 10 10
6 .Today – Algorithm Analysis Review math for algorithm analysis Exponents and logarithms, floor and ceiling Analyzing code Big-O definition Using asymptotic analysis (continue next time ) Set ourselves up to analyze why we use Heaps for Priority Queues (continue later this week) 6 CSE373: Data Structures & Algorithms Winter 2017
7 .Review of Logarithms log 2 x =y if x=2 y (so, log 2 1,000,000 = “a little under 20”) Just as exponents grow very quickly, logarithms grow very slowly Log base B compared to log base 2 doesn’t matter so much In computer science we use base 2 because it works nicely with binary and how a computer does math. we are about to stop worrying about constant factors In particular, log 2 x = 3.22 log 10 x 7 CSE373: Data Structures & Algorithms Winter 2017
8 .Review of log properties log(A*B) = log A + log B So log( N k )= k log N log(A/B) = log A – log B log(log x) is written log log x Grows as slowly as 2 2 grows quickly (log x)(log x) is written log 2 x It is greater than log x for all x > 2 It is not the same as log log x 8 CSE373: Data Structures & Algorithms y Winter 2017
9 .Review of floor and ceiling 9 CSE373: Data Structures & Algorithms Floor function: the largest integer < X Ceiling function: the smallest integer > X Winter 2017
10 .Comparin g Algorithms When is one algorithm (not implementation ) better than another? Various possible answers (clarity, security, …) But a big one is performance : for sufficiently large inputs , runs in less time or less space Large inputs (n) because probably any algorithm is “fine” for small inputs Answer will be independent of CPU speed, programming language , coding tricks, etc . 10 CSE373: Data Structures & Algorithms Winter 2017
11 .Comparin g Algorithms Example Given the above list, search for 3, which is better? binary search linear search 11 CSE373: Data Structures & Algorithms Winter 2017 4 2 5 1 8 6 10 9 3 7 1 2 3 4 5 6 7 8 9 10 Given the above list, search for 3, which is better? binary search linear search
12 .Analyzing Algorithms As the size of an algorithm’s input grows: How much longer does the algorithm take ( time ) How much more memory does the algorithm need ( space ) Ignore constant factors, think about large input: there exists some input size n 0 , that for all input sizes n larger than n 0 , binary search is better than linear search on sorted input Analyze code to compute runtime, then look at how the runtime behaves as n gets really large (asymptotic runtime) 12 CSE373: Data Structures & Algorithms Winter 2017
13 .Analyzing Code “Constant time” operations: Arithmetic, Variable Assignment, Access one Java field or array index, etc Complex operations (approximation ): Consecutive Statements: Sum of time of each statement Conditionals: Time of condition + max( ifBranch , elseBranch ) Loops: Number of iterations ∗ Time for Loop Body Function Calls: Time of function’s body 13 CSE373: Data Structures & Algorithms Winter 2017
14 .Example What is the runtime of this pseudocode : x := 0 for i =1 to N do for j=1 to N do x := x + 3 return x 14 CSE373: Data Structures & Algorithms Winter 2017
15 .Example Solution What is the runtime of this pseudocode : x := 0 for i =1 to N do for j=1 to N do x := x + 3 return x 1 assignment + (N iterations of loop * (N iterations of loop * 1 assignment and math)) 1 return 1 + (N * (N * 1)) + 1 = N 2 + 2 However, what we care about here is the N 2 part. Let’s look at asymptotic runtimes to see why. 15 CSE373: Data Structures & Algorithms Winter 2017
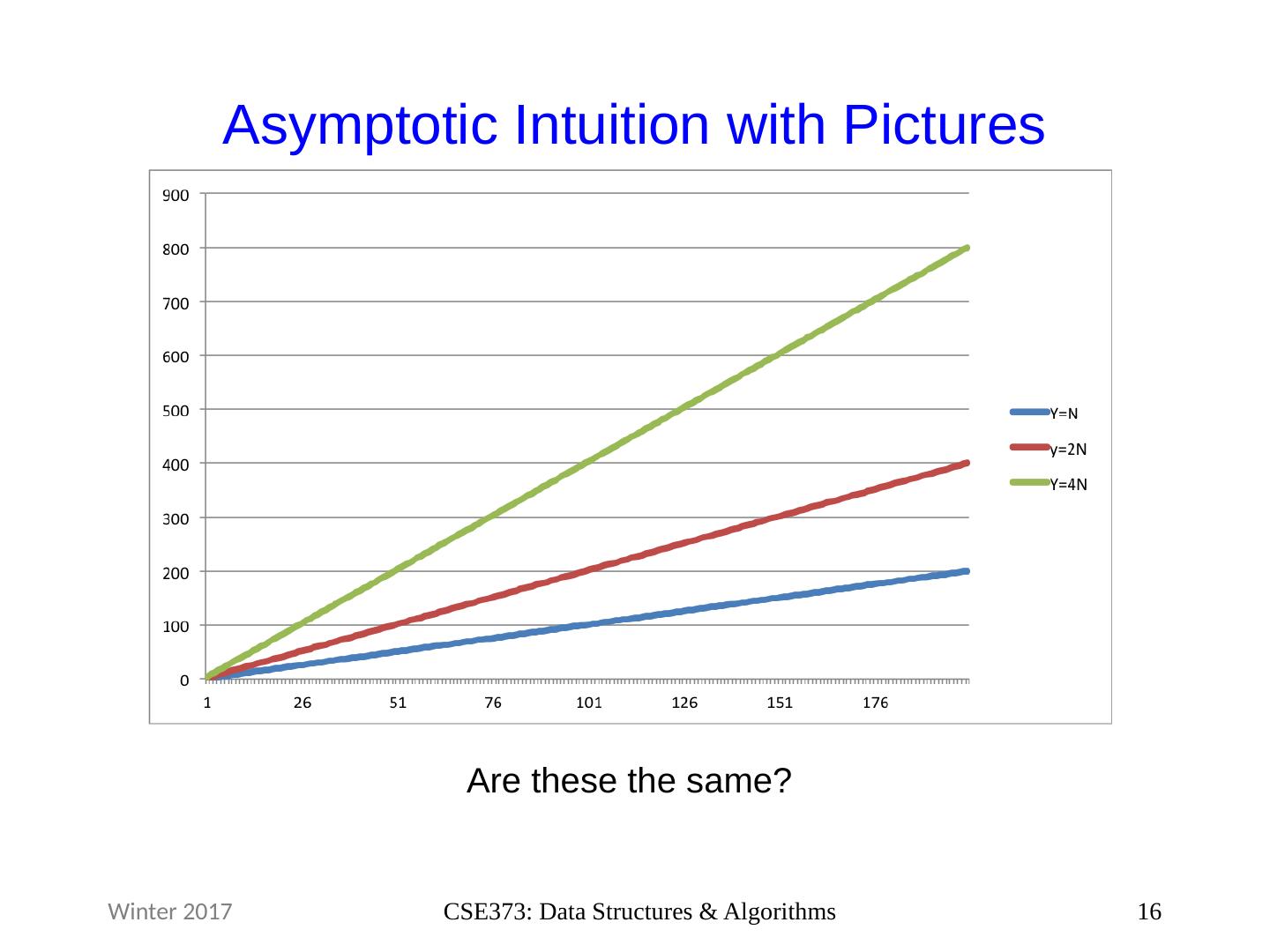
16 .Asymptotic Intuition with Pictures 16 CSE373: Data Structures & Algorithms Winter 2017 Are these the same?
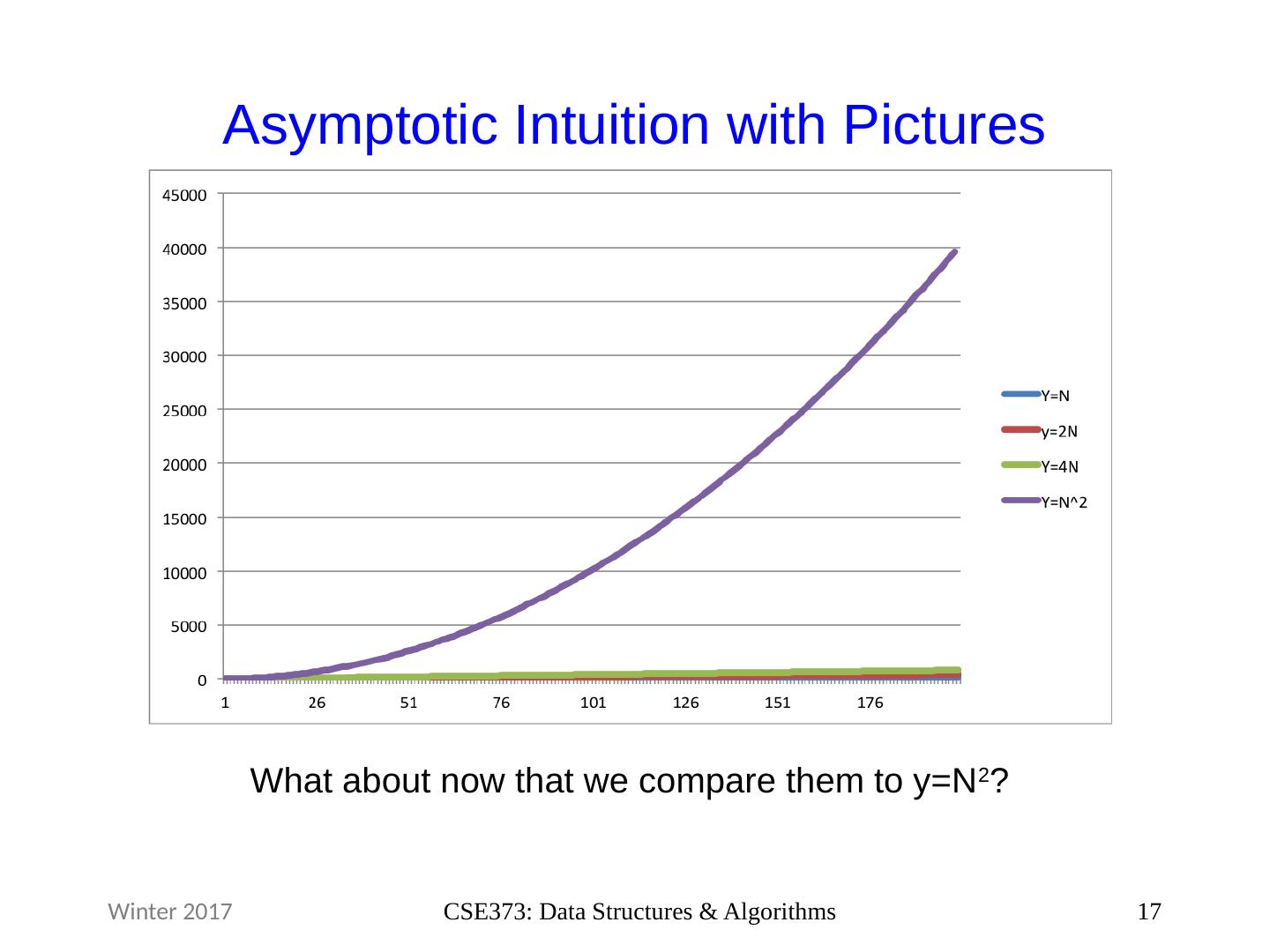
17 .Asymptotic Intuition with Pictures 17 CSE373: Data Structures & Algorithms Winter 2017 What about now that we compare them to y=N 2 ?
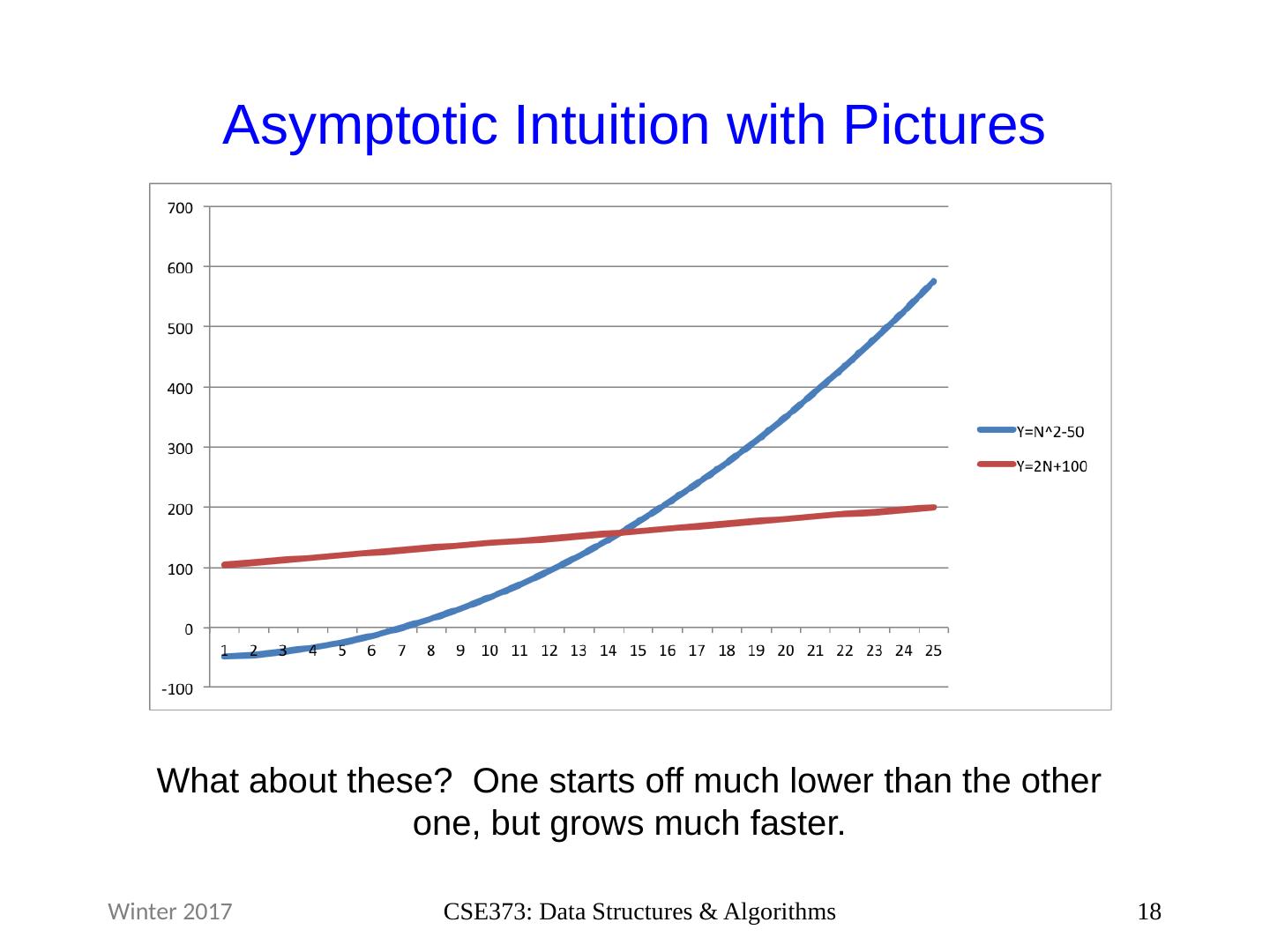
18 .Asymptotic Intuition with Pictures 18 CSE373: Data Structures & Algorithms Winter 2017 What about these? One starts off much lower than the other one, but grows much faster.
19 .Asymptotic Notation About to show formal definition, which amounts to saying: Calculate Runtime by analyzing code Eliminate low-order terms Ignore constants and coefficients Examples: 4 n + 5 0.5 n log n + 2 n + 7 n 3 + 2 n + 3 n n log (10 n 2 ) 19 CSE373: Data Structure & Algorithms Winter 2017
20 .Examples with Big -O Asymptotic Notation True or F alse ? 3n+10 ∈ O(n) 4+2n ∈ O(1) 20-3n ∈ O( n 2 ) n +2logn ∈ O( logn ) logn ∈ O(n+2logn ) 20 CSE373: Data Structures & Algorithms Winter 2017
21 .Examples with Big- O Asymptotic Notation Solutions True or F alse ? 3n+10 ∈ O(n) True (n = n) 4+2n ∈ O(1) False : (n >> 1) 20-3n ∈ O( n 2 ) True: (n ≤ n 2 ) n +2logn ∈ O( logn ) False : (n >> logn ) logn ∈ O(n+2logn) True: ( logn ≤ n+2logn) 21 CSE373: Data Structures & Algorithms Winter 2017
22 .Formally Big- O Definition: g( n ) is in O( f( n ) ) if there exist constants c and n 0 such that g( n ) c f( n ) for all n n 0 To show g( n ) is in O( f( n ) ) , pick a c large enough to “cover the constant factors” and n 0 large enough to “cover the lower-order terms” Example: Let g( n ) = 3 n 2 +17 and f( n ) = n 2 c =5 and n 0 =10 is more than good enough This is “less than or equal to” So 3 n 2 +17 is also O ( n 5 ) and O (2 n ) etc. 22 CSE373: Data Structure & Algorithms Winter 2017
23 .Big- O We use O on a function f( n ) (for example n 2 ) to mean the set of functions with asymptotic behavior less than or equal to f( n ) So (3 n 2 +17) is in O ( n 2 ) 3 n 2 +17 and n 2 have the same asymptotic behavior What it means: For your runtime, asymptotically, O(function) is the family of functions that defines the upper bound. There is a size of input ( n 0 ) and a constant factor ( c ) you can use to make O(function) strictly larger than your runtime. 23 CSE373: Data Structure & Algorithms Winter 2017
24 .Examples using formal definition A valid proof is to find valid c and n 0 : Let g( n ) = 1000 n and f( n ) = n 2. The “cross-over point” is n =1000 So we can choose n 0 =1000 and c =1 Many other possible choices, e.g., larger n 0 and/or c Let g( n ) = n 4 and f( n ) = 2 n. W e can choose n 0 =20 and c =1 24 CSE373: Data Structure & Algorithms Definition: g( n ) is in O( f( n ) ) if there exist constants c and n 0 such that g( n ) c f( n ) for all n n 0 Winter 2017
25 .What’s with the c The constant multiplier c is what allows functions that differ only in their largest coefficient to have the same asymptotic complexity Example: g( n ) = 7 n +5 and f( n ) = n For any choice of n 0 , need a c > 7 (or more) to show g( n ) is in O( f( n ) ) 25 CSE373: Data Structure & Algorithms Definition: g( n ) is in O( f( n ) ) if there exist constants c and n 0 such that g( n ) c f( n ) for all n n 0 Winter 2017
26 .Big-O: Common Names O (1) constant (same as O ( k ) for constant k ) O ( log n ) logarithmic O ( n ) linear O(n log n ) “ n log n ” O ( n 2 ) quadratic O ( n 3 ) cubic O ( n k ) polynomial (where is k is any constant: linear, quadratic and cubic all fit here too.) O ( k n ) exponential (where k is any constant > 1) Note : “exponential” does not mean “grows really fast”, it means “grows at rate proportional to k n for some k >1 ”. Example: a savings account accrues interest exponentially ( k =1.01? ). 26 CSE373: Data Structures & Algorithms Winter 2017
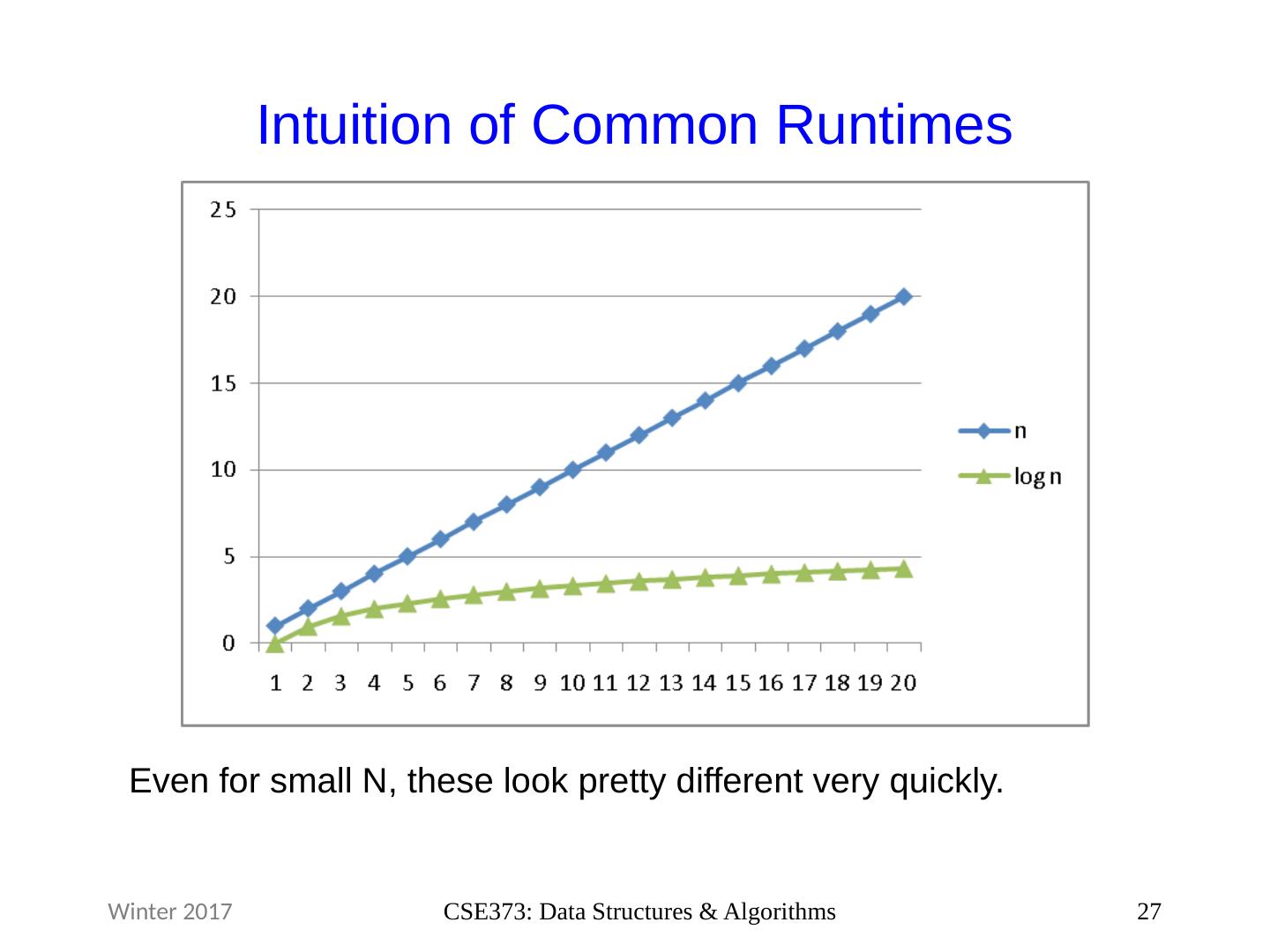
27 .Intuition of Common Runtimes 27 CSE373: Data Structures & Algorithms Winter 2017 Even for small N, these look pretty different very quickly.
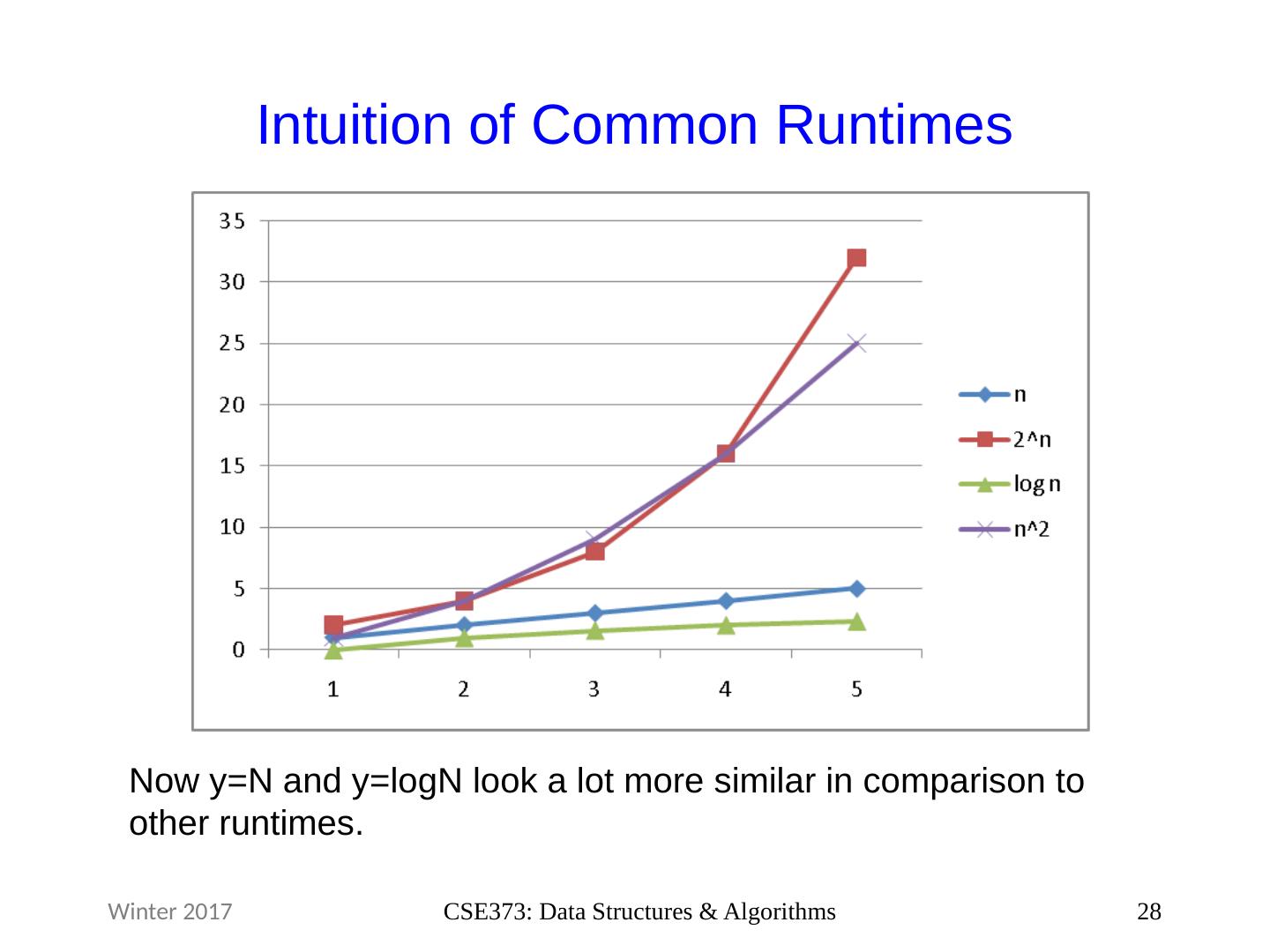
28 .Intuition of Common Runtimes 28 CSE373: Data Structures & Algorithms Winter 2017 Now y=N and y= logN look a lot more similar in comparison to other runtimes.
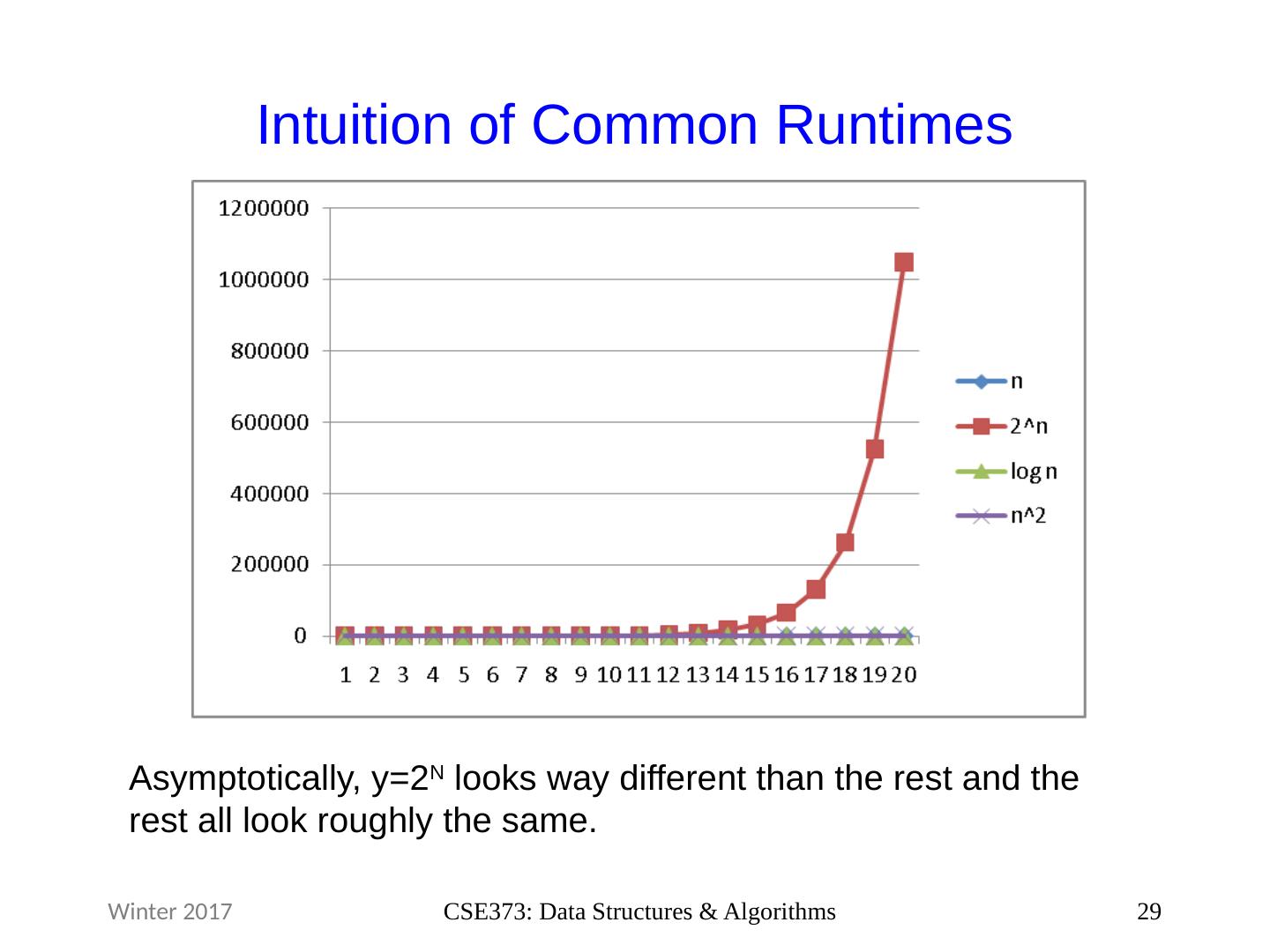
29 .Intuition of Common Runtimes 29 CSE373: Data Structures & Algorithms Winter 2017 Asymptotically, y=2 N looks way different than the rest and the rest all look roughly the same.