概率论与数理统计第十二章---假设检验

1 . 第十一章 假设检验  假设检验的基本原理  显著水平检验法与正态总体检验 

2 . 第十一章 假设检验 一、检验问题的提法 假设检验是即同估计密切联系，但又有重要区别的一种推 断方法。 例如：某种电子元件寿命 X 服从参数为 λ 的指数分布，随机抽 取其中的 n 件。测得其寿命数据， 问题⑴，这批元件的平均寿命是多少？ 问题⑵，按规定该型号元件当寿命不小于 5000(h)h)) 为合 格，问该批元件是否合格？ 问题⑴是对总体未知参数 μ=E(X)=1/E(h)X)=E(X)=1/1/λ 作出估计。回答 “ μ 是多少？”，是定量的。问题⑵则是对假设“这批元件合格” 做出接受还是拒绝的回答，因而是定性的。 

3 . 第十一章 假设检验 对上述例子，还可做更细致考察，设想如基于一次观察 数据算出 μ 的估计值 ˆ 5001(h) ，我们能否就此接受“这批 元件合格”的这一假设呢？尽管 但这个估计仅仅 ˆ  5000(h), 是一次试验的结果，能否保证下一次测试结果也能得到 μ 的 估计值大于 5000 呢？也就是说从观察数据得到的结果 ˆ 5001 与参考值 5000 的差异仅仅是偶然的呢？还是总体均值 μ 确实 有大于 5000 的“趋势”？ 这些问题是以前没有研究过的。一般而言，估计问题 是回答总体分布的未知参数是多少？或范围有多大？而假设 检验问题则是回答观察到的数据差异只是机会差异，还是反 映了总体的真实差异？因此两者对问题的提法有本质不同。 

4 . 第十一章 假设检验 二 . 原假设和备择假设 下面通过一个例子介绍 原假设和备择假设 

5 . 例 1( 酒精含量 ) 一种无需医生处方即可达到的 治疗咳嗽和鼻塞的药。按固定其酒精含量为 5﹪. 今从一出厂的一批药中随机抽取 10 瓶 , 测试其酒 精含量得到的 10 个含量的百分数 : 5.01, 4.87, 5.11, 5.21, 5.03, 4.96, 4.78, 4.98, 4.88, 5.06 如果酒精含量服从正态分布 N(h)μ,0.00016), 问 该批药品的酒精含量是否合乎规定 ? 任务 : 通过样本推断 X 的均值 μ 是否等于 5. 假设 : 上面的任务就是要通过样本去检验“ X 的均值 = 5” 这样一个假设是否成立 .( 在数理统计中把“ X 的均 值 μ=5” 这样一个待检验的假设记作“ H0:μ=5” 称为 “原假设”或 “零假设” . 表明数据的“差异”是偶然的 , 总体没有 “变异”发生 . 

6 . 原假设的对立面是“ X 的均值 μ≠10” 记作“ H1: μ≠10” 称为“对立假设”或“备择假设” . 表明数据的 “差异”不是偶然的 , 是总体 “变异”的表现 . 把它们合写在一起就是 :H0:μ=10 H1:μ≠10 原假设 H0 表明含量符合规定，这个 5﹪ 也称之 为期望数，尽管 10 个数据都 5﹪ 与有出入，这只是 抽样的随机性所致 ; 备择假设 H1 表明总体均值 μ 已 经偏离了期望数 5﹪ ，数据与期望数 5﹪ 的差异是 其表现 . 假设检验 必须在原假设与备择 的任务 假设之间作一选择 

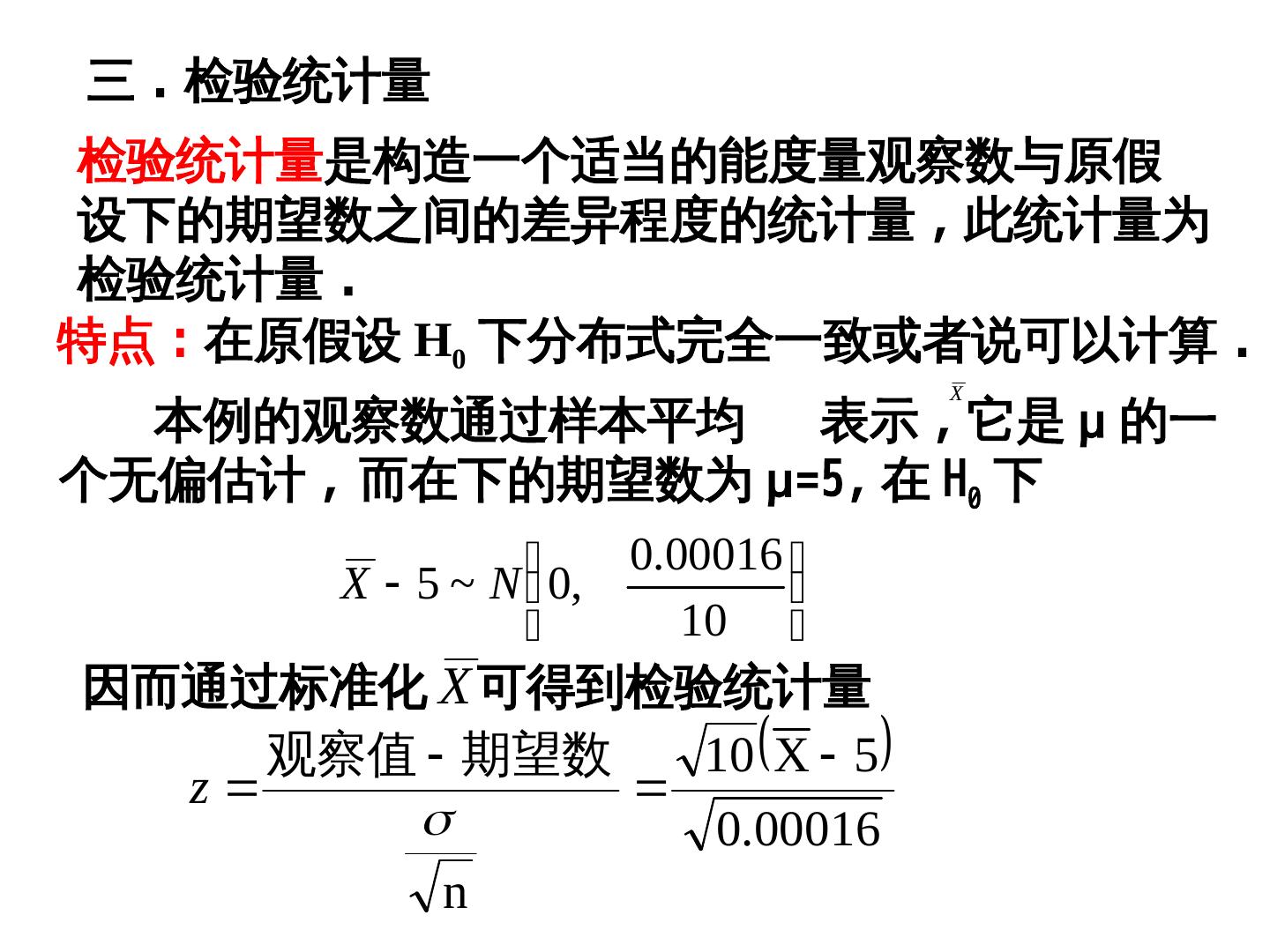
7 .三 . 检验统计量 检验统计量是构造一个适当的能度量观察数与原假 设下的期望数之间的差异程度的统计量 , 此统计量为 检验统计量 . 特点 : 在原假设 H0 下分布式完全一致或者说可以计算 . X 本例的观察数通过样本平均 表示 , 它是 μ 的一 个无偏估计 , 而在下的期望数为 μ=5, 在 H0 下  0.00016  X  5 ~ N  0,   10  因而通过标准化 X 可得到检验统计量 观察值  期望数 10  X  5 z   0.00016 n 

8 .四 . 否定论证及实际推断原理 否定论证是假设检验的重要推理方法 , 其要旨是 : 先假定原假设 H0 成立 , 如果从试验观察数据及此假定 将导致一个矛盾的结果 , 则必须否定这个原假设 ; 反之 , 如果不出矛盾的结果 , 就不能否定原假设 . 从试验数据判断是否导致一个矛盾的结果 , 一个重 要的依据是小概率事件的实际推断原理 . 看例 1, 由 观察数据 , 可算得的X 观察值为 4.989, 代入统计 量 Z 的表达式 , 得 Z 的观察值为  10 0.011 0.0348 Z   2.7509 0.00016 0.01265 

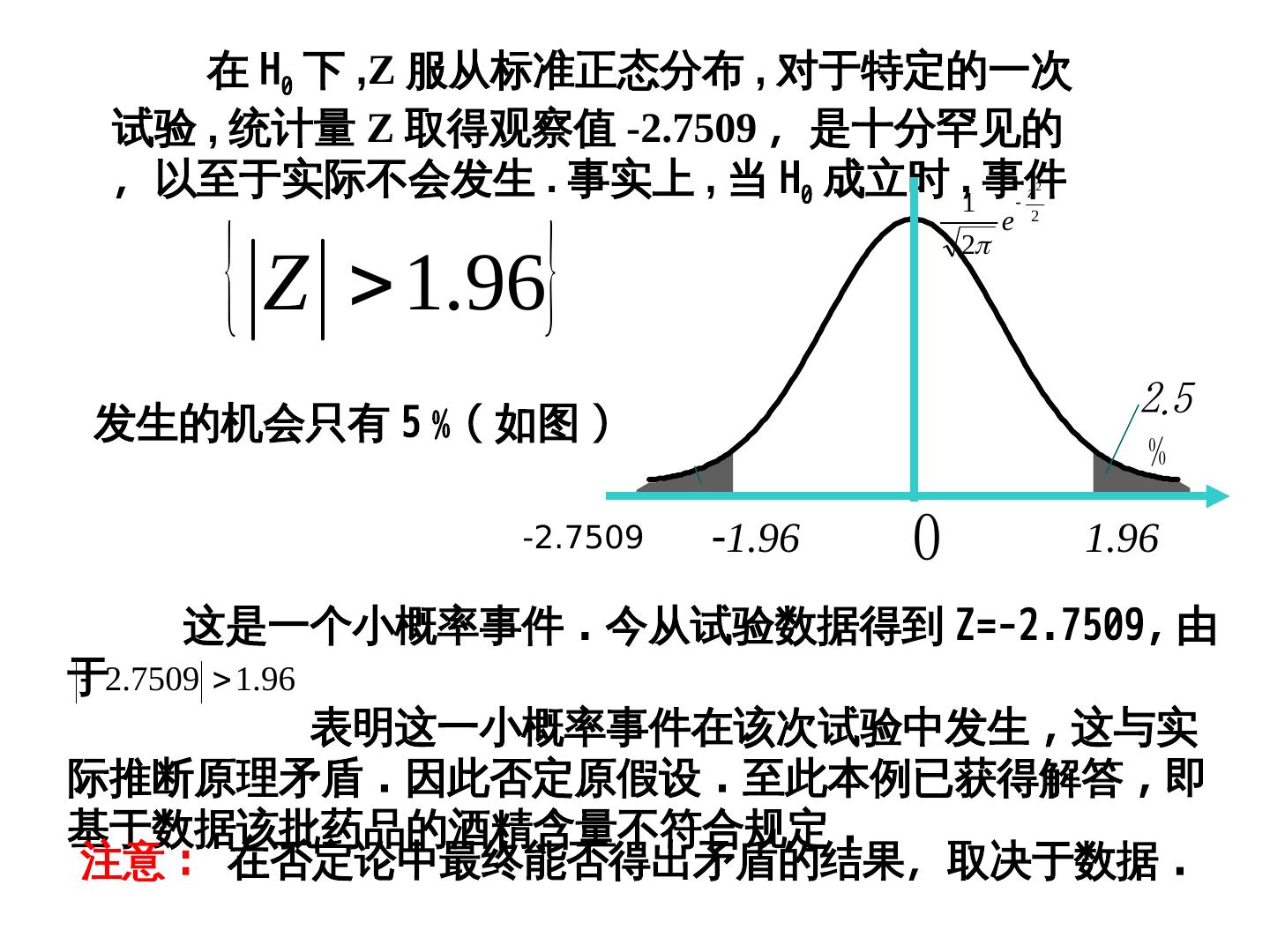
9 . 在 H0 下 ,Z 服从标准正态分布 , 对于特定的一次 试验 , 统计量 Z 取得观察值 -2.7509 ，是十分罕见的 ，以至于实际不会发生 . 事实上 , 当 H0 成立时 ,1 事件  z2 Z  1.96 e 2 2  发生的机会只有 5﹪( 如图 ) ﹪ -2.7509 1.96  1.96 这是一个小概率事件 . 今从试验数据得到 Z=-2.7509, 由 于  2.7509  1.96 表明这一小概率事件在该次试验中发生 , 这与实 际推断原理矛盾 . 因此否定原假设 . 至此本例已获得解答 , 即 基于数据该批药品的酒精含量不符合规定 . 注意 : 在否定论中最终能否得出矛盾的结果，取决于数据 . 

10 . 假设检验的两类错误 第二节 显著水平检验法与正态总体检验 所作判断 接受 H0 拒绝 H0 真实情况 H0 为真 正确 第一类错误 (弃 真) H0 为假 第二类错误 正确 (取 伪) 注意 : 不可能消除这两种错误 , 而只能控制发生 这两类错误之一的概率 . 

11 . 第二节 显著水平检验法与正态总体检验 假设 H0 与 H1 从一开始就不是“平等的” . 在很多情况下 , 人们希望通过收集数据拒绝 H0, 从而达到接受 H1 的目的 . 因而控制犯第一类错误概率就变得十分重要了 , 使得拒绝 了一个真实的 H0 的可能性降低到一个我们能接受的程度 . 二 . 显著水平检验法 显著水平检验法 : 在数据收集之前就已经设定好一 个 检验规则 , 即文献上称之为拒绝域 R, 使得当样本观察值落 入对拒绝域 R 的要求是 : 在 H0 下 { 样本落入 R} 为一小概率 事件R, 就拒绝 R0. 挤兑预先给定的 0<α<1 有 P({ 样本落入 R}|H0)≤ α 

12 .例 3 某降价盒装饼干，其包装上的广告上称每盒质量为 269g. 但有顾客投诉，钙饼干质量不足 269g 。为此质检部门从准备出 厂的一批盒装饼干中，随机抽取 30 盒，由测得的 30 个质量数据 算出样本平均为 268. 假设盒装饼干质量服从正态分布 N(μ ， 22 ), 以显著水平 α=0.05 检验该产品广告是否真实 . 解 : 依题意 , 可设原假设 H0:μ=269 备择假设 H1:μ<269 X 作为未知参数 μ 的点估计 , 因此 X  269 偏小应该拒绝 H0. 若 H0 成立 ,  22  X ~ N  269.   30  则有 Z  30  X  269 2 则在下 Z~N(0,1), 即 Z 的分布已知，因而 Z 可以做检验统计量， 偏小等价于 Z 偏小，从而得到拒绝域的形式如下  30  X  269  R   k 其中 k 待定，称之为临界值 .  2  

13 . α=E(X)=1/0.05, 为求显著水平 0.05 的检验 , 只需选取 k 使得 P Z  k | H 0  0.05 查表可得 k   0.95  1.645 因而得到水平 0.05 检验的拒绝域  30  X  269  R    1.645  2  代入数据得 Z=-2.74, 显然小于临界值 -1.645, 因而依据检验 规则应该拒绝 H0, 即该盒装广告有不实广告行为 . 总结求解步骤 

14 . 第二节 显著水平检验法与正态总体检验 三 . 正态总体的显著水平检验 例 4( 例 3 续 ) 在上例中，若盒装饼干重量服从正态分 布 N(μ,σ2), μ 与 σ2 均未知，已知样本平均 X 268 修正样本标准差为 S  1.8 ，求解相同的问题 . 此时不能用使用 Z 作为统计量 , 因为 : 30  X  269  Z  其中 σ 未知 , 今用 S* 代替 σ, 得到 t 的统计量 S * 30  X  269  T S 由正态总体抽样分布基本定理可知 : 

15 . 第二节 显著水平检验法与正态总体检验 在 H0 下 : T ~ t ( 29), 同上例作相同的分析 , 可得到拒绝域为 R  T  k  , 临界值通过查自由度为 29 的 t 分布表可得到 k  t0.95 ( 29)  1.699. 最后计算 T 的观察值 30  268  269  t  3.044 1.8