- 快召唤伙伴们来围观吧
- 微博 QQ QQ空间 贴吧
- 文档嵌入链接
- 复制
- 微信扫一扫分享
- 已成功复制到剪贴板
概率论与数理统计第十一章---区间估计
展开查看详情
1 .第十一章 区间估计 置信区间 正态总体下的置信区间
2 . 第一节 置信区间 对应总体的某一个样本观测值,我们可以得到点估计量 ˆ 的一个观测值,但是它仅仅是参数 θ 的一个近似值 . 由于 ˆ 是一个随机变量,它会随着样本的抽取而随机变 化,不会总是和 θ 相等,而存在着或大、或小,或正、或负 的误差 . 即便点估计量具备了很好的性质,但是它本身无法 反映这种近似的精确度,且无法给出误差的范围 . 为了弥补这些不足,我们希望估计出一个范围,并知道 该范围包含真实值的可靠程度 . 这样的范围通常以区间的形 式给出,同时还要给出该区间包含参数 θ 真实值的可靠程度 . 这种形式的估计称之为区间估计 .
3 . 第一节 置信区间 例 对明年小麦的亩产量作出估计为 : 明年小麦亩产量八成为 800-1000 斤 . 若设 X 表示明年小麦亩产量 , 则估计结果为 P(800≤X≤1000)=80% 区间估计
4 . 第一节 置信区间 例 1某农作物的平均亩产量 X( 单位 ) 服从正态分布 N(μ,σ2), 今随机抽取 100 亩进行试验 , 观察其亩产量值 x1,x2,…,x100, 基此算出 , 因此 x 500( kg ) μ 的点估计值为 500. 由于抽 样的随机性 , μ 的真值与 的值总有误差 x , 我们希望以 95% 的可靠度估计 与 x μ 的最大误差是多少 ? 2 因为 , x ~ N ( , 从而存在 ) c>0, 使得 , n P (| X |c) 0.95 因此 ,这个 c 就是可允许的最大误差
5 . 第一节 置信区间 定义 设 X1,X2,…,Xn 是来自总体 f(x,) 的样本 , 未 知 , 对于任给( 0< <1), 若有统计量 ( X 1 , X 2 ,..., X n ), ( X 1 , X 2 ,..., X n ), 使得 P { } 1 则称随机区间 [ , ]为的双侧 1 的置信区间 ,1 为置信水平 , θ,和θ分别称为置信度为1 α的置信上限和置信下的置信上限和置信下限。
6 . 几点说明 1 、参数的置信水平为 1- 的置信区间( 1 , 2 ) 表示该区间有 100 ( 1- ) % 的可能性包含总体参 数的真值。 2 、不同的置信水平, 参数的置信区间不同。 3 、置信区间越小, 估计越精确, 但置信水平会降低; 相反, 置信水平越大, 估计越可靠, 但精确度会降 低, 置信区间会较长。一般:对于固定的样本容量, 不能同时做到精确度高( 置信区间小), 可靠程度也 高( 1- 大)。如果不降低可靠性, 而要缩小估计范 围, 则必须增大样本容量, 增加抽样成本。
7 . 第一节 置信区间 在上述讨论中, 对于未知参数 , 我们给出两个 统计量 , , 得到 的双侧置信区间( , ). 但在一 些实际问题中, 例如, 对于设备, 元件的寿命来说, 平均寿命长是我们所希望的, 我们关心的是平均寿 命 的"下限", 与此相反, 在考虑化学药品中杂质含 量的均值 E(X )时, 我们常关心参数 E(X )的"上限". 这就引出了单侧置信区间的概念.
8 . 第一节 置信区间 对于给定值 (0< <1), 若由样本 ( X 1 , X 2 ,, X n ) 确定的 统计量 ( X 1 , X 2 ,, X n ) , 对于任意 满足 P{ }1- , 称随机区间(- , )是 的置信水平为 1- 的单侧置信 区间, 称为 的置信水平为 1- 的单侧置信上限. 对于给定值 (0< <1), 若由样本 ( X 1 , X 2 ,, X n ) 确定的统 计量 ( X 1 , X 2 ,, X n ) , 对于任意 满足 P{ > }1- , 称随机区间( , )是 的置信水平为 1- 的单侧置信区 间, 称为 的置信水平为 1- 的单侧置信下限.
9 . 对于给定的置信度 , 怎样根据样本来确定未知参 数 θ 的置信区间 , 就是参数 θ 的区间估计问题 . 求 未知参数 θ 的置信区间的一般方法:(枢轴变量法) 以例 1 为例, μ 的点估计 X ( 也是极大似然估计 ) 有 分布 2 def nX X ~ N , G X , ~ N 0,1 n 对于给定 α=0.05 ,可通过查正态分布表得: P G X, 1.96 1 2 由随机事件的等价性 G X , X 1.96 n P X 1.96 , X 1.96 n n c值 置信区间 X c, X c
10 .G X , 称为枢轴函数,它有以下两个特点: 1. 枢轴函数除含有关心的未知参数 μ 外,不再有 其他未知参数; 2. 枢轴函数的分布式完全已知的或完全可以确定。
11 . 第一节 置信区间 对于给定的置信度 1 ,怎样根据样本来确定 未知参数θ的置信区间 的置信区间 (ˆ1 ,ˆ2 ) ,步骤如下: (1)先求出未知参数θ的置信区间 的一个点估计 ( X 1 , X 2 ,..., X n ) . (2)构造一个 含有未知参数 θ的置信区间 而不含有其他未 知参数的枢轴函数 G G ( X 1 , X 2 ,, X n , ) ,且已知其分 布. (3)对给定的置信度 1 ,根据 G ( X 1 , X 2 , , X n ; ) 的分布定出分位点 a 和 b,使得 P a G ( X 1 , X 2 , , X n ) b 1
12 . 第一节 置信区间 (4)将不等式 a G ( X 1 , X 2, , X n ; ) b 中解出 θ的置信区间 ,得 出其等价形式 X 1 , X 2 ,, X n X 1 , X 2 ,, X n 这时必有 P ( X 1 , X 2 , , X n ) ( X 1 , X 2 ,, X n ) 1 于是 ( , ) ,即为θ的置信度为θ的置信度为的置信度为θ的置信度为1 的置信区间.
13 .例 1某农作物的平均亩产量 X( 单位 ) 服从正态分布 N(μ,σ2), 今随机抽取 100 亩进行试验 , 观察其亩产量值 x1,x2,…,x100, 基此算出 , 因此 x 500( kg ) μ 的点估计值为 500. 由于抽 样的随机性 , μ 的真值与 的值总有误差 x , 我们希望以 95% 的可靠度估计 与 x μ 的最大误差是多少 ? 2 解 因为 , x ~ N ( , 此处 ) , n=100, 因此 n def n(X ) G( X , ) ~ N (0,1) 对于给定的 1 0.95 0.05 G ( X , ) 1.96 | X |1.96 n P ( [ X 1.96 , X 1.96 ]) 1 n n 因此 , 1.96 就是 c 值, 置信区间 [ X c, X c ] n
14 . 第二节 正态总体下的置信区间 单个正态总体 N(μ,σ2) 的情形 一、均值估计(均值 μ 的置信区间) X1,X2,…,Xn 为取自 N(μ,σ2) 的样本 , 求 μ 的 1-α 置信区间 1. σ2 已知时 n(X ) X 是的一个点估计,U ~ N (0,1) 因此U是枢轴函数, 当k u1- / 2时 P (| U |k ) 1 σ σ | U |k等价于 {μ [X - k ,X k ]} n n σ σ 的1 - 置信区间为θ的置信度为:[ X -k ,X k ] n n
15 . 第二节 正态总体下的置信区间 单个正态总体 N(μ,σ2) 的情形 2. σ2 未知时 1 2 2 用S * 作的估计 t0 t0 n(X ) 得到枢轴函数为θ的置信度为, T * ~ t (n 1) S 取k t1- / 2 (n 1), P (| T |k ) 1 S* S* 的1 - 置信区间为θ的置信度为:[X-k ,X k ] n n
16 . 第二节 正态总体下的置信区间 单个正态总体 N(μ,σ2) 的情形 例 为估计一批钢索所能承受的平均张力(单位: kg/cm2 ) , 从中随机抽取 10 个样品作试验,由实验数据算出 x 6.720 , 假定张力服从正态分布,求平均张力的置信水平 S * 220, 为 95% 的置信区间 . 解 平均张力的95%的置信区间为θ的置信度为: 此处未知, S* S* [ X -t0.975 (n 1) ,X t0.975 (n 1) ] n n 代入数据 x 6720, S * 220, n 10, 查表t0 .975 2.2622 平均张力的置信区间的观察值是 [6562.6185, 6877.6815]
17 . 第二节 正态总体下的置信区间 单个正态总体 N(μ,σ2) 的情形 二、方差的估计(方差 σ2 的置信区间) X1,X2,…,Xn 为取自 N(μ,σ2) 的样本 , 求 σ2 的 1-α 置信区间 1. μ 已知时 2 2 1 n 2 n 2 σ ( X i ) 是 的点估计,且 2 2 2 ~ ( n) n i 1 因此 2 是枢轴函数, 容易找到a b,使得 P (a 2 b) 1 一般取 a χ α2 (n),b χ 2 α (n) 1 2 2 2 2 n σ n σ 此时对应的 2的1 - 置信区间为θ的置信度为:[ , ] b a
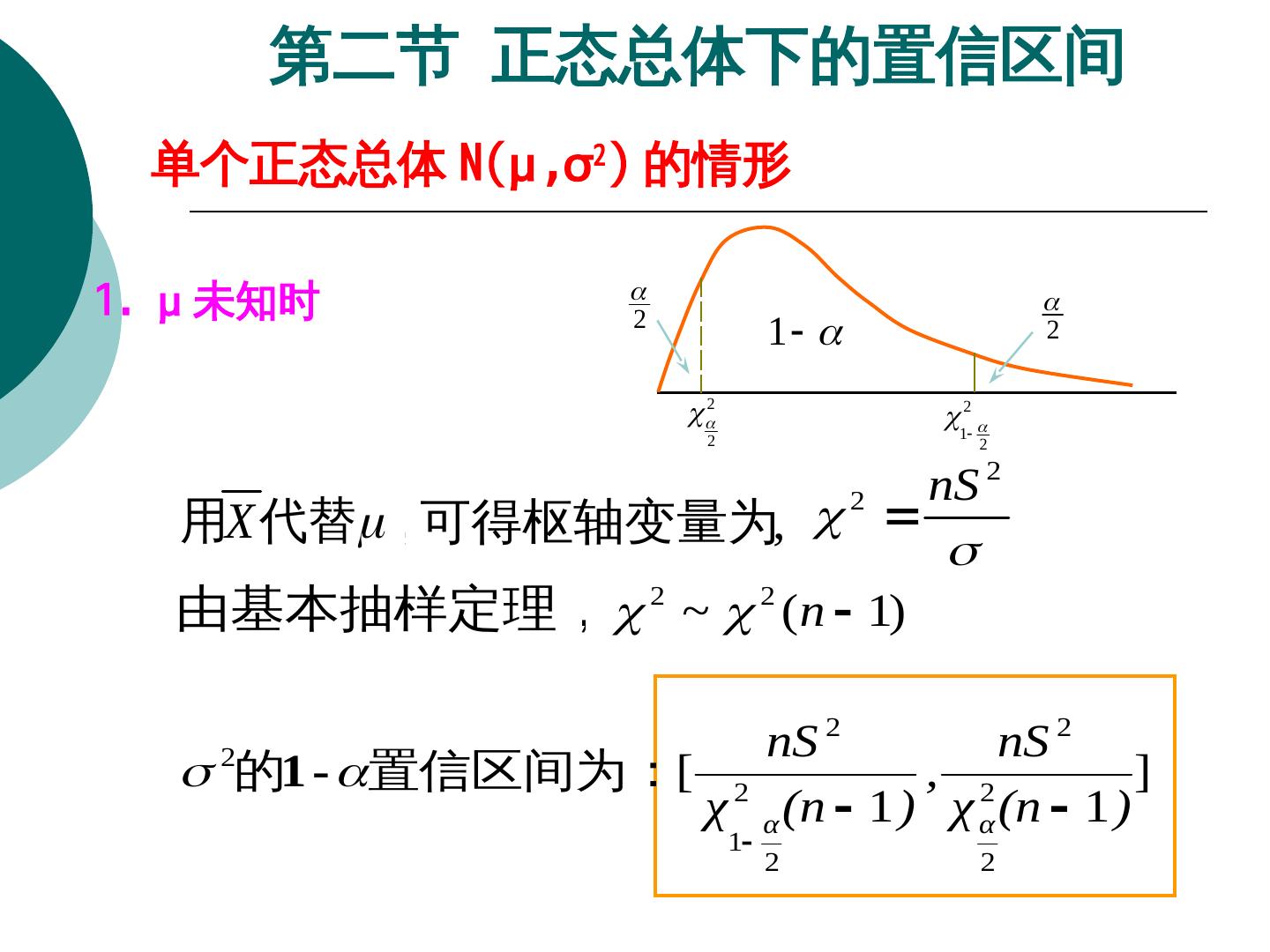
18 . 第二节 正态总体下的置信区间 单个正态总体 N(μ,σ2) 的情形 1. μ 未知时 2 1 2 2 12 2 2 2 2 nS 用X 代替,可得枢轴变量为θ的置信度为, 由基本抽样定理, 2 ~ 2 (n 1) 2 2 nS nS 2的1 - 置信区间为θ的置信度为:[ 2 , 2 ] χ α (n 1 ) χ α (n 1 ) 1 2 2
19 . 第二节 正态总体下的置信区间 两个正态总体 N(μ1,σ12), N(μ2,σ22) 的情形 设 X1,X2,…,Xm 为取自 N(μ1,σ12) 的样本 , Y1,Y2,…,Yn 为取自 N(μ2,σ22) 的样本 , 且( X1,X2,…,Xm ,)与 ( Y1,Y2,…,Yn )相互独立,求二总体均值差 μ1- μ2 的 1-α 置信区间
20 . 第二节 正态总体下的置信区间 两个正态总体 N(μ1,σ12), N(μ2,σ22) 的情形 μ1- μ2 的置信区间 1. σ12, σ22 已知时 12 22 X Y 是1 2的点估计,且由 X Y ~ N ( 1 2 , ) m n X Y ( 1 2 ) 可导出枢轴函数为θ的置信度为 U 2 2 , 1 2 1 m 1 m m n 此处, X X i , Y Yi m i 1 n i 1 1) 取k u1- / 2,有 P (| U |k ) 1 显然,U ~ N(0, 1 2的1-α置信区间为θ的置信度为: σ 12 σ 22 σ 12 σ 22 [X Y μ α ,X Y μ α ] 1 2 m n 1 2 m n
21 . 第二节 正态总体下的置信区间 两个正态总体 N(μ1,σ12), N(μ2,σ22) 的情形 2. σ12=σ22=σ2 未知时 m n 1 记, S w2 [ ( X i X ) 2 (Yi Y ) 2 ], m n 2 i 1 j 1 X Y (μ1 μ2 ) 令 T 2 2 , T ~ t ( m n 2) σ σ Sw 1 2 m n 1 2的1-α置信区间为θ的置信度为: σ 12 σ 22 σ 12 σ 22 [ X Y kS w ,X Y kS w ] m n m n 其中 k t1- / 2(m n 2 )
22 . 第二节 正态总体下的置信区间 两个正态总体 N(μ1,σ12), N(μ2,σ22) 的情形 例 甲、乙两台机床加工同一种零件,今在机床甲加工的零 件中随机抽取 9 件,在乙加工的零件中随机抽取 6 件,分 别测量零件的长度(单位: mm ),由测得的数据可算出 *2 *2 x 2.0648, y 2.0594, S 0.245, S 0.257. 1 2 假定零件长度服从正态分布,试求两台机床加工零件长 度的均值差 μ1-μ2 的水平为 95% 的置信区间。 解 令 n1=9, n2=6 1 Sw [8 0.245 5 0.357] 0.5367 13 1 1 k t0.975 (13) 2.1604 9 6 水平为 95% 的 μ1-μ2 的置信区间为 [-0.6056 , 0.6164]
23 .例1 某工厂生产一批滚珠 , 其直径 X 服从正态 分布 N( 2), 现从某天的产品中随机抽 取 6 件 , 测得直径为 15.1 , 14.8 , 15.2 , 14.9 , 14.6 , 15.1 (1) 若 2=0.06, 求 的置信区间 (2) 若 未知 , 求 的置信区间 2 置信水平 (3) 求方差 2 的置信区间 . 均为 0.95 解 (1) X ~ N ( , 0.06 / 6) 即 N ( ,0.01) X ~ N (0,1) u1 u0.975 1.96 0.1 2
24 . 的置信区间为 0.1 0.1 ( 14.95 1.96 , 14.95 1.96 ) 6 6 X (2) 取T S * ~ t (5) 查表 t0.975 (5) 2.5706 6 由给定数据算得 x 14.95 6 *2 1 s ( xi 6 x ) 0.051. s 0.226 2 2 * 5 i 1
25 . 的置信区间为 * * s s (x t0.975 (5), x t0.975 (5) ) 6 6 (14.71, 15.187 ) 5S 2 (3) 选取枢轴量 K 2 ~ 2 (5) s 2 0.051. 2 2 查表得 0.025 (5) 12.831, 0975 (5) 0.832 2 的置信区间为 2 2 5s 5s ( 2 , 2 ) ( 0.0199 , 0.3069 ) 0.025 (5) 0.975 (5)