- 快召唤伙伴们来围观吧
- 微博 QQ QQ空间 贴吧
- 文档嵌入链接
- 复制
- 微信扫一扫分享
- 已成功复制到剪贴板
概率论与数理统计第九章--统计量和抽样分布
展开查看详情
1 .第九章 统计量和抽样分布 统计量 常用统计量 抽样分布
2 . 第一节 统计量 样本是进行统计推断的依据,在应用时,往往不是 直接使用样本本身,而是针对不同的问题构造样本的适 当函数,利用这些样本的函数进行统计推断。 样本来自总体,样本的观测值中含有总体各方面的 信息,但这些信息较为分散,有时显得杂乱无章。为了 将这些分散在样本中的有关总体的信息集中起来以反映 总体的各种特征,需要对样本进行加工,表和图是一类 加工形式,它使人们从中获得对总体的初步认识。当人 们需要从样本获得对总体各种参数的认识时,最常用的 加工方法是构造样本函数,不同函数反映总体的不同特 征。
3 . 第一节 统计量 例 以下是某厂生产机器零件的质量( Kg ) 215 , 227 , 216 , 192 , 207 , 207 , 214 , 218 , 205 , 200 187 , 185 , 202 , 218 , 195 , 215 , 206 , 202 , 208 , 210 算术平均值为: 206.45 样本标准差为: 9.97
4 . 第一节 统计量 统计量 完全由样本确定的量 从数学观点来看,统计量是样本的函数 定义:设 (XX1,X2,…,Xn) 是来自总体 X 的一个样本 ,f(XX1,X2,…,X n) 是关于 X1,X2,…,Xn 的一个连续函数且 f(XX1,X2,…,Xn) 中 不 例 若 含有何未知参数 , 则称 f(XX1,X2,…,Xn) 是样本 (XX1,X2,…, X 1 , X 2 , , X n 是一个样本,则 Xn) n n (的一个统计量 1) X , X i2 i 以及 Fn ( x ) 都是统计量; i 1 i 1 . ( 2 ) 若 μ,σ2 未知时, X1- μ,X1/σ 都不是统计量 . 设 (Xx1,x2,…,xn ) 是相应于样本 (XX1,X2,…,Xn ) 的样本值 , 则 f(Xx1,x2,…,xn) 称是 f(XX1,X2,…,Xn) 的观察值 .
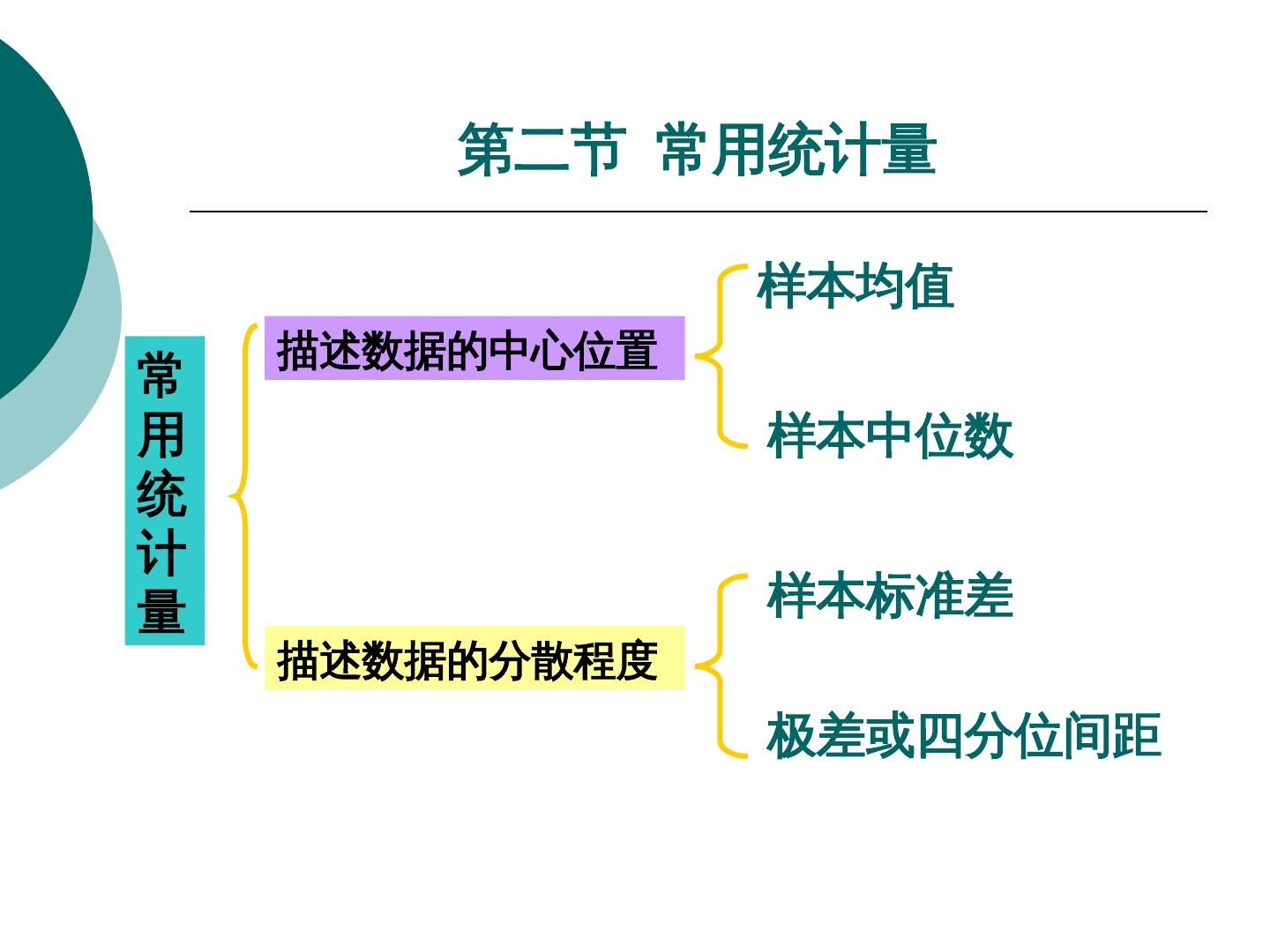
5 . 第二节 常用统计量 样本均值 描述数据的中心位置 常 用 样本中位数 统 计 量 样本标准差 描述数据的分散程度 极差或四分位间距
6 . 第二节 常用统计量 设 ( X 1 , X 2 ,, X n ) 是来自总体 X 的容量 为 n 的样本 , 称统计量 1 n 样本均值 X Xi n i 1 n 1 2 样本方差 S Xi X 2 n i 1 样本标准差 S 1 n n i 1 Xi X 2 返回
7 . 第二节 常用统计量 样本中位数 : 若将数据从小到大排列 , 中位数就是 居于中间位置的数 为样本 计算 : 设 ( X 1 , X 2 , , X n ) , 当其取值为 ( x1 , x 2 , , x n ) 时 x(1) x( 2 ) x( n ) 是数据 , 由小到大的重排 , 则中位数可如下计 ( x1 , x 2 , , x n ) 算 x n 1 , 当n为奇数 ( 2 ) med 1 ( x( n ) x( n 1) ) 当n为偶数 2 2 2 返回
8 . 第二节 常用统计量 极差 : R X ( n ) X (1) 其中 , X (1) min { X i }, X ( n ) max { X i } 1i n 1i n 直观意义 : R 即数据振幅 , 振幅越大说明数据越分散 四分位间距 H QU QL : 注 : 此处 ,QL<QU, 分别使 QL 的左、右数据比及分别使 QU 的 右、左数据比为 1:3, 也称 QL,QU 为数据的上下四分 位 数。依定义 H 是区间( QL,QU )的间距,而此区间 正 返回 好含有 50% 的数据,因此 H 是相对于中位数的数据分
9 . 第二节 常用统计量 样本相关系数 n 样本相关系数 : (x i 1 i x )( yi y ) rxy SxS y 其中 分别为数据 x, y {xxi} , {xyj} 的样本均值 , 而 Sx , Sy 则 分别为样本标准差 , 1.|rxy|≤1 称数据极大相关; 2. 当 rxy=±1 时 3. 当 rxy=0 时称数据不相关; 称数据为正相关; 4. 当 rxy>0 时 称数据为负相关 . 5. 当 rxy<0 时
10 .
11 . 统计量 是样本 的 f ( X 1 , X 2 ,..., 是样本 的 Xn) X 1 ,的不含任何 X 2 ,..., X n 未知数的函数,它是一个随机变量 是样本 的 统计量 是样本 的的分布称为抽样分布。 由于正态总体是最常见的总体,因此这里主要讨 论正态总体下的抽样分布 . 由于这些抽样分布的论证要用到较多的数学知识 ,故在本 的节中,我们主要给出有关结论,以供应用 .
12 . 第三节 抽样分布 抽样分布 设总体中个体总数为 N ,样本容量为 n(Xn 定理 1 〈N ) 且总体有有限均值 μ, 方差 σ2, 则 (1) E ( X ) (2) 有放回抽样 (X ) n N n 无放回抽样 ( X ) N1 n
13 . 数理统计中常用的分布除正态分布外,还有 三个非常有用的连续型分布,即 2 分布 t 分布 数理统计的三大分布 (X 都是连续 F 分布 型 ). 它们都与正态分布有密切的联系 . 在本章中特别要求掌握对正态分布、 2 分 布、 t 分布、 F 分布的一些结论的熟练运用 . 它们是后面各章的基础 .
14 . 第三节 抽样分布 χ2 分布 1. 定 义 为 n 个独立的标准正态随机变量 X 1 , X 2 ,, X n 设 , 称随机变量 n U X i2 i 1 的分布为自由度 n 的 χ2分布,记为 U ~ 2 ( n) f ( x) n 1 密度函数的图象如右图 n 4 n 10 0 x 2分布的概率密度函数
15 . 第三节 抽样分布 χ2 分布 n = 1 时 , 其密度函数 1.2 为 1 1 1 x 0.8 x e , 2 2 x 0 0.6 f ( x) 2 0.4 0, x 0 0.2 2 4 6 8 10 n = 2 时 , 其密度函数 为 1 2x 0.4 e , x0 f ( x) 2 0.3 0, 0.2 x 0 0.1 为参数为 1/2 的指数分布 2 4 6 8 10
16 . 第三节 抽样分布 χ2 分布 一般自由度为 n 的 2 ( n ) 的密度函数为 1 2x n2 1 f ( x) n2 n e x , x 0 n 1 f ( x) 2 ( 2 ) n 4 0, x 0 n 10 其中, ( x ) 0 t x 1e t dt 0 2分布的概率密度函数 x 在 x > 0 时收敛,称为函数,具有性质 ( x 1) x( x), (1) 1, (1 / 2) (n 1) n ! (n N )
17 . 第三节 抽样分布 χ2 分布 2. 性 质 1 E U n, DU 2n 证明 2 若X 1 2 (n1 ), X 2 2 (n2 ), X 1 , X 2 相互独立, 则 X 1+X 2~ 2 (n1+n2 ) 性质2称为 2分布的可加性,可推广到有限个的情形: m m 设U i ~ 2 (ni ), 且 U1 ,U 2 U m 相互独立,则 i ( ni ) U ~ i 1 2 i 1
18 . n 证 1 设 (n) X 2 2 i X i ~ N (0,1) i 1,2, , n i 1 X 1 , X 2 , , X n 相互独立 , 2 则 E ( X i ) 0, D( X i ) 1, E ( X ) 1 i n 2 E U E X i n i 1 1 4 x2 4 E( X ) i x e 2 dx 3 2 2 4 2 2 D ( X ) E ( X ) E ( X ) 2 i i i n 2 DU D X i 2n 返回 i 1
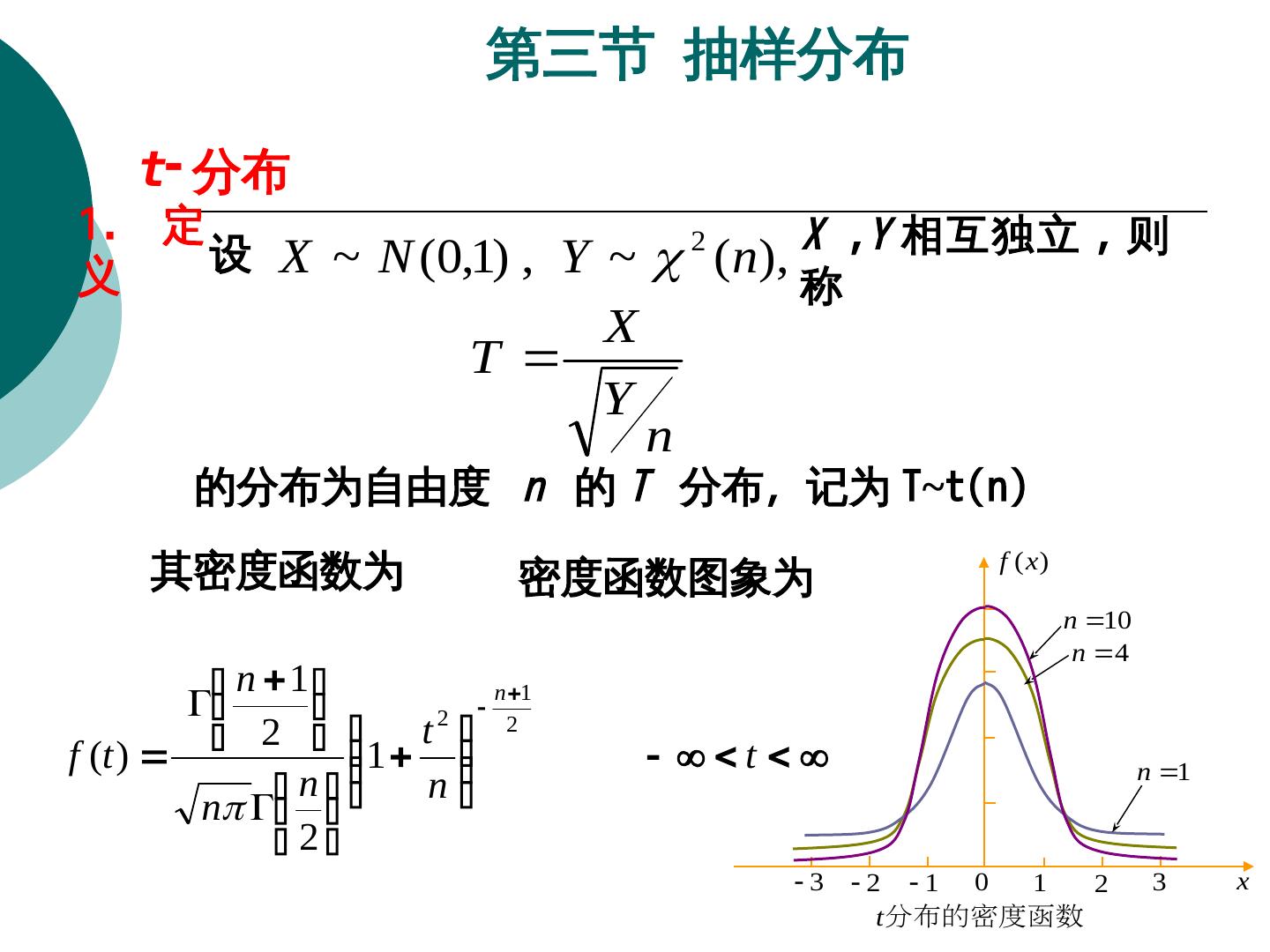
19 . 第三节 抽样分布 t- 分布 1. 定 设 X ~ N (0,1) , Y ~ 2 ( n), X ,Y 相互独立 , 则 义 称 X T Y n 的分布为自由度 n 的 T 分布,记为 T~t(Xn) 其密度函数为 密度函数图象为 f ( x) n 10 n 4 n 1 n 1 2 2 2 t f (t ) 1 t n 1 n n n 2 3 2 1 0 1 2 3 x t分布的密度函数
20 .t- 分布 第三节 抽样分布 2. 性质 : (X1) f(Xt) 关于 t=0(X 纵轴 ) 对称。 (X2) f(Xt) 的极限为 N(X0 , 1) 的密度函数,即 2 t lim f ( t ) ( t ) 1 e 2 , x n 2
21 . 第三节 抽样分布 F - 分布 1. 定义 若 U ~2(Xn),V~2(Xm)) , U,V 独立,则称 U /n F ~ F ( n, m). V /m 的分布为自由度 (Xn,m)) 的 F 分布 , 记为 F~F(Xn,m)). 其概率密度为 概率密度函数图象为 f x n 1 n 2 n1 1 n=20,m=∞ n1 / 2 ( 2 )( n1 / n 2 ) y 2 n=20,m=25 , y 0 h ( y ) n1 n n ( 2 ) ( 2 )(1 1 y )( n1 n 2 ) / 2 n=20,m=10 2 n2 0, y 0 0 1 2 x F分布的密度函数
22 . 第三节 抽样分布 正态总体的抽样分布 设XX1,X 2 ,...,X n是来自正态总体N(μN(μ,μ,σ2 )的样本,即它们 是独立同分布的,皆服从N(μ,N(μ,μ,σ2 ).我们有 定理 2 证明 (1 X ~ N ( , ); ) n n 1 ( 2 ) X与S 2 ( X i X ) 2 相互独立; n i 1 n nS 2 i ( X X ) 2 (3) i 1 ~ 2 ( n 1) 2 2
23 .证明( 1 ) 1 n 1 n E ( X ) E ( X i ) E ( X i ) n i 1 n i 1 1 n 1 n 1 2 D( X ) D( X i ) 2 D( X i ) n i 1 n i 1 n 2 故有 X ~ N ( , ). n 返回
24 .例 : 设X 1 , X 2 ,..., X n 是来自总体X ~ N ( , 2 )的样本, X与S 2 分别为其样本均值与样本方差, 则 ( X ) T ~ t (n 1) 2 S ( / n-1) 2 X n ( X ) 证明 因为 X ~ N ( , ) , 即 ~ N (0,1) n / n n nS 2 i 1 i 2 ( X X ) 2 又 2 2 ~ (n 1) 且它们表示的随机变量是相互独立的 , 故 X X n T ~ t (n 1) 2 2 S (n 1) nS (n 1) 2
25 .例: 设XX 1 ,X 2 ,...,X m 是来自总体X ~ N(μμ1 ,σ2 )的一个样本 的,X 与S 2X 分 别为其样本 的均值与样本 的 方差;Y1 ,Y2 ,...,Yn是来自总体Y ~ N(μμ2 ,σ2 ) 的一个样本 的,Y 与S 2Y 分别为其样本 的均值与样 本 的方差; 1 m 1 n 1 m 1 n X Xi Y m i 1 n i 1 Yi S ( X i X ) S 2 (Yi Y ) 2 1 2 m i 1 2 2 n i 1 mS12 nS 22 S w2 mn 2 则随机变量 ( X Y ) ( 1 2 ) T ~ t ( m n 2) 1 1 Sw m n
26 . 2 2 证明 : (X1) 因 X ~ N ( 1 , ) Y ~ N (2 , ) m n 为 所以 ( X Y ) ( 1 2 ) V ~ N (0,1) 1 1 m n (X2) 因为 mS 12 nS 22 ~ 2 (m 1) ~ 2 (n 1) 2 2 所以 mS12 nS 22 U 2 2 ~ 2 ( m n 2) (X3) 故 T V ( X Y ) ( 1 2 ) ~ t (m n 2) U /(m n 2) 1 1 Sw m n
27 . 2 2 1 m 1 n 例: *2 S1 (Xi X ) *2 S2 (Yi Y ) m 1 i 1 n 1 i 1 *2 S 则 F 1 *2 S ~ F (m 1, n 1) 2
28 . 第三节 抽样分布 极限分布 设总体有有限均值 μ 及方差 σ2 , X1 , X2,…Xn 是样本, 则由中心极限定理,当 n→∞, 有 n( X ) L N (0,1) 因此,统计量 2 有渐进分布 X N ( , ) n
29 .例 某镇有 25000 户家庭,平均拥有汽车 1.2 辆,标准差为 0. 90 辆 , 他们中 10% 没有汽车 . 今有 1600 户家庭的随机样本 , 问 在样本 中 9% 和 11% 之间的家庭没有汽车的概率是多少 ? 解 引入新变量 1, 第i个样本家庭无汽车i个样本家庭无汽车个样本家庭无汽车 X 0, 第i个样本家庭无汽车i个样本家庭无汽车个样本家庭无汽车 X 1 , X 2 ,, X n 是相互独立的, 而且n N , 可以看成有放回抽样,样本中无汽车家庭的比例为 X 2 X ~ N ( , ) p=0.1, μ=0.1 σ=0.3, n 40 (0.09 0.1) n ( X ) 40 (0.11 0.1) P(9% X 11 %) P( ) 0.3 0.3 40 (0.11 0.1) 40 (0.09 0.1) ( ) ( ) 0.3 0.3 0.8164