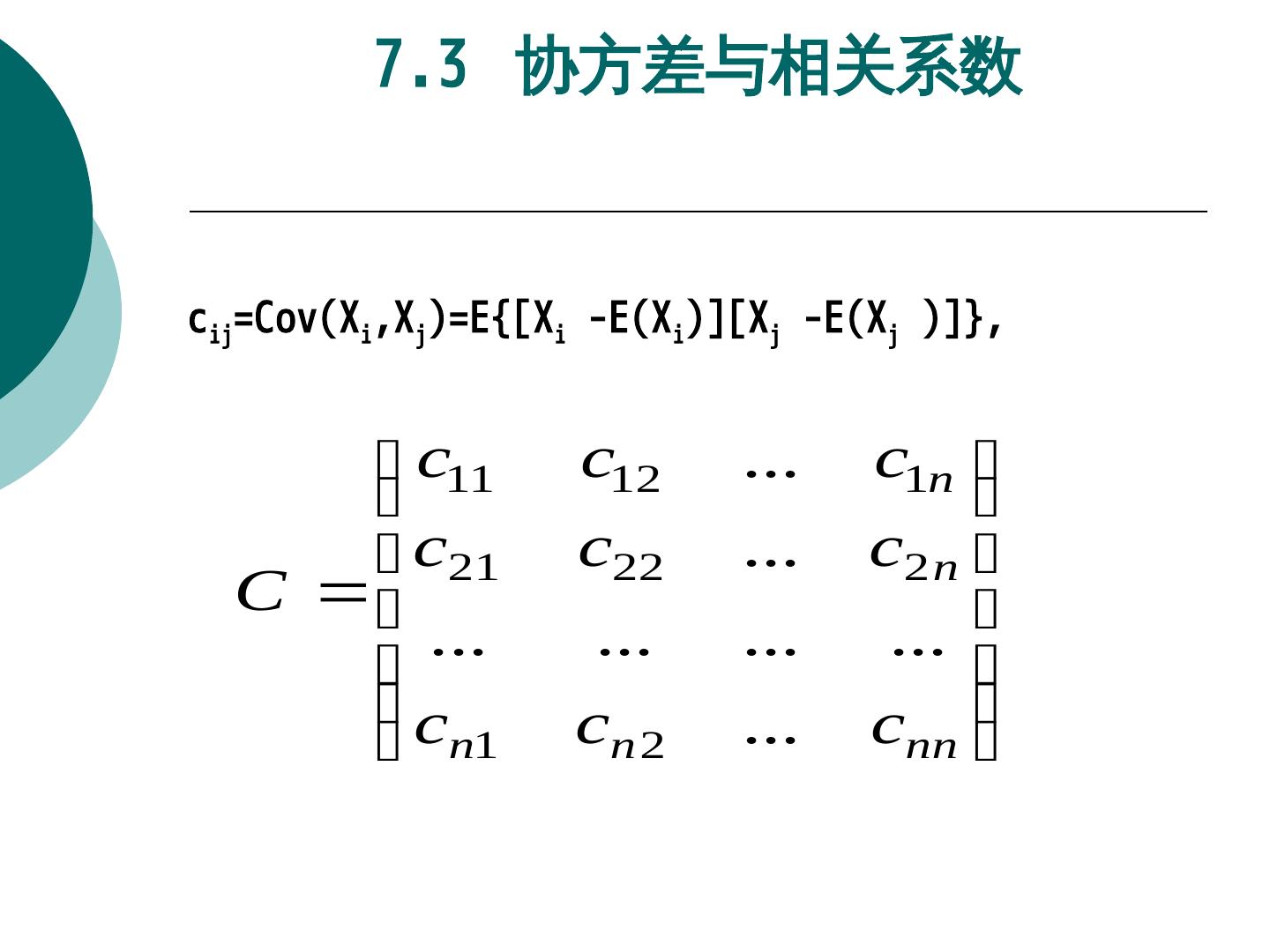
- 快召唤伙伴们来围观吧
- 微博 QQ QQ空间 贴吧
- 文档嵌入链接
- 复制
- 微信扫一扫分享
- 已成功复制到剪贴板
概率论与数理统计第七章--随机变量的数字特征
展开查看详情
1 . 第七章 随机变量的数字特征 前面讨论了随机变量的分布函数,我们看到分布 函数能够完整地描述随机变量的统计规律。然而在许 多实际问题中,随机变量的分布并不容易求得,并且 有时不需要去完全考察随机变量的变化情况,而只需 要知道随机变量的某些特征,因而不需要求出它的分 布函数。 例如 1 、在评定某一地区粮食产量的水平时,在许多场合 只要知道该地区的平均产量; 2 、在研究水稻的品种优劣时,时常是关心稻穗的平 均稻谷粒数;
2 . 第七章 随机变量的数字特征 3 、在检查一批棉花的质量时,既需要注意纤维的平均 长度,又需要注意纤维长度与平均长度的偏离程度,平 均长度较大、偏离程度较小,质量就较好。 从上面的例子看到,与随机变量有关的某些数值,虽 然不能完整地描述随机变量,但能描述随机变量在某些 方面的重要特征。随机变量的数字特征就是用数字表示 随机变量的分布特点,在理论和实践上都具有重要的意 义。
3 .第七章 随机变量的数字特征 数学期望 方差和标准差 协方差和相关系数 切比雪夫不等式及大数定理 中心极限定理
4 . 7.1 随机变量的数学期望 一、离散型随机变量的数学期望 从平均数说起,设以数据集 {2 , 3 , 2 , 4 , 2 , 3 , 4 , 5 , 3 , 2} 为总体,求其平均数(设为 μ ) μ= ( 2+3+2+4+2+3+4+5+3+2 ) /10 = ( 2×4+3×3+4×2+5×1 ) /10 =2×4/10+3×3/10+4×2/10+5×1/10 =3 概括得: xi f i i 1
5 . 7.1 随机变量的数学期望 一、离散型随机变量的数学期望 下面我们逐步分析如何由分布来求“均值”: ( 1 )算术平均:如果有 n 个数 x1,x2,…,xn ,那么求这 n 个数的算术平均,只需将此 n 个数相加后除以 n ,即 1 n 1 1 1 x xi x1 x2 xn . n i 1 n n n ( 2 )加权平均:如果这 n 个数中有相同的,不妨设其中有 ni 个取值为 xi(i=1,2,…,k) ,列表为 取值 x1 x2 xk 频数 n1 n2 nk n1 n2 nk 频率 n n n 1 k k ni n1 n2 nk n i 1 ni xi xi x1 x2 xk i 1 n n n n
6 . 7.1 随机变量的数学期望 一、离散型随机变量的数学期望 其实,这个“加权”平均的权数 ni/n 就是出现数值 xi 的频率,而频率在 n 很大时,就稳定在其概率附近 。3 )对于一个离散随机变量 X ,如果其可能取值为 x ( 1 ,x2,…,xn ,若将这 n 个数相加后除以 n 作为“均值”, 则肯定是不妥的,原因在于 X 取各个值的概率是不同 的,概率大的出现的机会就大,在计算中其权数就应 该大。 用取值的概率作为一种“权数”作加权平均是十分合理的 。
7 . 7.1 随机变量的数学期望 一、离散型随机变量的数学期望 1.定义 设离散随机变量X的分布律为 p ( xi ) P( X xi ) pi , i 1, 2, , n, X x 1 x 2 … xn … 如果 | x | p i 1 i i P p1 p2 … pn … 则称 E ( X ) p1 x1 p2 x2 pk xk pk xk k 为随机变量 X 的数学期望,或称为该分布的数学期望 , 简称期望或均值。 若级数 | xi | pi不收敛 , 则称 X 的期望不存在。 i 1
8 . 7.1 随机变量的数学期望 一、离散型随机变量的数学期望 注释 (1) X 的期望 E(X) 是一个数,它形式上是 X 的可能值 的加权平均,其权重是其相应的概率,实质上它体现了 X 取值的真正平均,为此我们又称它为 X 的均值。因为 它完全由 X 的分布所决定,所以又称为分布的平均值。 (2) E(X) 作为刻划 X 的某种特性的数值,不应与各项的 排列次序有关。所以,定义中要求级数绝对收敛。
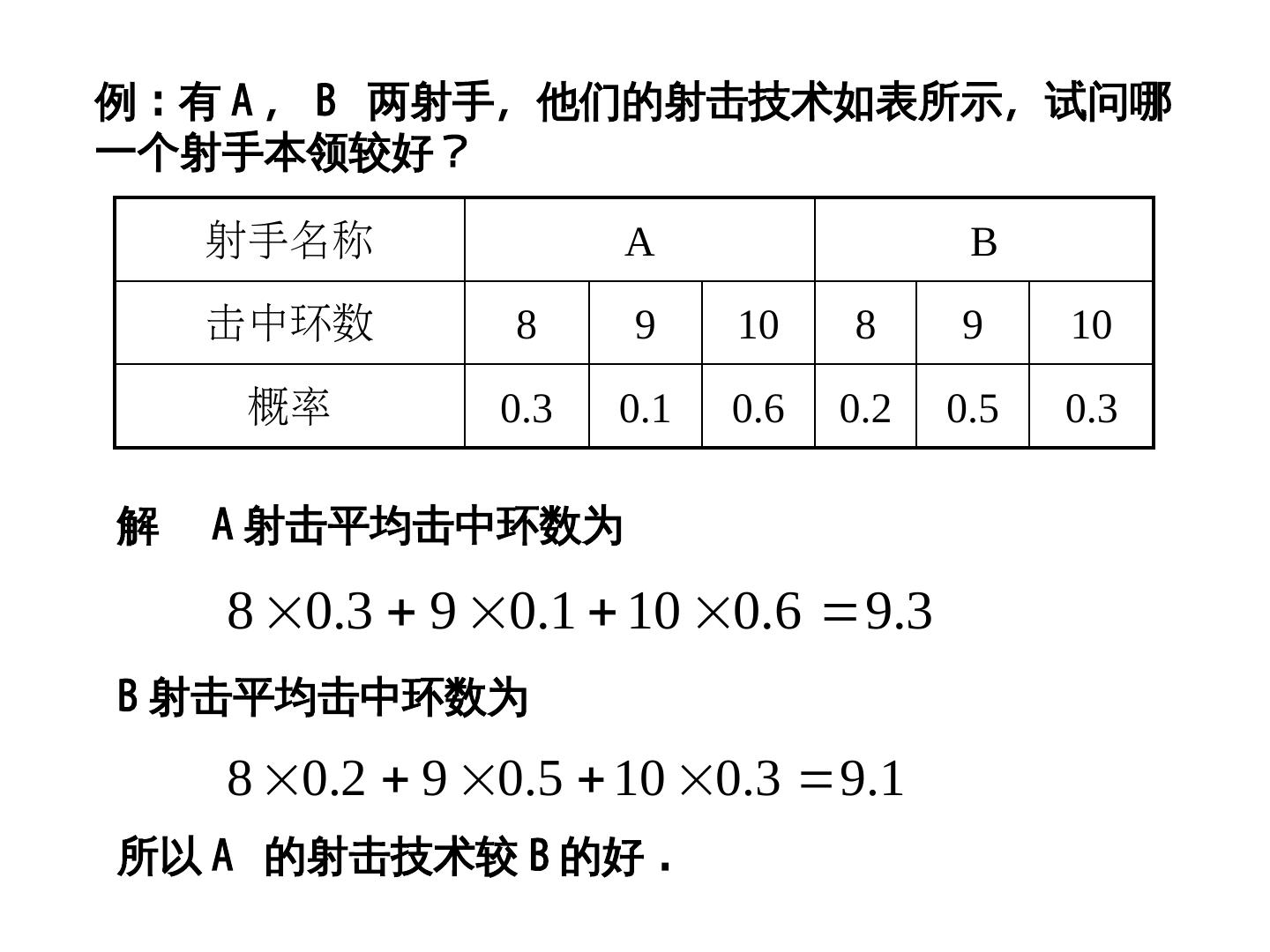
9 .例 : 有 A , B 两射手,他们的射击技术如表所示,试问哪 一个射手本领较好? 射手名称 A B 击中环数 8 9 10 8 9 10 概率 0.3 0.1 0.6 0.2 0.5 0.3 解 A 射击平均击中环数为 8 0.3 9 0.1 10 0.6 9.3 B 射击平均击中环数为 8 0.2 9 0.5 10 0.3 9.1 所以 A 的射击技术较 B 的好 .
10 .例 : 设有某种产品投放市场,每件产品投放可能发生三 种情况:按定价销售出去,打折销售出去,销售不出 去而回收。根据市场分析,这三种情况发生的概率分 别为 0.6 , 0.3 , 0.1 。在这三种情况下每件产品的 利润分别为 10 元, 0 元,- 15 元(即亏损 15 元)。 问厂家对每件产品可期望获利多少? 解 : 设 X 表示一件产品的利润(单位元), X 是随机变 量,且 X 的分布律为 X 10 0 -15 P 0.6 0.3 0.1 依题意,所要求的是 X 的数学期望 E(X)=10×0.6+0×0.3+(-15)×0.1=4.5( 元 )
11 . 7.1 随机变量的数学期望 一、离散型随机变量的数学期望 2. 几种典型的离散型随机变量的数学期望 i. X 服从参数为 p 的 (0,1) 分布:X 0 1 E(X)=0×(1-p)+1×p=p ; P q p ii. 若 XB(n,p), 则 E(X)=np ; 证明: X 的分布律为 P{ X k } C nk p k q n k k 0,1,2,...., n. n n n! E ( X ) k C nk p k q n k k p k q n k k 0 k 1 k ! ( n k )! np n n 1! p k 1 q n k k 1 k 1! ( n k )! n np C nk 11 p k 1q n k np( p q ) n 1 np . k 1
12 . 7.1 随机变量的数学期望 一、离散型随机变量的数学期望 2. 几种典型的离散型随机变量的数学期望 iii. 若 XP(λ)) ,则 E(X)=λ) 。 证明: X 的分布律为 k e P { X k } k 0,1,2,..... k! k e k e E ( X ) k k 0 k! k 1 k 1! k 1 e e e k 1 k 1!
13 . 7.1 随机变量的数学期望 二、连续型随机变量的数学期望 1. 定义 设连续型随机变量 X 的概率密度为 f(x) , 如果 | x | f ( x) dx 则称 EE( (XX) ) xfxf( (xx)dx )dx 为随机变量 X 的数学期望,记为 E(X).
14 .例 : 设随机变量 X 的概率密度函数为 2 x, 0 x 1 f ( x ) 0, 其他 试求 X 的数学期望 1 解 E ( X ) xf ( x)dx x 2xdx 0 1 2 31 2 2 x dx x 2 0 3 0 3
15 . 7.1 随机变量的数学期望 二、连续型随机变量的数学期望 2. 几种典型的连续型随机变量的数学期望 i. 若 XR(a,b), 则 E(X)=(a+b)/2. 证: X 的概率密度为 1 x (a , b) f ( x ) b a 0 x (a , b) 1 b a b E ( X ) xf ( x )dx x dx a b a 2
16 . 7.1 随机变量的数学期望 二、连续型随机变量的数学期望 2. 几种典型的连续型随机变量的数学期望 ii. 若 XN(µ,σ2) ,则 E(X)=μ. 证: X 的概率密度为 x 2 1 2 2 f ( x) e 2 x 2 1 E ( X ) xf ( x )dx x e 2 2 dx 2 x 令 t , t2 t 2 1 E( X ) t e 2 dt e 2 dt . 2 2 特别地,若 XN(0,1) ,则 E(X)=0.
17 . 7.1 随机变量的数学期望 二、连续型随机变量的数学期望 2. 几种典型的连续型随机变量的数学期望 iii. 若 X 服从参数为 λ) 的指数分布,则 E(X)=1/λ) . 证: X 的概率密度为 e x x 0 f ( x ) 0 x 0 1 E ( X ) xf ( x)dx e x dx 。 0
18 . 7.1 随机变量的数学期望 三、随机变量的函数的数学期望 定理 设 Y 是随机变量 X 的函数 :Y=g(X)(g 是连续函数 ) , (1) X 是离散型随机变量,它的分布律为 P{X=xk}=pk , g xk p k k=1 , 2 ,…, k 1 若 E (Y ) E ( g ( X绝对收敛, )) g xk pk k 1 则有 (2) X X 是连续型随机变量,它的概率密度为 f(x) , 若 g ( x) f ( x)dx 绝对收敛, 则有 E (Y ) E[ g ( X )] g ( x ) f ( x )dx
19 .例 已知随机变量 X 的分布律如下 X -2 -1 0 1 2 P 0.2 0.1 0.1 0.3 0.3 求 Y X 2 的数学期望。 2 2 Y X 的分布律为 X ( 2) 2 ( 1) 2 02 12 22 解 P 0.2 0.1 0.1 0.3 0.3 对相同的值合并,并把对应的概率相加,可得 X2 0 1 4 P 0.1 0.4 0.5 2 所以 E (Y ) E ( X ) 0 0.1 10.4 4 0.5 2.4 2 或 E (Y ) E ( X ) ( 2) 2 0.2 ( 1) 2 0.1 0 2 0.1 12 0.3 22 0.3 2.4
20 .例:某公司生产的机器其无故障工作时间 X 有密度函数 1 , x 1; f ( x ) x 2 0, 其他. 公司每出售一台机器可获利 1600 元 , 若机器售出后使用 1.2 万 小时之内出故障 , 则应予以更换 , 这时每台亏损 1200 元 ; 若在 1.2 到 2 万小时之间出故障 , 则予以维修 , 由公司负担维修费 400 元 ; 在使用 2 万小时以后出故障 , 则用户自己负责 . 求该公司售出每 台机器的平均获利 . 解 :设 Y 表示售出一台机器的获利 . 则 1200, 0 x 1.2; Y g(x) 1200, 1.2 x 2; 1600, x 2. 1.2 1 2 1 1 E (Y ) E ( g ( x)) 1200 2 dx 1200 2 dx 1600 2 dx 1 x 1.2 x 2 x 1000
21 . 7.1 随机变量的数学期望 三、随机变量的函数的数学期望 定理 : 设 Z 是随机变量 X,Y 的函数 Z=g(X,Y) (g 是连续函 数 ). (1) 设二维随机变量 (X,Y) 的分布律为 P{ X xi , Y y j } pij i, j 1,2,... 若 | g(x , y ) | p j i i j ij 则 E ( Z ) E[ g ( X , Y )] g ( xi , y j ) pij j i (2) 设二维随机变量 (X,Y) 的分布密度为 f(x,y), 若 | g ( x, y) | f ( x, y)dxdy 则 E ( Z ) E[ g ( X , Y )] g ( x, y ) f ( x, y )dxdy
22 .例: 设( X,Y )的联合分布律如下, Z=XY ,求 E(Z). X 1 2 3 Y 0 0.1 0.15 0.25 1 0.25 0.15 0.1 解 E ( Z ) 10 0.1 110.25 2 0 0.15 2 10.15 3 0 0.25 3 10.1 0.85
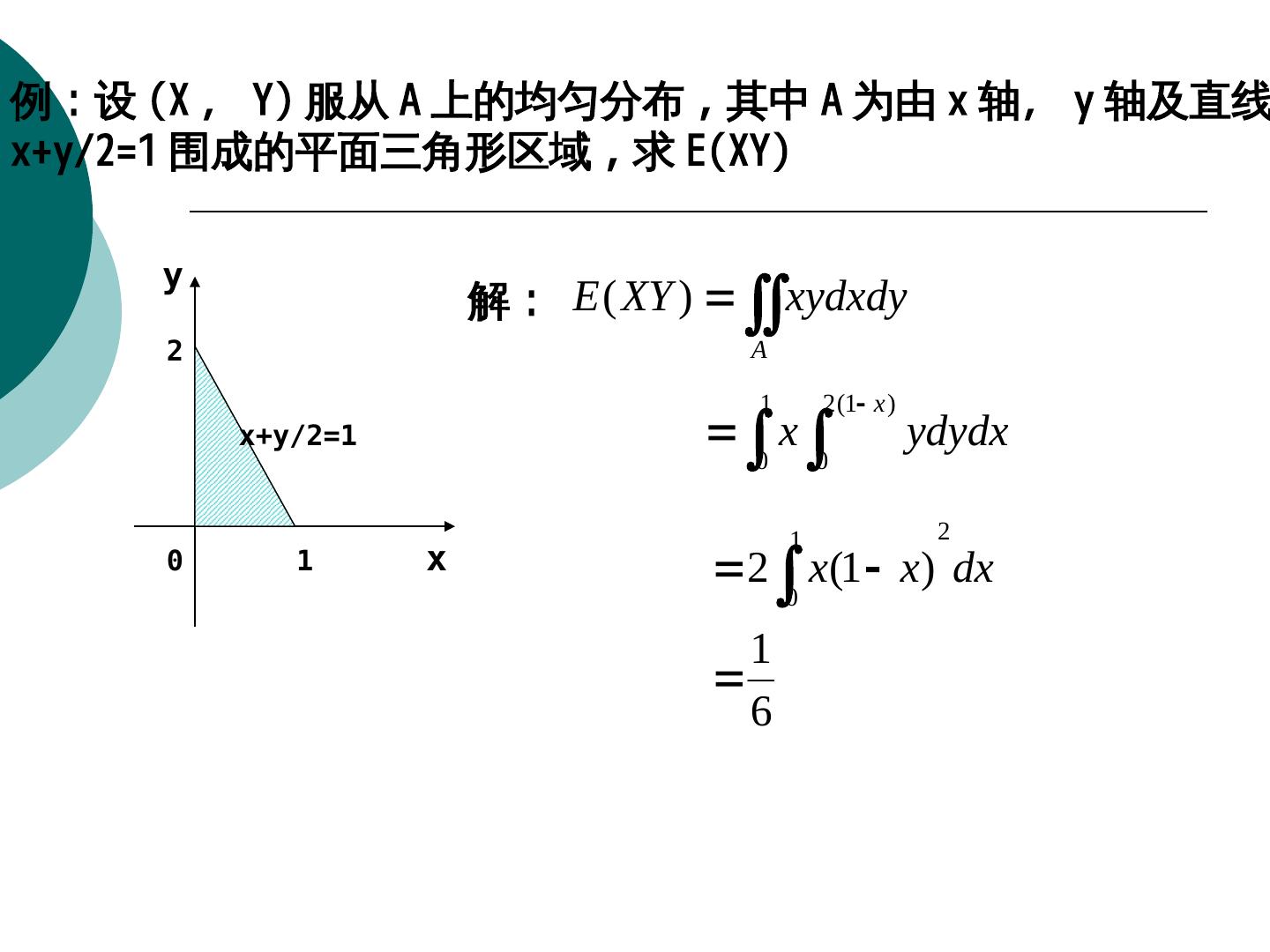
23 .例:设 (X , Y) 服从 A 上的均匀分布 , 其中 A 为由 x 轴, y 轴及直线 x+y/2=1 围成的平面三角形区域 , 求 E(XY) y 解: E ( XY ) xydxdy 2 A 1 2 (1 x ) x+y/2=1 x ydydx 0 0 1 2 0 1 x 2 x(1 x) dx 0 1 6
24 . 7.1 随机变量的数学期望 四、数学期望的性质 1. 若 C 是常数 , 则 E(C)=C. 2. 设 X,Y 是两个随机变量 , 若 E(X),E(Y) 存在 , 则对任 意的实数 a 、 b, E(aX+bY) 存在 , 且有 E(aX+bY)=aE(X)+bE(Y) 3. 设 X,Y 是互相独立的随机变量 , 则有 E(XY)=E(X)E(Y) 性质 2 、 3 都可推广到有限个互相独立的随机变量之积 的情况 .
25 . 7.1 随机变量的数学期望 四、数学期望的性质 性质 2 E(aX+bY)=aE(X)+bE(Y) 证明 (1) 设离散型随机变量 (X,Y) 的联合分布律和边缘 分布律分别为 P{X=xi,Y=yj}=pij, i,j=1,2,… P{X=xi}=pi., i=1,2,… P{Y=yj}=p.j, j=1,2,… 则 E (aX bY ) (axi by j ) pij axi pij by j pij i 1 j 1 i 1 j 1 j 1 i 1 a xi pi. b y j p. j aE ( X ) bE (Y ) i 1 j 1
26 . 7.1 随机变量的数学期望 四、数学期望的性质 性质 2 E(aX+bY)=aE(X)+bE(Y) (2) 设连续型随机变量 (X,Y) 的联合概率密度和边缘概率 密度分别为 f(x,y) 和 fX(x), fY(y) 则 E (aX bY ) (ax by) f ( x, y)dxdy axf ( x, y)dxdy byf ( x, y)dxdy ax[ f ( x, y )dy]dx by[ f ( x, y )dx]dy axf X ( x)dx byfY ( y )dy aE ( X ) bE (Y )
27 . 7.1 随机变量的数学期望 四、数学期望的性质 性质 3 如 X,Y 是互相独立 , 则 E(XY)=E(X)E(Y) 证明 (1) 设离散型随机变量 (X,Y) 的联合分布律和边缘 分布律分别为 P{X=xi,Y=yj}=pij, i,j=1,2,… P{X=xi}=pi., i=1,2,… P{Y=yj}=p.j, j=1,2,… 则 E ( XY ) xi y j pij xi y j pi. p. j i 1 j 1 i 1 j 1 xi pi. y j p. j E ( X ) E (Y ) i 1 j 1
28 . 7.1 随机变量的数学期望 四、数学期望的性质 性质 3 如 X,Y 是互相独立 , 则 E(XY)=E(X)E(Y) (2) 设连续型随机变量 (X,Y) 的联合概率密度和边缘概率 密度分别为 f(x,y) 和 fX(x), fY(y) 则 E ( XY ) xyf ( x, y )dxdy xyf X ( x) fY ( y )dxdy xf X ( x)dx yfY ( y )dy E ( X ) E (Y )
29 .例:将 n 个球随机地放入 M 个盒子中去,设每个球放入各个盒子 是等可能的,求有球盒子数 X 的期望 M 解: 记 X i 1, 第i个盒有球. ; 0, 第i个盒无球.. i=1,2,…,M, 则 X X i i 1 (M 1) n 1 n P(X i 0) n (1 ) M M 1 n P ( X i 1) 1 (1 ) M 因而 E ( X i ) 1P ( X i 1) 0 P ( X i 0) 1 n 1 (1 ) M M 1 n E ( X ) E ( X i ) M (1 (1 ) ) i 1 M