概率论与数理统计第六章---随机变量的函数及其分布

1 .第六章 随机变量的函数及其分布  一维随机变量的函数及其分布  二维随机变量的函数的分布 

2 . §6.1 一维随机变量的函数及其分布  背景 在许多实际问题中 , 常常需要研究随机变量的函数 的分布问题 , 例 : ☆ 　测量圆轴截面的直径 d, 而关心的却是截面积： 1 2 S  d 4 d 为随机变量 , S 就是随机变量 d 的函数。 ☆ 在统计物理中 , 已知分子的运动速度 x 的分布 , 求其动 能： 1 y  mx 2 的分布。 2 一般地，设 y=g(x) 是一元实函数， X 是一个随机变量，若 X 的 取值在函数 y=g(x) 的定义域内，则 Y=g(X) 也为一随机变量。 

3 .密度函数 随机变量 分布函数 f X ( x) X F X ( x) fY ( y ) Y g ( X ) FY ( y ) 随机变量的函数 

4 . §6.1 一维随机变量的函数及其分布 　若 X 为离散型 随机变量 随机变量 , 其分布律为 X x1 x2 x3 ．．．．．．． xn ．．． pk ． p p2 p3 ．．．．．．． pn ．．．． 1 g(x) 是一个已知函数， Y=g(X) 是随机变量 X 的函数， 则随机变量 Y 的分布律为 Y g( x1) g( x2) g( x3) ．．．．． g (xn) ．．．． pk p1 p2 p3 ．．．．． pn ．．．． 如果 g( x i ) 与 g( x j ) 相同，此时将两项合并，对应概率相加． 

5 .例 设随机变量 X 的分布律为 X －1 0 1 2 求 Y=2X2 +1 的分布律． p 0.2 0.3 0.4 0.1 解 由题设可得如下表格 x -1 0 1 2 Y=2x2+1 3 1 3 9 概率 0.2 0.3 0.4 0.1 所以， y=2x2+1 的分布律为 Y 1 3 9 p 0.3 0.6 0.1 

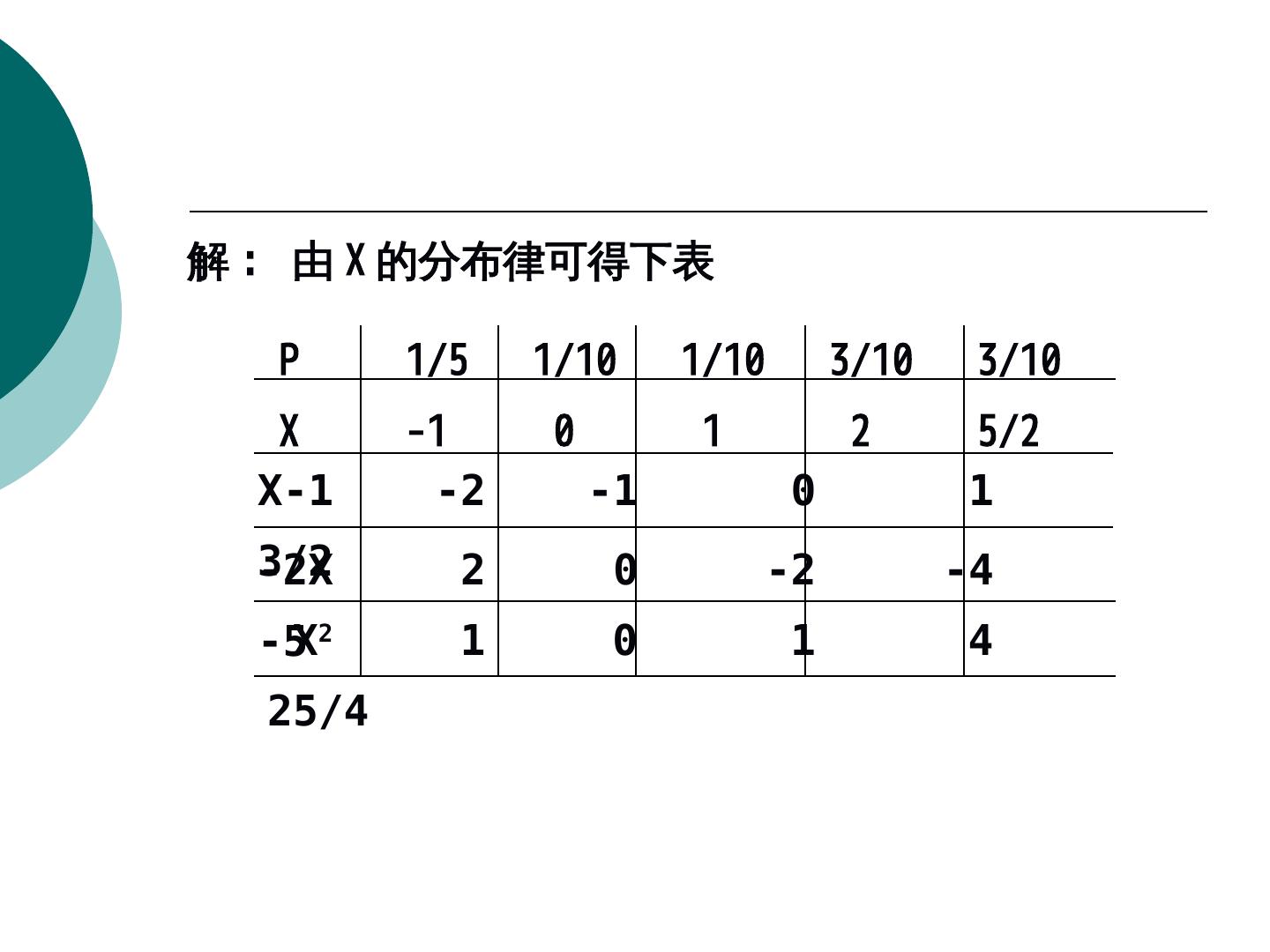
6 .例 : 设离散型随机变量 X 的分布律为 X -1 0 1 2 5/2 P 1/5 1/10 1/10 3/10 3/10 求 (1)Y=X-1; (2)Y=-2X; (3)Y=XY=X-1; (2)Y=X-1; (2)Y=-2X; (3)Y=XY=-2X; (3)Y=X-1; (2)Y=-2X; (3)Y=XY=X2 的分布律 

7 .解 : 由 X 的分布律可得下表 P 1/5 1/10 1/10 3/10 3/10 X -1 0 1 2 5/2 X-1 -2 -1 0 1 3/2 -2X 2 0 -2 -4 -5X2 1 0 1 4 25/4 

8 . 6.1 一维随机变量的函数及其分布 一、离散型随机变量 (1)Y=X-1; (2)Y=-2X; (3)Y=X Y=X-1 的分布律为 Y -2 -1 0 1 3/2 P 1/5 1/10 1/10 3/10 3/10 (2)Y=X-1; (2)Y=-2X; (3)Y=X Y=-2X 的分布律为 Y 2 0 -2 -4 -5 P 1/5 1/10 1/10 3/10 3/10 (3)Y=X-1; (2)Y=-2X; (3)Y=X Y=X2 的分布律为 Y 0 1 4 25/4 P 1/10 3/10 3/10 3/10 

9 . 若 X 为一个连续型 随机变量随机变量，其概率密度函数为 f ( x) 。 y = g(x) 为一个已知的连续函数，求随机变量 Y=g(X ) 的概率密度函数  一般方法 (1) 求 Y 的分布函数 FY(y) 根据分布函数的定义 FY ( y ) FY(y)=P{Y≤y}=P{g(X)≤y}   FY  y   P X  I g   f X ( x)dx   Ig g ( x ) y f X ( x)dx (2) 对 FY(y) 求导，得到 fY(y) fY ( y ) FY( y ) 

10 . 6.1 一维随机变量的函数及其分布 二、连续型随机变量 例：设随机变量 X 服从区间 (0 ， 1)Y=X-1; (2)Y=-2X; (3)Y=X 上的均匀分布 . 试求 Y=X2 的密度函数 . 解 当 y<0 时 ,P(XP(X2≤y)Y=X-1; (2)Y=-2X; (3)Y=X=0 FY ( y ) 0  y 1dx  y , 0  y  1 f X ( x)dx  0 y 当 y≥0 时 ,P(XP(X2≤y)Y=X-1; (2)Y=-2X; (3)Y=X= FY ( y)  y  1, 其他 于是 Y 分布函数为  0, y0  FY ( y )  y, 0 y 1  1, 其他   1 '  , y0 因此 fY ( y )  FY ( y )  2 y  0, 其他  

11 . 设随机变量 X 的密度函数为 x  ,0  x  4 f ( x )  8  0, 其它 求 : 随机变量 Y=2X+8 的概率密度。 解（ 1 ） 先求 Y=2X+8 的分布函数 FY (y). FY ( y) P(Y y) P(2X  8 y) y 8 y 8 P(X  2 )    2 f ( x)dx 

12 .（ 2 ） 求 Y=2X+8 的概率密度   y  8  y  8 fY ( y ) FY( y )  f     2  2  1 y 8 1 y 8    , 0 4  8  2  2 2  0, 其它   y 8  , 8  y  16  32  0, 其它 

13 . 6.1 一维随机变量的函数及其分布 二、连续型随机变量 例：设随机变量 X 服从正态分布， X~N(0 ， 1)Y=X-1; (2)Y=-2X; (3)Y=X ，试求随机 变量函数 Y=|X| 的密度函数 解 X 的密度函数为 1  x2 / 2 f  x  e (  x  ) 2 于是 Y 分布函数为  P( y  X  y ), y  0; FY  y  P(Y  y ) P( X  y )   0, y 0. x2 y y 1 2 P( y  X  y )   f X ( x)dx   e dx y y 2  2 y 2  e 2 , y0 因此 fY ( y )  FY ( y )   '  0, 其他  

14 . §6.1 一维随机变量的函数及其分布 二、连续型随机变量 当函数 y=g(x)Y=X-1; (2)Y=-2X; (3)Y=X 可导且为严格单调函数时，我们有 下面一般结果 2. 特殊方法 定理 设随机变量 X 具有概率密度 fX(x)Y=X-1; (2)Y=-2X; (3)Y=X ，又设函 数 g(x)Y=X-1; (2)Y=-2X; (3)Y=X 单调（恒有 g(x)Y=X-1; (2)Y=-2X; (3)Y=X>0 或恒有 g(x)Y=X-1; (2)Y=-2X; (3)Y=X<0)Y=X-1; (2)Y=-2X; (3)Y=X ，且处 f Y  y  f X  h  y   h y  处可导，则 Y=g(x)Y=X-1; (2)Y=-2X; (3)Y=X 的概率密度为 其中 x=h(y)Y=X-1; (2)Y=-2X; (3)Y=X 为 y=g(x)Y=X-1; (2)Y=-2X; (3)Y=X 的反函数， 

15 . 6.1 一维随机变量的函数及其分布 二、连续型随机变量 例 : 设随机变量 XN(μ ， σ2)Y=X-1; (2)Y=-2X; (3)Y=X,P(X 试证明 X 的线性函数 Y= kX+b(k≠0)Y=X-1; (2)Y=-2X; (3)Y=X 也服从正态分布。 证明： X 的概率密度为 1 f X  x    x    / 2 2 2 e    x   2  现在 y=g(x)Y=X-1; (2)Y=-2X; (3)Y=X=kx+b ，由这一式子解得 x=h(y)=(y-b)/k 由定理得 Y=kX+b 的概度密度为 1 y b fY ( y )  fX ( )    y   k k 

16 . 6.1 一维随机变量的函数及其分布 二、连续型随机变量 2  y b     k 1 1   即 fY ( y )  e 2 2 | k | 2   y  ( b  k )  2 1 1  2 ( k ) 2  e    y   | k |  2 所以 Y=kx+b~N(kμ+b , k22 ) 特别，在上例中取 k=1/ ,P(X b= -μ/ 得 X  Y  ~ N (0,1)  

17 . 6.1 一维随机变量的函数及其分布 二、连续型随机变量 例：设随机变量 X 服从参数 λ=1 的指数分布，求随机变量函数 Y=eX 的密度函数 解 由于 X 服从参数为 1 的指数分布，因此其密度函数为  e x x  0; f  x    0 其他 函数 y=ex 为一个单调增加且有一阶连续导数的函数， 其反函数 x=h(y)Y=X-1; (2)Y=-2X; (3)Y=X=lny,P(Xh’(y)Y=X-1; (2)Y=-2X; (3)Y=X=1/y  1  , y 1 因此 f Y ( y) f X (h ( y)) | (h ' ( y)) | y 2  0, y 1 

18 . 6.1 一维随机变量的函数及其分布 二、连续型随机变量 例：假设由自动线加工的某种零件的内径（单位 :mm ）服从正态分服从正态分 布 N （ 11 ， 1 ）服从正态分，内径小于 10 或者大于 12 为不合格品，其余为 合格品，销售每件合格品获利，销售每件不合格品则亏损，已知 销售利润 Y （单位：元）服从正态分与销售零件的内径 X 有如下关系：   1, X  10;  Y  20, 10  X 12;   5, X  12.  试求 Y 的分布律 

19 . 6.1 一维随机变量的函数及其分布 二、连续型随机变量 解 P(Y=-5)Y=X-1; (2)Y=-2X; (3)Y=X= P(X>12)Y=X-1; (2)Y=-2X; (3)Y=X=1-P(X≤12)Y=X-1; (2)Y=-2X; (3)Y=X 12  11 1  Φ ( ) 1  Φ (1) 1  0.84 0.16 1 P(Y=-1)= P(X<10) 10  11 Φ ( ) Φ ( 1) 1  Φ (1) 1  0.84 0.16 1 P(Y=20)Y=X-1; (2)Y=-2X; (3)Y=X= P(10≤X≤12 12  11 10  11 Φ ( ) Φ( ) 1 1 Φ (1)  Φ ( 1) 0.68 综合得 Y 的分布律为 Y -5 -1 20 p 0.16 0.16 0.68 

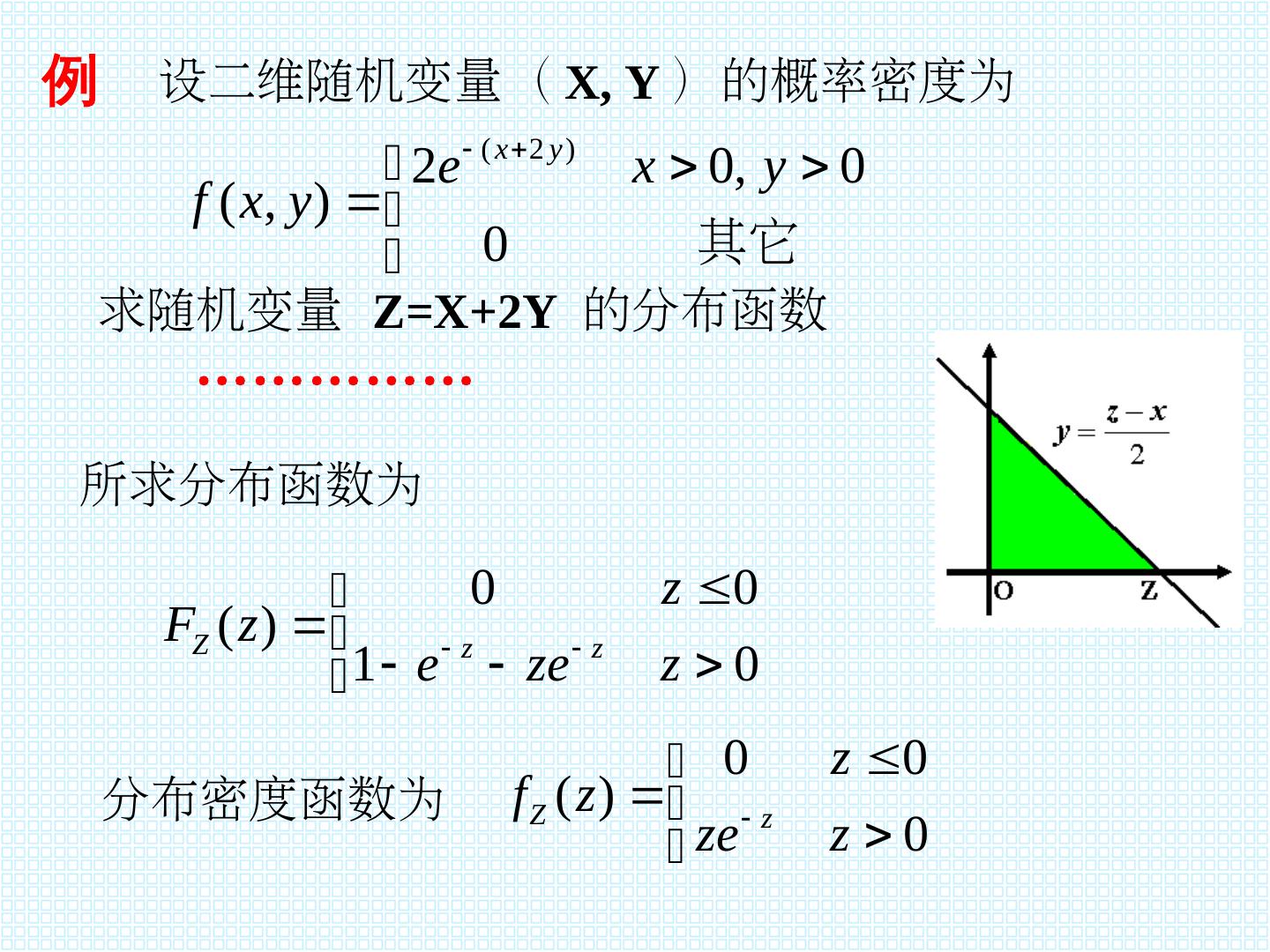
20 . §6.2 二维随机变量的函数的分布 引 言 上节的内容可推广到多维随机变量 : (X1,P(X…,P(XXn)Y=X-1; (2)Y=-2X; (3)Y=X 为 n 维随机变量 ,P(XY 是 X1,P(X…,P(XXn 的函数 Y=g(x1,P(X x2,P(X…,P(X xn)Y=X-1; (2)Y=-2X; (3)Y=X 是一维随机变量 . 现在的问题是如何由 (X1,P(X…,P(XXn)Y=X-1; (2)Y=-2X; (3)Y=X 的 分布 ,P(X 来求出 Y 的分布 . 设 (X,P(XY)Y=X-1; (2)Y=-2X; (3)Y=X 为二维随机变量 ,P(X g(x,P(Xy)Y=X-1; (2)Y=-2X; (3)Y=X 为二元函数， 那么 Z=g(X,P(XY)Y=X-1; (2)Y=-2X; (3)Y=X 是一维随机变量 ,P(X 且由（ X ， Y ）服从正态分的 分布就可定出 Z 的分布 . 

21 . 6.2 二维随机变量的函数的分布 一、 (X,P(XY)Y=X-1; (2)Y=-2X; (3)Y=X 为二维离散型随机变量 设 (X,P(XY)Y=X-1; (2)Y=-2X; (3)Y=X 为二维离散型随机变量 ,P(X 其分布律为 pij=P(X=xi,P(XY=yj)Y=X-1; (2)Y=-2X; (3)Y=X (i,P(Xj=1,P(X2,P(X…)Y=X-1; (2)Y=-2X; (3)Y=X g(x,P(Xy)Y=X-1; (2)Y=-2X; (3)Y=X 是一个二元函数， Z=g(X,P(XY)Y=X-1; (2)Y=-2X; (3)Y=X 是二维随机变量 (X,P(XY)Y=X-1; (2)Y=-2X; (3)Y=X 的函数，则随机变量 Z 的分布律为： P(Z=g(xi,P(Xyj)Y=X-1; (2)Y=-2X; (3)Y=X)Y=X-1; (2)Y=-2X; (3)Y=X=pij (i,P(Xj=1,P(X2,P(X…)Y=X-1; (2)Y=-2X; (3)Y=X 注 : g(xi,P(Xyj)Y=X-1; (2)Y=-2X; (3)Y=X 取相同值对应的那些概率要合并相加 

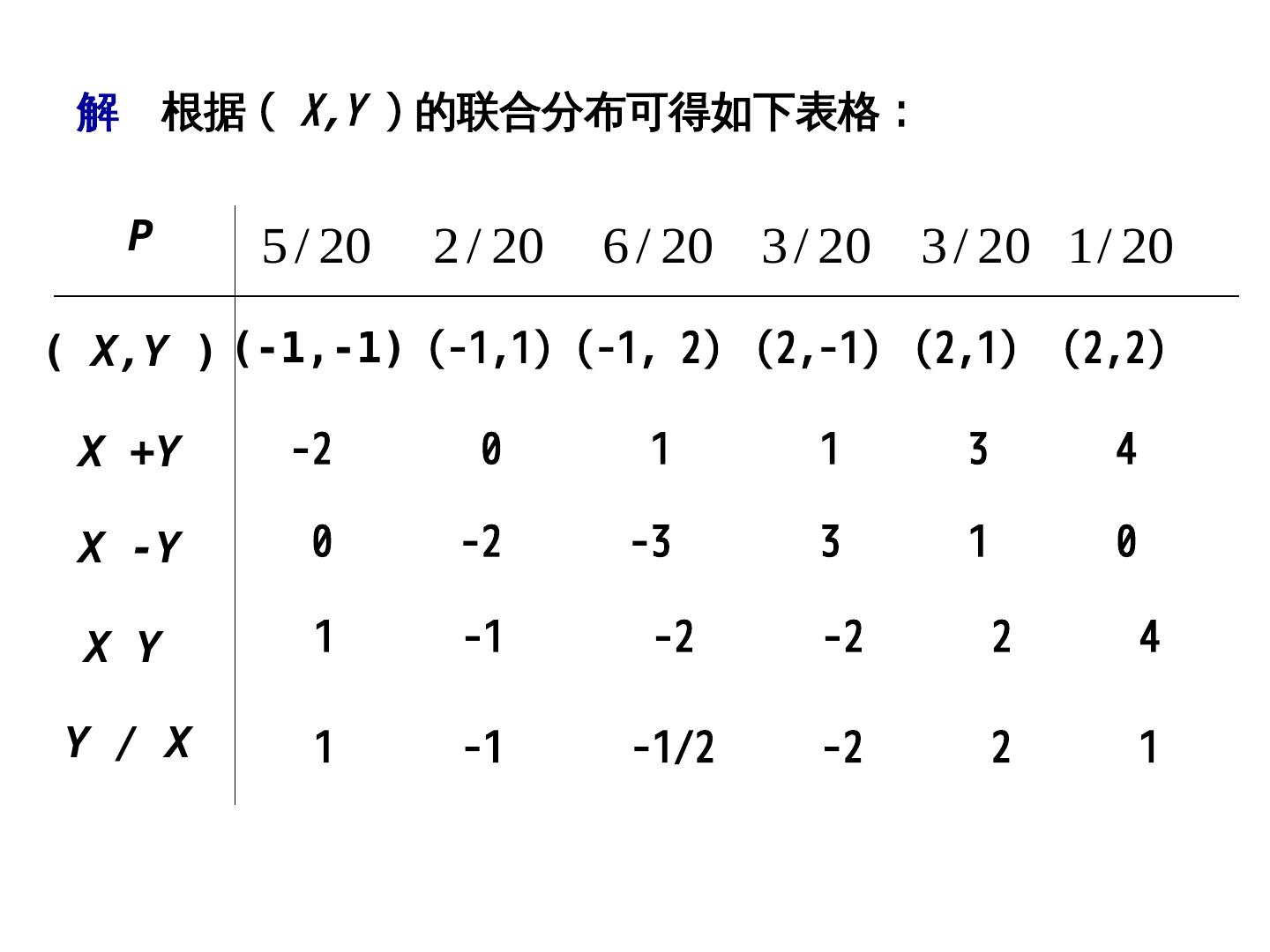
22 . 6.2 二维随机变量的函数的分布 一、 (X,P(XY)Y=X-1; (2)Y=-2X; (3)Y=X 为二维离散型随机变量 例 设二维随机变量 ( X,P(XY )Y=X-1; (2)Y=-2X; (3)Y=X 的概率分布为 Y -1 1 2 X -1 5 20 2 20 6 20 3 20 3 / 20 1 20 2 求 X  Y , X  Y , XY , Y X 的概率分布 

23 . 解 根据 ( X,P(XY )Y=X-1; (2)Y=-2X; (3)Y=X 的联合分布可得如下表格： P 5 / 20 2 / 20 6 / 20 3 / 20 3 / 20 1 / 20 ( X,Y ) (-1,-1) (-1,P(X1)Y=X-1; (2)Y=-2X; (3)Y=X (-1,P(X 2)Y=X-1; (2)Y=-2X; (3)Y=X (2,P(X-1)Y=X-1; (2)Y=-2X; (3)Y=X (2,P(X1)Y=X-1; (2)Y=-2X; (3)Y=X (2,P(X2)Y=X-1; (2)Y=-2X; (3)Y=X X +Y -2 0 1 1 3 4 X -Y 0 -2 -3 3 1 0 X Y 1 -1 -2 -2 2 4 Y / X 1 -1 -1/2 -2 2 1 

24 .故得 X+Y -2 0 1 3 4 P 5 / 20 2 / 20 9 / 20 3 / 20 1 / 20 X-Y -3 -2 0 1 3 P 6 / 20 2 / 20 6 / 20 3 / 20 3 / 20 

25 .故得 XY -2 -1 1 2 4 P 3 / 20 2 / 20 5 / 20 9 / 20 1 / 20 X/Y -2 -1 1/2 1 2 P 3 / 20 2 / 20 6 / 20 6 / 20 3 / 20 

26 .例 : 设 (X,P(XY)Y=X-1; (2)Y=-2X; (3)Y=X 的联合分布律为 Y X 0 1 2 3 4 5 0 0 0.01 0.03 0.05 0.07 0.09 1 0.01 0.02 0.04 0.05 0.06 0.08 2 0.01 0.03 0.05 0.05 0.05 0.06 3 0.01 0.02 0.04 0.06 0.06 0.05 求 (1)Y=X-1; (2)Y=-2X; (3)Y=XV=Max(X,P(XY)Y=X-1; (2)Y=-2X; (3)Y=X ； (2)Y=X-1; (2)Y=-2X; (3)Y=XU=Min(X,P(XY)Y=X-1; (2)Y=-2X; (3)Y=X ； (3)Y=X-1; (2)Y=-2X; (3)Y=XW=X+Y 的分布律 。 

27 . 解 : (1)Y=X-1; (2)Y=-2X; (3)Y=X V=Max(X,P(XY)Y=X-1; (2)Y=-2X; (3)Y=X 可能取值为： 0 ， 1 ， 2 ， 3 ， 4 ， 5 P{V=0}=P{X=0,Y=0}=0 ； P{V=1}=P{X=0,Y=1}+P{X=1,Y=0} +P{X=1,Y=1} =0.01+0.01+0.02=0.04 ； 所以 V 的分布律为 V 0 1 2 3 4 5 P 0 0.04 0.16 0.28 0.24 0.28 V=0 V=1 V=2 V=3 V=4 V=5 X 0 1 2 3 4 5 Y 0 0 0.01 0.03 0.05 0.07 0.09 1 0.01 0.02 0.04 0.05 0.06 0.08 2 0.01 0.03 0.05 0.05 0.05 0.06 3 0.01 0.02 0.04 0.06 0.06 0.05 

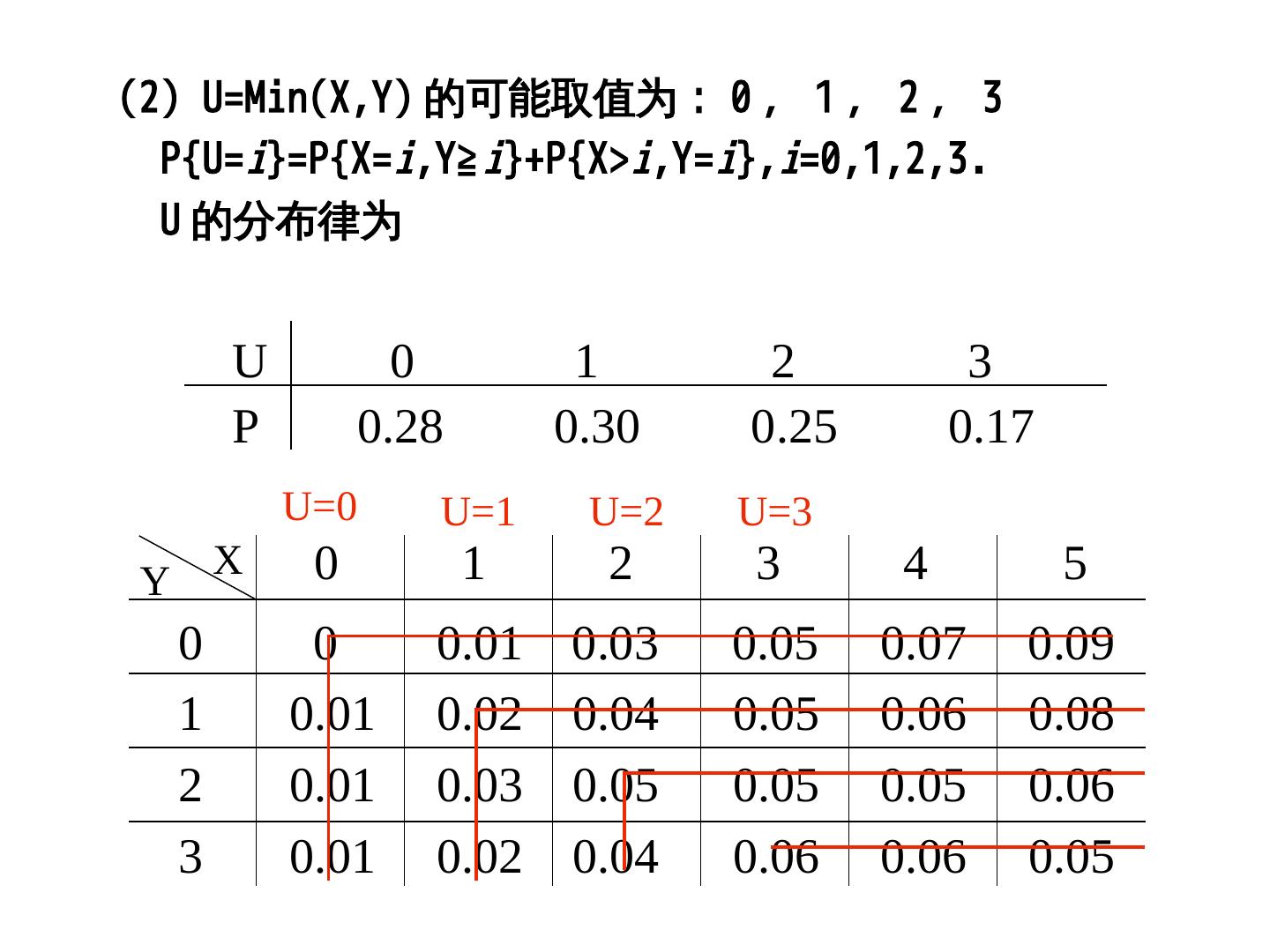
28 .(2)Y=X-1; (2)Y=-2X; (3)Y=X U=Min(X,P(XY)Y=X-1; (2)Y=-2X; (3)Y=X 的可能取值为： 0 ， 1 ， 2 ， 3 P{U=i}=P{X=i,P(XY≧i}+P{X>i,P(XY=i},P(Xi=0,P(X1,P(X2,P(X3. U 的分布律为 U 0 1 2 3 P 0.28 0.30 0.25 0.17 U=0 U=1 U=2 U=3 Y X 0 1 2 3 4 5 0 0 0.01 0.03 0.05 0.07 0.09 1 0.01 0.02 0.04 0.05 0.06 0.08 2 0.01 0.03 0.05 0.05 0.05 0.06 3 0.01 0.02 0.04 0.06 0.06 0.05 

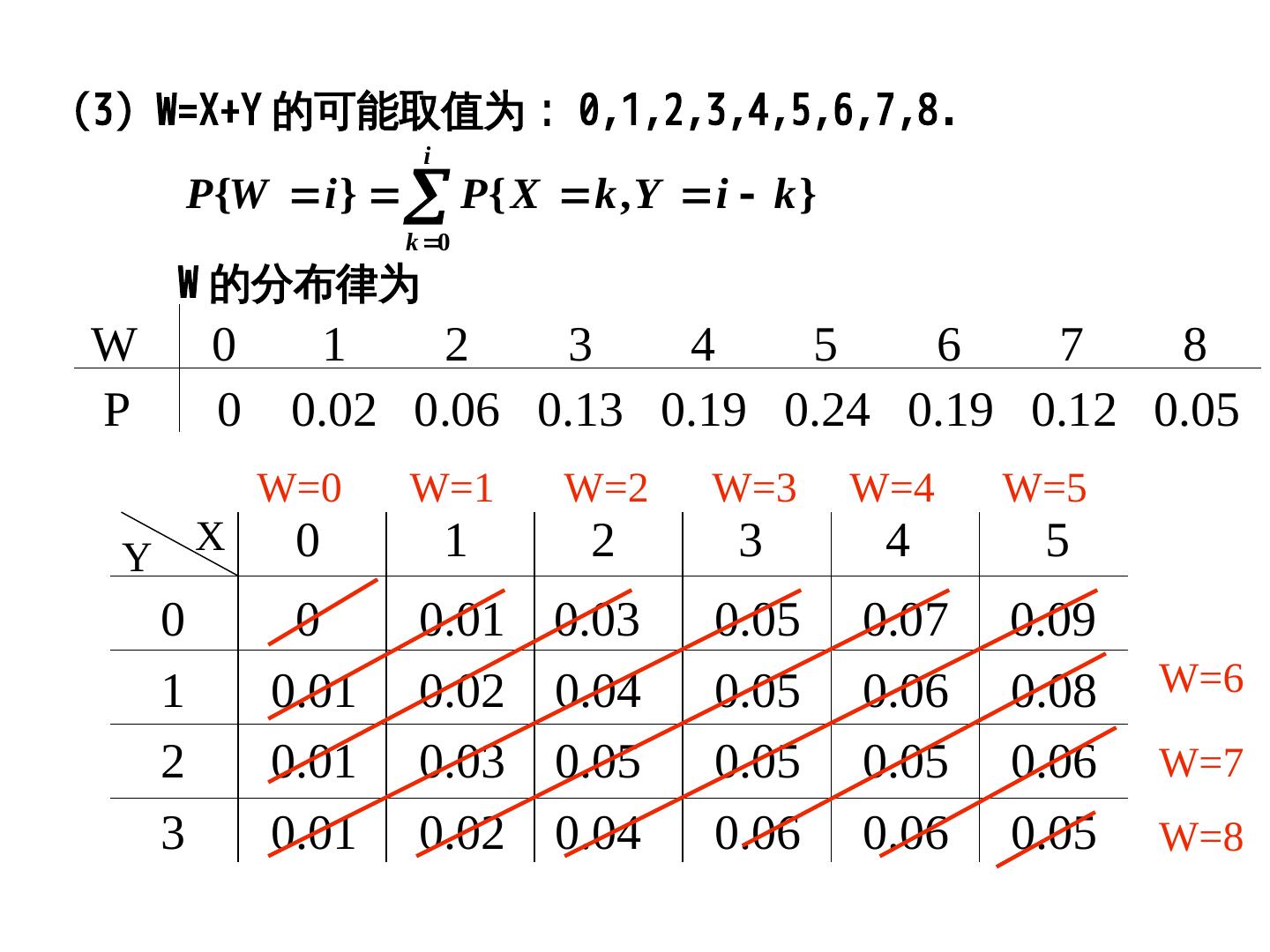
29 .(3)Y=X-1; (2)Y=-2X; (3)Y=X W=X+Y 的可能取值为： 0,P(X1,P(X2,P(X3,P(X4,P(X5,P(X6,P(X7,P(X8. i P {W  i }   P{ X  k , Y  i  k } k 0 W 的分布律为 W 0 1 2 3 4 5 6 7 8 P 0 0.02 0.06 0.13 0.19 0.24 0.19 0.12 0.05 W=0 W=1 W=2 W=3 W=4 W=5 Y X 0 1 2 3 4 5 0 0 0.01 0.03 0.05 0.07 0.09 1 0.01 0.02 0.04 0.05 0.06 0.08 W=6 2 0.01 0.03 0.05 0.05 0.05 0.06 W=7 3 0.01 0.02 0.04 0.06 0.06 0.05 W=8